基金项目:地震科技星火计划项目(XH18036)、国家自然科学基金(51578024)联合资助.
(1.重庆市地震局,重庆 401147; 2.北京工业大学 工程抗震与结构诊治北京市重点实验室,北京 100124; 3.江苏省射阳县高级中学,江苏 盐城 224300; 4.北京工业大学,北京 100124)
(1.Chongqing Earthquake Agency,Chongqing 401147,China)(2.Beijing Key Lab of Earthquake Engineering and Structural Retrofit,Beijing University of Technology,Beijing 100124,China)(3.Jiangsu Sheyang High School,Yancheng 224300,Jiangsu,China)(4.Beijing University of Technology,Beijing 100124,China)
Ground motion; Time-frequency characteristics; Wavelet transform; Frequency non-stationary
备注
基金项目:地震科技星火计划项目(XH18036)、国家自然科学基金(51578024)联合资助.
对美国NGA数据库中的3 551组地震记录按场地条件、震级、震中距进行了分组,采用一维连续小波变换得到每条记录的小波功率谱。研究任意时间处小波功率谱最大值所对应的主频率,并对每个地震动分组内的主频率值做一定时间窗内的均方根处理,分别采用线性函数、指数函数和指数三角函数模型来拟合得到的主频率随时间变化的曲线,最后分析了场地条件、震级和震中距对频率时变曲线的影响,并给出了每个分组内水平向和竖直向地震动主频率随时间变化的模型参数。结果 表明:地震动主频率随时间的增大逐渐减小,但是竖直向要比水平向衰减得快一些。
In this paper,3 551 sets of earthquake records from the NGA database were grouped according to the site condition,the moment magnitude and the epicentral distance. And then the wavelet spectrum of each earthquake record was calculated by using one-dimension continuous wavelet transform. In order to obtain time-frequency statistical characteristics of ground motion for engineering applications,the time dependent predominant frequencies corresponding to the maximum values of wavelet spectrum at every time were considered. And the root mean square of the predominant frequencies within a short time window in every group of ground motion was computed to obtain time series curves of predominant frequency. The results show that the predominant frequency of ground motion gradually decreases with the increasing of time,and the time series of predominant frequency in vertical component seems more remarkable than that in the horizontal component. Furthermore,a linear model,together with an exponential model and an exponential trigonometric model were used to fit the time series curves of the predominant frequency. Meanwhile,the effects of site condition,moment magnitude and epicentral distance on the time-varying curves of the predominant frequency were analyzed. Finally,the fitting parameters of the time series curves of predominant frequency in horizontal and vertical directions in each group were given.
引言
早在20世纪60年代,工程界就意识到实际地震动不仅在时域具有非平稳性,其频率成分也是非平稳的。但由于将平稳或强度非平稳模型用于线性结构分析,就能够得到满意的结果,因此地震动频率含量变化对结构的影响未能得到足够重视。近年来,大震经验逐渐积累,重大工程数量剧增,结构非线性计算势在必行,而频率非平稳地震波的输入则是决定计算结果正确与否的关键。因此,研究地震动非平稳特性不仅是地震动自身规律研究的要求,更重要的是满足建筑物抗震设计的要求。如何既考虑输入的时频非平稳特性,又能兼顾工程实际的需要,是国内外学者一直努力探索的研究课题之一。
目前地震工程领域研究较多的是一类特殊的调制过程,即均匀调制过程(胡聿贤,周锡元,1962; Housner,Jennings,1964; Iyengar,Iyengar,1969)。均匀调制模型从20世纪60年代开始研究,经过不断的发展和完善,已在工程结构抗震分析和设计中获得广泛应用(霍俊荣等,1991; 金星,廖振鹏,1994; 屈铁军等,1994; Yoshimoto,et al,1997; Zhou,Yu,2008)。但是这种模型只反映了地震动的强度非平稳特征,没有反映其频率非平稳特征,从更合理的模拟真实地震动的角度考虑,有必要引入一般的调制随机过程数学模型。但是,把地震动作为一般的非平稳随机过程处理是极为困难的,因此研究者一直试图用简单的数学模型近似解决这一问题。Priestley(1965)提出了渐进功率谱的概念,并在其后的研究中继续发展,为非平稳随机信号谱提供了清晰的物理解释。但在计算过程中,复调制函数的确定比较困难,为此Nakayama等(1994)采用窄带和低通滤波,直接生成复调制函数用于结构抗震可靠分析。Yilmaz和Bayrak(2013)总结了地震加速度记录的几种时频分析方法,并采用短时傅里叶和维格纳分布对Georgia地震的数据进行了时频分析(Yilmaz,Bayrak,2011,2013)。近年来,渐进功率谱已被应用于人工地震波的模拟(张翠然,陈厚群,2007)。现在较成熟的时-频非平稳信号分析工具有时变功率谱(包括渐进功率谱、瞬时功率谱和小波功率谱等)、小波变换、Wigner-Ville分布、ARMA模型和Hilbert-Huang变换等,但在实际工程应用中,都存在一些局限性(曹晖等,2002; 李中付等,2001; 朱继梅,2000; 谢皓宇等,2019)。小波变化的局限性就在于混频问题,袁美巧等(2010)通过调整混频顺序,解决了这个问题。需要指出的是,小波变换克服了短时傅里叶变换在单分辨率上的缺陷,具有多分辨率分析的特点,在时-频都有表征信号局部信息的能力,时间窗和频率窗都可以根据信号的具体形态动态调整。一般情况下,在低频部分(信号较平稳)可以采用较低的时间分辨率,而提高频率分辨率,在高频情况下可以用较低的频率分辨率来换取精确的时间定位。本文利用小波分析的方法实现强震记录的时频分析,旨在给出既能够反映地震动时频统计特性,又便于工程应用的模型。
1 数据来源及分组
本文采用的数据来源于美国NGA数据库的强震记录(Chiou et al,2008)。该数据库收录了1935—2003年发生于板内地震活跃区的175个浅源地震事件,共计3 551组10 580条(2个水平方向和1个竖直向,部分分量数据缺失)自由场地加速度记录。首先对这些强震记录进行筛选和分组,去除其中场地条件不明的记录,最终选取其中3 541组共计10 545条地震加速度记录用于研究。在对地震动时-频特性的分析中,主要考虑了3个影响因素,即场地条件、震中距及震级大小,并依据这3个影响因素将全部地震记录进行了分组。
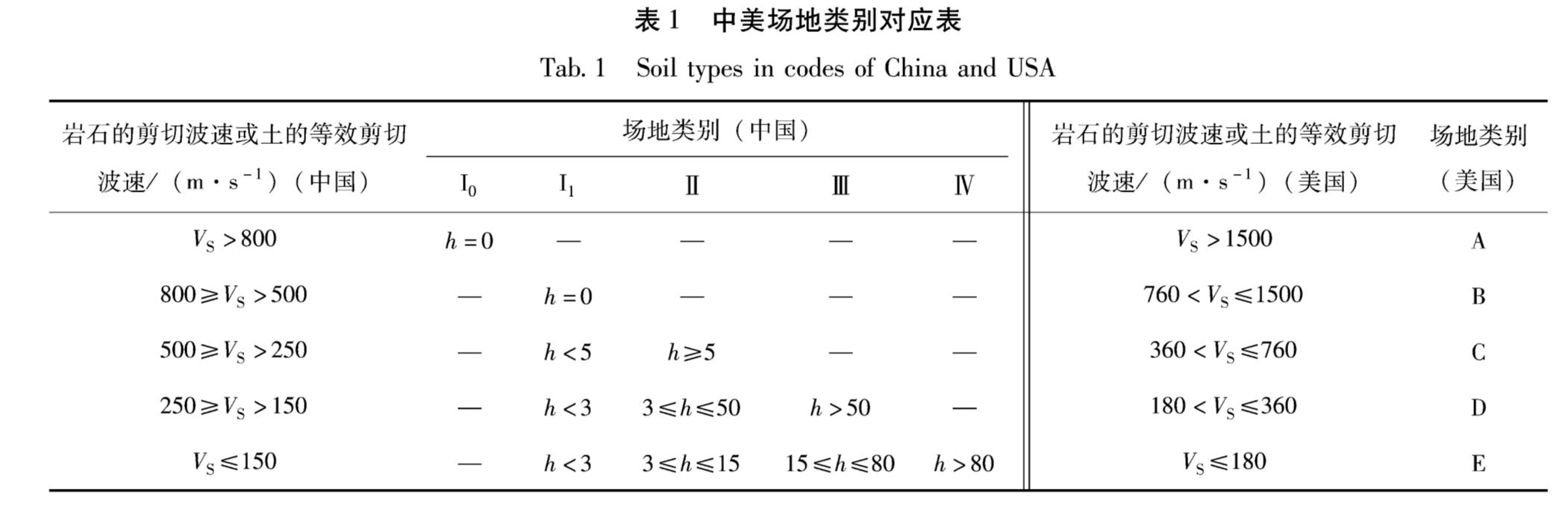
1.1 场地条件《建筑抗震设计规范》(GB 50011—2010)根据土层等效剪切波速和场地覆盖层厚度将场地划分为4类。在计算等效剪切波速VSE时,所取的深度是覆盖层厚度与20 m之间的较小值,因此认为20 m内的折算剪切波速VSE20近似等于VSE。在NGA数据库中,给出了VSE30的剪切波速值,吕红山和赵凤新(2007)研究认为剪切波速值VSE20与VSE30之间有一定的对应关系,如果以VSE30为场地条件的划分指标,那么对应我国规范中的Ⅰ,Ⅱ,Ⅲ,Ⅳ类场地的分界值分别为500,250和150 m/s,见表1。
1.2 震级大小采用0.5的震级间隔对震级进行划分,将震级划分为5个震级档:M5.5~6.0,M6.0~6.5,M6.5~7.0,M≥7.0。
1.3 震中距R采用20 km的间隔对震中距进行划分,划分为0~20 km,20~40 km,40~60 km,60~80 km,80~100 km和≥100 km共6个震中距范围。
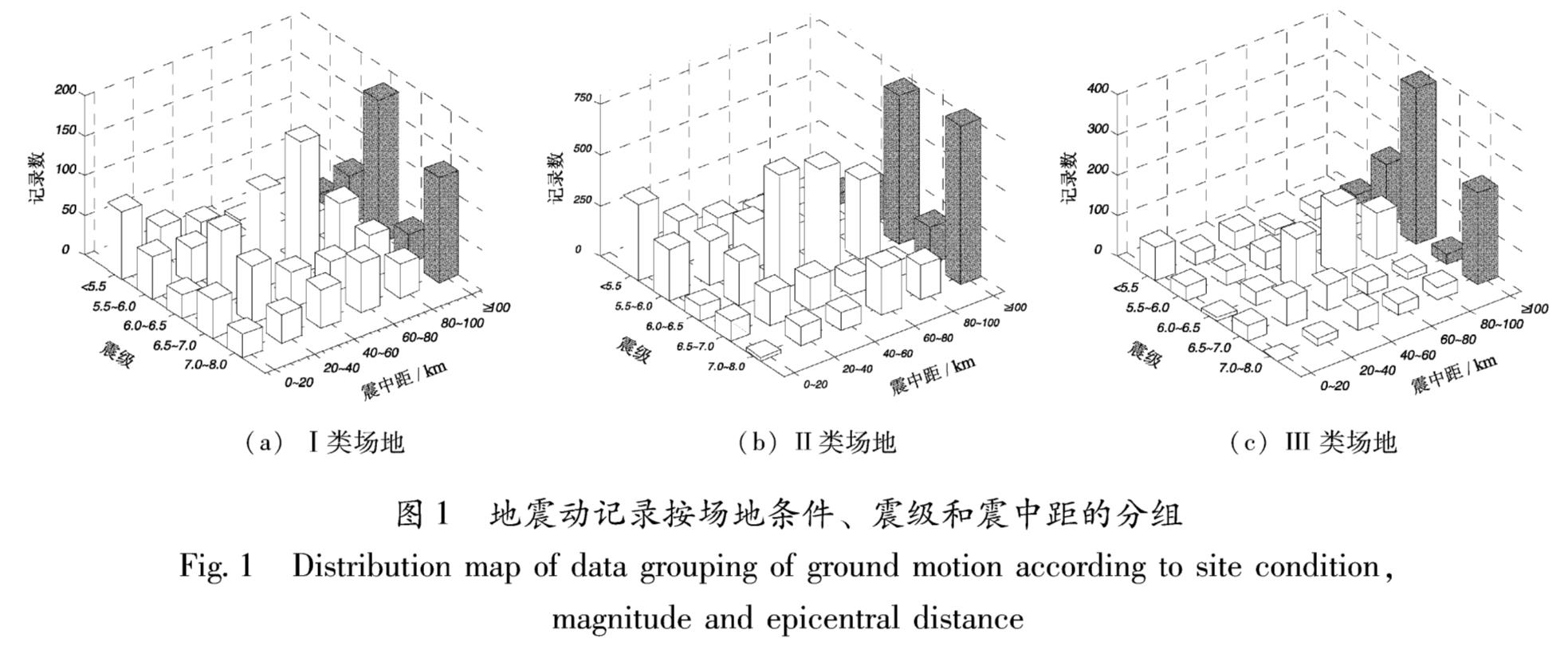
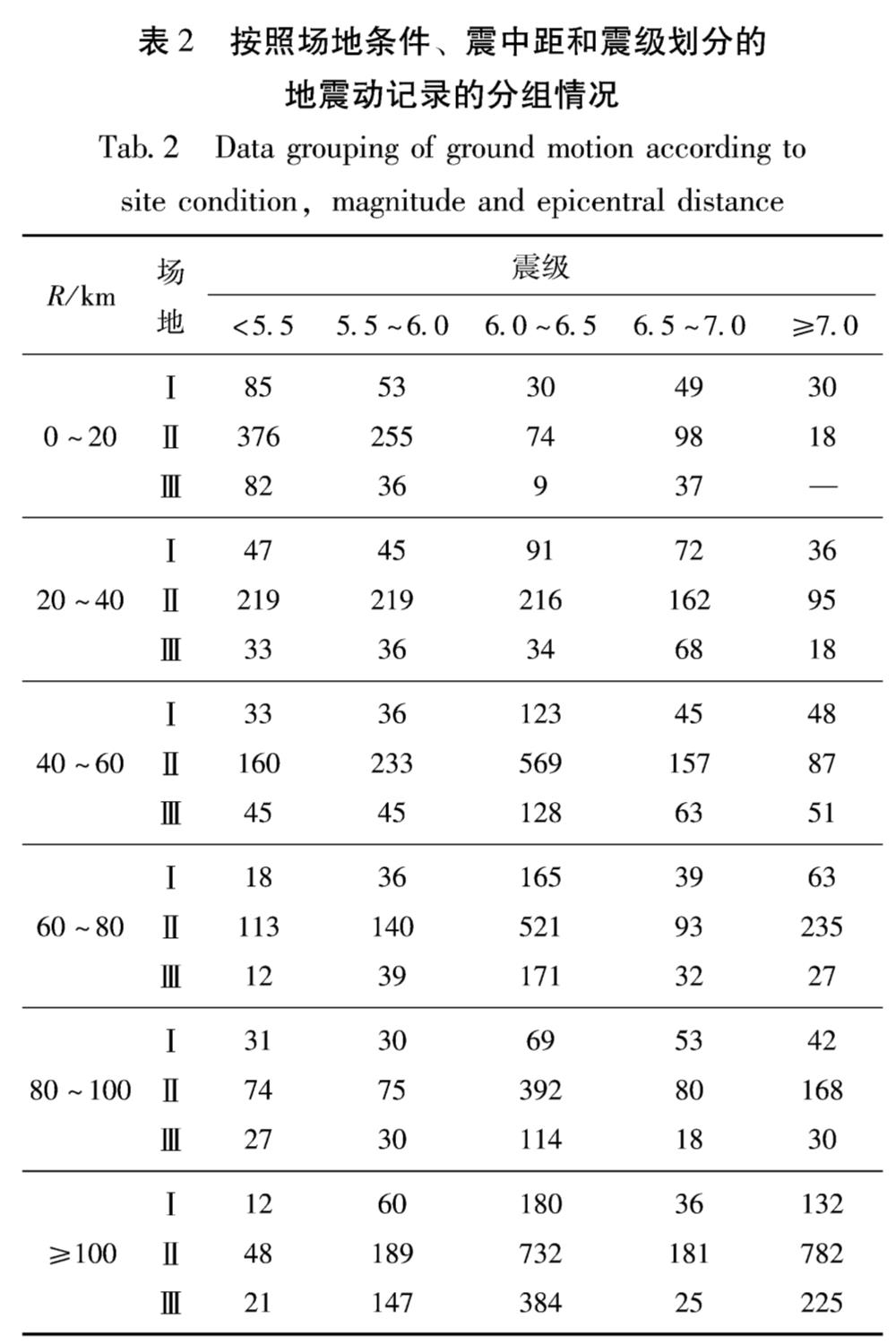
需要说明的是,由于相应于Ⅳ类场地的地震动记录只有8组,本文将这8组记录归入Ⅲ类场地进行统计分析。地震动记录按照震级、震中距以及场地条件进行分组的具体情况如图1所示。从图中可以看出,按照这3个影响因素,可将地震动分为90组,每组包括2个水平方向和1个竖直方向,见表2。
图1 地震动记录按场地条件、震级和震中距的分组
Fig.1 Distribution map of data grouping of ground motion according to site condition,magnitude and epicentral distance2 小波变换和小波基函数的选取
时-频分析的基本任务是建立一个以时间和频率为变量的二维联合分布函数。本文采用小波变换(杨福生,1999)得到时-频分布来讨论地震动的时-频非平稳特性。
小波变换的基本思想来源于函数的伸缩和平移,伸缩可以在不同的分辨率下分解信号,平移可以把这组信号作为窗,观察所关心的部分。小波基函数通过平移和伸缩,得到具有可变时间和频率分辨率的正交函数族,即在低频时具有高的频率分辨率和低的时间分辨率,在高频时具有低的频率分辨率和高的时间分辨率。
对于小波变换来说,小波基函数的选取至关重要。一般当ψ(t)∈L2(R)满足允许条件的函数便可以用作小波基,允许条件是:
CΨ=∫+∞∫-∞(〖JB<1|〗Ψ(ω)〖JB>1|〗2)/(〖JB<1|〗ω〖JB>1|〗) dω<∞(1)
式中:Ψ(ω)是ψ(t)的傅里叶变换。
但实际中往往要求更高些,在不同的应用领域,小波基的选取标准不同,不同的小波基适用于不同的具体情况。即使在同一应用领域,小波基的选取也没有形成统一的标准。小波基的选取除了满足以上一般原则外,还需根据具体分析对象进行考虑。对工程场地有影响的地震动加速度记录周期主要集中在3 s内,因此本文选取复Morlet小波cmor Fb-Fc作为小波基函数,其表达式为:
ψ(t)=1/((πFb)1/2)e2iπFc*te(-t2)/(Fb)(2)
式中:Fb是小波基ψ(t)的带宽; Fc是小波基ψ(t)的中心频率,本文取Fb=2,Fc=1。
由小波基通过平移和伸缩产生小波函数:
ψa,b(t)=1/((〖JB<1|〗a〖JB>1|〗)1/2)ψ((t-b)/a),a,b∈R,a≠0(3)
式中:a为伸缩因子(或尺度因子); b为平移因子。尺度a越大,表示对应着拉伸的小波函数在时间上越长,具有较小的频率窗、较高的频率分辨率,主要获取信号的低频特性; 尺度a越小,表示对应着压缩的小波函数在时间上越短,具有较大的频率窗、较低的频率分辨率,主要获取信号的高频特性。
对地震动加速度记录f(t)做小波函数为ψ(a,b)(t)的连续小波变换,得到关于时间和尺度的小波系数为:
Wf(a,b)=∫+∞∫-∞f(t)ψ(a,b)(t)^-dt=
1/((〖JB<1|〗a〖JB>1|〗)1/2)∫+∞∫-∞f(t)ψ((t-b)/a)^-dt(4)
式中:ψa,b(t)^-是小波函数ψa,b(t)的共轭。
将尺度换算成频率:
Fa=(Fc·fs)/a(5)
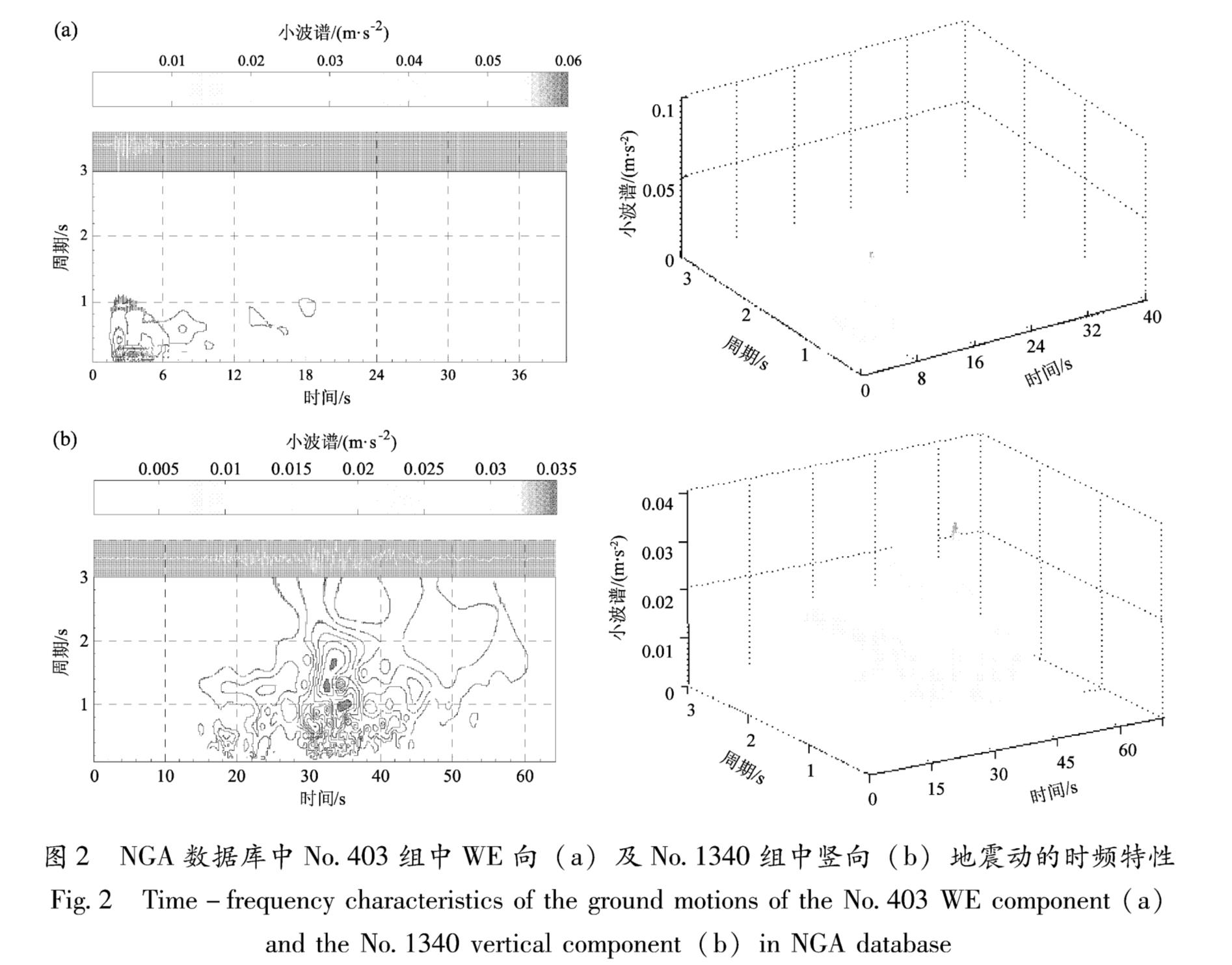
式中:a是尺度因子; Fa是a对应的实际频率; Fc是小波基的中心频率; fs是加速度记录f(t)的采样频率,从而得到关于时间和频率的小波功率谱,如图2所示,周期在3 s内具有较高的分辨率。
用一维连续小波变换对每条地震动记录进行地震动的小波功率谱研究,图2为NGA数据库中No.403组中WE向和No.1340组中竖向地震动记录的时频特性。
3 地震动频率的时变特性分析
3.1 地震动持续时间长度地震动加速度时程的持续时间与场地条件、震级、震中距等因素有关,因此,针对不同的影响条件,需要选择合适的持续时间范围。由地震动的强度包络函数模型,可知地震动的持续时间t=t1+ts+tc,其中t1为上升段的时间长度,ts为平稳段的时间长度,tc为衰减段的时间长度。胡聿贤(2003)研究认为,若在包线下降段时刻t处,强度包络线函数f(t)=e-c(t-t1-ts)=k时,地震动终止,其中,参数k通常取为0.1~0.5。本文通过对各组内地震动时程的强度包线的研究和分析,取k=0.3,衰减段的持续时间为:
tc=-(lnk)/c(6)
式中:c为下降段的衰减系数,按照本文不同分组内统计计算结果取值。
统计每个地震动分组内的t1,ts和tc,以t≥t1+ts+tc的原则选取地震动持续时间的长度,并考虑实际地震震级和震中距对持续时间的影响,最终得到不同分组内的持续时间,见表3。
需要特别说明的是,在Ⅲ类场地条件下,震级为6.5~7.0,震中距为80~100 km范围内的记录比较少,且时长都不超过40 s,因此本文仅将40 s作为该组内的时间长度进行分析。
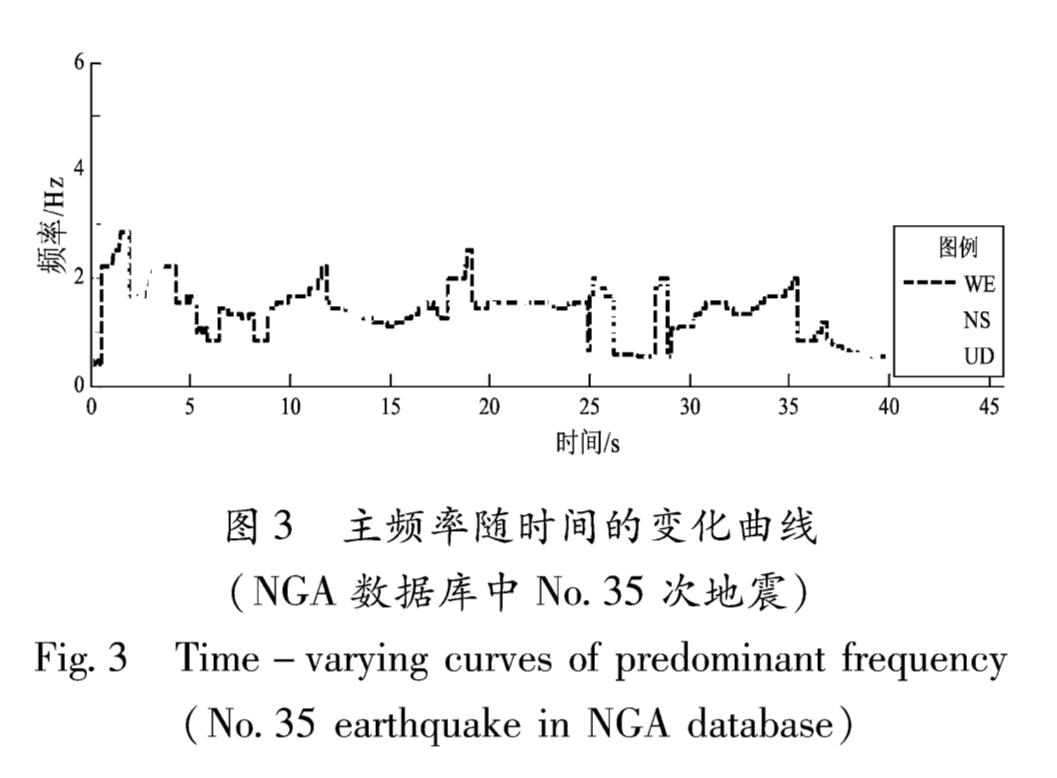
3.2 频率的时变特性分析为了能便于工程应用的地震动时-频特性统计,笔者仅考虑任一时间t处相应于小波功率谱最大值所对应的频率,即主频率随时间变化的曲线(图3)。
图3 主频率随时间的变化曲线(NGA数据库中No.35次地震)
Fig.3 Time-varying curves of predominant frequency(No.35 earthquake in NGA database)从图3可以看出,主频率随时间的变化过于离散,很难直接投入工程应用。鉴于此,笔者采用一个固定的时间窗Δt=0.5 s 作为移动窗的窗宽,将移动窗从t=0开始,对相同组内、相同方向的每一条频率时变曲线进行扫描,求出每一个窗宽内频率的均方根RMS值(高丽霞等,2006),即:
f=((f 21+f 22+…+f 2n)/n)1/2(7)
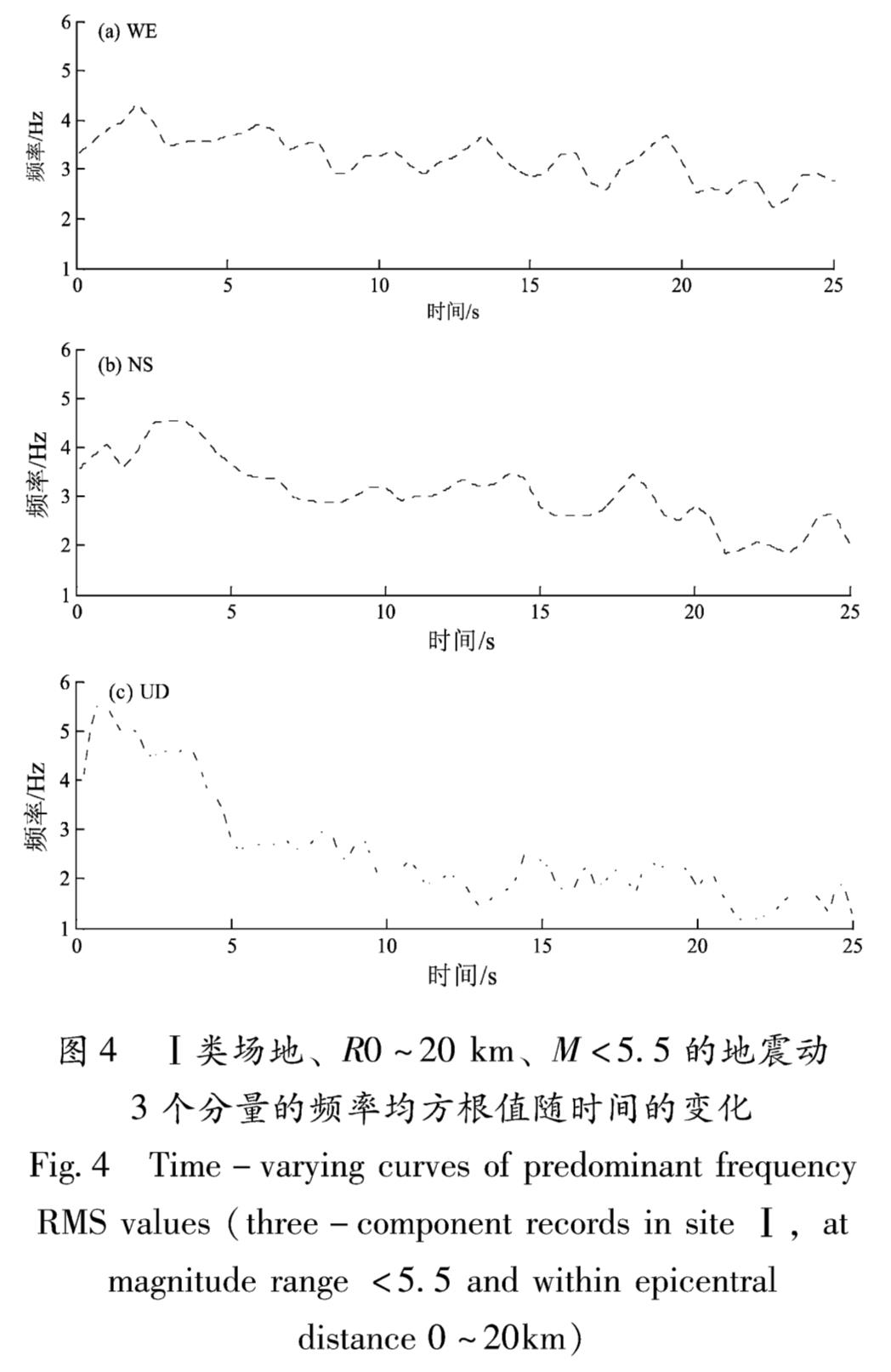
式中:n为移动窗内频率的个数,从而得到不同地震动分组内的频率时变曲线,如图4所示。
由图4可见,水平向的频率时变规律具有相似性。对台湾集集地震记录的有关研究表明水平向和竖向记录的地震动特性差别很大(王国权等,2001),因此本文在研究地震动时-频特性时,对水平向和竖向的加速度记录分别讨论,并且在讨论中不再区分2个水平向的方向。通过对水平向和竖向的每条地震动记录的主频的时变分析可以看出,无论是水平向还是竖向,地震动的主频率随时间的增大都逐渐减小,并且竖向记录比水平向记录随时间衰减更快。为了进一步了解地震动主频率的时变特性,笔者按照不同的分组进行了对比和分析,并分别选取式(8)给出的线性函数模型、指数函数模型、和指数三角函数模型:
f={a0+a1t
a0+a1e-bt
a0+a1e-btsin(ωt)(8)
图4 Ⅰ类场地、R0~20 km、M<5.5的地震动3个分量的频率均方根值随时间的变化
Fig.4 Time-varying curves of predominant frequency RMS values(three-component records in site Ⅰ,at magnitude range <5.5 and within epicentral distance 0~20km)对地震动主频的时变曲线进行拟合,得到不同拟合模型的参数,通过对比不同拟合情况,得到拟合误差可接受范围内相对比较简单的拟合方法。通过对拟合后各组地震动频率时变曲线的分析和比较,可得到以下几点认识:
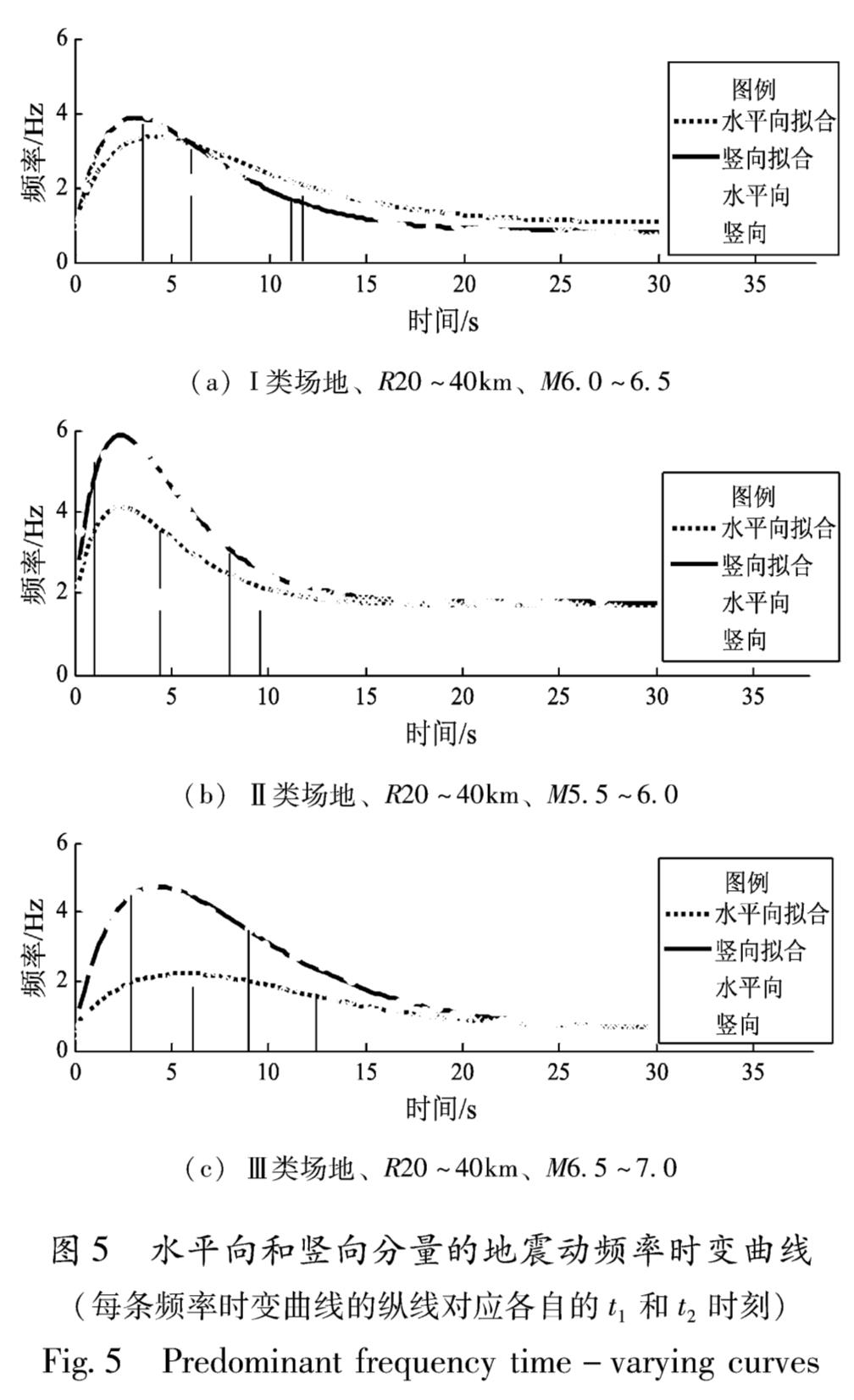
(1)在相同场地条件下,同一震级和震中距范围内,水平向与竖向记录的频率时变曲线的比较如图5所示,水平向和竖向的地震动主频率的整体趋势都是随时间递减的,但竖向主频率时变曲线衰减得更快,其前段频率大约是末端频率的4倍,水平向频率时变曲线的前段频率大约是末端频率的3倍。Ⅱ类场地(图5b)和Ⅲ类场地(图5c)条件下,竖向记录的高频成分比水平向记录的多,但Ⅰ类场地(图5a)条件下,大约一半的竖向记录具有更多的高频成分。
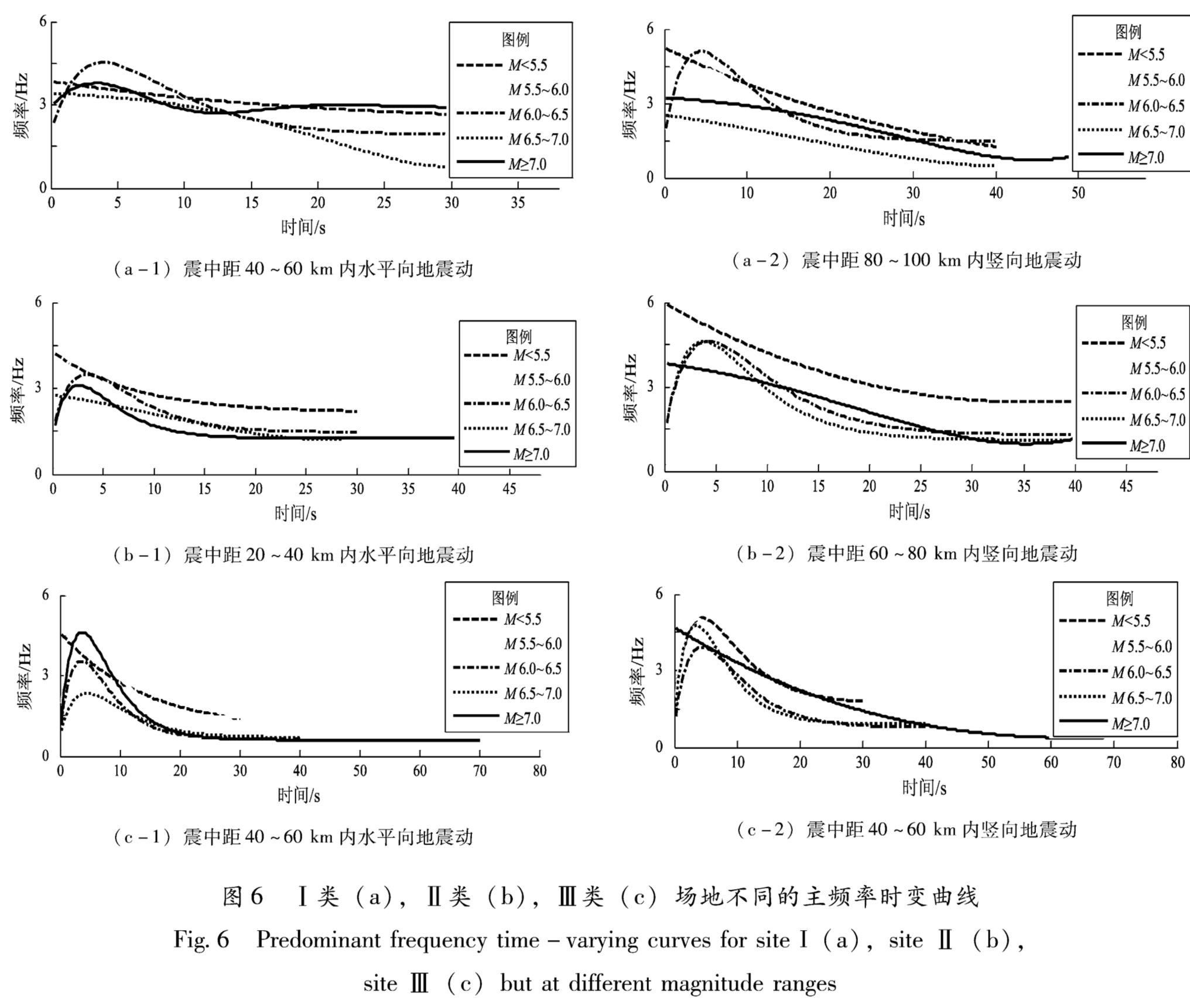
(2)在相同场地条件下,对于同一震中距范围内的水平向和竖向加速度记录,震级对频率时变曲线的影响如图6所示,由图可见,地震动主
图5 水平向和竖向分量的地震动频率时变曲线(每条频率时变曲线的纵线对应各自的t1和t2时刻)
Fig.5 Predominant frequency time-varying curves频率变化曲线的前段和末端频率的比值随震级的变化不规律,也即衰减快慢随震级的变化并不规律。在Ⅰ类场地(图6a)和Ⅱ类场地(图6b)条件下,水平向和竖向频率时变曲线衰减最快的震级范围多集中在M6.0~7.0; 在Ⅲ类场地(图6c)条件下,水平向和竖向频率时变曲线在M≥7.0时衰减得最快。频率随震级的变化没有明确的变化趋势。水平向记录中,主频率最大值多集中在M<5.5的分组中(70%左右),若只考虑Ⅰ类和Ⅱ类场地的情况,这种比例高达80%,这说明在Ⅲ类场地条件下震级对水平向记录频率的影响更复杂。对于竖向记录,其主频率最大值位于M<5.5的情况占80%以上。此外,地震动主频率的最小值多位于在M>6.5的情况(占80%以上)。由图6可以看出,其结果基本上符合较小震级的地震动具有更多的高频成分,较大震级的地震动具有更多的低频成分的认识。
图6 Ⅰ类(a),Ⅱ类(b),Ⅲ类(c)场地不同的主频率时变曲线
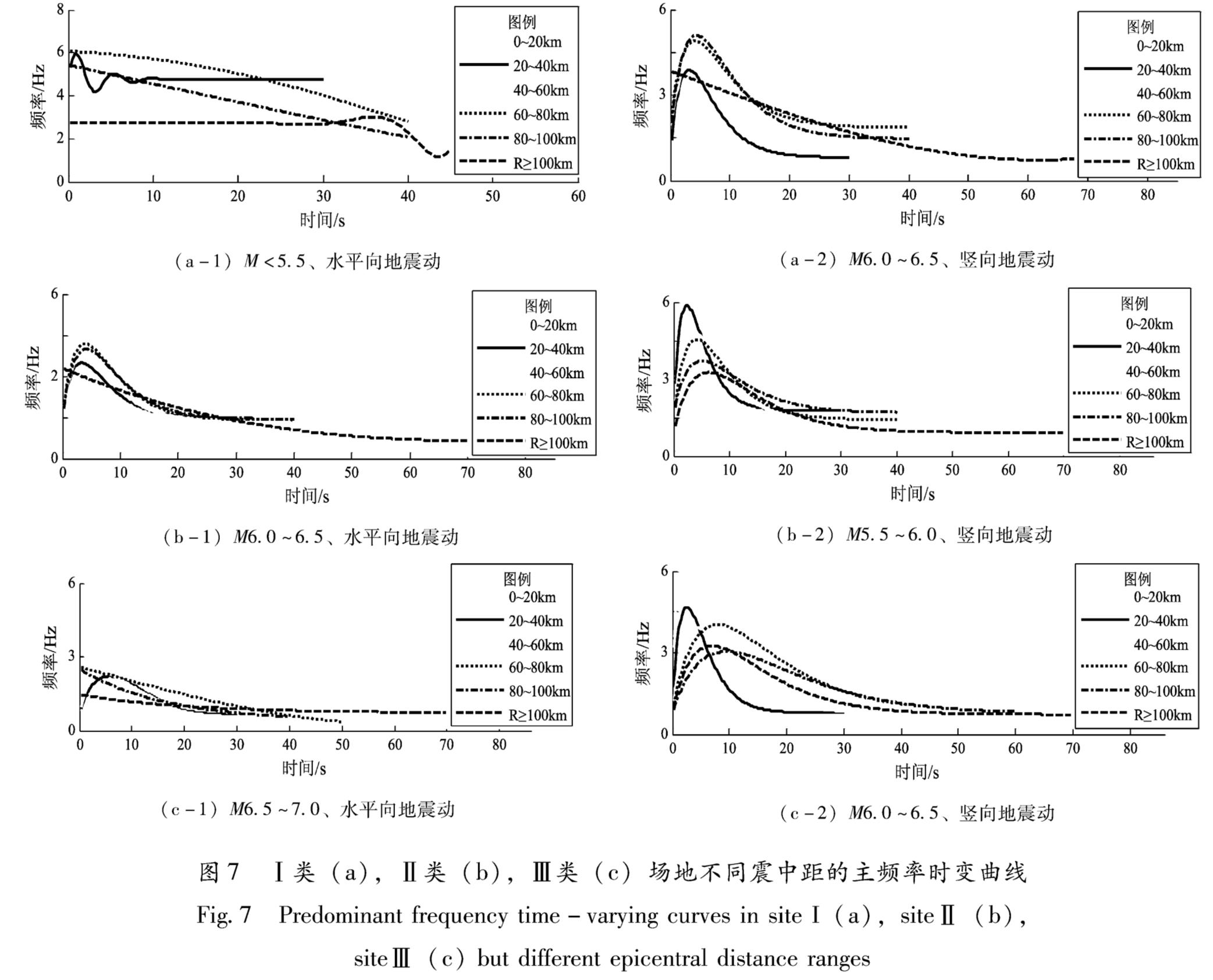
Fig.6 Predominant frequency time-varying curves for site I(a),site Ⅱ(b),site Ⅲ(c)but at different magnitude ranges(3)在相同场地条件下,对于同一震级范围内的水平向和竖向加速度记录,震中距对频率时变曲线的影响如下:地震动主频变化随震中距的变化不规律,在Ⅰ类场地条件下,水平向频率时变曲线在R60~80 km衰减得最快,而竖向频率时变曲线在R0~20 km衰减得最快; 在Ⅱ类场地条件下,R≥100 km的频率时变曲线衰减得最快; 在Ⅲ类场地条件下,R60~80 km的频率时变曲线衰减得最快。频率随震中距的增加变化较复杂,没有规律的变化趋势。水平向记录的主频率最大值多集中在R60~80 km(占50%以上),而竖向记录的主频率最大值集中在R60~80 km的只占20%左右,大约40%是集中在R0~20 km。由图7可知,在60 km内,随着震中距的增加,频率的变化不规律,R>60 km后,频率随着震中距的增加呈减小的趋势。说明在相同场地条件下,同震级的地震动在一定的距离范围外,随着震中距的增加,具有更多的低频成分。
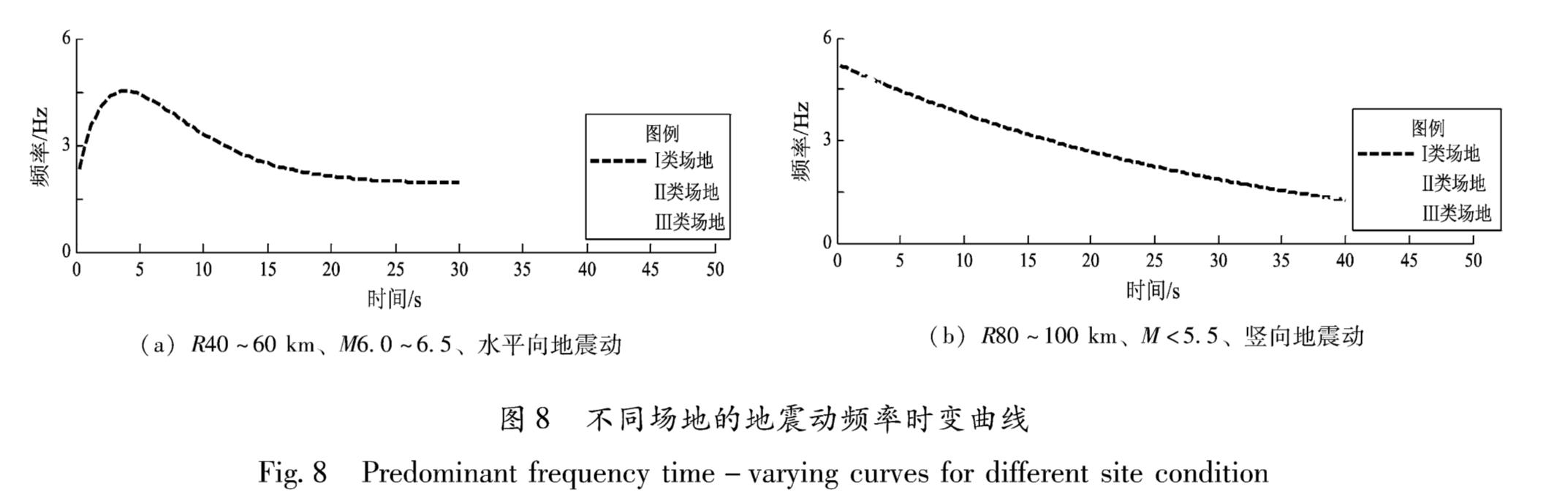
(4)对于相同震级和震中距范围内的水平向和竖向加速度记录,场地条件对主频率时变曲线的影响如下:随着场地变软,水平向地震动的主频率整体上有减小的趋势(图8a),这种情况在50%以上,这说明在Ⅰ类场地条件下水平向地震动的高频成分较多,而在Ⅲ类场地条件下水平向地震动的低频成分更丰富。但是竖向地震动的主频率随场地变软呈减小趋势的却只占不到20%,即竖向频率随场地条件的变化规律并不明显,但总体上也符合在Ⅲ场地条件下具有更多低频成分的规律(图8b)。
图7 Ⅰ类(a),Ⅱ类(b),Ⅲ类(c)场地不同震中距的主频率时变曲线
Fig.7 Predominant frequency time-varying curves in site I(a),siteⅡ(b),siteⅢ(c)but different epicentral distance ranges4 用于工程应用的频率时变模型
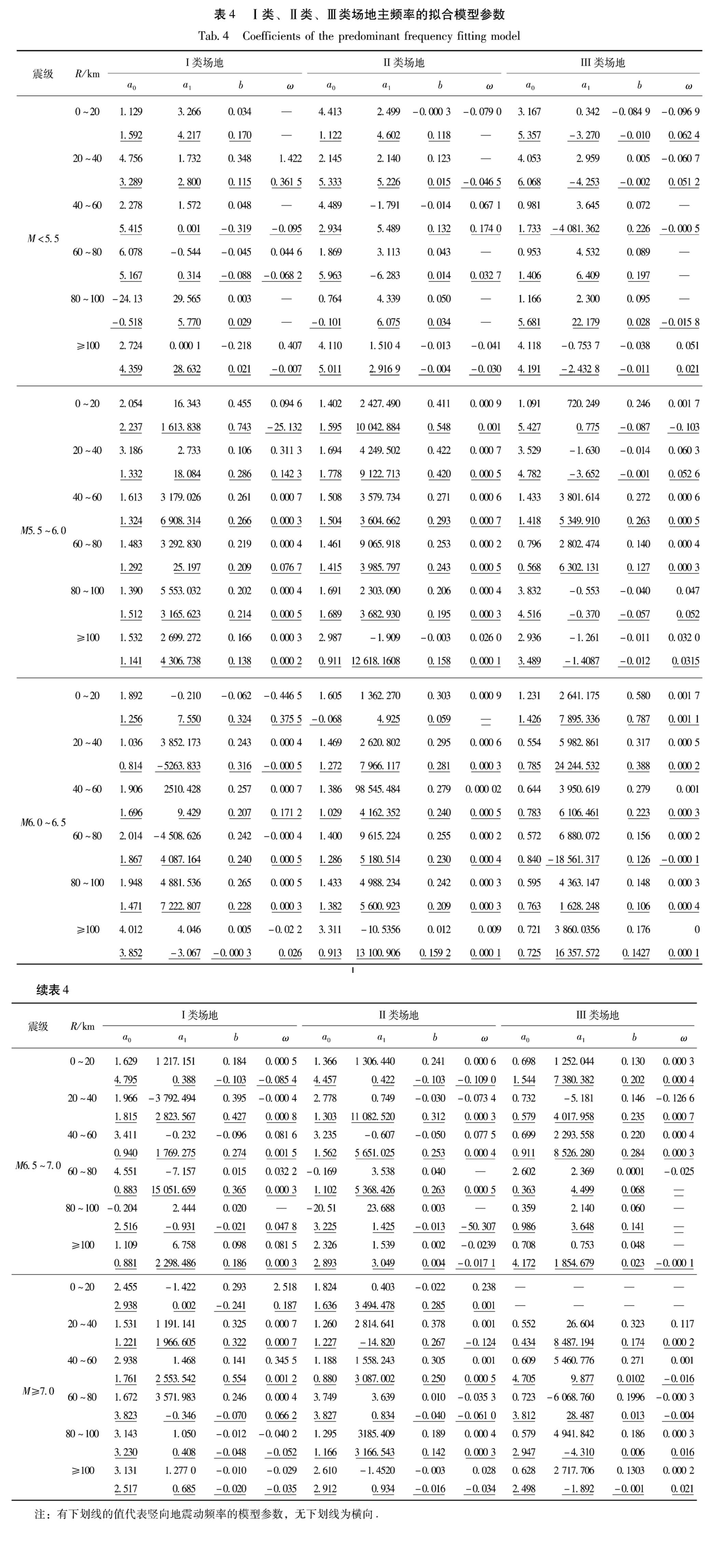
为了便于工程应用,如在地震动的人工拟合中考虑频率的非平稳特性,本文对主频率随时间的变化规律进行非线性最小二乘法拟合,得到频率随时间呈指数衰减的模型f=a0+a1e-btsin(ωt)或f=a0+a1e-bt的参数。表4为不同场地条件下各地震动分组内主频率随时间衰减的模型参数,其中有下划线的值代表竖向地震动频率的模型参数,无下划线的值则对应水平向地震动的模型参数。这些模型可以给工程应用提供一定的参考依据。
5 结论
本文对3 541组强震记录按照场地条件、震级、震中距进行分组,基于一维连续小波变换分析了地震动在不同条件下的频率时变特性,主要得出以下结论:
(1)给出了便于工程应用的地震动频率的时变模型,即定量地给出地震动频率随时间的变化规律,为地震动加速度时程的拟合以及结构的非线性反应分析提供了参考依据。
(2)得到地震动频率变化的统计特性:①水平向和竖向的频率时变曲线整体上都随时间呈递减趋势,且竖向衰减得更快些,大多数情况下竖向记录的高频成分比水平向记录的相应成分要多。②震级和震中距对频率时变特性的影响都比较复杂,但基本上都符合较小震级的地震动具有更多的高频成分,而较大震级的地震动具有更多的低频成分这一认识。竖向记录多在R0~20 km具有最大的频率值,而水平向记录多在R60~80 km具有最大的频率值。
(3)场地条件对频率时变特性的影响要规律得多,随着场地变软,水平向记录的频率整体上有减小的趋势,竖向记录的频率随场地的变化规律不如水平向记录那么明显,但总体上也符合在Ⅲ类场地条件下具有更多的低频成分这一认识。
特别感谢俞言祥研究员对本论文的悉心指导!
- 曹晖,赖明,白绍良.2002.基于小波变换的地震地面运动仿真研究[J].土木工程学报,35(4):40-46.
- 高丽霞,周锡元,董娣,等.2006.加速度均方根地震动统计研究[J].防灾减灾工程学报,26(3):251-256.
- 胡聿贤,周锡元.1962.弹性体系在平稳和非平稳化地面运动下的反应[M].北京:科学出版社,33-50.
- 胡聿贤.2003.地震安全性评价技术教程[M].北京:地震出版社.
- 霍俊荣,胡聿贤,冯启民.1991.地面运动时程强度包线函数的研究[J].地震工程与工程振动,11(1):1-12.
- 金星,廖振鹏.1994.地震动强度包线函数的理论研究[J].地震学报,16(4):519-525.
- 李中付,华宏星,宋汉文,等.2001.一维信号的模态分解与重构研究[J].数据采集与处理,16(3):324-329.
- 吕红山,赵凤新.2007.适用于中国场地分类的地震动反应谱放大系数[J].地震学报,29(1):67-76.
- 屈铁军,王君杰,王前信.1994.局部场地上地震动的强度包络线函数的特性研究[J].地震工程与工程振动,14(3):68-80.
- 王国权,周锡元,马宗晋,等.2001.921台湾地震近断层强地面运动的周期和幅值特性[J].工程抗震,(1):30-36.
- 谢皓宇,本田利器,郑万山.2019.复连续小波变换实现地震波在任意时一频域随机相位的方法[J].地震研究,42(4):510-515.
- 杨福生.1999.小波变换的工程分析与应用[M].北京:科学出版社.
- 袁美巧,俞瑞芳,俞言祥.2010.满足时-频统计特性的地震动时程调整[J].应用基础与工程科学学报,18(增刊1):162-172.
- 张翠然,陈厚群.2007.非平稳地震动时程的渐进谱研究[J].水利学报,38(12):1475-1481.
- 朱继梅.2000.非稳态振动信号分析[J].振动与冲击,19(1):87-91.
- Chiou B,Darragh R,Gregor N,et al.2008.NGA project strong-motion database[J].Earthquake Spectra,24(1):23-44.
- Housner G W,Jennings P C.1964.Generation of artificial earthquake[J].Journal of the Enginerring Mechanics Division,90(EM1):113-150.
- Iyengar R N,Iyengar K T S R.1969.A nonstationary random process model for earthquake accelerograms[J].Bulletin of the Seismological Society of America,59(3):1163-1188.
- Nakayama T,Fujiwara H,Komat S S,et al.1994.Nonstationary response and reliability of linear systems under seismic loadings[C].Rotterdam:Structural Safety & Reliability.2179-2186.
- Priestley M B.1965.Evolutionary spectra and non-stationary processes[J].Journal of the Royal Statistical Society,27(2):204-237.
- Yoshimoto K,Sato S,Ohtake M.1997.Three-component seismogram envelop synthesis in randomly inhomogeneous semi-infinite media based on the single scattering approximation[J].Physics of the Earth and Planetary Interiors,104(1-3):37-61.
- Zhou X Y,Yu R F.2008.Mode Superposition method of non-stationary seismic response for non-classically damped system[J].Journal of Earthquake Engineering,12(3):473-516.
- Yilmaz S,Bayrak Y,2011.Applications of various time-frequency analysis methods to earthquake accelogram records[C].Budapest,Hungary:6th Congress of the Balkan Geophysical Society,First Poster Session III,31-35.
- Yilmaz S,Bayrak Y.2013.Time-frequency analysis of georgia earthquake(25 December 2012)07 October 2013[C].Tirana:7th Congress of the Balkan Geophysical Society,Seismology and Lithosphere(Poster),18910-18914.
- GB 50011—2010,建筑抗震设计规范[S].