基金项目:国家重点研发计划(2018YFE0109700,2017YFC1500502)、中国地震台网中心2019年度青年科技基金(QNJJ201902)、中国地震局2019年度震情跟踪定向工作任务(2019010201)联合资助.
(1.中国地震台网中心,北京 100045; 2.新疆维吾尔自治区地震局,新疆 乌鲁木齐 830011)
(1.China Earthquake Networks Center,Beijing 100045,China)(2.Xinjiang Uygur Autonomous Region Eorthquake Agency,Urumqi 830011,Xinjiang,China)
Singular Spectrum Analysis(SSA); fixed-point deformation; assessment of earthquake forecast
备注
基金项目:国家重点研发计划(2018YFE0109700,2017YFC1500502)、中国地震台网中心2019年度青年科技基金(QNJJ201902)、中国地震局2019年度震情跟踪定向工作任务(2019010201)联合资助.
基于奇异谱分析算法,以新疆东风煤矿钻孔倾斜EW分量和巴里坤水平摆倾斜NS分量为例,在去除典型干扰及长周期趋势变化的基础上,拟合观测资料背景年变序列。对于残差时间序列,结合震例进行动态R值检验,自动提取破年变异常特征时段,递归求解出了最高R值评分对应的异常判定准则。进而自动识别出具有最佳映震效能的破年变异常时段,实现了破年变异常判定的自动化和定量化,提高了前兆异常信号识别的可靠性和准确性。
Based on the Singular Spectrum Analysis(SSA)and the EW component of borehole tilt data in Xinjiang Dongfeng coal mine station,the NS component of quartz horizontal pendulum tiltmeter in Xinjiang Balikun station,this study has realized the fitting of the background annual variation information of the observation data by eliminating the typical interference and long period trend changes.The dynamic R value test was performed on the residual time series combined with the earthquake examples,and the annual cycle breaking anomalies are automatically extracted.At the same time,the anomaly determination criterion corresponding to the highest R value score is recursively solved.Then the annual cycle breaking periods are automatically identified with the best reflection performance on earthquakes,and the automation and quantification of the determination of anomalies are realized.Under the current level of knowledge and conditions,the reliability and accuracy of precursory abnormal signal recognition have been improved.
引言
近年来,不同学者对多种类型的定点形变异常识别、判定及映震效能检验工作做了大量研究(牛安福等,2013; 杨玲英等,2014; 崔青发等,2014; 刘琦等,2016; 马栋等,2019),破年变类异常是其中的一个重要部分。目前该类异常的判定大多采用基于分析人员主观经验的曲线形态辨识法,不同的人对于同一个异常的认定具有不同的看法,导致异常的判定准则及预报效能缺乏定量化的表达。随着前兆台网的密集布设,时间序列数据的积累量已经达到TB级,为实现海量观测数据的快速高效提取,迫切需要研究针对不同异常类型、切实可行的自动识别算法。
破年变异常的提取以正常年变的拟合为基础,目前常用的方法有距平法和滑动傅里叶方法。距平法年变拟合通过不同年份内同一天内的观测取平均值构建标准背景年变序列,其振幅是固定不变的; 滑动傅里叶方法受正余弦波假定的约束,对于非正弦波及非平稳的时间序列周期成分的识别不稳定。奇异谱分析(singular spectrum analysis,SSA)是在Karhumen-Loeve分解理论的基础上发展起来的(Vautard et al,1992),是从时间序列的动力重构出发的自适应分析方法。该方法无需先验信息(江志红,丁裕国,1998),不仅能对信号的不同频率进行识别,还可以按照信号能量的大小进行严格排序,稳定识别非正弦波的周期信号,比传统的频谱分析更具优势(赵佳佳等,2017)。该方法适应面广、物理意义清晰,广泛应用于气象学、海洋学等领域(吴洪宝,1997; 余锦华,丁裕国,2001; 李亚伟等,2010)。近年来在大地测量学及地形变数据处理领域也有了初步应用:①数据预处理应用方面,王解先等(2013)利用SSA分析方法对中国地壳运动观测网络GPS数据服务提供的测站坐标时间(NEU,以BJFS站为例)序列进行了补缺,并根据降噪重构序列提取了坐标时间序列中的趋势和周期成分。②干扰信息提取方面,赵佳佳(2017)将SSA应用于实际倾斜应变固体潮数据的处理中,结果表明SSA能有效提取数据中的长周期成分和固体潮各潮波,有效分离数据中的干扰成分,对干扰排除和异常提取具有一定的参考意义。③周期成分重构与分析方面,李世友等(2018)利用SSA分析算法提取了大坝变形时间序列的趋势和周期分量,分析了各分量与时效、温度和水位因子的关联性; 张旺等(2017)改进了传统SSA的“相移现象缺点”,提出一种新的“SSA-PD”分析方法,并应用该方法对GNSS坐标时间序列中的趋势项和季节项进行了分析; 姚宜斌等(2016)利用SSA方法提取出电离层TEC时间序列中除去异常扰动以及观测噪声部分的日周期部分作为主要成分,在此基础上对震前电离层异常进行了探测与分析。
SSA方法在对时间序列趋势项和周期项的识别、提取等方面具有显著的优势。因此,利用SSA方法进行背景年变序列的拟合研究,既能克服传统距平法年变拟合振幅不准确的缺陷,又能克服滑动傅里叶变换方法严重依赖于正余弦重构的不稳定性问题。本文基于SSA方法,以新疆东风煤矿钻孔倾斜EW分量和巴里坤水平摆倾斜NS分量为例,在去除典型干扰及长周期趋势变化的基础上,对观测资料背景年变序列进行拟合。
1 奇异谱分析(SSA)基本原理计算方法
SSA的实现过程主要分为构建时间滞后矩阵(轨迹矩阵)、奇异值分解(SVD)、分组重构、对角平均4大步骤(赵佳佳等,2017),具体操作过程如下。
1.1 构建时间滞后矩阵X给定嵌入长度L,即窗口长度,构建给定时间序列Xi=(xi,…,xi+L-1)T[KG*2](1≤i≤k)的轨迹矩阵XL×K,其中K=N-L+1,1<L≤N/2,计算方法见下式:
X=[X1:…:Xk]=(xij)L,Ki,j=1=[JB([][HL(4:1,*2/3; 2,*2/3; 3,*2/3; 4,*2/3]x1[]x2[]…[]xN-L+1
x2[]x3[]…[]xN-L+2
[][][]
xL<[]xL+1[]…[]xN[HL)][JB)]]
SSA实现的过程需要确定2个重要参数——嵌入维度L和重构阶次P。嵌入维度L的选择直接影响SSA分解信号的效果,研究表明:若L较小,将会导致信号分解不彻底; 反之,将会使低频信号的分解产生谱裂现象(Vautard et al,1992)。对于待提取年变信号的观测数据,L的选取一般为年变周期的整数倍,这样分解效果较好。经过试验,本文设置L为整周年天数365 d。原始曲线如果存在显著的趋势,先利用高阶小波去除长周期趋势项,根据奇异谱曲线动态选取重构阶次P,确保重构序列位于年频段范围。
1.2 计算奇异值及特征向量设矩阵[WTHX]B=XXT,其中[WTHX]XT为轨迹矩阵[WTHX]X的转置。接下来计算矩阵B的所有特征值λi及其特征向量Ui,按照降序将特征值排列为λ1,λ2,…,λL(λ1≥λ2≥…≥λL≥0),其对应的特征向量分别为[WTHX]U1,U2,…,U[WTBX]L。
i=[WTHX]XT[WTHX]Ui/[KG-*3][KF(]λi[KF)](i=1,2,…,d)(2)
式中:[WTHX]U[WTBX]i和[WTHX]V[WTBX]i是轨迹矩阵[WTHX]X的左右特征向量; d=L*; L*=min{L,K}; 轨迹矩阵[WTHX]X可以由初等矩阵按照下式合成:
X=X1+X2+…+X[WT]d(3)
式中:初等矩阵[WTHX]X[WTBX]i=λi[KF)][WTHX]U[WTBX]i VTi, rank(Xi)=1, 而[KG-*3] λ1≥[KG-*3][KF(]λ2[KF)]≥…≥[KG-*3][KF(]λL≥0为时间序列[WTHX]X的奇异谱(Broomhead,King,1986; Shen,Li,2012)。由最大特征值及其对应的特征向量计算得到的初等矩阵,对应于原始时间序列的最大变化方向,反之则视为噪声。
1.3 分组将初等矩阵[WTHX]Xi的下标(i=1,2,…,d)分成p个不相交的子集I1,I2,…,Ip, 设I={i1,i2,…,im}, 则:
X*=XI1+XI2+…+XIp=(x*ij)L,Ki,j=1(4)
选取集合I1,I2,…,Ip的过程即为分组。研究表明,奇异值接近的2个初等矩阵重构得到一个具有优势周期的成分。通过求解并观测奇异值的分布情况,对观测时间序列分组重构,进而通过快速傅里叶变化(FFT)对重构的年变序列进行周期检验,确保其优势周期位于年频段范围内。
1.4 对角平均通过上述计算得到的重构矩阵[WTHX]X*,需要进行对角平均计算(Zhigljavsky,2010),从而得到一个重构的时间序列y1,y2,…,yN,展开后的计算方法为:yk=[JB({][SX(]1[]k[SX)]∑[DD(]k[]m=1[DD)]x*m,k-m+1 1≤k≤L*
[SX(]1[]L*[SX)]∑[DD(]L*[]m=1[DD)]x*m,k-m+1 L*≤k≤K*
[SX(]1[]N-K+1[SX)] ∑[DD(]N-K*+1[]m=K-K*+1[DD)]x*m,k-m+1[KG*1]K*≤k≤N[JB)]
式中:L*=min{L,K}, K*=max{L,K}。
2 R值检验基本原理及其计算方法
R值评分方法(许绍燮,1989; 张国民等,2002; 闫伟等,2019)是当前普遍认可和使用的地震效能评价方法,其计算方法如下式:
R=[SX(]c1[]c2[SX)] -[SX(]t1[]t2[SX)](6)
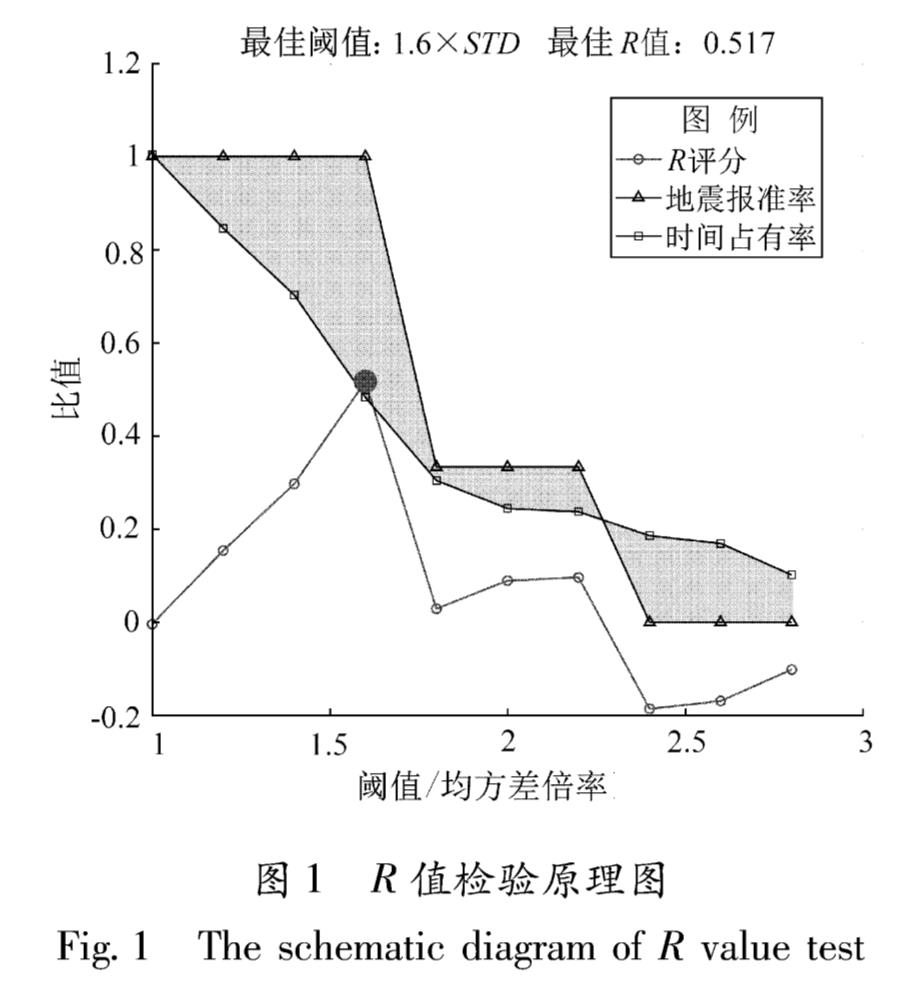
式中:c1为报准地震的次数; c2为应预测的地震总次数; t1为预测占用时间; t2为预测总时间。其基本原理如图1所示。R>0表示预报有效,且R值越大效果越好,最大值为1; R=0表示预报无意义; R<0为预报无效。另外结合统计分布检验,利用报准、漏报地震的个数,可以计算出大于97.5%置信度的R临界值R0,当R>R0时,认为其预测的有效性高于自然发生概率,该测项具有较高的预测效能。
3 技术路线
本文的基本思路和算法流程如图2所示:
(1)首先加载数据,并对原始观测数据进行预处理,包括去突跳、台阶及插值补缺等。
(2)对预处理数据进行滑动傅里叶周期显著性检验,若不显著,先进行高阶小波去趋势处理,进而将具有显著周期的观测数据进行奇异谱分析(SSA)。
(3)设置初始的异常判定阈值S0,按此阈值提取残差时间序列(原始观测值减去趋势和SSA拟合年变成分)的超限部分。
(4)设置初始预测时间阈值T0,将超限的时间点加时间初始阈值T0得到预警时段,检索震例并代入R值公式计算得到R00。
(5)增加预测时间步长step1,循环进行上述R值检验,得到对应于同一异常判定阈值、不同预测时间的R值序列[R00,R01,…,R0n-1]。
(6)增加异常判定阈值步长step2,按照步骤(5)重新遍历预测时间段集合并进行R值检验,得到[R10,R12,…,R1n-1]。
(7)以此递推,求得异常判定阈值、预测时间滑动下的二维R值序列数组,将[T1,T2,…,Tm]与[S1,S2,…,Sn]、R值序列之间的关系拟合成连续的二维曲面,取R值的最高点所对应的阈值T、S作为该测项异常提取和地震预测的标准。
4 实验结果
奇异值的选取需根据奇异谱曲线的形态确定,因此本文设计了一套可以交互选取奇异值进行年变成分重构的计算程序。该程序主要分为“奇异谱分析SSA”和“R值递归检验”两大模块,其中SSA模块提供了数据预处理(包括去除台阶、突跳和趋势项)、预览、奇异值选取、重构序列周期检验以及原始及处理结果可视化几个功能,支持交互确定重构参数。以新疆东风煤矿钻孔倾斜EW和目前存在显著破年变异常的巴里坤水平摆倾斜NS分量为例,简要介绍提取过程并分析结果。
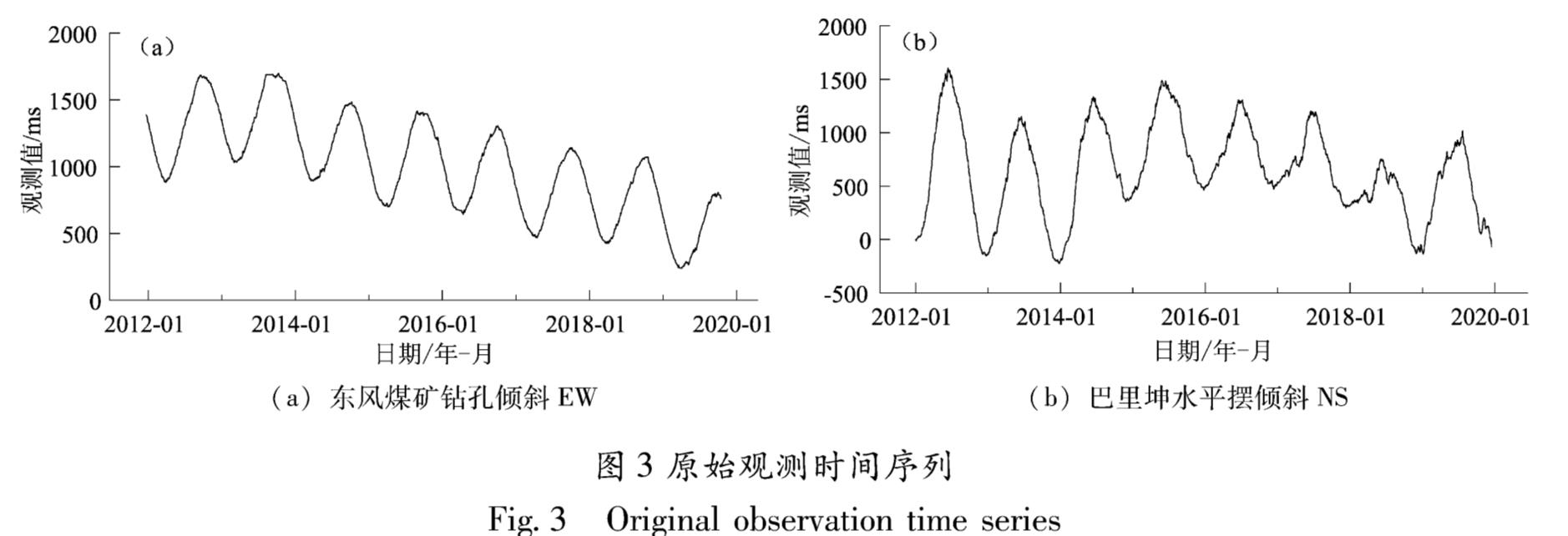
4.1 数据预处理及残差序列SSA图3原始观测时间序列显示,2个测项在年变的基础上叠加了显著的趋势项变化,其中东风煤矿钻孔倾斜EW存在单一的西倾趋势(图3a),而巴里坤水平摆倾斜NS存在多个线性变化趋势(图3b)。因此,首先利用db5小波进行高阶滤波,去除长周期的趋势变化,进而对变化相对平稳的去趋势时间序列做奇异谱分析。
去趋势时间序列的奇异谱曲线显示(图4a),2个测项的第1,2个奇异值位于噪声平台的上方,占比较高且存在显著的周期台阶,因此取重构阶次P为[1,2],重构结果见图4b,c中红色和蓝色虚线部分,灰色曲线为去趋势后的观测时间序列。从图4中可以看出,东风煤矿钻孔倾斜EW分量去掉趋势项后,部分年份如2013,2016年,明显偏离SSA重构得到的年周期变化规律,出现破年变信号; 巴里坤水平摆NS的多个长周期趋势
图4 奇异谱曲线(a)及SSA年变重构结果(b)(c)
Fig.4 Singular spectral analysis curve(a)and results of annual variation reconstruction based on the SSA algorithm(b)(c)项,使得趋势转折与破年变变化混在一起难以区分,通过去趋势并结合SSA重构的结果来看,2017,2018以及2019年均存在显著的破年变异常,与笔者从原始曲线观测到的破年变异常年份基本一致,只是幅度略有差异。
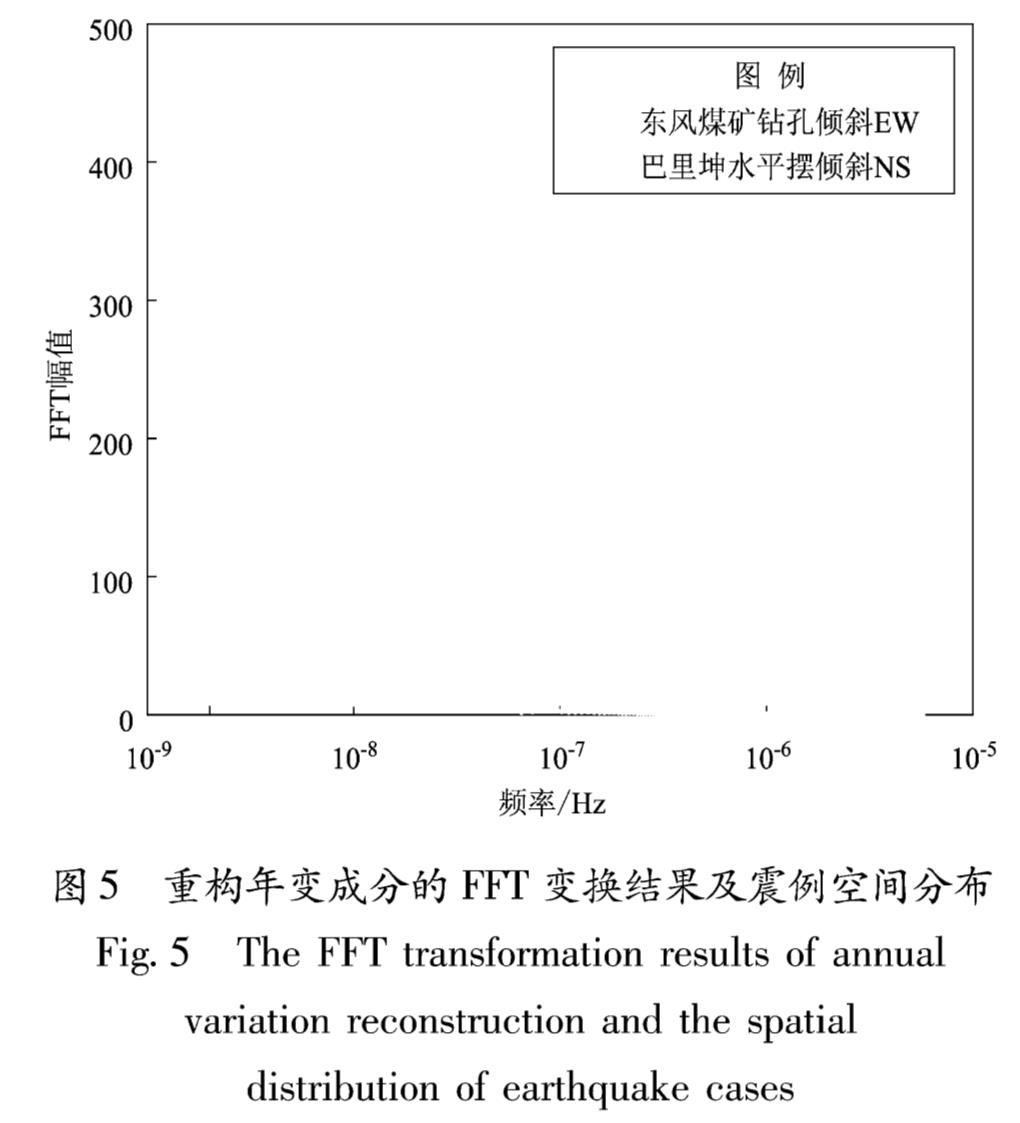
对SSA算法重构得到的年变时间序列做快速傅里叶变换(FFT)的结果显示(图5),2个测项通过SSA重构后的时间序列,其优势周期均为372 d,这表明重构时间序列成功分离出了原始曲线中年频段的成分。将去趋势的观测序列与重构时间
图5 重构年变成分的FFT变换结果及震例空间分布
Fig.5 The FFT transformation results of annual variation reconstruction and the spatial distribution of earthquake cases序列做差,得到了去趋势和年变(SSA重构的正常年变)后的残差时间序列,在此基础上进行动态R值检验。
4.2 震例回溯及动态R值检验取台站周边200 km范围内5级以上、300 km范围内6级以上地震(Dobrovolsky et al,1979),作为输入震例进行R值检验,检索到的震例及台站的空间分布情况如图6所示,2个蓝色圆圈分别代表了以台站为中心的200,300 km的圆形震例检索区。
动态R值检验过程对应于2个互相嵌套的循环,需要设置2个循环变量:
(1)异常判定阈值
通常取均值加减几倍的均方差作为异常判定的标准,但不同观测方法、不同台站测项的信噪比差别较大,取单一的阈值会漏掉部分异常信息,或引入部分噪声信息。因此本文将上述异常判定阈值扩大到某一个动态范围,循环进行R值检验,根据检验结果确定最佳阈值。本例中设定阈值范围为1~3倍的均方差,循环步长设为0.1倍的均方差。
(2)预测时间
预测时间即异常从开始到结束所持续的时间,通过循[JP2]环设定该变量并进行R值检验,可以得到某一观测具有最佳预测效能的预测时间取值,本文设定该变量的取值范围0~720 d,循环步长为10 d。
循环计算后得到了“R值-异常判定阈值-预
图6 震例空间分布(此2例中均无漏报地震)
Fig.6 Spatial distribution of earthquake cases(There was no under reported earthquake in both cases)测时间”的空间插值图像(图7a,8a),其色标代表了不同的异常判定阈值-预测时间组合所对应的预测效能检验结果,即R值评分,取值范围-1~1。从中可以看到不同组合的明显差异性,图中黑色圆点代表了R值最高点,将对应的异常判定阈值及预测时间代入残差时间序列,提取异常特征时段进行R值检验,得到了具有最佳映震效能的异常识别及震例回溯结果如图7b,8b所示。
图7 东风煤矿钻孔倾斜EW动态R值扫描(a)与异常自动识别结果
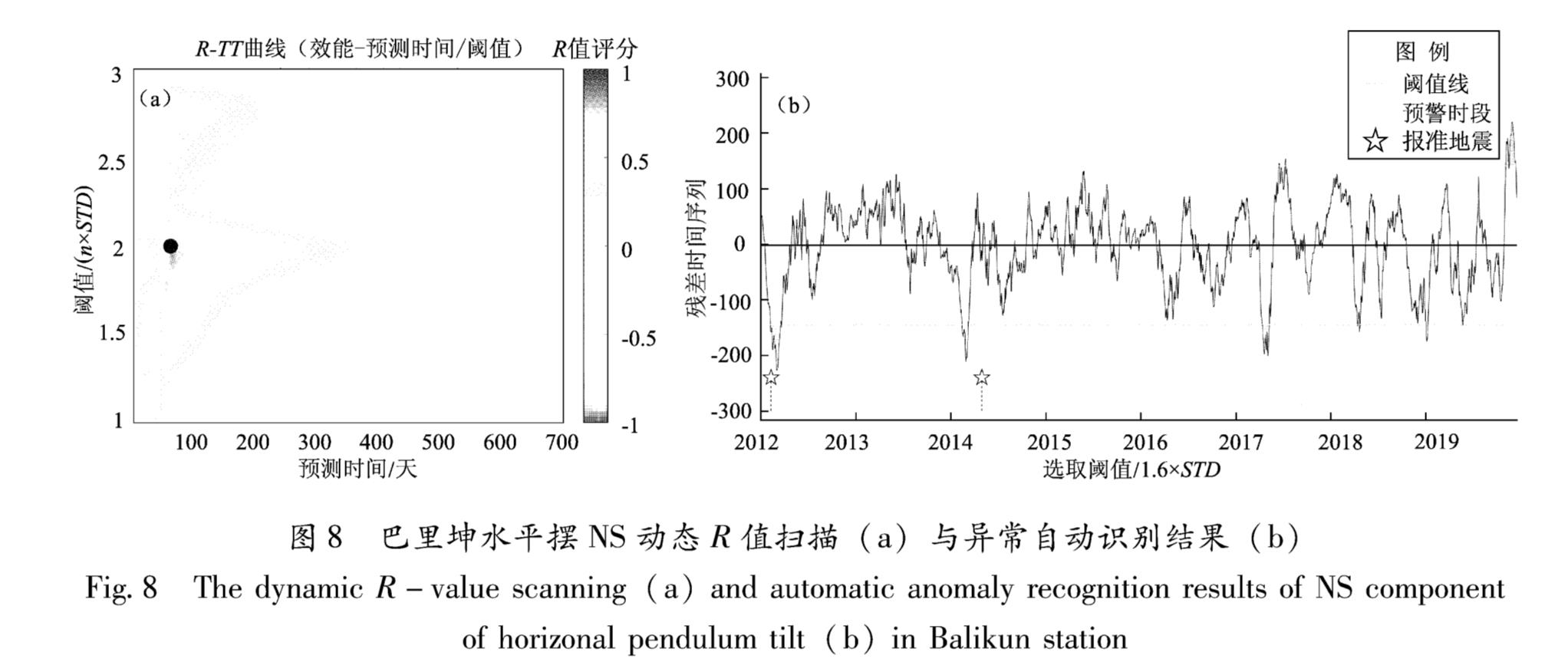
Fig.7 The dynamic R-value scanning(a)and automatic anomaly recognition results of EW component of borehole tilt(b)in Dongfeng coal mine station图8 巴里坤水平摆NS动态R值扫描(a)与异常自动识别结果(b)
Fig.8 The dynamic R-value scanning(a)and automatic anomaly recognition results of NS component of horizonal pendulum tilt(b)in Balikun station图7b,8b中蓝色虚线为具有最佳R值评分的异常判定阈值线,黑色实线为数据均值线。从动态检验的结果来看:①上述2个测项具有最佳预测效能的异常判定阈值分别为均值加减1.6倍、2倍的均方差; ②异常出现后最佳预测时间分别为91 d,61 d,目前2个测项均处在异常阶段; ③东风煤矿钻孔倾斜EW的破年变异常对其周边300 km内的5级以上地震具有较好的映震效能,震例主要集中在台站的ES方向; ④巴里坤水平摆倾斜NS破年异常主要对应200 km内的5级以上地震,震例较少且无优势集中方向; ⑤应用本研究中的方法提取的破年变异常,东风煤矿钻孔倾斜EW破年变异常的预测效能大于97.5%置信度的临界值R0,预测结果较为可靠; 而巴里坤水平摆倾斜NS虚报率较高,小于临界值R0,虽然目前处于异常时段,但信度较低,建议参考使用。
5 结论与讨论
本文通过对去除长周期趋势变化的平稳时间序列进行SSA分析,得到了基于SSA的正常年变时间序列的拟合; 在此基础上,对扣掉趋势变化和年变成分的变化部分做动态R值检验,从震例回溯和统计的角度,得到了具有最佳映震效能的预测参数组合,即异常判定阈值和时间预测准则。应用该准则,可以跟踪该测项未来的异常变化情况,并结合R值评分和以往的震例对应情况,给出相应的预测意见,对异常判定的定量化和自动化工作具有一定的参考价值。
基于以上研究,对未来工作提出如下的建议:
(1)进一步论证SSA算法中嵌入维度L和重构阶次P对年变重构的影响,并给出更加合理的参数设置。
(2)对比不同研究方法对原始数据去趋势处理的结果及可靠性,优选出最佳的趋势拟合方案,确保该处理过程的可靠性。
(3)目前震例的选取采用的是经验做法,单从与台站的距离和震级两个方面作为约束,不同台站对周边地震的反映具有特异性,因此需要结合具体地质构造背景,利用数据挖掘等方法综合确定针对某一特定台站和测项的震例,输入动态R值检验模块求解最佳预测参数组合。[KH1*4D]
- 崔青发,韩晓飞,张璐,等.2014.西安台体应变对汶川大地震的响应分析[J].大地测量与地球动力学,34(4):96-101.
- 江志红,丁裕国.1998.奇异谱分析的广义性及其应用特色[J].气象学报,56(6):736-745.
- 李世友,王奉伟,沈云中.2018.大坝变形时间序列的奇异谱分析[J].测绘通报,(9):64-68.
- 李亚伟,詹卫华,卫东山,等.2010.流域年径流时间序列的奇异谱分析[J].水电能源科学,28(10):19-22.
- 刘琦,闫伟,李智蓉,等.2016.南北地震带定点形变前兆异常指标初建[J].地震,36(4):76-88.
- 马栋,马利军,侯晓真,等.2019.华北地区地壳形变连续观测灵敏台站研究[J].地震研究,42(3):405-410.
- 牛安福,顾国华,曹景鹏,等.2013.芦山MS7.0地震前远、近场形变时空演化特征研究[J].地震学报,35(5):670-680.
- 王解先,连丽珍,沈云中.2013.奇异谱分析在GPS站坐标监测序列分析中的应用[J].同济大学学报(自然科学版),41(2):282-288.
- 吴洪宝.1997.奇异谱和多通道奇异谱分析[J].气象教育与科技,(4):1-10.
- 许绍燮.1989.地震预报能力评分[G].地震预报方法实用化研究文集地震学专辑.北京:地震出版社,586-589.
- 闫伟,刘桂萍,黎明晓,等.2019.短期地震预测准确性的定量评价方法[J].地震学报,41(3):399-409.
- 杨玲英,张欢,毛先进,等.2014.永胜台对汶川8.0级地震的倾斜响应与异常分析[J].地震研究,37(4):628-633.
- 姚宜斌,翟长治,孔建,等.2016.2015年尼泊尔地震的震前电离层异常探测[J].测绘学报,45(4):385-395.
- 余锦华,丁裕国.2001.近百年全球平均地面气温准周期信号及其长期演变特征的分析[J].大气科学,25(6):767-777.
- 张国民,刘杰,石耀霖.2002.年度地震预报能力的科学评价[J].地震学报,24(5):525-532.
- 赵佳佳,陈志遥,张燕,等.2017.奇异谱分析在倾斜应变数据处理中的应用研究[J].大地测量与地球动力学,37(5):541-545.
- 张旺.2017.基于改进奇异谱分析方法提取GNSS坐标序列趋势项及季节项信息[D].成都:西南交通大学.
- Broomhead D S,King G P.1986.Extracting qualitative dynamics for experimental data[J].Physica D,20(2-3):217-236.
- Dobrovolsky I P,Zubkov S I,Miachkin V I.1979.Estimation of the size of earthquake preparation zones[J].Pure and Applied Geophysics,117(5):1025-1044.
- Shen Y Z,Li W W.2012.Spatio temporal related signal and noise analysis of GPS monitoring series of the base stations in China[R].International Union of Geodesy and Geophysics Conference.
- Vautard R,Yiou P,Ghil M.1992.Singular-Spectrum Analysis:A Toolkit for Short,Noisy Chaotic Signals[J].Physica D Nonlinear Phenomena,58(1):95-126.
- Zhigljavsky A.2010.Singular spectrum analysis for time series:Introduction to this special issue[J].Statistics and its Interface,3(3):255-258.