收稿日期:2020-03-28
基金项目:国家重点研发计划(2018YFC0705602)资助.
基金项目:国家重点研发计划(2018YFC0705602)资助.
铁基形状记忆合金混凝土框架节点可恢复变形性能分析*
(1.沈阳建筑大学 土木工程学院,辽宁 沈阳 110168; 2.大连理工大学 建设工程学部,辽宁 大连 116024)
Resilient Performances Analysis of Fe-SMA Reinforced Frame Joints
YAN Shi1,DU Changhong1,XIAO Zhengfeng1,JANG Xinxin1,NIU Jian1,2
(1.School of Civil Engineering,Shengyang Jianzhu University,Shenyang 110108,Liaoning,China)(2.Faculty of Infrastructure Engineering,Dalian University of Technology,Dalian 116024,Liaoning,China)
Fe-SMA frame joints; resilient performances; superelasticity; seismic performances; pseudo-static loading; residual deformation
备注
摘要
全文
图/表
参考文献
罕遇地震作用下混凝土框架梁柱节点残余变形的不断累积是造成其破坏的主要原因之一,如何减小动力循环荷载作用下节点的残余变形,提升其可恢复变形能力具有重要的意义。利用超弹性铁基形状记忆合金(SMA)代替普通钢筋,不仅可使节点具有较大延性,还能保持较高耗能和可恢复变形能力。为了系统地分析新型节点的地震可恢复变形性能,利用OpenSEES系统平台建立一种相关节点的有限元模型,数值模拟普通配筋节点和铁基SMA筋节点模型在拟静力荷载作用下的内力和变形规律,并与试验结果进行比较; 进一步分析了新型节点不同轴压比等参数下滞回性能,得到了极限承载力、刚度、阻尼、残余变形等变化规律,明确了可恢复变形性能。结果 表明:所建立的模型能较好地反映新型节点的滞回性能和可恢复变形性能的变化规律,所提出SMA混凝土节点具有更好的抗震性能和可恢复地震变形能力,残余变形减小50%左右。
The continuous accumulation of concrete frame structure beam-column joint residual deformations under major earthquakes is one of the main causes for structural destructions.How to reduce residual deformations of the beam-column joints under dynamic cyclic loading and improve their earthquake resilient performances(ERPs)is of great significance.Shape memory alloy(SMA)rebars with the superelasticity can replace ordinary rebars in beam-column joints in concrete frame structures to greatly increase the ductility while maintaining high energy dissipation capacity and high ERPs.In order to systematically analyze the seismic resilient deformation performance,the OpenSEES system platform is used to establish a finite element model(FEM)of corresponding joints,numerically simulating internal forces and deformation laws of ordinary beam-column joints and iron-based SMA beam-column joint under pseudo-static loading,and comparing with the test results.After the model updating,the hysteresis performances of the novel joints under different parameters such as compression ratios are further investigated,obtaining the law of the ultimate bearing capacity,stiffness,damping,residual deformation,and the resilient deformation capacity.The results show that the established model can better reflect the law of the hysteresis performances and resilient deformation capacity,and the proposed novel joint has better seismic performances and resilient deformation capacity as well as obviously reduced residual deformation than the normal joints.
引言
在钢筋混凝土框架结构中,梁柱节点是重要的承重构件,起到传递弯矩、剪力和轴力的枢纽作用,对结构抗震性能产生重要影响。混凝土梁柱节点要满足“强节点”的要求,通常在节点处配置钢筋较多,施工难度较大、受力复杂、容易发生脆性破坏,且在较大荷载作用下可能会发生核心区的剪切破坏,以及节点区钢筋锚固失效引起的梁柱构件的弯曲破坏等。塑性变形的不断积累是导致节点破坏的主要因素之一,如何提高节点的可恢复变形能力以减小其塑性损伤积累是急需解决的问题。形状记忆合金(shape memory alloy,简称SMA)材料是一种新兴智能材料,超弹性SMA具有很强的变形能力,伸长率可达6%以上,且在所受外荷载作用未明显减少的情况下,其极限伸长率能达到20%左右,而且卸载后具有很小的残余变形。用超弹性SMA筋替代部分普通钢筋布置在节点中,使其具有更好的延性和可恢复变形性能,会显著提高其抗震能力。
国内外学者己对普通钢筋混凝土框架节点进行了较多试验研究(张健新等,2020; 潘毅等,2018),但是对于框架节点有限元模型的研究相对较少(Hwang,Lee,1999; Pantelides,2002; Altoontash,2004; 江传良,2006; Celik,Ellingwood,2008),对于利用超弹性SMA筋的框架节点的数值分析研究更是鲜有报道。目前,采用商业软件ANSYS或ABAQUS等有限元方法分析节点力学性能较为常见,其运算量相对较大,且大多只是与骨架曲线吻合较好,较难模拟出节点的滞回性能(Favvata et al,2008),而利用OpenSEES地震分析平台采用杆系结构进行有限元分析,不仅运算速度快、建模快捷和精确度高,而且力学概念清楚。因此,本文利用OpenSEES地震分析平台开展拟静力荷载作用下的SMA混凝土节点滞回性能分析。
1 梁柱节点试验设计
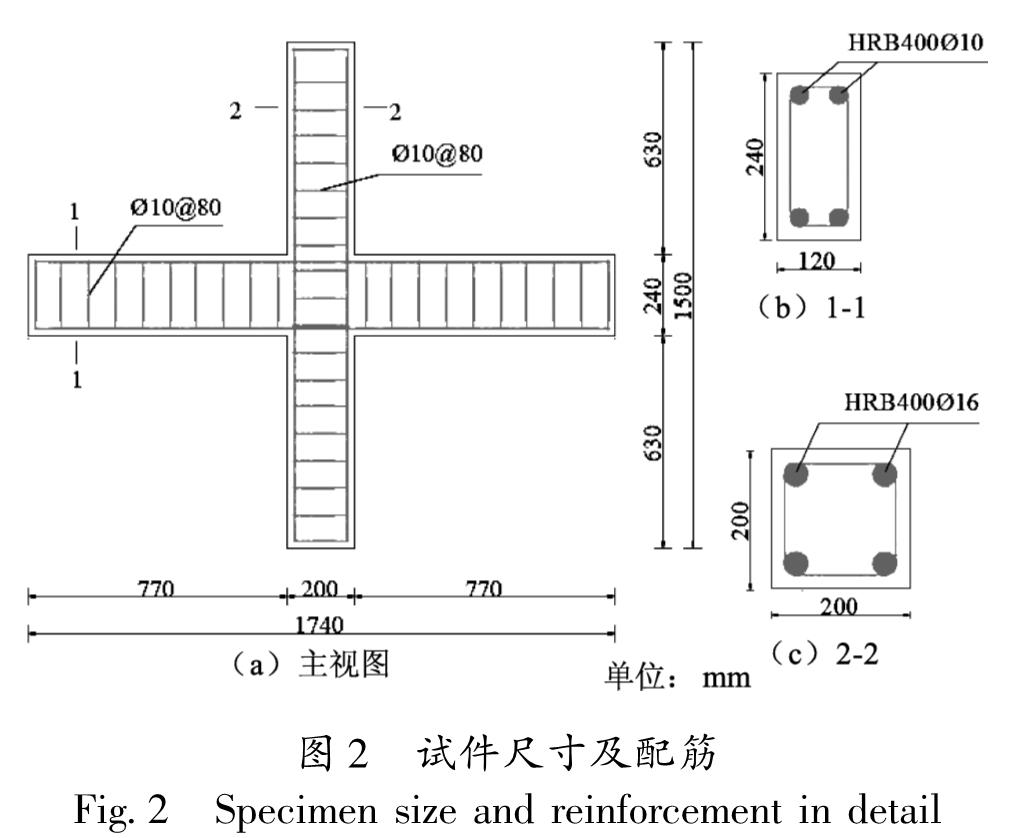
对普通梁柱节点和配有铁基SMA筋节点进行拟静力试验研究(肖正峰,2018)。共制作了4组试件,按比例1:2进行缩尺,梁和柱的几何尺寸(长×宽×高)分别为770 mm×120 mm×240 mm和1 500 mm×200 mm×200 mm。纵筋均采用对称配置,普通受力纵筋均为HRB400,箍筋均为HPB300,梁柱保护层均为20 mm,编号分别是XJD-1、SJD-1、SJD-2和SJD-3,其中,XJD
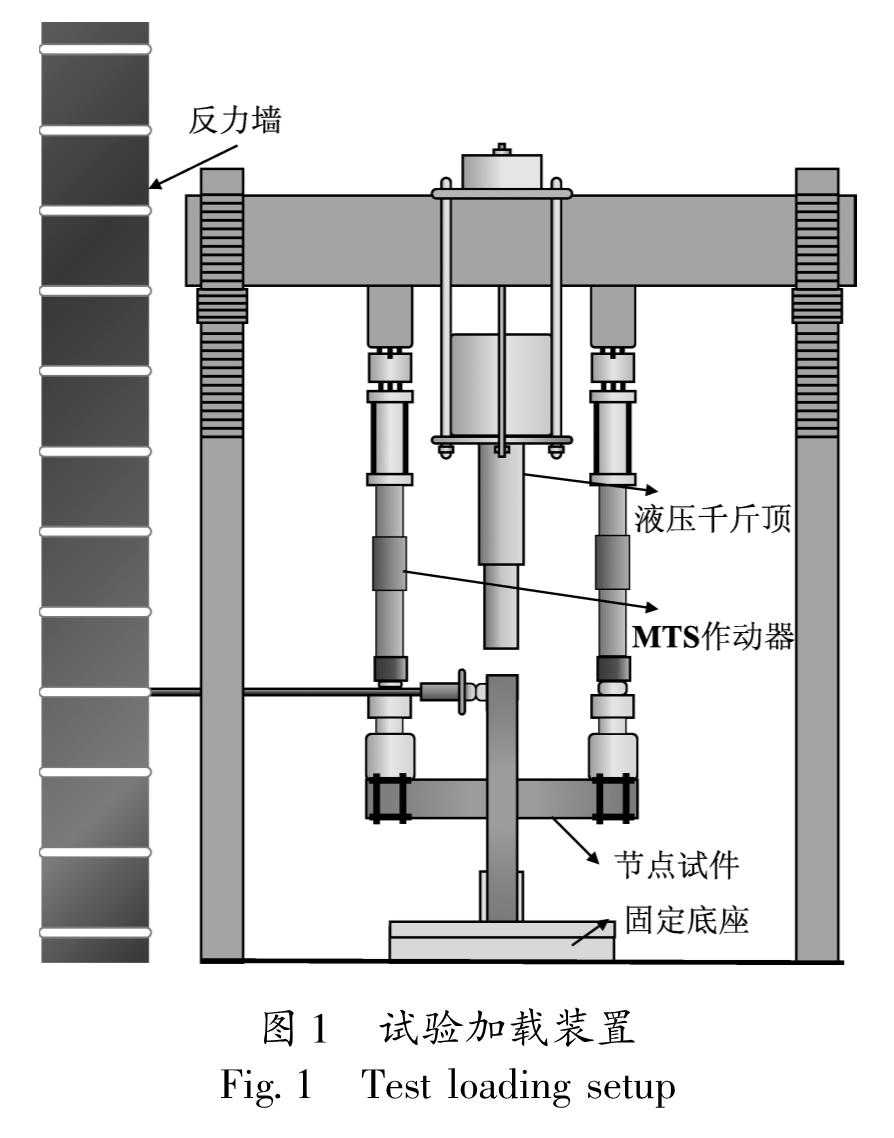
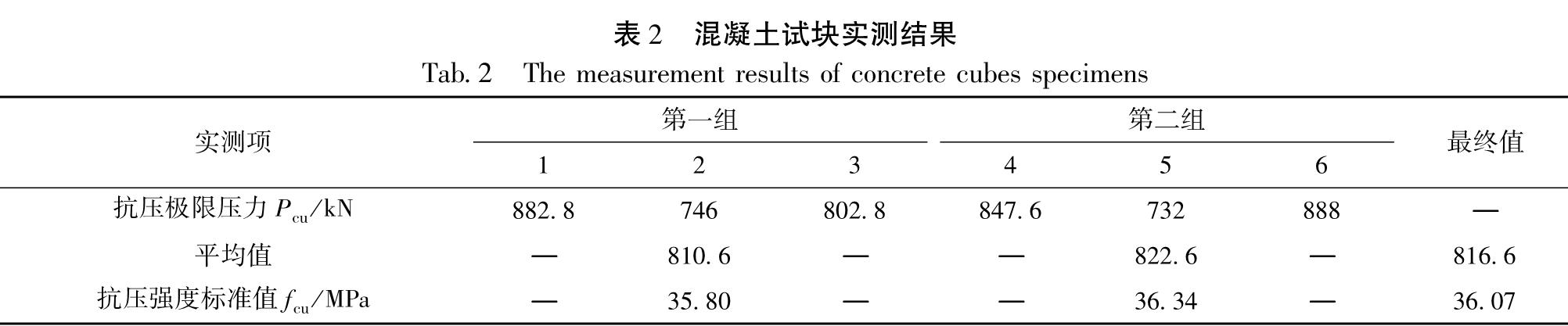
-1为普通钢筋节点,SJD-1、SJD-2和SJD-3采用不同直径的铁基SMA作为梁纵筋。设计轴压比均为0.3,混凝土强度为C30,采用力—位移混合加载方案,加载装置图如图1所示,试件具体尺寸及配筋分别如图2和表1所示,混凝土、钢筋及铁基SMA筋材性试验数据分别见表2～4。
试验得到节点梁端的荷载-位移和荷载-应变滞回曲线等,破坏主要发生在梁靠近节点核心区的端部,呈外区破坏的特点。另外,由于SMA筋表面光滑,与混凝土之间的粘结力较弱,当滞回循环次数较大时,SMA有发生粘结破坏的趋势。
图1 试验加载装置
Fig.1 Test loading setup
图2 试件尺寸及配筋
Fig.2 Specimen size and reinforcement in detail
表1 试件配筋表
Tab.1 Specimen reinforcement table
表2 混凝土试块实测结果
Tab.2 The measurement results of concrete cubes specimens
表3 钢材性能指标
Tab.3 The performance of reinforcement
表4 Fe-Mn-Si基合金材料性能
Tab.4 Fe-Mn-Si based alloy material properties2 梁柱节点数值模拟分析
3 模拟验证及参数分析
4 结论
基于OpenSEES平台,对节点进行数值模拟,并与试验结果进行对比分析,验证模拟结果准确性,并进一步考虑SMA筋直径和轴压比这2个主要参数对铁基SMA梁柱节点抗震性能与可恢复变形性能的影响,得出以下主要结论:
(1)SMA筋节点的残余变形要远小于普通钢筋节点,故SMA筋节点的可恢复变形性能要优于普通钢筋节点。SMA筋的锚固性能对节点的变形可恢复能力有一定的影响。
(2)在一定范围内,随着SMA筋直径的增大,SMA筋节点的屈服强度和极限荷载增大,并且刚度退化趋缓,滞回曲线所围面积增大,耗能能力越好,残余变形比越小,节点的变形可恢复能力越好。
(3)对于破坏发生在梁端的框架节点而言,在一定范围内,轴压比对试件的屈服强度和极限强度影响不显著,耗能能力和残余变形比基本不随轴压比的改变而改变。
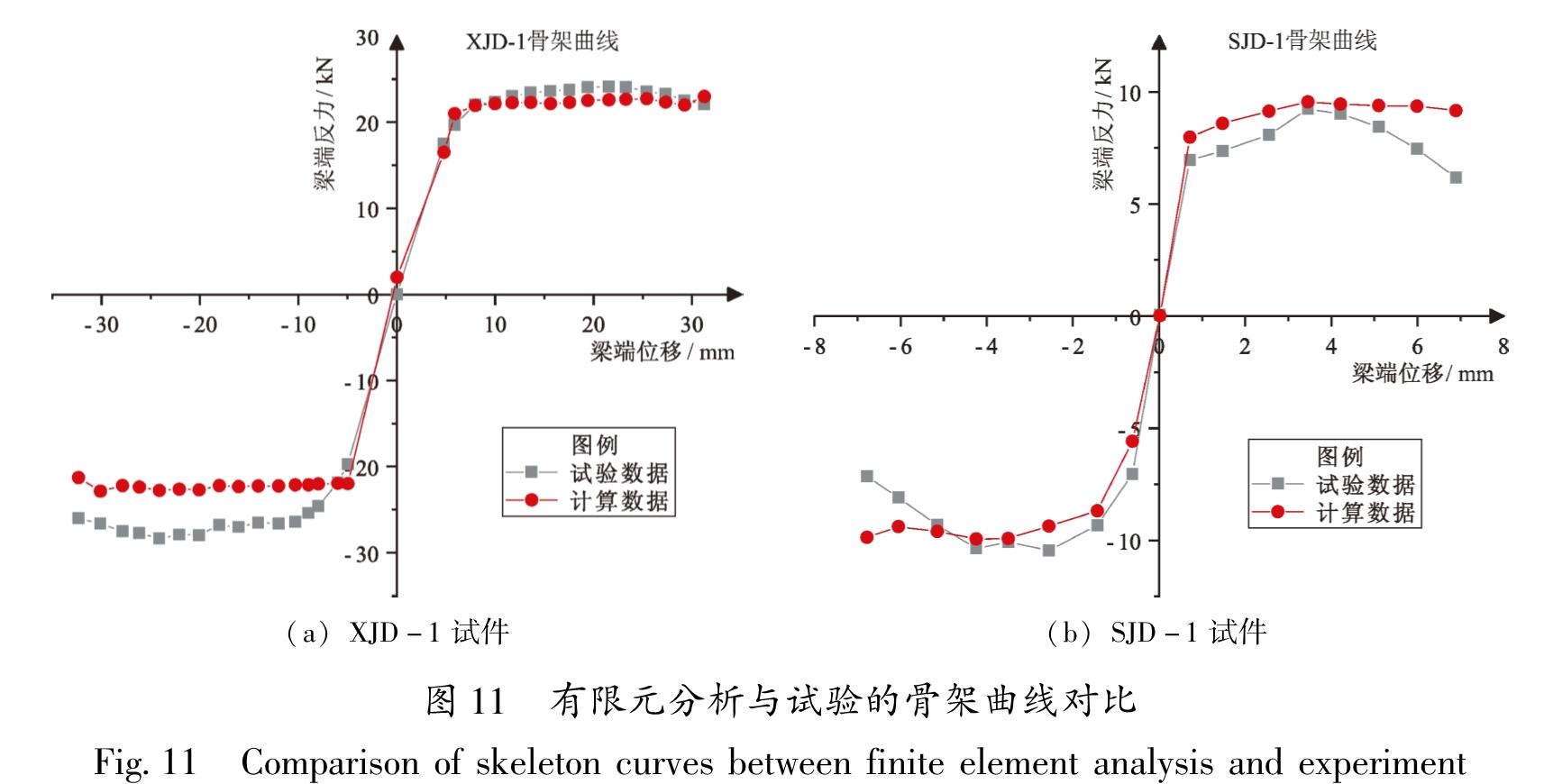
3.1 模拟验证建立按照实际试验位移两点加载的两个梁柱节点模型(XJD-1和SJD-1),并进行有限元分析,得到构件梁左端力—位移的滞回曲线、骨架曲线与相应试验结果的比对,如图 10和图 11所示。
图 10 有限元分析与试验的滞回曲线对比
Fig.10 Comparison of hysteresis curves between finite element analysis and experiment
图 11 有限元分析与试验的骨架曲线对比
Fig.11 Comparison of skeleton curves between finite element analysis and experiment由图 10,11可见,试验和模拟得到的滞回曲线和骨架曲线在弹性阶段和屈服阶段基本一致,但达到极限阶段后的下降段模拟稍差。由于现场试验影响因素较多,相比理想化的有限元模型在加卸载、测量以及试件约束等方面有一定的差异,故试验和模拟的滞回曲线、骨架曲线有一些差距,但对于要关注的屈服强度、极限强度、残余变形、滞回耗能等方面来说还是能够有效验证有限元模拟的准确性和可行性,吻合相对较好。
SMA筋并不能提高构件的承载能力和延性,主要原因是SMA筋表面光滑,粘结性能弱于普通钢筋,在接近极限荷载时,SMA筋可能有相对滑移产生。但是,SMA筋节点试件的残余变形要远小于普通钢筋混凝土节点。
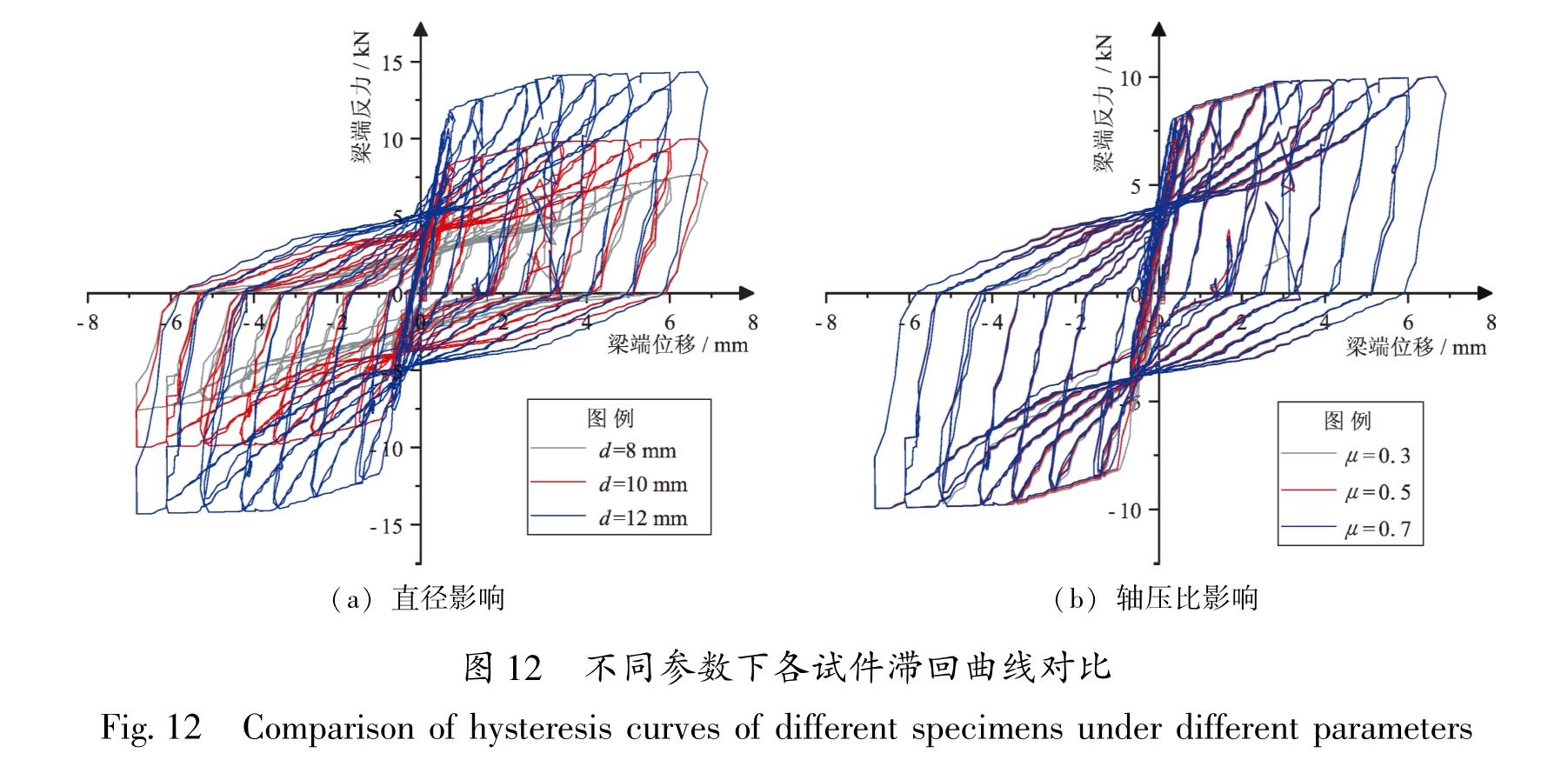
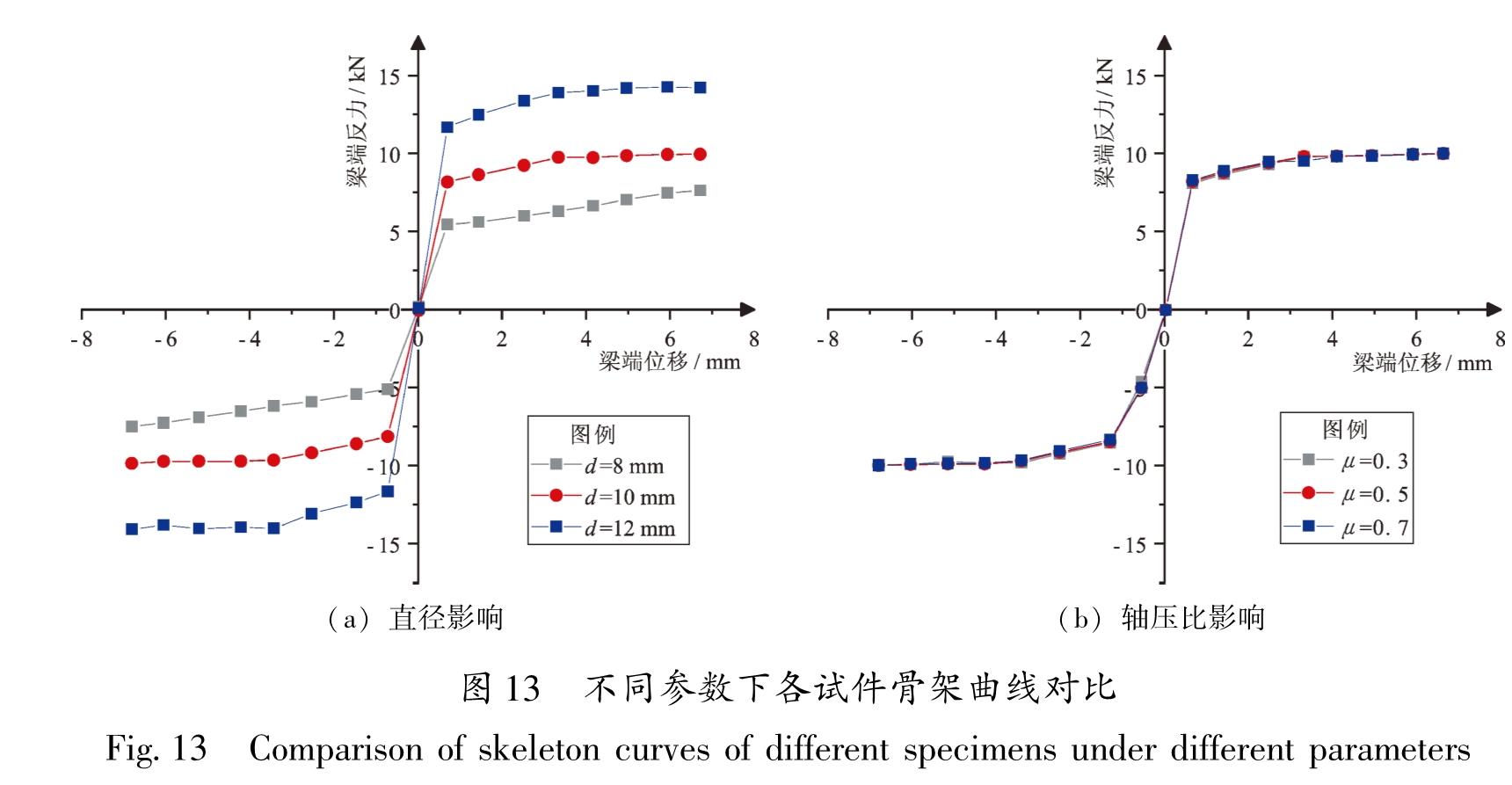
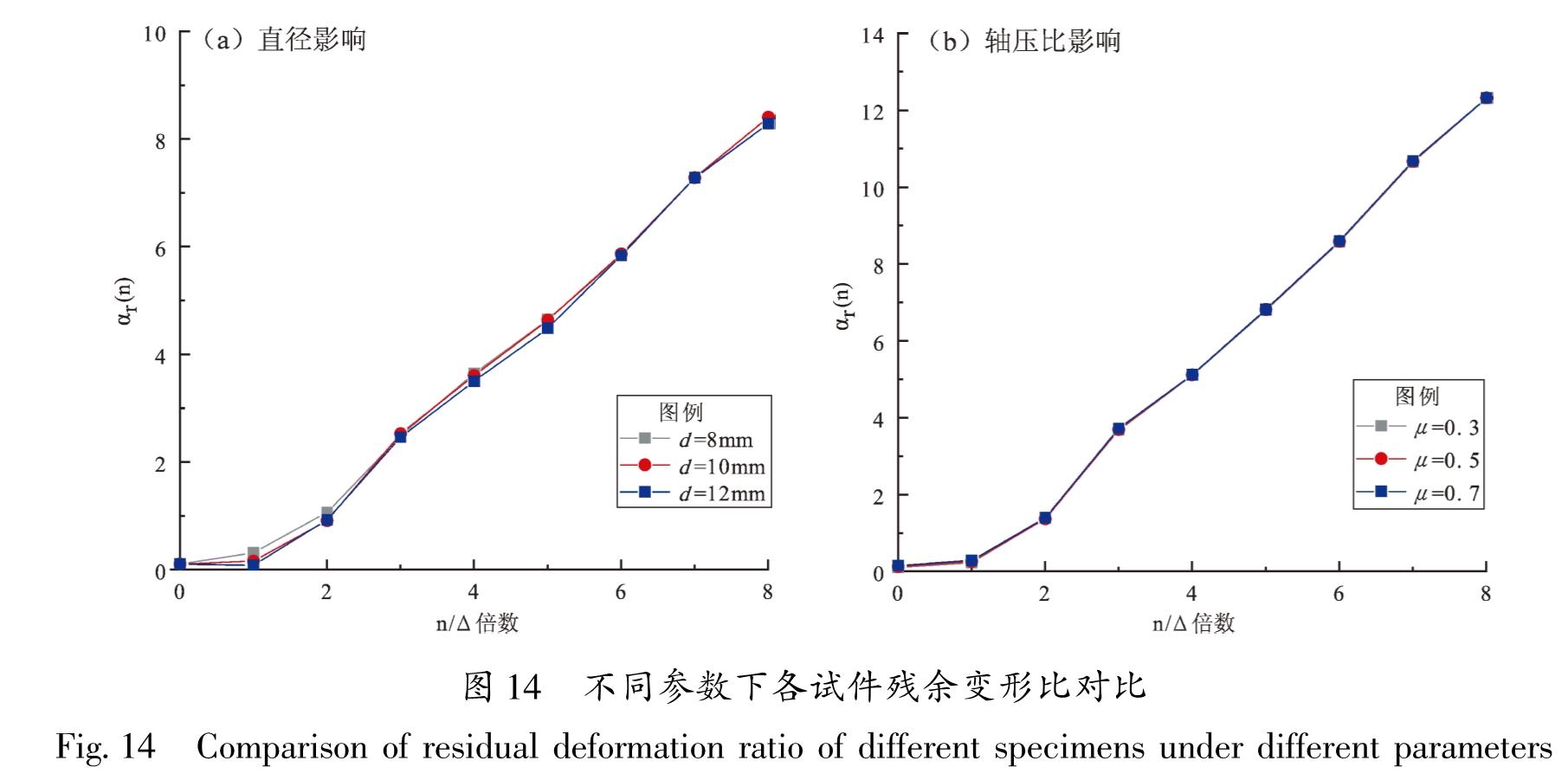
3.2 参数分析数值模拟和试验结果比较吻合,证实了基于OpenSEES非线性对普通梁柱节点和铁基SMA筋梁柱节点有限元分析的有效性。为进一步扩大适用范围,选取铁基SMA筋节点的SMA筋直径和轴压比为主要影响参数,分析其对滞回性能和自复位性能的影响。取试件SJD-1为分析试件,SMA筋直径d=10 mm且设计轴压比μ=0.3,保持其它条件不变,使用SJD-1的加载方式,分别进行SMA筋直径d=8 mm和d=12 mm和设计轴压比μ=0.3和μ=0.5的SMA节点在低周反复加载条件下有限元数值分析,计算得到的各试件的滞回曲线、骨架曲线和残余变形比分别如图 12～14所示。残余变形比αr(n)为:
αr(n)=(Δr(n))/(Δy)(7)
式中:Δr(n)为卸载后荷载为零时结构产生的不可恢复的残余变形,在满足抗震要求时,该值越小,构件的可恢复变形性能越好; Δy为屈服位移。
3.2.1 不同SMA筋直径的SMA梁柱节点对比分析(1)承载能力:在弹性范围内,骨架曲线不重合,说明弹性阶段SMA筋直径这一参数的变化对试件的刚度有一定影响; 在一定范围内随着SMA筋直径的增大,屈服强度和极限荷载增大,并且刚度退化趋缓。
(2)耗能能力:在一定范围内随着SMA筋直径的增大,其滞回曲线所围面积也增大,说明试件的耗能能力也就越好。
(3)残余变形:在一定范围内随着SMA筋直径的增大,其残余变形比逐渐减小,但减小的程度不大,试件的变形可恢复能力趋好但也不显著。
图 12 不同参数下各试件滞回曲线对比
Fig.12 Comparison of hysteresis curves of different specimens under different parameters
图 13 不同参数下各试件骨架曲线对比
Fig.13 Comparison of skeleton curves of different specimens under different parameters
图 14 不同参数下各试件残余变形比对比
Fig.14 Comparison of residual deformation ratio of different specimens under different parameters3.2.2 不同设计轴压比的SMA梁柱节点对比分析(1)承载能力:在一定范围内,轴压比对试件的屈服强度和极限强度影响不显著。
(2)滞回面积:在0.3～0.7范围内,轴压比对试件的耗能作用影响不显著。
(3)残余变形:残余变形比基本不随轴压比的改变而改变,可以认为影响不大。
- 江传良.2006.碳纤维布加固钢筋混凝土框架节点的试验研究[D].广州:广州大学.
- 江见鲸,李杰,金伟良.2006.高等混凝土结构理论[M].北京:中国建筑工业出版社.
- 潘毅,陈侠辉,王涵平,等.2018.无黏结预应力装配式框架结构地震易损性分析[J].哈尔滨工业大学学报,50(6):71-77.
- 吴健秋.2007.基于OpenSEES的梁-柱节点单元的适用性和定参方法研究[D].重庆:重庆大学.
- 肖正峰.2018.形状记忆合金混凝土梁柱节点抗震性能研究[D].沈阳:沈阳建筑大学.
- 张健新,丁传林,戎贤,等.2020.装配式高强钢筋钢纤维混凝土框架节点抗震性能试验研究[J].土木与环境工程学报(中英文),42(2):157-164.
- Altoontash A.2004.Simulation and damage models for performance assessment of reinforced concrete beam-column joints[D].Stanford:Stanford University.
- Celik O C,Ellingwood B R.2008.Modeling beam-column joints in fragility assessment of gravity load designed reinforced concrete frames[J].Journal of Earthquake Engineering,12(3):357-381.
- Eligehausen R,Popov E P,Bertero V V.1983.Local bond stress-slip relationships of deformed bars under generalized excitations[R].PEERC Report,University of California,Berkeley,83/23.
- Favvata M J,Izzuddin B A,Karayannis C G.2008.Modelling exterior beam-column joints for seismic analysis of RC frame structures[J].Earthquake Engineering & Structural Dynamics,37(13):1527-1548.
- Filippou F C,Issa A.1988.Nonlinear analysis of reinforced concrete frames under cyclic load reversals[R].Berkeley:Earthquake Engineering Research Center Report,88-12.
- Filippou F C,Popov E P,Bertem V V.1983.Effects of bond deterioration on hysteretic behavior of reinforced concrete joints[R].Berkeley:Earthquake Research Center,University of California.
- Hawkins N M,Lin I J,Jeang F L.1982.Local bond strength of concrete for cyclic reversed loadings[M].Bond in Concrete,Bartos P(editor),Applied Science Publishers Ltd.,London,151-161.
- Hwang S J,Lee H J.1999.Analytical model for predicting shear strengths of exterior reinforced concrete beam-column joints for seismic resistance[J].ACI Structural Journal,96(5):846-858.
- Lowes L N,Altoontash A.2003.Modeling reinforced concrete beam-column joints subjected to cyclic loading[J].Journal of Structural Engineering,129(12):1686-1697.
- Mari A,Scordelis A.1984.Nonlinear geometric dependent analysis of three dimensional material and time reinforced and prestressed concrete frames[R].Berkeley:Department of Civil Engineering,University of California.
- Menegotto M.1973.Method of analysis for cyclically loaded RC plane frames including changes in geometry and non-elastic behavior of elements under combined normal force and bending[C].Zurich:International Association for Bridge and Structural Engineering.
- Mitra N.2007.An analytical study of reinforced concrete beam-column joint behavior under seismic loading[D].Washington:University of Washington,1-136.
- Pantelides C P.2002.Assessment of reinforced concrete building exterior joints with substandard details[D].Berkeley:Pacific Earthquake Engineering Research Center,College of Engineering,University of California.
- Park Y J,Ang A H-S.1985.Mechanistic seismic damage model for reinforced concrete[J].Journal of Structural Engineering,ASCE,111(4):722-739.
- Shima H,Chou L L,Okamura H.1987.Bond characteristics in post-yield range of deformed bars[J].Concrete Library of JSCE,10:113-124.
- Vecchio F J,Collins M P.1986.The modified compression-field theory for reinforced concrete elements subjected to shear[J].ACI Structural Journal,83(2):219-231.
- Viawanthanatepa S,Popov E P,Bertero V V.1979.Effects of generalized loadings on bond of reinforcing bars embedded in confined concrete blocks[R].Berkeley:PEER Report,University of California,1-223.
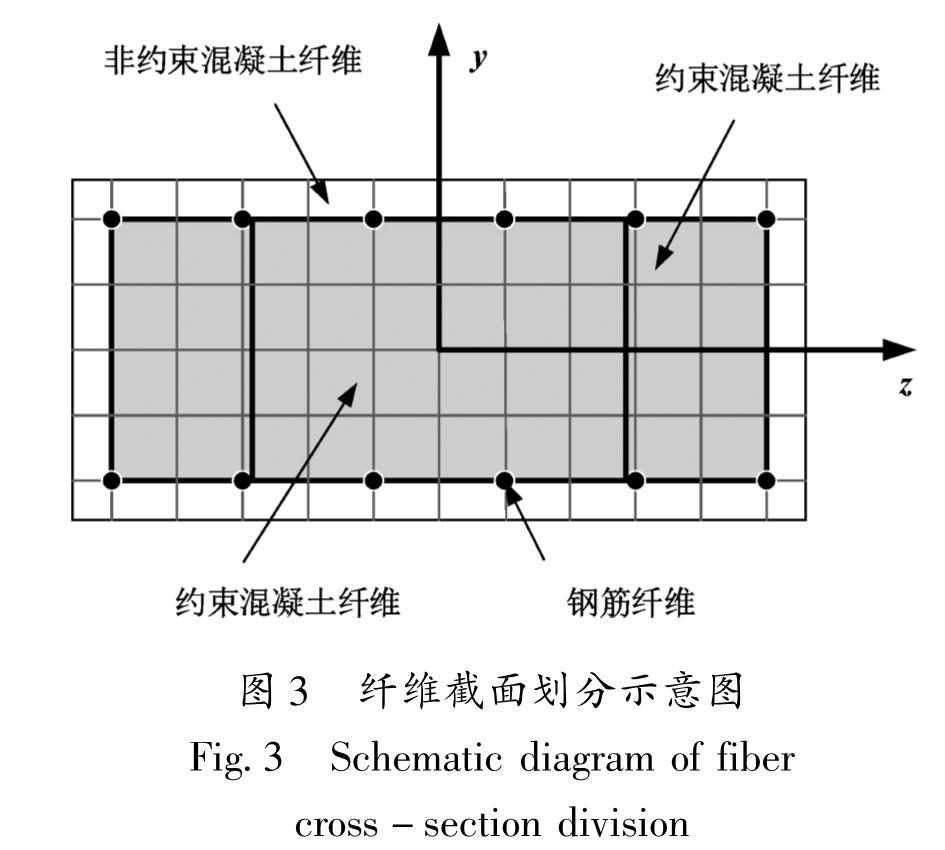
2.1 纤维截面OpenSEES中纤维截面模型最早是由Taucer开发的。该模型在变形过程中忽略时间、温度和湿度等因素引起的构件受力变化,假定构件的截面始终保持平截面。但由于钢筋混凝土材料的非均匀质性,所以可能存在裂缝,严格来说,平截面假定不成立,但试验结果表明,沿构件轴线取出一段长度的平均应变在构件截面上的分布仍然基本符合平截面假定(江见鲸等,2006),纤维模型是目前进行结构弹塑性分析使用最为广泛的模型之一。
图3 纤维截面划分示意图
Fig.3 Schematic diagram of fiber cross-section division基于平截面假定,可将混凝土节点截面划分成一定数目的小纤维束,包括非约束混凝土纤维束、约束混凝土纤维束、普通钢筋纤维束和铁基SMA筋纤维束等,将对应非约束混凝土、约束混凝土、钢筋和选定的SMA筋本构关系分别赋予对应的纤维束,并根据截面的弯曲应变和轴向应变求出每一根纤维的应变,进而可以得到每根纤维的应力,最终计算出截面的刚度,如图3所示。
2.2 梁柱单元选择基于有限单元方法形成的杆系模型,最常用的是由Mari和Scordelis(1984)提出的基于位移的梁柱单元模型和由Filippou和Issa(1988)提出的基于力的梁柱单元。基于位移的梁柱单元由于插值函数不能很好描述纤维端部屈服后单元的曲率分布情况,且在单元层次上不能迭代计算,因此收敛速度慢且精度稍低,不能很好地描述非线性行为,要到达需要的效果,需要在非弹性区域使用非常细的划分。而基于力的梁柱单元可不受线性曲率分布的限制,不需要再细分单元,能同时满足力平衡方程和变形协调条件,故基于力的梁柱单元精度较高,使用一个单元就可模拟一个构件,通过选取合理数量的积分点就能达到足够的精度,并且计算效率也大幅提高。因此,本文选用基于力的非线性梁柱单元模拟梁柱构件。
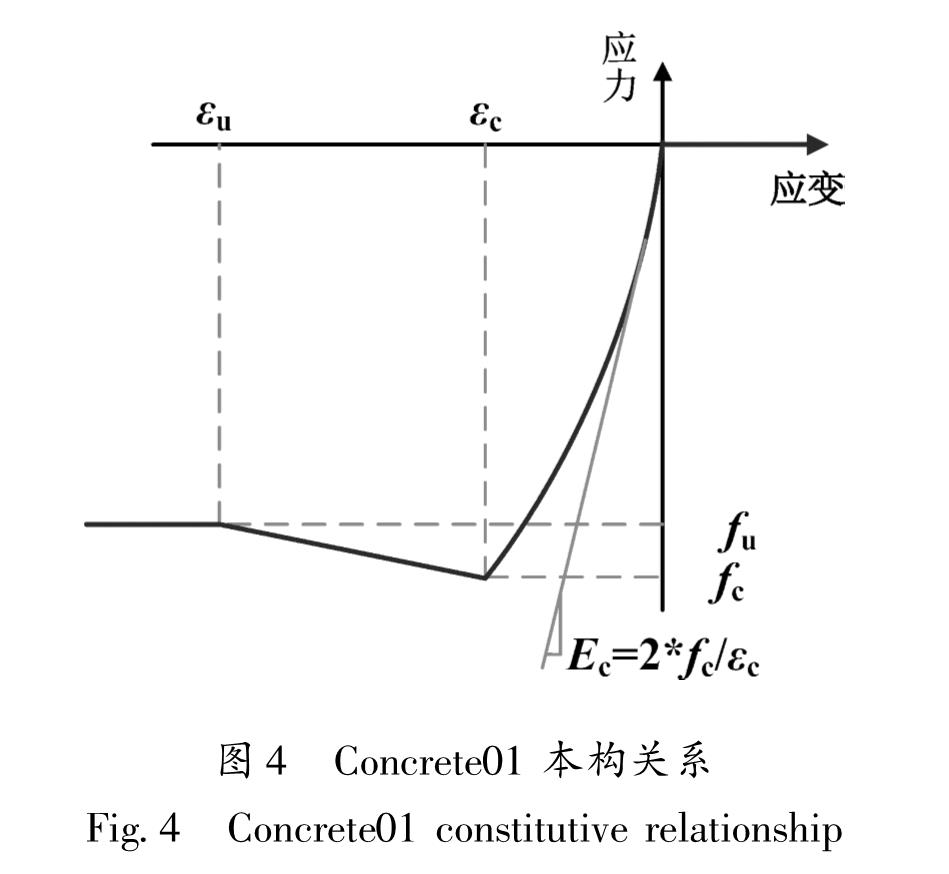
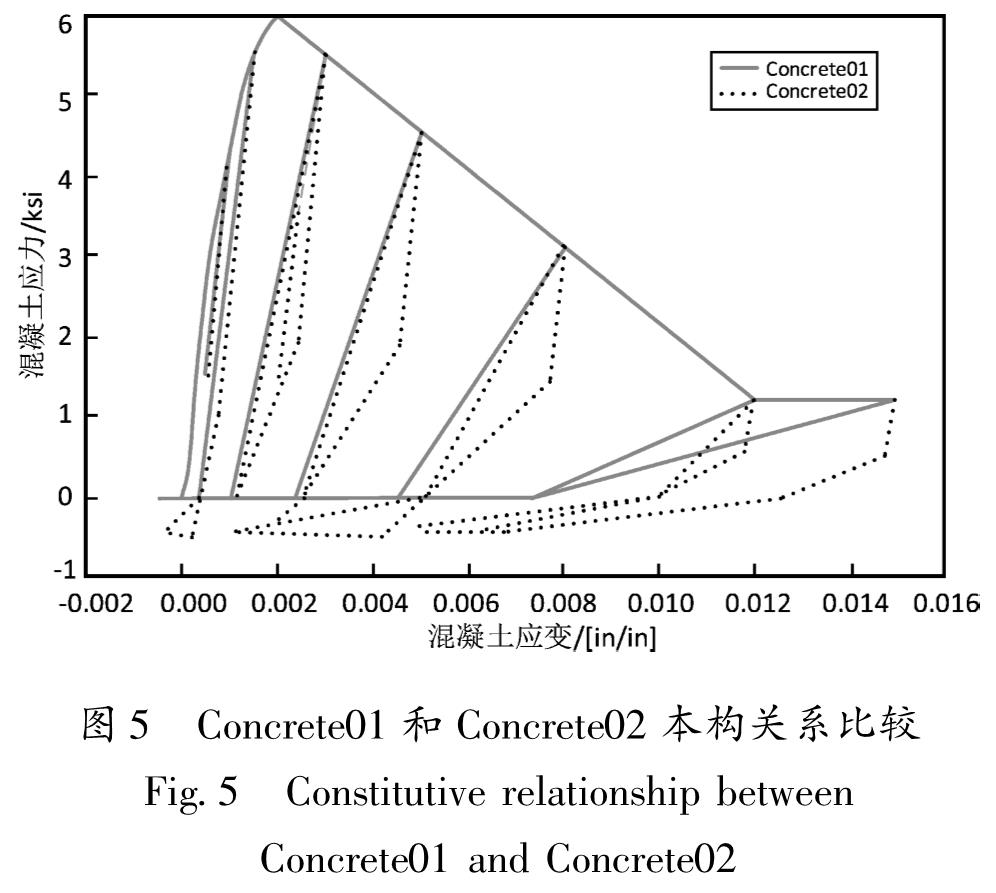
2.3 材料本构选择2.3.1 混凝土本构OpenSEES中有2个常用的混凝土本构模型:Concrete0l Material 和Concrete02 Material,两者的区别主要在于Concrete02可以考虑混凝土的受拉性能。但对于梁柱节点来说,混凝土的抗拉能力基本忽略,故拟采用Concrete0l本构模拟混凝土,如图4所示,Concrete0l和Concrete02的滞回规则如图5所示。计算时对于约束混凝土可按下述方法计算,而对于非约束的保护层混凝土仅需将体积配箍率取为0。
图4 Concrete01 本构关系
Fig.4 Concrete01 constitutive relationship
图5 Concrete01和Concrete02本构关系比较
Fig.5 Constitutive relationship between Concrete01 and Concrete02混凝土本构方程及相关参数的计算方法如下文所示。
受压曲线段方程为:
σc=kfc'[(2εc)/(0.002k)-((εc)/(0.002k))2](εc≤0.002k)(1)
线性软化段方程为:
σc=kfc'[1-Zm(εc-0.002k)]≥0.2kfc'(εc≤0.002k)(2)
箍筋约束对混凝土受压强度的提高系数为:
k=1+(ρsfyh)/(fc')(3)
受压下降段斜率为:
Zm=(0.5)/((3+0.29fc')/(145fc'+3/4 ρs((h')/(sh))1/2-0.002k))(4)
对于约束混凝土,其峰值点应变0.002 k所对应的强度为素混凝土乘以k受约束混凝土的极限应变为:
εu=(0.8)/(zm)+0.002k>0.004+0.9ρs[(fyh)/(300)](5)
约束混凝土受拉强度为:
fct=0.25(fc')1/2<kfc'[1-Zm(εc-0.002k)](6)
式中:εc为混凝土的压应变; σc为混凝土压应变εc对应的压应力; ρs为体积配箍率; fyh为箍筋的屈服强度(MPa); fc'为混凝土的圆柱体抗压强度(MPa); h'为核心区混凝土宽度从箍筋外边缘算起(mm); sh为箍筋间距(mm)。
对于循环往复荷载作用下的混凝土构件,还需要模拟混凝土构件的滞回规则。非约束混凝土压碎即退出工作,一般受压应变εu超过0.04,应力值设为0。
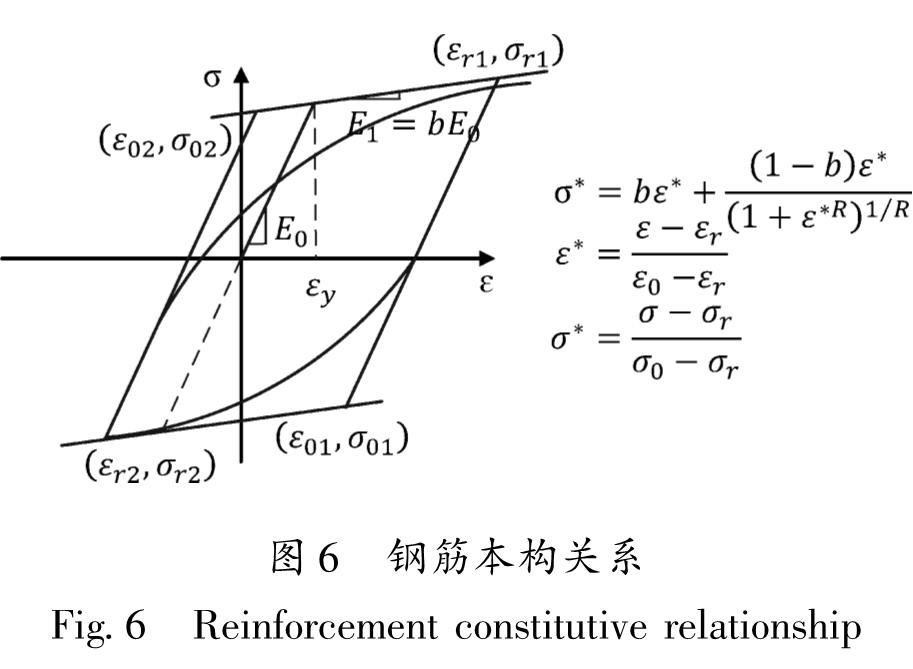
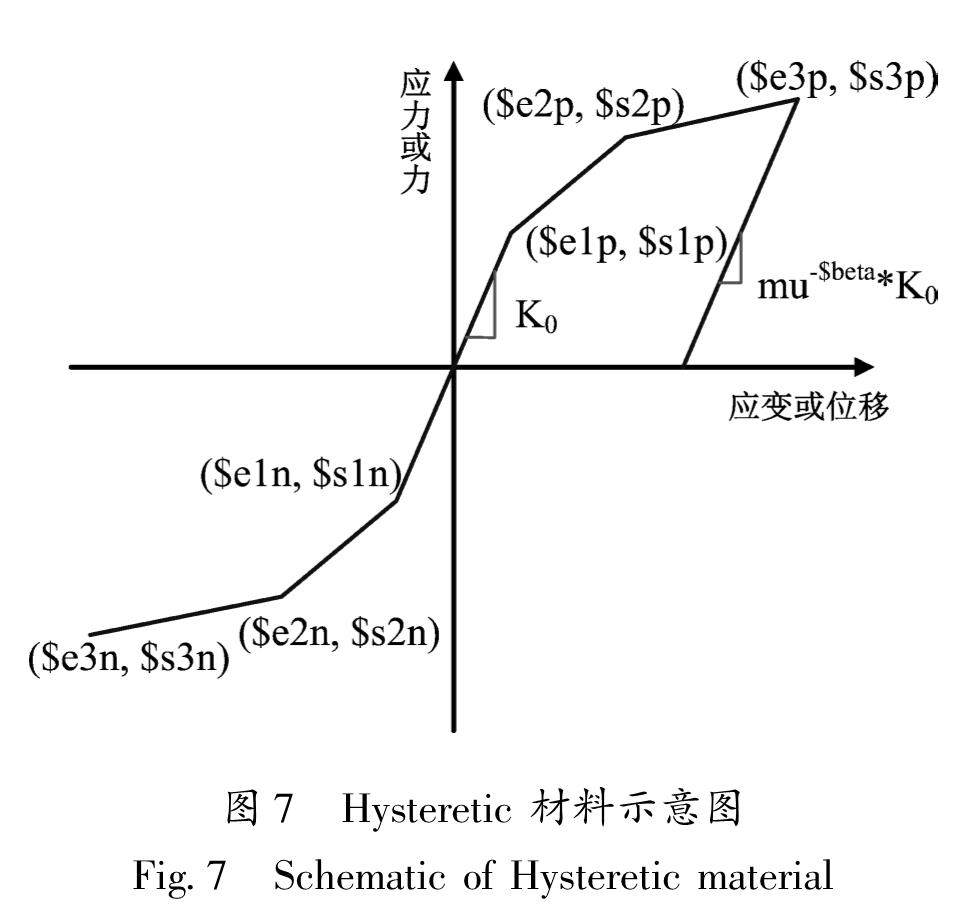
2.3.2 普通钢筋及SMA筋本构关系普通钢筋选用Stee102模型,如图6所示,最初由Menegotto(1973)提出,又经过Filippou等(1983)修正,其骨架曲线为双折线形。该模型能考虑各向同性应变硬化影响,同时也能够较好地反映Bauschinger效应。采用Hysteretic Material来模拟SMA筋的应力-应变关系,认为超弹性SMA是一种单轴双线性滞回材料,正向和反向加载各有3个特征点,通过设置这些参数可以较为准确地模拟出SMA筋良好的滞回耗能和变形可恢复的性能,如图7所示。
图6 钢筋本构关系
Fig.6 Reinforcement constitutive relationship
图7 Hysteretic 材料示意图
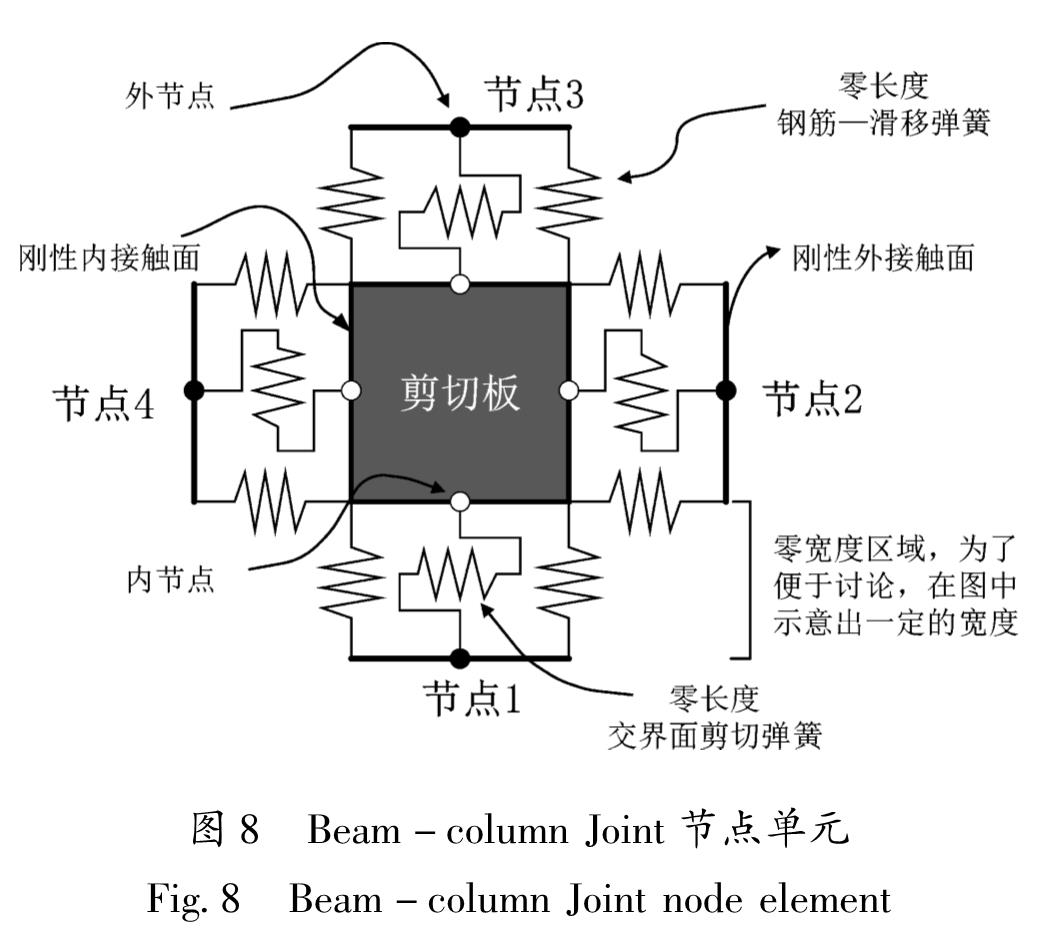
Fig.7 Schematic of Hysteretic material2.4 梁柱节点单元选择选用由Lowes和Altootash(2003)提出,并由Mitra(2007)改进,基于OpenSEES开发的一种二维宏观柔性节点模型,如图8所示。吴健秋(2007)阐述了关于节点内部变形分量与荷载分量,节点单元内部平衡原理等问题。
该模型中的3种组成元件可分别模拟节点的3种主要的破坏机制:一个核心区剪切板元件来模拟由节点核心区混凝土剪切变形引起的节点的刚度和强度退化; 8个零长度的钢筋滑移弹簧元件来模拟贯穿节点核心区的梁、柱纵向钢筋的锚固不足引起的梁柱节点的刚度和强度退化; 4个节点区与梁柱单元交界面的零宽度剪切弹簧元件来模拟地震作用下交界面处开裂造成的剪力传递能力退化。这3种元件协同工作来模拟地震作用下节点的非线性受力特性,故精确定义这3个元件的参数对精细化建模的结果有直接影响。
图8 Beam-column Joint节点单元
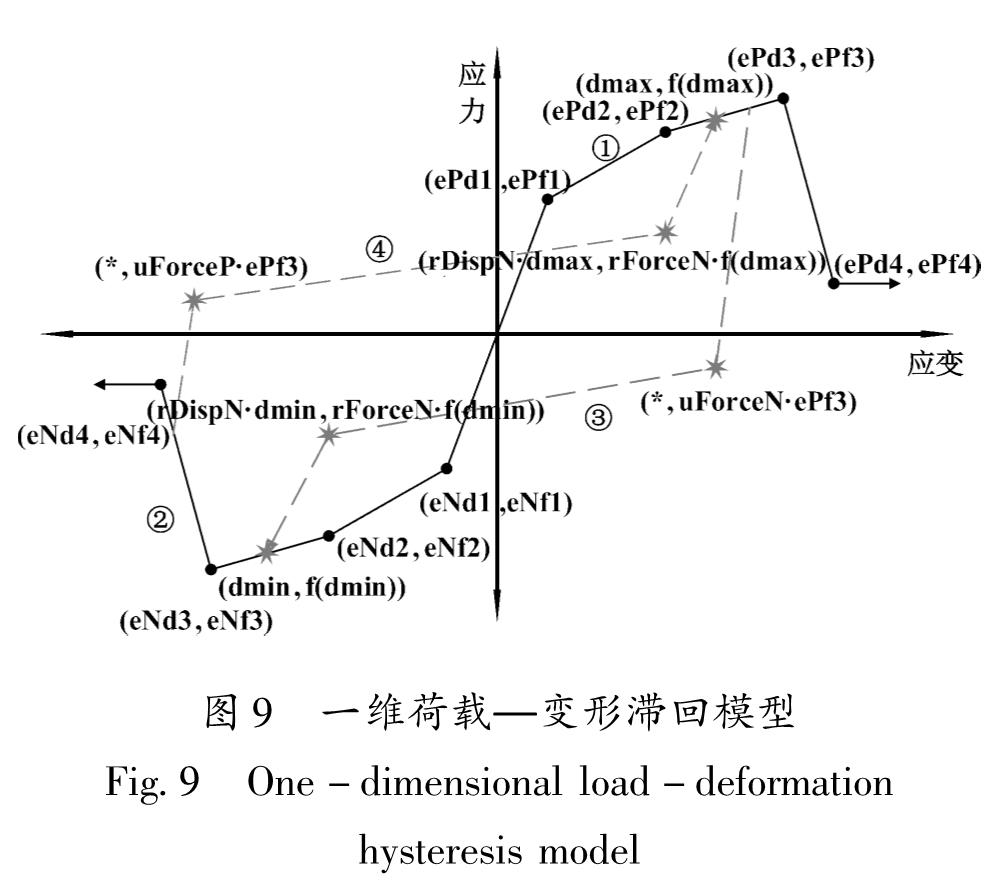
Fig.8 Beam-column Joint node element2.4.1 核心区剪切板元件参数确定选用OpenSEES中的一维荷载—变形滞回模型(Pinching4)来模拟节点剪切板的剪切应力应变关系和钢筋与混凝土之间的粘结滑移,实现节点的荷载—位移曲线明显的捏缩特性,如图9所示。
Pinching4命令中16个参数($ePf1～$eNd4)定义单调加载下多线型骨架包络曲线(图9中①和②所示)的8个特征点(Lowes,Altoontash,2003),基于Vecchio和Collins(1986)提出的修正压力场(MCFT)理论,并参考吴健秋(2007)关于剪切块剪应力—剪应变骨架骨架参数定义研究定参。
Pinching4命令中6个参数($rDispP～$uForceN)定义循环加载下三线型再加载—卸载路径(图9中③和④所示)的正负方向上起点,采用节点单元开发者Mitra(2007)在其博士论文中给出的建议值。
Pinching4命令中15个参数($gKl～$gFLim),每5个1组,形成3组损伤计算参数,分别定义卸载刚度的退化、再加载刚度的退化和强度的退化的3个损伤准则,在描述剪切块在滞回加载下的退化特征时,采用Park和Ang(1985)提出的广义破坏准则理论。
对强度和刚度退化参数的取值不做过多研究,直接采用Mitra(2007)在其博士论文中给出的建议值。
图9 一维荷载—变形滞回模型
Fig.9 One-dimensional load-deformation hysteresis model2.4.2 钢筋滑移元件定参选用Barslip Material来模拟钢筋滑移元件,该模型由Eligehausen等(1983)和Hawkins等(1982)提出,能够较好地模拟通过节点区水平和竖向钢筋的分布粘结力传入节点核心区引起的节点核心区梁、柱纵筋粘结滑移、锚固失效的现象(Shima et al,1987; Viawanthanatepa et al,1979)。
钢筋滑移元件能考虑混凝土强度、纵筋材料特性(屈服强度、极限强度、弹性模量、硬化率和钢筋直径)、节点截面尺寸和锚固强弱程度(强或弱)对钢筋应力—滑移的影响,进而分析对整个节点性能的影响。
2.4.3 交界面剪切弹簧元件定参现浇梁、柱与节点核心区交界面的抗剪刚度较大,假定该交界面之间为刚性连接,故交界面剪切弹簧元件可选用弹性模量无限大的线弹性材料来模拟。
计算模型的边界条件的设置及荷载施加的方式与试验情况一致。
