基金项目:地震科技星火计划项目(XH18044Y)、震情跟踪定向工作任务(2020010128)和国家自然基金项目(41574059)联合资助.
(1.中国科学与技术大学 地球和空间科学学院,安徽 合肥 230026; 2.云南省地震局,云南 昆明 650224; 3.南方科技大学 地球与空间科学系,广东 深圳 518055)
(1.School of Earth and Space Sciences,University of Science and Technology of China,Hefei 230026,Anhui,China)(2.Yunnan Earthquake Agency,Kunming 650224,Yunnan,China)(3.Department of Earth and Space Sciences,Southern University of Science and Technology,Shenzhen 518055,Guangdong,China)
numerical simulation; water level; towing depth; excitation energy; signal amplitude
备注
基金项目:地震科技星火计划项目(XH18044Y)、震情跟踪定向工作任务(2020010128)和国家自然基金项目(41574059)联合资助.
利用有限差分方法,对宾川气枪试验中激发条件对气枪信号振幅的影响进行数值模拟。结果 显示:水库水位对信号振幅的影响呈非线性关系,34 m为气枪激发试验的优势激发水位,能产生最强波形振幅能量,而水位变化的影响随距离缓慢减小。通过拟合给出了不同水位变化幅度与其产生的平均振幅变化率之间的幂函数关系,可为实际波形运用中去除水位变化的影响提供理论参考。波形振幅与激发能量及震源沉放深度呈近线性关系,即激发能量越大,震源沉放深度越深,气枪激发效果越好,越有利于进行远距离深穿透地下结构的探测。
Using the finite different method,we numerically simulate the effect of excitation factors on airgun signal in Binchuan Reservoir.The result shows that the relationship between the change of reservoir water level and airgun signal amplitude is nonlinear,there is an optimum water level range of 30~35 m for airgun firing test which can excitate the strongest energy of signal amplitude,in addition the influence of water level changing attenuates with distances.We also fit the power equation between the amplitude of water level changing and the average amplitude change rate it produced,so that we can use it to provide theoretical reference for removing the effect of water level changing in actual waveform application.The wave amplitude is linear with excitation energy and towing depth,that is the greater the energy and the deeper of the towing,the better the effect of excitation,the more conducive to detect remote and deep penetration underground structure.
引言
水库大容量非调制气枪阵列震源是通过在水中瞬间释放枪体中高压气体产生地震信号,具有激发效果好,可控性、操作性强的优势(Reasenberg,Aki,1974; 陈颙等,2007,2017; 陈颙,李宜晋,2007; 罗桂纯等,2006),是进行区域尺度深部结构探测的理想人工震源(Chen et al,2008; 林建民等,2008; 王伟涛等,2017)。利用气枪震源高度重复性及具有较高能量的特性可以动态监测区域波速变化(王宝善等,2011; Wang et al,2020),对地震预测研究具有重要意义。2012年云南宾川建成了全球首个陆地激发气枪震源发射台,随后在新疆呼图壁、甘肃张掖等地也建设了固定式气枪震源发射台,进行连续激发或密集台阵观测试验(王彬等,2016; 魏斌等,2016; 张元生等,2016),还在福建发展了船载式和移动式气枪震源系统,在长江安徽段开展了气枪震源流动激发试验,为区域尺度的地壳结构探测研究提供了有力工具(姚道平等,2016; 徐逸鹤等,2016; 王宝善等,2016)。
在陆地水库中进行气枪震源试验时,由于水深较浅、水域面积有限,气枪震源激发过程实为气枪源与浅水区相互作用的过程,共同构成浅水区气枪震源激发系统。近年来,很多研究表明,在浅水环境中激发产生的地震波会受到气枪源本身配置(气枪的容量、激发压力等)以及外部激发环境的影响,如气枪所在水库的水位变化、气枪震源的沉放深度等(Chen et al,2014)。Dragoset(2000)通过研究气枪震源激发信号特征,给出了激发信号与气枪容量、工作压力和沉放深度等激发参数之间的具体关系及经验公式; 唐杰等(2009)和林建民等(2010)均对2007年9月上关湖水库气枪激发试验中水听器记录的近场波形数据进行模拟和分析,发现气枪震源沉放深度、工作压力等不同激发条件对压力脉冲和气泡脉冲存在一定影响; 陈蒙(2014)基于宾川多次气枪试验,分析了不同激发压力、沉放深度和水库水位等因素对宾川气枪激发地震波的影响,发现水库水位变化的影响远远大于震源沉放深度的影响; 孙楠等(2017),Sun和Sun(2019)用雷克子波震源时间进行数值模拟,发现水库水位深度对波形振幅的影响是非线性的,激发能量和沉放深度与波形振幅近似呈线性关系; 胡久鹏等(2017)模拟不同水体形状对气枪激发波形的影响,发现水体形状对高频信号成分影响较强,对低频信号成分影响较弱。以上研究主要借助数值模拟方法,分析陆地水库气枪震源试验中不同激发条件的影响,可以此作为一种辅助手段为实际波形的分析应用提供依据。
水库激发气枪信号中,最大振幅是气枪信号的一个重要参数。在研究气枪震源对环境的破坏作用以及对水中生物的影响时,尤其是当气枪在浅水环境下激发时,对气枪激发信号最大振幅的研究具有重要的意义(林建民等,2010)。本文主要模拟有限水体中水位、激发能量、震源沉放深度等激发条件,对气枪信号最大振幅的影响特征,从而为水库激发气枪震源工作研究提供理论依据,这对于进一步深化气枪震源的应用意义重大。
1 数值模拟激发条件的影响
2 分析讨论
数值模拟结果显示,在近场面波传播速度小于体波传播速度,使模拟波形中由振幅更大的面波占主导,随着波形传播距离的增加,体波与面波到时差逐渐增大,P波和S波震相逐渐清晰; 在相对较远距离上的波形则会由P波和S波为主导。对于水位变化的模拟,当水位为13~40 m时,对振幅的影响呈非线性状态的; 水位为13~15 m时,振幅随水位增加而减小,这可能与其传播路径有关,在水中消耗能量更多,使得振幅变小; 当水位为15~34 m时,振幅随水位变化总体呈正相关,这是由于随着水库水位的增加,水对水库底的压强增大,水库底部面积也增大,使得水库底部所承受压力增大,而气枪信号的振幅与水库底部压力成正比,因此水位增加会引起气枪信号的振幅增大; 在水位为34 m时,达到最大波形振幅,该段水位就是气枪激发试验的优势激发水位; 当水位为20~40 m时,水面宽度不变,对应的Gaussian形状库体的边界会有相应的倾角变化,对于库体边界倾角变化所带来的影响,会在之后的工作中进行深入地分析。
在波形向外传播的过程中,由水位变化引起的振幅波动缓慢减小,表明水体效应的影响随距离逐渐减小。通过具体模拟不同幅度的水位变化,发现水体振荡会产生驻波效应,这种驻波使得波形振幅受水位的变化呈周期振荡形式,而其影响范围约为10倍水面宽度的距离,超过这个距离后,驻波效应逐渐消失,振幅变化逐渐减小。水位变化对波形水平向影响大于垂直向,可能是因为水平向的能量主要通过P波转换而来,而垂直向分量的能量主要通过S波转换而来,这与由图3得出的水平向传播速度更快,可能其P波转换波所占比重更大相吻合。因此,水平向受水位变化的影响更大,而垂直向相对更小。通过拟合不同水位变化幅度与其产生的平均振幅变化率,得到二者之间的幂函数关系,由此可以为实际波形运用中去除水位影响提供参考和理论依据。
水库大容量气枪试验中,气枪总容量一定时,激发压力与激发能量呈正比,模拟激发能量变化对波形振幅的影响与陈蒙(2014)关于宾川气枪信号特征的结论一致,激发能量与波形振幅成线性关系。当气枪工作压力增加时,激发产生的气泡内的压力增大,造成对应的气泡半径及气泡壁运动速度也相对较大,使得对应的气泡脉冲的振幅变大。
数值模拟震源沉放深度的变化对波场传播特征的影响结果显示:信号最大振幅与震源沉放深度总体呈线性递增的关系,这可能是因为气枪沉放深度越深、静水压越大、气泡激发和振荡过程中与水体的耦合越好,因此气枪激发声波能量越有效,使得接收的波形振幅越大。而震源沉放深度的影响效应随距离的增加在缓慢减小。
3 结论
水库大容量气枪激发震源信号对水位、激发能量和震源沉放深度等激发条件存在一定的依赖。通过本文数值模拟分析,得到以下结论:水库激发气枪震源试验中,水库水位对振幅的影响呈非线性状态,15~34 m时,振幅随水位变化总体呈正相关; 34 m为气枪激发试验的优势激发水位,能产生最大波形振幅能量。水位变化引起的振幅波动随距离的增加缓慢减小,在震中距为水面宽度10倍的范围内受水体振荡产生的驻波影响,振幅呈周期振荡形式变化,超过这个距离后驻波效应逐渐减小,且水位变化对水平向振幅的影响要大于垂直向。通过拟合不同水位变化幅度与其产生的平均振幅变化率,得到二者之间存在幂函数关系。因此,可以在实际波形运用中,参考水位变化幅度产生的振幅变化率,去除或尽可能减小水位变化带来的影响。波形振幅与激发能量及震源沉放深度呈近线性关系,即激发能量越大,震源沉放深度越深,气枪激发效果越好,越有利于进行远距离深穿透地下结构的探测。
本文通过数值模拟得到不同激发条件对水库气枪源信号的影响特征,能够为解释实际试验结论提供一定的参考意义,但该模拟中仍受到计算条件及成本的限制,仅采用了二维介质模型及参考震源时间函数进行计算,尚不能达到实际气枪激发试验中所呈现的激发条件的复杂精细程度,与实际气枪信号特征还存在一些定量的差异,因此,需要更为精细的模型介质、更精确的震源时间函数以及更优的计算方法进行模拟,从而为实际气枪震源信号的应用研究提供可靠的基础。
有限差分方法作为一种能够模拟地震波在复杂介质中传播的数值计算方法,将区域网格化,把网格点上的时、空数值用差商近似为偏微分项,将连续的偏微分方程转化成离散格点上值的差分方程。该方法具有简单直接、计算效率高的优点,能比较完善地解决地震勘探、强地面运动预测等研究中地球内部任意非均匀介质问题,准确高效地模拟符合真实地质条件的复杂地形的地震波传播(Zhang,Chen,2006; Sun et al,2017)。本文将利用有限差分方法数值模拟激发条件对气枪信号振幅的影响。
本文有限差分法采用同位网格的DRP/opt MacCormack差分格式,将MacCormack格式和DRP(Dispersion Relation Preserving)格式相结合,需要4个网格点的长度,具有4阶空间精度且网格分辨率高,通过前后各3个相邻点差分引入高频耗散,不仅可以消除奇偶失联现象,还可以获得中心差分的截断误差精度,从而正确地计算各项异性介质中地震波的传播过程(MacCormack,1969; Hixon,1997; Zhang et al,2012; Sun et al,2016),再结合体贴网格技术可以准确描述固液界面的起伏。在计算区域边界附近的网格点时,由于没有足够的相邻的计算格点,采用4阶空间精度的紧致MacCormack差分格式,结合牵引力镜像法(Zhang,Chen,2006)实施自由表面边界条件,在边界处计算应力分量和速度分量的空间导数。在计算区域的左右边界附近设定一定宽度的吸收层,使用简单稳定易于实现的指数衰减吸收层,在吸收层内将地震波场和波场衰减项相乘(Cerjan et al,1985),从而达到吸收波场的目的。
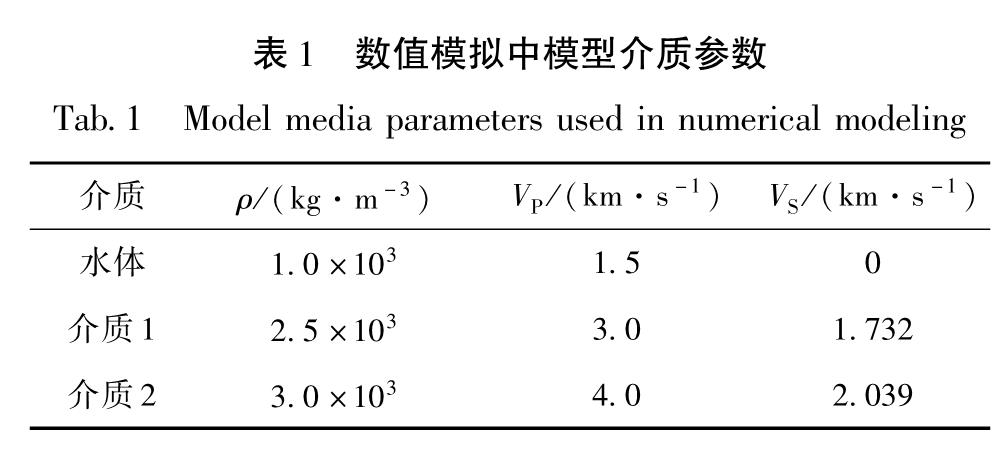
1.1 介质模型数值模拟中,研究区域为4 km×0.6 km大小的层状半空间介质(图1),水体位于距左侧边界0.25 km处的第一层,水体形状使用Gaussian函数z=b0exp[-(x-x0)2/a20]获得,水体的第二、三层均为固体介质。模拟中只考虑了弹性情况的几何扩散的衰减,未考虑非弹性的衰减,具体介质参数配置见表1。
将震源沉放于水体中,在距离水面10 m处,模拟水库中气枪震源沉放方式。在计算区域的地表面(0.35~4.0 km)设置一条测线,共放置92个检波器,用于研究激发条件变化对波形振幅的影响程度范围。在区域边界使用10层的指数衰减吸收层来吸收向外传播的波(图1)。
模拟时首先对区域进行网格化,网格大小设置为1 m×1 m,共2.4×106个网格,时间步长设置为0.1 ms,能够满足二维DRP/opt MacCormack格式的稳定性条件要求为:
t<0.93×h/Cmax(1)
式中:h是空间网格间隔; Cmax是介质的最大波速; 模拟时间长度总共为3 s,并行计算共占用60个核。对于模拟中震源时间函数的设置,考虑到水库作为有限水体,在其内部激发气枪信号后会产生气泡振荡,而气泡振荡的传播可能会受到有限水体边界的影响,使得向外传播的可能为气泡、水体与水库边界的耦合源,其震源时间函数尚不能明确。而在宾川气枪震源波形数据应用中,通常用发射台附近的参考台波形近似成源,进行反褶积运算,以此来消除由震源变化引起的
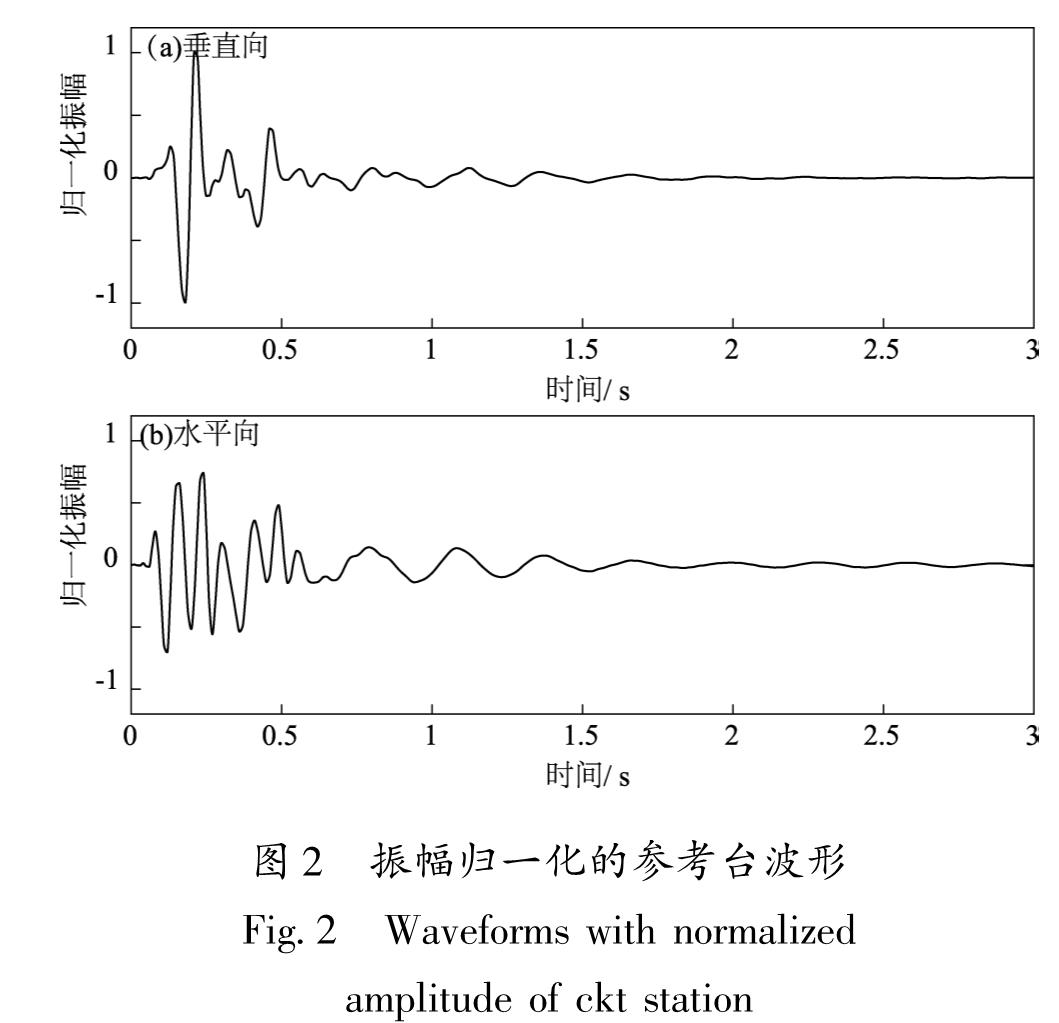
影响(翟秋实等,2016)。因此,本文选取宾川气枪发射台附近的参考台波形,用其垂直向最大振幅进行归一化后的波形形态,近似成震源时间函数进行数值模拟计算,其中归一化后的垂直向最大振幅约为水平向最大振幅的1.4倍(图2)。
1.2 数值模拟结果利用有限差分方法,模拟得到有限水体中不同水位、激发能量、震源沉放深度等激发条件时的波形信号,分析其最大振幅的变化特征,从而探究浅水环境下激发条件的影响。结果分析中,引用波形的最大振幅的相对变化率(以下简称 “振幅变化率”),表征激发条件变化时波形最大振幅的变化。
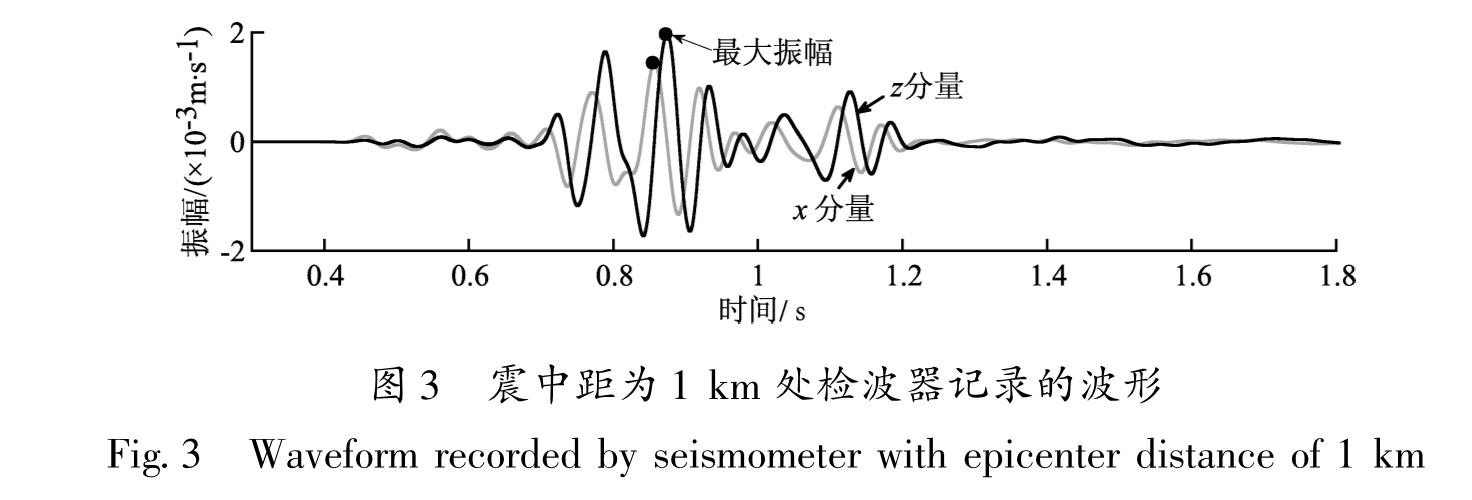
从距离震源1 km的检波器记录的波形可以看出(图3),x分量体波和面波的到时均比z分量的早,即在水平向传播速度更快。x分量的P波振幅比z分量的要大,而z分量的S波和面波振幅则更大。最大振幅分布在面波段,z分量的最大振幅约为x分量的1.4倍。从所有检波器接收的波形随距离的分布图(图4)可以看出,在不同距离均可以看到非常明显的面波,最大振幅分布在面波段,z分量的振幅比x分量大。
1.2.1 水体水位宾川气枪试验选取大银甸水库作为激发水体,其水位有显著的季节性变化(王彬等,2016)。
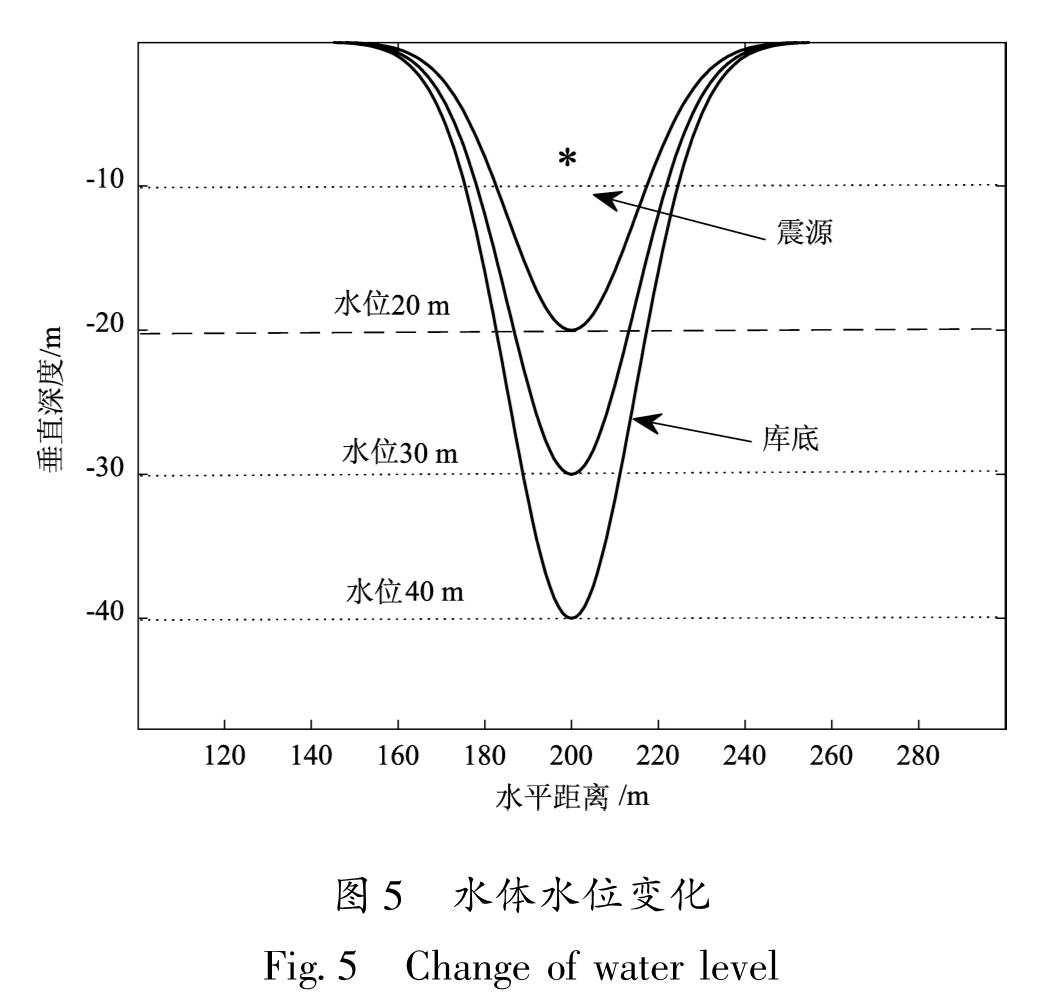
数值模拟中,水体形状使用Gaussian函数获得,水平面与地表面持平,保持震源到水面的距离为10 m不变,保持水平面宽度200 m不变,通过增加水库的深度引起水位的变化(图5)。
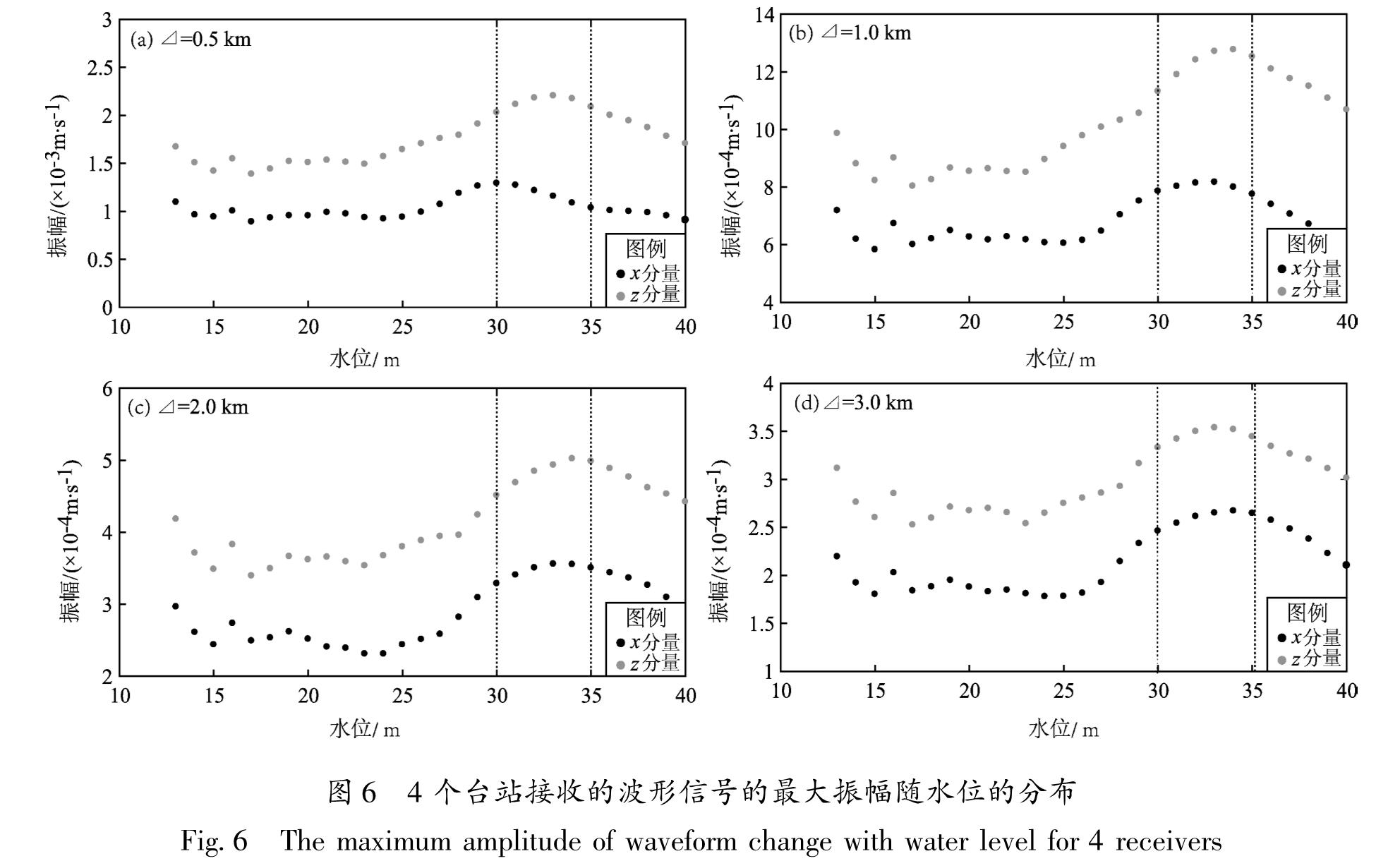
数值模拟水位范围为13~40 m,分别选取到水库右侧的距离Δ=0.5,1.0,2.0,3.0 km的4个接收台站,模拟波形最大振幅随水位的变化,
如图6所示,4个台站接收到的波形最大振幅随水位增加的变化均是非线性的,水平向和垂直向变化形态大致相同,垂直向最大振幅约为水平向最大振幅的1.4倍,这应该与所选取的震源时间函数的振幅最大值有关。Δ的增加,表示台站和水库距离变远,从图6纵坐标的振幅范围可以发现,最大振幅的整体变化形态减小,表明随着震中距增大,水位变化的影响逐渐减小。
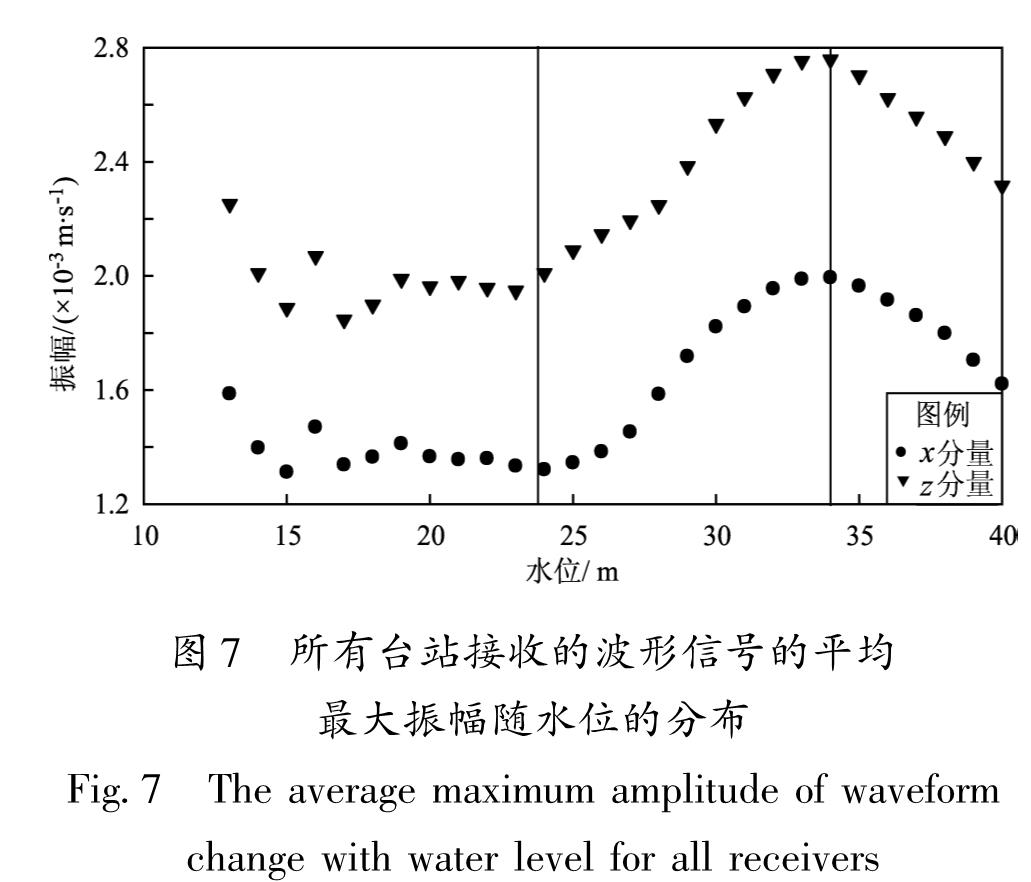
由于各个台最大振幅随水位的变化形态大致相同,对模拟得到的90个台的波形最大振幅求平均,得到不同水位对应的平静最大振幅的变化特征(图7)。从图7可知,在水位约为13~15 m时,振幅随水位增加而减小,呈负相关; 水位为17~19 m时,振幅随水位增加而增加,呈正相关; 水位为20~24 m时,呈负相关; 水位为25~34 m时,呈正相关; 水位为35~40 m时,呈负相关,水位约为33 m时波形振幅最大,即振幅激发能量最强,为优势激发水位。
当水位增加1 m时(图8),不同距离的波形的最大振幅变化显示,在震中距小于2 km范围内振幅变化率呈周期振荡,随着震中距的继续增加,周期振荡形式逐渐消失。这种周期性振荡可能与
图6 4个台站接收的波形信号的最大振幅随水位的分布
Fig.6 The maximum amplitude of waveform change with water level for 4 receivers图7 所有台站接收的波形信号的平均最大振幅随水位的分布
Fig.7 The average maximum amplitude of waveform change with water level for all receivers水体振荡产生的驻波向外传播的影响有关,随着震中距的增加,驻波效应也逐渐消失。水平分量的变化稍大于垂直分量的变化,表明水位变化对水平向的影响大于垂直向。水位增加1~7 m时,90个台站接收的波形振幅变化率显示(图9):水位变化幅度越大,波形振幅的变化率越大。在2 km范围内,振幅变化率随距离呈周期性振荡,也就是驻波振荡效应的影响范围约为水面宽度10倍的距离,也使得在某些距离处(如波谷处)接收到的波形受水位变化的影响特别小。
图8 水位增加1 m时振幅变化率随距离的分布
Fig.8 Distribution of amplitude changing rate with distance with water level increasing of 1 m图9 水位不同变化幅度引起的振幅变化率随距离的分布
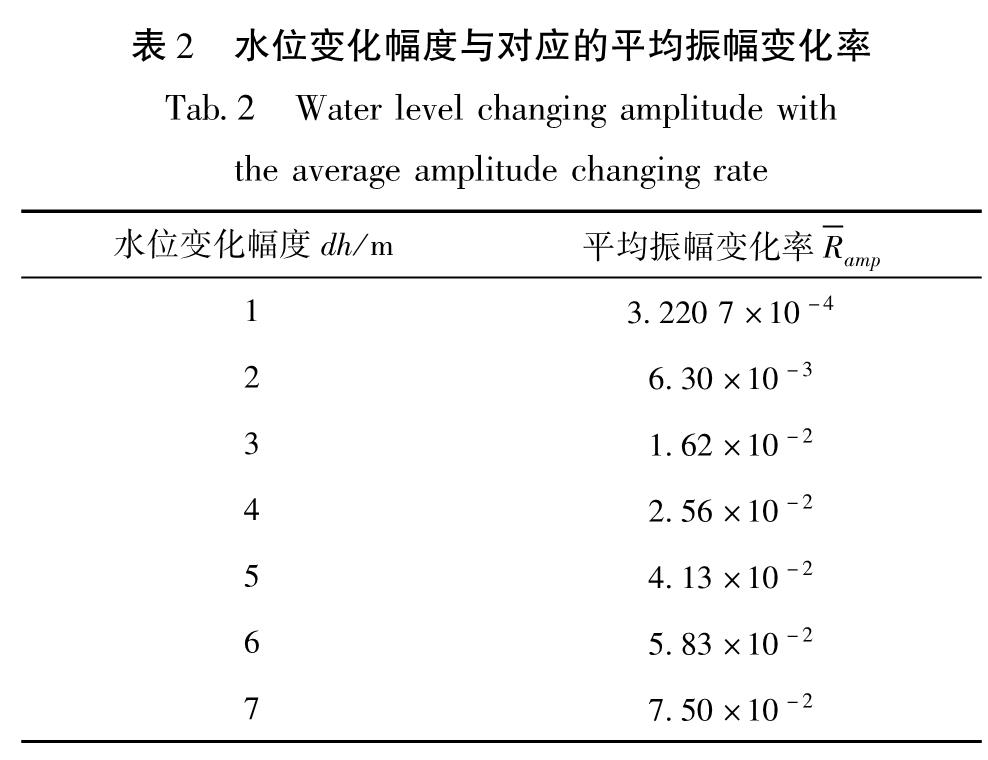
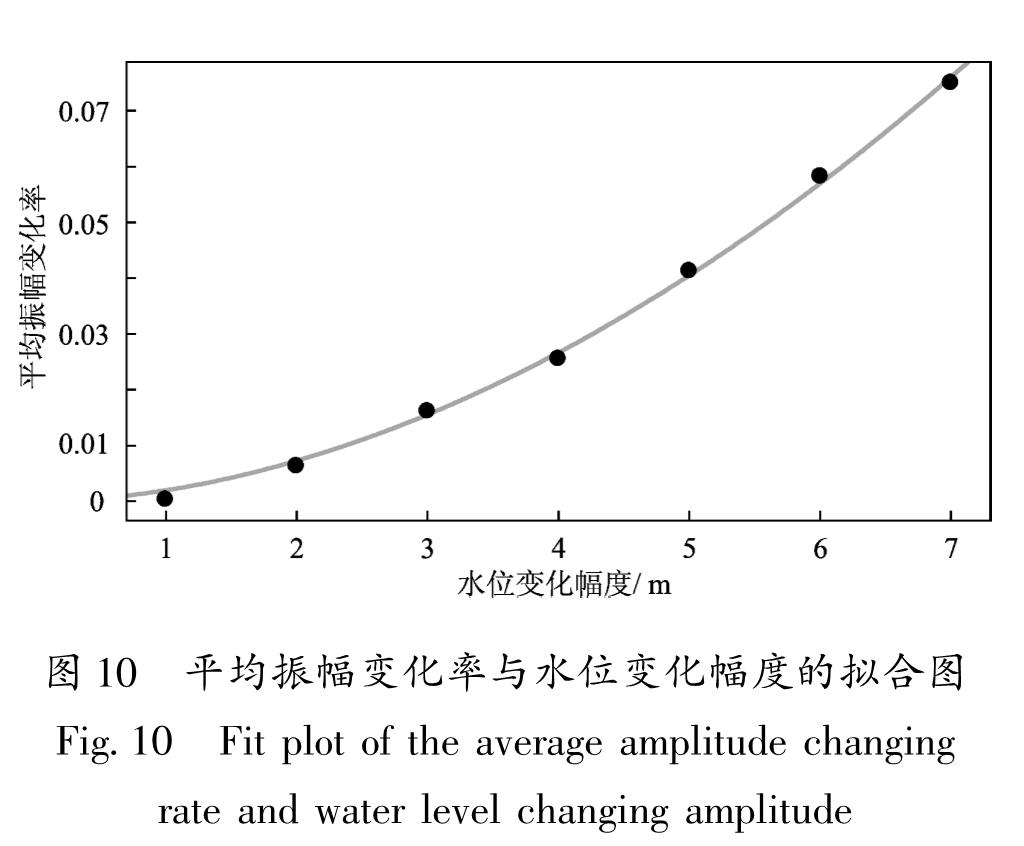
Fig.9 Amplitude changing rate induced by different water level changing amplitude with distance将水位变化分别为1~7 m时所有台站的振幅变化率进行平均,得到由水位变化引起的平均振幅变化率幅度(表2)。由表2可知,当水位增加1 m时,引起振幅变化率约为3.220 7×10-4。拟合水位变化幅度(dh)与平均振幅变化率(R^-amp),得到:
R^-amp=a·dhb(2)
式中:a=1.985×10-3; b=1.874; 拟合函数确定系数Rsquare=0.998 1,非常接近于1,表明拟合效果非常好,平均振幅变化率与水位变化幅度呈幂函数关系(图 10)。
1.2.2 激发能量在大容量气枪试验中,气枪震源的激发能量来源于高压气体,可通过Ronen(2002)方程从高压气体的容量和压力计算得出,其具体关系为:
E=P·Vln(P/P0)(3)
式中:E为气枪激发能量; V为气枪总容量; P为激发压力; P0为环境压力,一般是1个大气压。当V一定时,E与P成正比,因此可以通过模拟激发能量变化对波形振幅的影响来反映激发压力的影响。
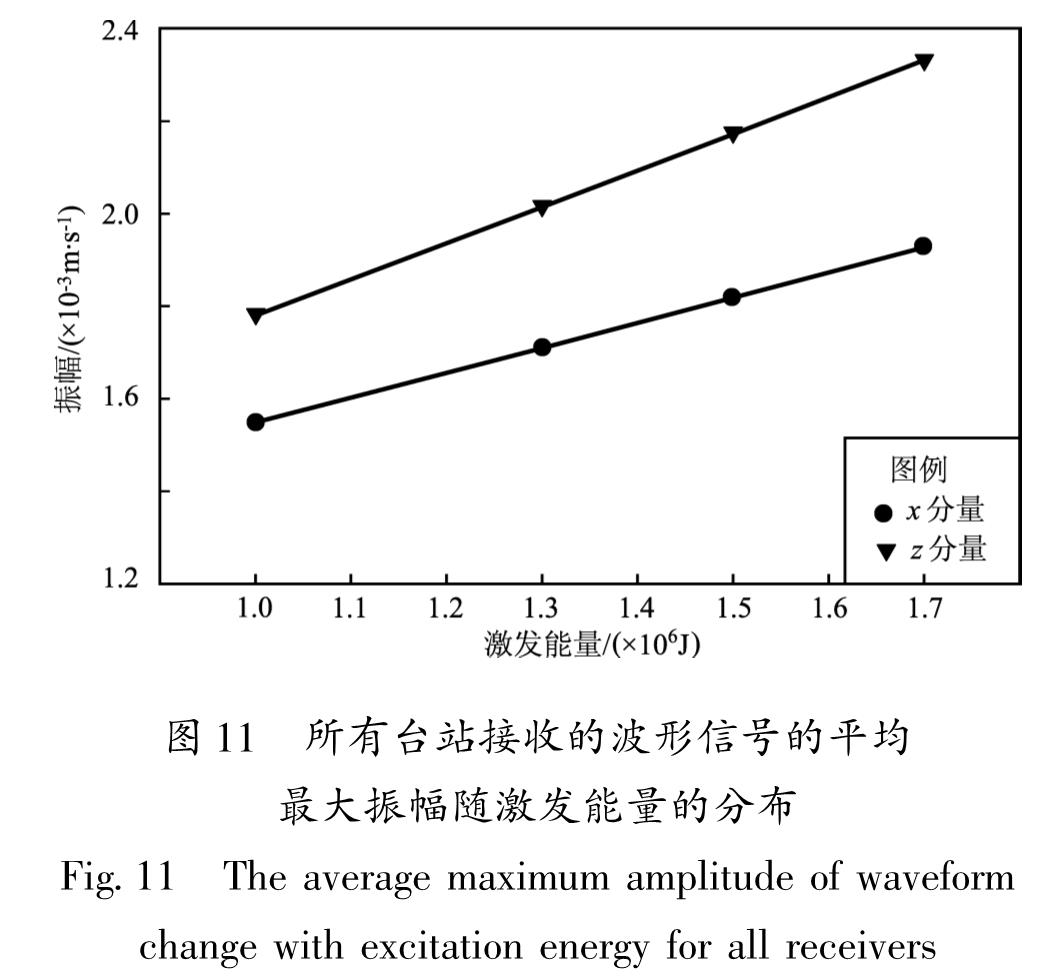
在其它激发条件不变的情况下,激发能量分别取1.0×106,1.3×106,1.5×106,1.7×106 J,根据能量震级转换,激发能量为1.3×106 J,相当于大约0.8级地震的能量。模拟结果(图 11)显示,信号振幅随气枪激发能量的增加而增加,二者呈近线性关系,且激发能量引起的振幅变化不受距离的影响。
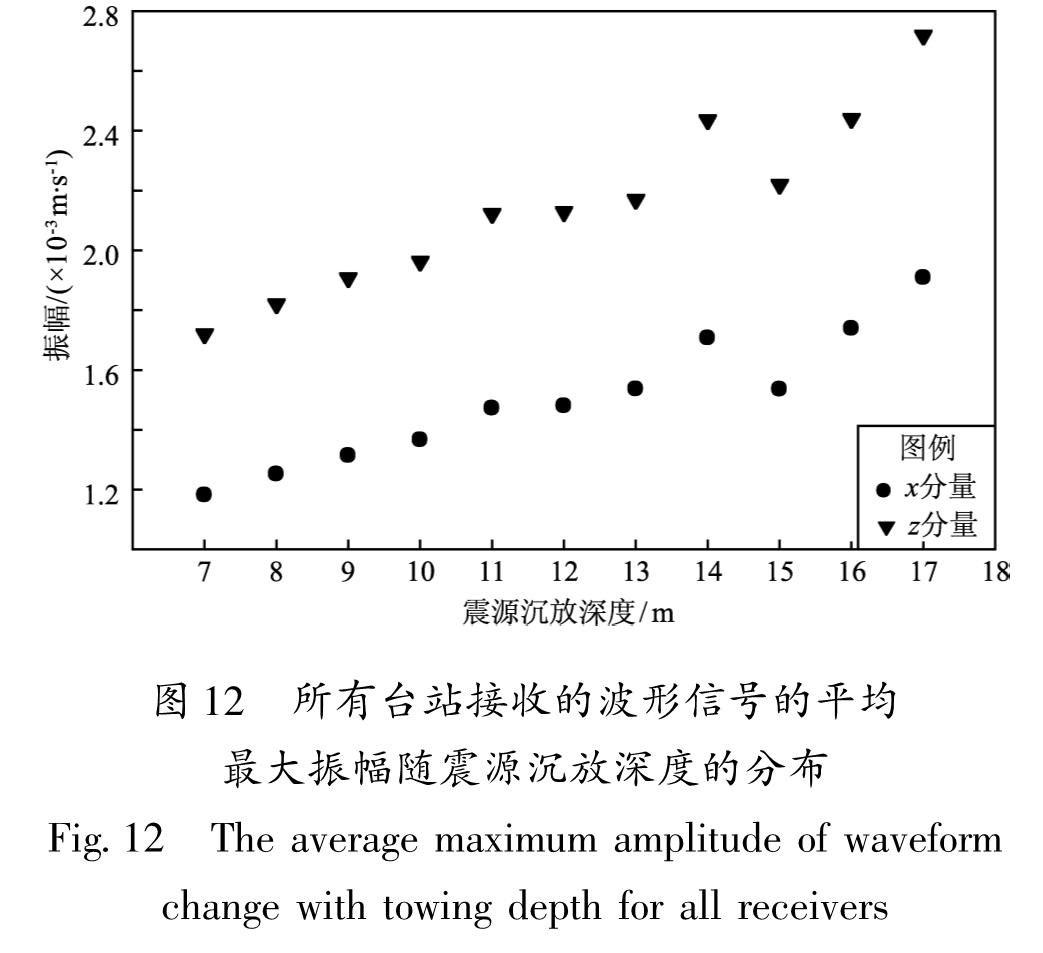
1.2.3 震源沉放深度气枪阵列的沉放深度决定了气枪阵列与水库底部和水面的距离,会对气枪地震信号产生影响。为了研究沉放深度对有限水体中气枪震源信号的影响,本文进行了不同沉放深度的情况模拟。激发条件一致时,固定水体水位为20 m,震源分别沉放于7~17 m处,结果显示,振幅随沉放深度增大而增大,且垂直向振幅大于水平向振幅(图 12)。
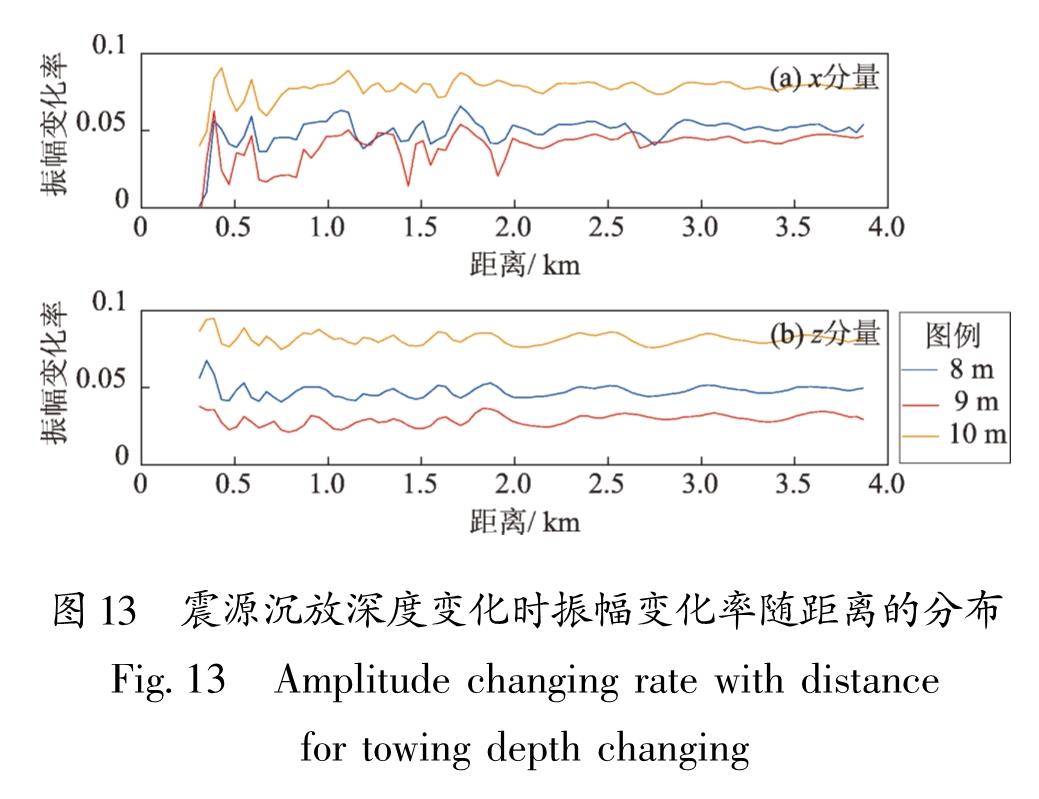
为了分析由震源沉放深度引起的振幅变化,选取震源沉放深度范围为8~10 m,改变其沉放深度,得到振幅变化率随距离的分布如图 13所示:水平向的变化幅度大于垂直向变化幅度,距离为2.0 km范围内的信号振幅变化率呈周期性振荡,距离大于2.0 km的信号振幅变化率则变化幅度较小。
图 12 所有台站接收的波形信号的平均最大振幅随震源沉放深度的分布
Fig.12 The average maximum amplitude of waveform change with towing depth for all receivers- 陈蒙.2014.利用水库大容量非调制气枪阵列进行区域尺度地下结构探测和监测[D].北京:中国地震局地球物理研究所.
- 陈颙,李宜晋.2007.地震波雷达研究展望:用人工震源探测大陆地壳结构[J].中国科学技术大学学报,37(8):813-819.
- 陈颙,王宝善,姚华建.2017.大陆地壳结构的气枪震源探测及其应用[J].中国科学:地球科学,47(10):1153-1165.
- 陈颙,张先康,丘学林,等.2007.陆地人工激发地震波的一种新方法[J].科学通报,52:1317-1321.
- 胡久鹏,王宝善,陈颙.2017.水体形状对陆地气枪激发信号的影响[J].地震研究,40(4):543-549.
- 林建民,王宝善,葛洪魁,等.2008.大容量气枪震源特征及地震波传播的震相分析[J].地球物理学报,51(1):206-212.
- 林建民,王宝善,葛洪魁,等.2010.大容量气枪震源子波激发特性分析[J].地球物理学报,53(2):342-349.
- 罗桂纯,王宝善,葛洪魁,等.2006.气枪震源在地球深部结构探测中的应用研究进展[J].地球物理学进展,21(2):400-407.
- 孙楠,孙耀充,庾汕.2017.含有限水体介质中地震波场数值模拟[J].地震研究,40(4):557-564.
- 唐杰,王宝善,葛洪魁,等.2009.大容量气枪震源的实验与模拟研究[J].中国地震,25(1):1-10.
- 王宝善,葛洪魁,王彬,等.2016.利用人工重复震源进行地下介质结构及其变化研究的探索和进展[J].中国地震,32(2):168-179.
- 王宝善,王伟涛,葛洪魁,等.2011.人工震源地下介质变化动态监测[J].地球科学进展,26(3):249-256.
- 王彬,李孝宾,刘自凤,等.2016.宾川地震信号发射台的震源系统、观测系统和观测结果[J].中国地震,32(2):193-201.
- 王伟涛,王宝善,蒋生淼,等.2017.利用气枪震源探测大陆浅部的地震学研究回顾与展望[J].地震研究,40(4):514-523.
- 魏斌,苏金波,王海涛,等.2016.新疆呼图壁人工水体大容量气枪信号发射台性能研究[J].中国地震,32(2):222-230.
- 徐逸鹤,王宝善,王伟涛.2016.利用固定台站分析长江激发气枪信号特征[J].中国地震,32(2):282-295.
- 姚道平,张艺峰,闫培,等.2016.台湾海峡大容量气枪震源海陆联测初探[J].地震学报,38(2):167-178.
- 翟秋实,姚华建,王宝善.2016.气枪震源资料反褶积方法及处理流程研究[J].地震研究,32(2):295-304.
- 张元生,郭晓,秦满忠,等.2016.甘肃祁连山主动源重复探测项目建设及震源重复性分析[J].中国地震,32(2):209-215.
- Cerjan C,Kosloff D,Kosloff R,et al.1985.A nonreflecting boundary condition for discrete acoustic and elastic wave equations[J].Geophysics,50(4):705-708.
- Chen M,Yang W,Wang W,et al.2014.Influencing factors of seismic signals generated by un-tuned large volume airgun array in a land reservoir[J].Earthquake Science, 27(4):365-376.
- Chen Y,Liu L B,Ge H K,et al.2008.Using an airgun array in a Land reservoir as the seismic source for seismotectonic studies in Northern China:experiments and preliminary results[J].Geophysical Prospecting, 56(4):601-612.
- Dragoset B.2000.Introduction to air guns and air-gun arrays[J].The leading Edge,19(8):892-897.
- Hixon R.1997.On Increasing the Accuracy of macCormack scheme for Aeroacoustic Applications[J].AIAA paper:29-39.
- MacCormack R W.1969.The effect of viscosity in hypervelocity impact cratering[J].Journal of Spacecraft and Rockets, 40(5):69-354.
- Reasenberg P A,Aki K.1974.A precises,continuous measurement of seismic velocity for monitoring in situ stress[J].Journal of Geophysical Research, 79(B2):399-406.
- Ronen S.2002.Psi,pascal,bars,and decibels[J].The Leading Edge,21:60-61.
- Sun N,Sun Y C.2019.Numerical simulation of the Binchuan airgun source affected by water body[J].Earthquake Research in China, 2019,33(2):208-219.
- Sun Y C,Zhang W,Xu J K,et al.2017.Numerical simulation of 2-D seismic wave propagation in the presence of a topographic fluid-solid Interface at the sea bottom by the curvilinear grid finite-difference method[J].Geophysical Journal International,210:1721-1738.
- Sun Y,Zhang W,Chen X.2016.Seismic-wave modeling in the presence of surface topography in 2D general anisotropic media by a curvilinear grid finite difference method[J].Bulletin of the Seismological Society of America,106(3):1036-1054.
- Wang B,Yang W,Wang W,et al.2020.Diurnal and semidiurnal P-and S-wave velocity changes measured using an airgun source[J].Journal of Geophysical Research:Solid Earth,125(1)doi:10.102912019JB01828.
- Zhang W,Chen X.2006.Traction image method for irregular free surface boundaries in finite difference seismic wave simulation[J].Geophysical Journal International,167(1):337-353.
- Zhang W,Zhang Z,Chen X.2012.Three-dimensional anisotropic seismic wave modeling in spherical coordinates by a collocated-grid finite-difference method[J].Geophysical Journal International, 188(3):1359-1381.