基金项目:国家自然科学基金(51969019,51468045)、水利部公益性行业科研专项(201401009)和江西省教育厅科技项目(GJJ160703)联合资助.
(1.南昌航空大学 土木建筑学院,江西 南昌 330063; 2.常德职业技术学院 土建系,湖南 常德 415006)
KiK-net台网强震记录; 地震动; 相干函数; 影响因素
(1.Department of Civil Engineering,College of Civil Engineering and Architecture,Nanchang Hangkong University,Nanchang 330063,Jiangxi,China)(2.Department of Civil Engineering,Changde Vocational Technical College,Changde 415006,Hunan,China)
KiK-net strong motion records; ground motion; coherency function; influencing factors
备注
基金项目:国家自然科学基金(51969019,51468045)、水利部公益性行业科研专项(201401009)和江西省教育厅科技项目(GJJ160703)联合资助.
基于KiK-net台网强震记录,探讨震级、震中距、场地类别及测点高差等对沿深度方向相干函数的影响规律。结果 表明:①水平分量的相干函数值随频率变化规律相同,竖向与水平分量间的差异较大; 相干函数值随频率和测点高差的增加而减小; Ⅲ类场地较之Ⅰ,Ⅱ类场地,所记录的相干函数值随频率增加而衰减的速度更快。②近场(R≤300 km)相干函数值大于远场(R>300 km); 震级对相干函数的影响规律不明显; 不同场地记录沿深度方向地震动相干性不同,建议选用王招招模型描述Ⅲ类场地地震动相干性,Harichandran模型描述Ⅰ,Ⅱ类场地地震动相干性。③基于日本“3·11”地震记录拟合得到了按震中距分段的相干函数模型参数值。
Based on the data of several stations in KiK-net strong-motion seismograph network,we discussed the influence of magnitude,epicenter distance,site classification,and the height difference between the surface and the underground measuring points on the coherence function of ground motion along the depth.The results showed that:① The variation law of coherency functions in two horizontal components with the frequency was similar,but the difference of coherency functions between vertical and horizontal components was significant.The coherency function decreased with the increasing of frequency and height difference,and the attenuation speed of coherency function in vertical component in the class Ⅲ site was faster than that of both the classⅠand classⅡ site with the increasing of the frequency.② The coherence function value of near-field(R≤300 km)is greater than that of far-field(R>300 km).The influence of magnitude on coherency function was not significant.The coherences of ground motion were different in different site,and different coherence function models should be used in different site types.We suggested that the coherence of ground motion in class Ⅲ site can be reflected by the function model of Wang Zhaozhao,and that in classⅠand Ⅱ sites can be reflected by the Harichandran function model.③ Based on the data of Japan “3·11” earthquake,we fit the parameters of the coherence function model in epicenter distance range.
引言
地震动在传播过程中受行波效应、频散效应、衰减效应等因素的影响,具有强烈的空间变化特性(Kiureghian,Neuenhofer,1992),常用频域相干性来描述。Matsushima(1975)提出了地震动相干函数的概念,随后国内外不少学者,如Somerville等(1991)、Hao等(1989)、Kiureghian(1996)、丁海平和宋贞霞(2010)、屈铁军(1995)、钟菊芳等(2005)探讨了地表测点间地震动的相干性,建立了一批实用的相干函数模型。由于相干函数模型的影响因素较多,不同学者分别进行了探讨,如王招招(2012)研究了测点深度、场地条件、震中距大小对地震动相干函数影响规律,提出了经验相干函数模型; 曾庆龙(2012)分析了震源特性的影响,给出了相干函数模型参数的取用原则; 吴边(2015)建议深入研究相干函数模型中各影响因素(如场地因素、震源因素等)的影响规律; Tsai和Liu(2017)通过分析5个井下台阵记录,认为水平和竖向地震动传播存在明显差异; 马俊玲等(2018)得出随台站间距d的增大,整条记录的相干系数降低越多; 尚静和丁海平(2019)探讨了震级和传播距离对相干函数的影响,发现震级对地震动相干性影响较大,传播距离影响不显著,震级小的相干性较好,震源距较小地震动相干性较小。
现有相干函数模型大都是基于密集台阵如SMART-1台阵记录的,少数是通过理论方法得到的。基于SMART-1密集台阵记录的相干函数模型通常只能用于描述与土层条件相类似的地表地震动相干性,描述沿深度方向地震动的相干性的合理性还有待论证。现有模型大都是利用Ⅰ,Ⅱ类场地的台站记录数据得出的,由于缺少Ⅲ,Ⅳ类场地台站地震资料,这两类场地地震动相干函数模型很少,描述地表与地下测点间地震动沿深度方向相干性的模型极少。为满足地下任意深度处确定地震动参数的需求,本文基于KiK-net强震台网记录,开展地表与地下测点间的地震动相干性分析,探讨震级、震中距、场地类别及测点高差对相干函数的影响规律; 通过对比分析不同相干函数模型的适用性,拟合得到能反映沿深度方向地震动相干性的相干函数表达式。
1 资料选取及相干函数值计算
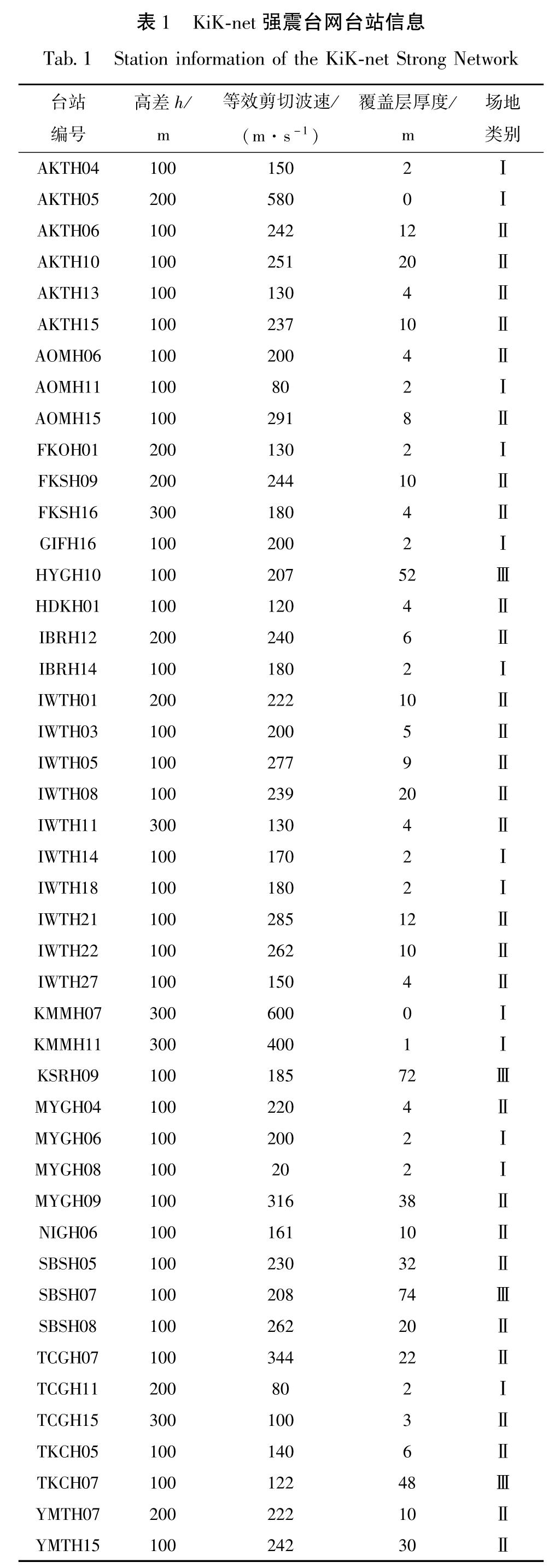
1.1 资料选取KiK-net强震台网于1997年开始运行,共有697个台站,每一个台站均设置了地表和地下基岩2个三分量测点(Aoi et al,2010; 解全才等,2020)。其中,地表与地下两个测点高差h分别为<100,100,100~200,200,200~300,300,>300 m,对应的台站数分别为1,229,235,83,68,15和66个。为了更加清晰地了解相干函数随测点高差和场地类别的变化规律,选取h分别为100,200和300 m的2类多组数据进行分析,一类为同一次地震——日本“3·11”大地震多个台站记录,另一类为2008年以后发生的M≥4.7、震中距R≤300 km的多个台站记录。台站的具体信息见表1,表中场地类别是参照日本防灾科学技术研究院网站的台站场地柱状图,并根据《建筑抗震设计规范》(GB 50011—2010)场地分类标准所确定。
1.2 相干函数值的计算地震动相干函数定义为(Harichandran,Vanmarcke,1986):
γjk(ω,d)={(Sjk(ω,d))/((Sjj(ω)Skk(ω))1/2), Sjj(ω)Skk(ω)≠0
0, Sjj(ω)Skk(ω)=0(1)
式中:γjk(ω,d)为相干函数; Sjj(ω)和Skk(ω)分别为第j个和第k个测点的自功率谱密度函数; Sjk(ω,d)为测点间距为d的第j个和第k个测点间的互功率谱密度函数。
在对密集台阵记录数据进行统计分析时,一般采用迟滞相干函数(李杰,廖松涛,2003):
〖JB<1|〗γ(ω,d)〖JB>1|〗={(〖JB<1|〗Sjk(ω,d)〖JB>1|〗)/((Sjj(ω)Skk(ω))1/2), Sjj(ω)Skk(ω)≠0
0, Sjj(ω)Skk(ω)=0(2)
迟滞相干函数反映了两测点间的地震动相关程度,其值介于0~1,相干函数值越接近1,说明两测点间地震动的相关性越强。
2 基于日本“3·11”地震记录的相干性分析
3 多次地震的相干函数影响因素分析
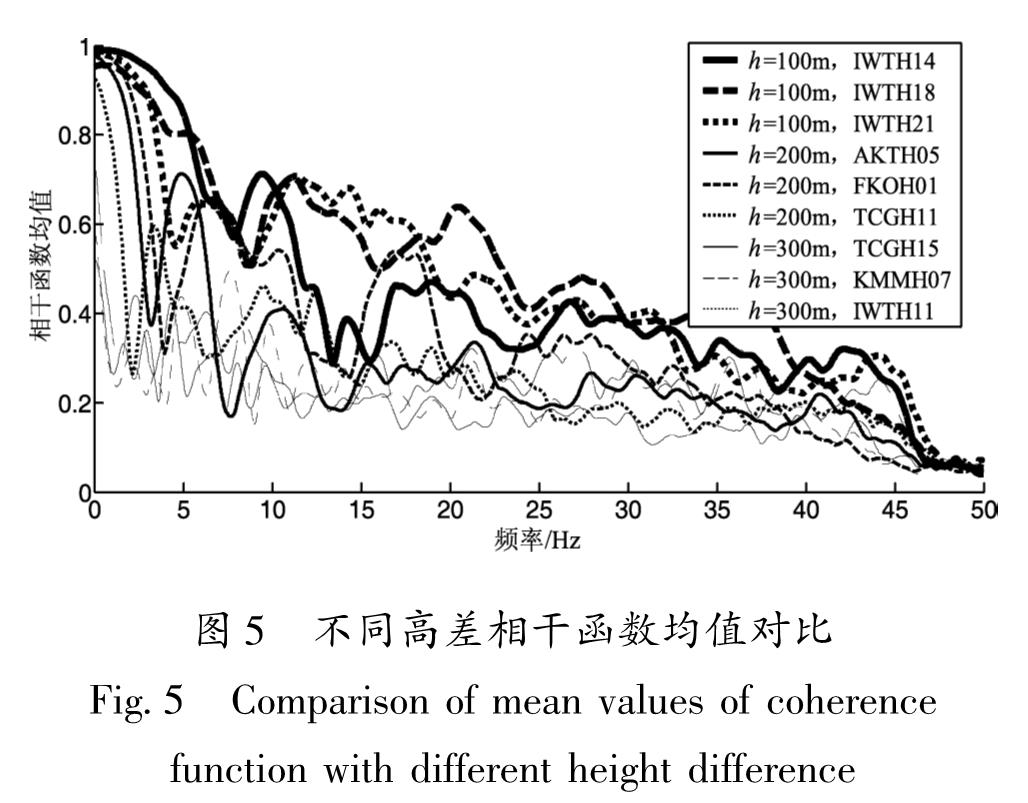
3.1 测点高差在Ⅰ,Ⅱ类场地上选取测点高差h分别为100,200及300 m的台站各3个,每个台站取20次M≥5.0,R≤250 km地震的水平分量进行分析。分析结果表明:相干函数值随h增加而减小,当f<5 Hz时衰减明显,随f增加衰减趋势减弱; 当f>7 Hz时,h=200 m和h=300 m的记录相干函数值接近。f相同时,相同高差相干函数值表现出较大的离散性,且随f增加离散性明显增大。
每个台站20次地震相干函数平均值随频率变化的对比如图5所示,从图中可以看出,当f一定时,相干函数值随h的增大而减小,这与测点间距对两地表测点间水平方向地震动相干性的影响规律类似。虽然同等高差的不同台站间相干函数值表现出一定的离散性,但对规律影响不大。高差越大,相干函数值随f衰减的速度越快,当f≥10 Hz时,h=200 m和h=300 m的记录相干函数值衰减到0.4,为弱相关。
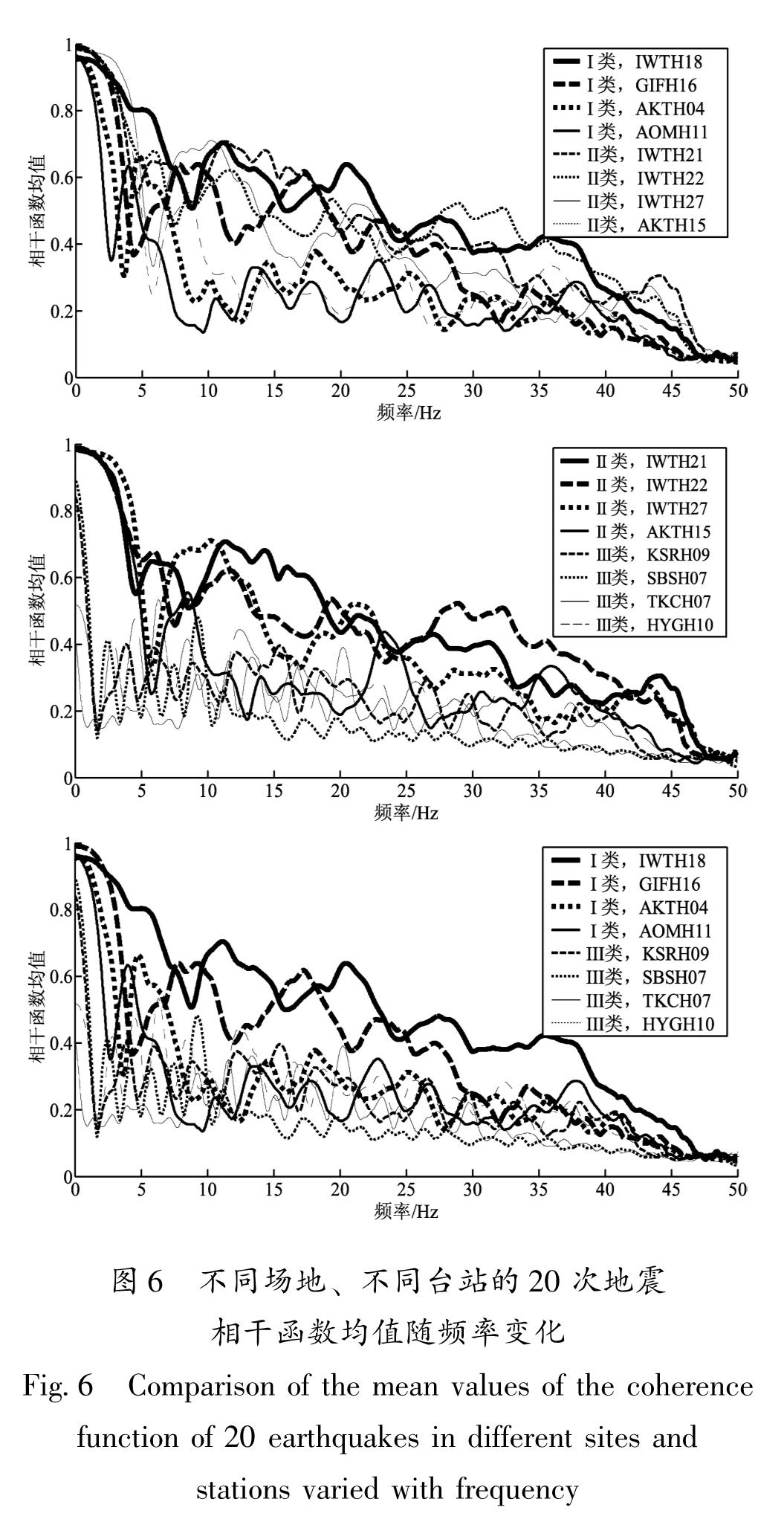
3.2 场地类别本文对Ⅰ,Ⅱ及Ⅲ类场地均选取h=100 m,M≥5.0的20次地震记录进行相干函数值变化规律对比分析,每类场地各选取4个台站,不同场地各个台站20次地震水平分量相干函数均值对比如图6所示。由图6可见,Ⅲ类场地记录的相干函数值比Ⅰ,Ⅱ类场地的小,且随f增加衰减更快。Ⅰ类场地不同台站间相干函数值离散性较大,Ⅰ,Ⅱ类场地记录相干函数值的变化规律相似。当f≤5 Hz时,Ⅰ,Ⅱ类场地记录相干函数值随f增加衰减慢,f>5 Hz时有明显的振荡现象,总体趋势为随f增加而减小。Ⅰ类场地比Ⅱ类场地记录的相干函数值稍小,两者的差异小于Ⅰ类与Ⅲ类场地的差值。
图6 不同场地、不同台站的20次地震相干函数均值随频率变化
Fig.6 Comparison of the mean values of the coherence function of 20 earthquakes in different sites and stations varied with frequency对比Ⅰ,Ⅲ类场地和Ⅱ,Ⅲ类场地记录相干函数值变化规律发现,场地类别对沿深度方向地震动相干函数值影响明显。Ⅲ类与Ⅰ,Ⅱ类场地记录的相干函数值有明显的不同,相同测点高差Ⅲ类场地记录的相干函数值的平均值小于Ⅰ,Ⅱ类场地的相应值。Ⅲ类场地记录相干函数值随f增加而衰减的速度快于Ⅰ,Ⅱ类场地。当f=2 Hz时,Ⅲ类场地记录相干函数平均值只有0.3,而Ⅰ,Ⅱ类场地记录的相干函数平均值为0.7~0.8,在f=30 Hz左右才降为0.3。
分析认为,Ⅲ类场地条件比Ⅰ,Ⅱ类场地条件更为复杂,Ⅲ类场地上的测点记录受深厚冲积土层对地震波的吸收和放大效应的综合影响显著,不同台站的测点记录的频谱成分差异性大,从而使得多次地震的平均相干函数值变化规律表现出与Ⅰ,Ⅱ类场地上的记录的相干函数值不一致。
3.3 震中距鉴于震中距不同,其它参数都相同的地震很少,本文选取h=100 m的5个台站,每个台站在R≤150 km和150 km<R≤250 km这2组震中距范围内各选20次4.9≤M≤5.9地震记录,分析震中距对沿深度方向相干函数的影响。
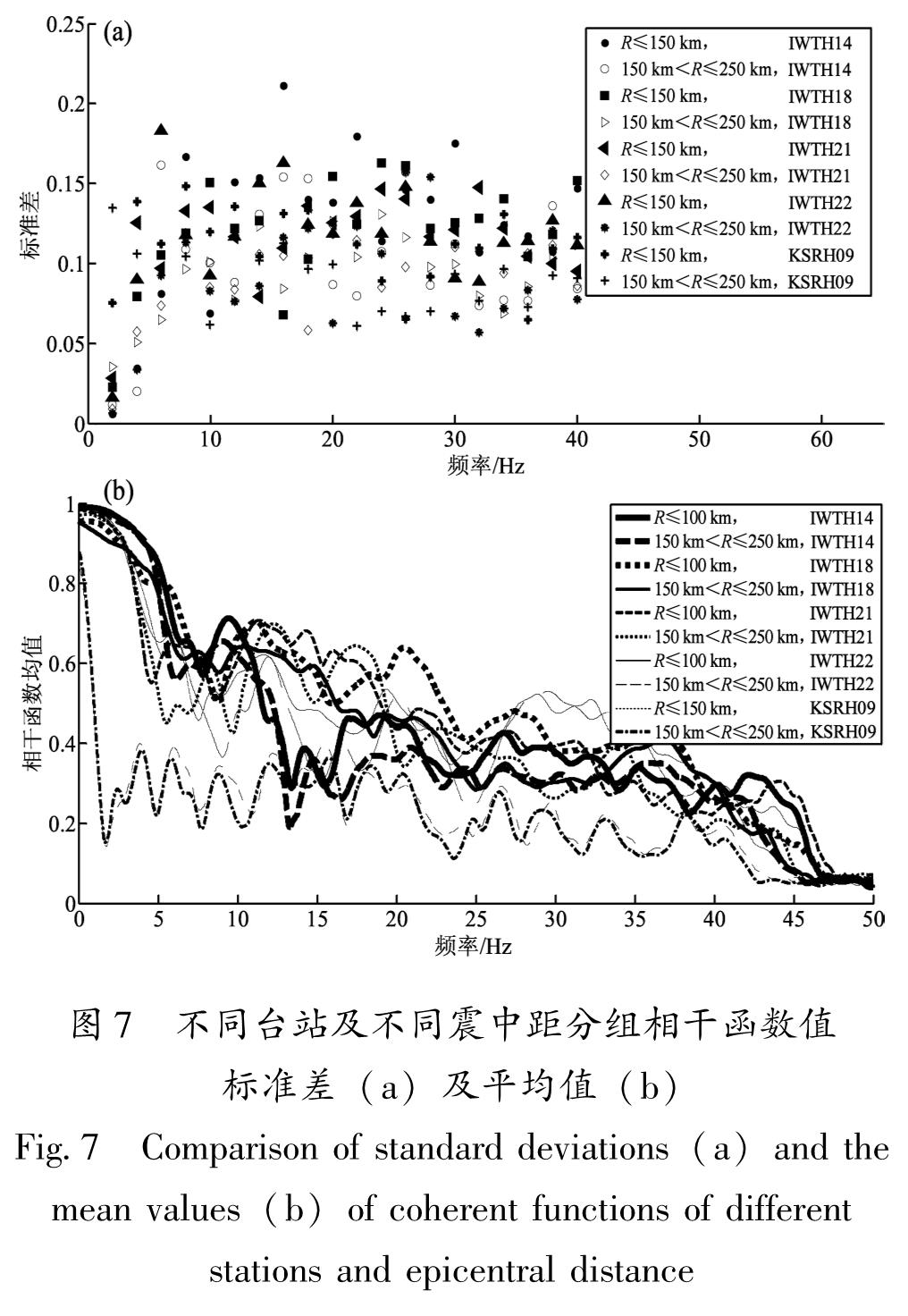
从计算结果来看,不同震中距分组、不同台站的相干函数值表现出一定的离散性。不同台站及震中距分组内20次地震20个频率点相干函数标准差如图7a所示,其相干函数均值随频率的变化如图7b所示。由图7a可知,不同震中距分组20次地震相干函数值在f≤40 Hz时差别较小,尤其在f≤3 Hz时,有8组记录的相干函数标准差在0.05内; f≤5 Hz时,所有记录的标准差都在0.15范围内; 随f增加相干函数值标准差有所增加,但最大值小于0.25,且基本在0.10附近。说明同一个震中距分组内不同地震之间的相干函数值的离散性均较小。不同震中距分组内相干函数值离散性不一样,150 km<R≤250 km记录的相干函数值的标准差总体要小于R≤150 km的标准差,说明近震地震动相干函数的波动要比中远震大。由图7b可知,震中距对沿深度方向上的地震动相干性影响总体比较小。当f≤5 Hz时,相干函数值基本相同,说明R≤250 km时,R对低频段沿深度方向相干函数影响较小,几乎可以忽略; f>5 Hz时,R越大,相干函数值越小,但这种变化的幅度不大。
3.4 震级选取Ⅰ,Ⅱ类场地R≤250 km范围内各2个台站M5.0左右(中强震)和M≥6.0(强震)2个震级段的20次地震记录,分析震级对沿深度方向相干函数的影响。
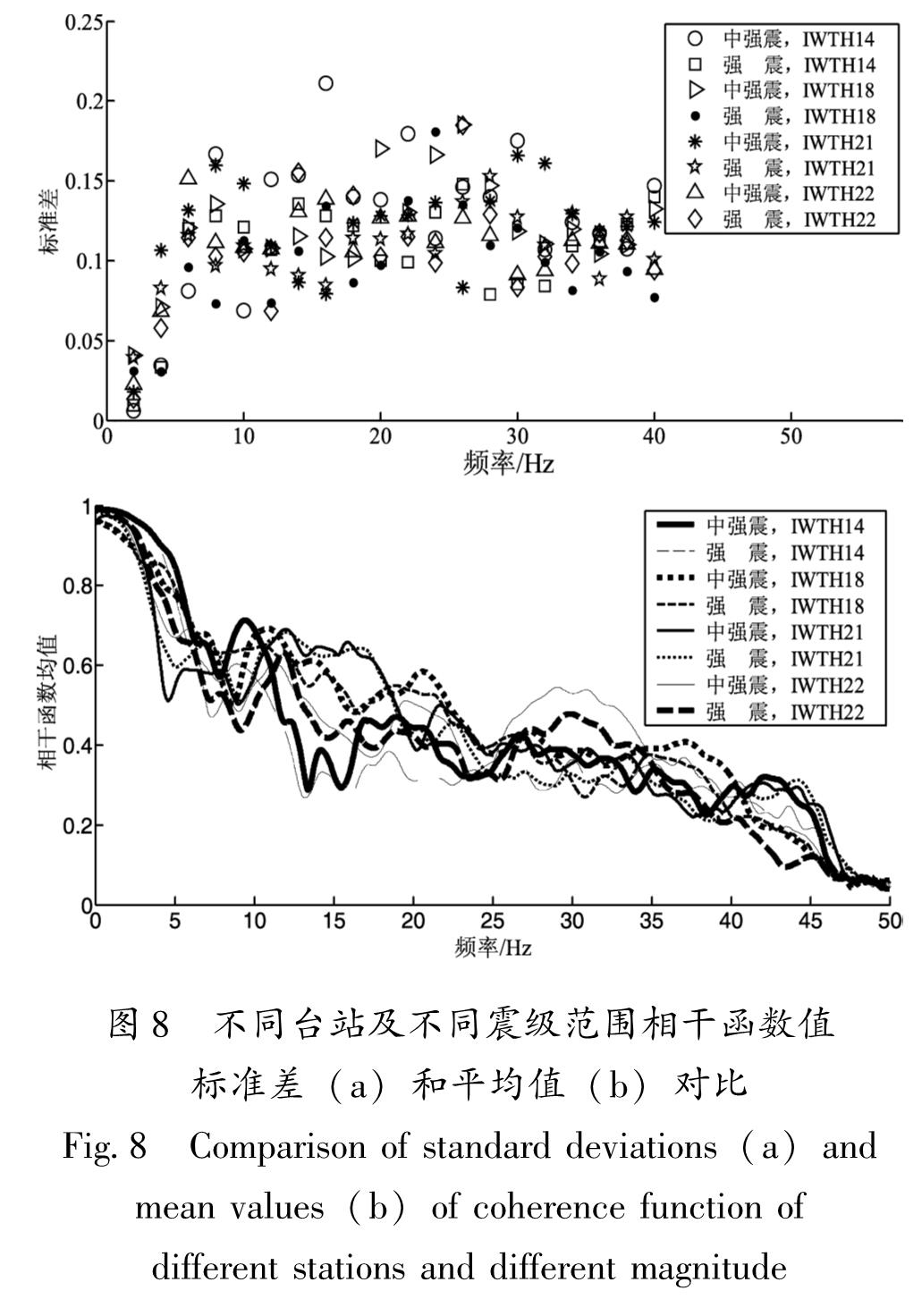
不同台站、不同震级分组的20次地震的相干函数标准差及其平均值如图8所示。由图8a可见,各震级分组内相干函数标准差大部分在0.1~0.15,当f≤3 Hz时,各震级分组的相干函数标准差小于0.05; 当f≤5 Hz时,大部分在0.1以下; f>5 Hz时,标准差变大,大部分在0.1~0.15。20个频率点中,强震的标准差小于中强震标准差的频率点数分别为:IWTH14台有12个,IWTH18台有14个,IWTH21台有13个,IWHT22台有13个,总体上强震的离散性要小一些。在震级分段时,选取的中强震大部分在M5.0左右,而选取的强震范围比较大(M≥6.0),且大部分在M6.0~7.0。强震的标准差没有表现出很大的差异,可以间接看出,当R≤250 km时,震级对地震动相干性影响较小。从图8b可知,中强震、强震的相干函数值变化规律相似,只在个别频率点有微小差异,f≤5 Hz时,不同震级段相干函数值差别很小; f>20 Hz时,震级越大相干函数值反而越小,但减小不多,说明震级对相干函数值影响规律不明显。
4 相干函数模型分析
地震动相干函数模型的合理性将直接影响多点输入地震场的空间变化性的描述。通过对地震动相干函数影响因素以及相干函数值随频率和距离的变化规律分析,建立一套实用的相干函数模型用于工程地震动输入参数的确定,是地震动空间变化性研究的最终目的。对比已有经验和半经验半理论相干函数模型可以发现:基于不同相干函数模型计算得到的相干函数值有较大差异; 即便是依据相同台阵(如SMART1台阵)记录提出的相干函数模型也存在明显的差异。因此,在实际工程应用中如何选取合理的模型仍需要深入探讨。
4.1 现有地震动相干函数模型的适用性分析国内外学者基于不同台阵记录资料先后提出了多组经验相干函数模型,选6组不同类型的相干函数模型进行KiK-net记录沿深度方向相干函数的适用性分析:
(1)丁海平和宋贞霞(2010)模型(简称D Model)
〖JB<1|〗ρ(f,d)〖JB>1|〗=exp[-(a+bf 2)d](3)
式中:a=9.8×10-6,b=4.79×10-5。
(2)Harichandran(1991)模型(简称H Model)
〖JB<1|〗γ(ω,d)〖JB>1|〗=Aexp{-(2d(1-A))/(ak)[1+
(ω/(2πf0))b]0.5}+(1-A)(4)
式中:A=0.736; ak=766; f0=1.09; b=2.78。
(3)Luco和Wong(1986)模型(简称L-W Model)
〖JB<1|〗γ(ω,d)〖JB>1|〗=exp(-α2ω2d2)(5)
式中:α=0.000 25。
(4)冯启明和胡聿贤(1981)模型(简称F-H Model)
〖JB<1|〗γ(ω,d)〖JB>1|〗=exp[-(k1ω+k2)d](6)
通过日本荒川台阵记录分析得到k1=4×10-5 s/m; k2=1.9×10-3 s/m 。
(5)Menke等(1990)模型(简称M Model)
〖JB<1|〗γ(ω,f)〖JB>1|〗=exp(-αfd)(7)
式中:α=0.000 25~0.000 7。
(6)王招招(2012)模型(简称W Model)
〖JB<1|〗ρ(f,h)〖JB>1|〗=exp{-[a+bRchd(f-f1)2]h}(8)
f1=αexp(βR)[1-exp(δh2)] (9)
式中:a=0.010 06; b=0.000 59; c=0.639 60; d=-1.284 8; α=14; β=-0.008; δ=-0.000 45; 震中距R取50 km。
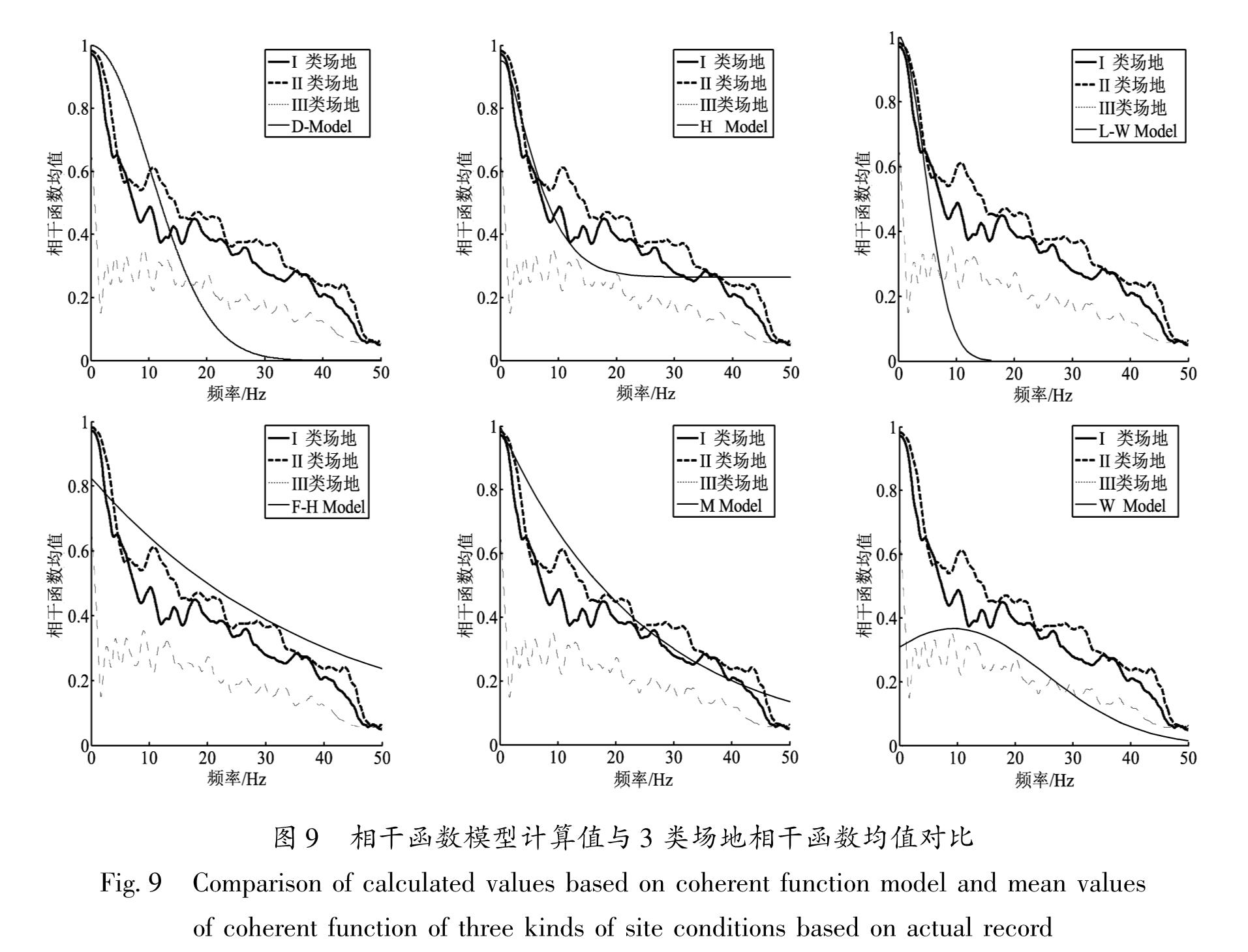
6组模型中依据沿深度方向记录相干函数值推求的相干函数模型只有D Model和W model,其它4组均是反映地表测点间沿水平方向变化的相干函数模型。图9为基于相干函数模型计算值与3类场地上相干函数均值的对比。从图9可见,由Ⅲ类场地数据与由Ⅰ,Ⅱ类场地数据拟合得到的函数模型差别较大,说明了Ⅲ类与Ⅰ,Ⅱ类场地的相干函数值差别较大。描述地表测点间水平方向上地震动相干性的4个函数模型,在某些频段也能较好地描述沿深度方向地震动相干函数随频率的变化规律。
图9 相干函数模型计算值与3类场地相干函数均值对比
Fig.9 Comparison of calculated values based on coherent function model and mean values of coherent function of three kinds of site conditions based on actual recordD Model中模型值在f≤15 Hz时明显大于3类场地记录的相干函数值,在f>15 Hz时比记录的相干函数值小。相比较而言,H Model能较好地反映Ⅰ,Ⅱ类场地记录的沿深度方向上相干函数变化规律,其模型值在f≤10 Hz时接近记录相干函数值,在f>10 Hz时稍小于记录的相干函数值。f≤5 Hz时,L-W Model与Ⅰ,Ⅱ类场地记录相干函数值较吻合,但当f>5 Hz时,模型值小于记录相干函数值,并衰减很快,f=15 Hz时,其模型值接近于0,这与记录相干函数值不符。在f<2 Hz时,F-H Model中模型值小于记录相干函数值,在f≥2 Hz时大于Ⅰ,Ⅱ类场地记录相干函数值。当f≤10 Hz时,M Model模型值大于记录相干函数值,当f>20 Hz时与记录相干函数值拟合较好。W Model模型值与记录值在零频处有差异,总体上比较符合,能较好地反映Ⅲ类场地记录相干函数值的变化规律。分析认为:在某些频段内5组相干函数模型均能较好地描述Ⅰ,Ⅱ类场地记录相干函数值随频率和距离的变化规律,但很难确定最能反映Ⅰ,Ⅱ类场记录沿深度方向上相干函数的变化规律的最优模型。
4.2 Ⅰ,Ⅱ类场地记录相干函数模型及参数的确定采用基于1stOpt软件平台的通用全局优化算法中的Levenberg-Marquardt算法进行回归分析。从图 10来看,4组模型中H Model拟合效果较好,其均方差和残差平方和明显比其它模型小。4种模型拟合优度系数r2虽然相差不大,但H Model拟合优度系数相对要高,建议选H Model用以描述Ⅰ,Ⅱ类场地记录沿深度方向上地震动相干函数的变化规律。
图 10 4种模型的拟合优度系数(a)、残差平方和(b)及均方差(c)对比
Fig.10 Comparison of goodness coefficient(a),residual difference(b)and mean square error(c) of four coherent function models震中距对沿深度方向的地震动相干函数有一定的影响,在建立相干函数模型时要考虑这种影响。由前述分析可知,R≤300 km分组内相干函数值普遍大于R>300 km相应值,在震中距分组内的相干函数值变化较小。据此,建议依据震中距将记录分为R≤300 km和R>300 km,分别进行Ⅰ,Ⅱ类场地记录相干函数模型参数的拟合。对基于h=100 m的台站记录的日本“3·11”地震数据进行模型参数拟合,取各台站模型参数拟合值的均值作为模型参数的建议取值,见表2。
4.3 Ⅲ类场地记录相干函数模型W Model考虑了震中距的影响,较适于描述Ⅲ类场地相干函数的变化规律。为进一步了解W Model
的适用性,将模型值与SBSH07和KSRH09台站8次地震记录的相干函数值进行对比。结果表明,震中距对f≤10 Hz模型的相干函数值影响很小; f>10 Hz相干函数值随震中距增大的衰减加快,震中距越大相干函数值越小。W Model计算值与记录相干值除在零频处差异较大外,在其它频率点均较接近,函数模型能较好地反映Ⅲ类场地上深度方向的相干函数值随震中距、频率及测点高差的变化规律。
5 结论
本文基于KiK-net强震台网记录数据,选取了两大类多组数据,分析了震级、震中距、测点高差及场地类别等因素对地震动相干函数的影响规律,并进行地震动三分量间的相干函数值对比分析; 对比了6组地震动相干函数模型用于描述沿深度方向地震动相干性的适用性,给出了考虑震中距影响的相干函数模型及参数取值的建议。通过分析得到以下结论:
(1)水平分量相干函数差异小,水平与竖向分量相干函数值随频率变化规律差异大; 竖向分量相干函数值随频率变化的振荡幅度比水平分量大。高差相同时,f>20 Hz竖向分量函数值大于水平分量。
(2)随高差增大沿深度方向相干函数值减小,水平分量衰减速度大于竖向分量,相干函数值随频率增加而衰减的速度也加快。
(3)不同场地类别对沿深度方向相干函数影响程度不同,Ⅲ类场地记录水平分量相干函数值随频率增加而衰减的速度比Ⅰ,Ⅱ类场地快。其它条件相同时,Ⅰ,Ⅱ类场地记录相干函数值随频率变化规律相似; Ⅲ类场地记录相干函数值明显小于Ⅰ,Ⅱ类场地的相应值。
(4)震中距对沿深度方向地震动相干函数的影响不可忽略。同一台站远震相干函数值离散性要比近震的小。R≤300 km的相干函数值大于R>300 km的相应值,R>300 km的相干函数值比较接近。
(5)震级对沿深度方向上地震动相干性的影响规律不明显。
(6)建议选用W Model描述Ⅲ类场地记录沿深度方向相干函数变化规律; 选用H Model模型描述Ⅰ,Ⅱ类场地记录沿深度方向相干函数变化规律; 考虑震中距的影响,建议按R≤300 km和R>300 km分段选取Ⅰ,Ⅱ类场地记录相干函数模型参数值。
2011年3月11日,日本东北部海域发生里氏9.0级地震,本文选用该次地震的记录资料进行相干性分析,以减少震源因素对相干函数的影响。由于Ⅱ类场地上台站记录数据较多,开展不同分量间的差异性分析和测点高差及震中距对沿深度方向地震动相干函数的影响分析时,只取Ⅱ类场地记录资料。
2.1 地震动分量选取150 km≤R≤250 km,h=100 km的6个台站记录进行分析,其三分量相干函数值随频率f变化情况如图1所示。由图1可知:①地表土层与地下基岩测点间三分量地震动的相干函数值在低频段(f≤5 Hz)变化规律几乎相同; 但随着f的增加,不同分量间地震动相干函数值的差异性逐渐凸显。②两水平分量相干函数值的变化规律较为接近,虽有振荡,但总体趋势表现为随f的增加而减小; 在整个研究频段内,二者的差异性不存在明显的随f增加而增大的现象,最大差异出现在中频段。③竖向与水平分量的相干性差异较大,竖向分量相干函数值在f≤12 Hz时随f增加而减小,12 Hz<f<25 Hz时随f增加而增大,f>25 Hz后,总体呈下降趋势; 竖向分量相干函数值在f≤5 Hz时比水平分量相干函数值稍大,10 Hz<f<15 Hz时小于水平分量,f>20 Hz时明显大于水平分量。竖向分量地震动高频部分的相干函数值较高,这与两地表测点间相干函数值随f增加而迅速减小的变化规律明显不同。综上可知,地表土层测点与地下基岩测点间的不同分量地震动相干函数值随f的变化规律不完全遵循两地表测点间的相干性随频率的变化规律,尤其是竖向分量的相干函数值。
2.2 测点高差选取高差h为100,200和300 m的台站,由于不同台站所处的位置不同,很难找到R相同的台站,且h为200 m和300 m台站较少。因此选取了对应每个h值都在250 km≤R≤360 km范围内的4个台站记录进行分析。图2为f分别为1,3,5,7,15及25 Hz的相干函数值随高差变化。
图1 不同台站三分量相干函数值随频率变化
Fig.1 Comparison of the coherence function values in three components at different stations varied with frequency由图2可知,相干函数值随h增加而减小。不同地震分量间相干函数值在不同频率随h的衰减规律不同。f≤5 Hz时,水平和竖向分量相干函数值呈明显的随h增加而衰减的趋势; 5 Hz<f<7 Hz时,水平分量相干函数值随h增加先减小后增大。这与相干函数在f为5和7 Hz左右振荡起伏较大有关,且不同的台站震中距的差别也对相干函数值造成了一定的影响。水平分量相干函数值随h增加而衰减的速率比竖向分量快,h为200和300 m时,竖向分量相干函数值大于水平分量,说明h对水平分量相干函数值的影响大于竖向分量。由于震中距和台站所处的局部场地条件有差别,在频率和高差相等的条件下,地震动水平和竖向分量的相干函数值都表现出一定的离散性。
2.3 震中距由于h=100 m时,Ⅱ类场地台站记录数据Rmin=158.70 km,所以选用150 km<R<500 km的记录进行分析。为便于对比,且保证每个分组内有6个台站记录,按R将台站记录分为3组:150 km<R<210 km为第1组,300 km<R<330 km为第2组,390 km<R<490 km为第3组。
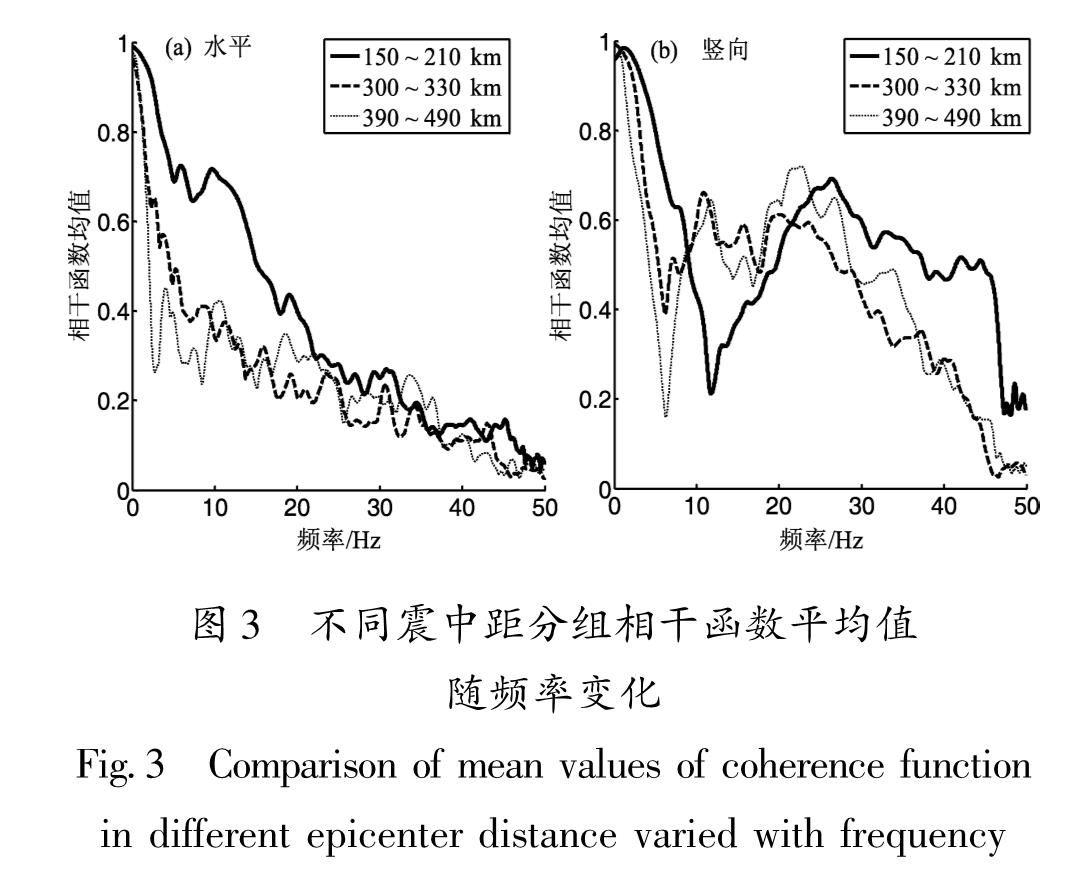
R对沿深度方向地震动相干函数值有一定的影响,且对水平和竖向分量相干函数值的影响程度不同。第2,3组水平分量相干函数值随f增加而衰减的速率较第1组快,且在f=5 Hz时衰减到0.5,第1组在f≥20 Hz时才衰减到0.5。当f≤20 Hz时,R对水平分量相干函数值影响较明显,R越大,相干函数值越小; 当f>20 Hz时,R对相干函数值影响很小。竖向分量的相干函数值在同一震中距分组内离散性较大,且离散程度随R的增加而增大。
同一震中距分组内6个台站记录的相干函数平均值随频率变化如图3所示,由图可见,f≤20 Hz时,第1组水平分量相干函数值要明显大于第2,3组; 0<f≤8 Hz和f≥20 Hz时,第1组竖向分量相干函数值也大于第2,3组。不同分组间相干函数值的差异表现为水平分量大于竖向分量,说明R对水平分量相干函数值的影响更大。300 km<R<330 km和390 km<R<490 km时,水平和竖向分量相干函数值较接近,说明当R≥300 km时R对相干函数影响小。
2.4 场地类别由于Ⅳ类场地上h=100 m的台站只有2个,且R相差较大,分别为284.91,631.67 km,所以只进行Ⅰ,Ⅱ和Ⅲ类场地的相干函数分析。
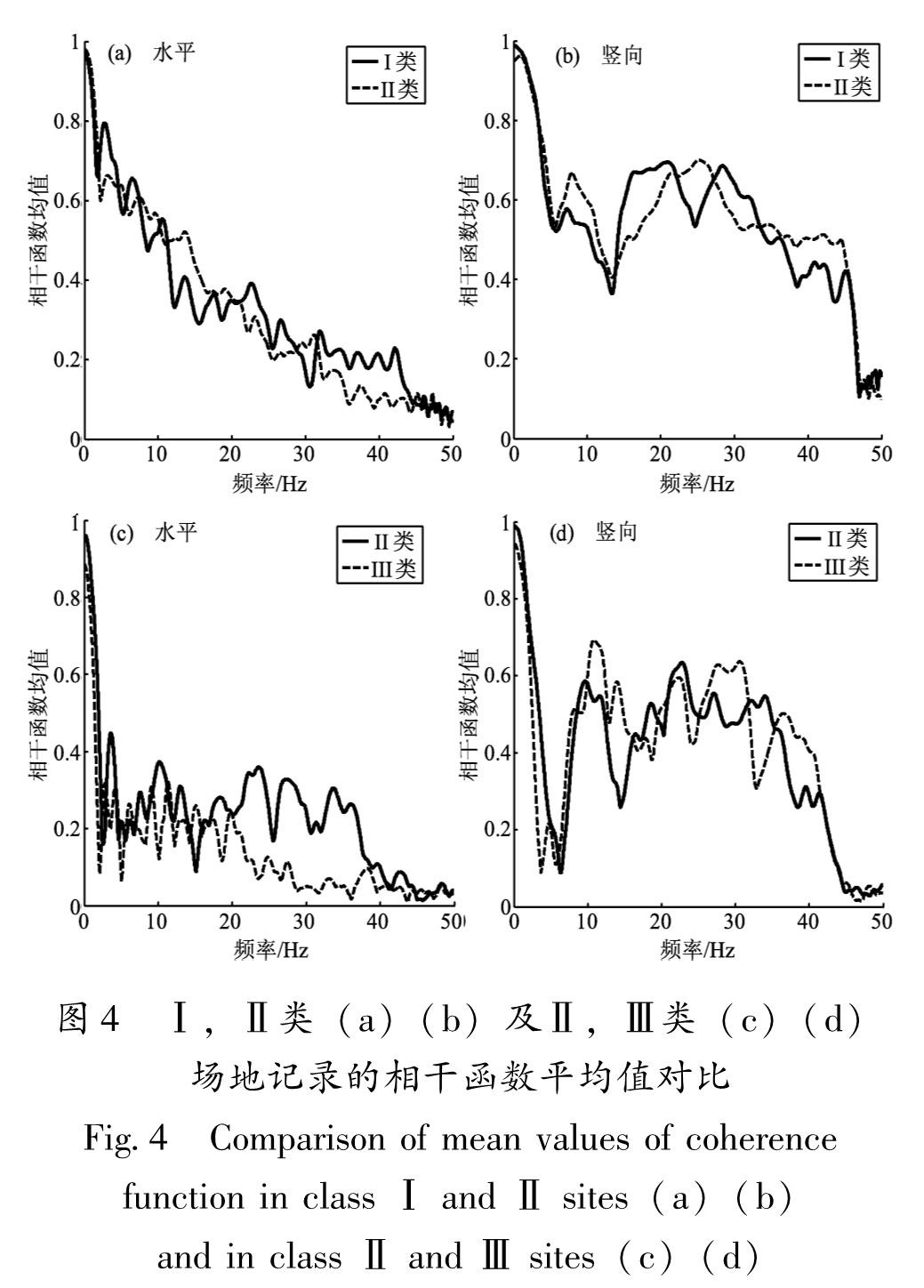
2.4.1 Ⅰ,Ⅱ类场地在Ⅰ,Ⅱ类场地上选取h=100 m,150 km≤R≤300 km的各6个台站记录进行分析。图4a,b为Ⅰ,Ⅱ类场地上的6个台站记录相干函数平均值对比。同一场地类别不同台站记录的相干函数值都表现出一定的离散性,主要是因为震中距以及不同台站间的局部场地条件不同。由图4a,b可见,无论是水平还是竖向分量,在同一频率,Ⅰ,Ⅱ类场地记录的相干函数值很接近,说明场地条件对这两类场地记录沿深度方向相干函数值影响很小。
2.4.2 Ⅱ,Ⅲ类场地鉴于Ⅰ,Ⅱ类场地记录的相干性值比较接近,且Ⅱ类场地台站多,本文仅开展Ⅱ,Ⅲ类场地的对比。由于Ⅲ类场地上h=100 m的台站只有4个,其中,有3个台站的R为425~470 km,另一个台站的R=936.45 km。考虑到震中距对相干函数的影响,取震中距接近的3个台站记录进行分析(图4c,d)。由图4c,d可见,Ⅱ,Ⅲ类场地记录的相干函数值随f变化的规律相似,水平分量相干函数值随f增加衰减很快,当f=3 Hz时,相干函数值已衰减到0.4左右,为弱相干。Ⅱ,Ⅲ类场地记录的竖向分量相干函数比水平分量相干函数衰减慢,Ⅲ类场地记录竖向分量相干函数值上下波动幅度更大,当f>10 Hz时,震荡现象更明显。Ⅲ类场地记录水平分量相干函数值的离散性比Ⅱ类场地的小,而Ⅲ类场地记录竖向分量相干函数值的离散性则比Ⅱ类场地的大。综上可见,无论是水平还是竖向分量,Ⅱ,Ⅲ类场地记录相干函数值差异不大,尤其当f<10 Hz时,这说明当R>400 km时场地类别对相干函数值影响小。
- 丁海平,宋贞霞.2010.震源参数对地震动相干函数的影响[J].振动与冲击,29(7):16-18.
- 冯启民,胡聿贤.1981.空间相关地面运动的数学模型[J].地震工程与工程振动,1(2):1-8.
- 李杰,廖松涛.2003.工程场地地震动相干函数的数值模拟[J].地震工程与工程振动,23(2):12-17.
- 马俊玲,罗翼,丁海平.2018.不同地震波波型对相干系数影响的对比分析[J].自然灾害学报,27(5):20-26.
- 屈铁军.1995.地面运动的空间变化特性研究及地下管线地震反应分析[D].哈尔滨:国家地震工程局力学研究所.
- 尚静,丁海平.2019.震级大小和传播距离对相干函数的影响[J].苏州科技大学学报(工程技术版),32(2):26-31.
- 王招招.2012.随深度变化的地震动相干性研究[D].大连:大连理工大学.
- 吴边.2015.地震动空间变化特征分析及模型化描述[D].重庆:重庆大学.
- 解全才,马强,张景发.2020.2016年日本熊本MW7.0地震强震动记录特征分析[J].地震研究,43(1):125-133.
- 曾庆龙.2012.地震空间相干函数模型及对单层球面网壳影响研究[D].哈尔滨:哈尔滨工业大学.
- 钟菊芳,胡晓,屈铁军.2005.同一测点不同地震动分量空间相干性分析[J].地震研究,28(4):378-382.
- Hao H,Oliveria C S,Penzien J.1989.Multiple-station ground motion processing and simulation based on SMART-I array data[J].Nuclear Engineering and Design,111(3):293-310.
- Harichandran R S,Vanmarcke E H.1986.Stochastic variation of earthquake ground motion in space and time[J].Journal of Engineering Mechanics,112(2):154-175.
- Harichandran R S.1991.Estimating the spatial variation of earthquake ground motion from dense array recordings[J].Structural Safety,10(1):219-233.
- Kiureghian A D,Neuenhofer A.1992.Response spectrum method for multi-support seismic excitations[J].earthquake Engineering and Structural Dynamics,21(8):713-740.
- Kiureghian A D.1996.A coherency model for spatially varying ground motions[J].Earthquake Engineering and Structure Dynamics,25(1):99-111.
- Luco J E,Wong H L.1986.Response of a rigid foundation to a spatially random ground motion[J].Earthquake Engineering and Structural Dynamics,14(6):891-908.
- Matsushima Y.1975.Spectra of spatially variant ground motion and associated transfer functions of soil foundation system[C].Proc 4th Japan Earthquake engineering symposium.Japan:Architectural Institute of Japan.
- Menke W,Lerner-Lam A L,Dubendorff B,et al.1990.Polarization and coherence of 5 to 30 Hz seismic wave fields at a hard-rock site and their relevance to velocity heterogeneities in the crust[J].Bulletin of the Seismological Society of America,80(2):430-449.
- Aoi S,Kunugi T,Nakamura H,et al.2010.New seismographs for Japanese strong motion network K-NET and KiK-net[C]//中国地球物理学会、中国地震学会.中国地球物理2010——中国地球物理学会第二十六届年会、中国地震学会第十三次学术大会论文集.
- Somerville P G,Melaren J P,Sen M K,et al.1991.The influence of site condition on the spatial incoherence of ground motions[J].Structural Safety,10:1-14.
- Tsai C C,Lui H W.2017.Amplification behavior of vertical motion observed from downhole arrays[C].Santiago:16th World Conference on Earthquake Engineering,24.
- GB 50011—2010,建筑抗震设计规范[S].