收稿日期:2020-05-19
基金项目:云南省地震局科技专项(2018ZX03)、国家重点研发计划项目(2018YFC1504503)和大中城市地震灾害情景构建重点专项(2016QJGJ09)联合资助.
基金项目:云南省地震局科技专项(2018ZX03)、国家重点研发计划项目(2018YFC1504503)和大中城市地震灾害情景构建重点专项(2016QJGJ09)联合资助.
基于公里网格单元的地震滑坡人员死亡率评估模型——以2014年鲁甸MS6.5地震为例*
(1.云南师范大学地理学部,云南 昆明650500; 2.云南省地震局,云南 昆明 650224; 3.中国地震局地质研究所,北京 100029)
地震滑坡; 人员死亡率; logistic模型; 公里网格; 鲁甸地震
Modeling and Testing Earthquake-induced Landslide Casualty Rate Based on a Grid in a Kilometer Scale:Taking the 2014 Yunnan Ludian MS6.5 Earthquake as a Case
BAI Xianfu1,2,NIE Gaozhong3,DAI Yuqian1,YU Qingkun2,LUO Weidong2,YE Liaoyuan1
(1.Faculty of Geography Science,Yunnan Normal University,Kunming 650500,Yunnan,China)(2.Yunnan Earthquake Agency,Kunming 650224,Yunnan,China)(3.Institute of Geology,China Earthquake Administration,Beijing 100029,China)
earthquake-induced landslides; casualty rates; logistic model; grid in a kilometer scale; Ludian MS6.5 earthquake
备注
摘要
全文
图/表
参考文献
为提高地震人员伤亡预评估的准确性,完善地震灾害损失评估模型,科学评估地震地质灾害可能造成的人员伤亡数量,以2014年鲁甸MS6.5地震滑坡人员死亡数据为样本,建立了一种基于公里网格单元的地震滑坡人员死亡率logistic回归模型。采用F检验法对所建模型的合理性进行检验,计算得到的F值无限接近于1,表明模型无限接近于完全模型,具有极好的数学统计意义。根据模型评估的死亡率反演得到鲁甸地震灾区滑坡致死人数为233人,比实际少17人,总精确度为93.20%,实际死亡人数与模型识别人数在空间上也有很好的一致性,说明计算得到的地震滑坡人员死亡率是实际死亡人数的良好指标。
To improve the accuracy of earthquake casualty assessment,we should improve the earthquake damage assessment system and scientifically assess the possible casualties caused by seismogeological disasters.For this purpose,we developed a logical regression model for earthquake landslide mortality based on 1 km×1 km grid cells using the death data in the landslides of the Yunnan Ludian MS6.5 earthquake in 2014.F-value test was used to examine the model's statistical portability.In the Ludian study area,the computed F-value was infinitely close to 1.This result proved that the model we developed is close to the real model in the Ludian area.According to the field investigation,the earthquake-induced landslides in the Ludian disaster area claimed 250 deaths,while we get 233 deaths by our new model,leaving the accuracy as 93.20%.Furthermore,the death places triggered by landslides are nearly consistent with the ones indicated by our model.This suggests that the computed earthquake-induced landslides mortality values are good indicators of real casualties.
引言
在多山地区发生地震,常会引发严重的滑坡灾害,导致大面积斜坡变形破坏(Pain,1972),可见,滑坡也是地震致人员伤亡的主要原因之一,如美国阿拉斯加大地震致130人死亡,其中48人死于地震滑坡(Keeper,1984)。1969年以来日本M≥6.9地震的死亡情况统计显示,一半以上死亡人数源于地震滑坡地质灾害(Kobayashi,1994)。迄今为止,国外出现的最大地震滑坡灾难性事件是1970年的秘鲁钦博特7.6级大地震,其所引发的滑坡掩埋了2个城市和一些村庄,造成至少2万人死亡(Plafker,1971)。地震滑坡在我国的云南地区也十分常见,几乎所有强烈地震都会引发大量滑坡,并造成不同程度的人员伤亡。如2006年云南昭通盐津2次5.1级地震致24人死亡,其中20人死于地震滑坡(白仙富等,2013); 2012年云南彝良MS5.7、5.6地震致81人死亡,有59人死于地震滑坡(白仙富等,2014); 2014年鲁甸MS6.5地震引发的滑坡共造成250人死亡和失踪; 2020年巧家MS5.0地震引发的滑坡造成2人死亡。从历史统计来看,云南地区发生的中强及以上地震导致的人员伤亡中,地震滑坡致死人数约占总死亡人数的25%～30%。地震滑坡已成为云南地区面临的主要灾害威胁之一。
如何科学评估地震滑坡可能造成的人员伤亡,完善地震灾害损失评估体系,提高地震人员伤亡评估的准确性,一直是地震灾害风险评估和震后高精准快速评估的难题之一。为评价地震滑坡危险性,许多学者建立了滑坡预测模型,主要分为两种:一是基于物理学和工程地质的模型,它是依据滑坡发生的物理机制,运用力学模型定量表达斜坡稳定性状态,如坡体极限平衡、Newmark位移分析和数值模拟等(张发明等,2002; 刘园园等,2013; 张杰等,2013); 二是基于历史滑坡数据的分析模型,通过分析历史滑坡失稳影响因素,依靠经验和数学算法推算未来发生滑坡的状况,如历史回归、信息量、专家打分等(赵建华等,2006; 白仙富等,2015)。这些研究成果可以对地震滑坡的危险性进行预测,但以此开展定量化的地震滑坡人员伤亡评估仍然困难重重。造成这种困难的原因有很多,如致死原因不明,或仅记录滑坡为致死原因但没有滑坡遇难者的具体位置,无法进行地震参数、滑坡位置、居民点位置与地震滑坡人员死亡数量的关系研究。地震滑坡死亡人数样本的不足和样本信息的粗犷导致在地震损失评估中,对地震滑坡死亡率的预测只能停留在专家经验估计的层面上,其准确性无法保证。因此,关于地震滑坡灾害易损性方面的研究较少,更没有形成基于地震滑坡危险性进行地震滑坡致死性定量研究的技术方法。鉴于此,本文通过对2014年鲁甸MS6.5地震滑坡人员死亡数据的详细收集和空间处理,开展基于公里网格单元的地震滑坡人员死亡率评估方法研究。
1 方法和数据
2 研究结果
2.1 地震滑坡死亡率影响因子分析根据实际调查得到的公里网格地震滑坡死亡人数和该公里网格的人口数计算得出鲁甸灾区各公里网格单元的地震滑坡死亡率,将得到的地震滑坡死亡率做为因变量,将地震滑坡危险性属性(即滑坡危险性等级)作为自变量,进行相关关系的判断。鲁甸地震灾区共包括10 395个公里网格人口数据,按照本文数据处理方法,得到10 395条地震滑坡死亡率信息,限于篇幅,仅给出部分结果(表2)。
为了判明所假设的公里网格单元地震滑坡死亡率与网格内的地震滑坡危险性属性有无关联,即是否独立,采用列联表对10 395个公里网格单元分析地震滑坡死亡率与每一类地震滑坡危险性属性的像元数量之间的相关性。我们把滑坡死亡率分为大于0和等于0两类,分别考虑不同地震滑坡危险性属性值(即地震滑坡死亡率影响因子)与死亡率分类之间的关系。
表2 鲁甸地震灾区公里网格单元属性表
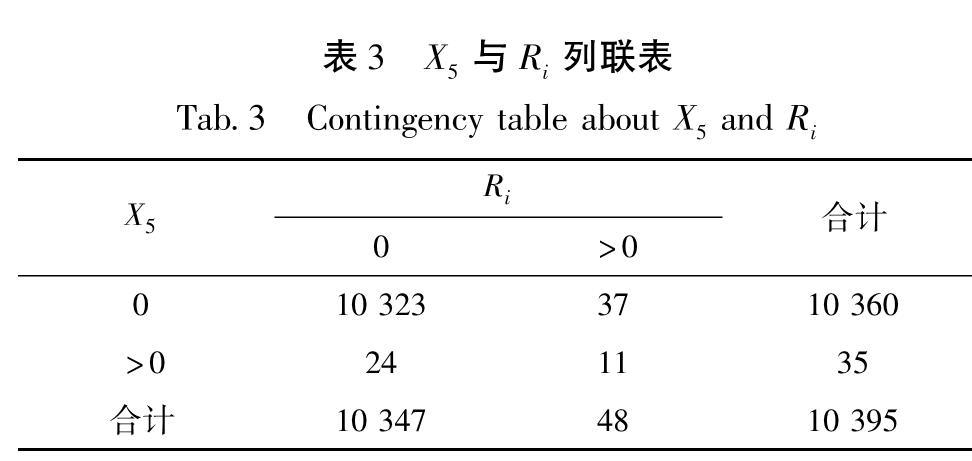
Tab.2 Property table of the Ludian earthquake stricken area in a kilometer scale对表3进行列联分析,原假设:X5与Ri独立; 备择假设:X5与Ri正相合; 检验P值为1.773×10-93; 相合系数:0.235 9; 结论:显著地有Xi的取值等于0,倾向于Ri的取值等于0; X5的取值大于0,倾向于Ri的取值大于0。
表3 X5与Ri列联表
Tab.3 Contingency table about X5 and Ri对表4进行列联分析,原假设:X4与Ri独立; 备择假设:X4与Ri正相合; 检验P值为4.67×10-184; 相合系数:0.371 8; 结论:显著地有X4的取值等于0,倾向于Ri的取值等于0; X4的取值大于0,倾向于Ri的取值大于0。
表4 X4与Ri列联表
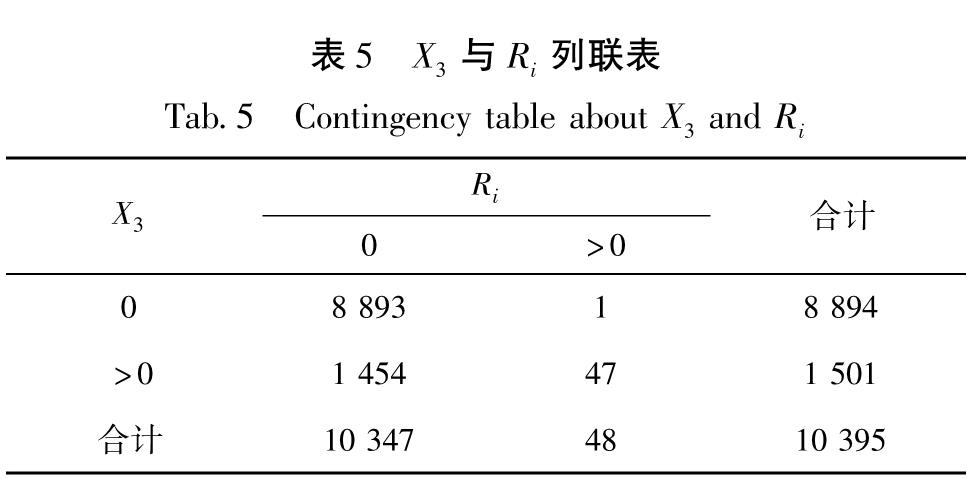
Tab.4 Contingency table about X4 and Ri对表5进行列联分析,原假设:X3与Ri独立; 备择假设:X3与Ri正相合; 检验P值为8.854×10-34; 相合系数:0.138 9; 结论:显著地有X3的取值等于0,倾向于Ri的取值等于0; X3的取值大于0,倾向于Ri的取值大于0。
表5 X3与Ri列联表
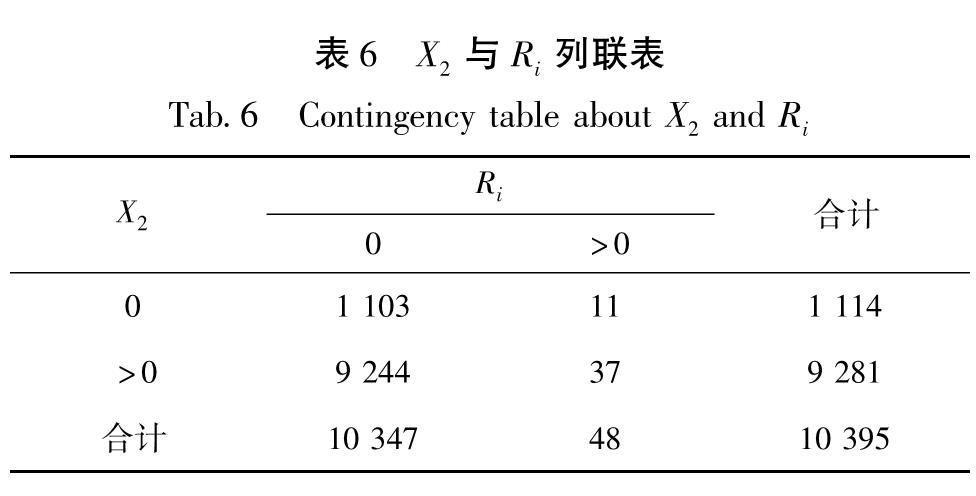
Tab.5 Contingency table about X3 and Ri对表6进行列联分析,原假设:X2与Ri独立; 备择假设:X2与Ri正相合; 检验P值为7.139×10-83; 相合系数:-0.032 89; 结论:显著地有X2的取值等于0,倾向于Ri的取值大于0; X2的取值大于0,倾向于Ri的取值等于0。
表6 X2与Ri列联表
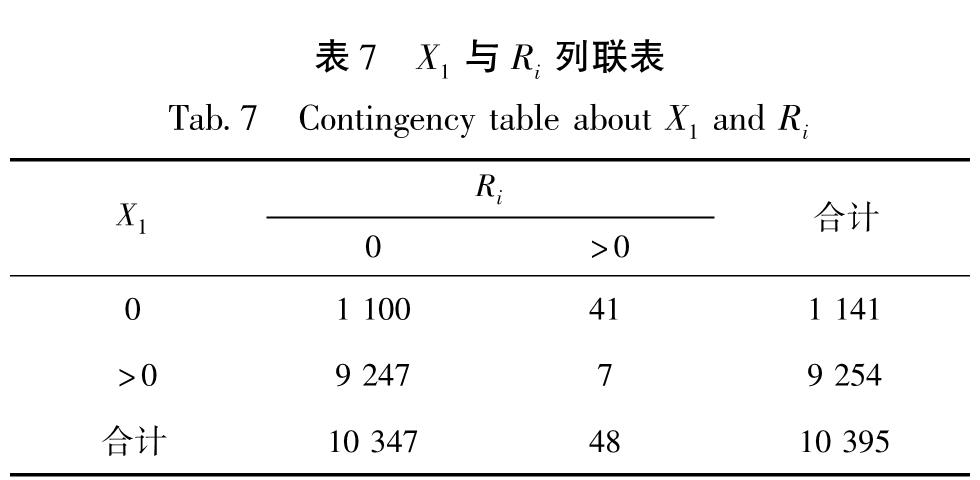
Tab.6 Contingency table about X2 and Ri对表7进行列联分析,原假设:X1与Ri独立; 备择假设:X1与Ri正相合; 检验P值为9.26×10-106; 相合系数:-0.032 89; 结论:显著地有X1的取值等于0,倾向于Ri的取值大于0; X1的取值大于0,倾向于Ri的取值等于0。
表7 X1与Ri列联表
Tab.7 Contingency table about X1 and Ri从表3～7可以看出,每一组的检验P值都远小于0.05,表明原假设不成立,即公里网格单元的地震滑坡死亡率与地震滑坡危险性属性相关。从相关系数看,X5、X4、X3与Ri有显著的正相合关系,在公里网格内,当X5、X4与X3的取值大于0时,Ri的取值倾向于大于0。X1、X2与Ri有显著的负相合关系,X1与X2的取值大于0时,Ri的取值倾向于等于0。
2.2 地震滑坡死亡率模型及其数学检验我们从鲁甸地震灾区的10 395个样本数据中选取45条数据(表2)及3 000条没有地震滑坡人员死亡的数据作为训练集,建立公里网格单元的地震滑坡人员死亡率logistic模型,其余的7 350条数据作为测试集对所建立模型进行合理性检验。本文通过R软件对各影响因子及系数进行回归计算,将回归结果代入式(3),得到地震滑坡死亡率与地震滑坡危险性属性的logistic回归关系:
本文采用F检验法对所建模型进行检验。只有F≥0.5,模型的合理性才不低于不合理性。检验的方式为:原假设H0(模型与完全模型无显著差异)对比备择假设H1(模型与完全模型有显著差异),看检验数据支持哪个命题,F值越小,拒绝原假设的理由越充分; 反之,接受原假设的理由越充分。在R软件中,鲁甸地震灾区公里网格地震滑坡人员死亡率训练集和测试集的F检验输出结果均为:[1]0,即F值无限接近1,表明模型无限接近完全模型,模型通过数学检验,具有较好的数学统计意义。
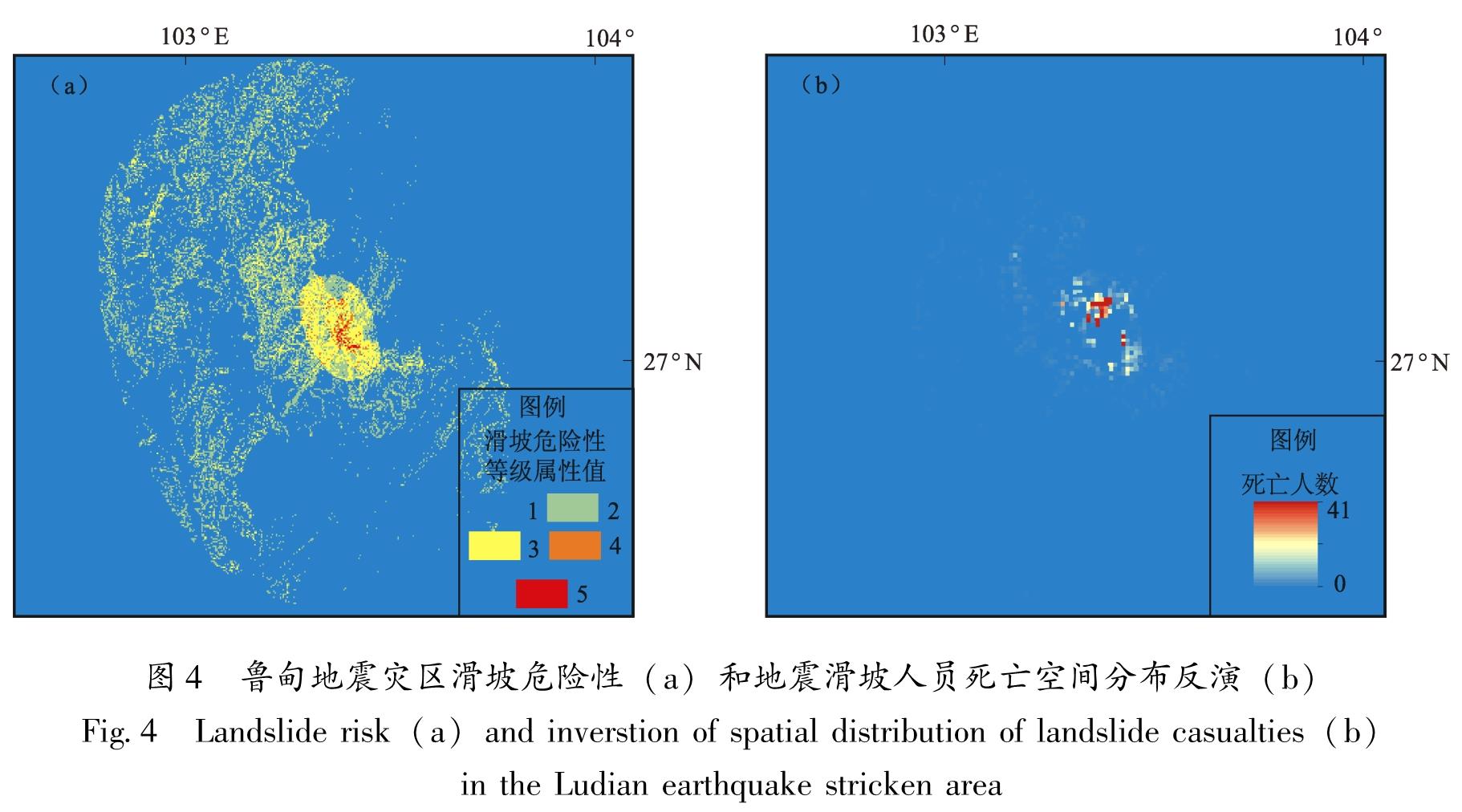
2.3 基于死亡率模型的公里网格死亡人数计算将公里网格的人口数和地震滑坡死亡率相乘来反演鲁甸地震滑坡死亡人数空间分布。从图4b可见,鲁甸地震滑坡公里网格死亡人数与实际滑坡人员死亡地点的空间分布非常接近。对鲁甸地震灾区公里网格内地震滑坡死亡人数的反演结果进行累加,结果为233人,比实际地震滑坡死亡和失踪人数(250人)少了17人,误差率为6.80%。由此可见,在鲁甸地震灾区,基于公里网格建立的地震滑坡死亡率是有效的,本文计算得出的地震滑坡人员死亡率是实际死亡人数的良好指标。
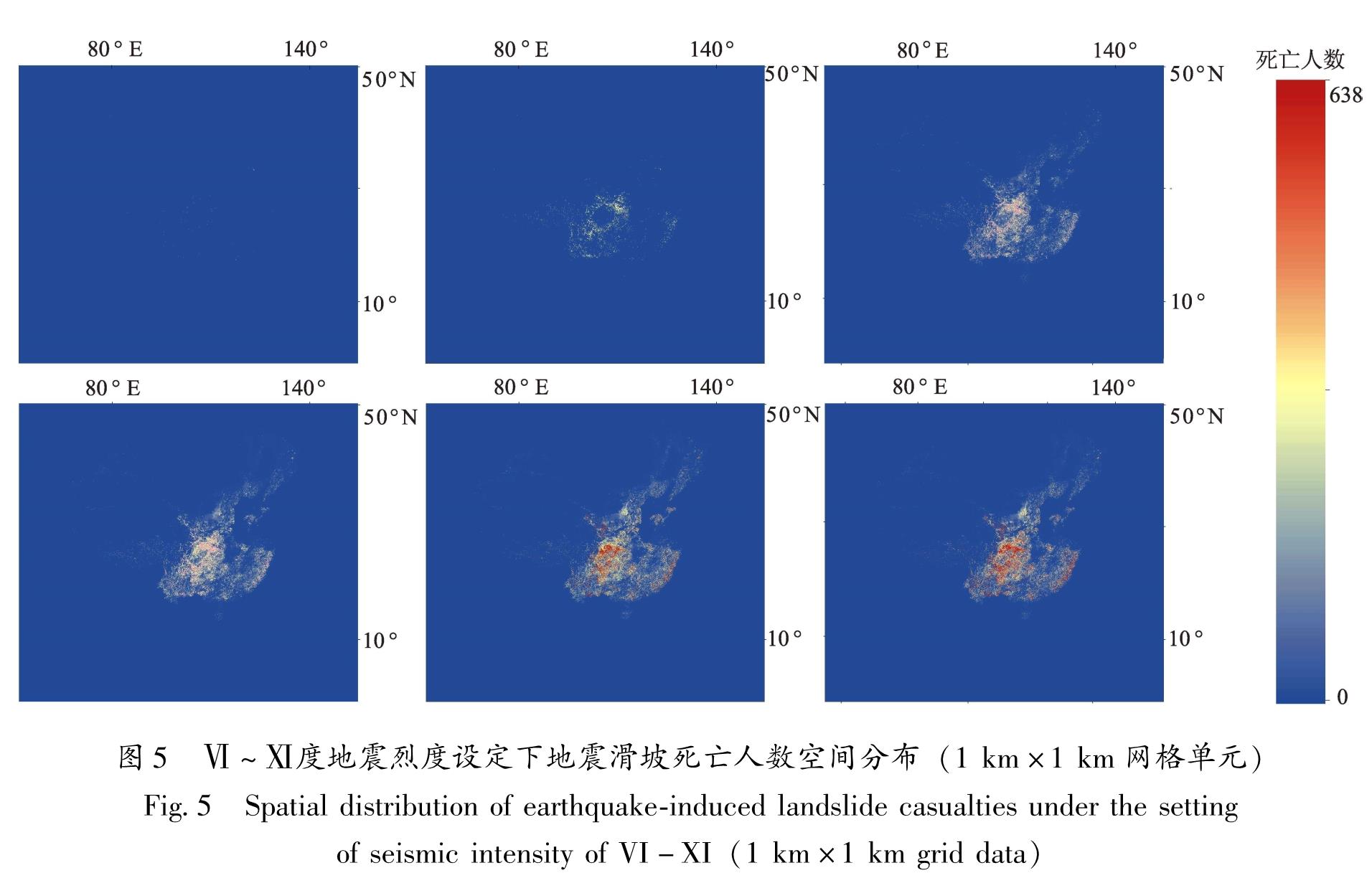
基于上述模型结果,使用2018年的公里网格人口数据和“重大地震灾害及其灾害链综合风险评估技术”课题产出的地震滑坡危险性等级预测数据来推算设定地震烈度为Ⅵ～Ⅺ度时我国及邻区地震滑坡公里网格死亡人数,得出各烈度设定下公里网格的地震滑坡死亡人数预测数据集。从图5可见,在地震烈度为Ⅵ度时,一般不会造成地震滑坡人员死亡,只有西南山区少量的公里网格
图4 鲁甸地震灾区滑坡危险性(a)和地震滑坡人员死亡空间分布反演(b)
Fig.4 Landslide risk(a)and inverstion of spatial distribution of landslide casualties(b) in the Ludian earthquake stricken area
图5 Ⅵ～Ⅺ度地震烈度设定下地震滑坡死亡人数空间分布(1 km×1 km网格单元)
Fig.5 Spatial distribution of earthquake-induced landslide casualties under the setting of seismic intensity of VI-XI(1 km×1 km grid data)有1～2人死亡。在Ⅶ度时,有地震滑坡死亡的公里网格数量增加,但最高死亡人数在10人以下。当烈度达到Ⅷ度时,公里网格的最高地震滑坡人员死亡数开始增加到10人以上,除了秦岭、大巴山、龙门山、横断山、乌蒙山、巫山、雪峰山等地区外,福建一带的武夷山地区地震滑坡死亡人数也开始增加。在Ⅸ度时,公里网格的地震滑坡死亡人数开始有较大增加,如太行山、吕梁山一带。设定地震烈度达到Ⅹ～Ⅺ度时,与Ⅸ度时相比,有地震滑坡人员死亡的公里网格空间分布范围没有太多增加,但公里网格内的死亡人数大幅增加。这两个烈度下,公里网格最高死亡人数相差很少,但Ⅺ度时有高死亡数量的网格数量明显比Ⅹ度时多。从总体来看,设定地震烈度为Ⅵ～Ⅺ度时,我国大陆地区公里网格的地震滑坡死亡人数空间分布与公里网格的人口数和滑坡危险性属性都有密切关系,是二者空间耦合的结果。具体到更小的省域,以云南为例,在相同地震烈度设定下,滇东北地区公里网格地震滑坡死亡人数总体比滇南、滇西南地区多,这与云南的地震实际较相符。
3 结论
为满足当前地震灾害风险分析和地震应急救援工作对准确评估地震滑坡死亡人数的迫切需求,本文提出了一种适用于公里网格单元的地震滑坡死亡率定量评估方法。该方法基于鲁甸地震滑坡死亡数据,使用GIS空间分析和统计功能进行数据处理,以此回归了针对公里网格单元的地震滑坡死亡率模型。基于公里网格人口数据和地震滑坡危险性等级数据建立的地震滑坡人员死亡率logistic回归模型本质上是一种统计模型,用训练集和测试集分别对模型进行F检验,输出结果均为:[1]0,即F值无限接近1,表明模型无限接近完全模型。鲁甸地震灾区地震滑坡实际造成250人死亡和失踪,模型评估结果为死亡233人,误差率为6.80%,且实际死亡人数与模型识别人数在空间上有很好的一致性。这说明计算出的地震滑坡人员死亡率是实际死亡人数的良好指标。在鲁甸地震灾区,基于公里网格建立的地震滑坡死亡率对该区域或对本次地震是有效的。
建立基于公里网格单元的地震滑坡死亡率logistic模型需要2个条件:①地震滑坡死亡率的对象尺度是1 km×1 km的规则网格; ②所使用的地震滑坡危险性数据是90 m×90 m的分级数据。而后者又包括2个条件,滑坡危险性数据是基于烈度为地震动影响参数的产品数据,滑坡危险性等级从低到高分为5个等级,相应的滑坡像元的属性值为1～5。当地震滑坡死亡率评估的基本单元尺度发生变化时,或所使用的地震滑坡危险性数据发生变化,或数据尺度发生变化时,这种方法的有效性会发生变化。
公里网格的地震滑坡人员死亡除了受使用数据尺度的影响之外,数据本身的精度也会影响模型的有效性。本模型仅仅使用了一种公里网格的数据对模型进行了测试,如果有更多技术层面的数据选择做比较时,或许能筛选出更为实用的公里网格人口数据。在地震滑坡死亡率评估模型建立中,我们只使用了logistic模型建立地震滑坡死亡率与地震滑坡危险性属性像元数量之间的关系,不同类型的模型会有不同的评估效果,如何开发不同的模型并筛选出更有效的模型是一个亟待解决的问题。
基于本文模型,对我国遭遇不同地震烈度下的公里网格地震滑坡死亡人数进行了推算,结合经验判断,该模型有其合理性。但该模型的建立基于鲁甸地震灾区,其检验效果只能说明对该次地震或这个区域的适宜性,当模型移植到其他区域时应该对模型进行本地化修正。如何对模型进行外延适用性检验和修正则是另一个亟待解决的问题。
本文提出基于公里网格单元的地震滑坡人员死亡率评估方法是对现有地震死亡人数评估方法不足的一种补充和完善,使地震滑坡死亡人数评估向定量化发展。但是由于历史数据资料不全等客观原因的影响,本研究更多的还是一种方法的探索。
- 安基文,徐敬海,聂高众,等.2015.高精度承灾体数据支撑的地震灾情快速评估[J].地震地质,37(4):1225-1241.
- 白仙富,戴雨芡,戴靖,等.2013.昭通地区地震灾害区域性特征分析[J].地震研究,36(4):514-524.
- 白仙富,戴雨芡,余庆坤,等.2014.彝良“9·07” MS5.7、5.6地震震亡人员研究[J].中国地震,30(4):571-582.
- 白仙富,戴雨芡,余庆坤,等.2015.地震滑坡危险性评估模型及初步应用[J].地震研究,38(2):301-312.
- 曹彦波,李永强.2018.云南地震应急关键技术与信息服务[M].昆明:云南科技出版社.
- 陈振拓,李志强,丁文秀,等.2012.面向防震减灾的人口数据空间化研究:以2007 年宁洱地震灾区为例[J].震灾防御技术,7(3):273-284.
- 邓树荣,张方浩,余庆坤,等.2019.一种地震应急响应级别判定方法[J].震灾防御技术,14(2):401-410.
- 丁文秀,张亦梅,陈振拓,等.2014.湖北省人口数据空间化及在巴东MS5.1地震灾情盲估中的应用[J].大地测量与地球动力学,34(3):28-30.
- 范强,巨能攀,解明礼,等.2019.2017年九寨沟MS7.0地震前后地质灾害风险对比[J].地震研究,42(3):419-427.
- 高娜.2015.地震应急辐射能力研究[D].北京:中国地震局地质研究所.
- 刘圆圆,王星华.2013.利用改进的Newmark方法探讨高陡岩质边坡稳定性[J].世界地震工程,(4):147-152.
- 裴强,夏超南,刘小庆,等.2018.预应力锚索抗滑桩支护边坡的地震动力响应分析[J].煤炭技术,37(9):57-58.
- 邱丹丹,牛瑞卿,赵艳南.2017.不同采样策略下地震滑坡敏感性分析研究[J].岩石力学与工程学报,36(S1):3101-3109.
- 魏连雨,李慧,董立颖,等.2016.河北承德黄土动剪切模量与阻尼比试验研究[J].地震研究,39(3):513-518.
- 吴玮莹,许冲.2018.2014年鲁甸MW6.2地震触发滑坡新编目[J].地震地质,40(4):1140-1148.
- 杨根云,周伟,方教勇.2019.基于信息量模型和数据标准化的滑坡易发性评价[J].地球信息科学学报,20(5):674-683.
- 易树健,李渝生,黄超,等.2018.金沙江杀威台子滑坡成因动力学特性研究[J].防灾减灾工程学报,38(2):297-304.
- 张超.2016.金沙江杀威台子古地震滑坡成因动力学机理研究[D].成都:成都理工大学.
- 张发明,陈祖煜,弥宏亮.2002.滑坡体稳定性评价的三维极限平衡方法及应用[J].地质灾害与环境保护,13(2):55-58.
- 张杰,侯定贵,张晓航,等.2013.地震诱发滑坡的数值模拟与敏感性分析[J].科学技术与工程,13(34):10254-10258.
- 张如前.2015.基于改进模糊聚类迭代和神经网络的边坡失稳预测方法[D].南昌:江西理工大学.
- 赵建华,陈汉林,杨树锋.2006.滑坡灾害危险性评价模型比较[J].自然灾害学报,15(1):128-134.
- An J W,Bai X F,Xu J H,et al.2015.Prediction of highway blockage caused by earthquake-induced landslides for improving earthquake emergency response[J].Natural Hazards,79(1):511-536.
- Keeper D K.1984.Landslides caused by earthquakes[J].Geological Society of America Bulletin,95(4):406-421.
- Kobayashi Y.1994.Effect of basal guided waves on landslides[J].Pure and Applied Geophysics,142(2):329-346.
- Pain C F.1972.Characteristics and geomorphic effects of earthquake-initiated landslides in the Adelbert Range,Papua New Guinea[J].Engineering Geology,6(4):261-274.
- Plafker G,Ericksen G E,Fernandez J.1971.Geological aspects of the May 31,1970,Peru earthquake[J].Bulletin of the Seismological Society of America,1(3):543-578.
1.1 研究方法1.1.1 研究假设地震滑坡人员死亡的致灾因子是地震滑坡体,但对一个确定的地点难以准确评估是否会发生滑坡,因此,我们选取地震滑坡危险性来表征造成人员死亡的地震滑坡这一影响参数。基于所收集的数据,本文提出以下假设:各公里网格单元的地震滑坡危险性等级属性是地震滑坡死亡率的影响因子,不同的滑坡危险性属性及其数量组合影响着地震滑坡死亡率的高低。公里网格的地震滑坡死亡率与其内部滑坡危险性等级数据各属性值像元数量之间的联系可抽象为:
Ri=f(li_ni)(1)
式中:Ri表示第i个公里网格单元的地震滑坡死亡率; f()表示推断的影响因素与Ri的关系; li_ni表示第i个公里网格单元上滑坡危险性栅格数据的属性值和像元数量。
1.1.2 地震滑坡死亡率理论模型将公里网格单元的地震滑坡死亡率与其内部每个滑坡危险性等级的像元数量之间的关系描述为函数f。根据影响因子的数据属性,函数f可以有不同的选择,式(1)可以进一步细化为:
Ri=f(l1i_n1i,l2i_n2i,…,lmi_nmi)(2)
式中:l1i_n1i～lmi_nmi是地震滑坡死亡率影响因子; l1i_n1i表示第i个公里网格单元内地震滑坡危险性等级为1的像元数量; l2i_n2i等以此类推。
理论上,公里网格地震滑坡死亡率最低为0,最高为1,且随着地震滑坡危险性属性的变化而相应地变化。我们进一步假定:地震滑坡死亡率与地震滑坡危险性属性变化之间存在logistic关系,则将式(2)表达为常用的logistic模型:
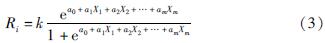
式中:Ri表示第i个各公里网格单元的地震滑坡死亡率,取值范围为0～1; k表示关系式函数的系数; X1～Xm分别表示第i个公里网格单元内地震滑坡危险性等级为1～m的像元数量。因此,只要求得式(3)中各参数系数,即可建立基于公里网格单元的地震滑坡死亡率模型。
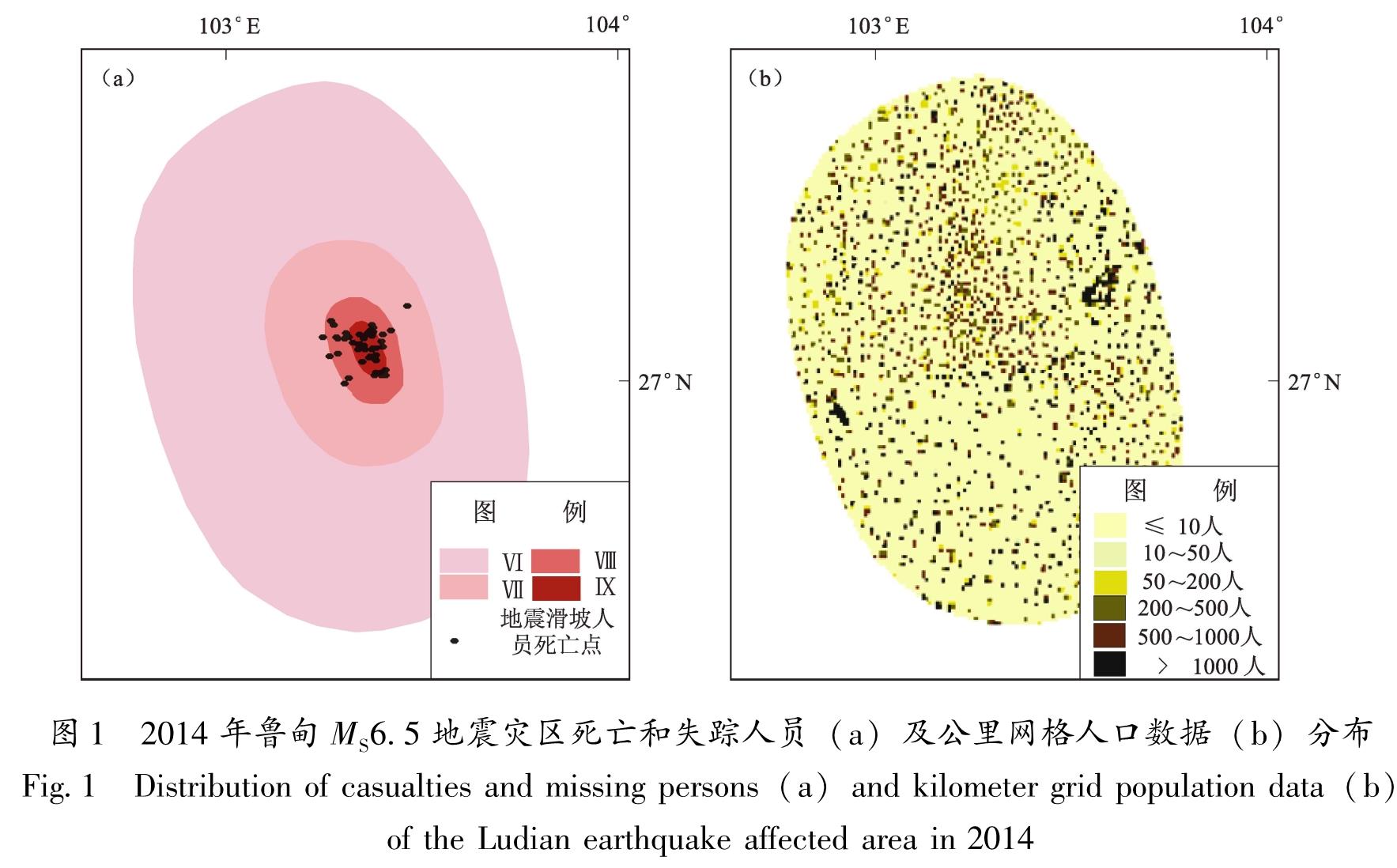
1.2 数据收集和处理1.2.1 数据收集2014年8月3日16时30分,云南省昭通市鲁甸县(27.10°N,103.34°E)发生MS6.5地震,地震诱发了大量的山体滑坡(吴玮莹,许冲,2018),造成134人死亡和116人失踪。鲁甸地震灾区是滇东北乃至整个西南高原山地的典型区域,具有一定的代表性。地震后,我们通过逐个调查地震现场,核实收集250位死亡和失踪人员的具体位置(图1a)。本文灾区是指地震现场调查后烈度为Ⅵ度及以上的区域(图1a); 人口数据来源于中国地震局地质研究所与中国科学院地理科学与资源研究所合作开发的产品,该产品的适用性已得到验证(陈振拓等,2012; 丁文秀等,2014; 安基文等,2015),选取地震发生之前的2010年度鲁甸地震灾区的公里网格人口数据(图1b)。
考虑到地震滑坡空间分布预测的困难,本文使用“十一五”国家科技支撑课题“重大地震灾害及其灾害链综合风险评估技术”产出的地震滑坡危险性评估模块来绘制地震灾区滑坡危险性分布预测图(白仙富等,2015),该模块可给出我国
图1 2014年鲁甸MS6.5地震灾区死亡和失踪人员(a)及公里网格人口数据(b)分布
Fig.1 Distribution of casualties and missing persons(a)and kilometer grid population data(b) of the Ludian earthquake affected area in 2014及邻区不同烈度设定下的地震滑坡危险性等级空间栅格数据,空间栅格数据精度为90 m×90 m(图2)。该数据集根据地震滑坡密度值(单位面积内的滑坡个数)将滑坡危险性分为5个等级,危险性等级从低到高的属性值依次为1～5,数据集
中每个栅格的属性值代表着该空间位置的地震滑坡危险性。该套数据集被多次试验性地应用于地震应急和地震灾害风险预评估,具有很好的合理性和实用性(白仙富等,2015; An et al,2015; 高娜,2015; 张如前,2015; 魏连雨等,2016;
图2 Ⅵ～Ⅺ度地震烈度设定下地震滑坡危险性等级空间分布(90 m×90 m栅格数据)
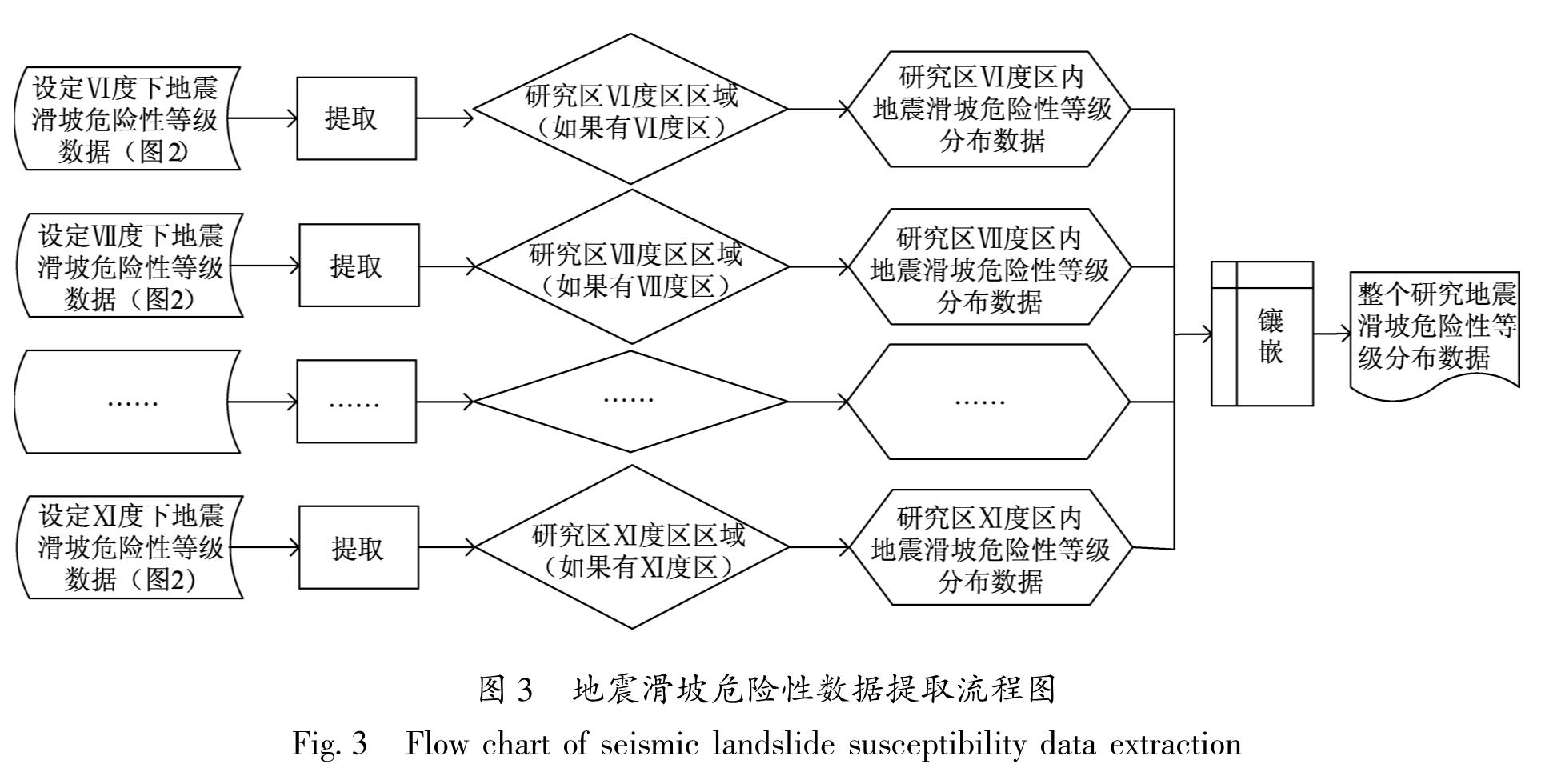
Fig.2 Spatial distribution of seismic landslide susceptibility under the setting of seismic intensity of VI-XI(90 m×90 m grid data)张超,2016; 邱丹丹等,2017; 裴强等,2018; 杨根云等,2018; 易树健等,2018; 曹彦波,李永强,2018; 范强等,2019; 邓树荣等,2019)。本文按照地震滑坡危险性数据提取流程(图3),利用鲁甸地震的烈度数据从地震滑坡危险性等级预测数据集中提取对应烈度区的内容,然后通过GIS镶嵌功能建立整个研究区地震滑坡危险性等级空间分布数据(图4a)。
图3 地震滑坡危险性数据提取流程图
Fig.3 Flow chart of seismic landslide susceptibility data extraction1.2.2 数据处理通过GIS的空间分析统计功能,以公里网格人口数据为基础,将每个公里网格内的地震滑坡死亡人数总和赋值给对应的网格作为网格的地震滑坡死亡人数属性。在对地震滑坡死亡人数赋值时,将地震滑坡造成的116个失踪人员等同于死亡人员,根据网格内的地震滑坡死亡人数计算该公里网格单元的地震滑坡死亡率。然后,通过GIS中的空间关联模块对各个公里网格内每一类地震滑坡危险性等级数据的像元数量进行统计,并将统计结果作为网格单元的地震滑坡危险性属性值赋值给对应的网格,使得每一个网格具有人口、地震滑坡死亡数、地震滑坡死亡率和地震滑坡危险性属性,见表1。表中FID表示字段的机器自动编码,一般从0开始; i表示第i个公里网格的机器自动编码数; Pi为人口字段名,表示第i个公里网格单元内的人口数; Di为地震滑坡死亡人数字段名,表示第i个公里网格单元内的地震滑坡死亡数; Ri为地震滑坡死亡率字段名,表示第i个公里网格单元内的地震滑坡人口死亡率,R通过D/P求得; X1～X5分别表示公里网格单元内地震滑坡危险性属性为1～5的字段名,X1表示地震滑坡危险性等级栅格数据像元属性值为1的字段名,Xi等以此类推; Ai1_Ii1 表示第i个公里网格单元内滑坡危险性等级栅格数据属性值为1的像元个数,Ai2_Ii2 等以此类推,在实际的属性表中,为一些非负的整数型数值。
表1 公里网格属性示例表
Tab.1 A sample table of grid properties in a kilometer scale
