基金项目:地震科技星火计划项目(XH20057,XH21034)、国家自然科学基金(51778590)及中国地震局地震预测研究所基本科研业务经费项目(2018IESLZ06)联合资助.
(1.兰州大学 土木工程与力学学院,甘肃 兰州 730000; 2.中国地震局兰州地震研究所,甘肃 兰州 730000; 3.中国地震局黄土地震工程重点实验室,甘肃 兰州 730000)
(1.College of Civil Engineering and Mechanics,Lanzhou University,Gansu 730000,Lanzhou,China)(2.Lanzhou Institute of Seismology,China Earthquake Administration,Gansu 730000,Lanzhou,China)(3.Key Laboratory of Loess Earthquake Engineering,China Earthquake Administration,Gansu 730000,Lanzhou,China)
scanning electron microscope; dynamic triaxial test; dynamic characteristics; structural characteristics
备注
基金项目:地震科技星火计划项目(XH20057,XH21034)、国家自然科学基金(51778590)及中国地震局地震预测研究所基本科研业务经费项目(2018IESLZ06)联合资助.
黄土的细观结构对其非线性动力参数具有重要影响。选取不同地区的典型原状黄土进行室内动三轴试验和扫描电镜(SEM)试验,利用PCAS孔隙图像识别与分析系统统计分析SEM图像,获取了黄土的孔隙细观结构参数,分析了孔隙细观结构参数与初始动弹性模量和阻尼比的关系。结果 表明:初始动弹性模量随着土体平均孔隙直径、表观孔隙率、分形维数和概率熵的增大而减小,其中平均孔隙直径和分形维数对初始动弹性模量的影响较为显著,表明土体内孔隙的大小及其排列对土体的动弹性模量具有明显的影响; 而阻尼比均随着土体平均孔隙直径、表观孔隙率、分形维数和概率熵的增大呈非线性增大,其与表观孔隙率和分形维数具有明显的相关性,表明孔隙数量及其排列形态对土的阻尼比影响较为明显。
The structural characteristics of loess are important influence factors of dynamic elastic modulus and damping ratio.In this paper,the typical undisturbed loess samples in different regions are selected for dynamic triaxial tests and SEM tests.We statistically analyzed SEM images to obtain microstructure parameters by using PCAS pore image recognition and analysis system,and studyed the relationship between pore mesostructure parameters and initial dynamic elastic modulus and damping ratio of loess.The results show that the initial dynamic elastic modulus decreases with the increase of the average pore diameter,fractal dimension,probability entropy,and apparent porosity of loess.Among these four parameters,the average pore diameter and fractal dimension have a significant effect on the initial dynamic elastic modulus of the loess,which shows that the size and arrangement of pores are the main influence parameters.However,the damping ratio increases nonlinearly with the increase of apparent porosity,fractal dimension,the average pore diameter,and probability entropy of the loess,which has an obvious correlation with apparent porosity and fractal dimension.It shows that the number of pores and the arrangement of pores have an obvious influence on the damping ratio of the loess.
引言
黄土是在干旱、半干旱气候条件下,形成于晚更新世和全新世的风成堆积物,其分布广泛且工程性质十分特殊。黄土在堆积过程中受控于特殊的物质来源、地质营力和沉积赋存环境等因素,形成了特殊的、以架空孔隙为主的多孔弱胶结结构(王兰民等,2003; 刘钊钊等,2019),因而具有欠压密性、湿陷性、震陷性等特点,给工程建设的施工和运营安全带来巨大的挑战。在我国,黄土广泛分布于西北、华北与东北地区,尤其集中分布在黄土高原的甘肃、陕西、山西、河南以及宁夏等地(王永焱,林在贯,1990),在长期内外地质营力的相互作用下形成了塬、梁、峁、阶地等典型的黄土地貌。同时,这些地区新构造运动强烈,地震活动频繁。根据中国地震动参数区划图(GB 18036—2015),黄土高原54%以上的区域和超过70%的城镇位于0.10 g(Ⅶ度设防)以上抗震设防区。且震害实例及研究表明,黄土在强震作用下表现出承载力迅速衰减和变形急剧增大的特性,由此造成的黄土滑坡、震陷、液化等地震地质灾害严重威胁着当地人民的生命财产安全和社会经济可持续发展。
动弹性模量和阻尼比可表征土体的动刚度特性,反映在外力作用下动应力-动应变的非线性和滞后性,是土体动力特性研究中的重要参数,也是场地地震反应分析中必不可少的研究内容(田堪良,2003)。黄土作为一种特殊土,其动弹性模量和阻尼比已得到国内外学者的广泛研究。骆亚生等(2000)对不同典型地区黄土进行动力特性试验分析,发现含水率、干密度、平均有效固结压力及结构性对动弹性模量影响明显; 王峻等(2010)认为含水率是黄土动力学性质中最主要的影响因素,胡仲有等(2010)发现原状黄土的阻尼比较重塑黄土受含水率影响更大; 王谦等(2017)对甘南地区次生黄土动本构关系进行研究,发现沉积环境不同,黄土动力特性有明显差异; 王建荣(1999)、王俊等(2011)研究了外部动荷载对黄土动力特性的影响,发现随机地震荷载不同,黄土动弹性模量和阻尼比不同,且均随振动频率的增高而增大,但原状黄土的动应力-动应变曲线仍服从双曲线模型。
结构性是黄土最重要的特征之一,黄土内部基本单元体大小、结构连结、孔隙大小、孔隙排列方式等均对黄土的宏观动力特性产生重要影响。李瑞宽等(2018)从微结构的角度揭示了围压和水分对黄土动力特性的影响特点,但其它影响因素并未涉及; 徐世民(2017)和冷冠军(2017)对黄土微结构参数与动弹性模量进行了研究,前者建立了宏观意义的结构性参数,但取样点相对较少; 后者则是在极限试验条件下对重塑土进行分析,广泛性和代表性不突出,且缺乏对阻尼比与细观结构参数关系的研究。因此,本文通过原状黄土动三轴试验,计算得到动弹性模量和阻尼比,基于SEM细观结构试验,利用PCAS孔隙图像识别与分析系统提取了原状黄土的细观结构参数,并分析原状黄土动弹性模量和阻尼比与细观结构参数之间的关系。
1 试样及试验方法
1.1 试样取备与基本物性指标为了研究细观结构参数对原状黄土弹性模量和阻尼比的影响,黄土样本分别取自甘肃省庆阳(QY)、通渭(TW)、陕西省宝鸡(BJ)、延安(YA)、洛川(LC)、山西省太原(TY)、吕梁(LL)、长治(CZ)以及河南省三门峡(SMX)的典型黄土场地。原状黄土取土试样高150 mm,直径80 mm,均为Q3黄土,取土深度4.5 m,取样过程中尽量避免土体扰动。按照《土工试验方法标准》(GB/T 50123—2019)测试得到黄土的基本物性指标,结果见表1。
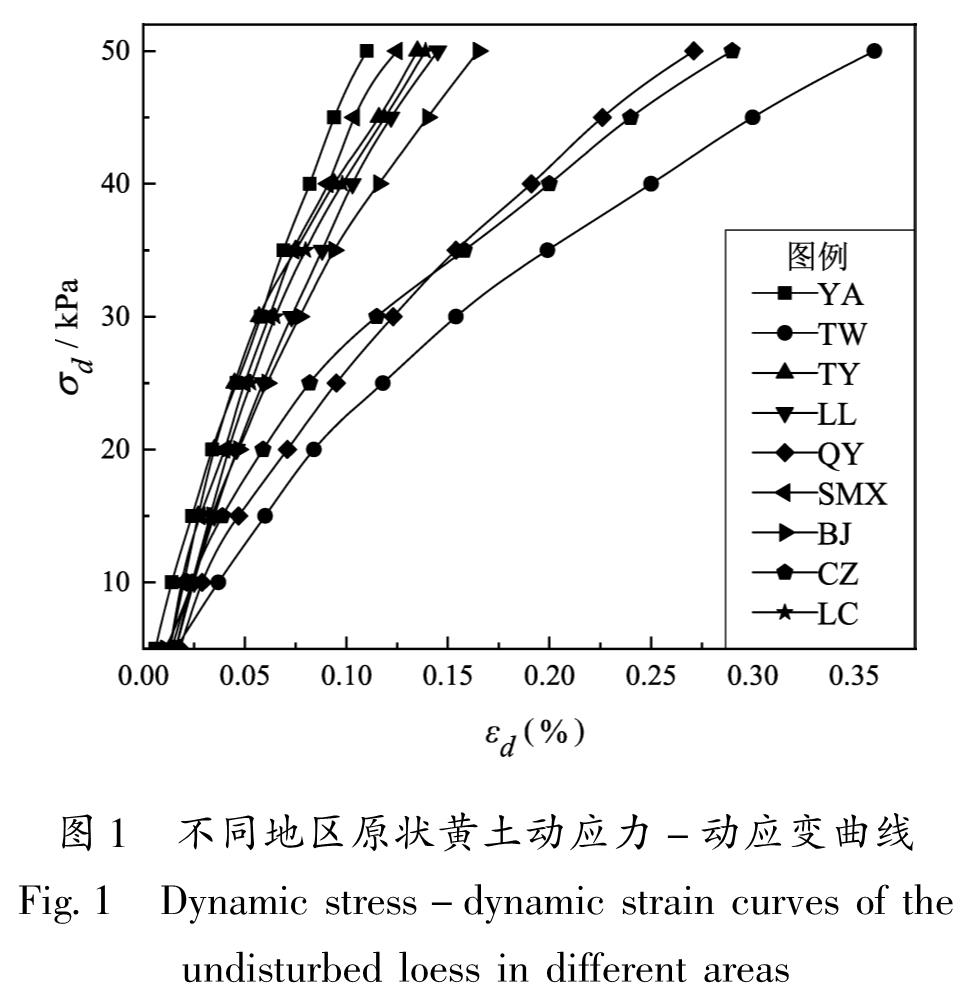
1.2 动三轴试验本文采用英国WF-12440型动三轴-扭剪试验系统开展动三轴试验,该系统通过气动伺服阀控制作动器实现静荷载和循环荷载加载,应变测量可精确至0.001%。参照《土工试验方法标准》(GB/T 50123—2019),试验前先将各取样点的黄土试样削制成高100 mm,直径50 mm的标准圆柱试样。采用各向异性固结模式对各试样进行固结,固结比Kc为1.69。待试样固结稳定后,在固结不排水条件下,采用多级加载方法对一个试样开展土样的动弹性模量和阻尼比测试,循环荷载选用频率为1 Hz的等幅正弦荷载(王谦等,2019),每级加载10次,各级荷载增幅为5 kPa,共加载10级,并实时记录动应力、动应变等试验数据。根据所得的动三轴试验数据绘制动应力-应变曲线(图1)。
1.3 扫描电镜试验对各组土样进行SEM细观结构测试,试验仪器采用KYKY-2800B型电子扫描显微镜。试验前,利用真空冷冻干燥仪将原状黄土进行干燥。人工掰取干燥后试样的断面,并选择平整的自然面作为试样测试面,试样底部用砂纸磨平,最终将试样制备成10 mm×10 mm×2 mm的方形薄片。将薄片用导电胶固定在试样托上,置于离子溅射仪中进行喷金处理,使得试样表面导电易于成像。将试样置于扫描电镜样品室中,设置电压为20 kV进行细观结构图像拍摄,拍摄倍数分别为100、200、400、500、800和1 000倍。为保证细观结构的足够信息量和准确度,各放大倍数均拍摄6~8张图像。
2 研究方法原理
黄土动应力-动应变关系符合Hardin-Drnevich双曲线模型(Hardin,Drnevich,1972):
σd=(εd)/(a+bεd)(1)
动弹性模量的定义为:
Ed=(σd)/(εd)(2)
整理式(1)和式(2)可得:
1/(Ed)=a+bεd(3)
式中:σd为轴向动应力; εd为轴向动应变; a为εd=0时对应的1/Ed,即初始动弹性模量Edmax的倒数; b为1/Ed~εd曲线的斜率,表征最大动应力幅σdmax的倒数。根据动三轴试验记录的动应力和动应变数据,可计算获得初始动弹性模量。
土的阻尼比D则由动应力-动应变滞回曲线求得,将动应力作用下的土体视为黏弹性体。黏弹性体在一个周期内的能量损耗可近似等于滞回圈所围面积(图2),根据其在周期性动荷载一次循环中消耗的能量与该循环中最大剪应变对应的能量之比,即通过计算滞回曲线围成区域的面积ΔF和ΔAOB的面积F得到阻尼比(Hardin,Drnevich,1972; Seed,Idriss,1970):

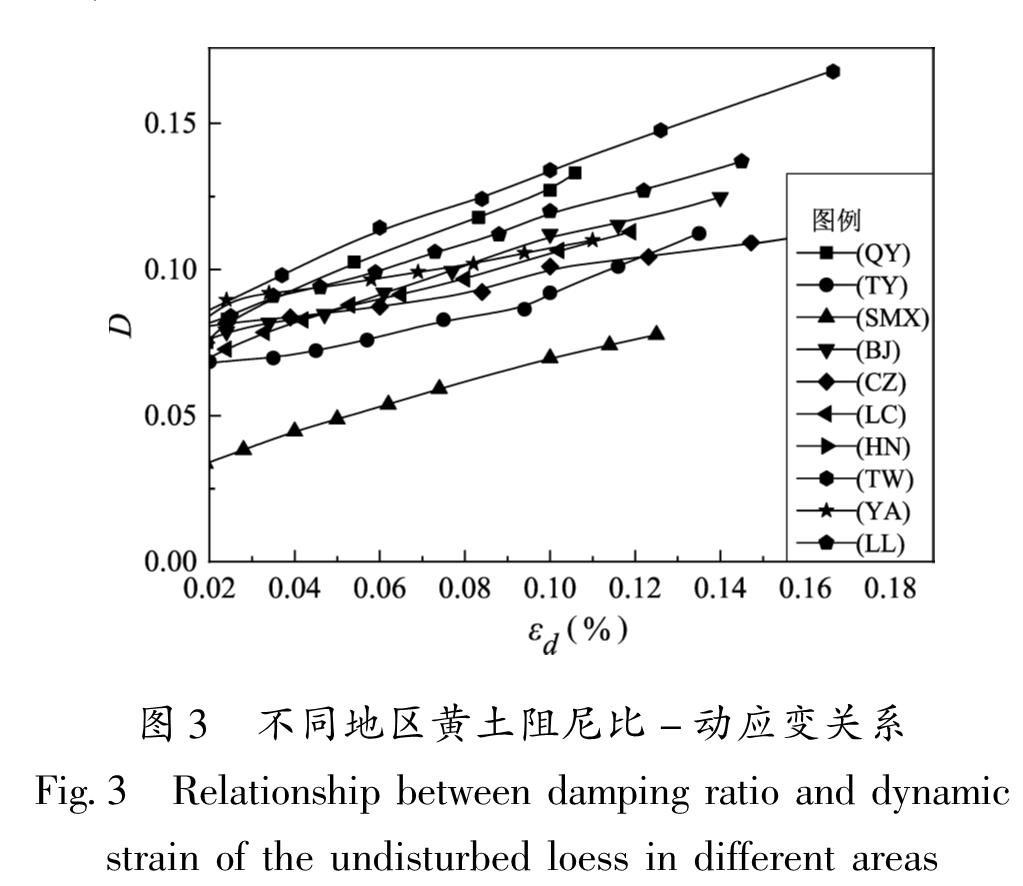
根据动三轴试验记录的动应变数据以及计算得到的各级荷载下的阻尼比,绘制D~εd关系曲线,如图3所示。
3 试验结果与分析
4 讨论
综合以上分析结果认为,黄土的结构性对初始动弹性模量和阻尼比有显著的影响。孔隙的大小、形状和排列细观结构参数与初始动弹性模量之间的相关系数均大于0.9,表观孔隙率与初始动弹性模量间相关系数为0.88,均有较好的相关性。孔隙直径越大、数量越多、颗粒间距越大,颗粒间连接变的薄弱,黄土中特殊的架空孔隙数量增多,而架空孔隙对黄土结构强度具有重要影响; 孔隙形状越复杂,颗粒表面起伏越大,颗粒间接触关系由面-面接触转变为点-面接触及点-点接触,颗粒表面在平面上呈犬牙交错,在空间上镶嵌排列形成粒间缝隙,结构密实度降低(李瑞宽等,2018; 安亮等,2019); 孔隙排列越混乱,土体在外界动应力作用下从无序变为有序的趋势越明显,同时,颗粒排列无序性增加,使得土体结构整体性降低,稳定性减弱。孔隙的大小、数量、形状细观结构参数与阻尼比相关系数之间的相关系数均大于0.9,具有较好的相关性。细观结构参数的变化通过影响颗粒间的错动能力、颗粒间的摩擦幅度以及应力波在土颗粒间的传播途径,进而影响了土体的阻尼比(谷天峰等,2011; Wang et al,2014)。但概率熵与阻尼比相关性为0.81,相关性较低,说明孔隙排列的有序化程度对土体阻尼比的影响不显著。
5 结论
通过对不同地区原状黄土进行动三轴试验和扫描电镜试验,分析了动弹性模量与阻尼比随细观结构参数变化的规律,可得以下结论:
(1)孔隙的大小和数量变化对黄土颗粒间接触关系及密实程度有重要影响,黄土的初始动弹性模量随着平均孔隙直径和表观孔隙率的增大而减小,且与平均孔隙直径之间具有明显的线性相关性; 阻尼比随着平均孔隙直径和表观孔隙率的增大呈非线性增大,其变化规律遵从二次函数关系。
(2)孔隙形状的复杂程度对黄土体结构均匀性影响显著,分形维数越大,初始动弹性模量越低,阻尼比呈先变大而后趋于平缓的趋势,形状变化对阻尼比的影响程度在阻尼比较小时更为明显; 初始动弹性模量和阻尼比与分形维数之间均具有良好的相关性。
(3)概率熵与动弹性模量之间呈明显的正相关关系,阻尼比随着概率熵的增大呈非线性增大,但概率熵对阻尼比的影响比平均孔隙直径、表观孔隙率、分形维数均小,孔隙排列的方向性对土体阻尼比影响较小。
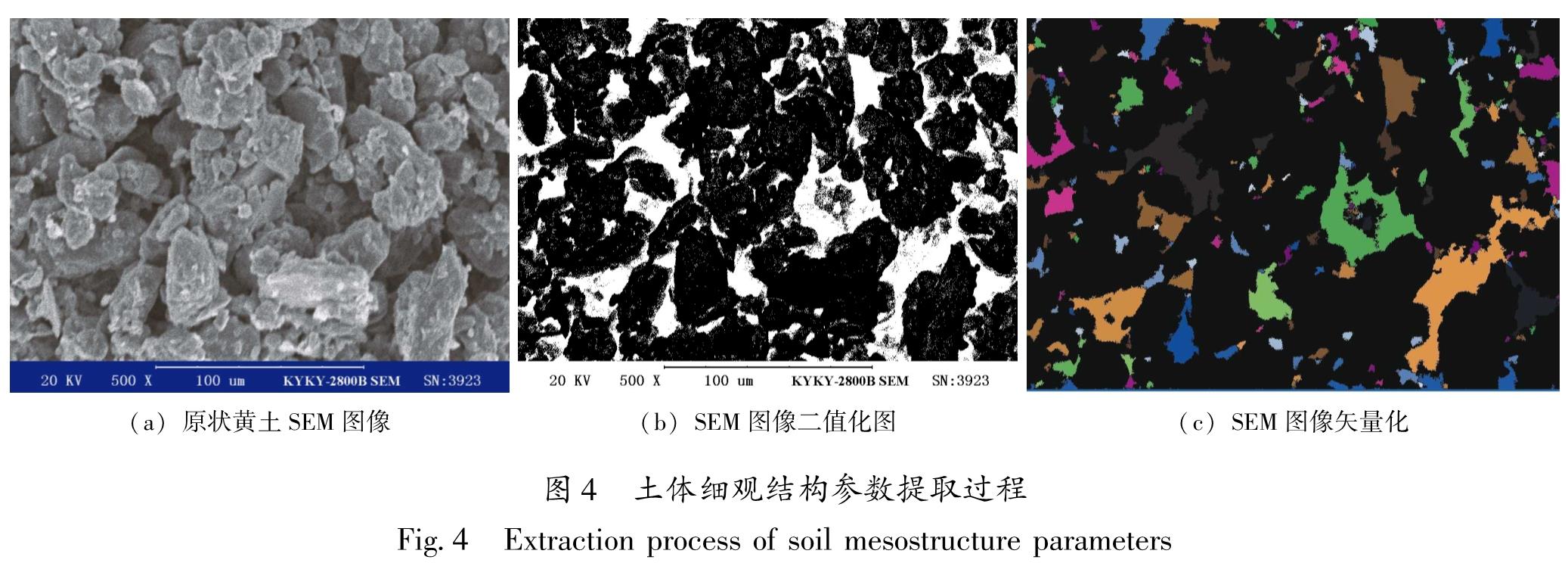
3.1 细观结构参数获取土体细观结构参数的获取依靠南京大学Liu等(2013)开发的PCAS孔隙图像识别与分析系统,该系统可准确识别电镜图像中的颗粒和孔隙,并统计细观结构参数。图4为土体细观结构参数提取过程中的各阶段的图像。获取细观结构参数时,首先对电镜图像进行二值化处理(图4b),为保证二值化图像能够准确反应电镜图像,对图像需调整灰度阈值,且为保证对比原则,将灰度阈值设置为一定值。在调整图像亮度和对比度一致的情况下,通过多人多次选择阈值,最终用取平均值的方法确定了灰度阈值。其次对二值化之后的图像进行矢量化处理(图4c),通过对图像进行腐蚀运算,以清除孔隙间的细小连接; 然后采用种子算法识别出各种子孔隙,再将剩余像素归并到种子孔隙上,从而得到真实孔隙分布。系统可以从处理后的SEM图像中自动提取孔隙几何形态参数和孔隙统计计算参数(Liu et al,2011)。
3.2 黄土细观结构参数对动力特性参数的影响本文计算获取初始动弹模量和0.1%应变下的阻尼比,并通过PCAS系统得到一系列细观结构参数,围绕孔隙的基本特征,从孔隙的尺寸、数量、形态特征、排列特征4个方面分析探讨细观结构参数与黄土动弹性模量和阻尼比之间的关系。
3.2.1 平均孔隙直径孔隙的尺寸大小是土体细观结构基本几何参数。对于规则的图形,可以用直径、长度、宽度等描述其大小,但对于土体而言,在绝大多数情况下孔隙形状极不规则,因而可通过Feret直径描述(Sezer et al,2008)。Feret直径定义为两条与孔隙以一定角度相切的平行直线间的距离,以不同角度相切形成不同区块。取各个孔隙最大Feret直径,计算平均值得到土体的平均孔隙直径。
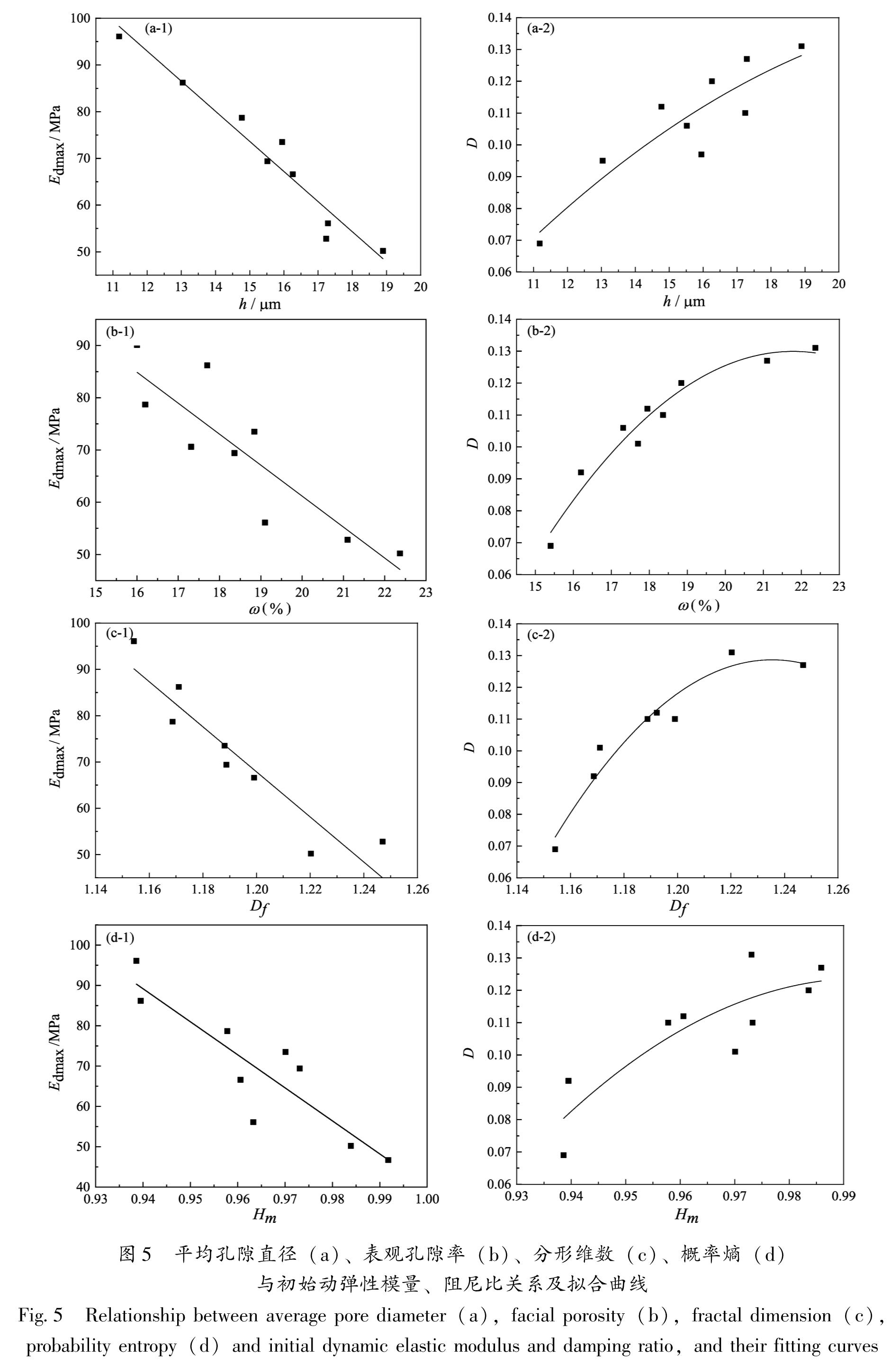
如图5a-1所示,随着平均孔隙直径增大,黄土初始动弹模量明显减小,这是由于平均孔隙直径较大时,土体颗粒间距变大,且颗粒连接方式以接触连接为主,易形成不稳定的架空孔隙,土体较松散; 在外部动应力作用下,土体骨架结构受到破坏,细小土颗粒易掉入孔隙内,导致土体结构失稳,变形势增加,因而土体初始动弹性模量较小。土体阻尼比反映动应力作用下能量因土的内部阻力而损失的性质。由5a-2可知,平均孔隙直径越大,阻尼比随之变大,且其变化趋势具有先增长较快后趋于平缓的特征。平均孔隙直径越大,土体结构越松散,土体内部颗粒错动摩擦机率越大,使得土体黏滞性越大,应力-应变滞回圈形状较为宽厚,阻尼比越大。分别对表观孔隙率与初始动弹性模量、阻尼比之间关系进行线性拟合,可得:
Edmax=-6.44h+170.30,R=0.96(5)
D=-3.39×10-4h2+0.017h-0.079
R=0.91(6)
式中:R表示相关系数。由此可知,平均孔隙直径对初始动弹性模量的影响符合线性关系,与阻尼比之间较好地符合多项式关系。
3.2.2 表观孔隙率表观孔隙率是表征单位面积孔隙占比的参数,用SEM图像范围内孔隙面积与图像面积之比表示(周建等,2014):
ω=(S孔隙)/(S图像)(7)
如图5b-1所示,随着表观孔隙率变大,黄土初始动弹性模量总体上呈减小的趋势,但受黄土不均匀性的影响,线性相关性较不明显; 由图5b-2可见,黄土的阻尼比随着表观孔隙率的增加仍呈先增大后渐趋平缓的特征,两者之间有良好的二次函数拟合关系,说明孔隙面积对土体阻尼比存在明显影响。表观孔隙率变大,表征土体中孔隙面积占比变大,在动应力作用下更易发生变形,且颗粒间摩擦消耗能量增多,从而使得初始动弹性模量降低、阻尼比增大。分别对表观孔隙率与初始动弹性模量、阻尼比之间关系进行拟合可得:
Edmax=-3.76ω+134.62,R=0.86(8)
D=-1.4×10-3ω2+0.006ω-0.53
R=0.97(9)
需要说明的是,表观孔隙率并不能全面地反映孔隙的数量情况。在相同的孔隙面积下,由于土体内的大、中、小孔隙的占比不同,导致黄土的结构强度存在显著差异; 同时,不同地区黄土颗粒之间胶结物的胶结强度也存在显著的差异,这可能是表观孔隙率与初始动弹性模量之间R<0.9的原因。
3.2.3 分形维数孔隙的细观形态特征是影响黄土结构的重要方面。形态特征主要表现为孔隙形状的复杂程度,分形是存在自相似性结构的几何形体,分形理论可处理复杂构型问题,而土体微结构存在自相似性,孔隙分形维数可以定量描述孔隙的复杂程度,采用面积-周长法定义分形维数Df(Cox,Budhu,2008):
lg(C)=Df /2·lg(S)+c1(10)
式中:C为孔隙周长; S为孔隙面积; 当Df=1时,所有孔隙的复杂程度相同; 当Df>1时,孔隙复杂程度增加,且孔隙形状的复杂程度随面积的增加而变大。
由于长治地区分形维数与其他地区相比呈较大离散性,为便于分析去除该点。分形维数与初始动弹性模量和阻尼比关系如图5c所示。由图5c可知,不同地区黄土的孔隙分形维数均大于1。根据分形维数的物理意义,当其较小时,表征孔隙形状复杂程度低,说明土体内颗粒排列较为整齐,结构较为稳定。随着分形维数增大,孔隙形状扭曲复杂,颗粒形态趋于混乱,集团化程度降低,颗粒间接触面积减小,连接趋于薄弱,土体均匀性变差,颗粒在动应力作用下易产生滑动,从而使得土体骨架易发生变形。同时,土颗粒间错动摩擦增加,使得土体在变形过程中消耗更多能量,因而土体初始动弹性模量减小,阻尼比增大。对分形维数与动弹性模量和阻尼比之间的关系进行拟合可得:
Edmax=-486.99Df+652.26,R=0.93(11)
D=-8.49D2f+20.99Df-12.83
R=0.95(12)
由此可知,孔隙形状的复杂程度与初始动弹性模量和阻尼比之间均有良好的相关性。
3.2.4 概率熵土体孔隙和颗粒的排列特征对土体结构有重要影响。熵是统计一个信源的平均信息量的指标,施斌(1997)将概率熵引入到粘性土的微细结构分析中,表征颗粒和孔隙排列的有序化程度。概率熵的计算公式为:

式中:n表示将0°~180°分成区间长度为α的等份区间的个数; Pi表示孔隙的长轴方向在某区间出现的概率; Hm的值域为(0~1),当Hm=0时,表示所有孔隙在同一方向上; Hm越大,孔隙排列的随机性越强。
由图5d-1可知,随着概率熵增大,土体初始动弹性模量减小。这是由于随着概率熵的增大,孔隙排列的无序性增强,在动应力作用下,由于孔隙排列需要适应外部变化而趋于稳定,逐渐向定向排列发展,使得土体结构改变,从而导致初始动弹性模量变小。从图5d-2可知,随着概率熵增大,土体阻尼比整体呈增大的趋势,但离散性相对较大。对概率熵与动弹性模量和阻尼比之间的关系进行拟合可得:
Edmax=-0.841.51Hm+881.76
R=0.92(14)
D=-14.27H2m+28.69Hm-13.96
R=0.84(15)
相比于平均孔隙直径、表观孔隙率、分形维数,概率熵与阻尼比之间的相关性较低,说明孔隙排列的复杂程度对阻尼比的影响较小。
- 安亮,邓津,郭鹏,等.2019.黄土微观参数指标与动弹性模量关联度研究[J].岩土工程学报,41(S2):105-108.
- 谷天峰,王家鼎,郭乐,等.2011.基于图像处理的Q3黄土的微观结构变化研究[J].岩石力学与工程学报,30(S1):3185-3192.
- 胡仲有,骆亚生,李焱.2010.不同地区黄土阻尼比变化特性试验研究[J].地震工程与工程振动,30(2):167-172.
- 冷冠军.2017.基于微观结构特征的咸阳黄土动力特性分析[D].长春:吉林大学.
- 李瑞宽,吴志坚,梁庆国,等.2018.考虑微结构特征的黄土动力特性影响因素研究[J].工程地质学报,26(4):84-93.
- 刘钊钊,钟秀梅,张洪伟,等.2019.典型地貌区原状黄土孔隙细观特征研究[J].水文地质工程地质,(2):148-155.
- 骆亚生.2000.中国典型黄土动力特性及其参数的试验分析[D].西安:西安理工大学.
- 施斌.1997.粘性土微观结构定向性的定量研究[J].地质学报,71(1):36-44.
- 田堪良.2003.黄土的结构性及其动力特性研究[D].西安:西北农林科技大学.
- 王建荣,张振中,王峻,等.1999.振动频率对原状黄土动本构关系的影响[J].地震工程学报,21(3):310-314.
- 王峻,石玉成,王杰民,等.2011.不同地震荷载作用下黄土震陷特性的对比分析[J].岩土工程学报,33(S1):102-105.
- 王峻,王强,王杰民.2010.震后黄土动力学特性试验研究[J].水文地质工程地质,37(4):68-72.
- 王兰民,石玉成,刘旭,等.2003.黄土动力学[M].北京:地震出版社,85-143.
- 王谦,李娜,王平,等.2017.甘南地区黄土的动模量与阻尼比特性研究[J].岩土工程学报,39(S1):192-197.
- 王谦,马金莲,马海萍,等.2019.饱和黄土动剪切模量和阻尼比的试验研究[J].岩石力学与工程学报,38(9):1919-1927.
- 王永焱,林在贯.1990.中国黄土的结构特征及物理力学性质[M].北京:科学出版社.
- 徐世民.2017.考虑微结构的黄土动力特性试验研究[D].兰州:中国地震局兰州地震研究所.
- 周建,邓以亮,曹洋,等.2014.杭州饱和软土固结过程微观结构试验研究[J].中南大学学报(自然科学版),45(6):1998-2005.
- Cox M R,Budhu M.2008.A practical approach to grain shape quantification[J].Engineering Geology,96(1-2):1-16.
- Hardin B O,Drnevich V P.1972.Shear modulus and damping in soils:Design equations and curves[J].Journal of the Soil Mechanics and Foundations Division,ASCE,98(7):667-692.
- Liu C,Shi B,Zhou J,et al.2011.Quantification and characterization of microporosity by image processing,geometric measurement and statistical methods:Application on SEM images of clay materials[J].Applied Clay Science,54(1):97-106.
- Liu C,Tang C S,Shi B,et al.2013.Automatic quantification of crack patterns by image processing[J].Computers & Geosciences,57(4):77-80.
- Seed H B,Idriss I M.1970.Soil moduli and damping factors for dynamic response analysis[R].University of California,Berkeley:Earthquake Engineering Research Center.
- Sezer G I,Ramyar K,Karasu B,et al.2008.Image analysis of sulfate attack on hardened cement paste[J].Materials and Design,29(1):224-231.
- Wang J D,Ren Q,Gu T F,et al.2014.The text analysis on the relationship between slide-zone loess porosity microstructure and dynamic parameters[J].Applied Mechanics and Materials,638-640:633-638.
- GB 18036—2015,中国地震动参数区划图[S].
- GB/T 50123—2019,土工试验方法标准[S].