在地电阻率观测中,为分析观测到视电阻率的变化和地下不同区域介质真电阻率变化之间的关系,钱家栋等(1985)提出了影响系数理论。多数情况下,地电阻率观测区可近似为分层均匀的电性结构(图1),对于n层结构,设第i层电阻率为ρ_i,厚度为h_i(i=1,2,…,n),其中底层厚度h_n→∞。在地表或地下采用对称四极或其它装置观测得到的视电阻率ρ_s是地下各层介质电阻率和厚度的函数,即:

ρ_s=f(ρ₁,ρ₂,…,ρ_x,h₁,h₂,…,h_n)(1)

假定各层厚度不变,视电阻率变化是由各层电阻率变化引起的,由式(1)求全微分并整理,得到:

式中:

式(2)表明,视电阻率的相对变化率等于各层介质电阻率相对变化率的加权求和,S_i即为第i层的加权系数,当第i层介质电阻率发生变化时,则该层对观测值变化率的贡献与S_i成正比。另一方面,若某两层介质电阻率的相对变化率相同,则影响系数较大的一层对观测值变化率的贡献也较大,因此将S_i称为影响系数(钱家栋等,1985)。

图1 水平层状电阻率结构模型
Fig.1 Model of the structure of horizontal stratified resistivity

地电阻率方法以设置于地表的固定装置系统所观测到视电阻率的时间变化为研究对象,影响系数理论强调了视电阻率的时间变化,它是由测区下方不同分区介质电阻率发生变化综合影响的结果。S_i也被称为响应系数(杨明芝等,1986)、权系数(许秀芬,姚福鑫,1980)或者灵敏度系数(Lu et al,1999)。影响系数理论的重要特点之一是:

这是一个重要的特性,它表明某些地层的影响系数减少时,其余一些地层的影响系数就会增加。目前,尚未见到有严格的科学论证。最简单的证明是,在测区下方各层介质电阻率相对变化相等的条件下,即式(2)中(Δρ_i)/(ρ_i)都相等时,地表固定装置系统的视电阻率相对变化应等于各层介质电阻率的相对变化,即:

因此。

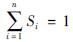但问题在于,若测区下方不同分区介质的电阻率变化率各不相等时,式(5)就不适用了。一些涉及该问题的早期文献(Seigel,1959; Roy,Poddar,1981; Wait,1981)曾声称,可以证明其影响系数满足式(4)这一关系,并且为诸多关于上述影响系数理论的文章所引用。笔者对这些早期文献进行了复核,发现它们对上述特性的证明,实际上与前述假设各分区电阻率变化率相等前提下的证明,在思路上是一致的。例如,Seigel(1959)根据导电介质中的直流电场理论有:

tρ_s(ρ₁,ρ₂,…,ρ_n)=f(tρ₁,tρ₂,…,tρ_n)(6)

式中:t为任意正数,说明视电阻率是各地层电阻率的一次齐次函数,Seigel(1959)、Roy和Poddar(1981)以及Wait(1981)证明上述特性时都使用了该齐次函数关系,根据齐次函数的欧拉定理,由式(6)可以得出:

然而从数学上看,式(6)描述的是各层电阻率的相对变化率都相等的一种特殊情形,即当各层电阻率都变化到原来的t倍时,视电阻率也将变化到原来的t倍,在这种情形下由式(2)也容易得到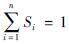。但实际中更常见的情况是各层电阻率的相对变化率并不相等,式(6)没有包含这种情形,即前人利用齐次函数关系所做的证明并不完善,没有回答当各层电阻率的相对变化率不相等时,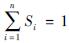是否仍然成立。

由于水平层状介质影响系数理论在地电阻率前兆观测和分析中具有重要的应用(许秀芬,姚福鑫,1980; 钱家栋等,1985; 赵和云等,1985; 杨明芝等,1986; Xue et al,1994; Lu et al,1999; 毛先进等,2014,2019; 解滔等,2016,2019),因此针对一维(即分层均匀)模型,本文给出无论各层电阻率的相对变化率是否相等的条件下,上述特性的证明。

对于分层均匀介质,地面上距点电流源r处的电位为(傅良魁,1991):

式中:T₁(m)是地面的电阻率转换函数; J₀(mr)是零阶贝塞尔函数; m是积分变量。

无论采用何种装置观测,视电阻率为:

式中:K为装置系数; I为供电电流强度; ΔU为测量电极之间的电位差。

以二极装置为例,据式(8)(9),可得:

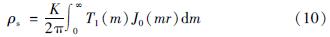
T₁(m)可以由地下各层界面的电阻率转换函数按如下递推关系得到(傅良魁,1991):

式中:T_i(m)是第i层顶面的电阻率转换函数。通过式(11)(12)的递推、复合关系,所得到的T₁(m)是各层电阻率(假定各层厚度不变)的函数,另外易知T_i(m)关于各层电阻率是可导的。

对比式(10)和式(1),可知式(1)右侧的函数关系f(·)由T₁(m)决定。因此,问题转化为:证明对任一m∈[0,∞),下式成立:

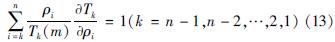
证明过程分为两步:

第一步为构造可微函数,其中,x,y为实数,α,β为常数,证明f(x,y)满足: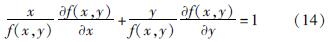

对f(x,y)求偏导有:

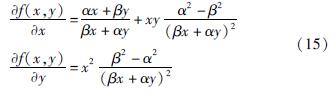
计算得到:

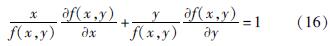
即式(14)成立。

第二步为采用归纳法证明式(13)成立。

当k=n-1时,由式(11)和(12)得到第n-1层顶面的电阻率转换函数为:

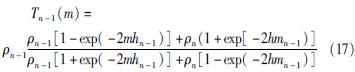
由式(17)可见,假定h_n-1不变,右边分子及分母中ρ_n-1和ρ_n的系数为常数,因此对确定的m,T_n-1(m)只是ρ_n-1,ρ_n的函数。为简洁起见,记T_n-1(m)=T_n-1, α_n-1=1-exp(-2mh_n-1), β_n-1=1+exp(-2mh_n-1)。则式(17)重写为:

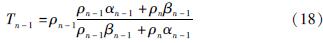
由式(18)可见,T_n-1作为ρ_n-1和ρ_n的函数,与前文中构造的函数f(x,y)在形式上完全相同,因此满足式(14),即:

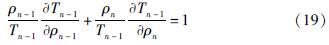
即k=n-1时,式(13)成立。

当k=n-2时,由式(12)得到第n-2层顶面的电阻率转换函数为:

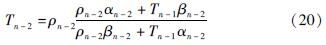
式中:α_n-2=1-exp(-2mh_n-2); β_n-2=1+exp(-2mh_n-2); 因T_n-1的复合关系,T_n-2是ρ_n-2,ρ_n-1和ρ_n的函数,利用复合函数的求导法则,有:

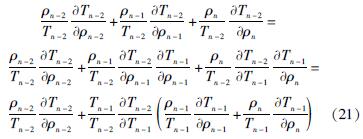
将式(19)带入式(21)右边最后一项得到:

从式(20)可见,T_n-2作为ρ_n-2和T_<sub>n-1的函数与 f(x,y)在函数形式上完全相同,因此满足式(14),即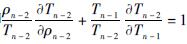,将其带入式(22)右边得到:

即k=n-2时,式(13)成立。

设当k=2时,式(13)成立,即:

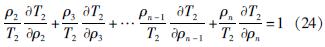
则当k=1时,由式(12)得到第1层顶面(地面)的电阻率转换函数T₁为:

式中:因T₂的复合关系,T₁是ρ₁,ρ₂,…,ρ_n的函数; α₁=1-exp(-2mh₁); β₁=1+exp(-2mh₁)。于是有:

将式(24)带入式(26)最后一项得到:

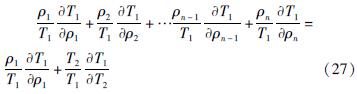
式(25)表明,T₁作为ρ₁和T₂的函数,与 f(x,y)在函数形式上完全相同,因此满足式(14),即

将其带入式(27)右边得到:

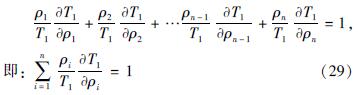
即k=1时,式(13)成立。

因此式(13)对k=n-1,n-2,…,2,1均成立。

以上证明过程中并没有用到式(4)的齐次函数关系,结合前文的分析,就证明了对于分层均匀结构,无论各层电阻率的相对变化率是否相等,各层影响系数的代数和都等于1。

井下观测(即供电电极和测量电极都在地下)时,水平层状介质视电阻率的计算也是归结为电阻率转换函数及相应的递推关系,虽然递推关系比地面观测复杂,但其电阻率转换函数表达式在形式上与地面观测时相同(葛为中,1994),因而采用上述方法可以证明井下观测时影响系数亦具有代数和等于1的特性,计算结果也证明了这一点(毛先进等,2014; 解滔等,2016)。

对一维(分层均匀)结构,通过构造一个与电阻率转换函数形式相同的辅助函数的方法,笔者证明了无论在地面还是井下观测,不管各层电阻率的相对变化率是否相等,各层电阻率影响系数的代数和都等于1,这是一个重要的特性,而前人只是在各层电阻率的相对变化率相等这一条件证明了影响系数具有这一特性。本文结果对于研究视电阻率的时间变化与地下各层介质电阻率的变化之间的定量关系是很有意义的。对于更为复杂的结构,能否从理论上对影响系数的这种特性给出一般性的证明还有待进一步研究。