基金项目:国家重点研发计划(2019YFE0112500),国家自然科学基金(51708518)和中国地震局地球物理研究所基本科研业务费专项(DQJB19B43、DQJB20X08)联合资助.
(1.中国地震局地球物理研究所,北京 100081; 2.北京工业大学 城市建设学部,北京100124)
(1.Institute of Geophysics,China Earthquake Administration,Beijing 100081)(2.Faculty of Architectnre,Civil and Transportation Engineering,Beijing University of Technology,Beijing 100124)
RID-passive,mega-sub controlled system; long-period ground motion; seismic response; seismic performance
备注
基金项目:国家重点研发计划(2019YFE0112500),国家自然科学基金(51708518)和中国地震局地球物理研究所基本科研业务费专项(DQJB19B43、DQJB20X08)联合资助.
引言
随着经济的快速发展,(超)高层建筑越来越多,体量也越来越大。巨型结构体系因其良好的整体性,新颖美观的结构形式等优点,在高层结构设计和研究中受到越来越多的关注。巨型结构由主、子两级结构构成,主结构由不同于常规梁、柱结构概念的巨型构件组成,子结构由常规构件组成,最后形成一种特殊结构体系(赵西安,1993)。1995年美国学者Feng首先提出巨-子结构控制体系的概念,即在巨型框架的基础上通过合理的设计放松主、子结构之间的侧向连接,使二者之间产生相对运动从而形成了巨型结构振动控制体系(Feng,Mita,1995; Chai,Feng,1997)。经过20多年的研究和发展,目前已有诸多针对巨型结构的减震措施,这类结构经过合理的设计或者施加减震装置,主结构与子结构都可达到良好的减震效果(王肇民等,1999; Lan et al,2000; Zhang et al,2005)。当子结构与主结构之间利用阻尼器装置连接时称之为巨-子结构消能控制体系,在普通地震动作用下,该结构体系能有效减小主结构及子结构的地震响应,具有很好的工程应用价值。但是已有研究中未考虑长周期地震动特性对巨-子结构消能控制体系地震响应的影响,长周期地震动作用下该体系的减震性能也缺乏深入研究。
长周期地震动是一种长持时且卓越周期较长的地震动。近场与远场均存在长周期地震动,其中,远场长周期地震动亦称远场类谐和地震动,近场长周期地震动则主要为近断层脉冲型地震动,而近断层脉冲型地震动又包括近断层向前方向性地震动与近断层滑冲型地震动两种形式(Kalkan,Kunnath,2006; Koketsu,Miyake,2008; 徐龙军等,2008; 王博等,2018; 贾路等,2019)。国内学者在长周期地震动特性方面已有诸多研究,俞言祥(2004)对长周期地震动研究的主要方法,即经验统计方法和震源模型方法进行了总结,并分析了它们的适用范围和存在的问题; 刘烁宇和李英民(2018)给出了盆地型长周期地震动的判别准则; 邵越风等(2017)以及李雪红等(2014)分别提出了区分长周期地震动和普通地震动的判定指标。
本文基于旋转惯容阻尼器(RID)实际物理质量较小,但能提供较大阻尼力的特性(Liu et al,2018),提出将RID附加到巨型结构体系形成RID-巨-子结构消能控制体系。基于强震动观测数据的统计分析,探讨长周期地震动与普通地震动特性的差异,在此基础上进一步研究长周期地震动对RID-巨-子结构消能控制体系地震响应的影响以及长周期地震动作用下该新型消能体系的减震性能。
1 长周期地震动特性研究
基于前人研究中普遍认为的远场类谐和地震动、近断层脉冲型地震动及普通地震动,各选取118条进行研究(李英民等,2018; 李雪红等,2014; 王博等,2013,2018; 徐龙军等,2008; 许立英等,2019),通过对比3类地震动的峰值、峰值比、持时以及频谱特性的异同得出长周期地震动与普通地震动的特征差异。其中地震动记录从太平洋地区地震工程研究中心(简称为PEER)中的NGA-West2强震动数据库进行下载。由于Wang等(2011)提出的自动基线校正方法具有效率高、自动化程度高等优点,本文采用该方法对加速度记录进行基线校正。
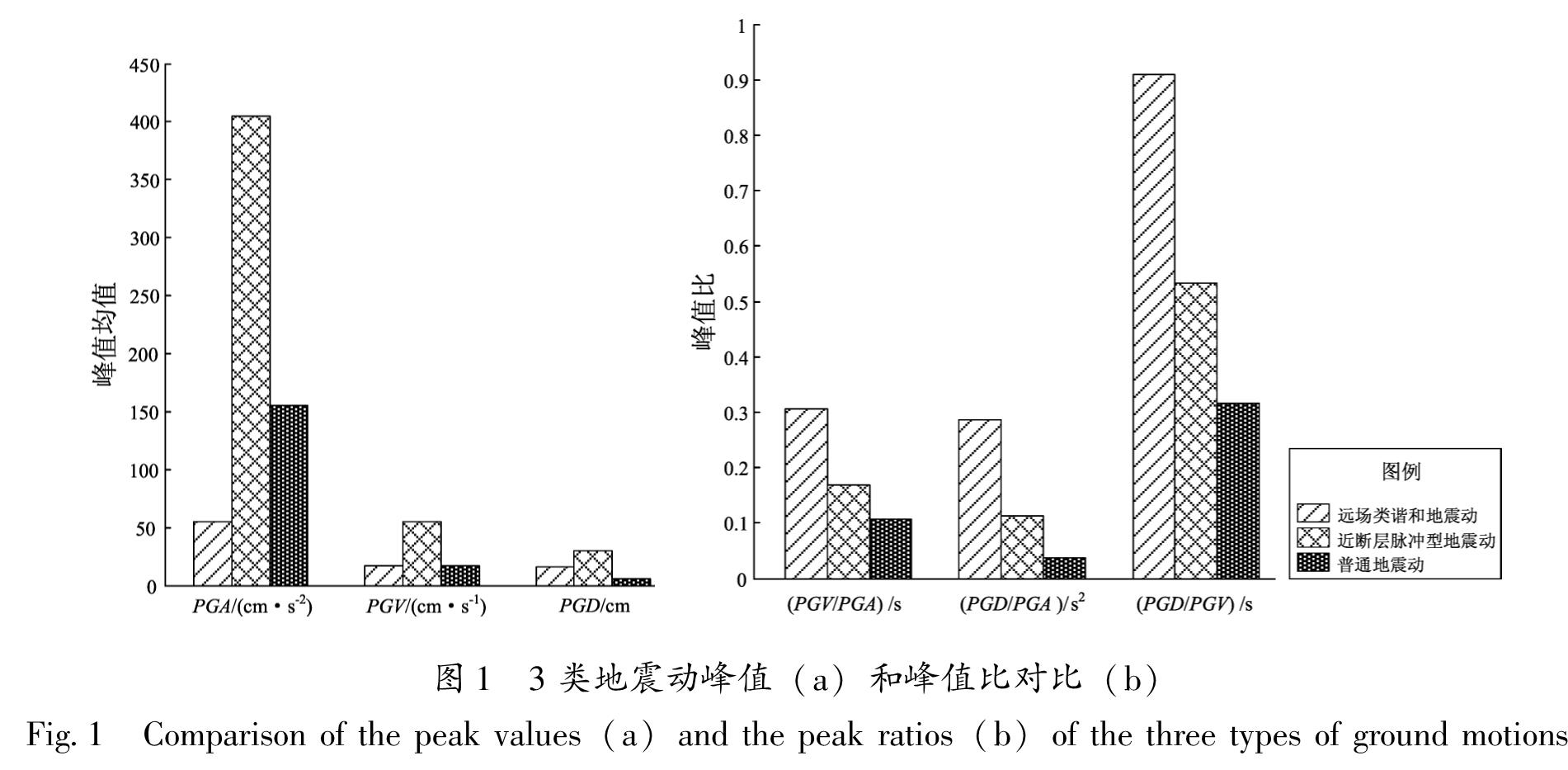
1.1 地震动峰值与峰值比强震记录的峰值与峰值比是地震动的基本特征参数,它们包含了大量与结构动力响应相关的信息。取3类地震动的峰值加速度PGA、峰值速度PGV以及峰值位移PGD,并对计算得到PGV/PGA、PGD/PGA和PGD/PGV进行对比分析(图1)。
图1 3类地震动峰值(a)和峰值比对比(b)
Fig.1 Comparison of the peak values(a)and the peak ratios(b)of the three types of ground motions由图1可以看出,近断层脉冲型地震动与普通地震动的PGA远大于远场类谐和地震动。近断层脉冲型地震动的PGA、PGV及PGD明显大于其它两类地震动; 远场类谐和地震动的PGA、PGV及PGD均相对较小; 普通地震动的PGA较大,但PGV与PGD相对较小。峰值比方面,长周期地震动的PGV/PGA、PGD/PGA和PGD/PGV均大于普通地震动,这说明在同时考虑不同峰值的情况下,长周期地震动的不同峰值间的相互影响较普通地震动大。
1.2 地震动持时本文采用地震时持时和相对持时来进行分析对比,相对持时采用90%能量持时,其定义为:地震动能量达到总能量的5%开始至达到总能量的95%之间所经历的时间,计算公式如下:

式中:I为总能量; T为地震动总持时; a(t)为地震动加速度时程。T2-T1即为计算得到的90%相对持时(胡聿贤,2006)。
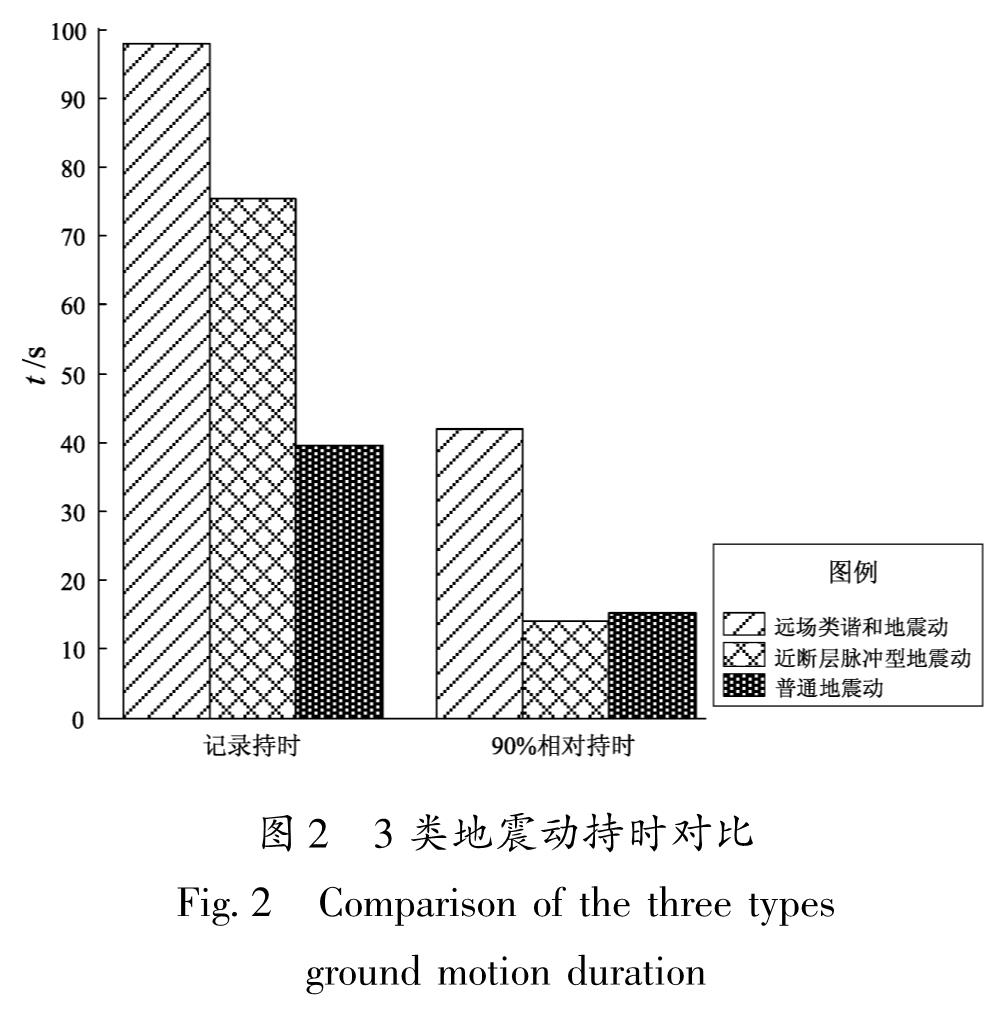
分别计算并获取强地震动及普通地震动的记录持时与90%相对持时如图2所示,由图可以看出,长周期地震动的记录持时明显长于普通地震动。其中,远场类谐和地震动的记录持时最长,其次为近断层脉冲型地震动。而在90%相对持时的对比中,远场类谐和地震动的相对持时最长,近断层脉冲型地震动与普通地震动的相对持时相差不大。
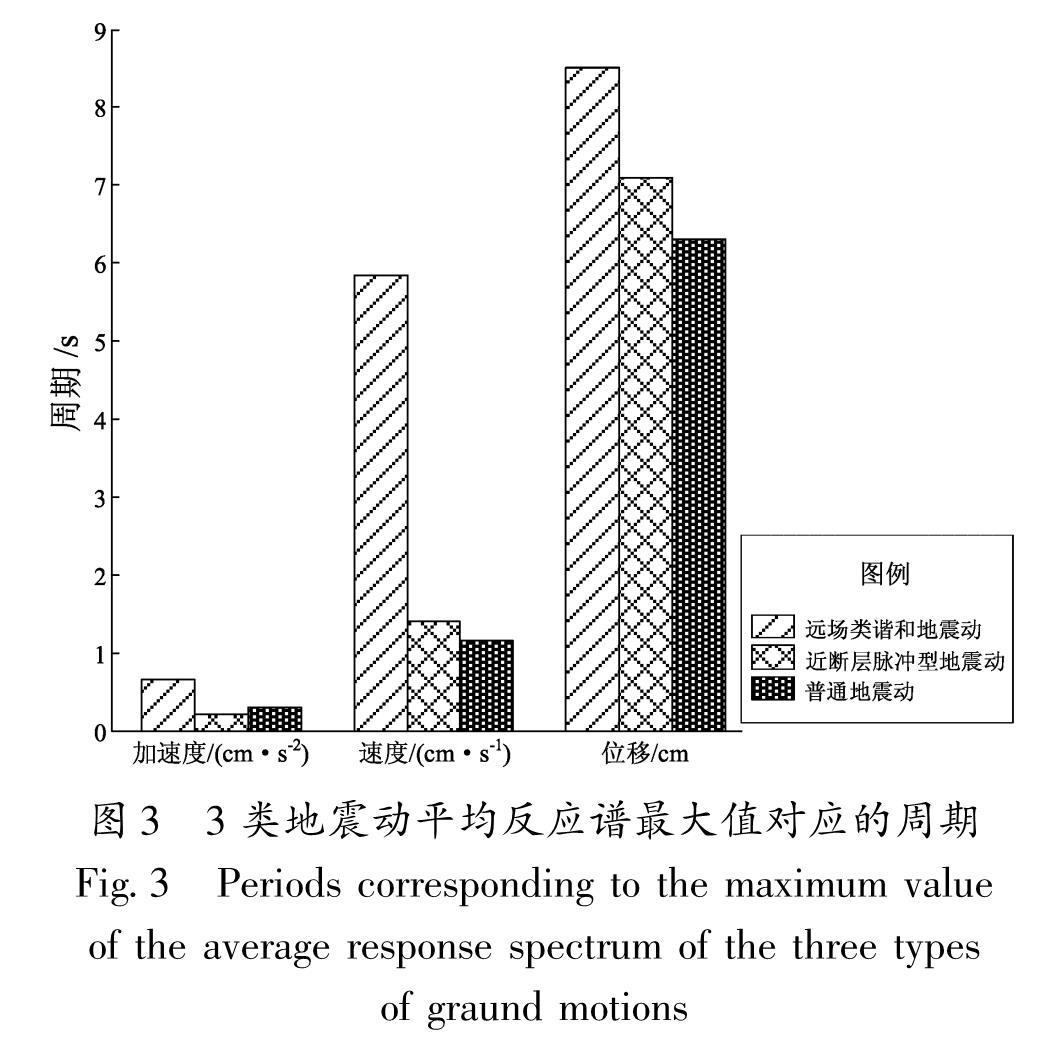
1.3 频谱特性分析与比较图3给出了3类地震动的平均加速度、平均速度及平均位移反应谱最大值所对应的周期的对比图。由图3可以看出,远场类谐和地震动平均加速度反应谱最大值对应的周期大于其它两类地震动。两类长周期地震动的平均速度及位移反应谱峰值对应的结构周期大于普通地震动,其中远场类谐和地震动平均速度及位移反应谱峰值对应的结构周期要较大。
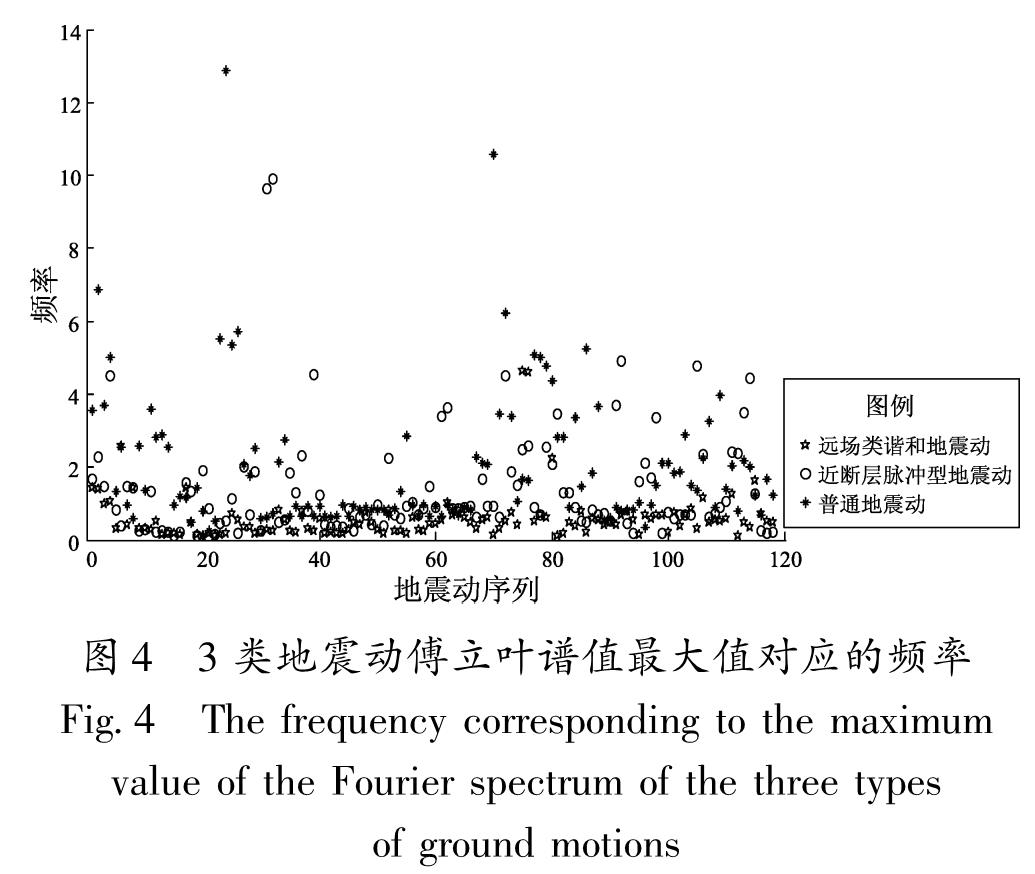
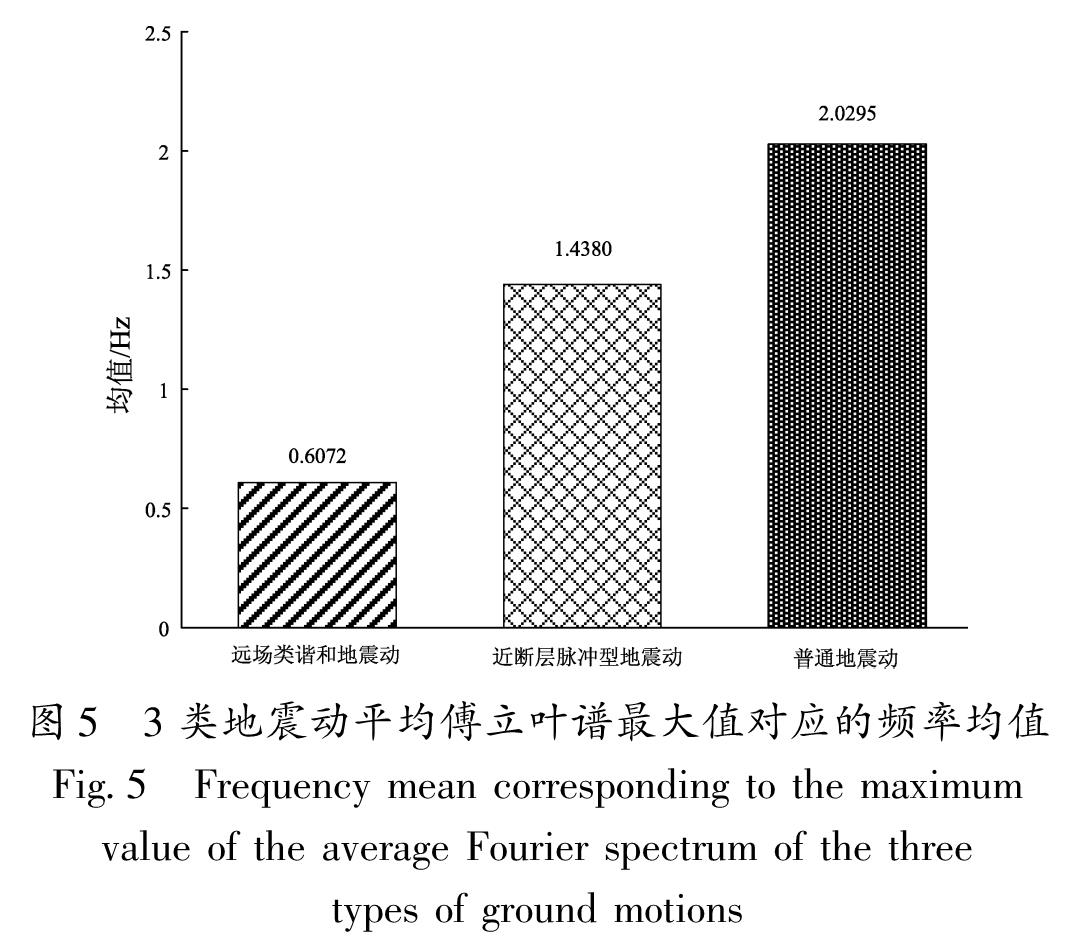
图4、5分别为3类地震动的傅里叶谱最大值对应的频率分布及频率均值的对比图。由图5可以看出,两类长周期地震动的傅里叶谱最大值对应的频率均值小于普通地震动,其中远场类谐和地震动的傅里叶谱最大值对应的频率均值最小,为0.607 2 Hz。且由图4可以看出,远场类谐和地震动的频率成分主要以低频为主,与其相比,近断层脉冲型地震动的频率分布范围更广。
本文在李祥秀等(2021)研究的基础上,进一步分析长周期地震动对RID-巨-子结构消能控制体系地震响应的影响以及长周期地震动作用下该体系的减震性能。
图3 3类地震动平均反应谱最大值对应的周期
Fig.3 Periods corresponding to the maximum value of the average response spectrum of the three types of graund motions图4 3类地震动傅立叶谱值最大值对应的频率
Fig.4 The frequency corresponding to the maximum value of the Fourier spectrum of the three types of ground motions2 长周期地震动对RID-巨-子结构消能控制体系地震响应影响的研究
3 长周期地震动作用下RID-巨-子结构消能控制体系减震性能研究
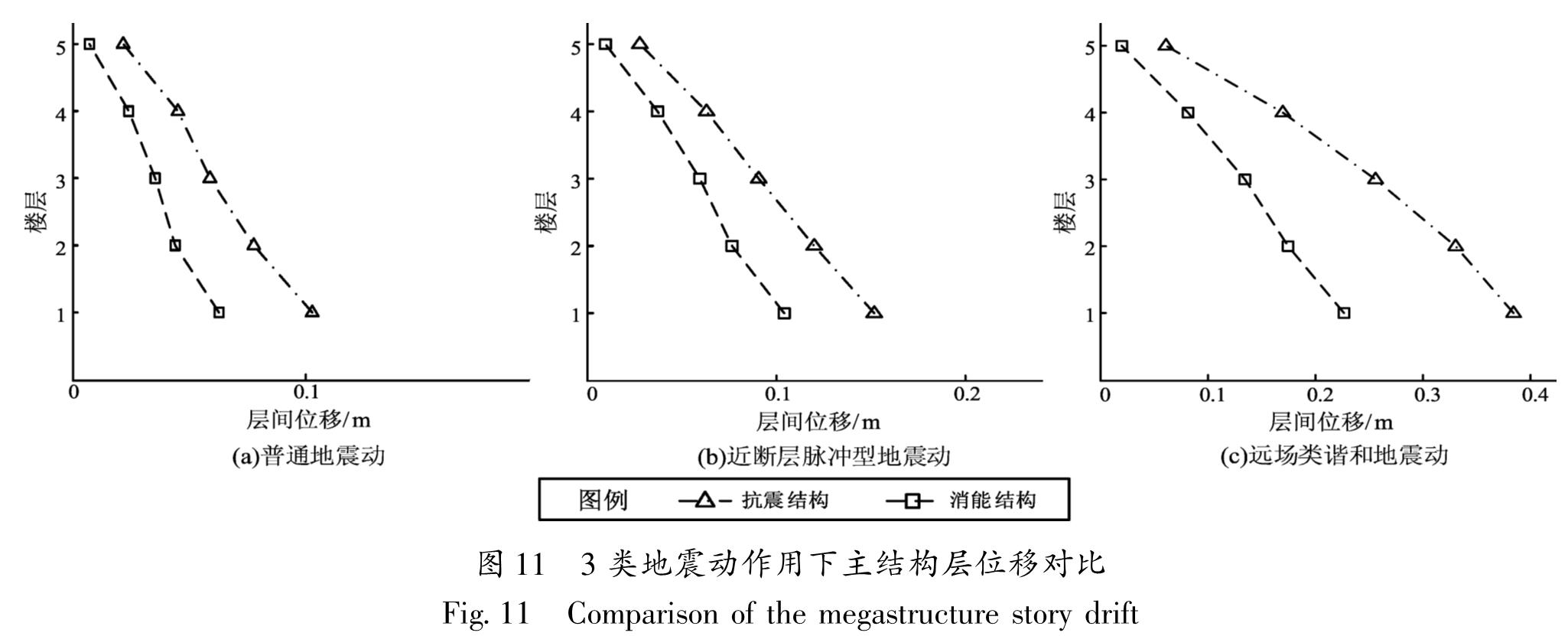
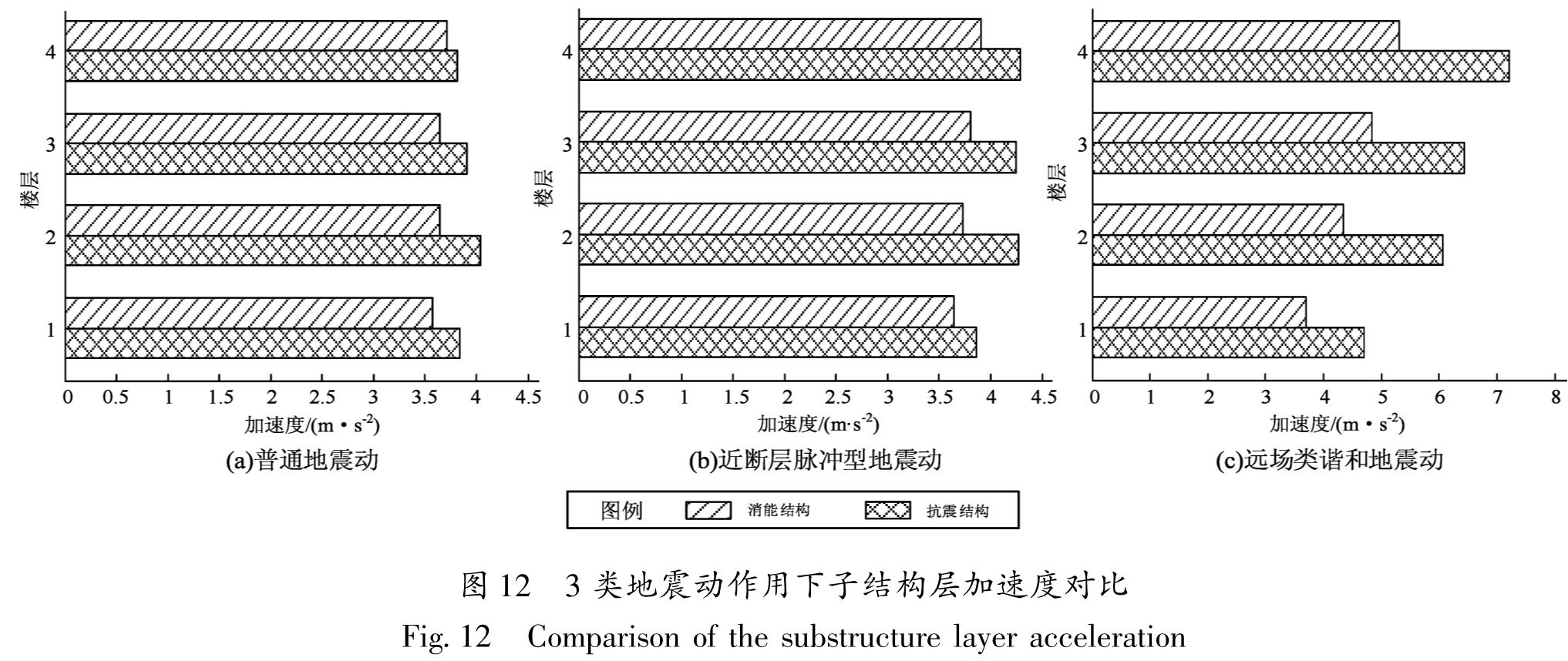
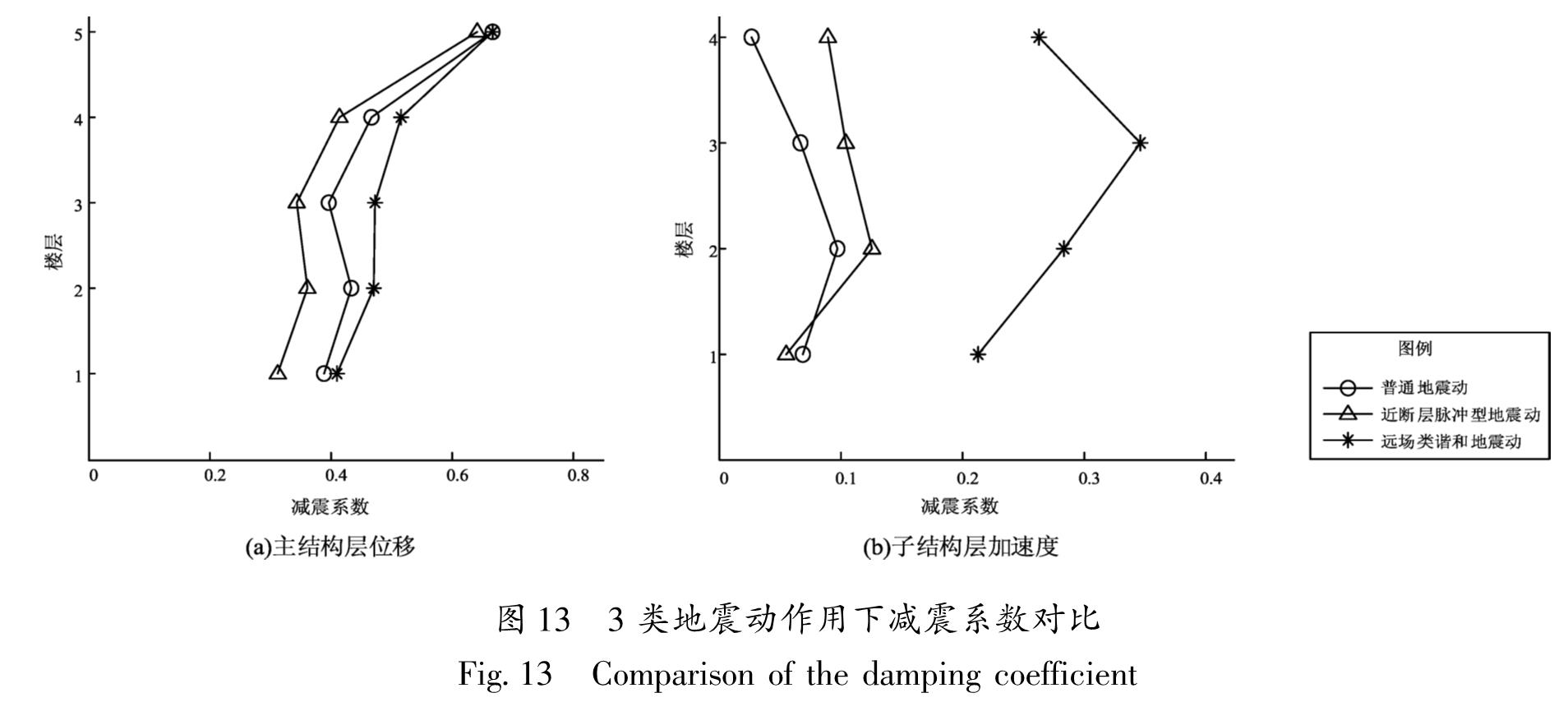
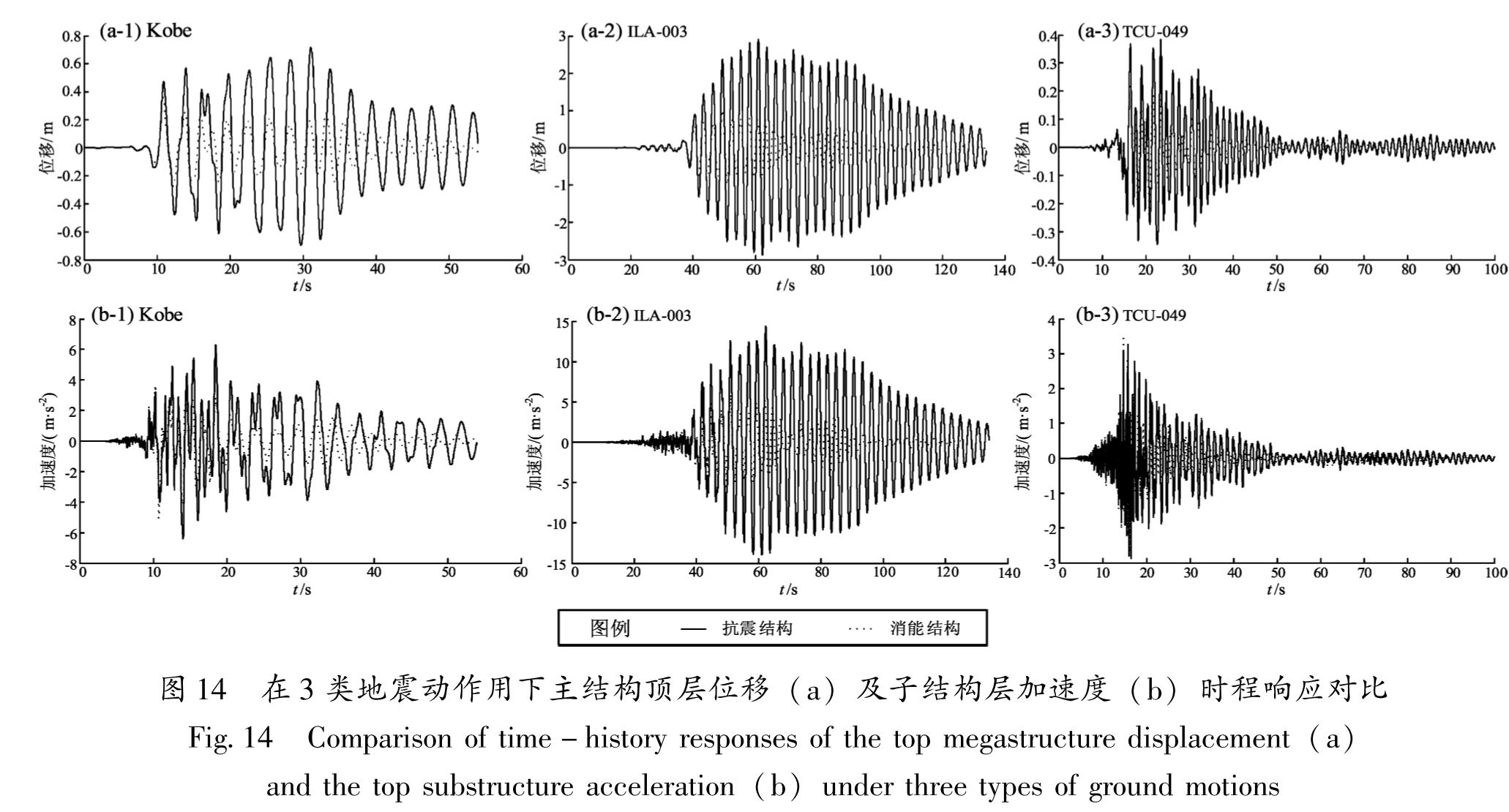
通过对比3类地震动作用下巨-子结构抗震体系及RID-巨-子结构消能控制体系地震响应的异同,研究在长周期地震动作用下RID-巨-子结构消能控制体系的减震性能。笔者分别给出在3类地震动作用下抗震结构和消能结构体系中主结构的层位移、子结构层加速度的均值对比(图 11、图 12)。同时,定义减震系数R=(抗震结构体系的地震响应-消能结构体系的地震响应)/抗震结构体系的地震响应,并给出在3类地震动作用下主结构层位移和子结构层加速度的减震系数对比(图 13)。再选取3类地震动记录各1条:远场长周期地震动为ILA003-EW、近断层脉冲型地震动为TCU049-EW、普通地震动为Kobe,研究RID-巨-子结构消能控制体系在长周期地震动作用下的时程响应(图 14)。
图 14 在3类地震动作用下主结构顶层位移(a)及子结构层加速度(b)时程响应对比
Fig.14 Comparison of time-history responses of the top megastructure displacement(a) and the top substructure acceleration(b)under three types of ground motions由图 11~14可以看出,在3类地震动作用下,RID-巨-子结构消能控制体系相对抗震体系而言能有效地减小主结构的层位移和子结构的层加速度,即在子结构与主结构之间施加RID能有效地减小在地震作用下结构体系的地震响应,且对主结构的层位移的减震效果更为明显。由图 13可以看出,当地震动记录的加速度峰值取值相同时,在远场类谐和地震动作用下RID-巨-子结构消能控制体系对主结构层位移和子结构层加速度的减震效果要优于在普通地震动和近断层速度脉冲型地震动作用下的减震效果。
4 结论
本文基于强震动观测数据的统计分析,研究了远场类谐和地震动、近断层速度脉冲型地震动两类长周期与普通地震动特性的差异。在此基础上,通过建立RID-巨-子结构消能控制体系的振动微分方程,分析了两类长周期地震动对该体系地震响应的影响,并研究了长周期地震动作用下RID-巨-子结构消能控制体系的减震性能。得到如下结论:
(1)两类长周期地震动的PGV/PGA、PGD/PGA和PGD/PGV要大于普通地震动的PGV/PGA、PGD/PGA和PGD/PGV,与普通地震动相比,长周期地震动有更大的峰值比; 在PGA的比较中,近断层速度脉冲地震动的PGA最大,远场类谐和地震动的加速度明显小于另外两类地震动。在地震动持时的比较中,远场类谐和地震动的记录持时最长,其次为近断层脉冲型地震动。而在90%相对持时的对比中,远场类谐和地震动的相对持时最长,近断层脉冲型地震动与普通地震动的相对持时相差不大; 在频谱特性方面,远场类谐和地震动的频率成分主要以低频为主,近断层脉冲型地震动的频率分布范围相对远场类谐和地震动而言分布更广。
(2)两类长周期地震动作用下,RID-巨-子结构消能控制体系的结构反应要大于普通地震动作用下的结构反应; 两类长周期地震动对主结构和子结构层位移的影响要明显大于对子结构层加速度的影响,且地震动记录的加速度峰值取值相同时,远场类谐和地震动对主结构层位移和子结构层位移、层加速度的影响要远大于近断层速度脉冲型地震动对其的影响。
(3)相对于巨-子结构抗震体系而言,在子结构与主结构之间施加RID阻尼器的消能结构体系能有效地减小结构体系在长周期地震动作用下的地震响应,减震效果明显。
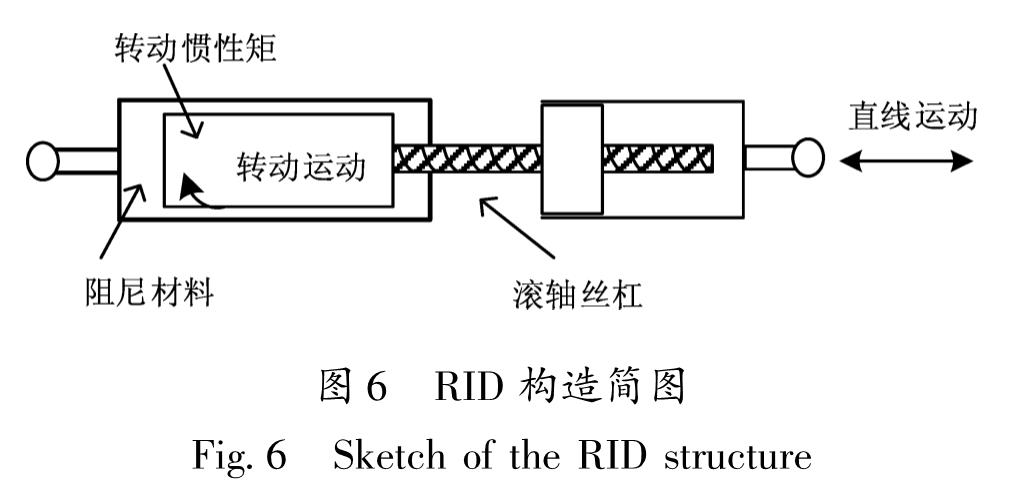
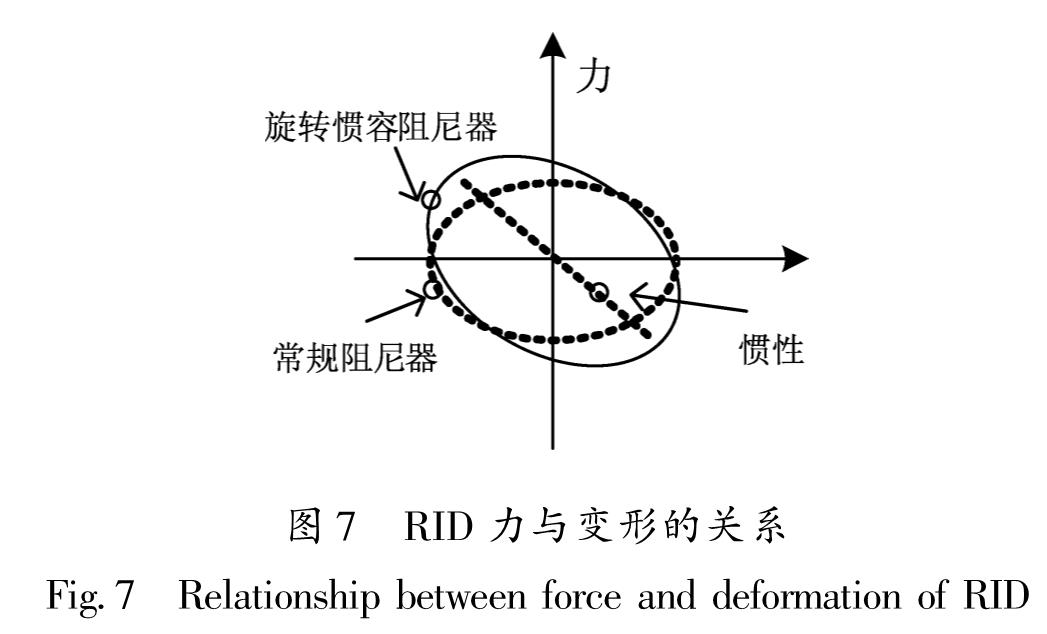
2.1 RID工作机理图6为RID的工作机理:通过滚轴丝杠等构件将直线运动转化为转动运动,当进行合理设计后可以起到位移放大作用,使更多的能量在管腔室内的阻尼材料作用下进行耗散。由于RID存在转动惯量,工作时将产生转动惯性力,随之带来“负刚度效应”。因此,RID最终的输出力包含粘滞力和“负刚度”力,其力与变形的曲线如图7所示。
2.2 分析模型及运动方程为了方便分析,本文采用串联质点系模型来模拟主结构,将每小层子结构分别简化为单个质点。在每一层子结构的顶部与主结构之间布置RID,RID用一个具有等效质量为b的惯容器和一个等效阻尼系数为cb的粘滞阻尼器来模拟,其产生的阻尼力为:

式中:
 分别为RID两端的加速度和速度。
分别为RID两端的加速度和速度。图8所示简化分析模型的运动方程为:

式中:

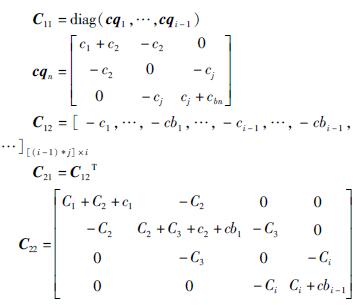
式中:mj、cj、kj分别为每层子结构的等效质量、等效阻尼及等效刚度; Mi、Ci、Ki分别为每层主结构的等效质量、等效阻尼和等效刚度; bj、cbj分别为RID的等效质量和等效阻尼系数; x=[xj xi]T,xj、xi分别为子结构与主结构相对地面的位移;
 为地震动加速度。2.3 典型工程概况
为地震动加速度。2.3 典型工程概况选取一典型工程作为算例(蓝宗建等,2002),主结构的模态阻尼比取值为0.05,主结构为5层,在2~5层主结构中均设置子结构。主结构的每层质量为9×105 kg、顶层质量为4.5×105 kg、层抗剪刚度为9×107 N/m。子结构的质量由质量比u决定,u定义为子结构与主结构质量的比值,取u=1,子结构的层剪切刚度取为4×108 N/m。每大层子结构中包含6层结构,且每层子结构的参数取值一致。利用MATLAB编制相关程序并计算可得主框架简化成串联质点系模型后结构的第一周期为2.008 2 s,
每大层子结构的基本周期为0.504 7 s。RID的等效质量b和等效阻尼系数cb按照李祥秀等(2021)的研究结果,分别取为2×104 kg、1×107,此时RID-巨-子结构消能控制体系的基本周期为2.718 0 s。
2.4 长周期地震动对RID-巨-子结构消能控制体系地震响应的影响以远场类谐和地震动、近断层脉冲型地震动以及普通地震动各118条作为输入,所有地震动的峰值加速度均调整至0.3 g,得出3类地震动作用下RID-巨-子结构消能控制体系中主结构的层位移的均值、子结构的层位移均值和层加速度均值。通过对比3类地震动作用下结构响应的异同,得出长周期地震动对RID-巨-子结构消能控制体系地震响应影响。
2.4.1 结构响应对比图9给出了在3类地震动作用下RID-巨-子结构消能控制体系中主结构层位移、子结构层位移和层加速度的均值对比图。由图9a可以看出,加速度峰值取值相同时,在两类长周期地震动作用下主结构的层位移明显大于普通地震动,其中远场类谐和地震动对主结构的层位移的影响较大。结合图9a、b可以看出,两类长周期地震动对主结构和子结构层位移的影响趋势一致,且在3类地震动作用下,消能结构体系中主结构与子结构层位移均呈现由底部到顶部递减的趋势。由图9c可以看出,加速度峰值取值相同时,两类长周期地震动作用下子结构的层加速度要大于普通地震动,且远场类谐和地震动对子结构层加速度的影响较大。在远场类谐和地震动作用下,RID-巨-子结构消能控制体系中子结构层加速度的大小均呈现由底部到顶部递增的趋势,而在普通地震动和近断层速度脉冲型地震动作用下,子结构层加速度的大小与所处楼层的位置相关性不大。
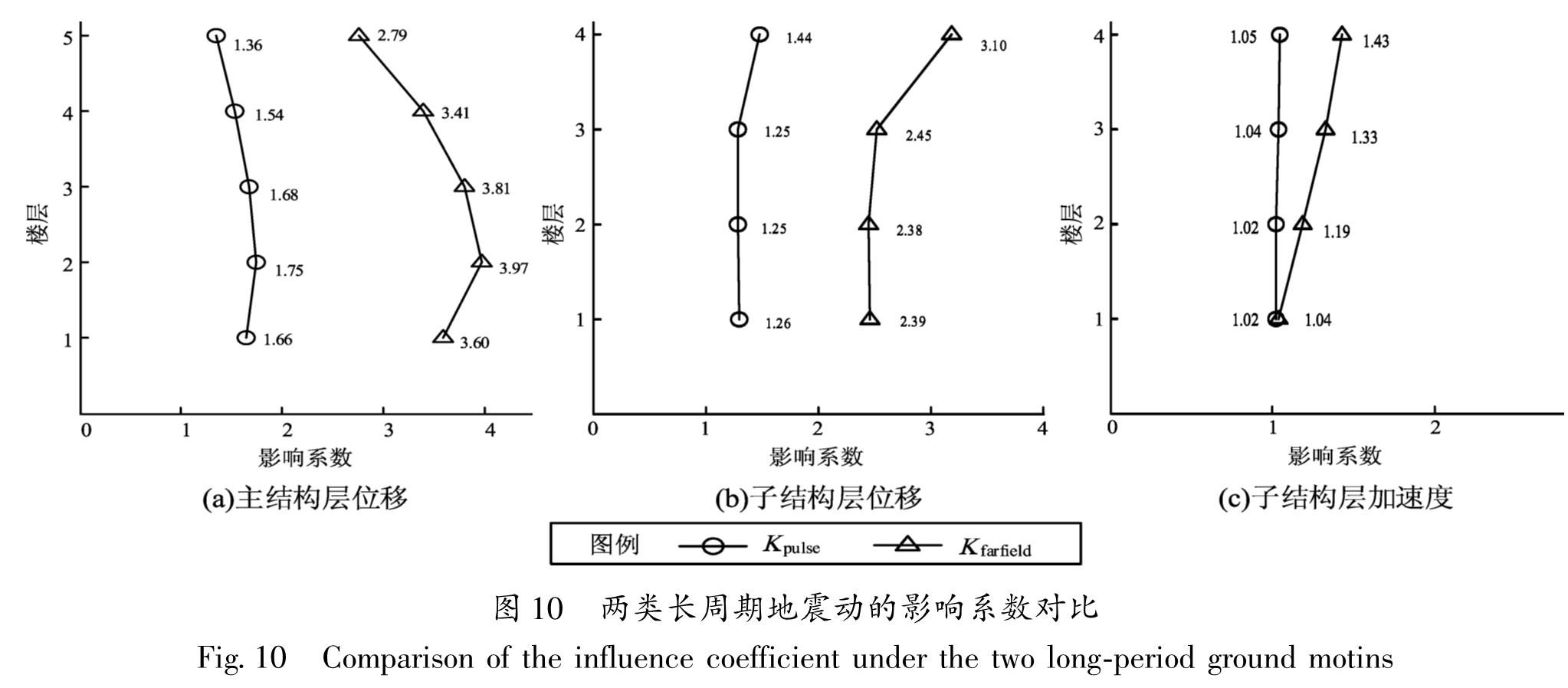
2.4.2 影响系数定义Kpulse为近断层速度脉冲型地震动相对于普通地震动对消能结构地震响应的影响系数,即二者结构最大响应之比。Kfarfield为远场类谐和地震动相对于普通地震动对消能结构地震响应的响应系数,即二者结构最大响应之比。两类长周期地震动对结构响应的影响系数对比如图 10所示,由图可见,加速度峰值取值相同时,两类长周期地震动对主结构和子结构层位移的影响明显大于对子结构层加速度的影响,且远场类谐和地震动对主结构层位移和子结构层位移、层加速度的影响要远大于近断层速度脉冲型地震动。
- 胡聿贤.2006.地震工程学[M].北京:地震出版社.
- 蓝宗建,田玉基,梁书亭,等.2002.钢筋混凝土巨型框架多功能减震结构的调频减振原理[J].工业建筑,32(1):4-6.
- 贾路,阮鑫鑫,刘章军.2019.近断层脉冲型地震动的降维模拟[J].地震研究,42(4):516-522.
- 李祥秀,刘爱文,刘良坤,等.2021.新型巨-子结构消能控制体系的动力特性及减震性能研究[J].振动与冲击,40(3):187-194.
- 李雪红,王文科,吴迪,等.2014.长周期地震动的特性分析及界定方法研究[J].振动工程学报,27(5):685-692.
- 李英民,赵晨晓,谭潜.2018.基于HHT地震动分量分离的长周期地震动界定方法[J].振动与冲击,37(7):164-171,219.
- 刘烁宇,李英民.2018.盆地型长周期地震动的判别准则[J].湖南大学学报:自然科学版,45(5):85-94.
- 邵越风,白国良,蒋连接.2017.基于EMD 与地震弹性反应谱的长周期地震动鉴别方法研究[J].世界地震工程,33(3):95-104.
- 王博,白国良,王超群,等.2013.基于Hilbert-Huang变换的长周期地震动能量时频分布比较研究[J].地震工程与工程振动,33(3):71-79.
- 王博,刘伯权,吴涛,等.2018.长周期地震动低频脉冲特性及反应谱分析[J].地震工程与工程振动,38(3):142-151.
- 王肇民,邓洪洲,董军.1999.高层巨型框架悬挂结构体系抗震性能研究[J].建筑结构学报,2(1):23-30.
- 许立英,刘宁,吴应雄.2019.基于抗震分析的长周期地震动的界定与选取[J].地震研究,42(4):569-578.
- 徐龙军,胡进军,谢礼立.2008.特殊长周期地震动的参数特征研究[J].地震工程与工程振动,28(6):20-27.
- 俞言祥.2004.长周期地震动研究综述[J].国际地震动态,(7):1-5.
- 赵西安.1993.钢筋混凝土高层建筑结构设计[M].北京:中国建筑工业出版社.
- Chai W,Feng M Q.1997.Vibration control of super tall buildings subjected to wind loads[J].International Journal of Nonlinear Mechanics,32(4):665-668.
- Feng M Q,Mita A.1995.Vibration control of tall buildings using mega-sub configuration[J].Journal of Engineering Mechanics,121(10):1082-1087.
- Kalkan E,Kunnath S K.2006.Effects of fling step and forward directivity on seismic response of buildings[J].Earthquake Spectra,22(2):367-390.
- Koketsu K,Miyake H.2008.A seismological overview of long-period ground motion[J].Journal of Seismology,12(2):133-143.
- Lan Z J,Wang X D,Dai H,et al.2000.Multifunctional vibration-absorption RC structures and their seismic response[J].Earthquake Engineering and Structural Dynamics,29(8):1239-1248.
- Liu L K,Tan P,Ma H T,et al.2018.A novel energy dissipation outrigger system with rotational inertia damper[J].Advances in Structural Engineering,21(12):1865-1878.
- Wang R,Schurr B,Milkereit C,et al.2011.An improved automatic scheme for empirical baseline correction of digital strong-motion records[J].Bulletin of the Seismological Society of America,101(5):2029-2044.
- Zhang X A,Wang D,Jiang J S.2005.The controlling mechanism and the controlling effectiveness of passive mega-sub-controlled frame subjected to random wind loads[J].Journal of Sound and Vibration,283(3-5):543-560.