水位对气压的传递函数可用于拟合气压响应函数,其振幅可作为气压效率。计算传递函数的步骤为:①确定水位、气压和固体潮信号的自功率谱和交叉谱; ②求解下列复线性方程组(Rojstaczer,1988a):

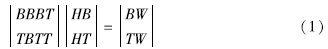
式中:BB和TT分别表示大气压力和固体潮的自功率谱; BT和TB分别表示大气载荷和固体潮之间的交叉谱和它的复共轭; BW表示大气载荷和水位的交叉谱; TW表示固体潮和水位之间的交叉谱; HB和HT分别表示水位与大气载荷和水位与固体潮之间的传递函数。

去除固体潮效应,计算传递函数的方法可以简化为:

BRF(f)=BW(f)/BB(f)(2)

振幅和相位可以表示为(Hussein et al,2013):

A^BRF=|BRF(f)|(3)

φ^BRF(f)=arctan{(imag[BRF(f)])/(real[BRF(f)])(4)

在使用传递函数时,往往需要使用滤波器对数据进行预处理,常用的有带通、低通、高通等滤波器,滤波器的截止频率与采样率有关,可以过滤掉3 cpd以上的高频噪音,或使用逐渐变小的汉宁窗,分成50%重叠率的频带进行平均等手段(Hussein et al,2013)。

Acworth和Brain(2008)通过地下水和气压的振幅比估计气压效率:

BE=(ρgΔh)/(ΔP)=(A(W))/(A(P))(5)

式中:A(W)为水位波动的振幅; A(P)为气压波动振幅。

但是在进行谐波调和分析计算气压效率时也需要识别并剔除固体潮响应,为此Acworth等(2015)提出利用离散傅立叶变换可以提取显著频率的振幅,并指示地下水对固体潮的响应。水位信号中S₂分量频率(2 cpd)以下的响应包括对大气潮的响应信号Z^GW-AT_S2和对固体潮响应信号Z^GW-ET_S2,即水头响应信号为:

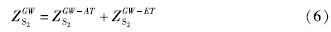
由于固体潮的M₂和S₂分量的振幅比是恒定的,水位对M₂分量的响应不会受大气压力的干扰,于是Z^GW-ET_S2可由Z^GW_M2计算得出:

气压效率可表示为:

在地下水存在补给、排泄或气压效率较低的系统中,气压波动与水位波动没有显著的相关性。为了更好地分解气压信号和固体潮信号,Acworth等(2016)采用谐波加和定理实现了突破,提出了一种利用消除固体潮响应来计算气压效率的新方法,指出响应振幅取决于两个驱动因素之间的相位差,只有当相位差等于0时,振幅才可以做简单的加减。

为了准确量化固体潮分量对地下水头的影响,可以通过计算固体潮在S₂分量下的振幅,用S₂分量下大气潮和固体潮之间的相位差来校正,气压效率的计算公式为:

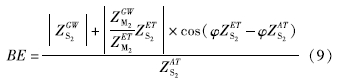
式中:S₂和M₂分量的振幅,可采用快速傅立叶变换获得(Acworth et al,2016)。

Rau等(2020)指出,Acworth等(2016)的方法是基于钻孔水位代表含水层孔隙压力的假设,即存在瞬时和无阻尼响应。在这种情况下,仅需要理论固体潮和气压潮驱动之间的相位差来校正地下水响应振幅。然而Hsieh等(1987)指出,固体潮M₂分量和井水位响应之间存在相位差,在利用地下水位对气压潮的响应中量化BE时,还必须考虑相位延迟(Rau et al,2020)。

考虑地下水位与孔隙压力的关系,阻尼大小可以用它们的振幅比A^r_S2计算,方法采用Hsieh等(1987)和Rojstaczer(1988b)的理论公式,即:

式中:Z^PP_S2为孔隙压力对S₂波响应信号; f_S2为S₂波的频率; T为导水率; S为储水率; r_w为井半径; r_c为套管半径。

振幅和相位变化都受到水力传导系数的影响,对于承压层A^r_S2>0.99,即渗透系数K>1×10^-5 m/s,阻尼造成的误差可以忽略,然而在渗透系数较小的条件下A^r_S2显著降低,计算气压效率时便需要考虑地下水位与孔隙压力的关系,所以更客观的气压效率的计算方法如下:

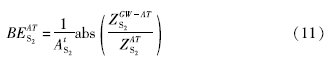
值得注意的是,Rau等(2020)在提出谐波信号时采用了谐波最小二乘法,计算公式为:

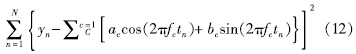
式中:N是离散样本数; y_n是时间t_n的样本值; C是频率为f_c的潮汐分量C的总数,通过最小二乘法拟合出参数a_c和b_c作为复数信号的实部和虚部。

Schweizer等(2021)比较了离散傅立叶变换和谐波最小二乘法提取谐波分量特性的能力,通过验证两个具有不同特征的真实数据集的模型,发现Rau等(2020)使用的谐波最小二乘法在各方面都优于前人使用的离散傅立叶变换。谐波最小二乘法在未来也会得到更多应用。

由于承压层之上存在包气带,气压传递会受到气体扩散系数的影响,从而造成气压效应的滞后; 在较厚或低渗透性的区域,包气带会导致周期性信号产生较大的衰减和相移。针对这种响应的时间滞后,Rasmussen和Crawford(1997)根据Furbish早期的研究,提出了利用回归反卷积方法来计算地下水对大气压力的响应,气压效率可以表示为延迟响应的函数,可以用如下的卷积计算方法来计算气压响应函数(BRF)(Butler et al,2011):

式中:Δw(t)为无趋势水位; α_i和β_i为滞后i时的大气压力和固体潮的单位脉冲,通过最小二乘回归可以计算α_i、β_i; j为观测时间。

Butler等(2011)提出某一口井的气压响应函数并不是一成不变的,其形式可能取决于穿过渗流区的压力传播的性质。对于承压含水层,短期内(1 h)大气压力荷载由孔隙水承担,含水层对大气压力的变化不敏感,BRF(j)数值较低,随着压力波通过不饱和带,井水头与大气压力变化达到平衡状态,单位脉冲响应α_i逐渐减弱,响应达到稳定。

例如云南会泽井的气压响应函数(图1a),随着滞后时间的增大逐步稳定,反映所处的地层可能为承压含水层。当在潜水或半承压含水层时,井水位和孔隙水同时受到大气压中短周期信号产生的响应,随后大气压力被孔隙水分担一部分,导致井水位的延迟响应越来越小,在压力平衡后达到稳定。这类气压响应函数的特征表明含水层可能属于半承压或未承压的状态,如新10井(图1b)。

图1 12 h内云南会泽井(a)和6 h内新10井(b)气压响应函数
Fig.1 Barometric Response Function of Huize well in 12 hours(a)and Xinshi well in 6 hours(b)

Jacob(1940)通过建立一个理想均匀边界的弹性承压含水层,说明了气压和潮汐波动可以作为量化含水层弹性的指标,潮汐效率(荷载效率)或气压效率与储水率之间有直接关系。

气压效率为:

BE=(θK_s)/(θK_s+K_f)(16)

潮汐效率为:

TH=1-BE(17)

式中:θ为孔隙度; K_f为水的弹性模量; K_s为地层的弹性模量; ρ为水的密度,根据泰斯的储水率计算公式,储水率可由气压效率计算:

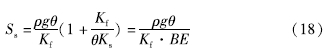
Bredehoeft(1967)提出水位对固体潮响应的振幅可以用于量化水文地质参数。假设忽略固体的可压缩性,近地表含水层的垂直应变取决于含水层的泊松比,含水层中钻孔水位变化和潮汐扰动的振幅变化之比是一个与储水率有关的定值:

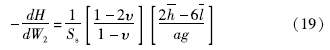
式中:dH为水位变化; dW₂为太阳或月球的干扰潮汐; S_s为储水率; υ为泊松比; h^-、l^-为洛夫数; a为地球半径; g为重力加速度。

当观测到的地球潮汐振幅有超过1 mm左右的水位变化时,那么地层一定是相对不可压缩的,固体的可压缩性是不可忽略的。所以Kamp 和 Gale(1983)考虑了固体可压缩性的影响,导出了通过固体潮和大气压力响应计算储水率的公式。如果固体是可压缩的,储水率可以写成:

S_s=(ρg)/(2Gγ)(α(1-2υ))/((1-υ))(20)

式中:γ为荷载效率; G为刚性模量; α为Biot-Willis常数。

Hsieh等(1987)通过理想承压含水层模型和开尔文函数解出了井水位对固体潮响应的解析解,发现振幅和相位是井半径、储水率和导水率的函数,为水文地质学家通过固体潮波动下水位记录计算含水层导水率提供了可能。

潮汐引起的水位波动振幅为:

相位为:

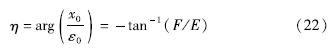
式中:x₀为水位波动振幅; ε₀为体应变波动的振幅; E、F由开尔文函数计算:

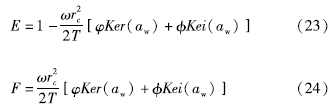
式中:φ、φ由a_w的一阶开尔文函数计算; Ker、Kei为零阶开尔文函数的实部和虚部; a_w由储水率、导水率、频率、井径计算得出:

在实际应用中可以通过原位应变仪测得潮汐作用引起的体应变,也可以通过理论固体潮计算得到,通过对水位和体应变进行傅立叶变换得到振幅和相位,再结合上述公式,可获得含水层的导水系数和储水率。

Roeloffs(1996)提出,在不排水条件下,假设忽略水流横向流动,只考虑垂向扩散,当气体能够扩散到整个潜水含水层时,气压效率为井水深和水力扩散系数的函数,可表示为:

式中:z为地表到含水层的距离; z_w为地表到井内水面的距离; c为水力扩散系数; υ_u为未排水地层的泊松比。

孔隙压与固体潮体应变的振幅比可表示为(Roeloffs,1996):

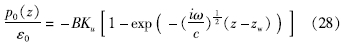
式中:p₀(z)为深度z时的孔隙压力; ε₀为固体潮体应变振幅。

Roeloffs(1996)指出,对于特定的潮汐分量主频率,ω(z-z_w)²/c可以用于反映含水层的承压性,当ω(z-z_w)²/c<0.2时,如果潮汐应变产生的扰动小于1/e,那么可以指示该含水层具有良好的承压性。

Rojstaczer(1988a)提出简化井-含水层模型,考虑气压变化的3个流动因素:①从地表到地下水位的非饱和带中的垂直气流; ②承压层内的垂直地下水水流; ③含水层和井孔之间的水平地下水水流。井水位对大气压力的响应大小取决于井的半径、含水层的水平向水力扩散率、包气带厚度和垂直气动扩散率以及潜水层(或部分承压层)垂直水力扩散率5个参数。这些水文地质参数与响应频率的关系如下。

在地表到地下水位的气流交换中,定义反映非饱和带厚度和气体扩散关系的频率参数R为:

R=(L²ω)/(2D_a)(29)

式中:L为地表到地下水位的距离; D_a为气体扩散系数。

在潜水面到含水层间的垂直水流交换中,定义反映潜水层厚度和水力扩散系数关系的频率参数Q为:

Q=(b'²ω)/(2D)(30)

式中:b'为潜水面到承压层上顶板的距离; D为垂直水力扩散系数。

在钻孔与含水层之间的水流交换中,定义反映井径与渗透系数关系的频率参数W为:

W=(r²_wω)/(Kb)(31)

式中:r_w为井半径; K为含水层渗透系数; b为含水层厚度。

在一般情况下,井水位对大气荷载的响应可以表示为:

x₀=-A/(ρg)+(p₀)/(ρg)-s₀(32)

式中:x₀为水位信号的振幅; A为大气压力信号的振幅; p₀为含水层中孔隙压力; s₀为井内水位降深。式(32)描述了井水位在频率域中的响应,井筒内水位的变化加上大气负荷(等效水位变化),等于远场孔隙压力(等效水位变化)减去井水位降深。

气压效率为响应频率的函数,气压效率可计算表示为响应函数的增益:

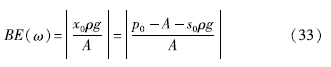
相位计算如下:

θ(ω)=arg((x₀ρg)/A)(34)

Rojstaczer和Agnew(1989)随后的研究中利用井水位对固体潮的响应来获取地壳应变,发现井水位对大气载荷和面应变响应的理论模型可以与交叉谱估计结合使用,进而估算含水层的弹性参数,如骨架压缩系数、孔隙率、储水率。水井对荷载和固体骨架应变的灵敏度和地层压缩性可表示为:

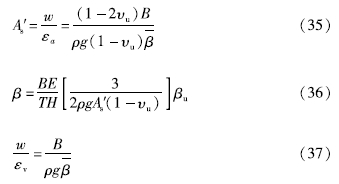
式中:w为水位变化; ε_v为固体骨架体应变; B为Skempton系数; β^-地层饱水时的压缩系数。

孔隙度可表示为:

φ=((β-β_u)(1-B))/(B(β_f-β_u))(38)

式中:β_f为液体压缩系数; β_u为固体压缩系数; β由面应变灵敏度和荷载效率计算得出。

由于含水层往往介于完全承压与完全不承压之间,Wang等(2018)提出了更具普适性的渗流模型,即考虑地下水水平流动和垂向的越流,在这种情况下,潮汐响应的振幅比为:

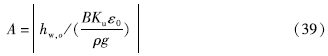
相位滞后表示为:

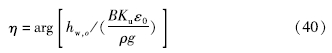
式中:h_w,o表示地下水的振幅,可通过修正Bessel函数和Laplce变化得到:

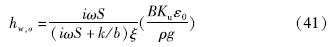
式中:S为储水率; k为弱透水层渗透系数; b为弱透水层厚度; ξ为导水率,井径的Bessel函数。

通过上述公式可以得到潮汐响应振幅、相移与导水系数、储水率和越流系数的关系。

地下水位动态经常受气压和固体潮变化的影响。这些干扰会对后续地下水位的动态分析造成误差(王丽亚等,2012)。即使在低水力梯度的包气带或非承压含水层中,气压的波动都会使地下水流动产生瞬时变化,从而影响地下水位测量的准确性。因此,在地下水流的研究中应考虑气压和固体潮的影响。利用回归反卷积法从水位中去除气压和固体潮效应在水位校正中已经进行了广泛应用,并取得了较好的效果(Rasmussen,Crawford,1997; Spane,2002; Toll,Rasmussen,2007)。

Rahi和Halihan(2013)提出利用频谱分析的方法可以判断含水层的类型:①非承压含水层的地下水信号存在S₂和K₁分量,但缺失M₂分量; ②半承压含水层地下水信号中S₂分量占主导,同时存在M₂分量; ③承压含水层中则有明显的M₂分量。尽管Rahi和Halihan(2013)没有给出定量的标准,但后续研究表明:当水位M₂分量的振幅大于1 mm时就可以指示含水层具备较好的承压性(Turnadge et al,2019)。前人的多个研究结果表明,谐波分析法是确定含水层类型的一种准确、低成本的方法(Hussein et al,2013; Rahi,Halihan,2013; Acworth et al,2015)。

Acworth等(2017)指出,当谐波分量S₂的地下水位与大气压力的相位差达到-180°时可以说明含水层具备良好的承压性。该研究指出地下水位的气压响应可以作为一种天然的示踪剂,有助于理解地下水系统的时空特征和概念,量化地质单元中多个含水层的承压状态和压缩储存特性。

前人通过地下水位对潮汐和气压的响应模型推导了许多水力参数的计算方法(Bredehoeft,1967; Hsieh et al,1987; Jacob,1940; Kamp,Gale,1983; Roeloffs,1996; Rojstaczer,Agnew,1989)。在后续的改良与应用中,Hussein等(2013)通过传递函数方法计算了含水层多个水文地质参数,并且根据结果提出了含水层脆弱性的评价方法,使地下水的气压响应方法成为半承压含水层脆弱性评估的有效工具。Xue等(2013)通过水位对气压潮响应来研究断裂带的水文地质结构,估算了断裂带的储水量和渗透率。Sun和Xiang(2019)等运用频谱分析,气压响应函数等手段计算了会泽井井水位对周期性荷载的响应灵敏度,说明响应灵敏度取决于其井结构和含水层渗透性。Sun和Xiang(2020)等通过比较不同模型,得出在气压荷载低频区,忽略非饱和带影响的模型拟合结果更优,特别是识别浅层地壳应变或应力的井。Qu等(2020a)研究了煤矿开采区地下水位对大气压力的响应,计算了煤矿上覆含水层的水力特性,证明了潮汐效应计算的水力特性有效半径与抽水试验相似。

基于地下水对气压响应的分析可以求解矿区、断裂带等特殊地层的水力特性参数,并且随着模型复杂性的提升,反演结果也更加客观。未来研究中可以对水力特性的有效范围开展进一步研究,探索其尺度效应的变化。

Rau等(2018)提出了一种基于耦合跨孔地震探测与地下水位气压效应来估算含水层储水率的新方法。该方法考虑了固体颗粒与骨架压缩性对储水率计算结果的影响,相比传统方法提高了计算的精度。Sun和Xiang(2019)利用井水位对大气压力的响应计算了地震对含水层系统垂向和水平向渗透率的影响,发现地震造成了地层渗透性的增大。地下水对潮汐和气压响应方法为研究浅层地壳介质渗透率变化及了解其各向异性分析提供一种新的途径。Zhang 等(2019)利用地下水位对大气压力和固体潮的响应,研究了地震对同一含水层系统中含水层和弱透水层渗透率和导水率的影响。说明地下水对气压响应分析同样适用于弱透水层的水力参数计算。

利用地下水对潮汐和气压的响应,结合地震分析可以改进水文地质概念模型(孙小龙等,2020a,b),加深对含水层断裂结构和形变的认识。通过分析地震前后地下水位相移和振幅的变化也为监测地震地下水前兆提供新的思路。