基金项目:国家自然科学基金项目(51908265、51768042)和红柳优秀青年人才资助计划(04-061810)联合资助.
(兰州理工大学 土木工程学院,甘肃 兰州 730050)
(School of Civil Engineering,Lanzhou University of Technology,Lanzhou 730050,Gansu,China)
continuous,rigid-frame bridge; construction process; equivalent load method; state of the internal force; seismic fragility
DOI: 10.20015/j.cnki.ISSN1000-0666.2022.0002
备注
基金项目:国家自然科学基金项目(51908265、51768042)和红柳优秀青年人才资助计划(04-061810)联合资助.
引言
近年来,随着我国城镇化水平的不断提高,对于交通基础设施建设的需求进一步加大,桥梁作为城市交通网络的枢纽工程得以飞速发展(石岩等,2021)。大跨度连续刚构桥因内力分布合理、跨越能力强和造价经济等优点在桥梁工程领域备受青睐(Peng,Zhang,2020; 郭昆霖等,2020; 赵秋红等,2019)。连续刚构桥一般采用悬臂施工法,施工过程复杂且持续时间较长,其成桥内力状态受施工过程影响不断变化(石岩等,2020; Shi et al,2021; 童磊等,2020)。另外,大跨度桥梁存在临近断层或跨越断层的可能性,鉴于以上因素,若不充分考虑大跨度连续刚构桥的真实内力状态而直接进行地震易损性分析,其分析结果将因未考虑初始内力而与实际情况相差甚远,对工程设计无参考价值。因此,研究真实内力状态下大跨度连续刚构桥在近断层地震动下的易损性情况十分重要。
地震易损性分析作为一种能直观反映地震动强度与结构损伤概率之间关系的评估方法,近些年被大量应用于桥梁结构的抗震分析研究(俎林,黄勇,2020; 李宏男等,2018)。李立峰等(2016)研究氯离子侵蚀效应对近海高墩连续刚构桥时变地震易损性的影响时,发现考虑纵筋锈蚀以后高墩的位移需求和曲率需求会显著增加; 庞于涛等(2018)对两座钢纤维混凝土连续刚构桥进行了地震易损性分析,发现钢纤维混凝土能够有效降低地震作用下桥梁结构的失效概率,提高其抗震性能; 赵凌志(2018)研究了高速铁路上双薄壁墩预应力混凝土连续刚构桥在施工过程中的地震易损性变化规律,以及桩土效应和悬臂效应对地震易损性的影响; 李吉涛等(2013)则以桥墩位移延性系数为指标分析了多点地震激励下大跨连续刚构桥的地震易损性。目前,连续刚构桥的地震易损性分析主要集中在特殊环境、材料和结构形式对易损性的影响,以及对损伤评价指标的探索等方面,而对于在数值模拟分析过程中如何考虑成桥内力状态以及考虑内力状态与否对连续刚构桥地震易损性分析影响方面的研[HJ1.95mm]究则较少。
为研究考虑内力状态的连续刚构桥地震反应及易损性情况,以一座主桥为大跨高墩连续刚构桥的实际工程为背景,考虑到采用MIDAS/Civil软件建立的弹性模型无法得到准确的非线性动力分析结果,而OpenSees软件又不擅于对桥梁施工过程进行模拟,故将两种软件进行联合建模。将从MIDAS/Civil施工阶段模型中经施工阶段分析得到的主梁和主墩的目标内力以等效荷载的方式施加于OpenSees动力分析模型,选取具有脉冲效应的近断层地震动进行增量动力分析(Incremental Dynamic Analysis,简称IDA),并重点分析桥墩的地震反应与损伤情况,以期为高烈度区连续刚构桥抗震设计和性能评估提供参考。
1 分析模型及内力状态
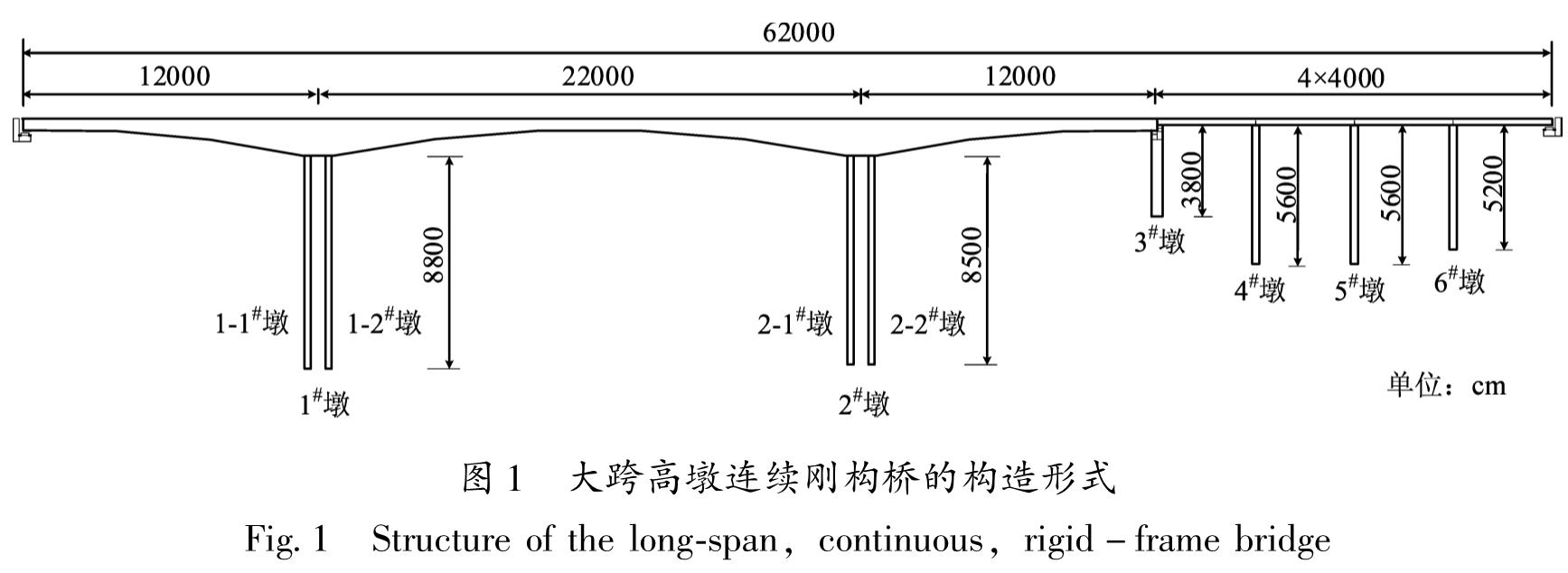
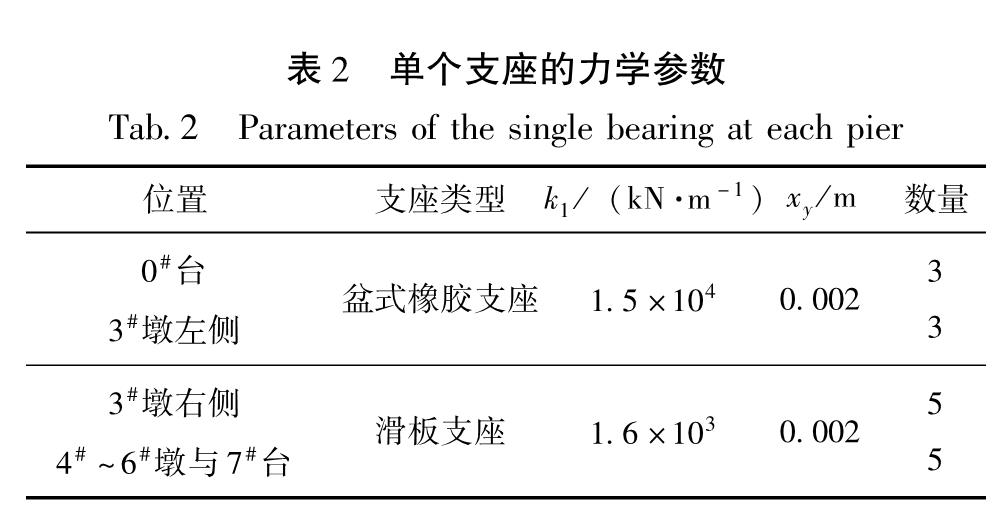
1.1 桥梁概况本文以某大跨高墩连续刚构桥为研究对象,其主桥是跨径为(120+220+120)m的3跨连续T型刚构,引桥是跨径为4×40 m的4跨简支T梁,如图1所示。主桥上部结构(主梁)为变截面单箱单室预应力混凝土箱梁,其顶板宽12 m,底板宽8 m; 引桥上部结构为等截面混凝土T梁,每跨5片; 全桥桥墩均为钢筋混凝土桥墩,1#~2#墩为双薄壁空心墩,3#~6#墩为单薄壁空心墩。主桥采用悬臂施工法进行施工,历时约460 d。主桥箱梁和引桥T梁采用C50混凝土,1#~6#墩采用C40混凝土; 箱梁采用Strand1860预应力钢绞线,共计452束。0#桥台、3#墩顶各设置3个盆式橡胶支座,7#桥台、3#~6#墩顶各设置5个滑板支座。桥址场地类别为II类,抗震设防烈度为9。
1.2 有限元模型及特征值分析为研究考虑内力状态与否对大跨高墩连续刚构桥地震易损性的影响,首先基于MIDAS/Civil软件建立2个考虑施工过程与否的全桥有限元模型,见表1。对于考虑施工过程的模型2,整个施工过程根据悬臂施工法划分成38个施工阶段,主桥的主要施工阶段为:主墩现浇—0#梁段施工—1#~32#梁段对称浇筑—边跨现浇段施工—边跨合龙—中跨合龙; 引桥在主桥中跨合龙完成以后整体导入,然后附加二期铺装荷载。不考虑桩土相互作用,桥墩墩底采用固结方式模拟。
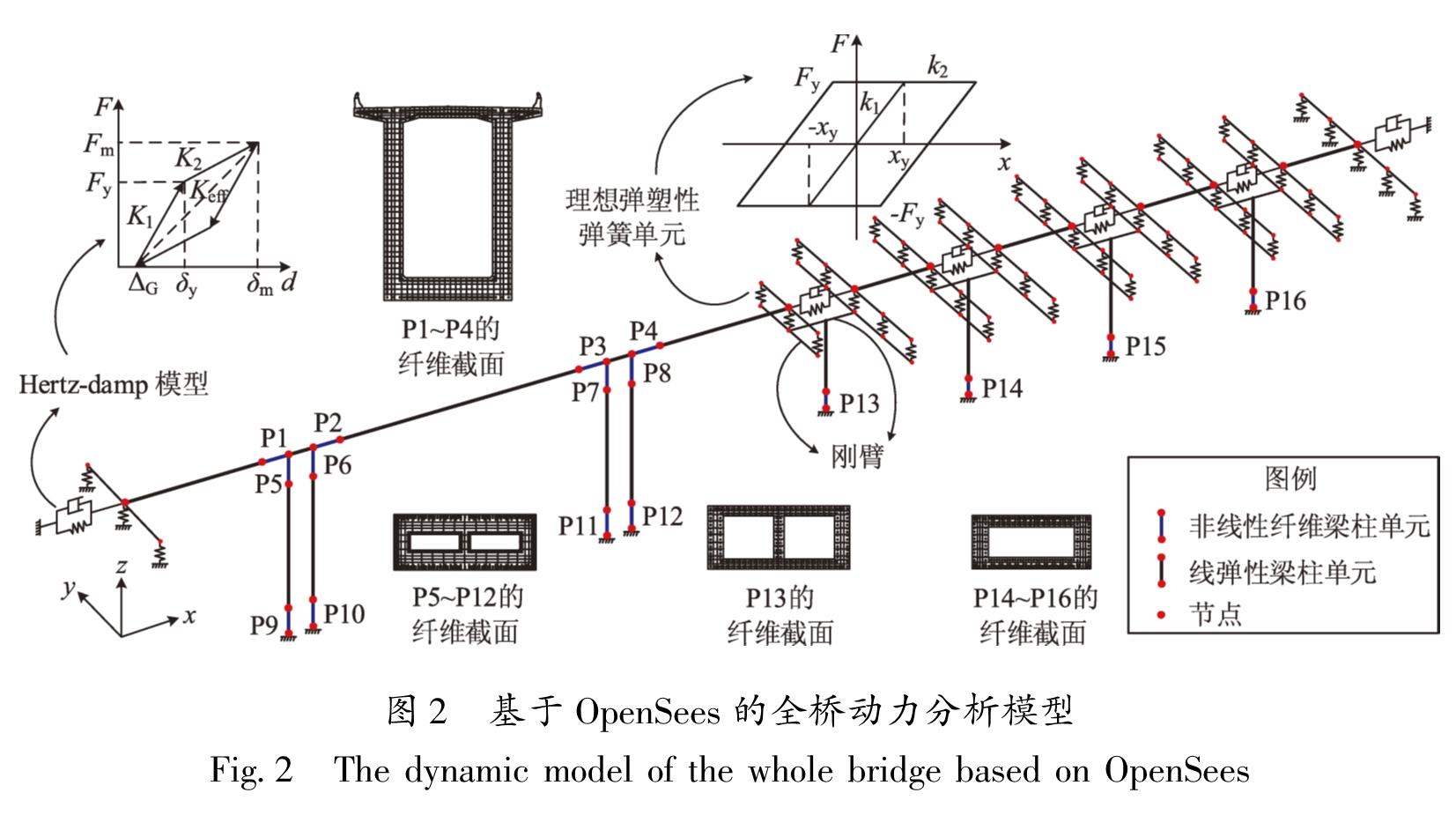
采用MIDAS/Civil软件建立的弹性模型无法进行非线性动力时程分析,故将其转化为基于OpenSees软件的非线性动力模型,如图2所示。关键受力部位(塑性铰区)包括主桥的主梁根部梁段(P1~P4)、主墩墩顶和墩底段(P5~P12)以及引桥桥墩的墩底段(P13~P16),采用基于位移的非线性纤维梁柱单元进行模拟。各关键位置处纤维截面的混凝土采用Concrete01材料,纵向钢筋采用Steel02材料; 纤维截面上的配筋与实际情况保持一致。假设非关键受力部位处于弹性状态且都采用弹性梁柱单元模拟,主梁和桥墩的弹性模量分别为3.45×104 MPa和3.25×104 MPa。主桥梁端设置3个支座单元,引桥梁端设置5个支座单元,各支座单元的力学参数详见表2。采用Hertz-damp模型(Guo et al,2017; Taflanidis,2011; Muthukumar,DesRoches,2006),考虑主桥和引桥梁体间、梁体与桥台背墙间的纵桥向碰撞作用,初始碰撞间隙为0.05 m; 由于强地震动作用下桥台和边墩处的横向挡块极易破坏,加之考虑到模型分析时的收敛性,故未考虑横桥向碰撞作用。桥梁模型的阻尼比取5%,并采用瑞利阻尼。
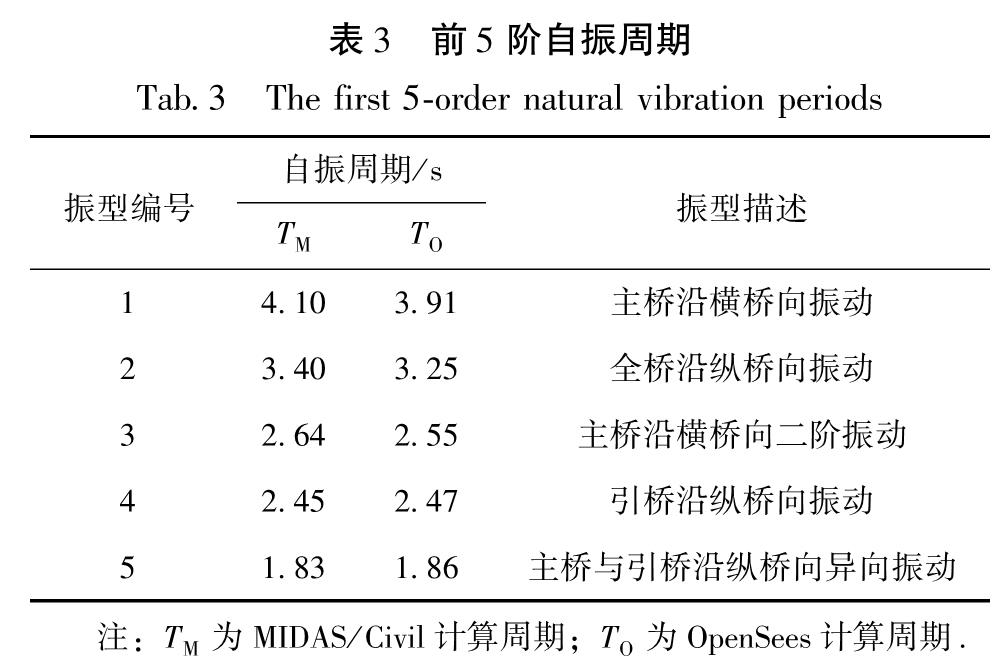
为确保所建立的OpenSees模型与MIDAS/Civil模型保持一致,对两种软件建立的同一模型的自振周期进行对比。从表3可知,前5阶自振周期最大周期差别率不超过5%,且此误差主要来源于软件差异,故证明了采用OpenSees软件所建动力分析模型的正确性。
表1 基于MIDAS/Civil软件建立的全桥有限元模型
Tab.1 Finite element models of the whole bridge based on MIDAS/Civil softwere1.3 等效荷载及内力状态利用MIDAS/Civil软件分析施工阶段得到主梁和主墩的目标内力状态(目标弯矩与目标轴力),参考Lin和Burns(1981)提出的等效荷载法对真实内力状态逐一进行分解与等效。其中,主梁目标轴力主要由预应力轴压作用引起,将相邻2个单元在同一节点处的轴力作差,即可得到主梁目标轴力对应的等效荷载。主梁目标弯矩主要由结构自重、二期铺装荷载和预应力竖弯作用提供,依据叠加原理,首先对各荷载作用进行分解,然后将结构自重和二期铺装荷载直接以节点荷载的形式附加在相应的节点处,而预应力的竖弯作用则以自重的某一倍数反向施加; 挂篮(吊篮)荷载等因素对最终阶段主梁弯矩的影响通过荷载系数加以考虑。从MIDAS/Civil模型中提取得到主梁各节点的结构质量和铺装质量(二期铺装荷载转化为质量),分别记为M1(x)、 M2(x), 则主梁目标弯矩对应的等效荷载计算公式为:
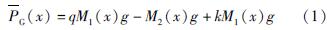
式中:
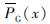 为主梁沿纵桥向第x个节点处的等效荷载,作用方向竖直向下; qM1(x)g为自重对应的等效荷载,其中q为自重系数,取值-1.04; -M2(x)g为二期铺装对应的等效荷载; kM1(x)g为预应力竖弯作用对应的等效荷载,其中k为荷载系数(1<k<2)。
为主梁沿纵桥向第x个节点处的等效荷载,作用方向竖直向下; qM1(x)g为自重对应的等效荷载,其中q为自重系数,取值-1.04; -M2(x)g为二期铺装对应的等效荷载; kM1(x)g为预应力竖弯作用对应的等效荷载,其中k为荷载系数(1<k<2)。将各模型中主梁目标弯矩的等效荷载附加到OpenSees模型并进行静力分析,可得到主梁的等效弯矩和主墩的非等效轴力,提取不同情况下主墩的非等效轴力,记为N'[KG-*3]Pm-n。从MIDAS/Civil中提取各模型下最终阶段的主墩墩顶节点轴力,记为NTPm-n; 提取墩底节点轴力,记为NBPm-n。则主墩各节点的轴力计算公式为:
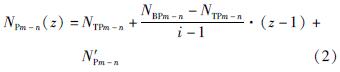
式中:m-n为主墩编号,其中m=1,2; n=1,2; z=1,2,…,i,表示沿墩高自上而下第z个节点; i为节点数,本模型1#墩(1-1#墩、1-2#墩)中i=23,2#墩(2-1#墩、2-2#墩)中i=22。依据叠加原理,给出主墩目标轴力对应的等效荷载计算公式为:
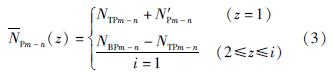
式中:当z=1时,N[TX-]Pm-n(1)为墩顶节点处的等效荷载; 当2≤z≤i时,N[TX-]Pm-n(z)为沿墩高自上而下第z个节点处的等效荷载,作用方向竖直向下。
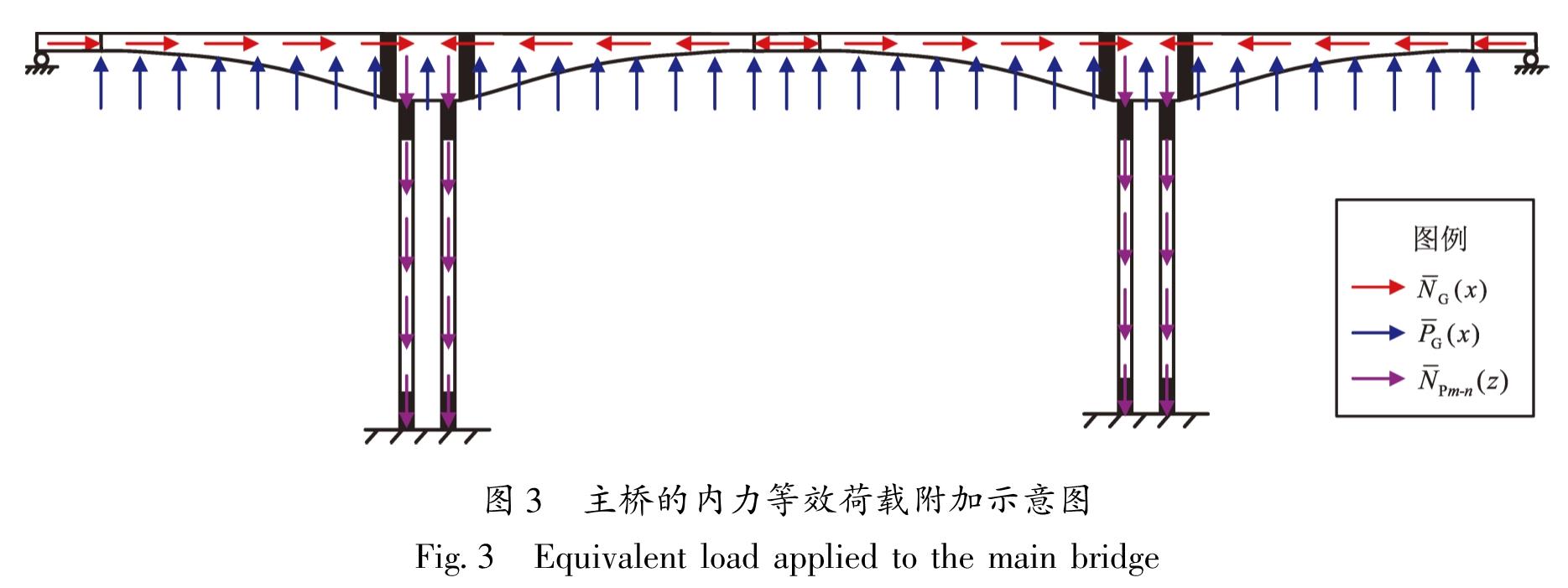
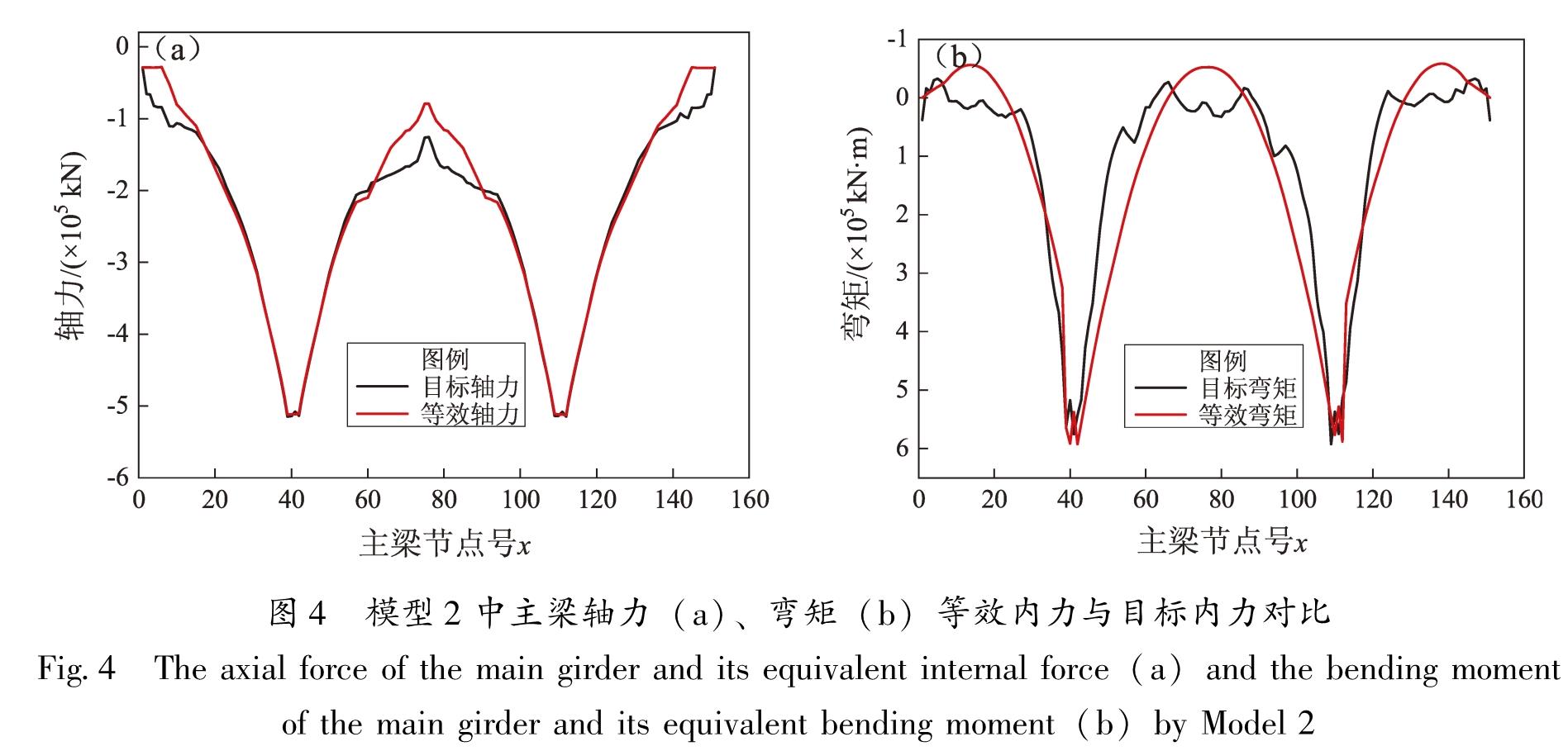
然后将计算得到的内力等效荷载分别施加于OpenSees动力分析模型,如图3所示。之后对OpenSees模型进行静力分析得到等效内力状态。图4给出了成桥初始阶段(模型2)主梁的等效内力与目标内力。从图中可见,所得等效内力与目标内力基本相等,进而验证了内力等效荷载的准确性,同时说明基于OpenSees建立的动力模型基本处于实际内力状态。
2 地震易损性分析方法
2.1 基于IDA的地震易损性方法结构的地震易损性,即结构发生某种破坏的超越概率。假设结构的地震需求D和抗震能力C均服从对数正态分布,以PGA为地震强度指标的地震易损性函数为:
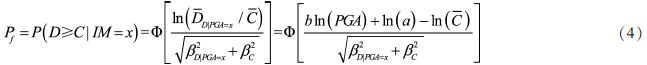
式中:Pf为失效概率; IM为地震强度指标,取峰值加速度PGA; x为给定的地震动强度参数; Ф为标准正态分布函数;
 表示在PGA=x下,地震需求D的中位值;
表示在PGA=x下,地震需求D的中位值; 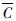 表示不同极限状态对应的结构抗震能力C的中位值,由不同破坏状态的界限值确定; a、b为回归系数; βD|PGA=x表示在PGA=x下,地震需求D的对数标准差; βc为抗震能力C的对数标准差。由于采用峰值加速度PGA作为地震强度指标,根据National Institute of Building Science(1999)所给建议,
表示不同极限状态对应的结构抗震能力C的中位值,由不同破坏状态的界限值确定; a、b为回归系数; βD|PGA=x表示在PGA=x下,地震需求D的对数标准差; βc为抗震能力C的对数标准差。由于采用峰值加速度PGA作为地震强度指标,根据National Institute of Building Science(1999)所给建议, 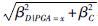 取为0.5(该经验值与桥梁的结构类型和损伤状态无关)。2.2 损伤指标的确定
取为0.5(该经验值与桥梁的结构类型和损伤状态无关)。2.2 损伤指标的确定根据National Institute of Building Science(1999)的规定,桥梁结构或构件在地震作用下的破坏状态共划分为5个等级,分别是:无损伤(None Damage,简称ND)、轻微损伤(Slight Damage,简称SD)、中等损伤(Moderate Damage,简称MD)、严重损伤(Extensive Damage,简称ED)及完全破坏(Complete Damage,简称CD)。损伤指标是对桥梁结构或构件的极限状态做出的定量描述,也是衡量其破坏程度的限值(Hose,Seible,1999; Park,Ang,1985)。现行的可用于描述桥梁破坏状态的损伤指标有很多,本文选取位移延性系数(Hwang et al,2000; Banon,Veneziano,1982)定义在地震作用下主桥的破坏状态,不同破坏状态及其描述见表4(Hwang et al,2001)。表4中,位移延性系数μΔ为地震作用下的墩顶最大相对位移Δ与墩底塑性铰区纵向钢筋首次屈服时的墩顶相对位移Δcy1之比; μ'[KG-*3]Δy为钢筋首次屈服时的位移延性系数; μΔy为截面等效屈服时的位移延性系数; μΔ4为截面边缘混凝土压应变εc首次达到0.004时的位移延性系数; μ<sub>Δmax为混凝土应变达到极限压应变εcu时的位移延性系数,可直接按μΔmax=μΔ4+3计算得到。
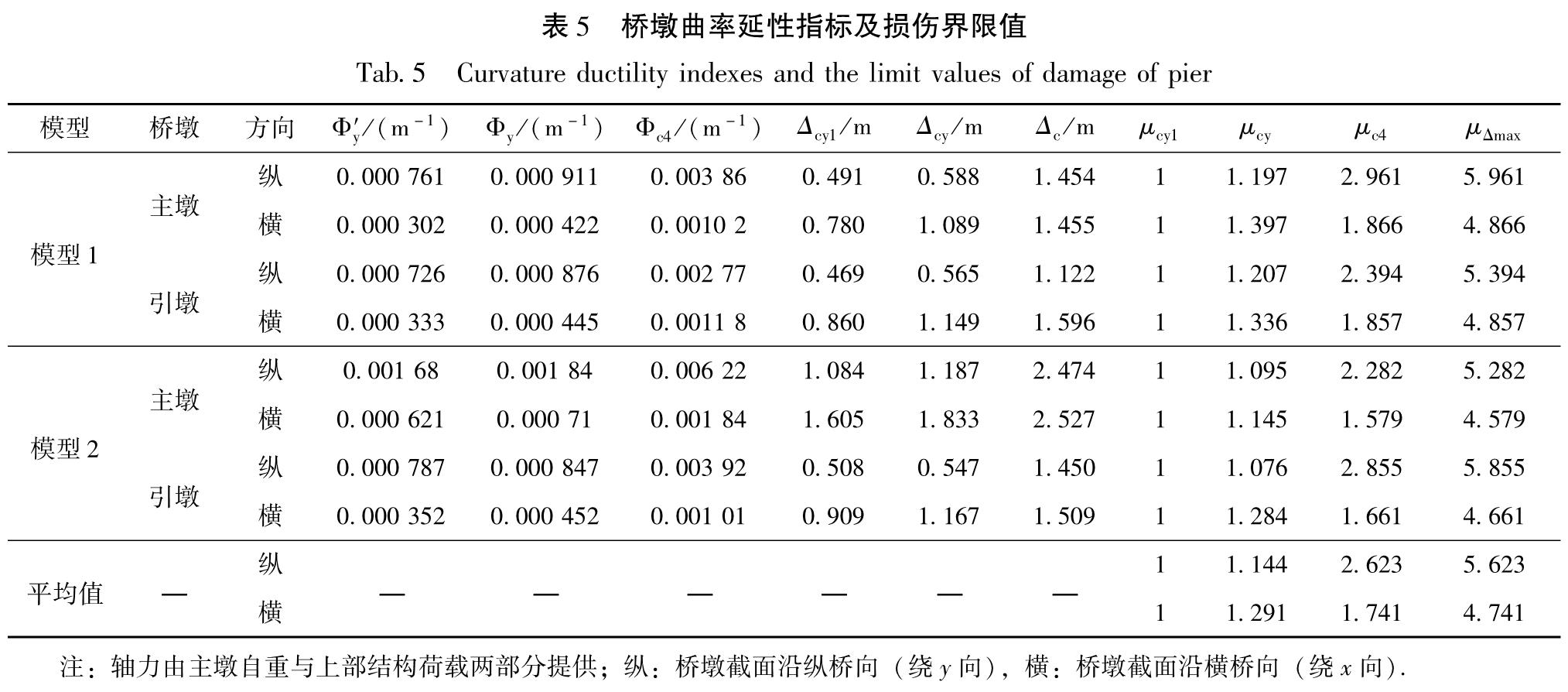
一般桥墩的非线性变形可通过塑性铰区截面的曲率延性能力来反映。塑性铰区的位置会因不同的桥墩形式而不同,如单柱墩的塑性铰区一般位于墩底,而刚构体系的桥墩沿纵桥向在墩顶和墩底都存在塑性铰区(马保林,2001)。根据已有研究可知,桥墩在不同破坏状态下的损伤界限值可利用墩底塑性铰区截面的曲率延性指标计算得到(HAZUS99,1999; Hwang,刘晶波,2004; Hwang et al,2001)。本文首先基于OpenSees软件对所有桥墩塑性铰区截面进行弯矩-曲率分析,得到弯矩-曲率曲线,然后从中提取曲率延性指标并计算局部位移延性能力,最后确定桥墩损伤界限值。其中等效塑性铰长度LP可依据《公路桥梁抗震设计细则》(JTG/T B02-01—2008)进行计算,并假设沿纵桥向主墩的反弯点在墩高1/2位置处。所得桥墩各项曲率延性指标和不同破坏状态下的损伤界限值见表5。
3 地震易损性分析
3.1 地震动选择及输入本文根据Baker等(2011)为美国太平洋地震工程中心(PEER)交通设施抗震研究提供的地震动记录数据库,选取场地条件相近、具有速度脉冲效应的40组典型近断层地震动记录作为输入,每组包含1个垂直断层方向地震动(SN)、1个平行断层方向地震动(SP)和1个竖向地震动(UP)。本文研究重点是桥梁初始内力的影响,所以默认桥梁是垂直断层走向,分别沿纵桥向(x方向)、横桥向(y方向)、竖向(z方向)输入各地震动分量,采用增量动力分析方法进行非线性时程分析,将每组记录中3个地震动分量的加速度峰值(PGA)以0.1 g为增幅,从0.2~1.5 g进行调幅。分析时各方向各PGA下,以40个地震反应峰值的平均值为讨论指标。
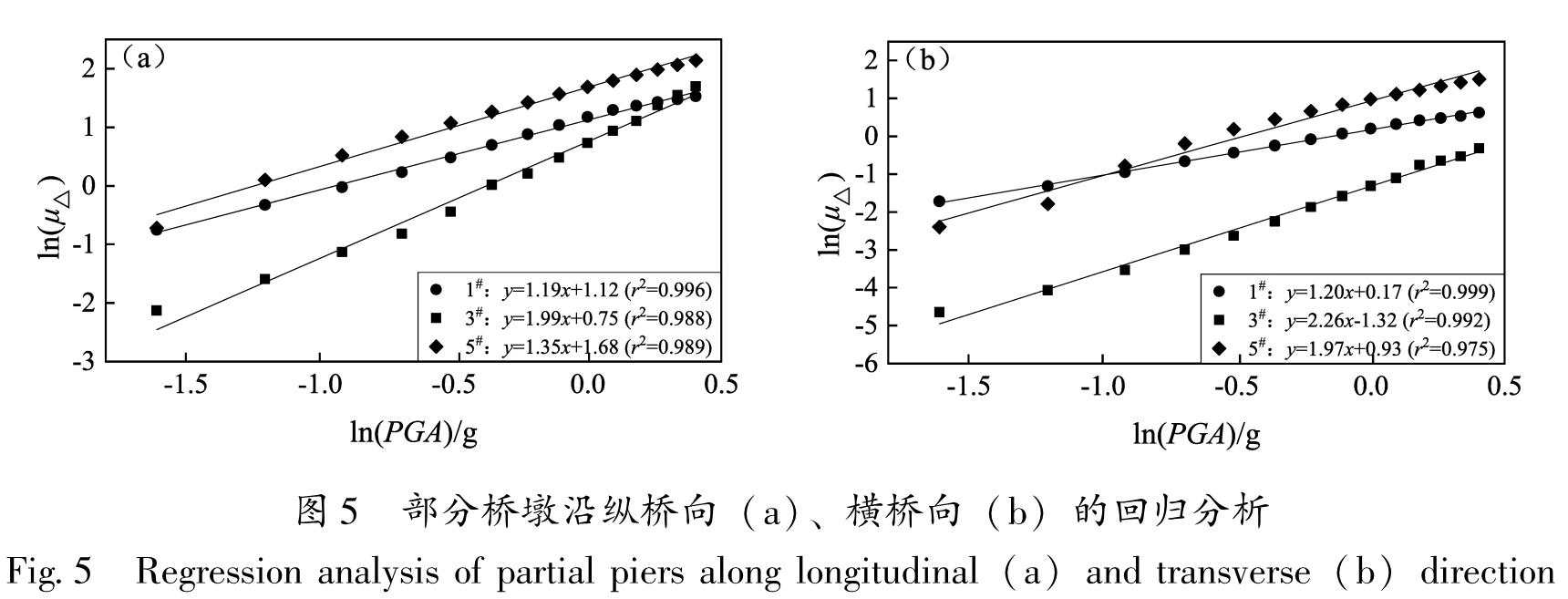
3.2 线性回归分析以PGA和位移延性系数的对数值作为横、纵坐标,采用最小二乘法对40组近断层地震动作用下的成桥阶段各桥墩沿纵、横桥向的位移反应平均值进行线性回归。图5给出了考虑内力状态时1#主墩、3#过渡墩和5#引桥墩的回归分析结果。结果显示,各散点集中分布在回归函数附近,且具有较高的回归相关系数r2,因此可以较准确地得到地震易损性曲线。
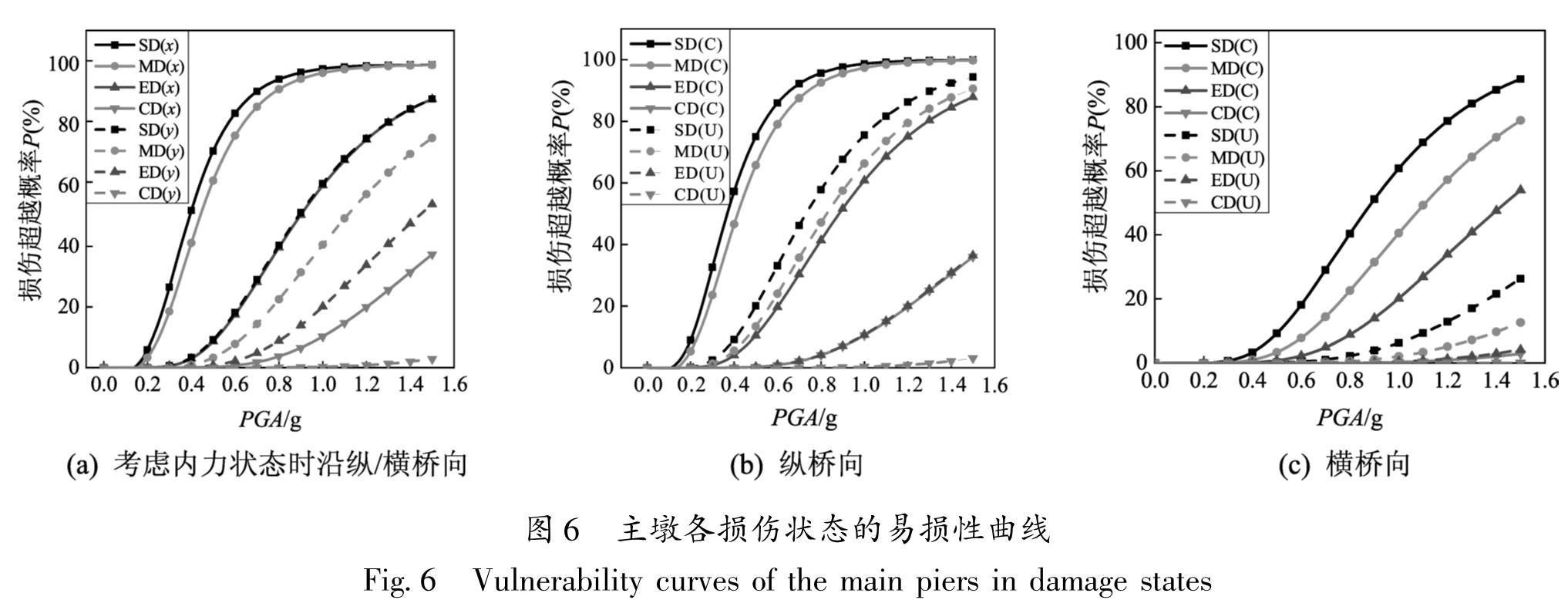
3.3 易损性分析由于1#主墩与2#主墩仅存在略微的墩高差,其受力大小、截面特性均相同,因此二者易损性曲线基本相同,故本文仅介绍1#主墩情况。为研究主墩易损性曲线变化规律,首先将考虑内力状态时1#主墩沿纵(x)、横(y)桥向各损伤状态的地震易损性曲线进行了对比,如图6a所示。图中显示:主墩沿纵、横桥向的地震易损性曲线变化规律相同,均随地震动强度的增加而上升,但同一种破坏状态下的损伤概率提升点总是先在纵桥向激发,横桥向则需要更大的PGA; 同时损伤概率沿横桥向增加速率较纵桥向小,因此主墩沿纵桥向的地震损伤概率总是大于横桥向。如PGA=0.4 g时,主墩沿纵桥向发生轻微破坏、中等破坏的概率较横桥向分别高约50%、40%; 当PGA=1.5 g时,主墩沿纵桥向发生完全破坏的概率能达到40%,而沿横桥向发生完全破坏的概率非常低。
进一步研究考虑内力状态与否对主墩沿纵、横桥向易损性曲线的影响(考虑与不考虑分别用C、U表示),如图6b、c所示,无论是沿纵桥向还是横桥向,不考虑内力状态时主墩在不同破坏状态下的易损性曲线均明显降低,即不考虑内力状态时将低估主墩的地震损伤概率。如在不考虑内力状态的情况下,PGA=0.4 g时主墩沿纵桥向发生轻微破坏、中等破坏的概率较考虑内力状态的情况分别被低估约50%、40%; PGA=1.0 g时主墩沿纵桥向发生严重破坏、完全破坏的概率较考虑内力状态的情况分别被低估50%、10%。
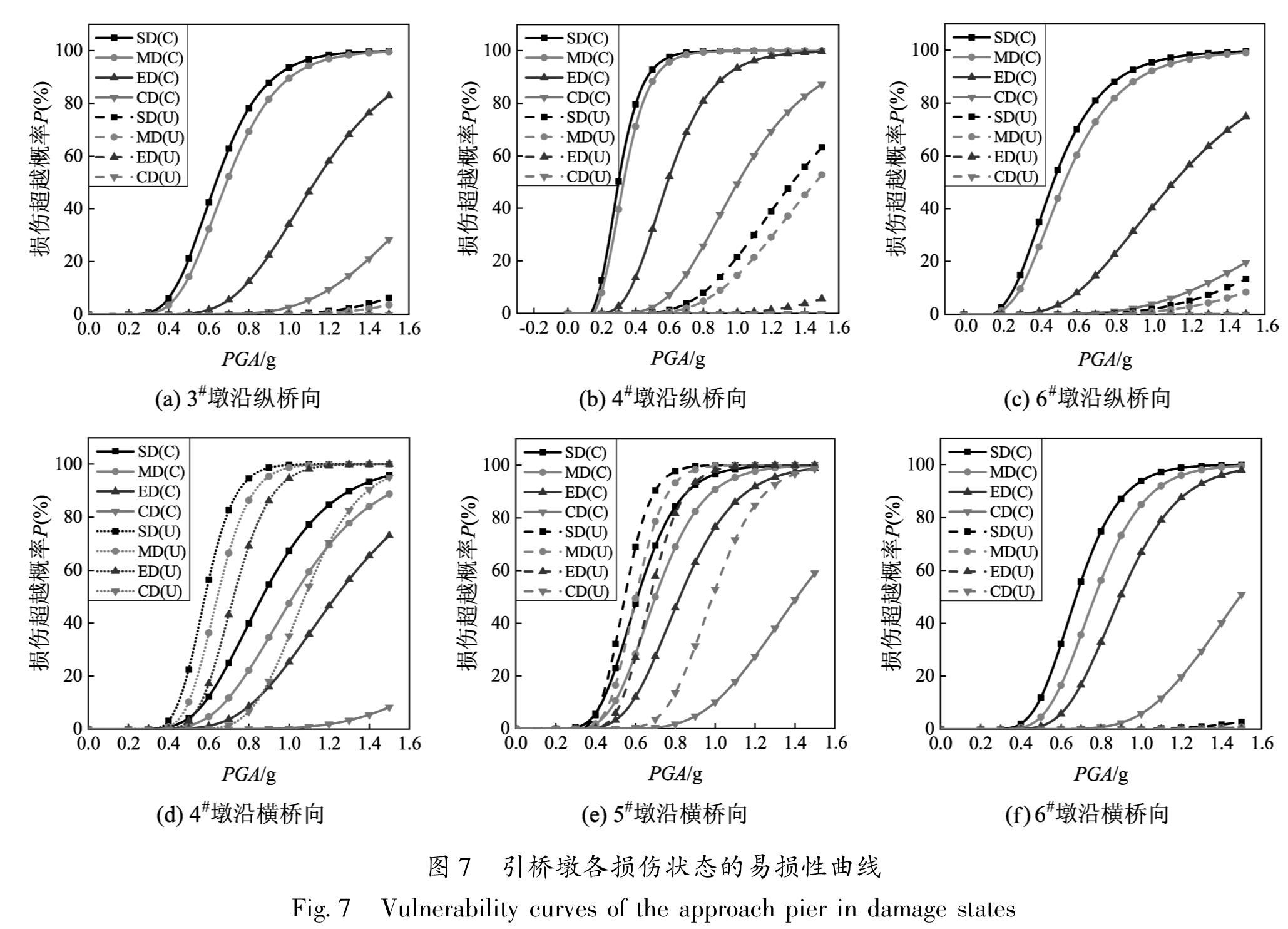
在研究考虑内力状态与否对引桥墩沿纵、横桥向地震易损性曲线的影响时,考虑到4#墩与5#墩的横截面大小、墩高及初始荷载都相等,同时3#墩在横桥向各损伤状态下的损伤概率非常小,故图7仅给出了部分引桥墩沿纵、横桥向的易损性曲线。从图中可以看出:沿纵桥向,各引桥墩的地震易损性曲线在不考虑内力状态的情况下远低于考虑内力状态的情况,即不考虑内力状态时将严重低估引桥墩的地震损伤概率,尤其对3#和6#墩,不考虑内力状态时最大损伤概率不足15%,损伤概率低估量明显较大。与沿纵桥向不同,4#和5#墩沿横桥向的地震易损性曲线在不考虑内力状态时较高,即不考虑内力状态时会高估4#和5#墩的地震损伤概率,而6#墩刚好相反,不考虑内力状态时6#墩的地震损伤概率不到10%,远小于考虑内力状态的情况。
4 结论
本文通过采用MIDAS/Civil和OpenSees两种软件联合建模的方法,对考虑内力状态的大跨度高墩连续刚构桥桥墩的地震反应与损伤情况进行了分析,得到以下主要结论:
(1)在连续刚构桥非线性动力分析中必须考虑施工过程和预应力作用对其成桥内力状态的影响,将基于等效荷载法计算得到的内力等效荷载施加到OpenSees动力分析模型上能够较好地反映真实内力状态。
(2)当考虑内力状态时,1#主墩与2#主墩的损伤概率基本相等; 主墩沿纵桥向损伤概率提升点对应较小PGA,且损伤曲线增长速率大,因此主墩沿纵桥向的损伤概率始终大于横桥向。
(3)考虑内力状态与否对主墩和引桥墩的地震易损性具有很大影响,不考虑内力状态的情况将严重低估主墩和引桥墩的地震损伤概率。在特定的PGA下,不考虑内力状态时主墩的损伤低估概率能达到50%; 对于6#引桥墩,不考虑内力状态时地震损伤概率不到10%,远小于实际情况。
(4)所采用的内力等效荷载方法较好地考虑了成桥内力状态,可为高烈度区连续刚构桥抗震设计和性能评估提供参考。但动力分析时采用了以平截面假设为基础的纤维梁柱单元,故未能考虑结构扭转和空间破坏作用,以及结构破坏所致的主梁预应力损失,这些工作还有待进一步研究。
- 郭昆霖,李小军,吴敬武,等.2020.地震行波对跨河谷高墩大跨桥梁地震反应的影响[J].地震研究,43(3):531-538.
- Hwang H,刘晶波.2004.地震作用下钢筋混凝土桥梁结构易损性分析[J].土木工程学报,37(6):47-51.
- 李宏男,成虎,王东升.2018.桥梁结构地震易损性研究进展述评[J].工程力学,35(9):1-16.
- 李吉涛,杨庆山,刘阳冰.2013.多点地震激励下大跨连续钢构桥易损性分析[J].振动与冲击,32(5):75-80.
- 李立峰,吴文朋,胡思聪,等.2016.考虑氯离子侵蚀的高墩桥梁时变地震易损性分析[J].工程力学,33(1):163-170.
- 马保林.2001.高墩大跨连续刚构桥[M].北京:人民交通出版社.
- 庞于涛,王建国,欧阳辉,等.2018.采用钢纤维混凝土的连续钢构桥地震易损性分析[J].哈尔滨工程大学学报,39(4):687-694.
- 石岩,李军,秦洪果,等.2021.桥梁双柱式排架墩抗震性能研究进展述评[J].中国公路学报,34(2):134-154.
- 石岩,张奋杰,韩建平,等.2020.高墩大跨度连续刚构桥典型施工阶段地震损伤分析[J].振动与冲击,39(22):89-95.
- 童磊,王东升,王荣霞.2020.汶川地震庙子坪特大桥主桥箱梁开裂震害分析[J].世界地震工程,36(3):161-171.
- 赵凌志.2018.高速铁路双薄壁墩混凝土连续刚构桥施工过程地震易损性分析[D].成都:西南交通大学.
- 赵秋红,李晨曦,董硕.2019.深水桥墩地震响应研究现状与展望[J].交通运输工程学报,19(2):1-13.
- 俎林,黄勇.2020.维修加固桥梁的抗震韧性评价方法[J].地震研究,43(3):522-530.
- Baker J W,Lin T,Shahi S K, et al.2011.New ground motion selection procedures and selected motions for the peer transportation research program[R].PEER Report,3.
- Banon H,Veneziano D.1982.Seismic safety of reinforced concrete members and structures[J].Earthquake Engineering and Structural Dynamics,10(2):179-193.
- National Institute of Building Science.1999.HAZUS99 User's manual[R].Washington D C:Federal Emergency Maragement Agency.
- Guo A X,Shen Y,Bai J L, et al.2017.Application of the endurance time method to the seismic analysis and evaluation of highway bridges considering pounding effects[J].Engineering Structures,131:220-230.
- Hose Y D,Seible F.1999.Performance evaluation database for concrete bridge components and systems under simulated seismic loads[M].California:Pacific Earthquake Engineering Research Center,University of California.
- Hwang H,Jernigan J B,Lin Y W.2000.Evaluation of seismic damage to Memphis bridges and highway systems[J].Journal of Bridge Engineering,5(4):322-330.
- Hwang H,Liu J B,Chiu Y H.2001.Seismic fragility analysis of highway bridges[R].Mid-Ameirica Earthquake Center Technical Report,MAEC-RR-4 Project.
- Lin T Y,Burns N H.1981.Design of prestressed concrete structures(3rd ed.)[M].New York:John Wiley & Sons,Inc.
- Muthukumar S,DesRoches R.2006.A hertz contact model with non-linear damping for pounding simulation[J].Earthquake Engineering and Structural Dynamics,35(7):811-828.
- Park Y J,Ang A H S.1985.Mechanistic seismic damage model for reinforced concrete[J].Journal of structural engineering,111(4):722-739.
- Peng Y C,Zhang Z X.2020.Development of a novel type of open-web continuous reinforced concrete rigid-frame bridge[J].Journal of Bridge Engineering,25(8):05020005.
- Shi Y,Li J,Qin H G,et al.2021.Correlation analysis of ground motion duration indexes and nonlinear seismic responses of a long-span continuous rigid-frame bridge with high-rise piers[J].Journal of Earthquake Engineering,25(4):1-21.
- Taflanidis A A.2011.Optimal probabilistic design of seismic dampers for the protection of isolated bridges against near-fault seismic excitations[J].Engineering Structures,33(12):3496-3508.
- JTG/T B02-01—2008,公路桥梁抗震设计细则[S].