基金项目:中国地震局工程力学研究所基本科研业务费专项(2021EEEVL0315)和国家重点研发计划项目课题(2019YFC1509301)资助.
(1.中国地震局工程力学研究所 地震工程与工程振动实验室,黑龙江 哈尔滨 150080; 2.哈尔滨工业大学(深圳)土木与环境工程学院,广东 深圳 518055)
(1.Key Laboratory of Earthquake Engineering and Engineering Vibration,Institute of Engineering Mechanics,China Earthquake Administration,Harbin 150080,Heilongjiang,China)(2.School of Civil and Environmental Engineering,Harbin Institute of Technology,Shenzhen,Shenzhen 518055,Guangdong,China)
thermal power plant; substations; beta function; damage ratio; seismic vulnerability
DOI: 10.20015/j.cnki.ISSN1000-0666.2022.0041
备注
基金项目:中国地震局工程力学研究所基本科研业务费专项(2021EEEVL0315)和国家重点研发计划项目课题(2019YFC1509301)资助.
引言
发电厂是电力系统的基础单元,在地震中如果遭受严重的破坏,不仅会造成直接经济损失,同时由于其发电功能丧失,供电终止,还将会引发一系列连锁危害,严重影响震后应急救援、人民生产生活和灾后重建工作。电力能源包含火电、水电、核电、风电、太阳能电等多种类型,其中火力发电是全球最广泛采用的发电方式,在中国使用率甚至达到了80%以上。因此,研究火力发电厂的地震易损性具有重要意义。
过去人们对火力发电厂的土建设施和发变电设备在结构设计、抗震措施和抗震能力评价等方面进行了大量研究(张治勇等,1999),如Wang等(2018)研究了火力发电厂的结构不规则性对其抗震性能的影响; Dai等(2018)通过单目标和多目标优化程序设计了火力发电场PMI系统; 还有学者采用增量动态分析方法对3个互联的高压变电站进行了抗震性能分析(Mohammadi,Tehrani,2014)等。对于火电厂的地震易损性研究,则是针对火电厂中个别土建设施或单体设备的易损性研究较多(周长东等,2017; 郑山锁等,2020)。然而,对于地震灾害预测、经济损失评估或地震保险工作而言,需要将火力发电厂作为一个独立的整体单元,根据其地震易损性矩阵中不同地震强度下不同破坏等级的破坏概率计算发电厂整体的地震损失,而不必详细研究火力发电厂中每个设施或设备发生的具体破坏情况。因此以火力发电厂作为整体单元的地震易损性矩阵,确定其在不同地震动强度下各破坏等级的概率,对于制定相应防灾政策和损失评估计算极其重要(马玉宏等,2015; 尹之潜,1996)。
由于火力发电厂组成构件较多且各类构件破坏原因和特点不同,以火力发电厂作为整体单元进行地震易损性分析是比较困难的事情。同时,相比于房屋建筑,火力发电厂实际震害资料以及整体破坏情况或经济损失的统计均较少,目前尚没有以火力发电厂为单元的地震易损性矩阵研究成果。美国应用技术委员会的ATC-25报告(ATC,1991)给出了火力发电厂在不同地震烈度下的破坏比曲线的计算式,但是依据此计算式依然不能得到火力发电厂的地震易损性矩阵,无法精细计算火力发电厂在不同地震动强度下发生各破坏等级的损失。
鉴于此,本文提出了一种计算火力发电厂地震易损性的方法。根据ATC-25报告中火力发电厂在不同地震烈度下的破坏比以及2008年汶川MS8.0地震中获得的变电站实际震害统计数据,使用Beta分布函数计算基于烈度的地火力发电厂震易损性矩阵,然后利用对数正态分布拟合地震易损性曲线,获得基于地震动峰值加速度的火力发电厂地震易损性矩阵,为火力发电厂地震风险评估和损失计算工作提供参考。
1 研究思路
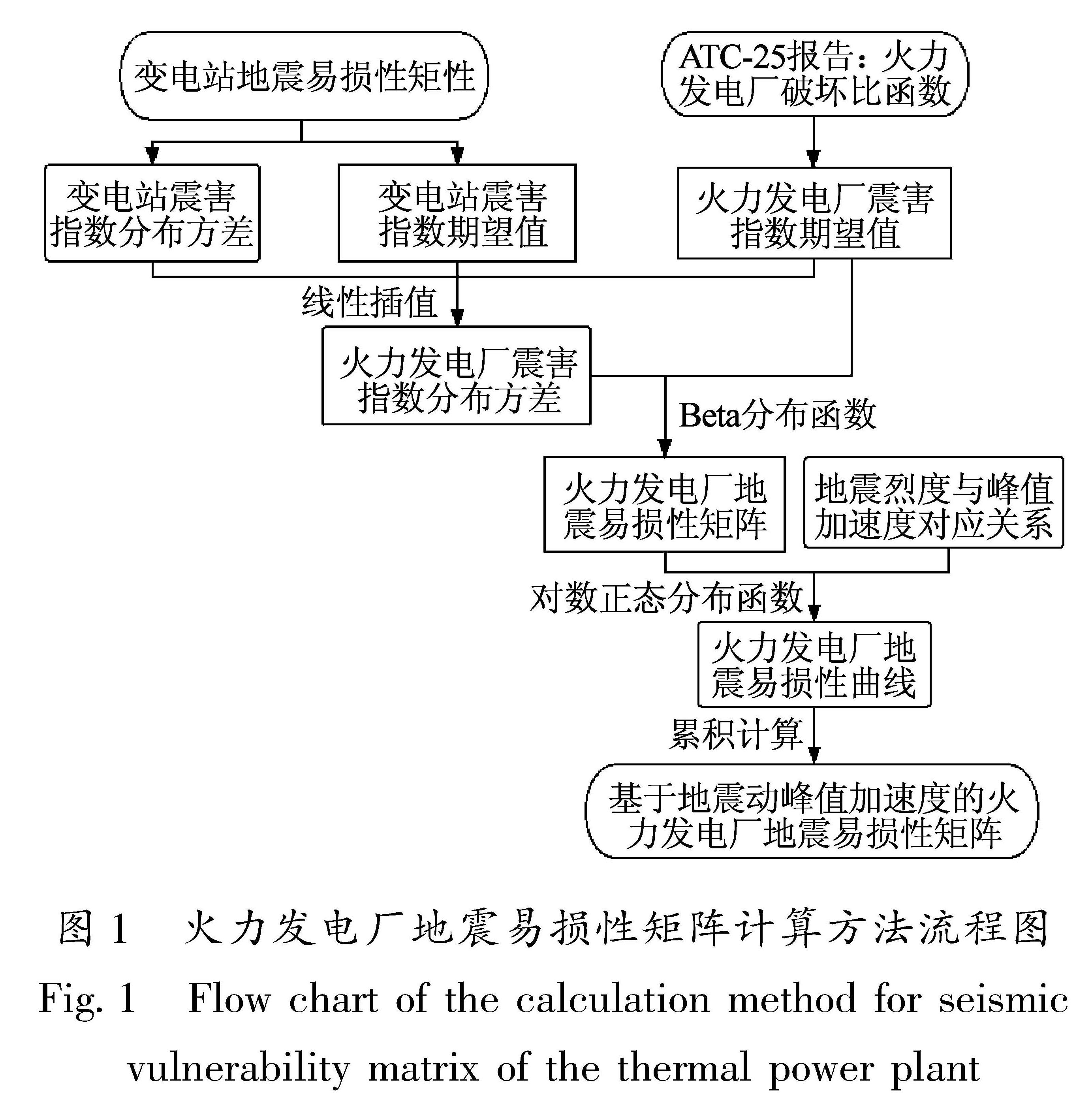
基于Beta分布函数的火力发电厂地震易损性研究思路为:①根据ATC-25报告中提出的火力发电厂的破坏比函数,确定不同地震烈度下火力发电厂的震害指数期望值。②由于变电站与火力发电厂构件组成和震害特点上具有诸多相同点,都是由建构筑物、电气设备以及室内监控设备(发电厂除监控设备外还包括机电设备)构成,因此假设火力发电厂和变电站在震害指数期望值相同时,其震害指数分布的离散性也相同。根据这一假设,基于变电站震害指数的期望值和分布方差,采用线性插值法求得与火力发电厂不同震害指数期望值相对应的震害指数离散分布方差。③以火力发电厂的震害指数期望值和方差为参数,使用Beta分布函数拟合基于地震烈度的火力发电厂地震易损性矩阵。④基于火力发电厂地震易损性矩阵和烈度与地震动峰值加速度的对应关系,使用对数正态分布累积函数拟合火力发电厂的地震易损性曲线,确定基于地震峰值加速度的火力发电厂的地震易损性矩阵。计算流程如图1所示。
2 拟合参数的确定
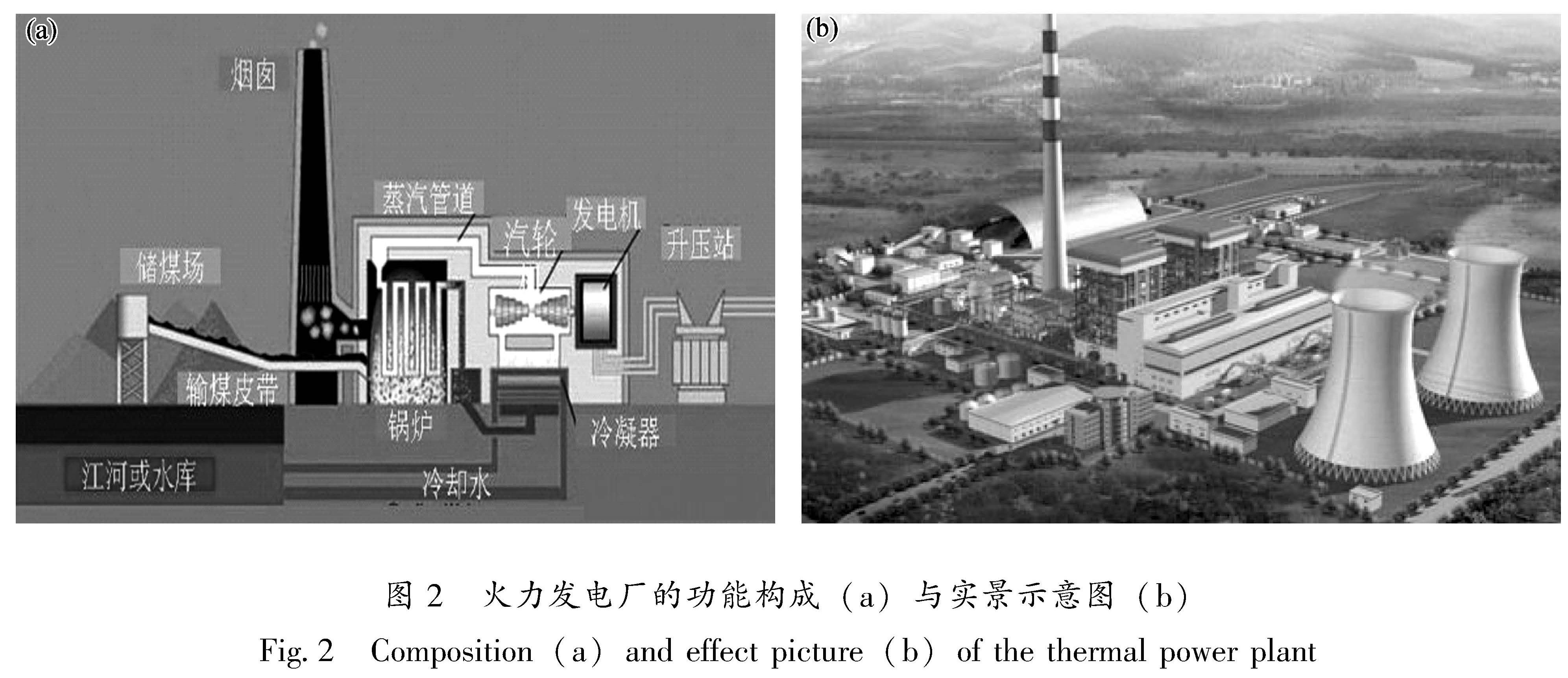
2.1 震害指数期望值火力发电厂的构成十分复杂,由燃料系统、燃烧系统、汽水系统、电气系统、控制系统5个系统组成。各种构件包括燃料室、燃烧室、汽机房、控制室、冷却塔、烟囱等各种土建设施和锅炉、发电机组以及各种变电设备和监控设备等。电厂的功能组成与实景示意如图2所示。
上述火力发电厂的设备设施可以分为3类:土建设施、机电设备、电气设备。ATC-25报告中对火力发电厂地震易损性进行了研究,在计算火力发电厂整体的地震破坏比时综合考虑了土建设施、机电设备和电气设备的破坏特点,提出了3类设施设备破坏比的计算公式并确定它们在发电厂中的权重占比。火力发电厂每一类设施设备破坏比计算公式为(ATC,1991):

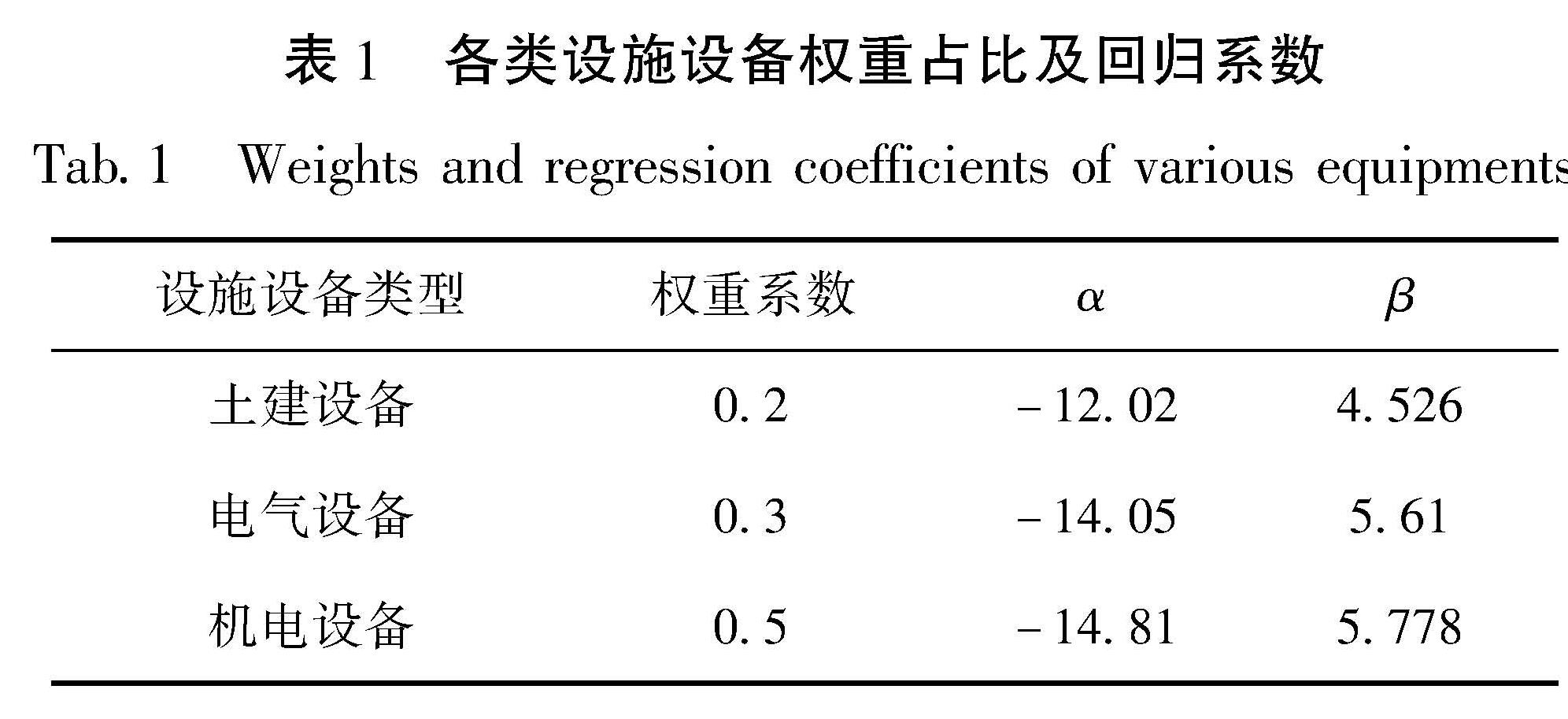
式中:DMG为破坏比; j为地震烈度; α、β为回归系数,各类设备的回归系数以及权重系数见表1。
由于不同设备使用功能和经济价值不同,因此不同设备的破坏在火力发电厂的整体破坏评价中占比不同,各类设备权重占比见表1。
由表1中各类设备权重占比和回归系数,结合火力发电厂设备地震破坏比计算公式,可得火电厂整体破坏比为:

式中:R(j)为地震烈度j下火力发电厂的破坏比; j为地震烈度。
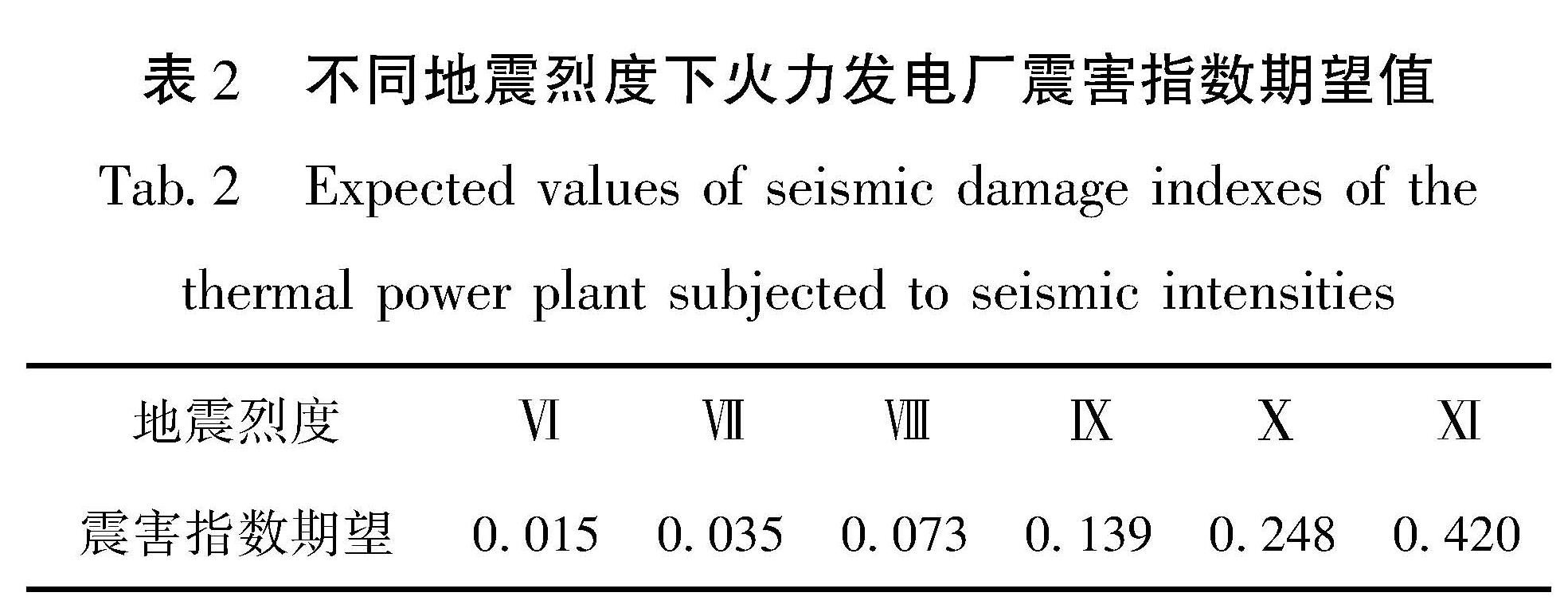
某地震动强度下的震害指数期望值是地震易损性矩阵中该地震动强度下各破坏等级所占比率与相对应破坏等级的震害指数加权平均之和,可以表示火力发电厂的整体破坏程度情况,与整体的破坏比具有相同的实际意义(胡聿贤,2006)。因此采用式(2)计算获得不同地震烈度下整体破坏比作为火力发电厂震害指数期望值(表2)。
2.2 震害指数分布方差变电站与火力发电厂在设备组成和震害特点上存在许多相似点:①变电站也是由变压器、控制设备等多种设备组合而成的主体,设备种类众多,主要可以分为土建设施、室外高压电气设备以及室内设备3类; ②在历史地震中,变电站的破坏原因主要分为两类:一是由于地震导致各类设施的直接损坏,二是由于土建设施损坏造成内部设施的间接损毁,与火力发电厂整体破坏的原因基本相同; ③110 kV及以上变电站的室外高压电气设备、室内设备以及土建设施的价值权重(刘如山等,2017)分别为0.671、0.201、0.128,与表1中火力发电厂各类设施经济价值权重相似。
由于变电站与火力发电厂在构件组成、破坏类型以及权重系数方面的相似性,本文假设火力发电厂和变电站的地震易损性矩阵在不同破坏等级分布的离散性比较接近,即二者的震害指数期望值相同时,其离散性也相同,即震害指数分布方差相同。由于目前尚无火力发电厂的地震易损性矩阵研究,其震害指数的分布方差未知。因此本文基于上述假设,采用已有变电站地震易损性矩阵中震害指数的分布方差,插值计算获得不同地震烈度下火力发电厂震害指数的分布方差。
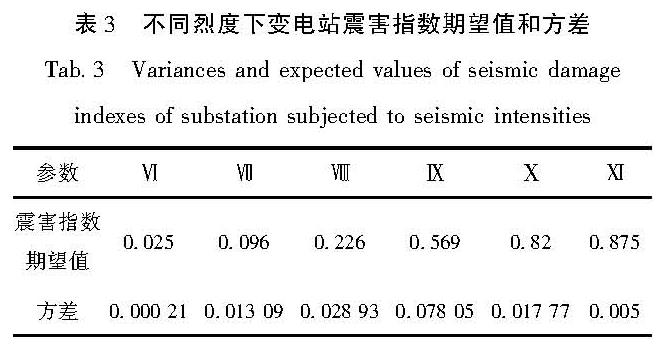
刘如山等(2021)对四川电网中110 kV及以上的121个变电站进行了统计分析,得到变电站的地震易损性矩阵,其不同地震烈度下变电站的震害指数期望值和分布方差见表3。
表3 不同烈度下变电站震害指数期望值和方差
Tab.3 Variances and expected values of seismic damage indexes of substation subjected to seismic intensities本文在已有变电站震害指数期望值、分布方差以及火力发电厂震害指数期望值的基础上,采取分段线性插值计算火力发电厂的震害指数分布方差为:
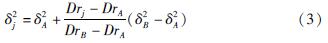
式中:Drj为j烈度下火力发电厂震害指数期望值; δ2j为j烈度下火力发电厂震害指数分布方差; DrA、DrB为变电站震害指数期望值; δ2A、δ2B为变电站震害指数分布方差。火力发电厂震害指数期望值和分布方差计算结果见表4。
3 基于地震烈度的地震易损性矩阵拟合
3.1 Beta函数性质多数随机变量的概率分布范围在一端或两端是无界的,但是在一些工程应用上,随机变量的数值可能具有下限和上限。在此情况之下,采用具有上限和下限的概率分布函数相对更为合适。如果随机变量是有界的,并且具有上限值和下限值,则适合选用Beta分布函数(Ang,Tang,2007)。
Beta函数的随机变量有上下限值,当自变量x的上下限区间为[0,1]时,称为标准Beta分布。标准Beta分布的概率密度函数为:
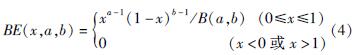
式中:a>0,b>0,B(a,b)表示为:

标准Beta分布函数的随机变量期望值为:

方差计算式为:
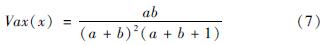
显然Beta分布概率密度函数在x∈[0,1]内符合全概率分布性质,即:

这与地震易损性矩阵中某烈度下结构各个破坏等级概率分布之和为1具有同样的性质。当其参数a和b不同且小于1时,标准Beta分布的概率密度函数都具有单峰值的性质。因此,如果将火力发电厂的震害指数Dr作为变量,就可以用Beta分布概率密度函数来拟合火力发电厂的地震易损性矩阵。这里,震害指数Dr是连续型变量。
3.2 基于地震烈度的地震易损性矩阵拟合刘如山等(2009)提出以地震动峰值加速度作为拟合参数,利用Beta分布函数对不同地震烈度下结构各破坏等级的概率分布进行拟合,研究房屋结构的地震易损性矩阵的方法,并应用于某些地区老旧房屋的地震易损性研究(Liu et al,2020)。由于地震易损性矩阵各个破坏等级概率密度之和为1,与标准Beta分布的概率密度函数具有同样的性质,上述研究结果也表明使用Beta分布函数拟合地震易损性矩阵拟合结果良好。因此本文将震害指数作为连续变量,以不同地震烈度下震害指数的期望值和分布方差为拟合参数,使用Beta分布函数拟合火力发电厂整体破坏情况的地震易损性矩阵方法过程如下:
由式(6)(7)中Beta分布函数参数a和b与期望值和方差的关系,可以推导出使用震害指数期望值和方差计算j烈度下Beta分布函数的参数aj和bj为:
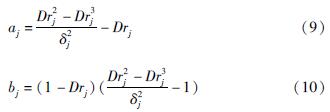
式中:Drj为j烈度下震害指数期望值; δ2j为j烈度下震害指数分布方差。
将参数aj、bj代入式(4),则j烈度下震害指数的Beta分布的概率密度函数可表示为:
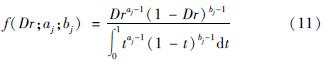
对火力发电厂在不同地震烈度下各破坏等级的破坏概率进行分段积分拟合,最终得到火力发电厂的地震易损性矩阵,公式为:
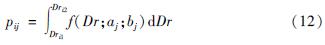
式中:Dr为震害指数连续型变量; pij为烈度j下发生i级破坏的概率值; Dri1、Dri2分别为i级破坏的震害指数区间下限值和上限值。
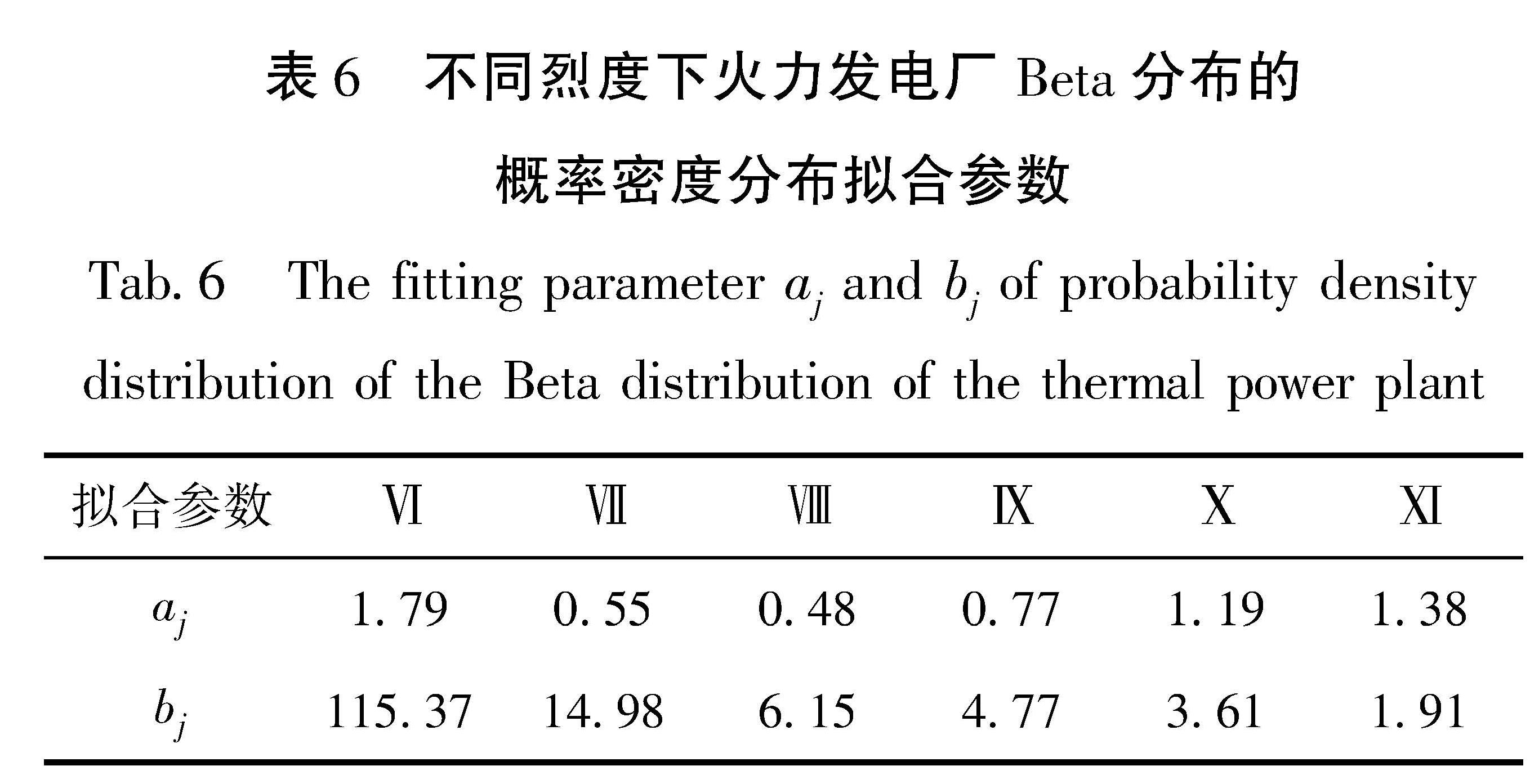
考虑到电力设施更强调功能性,这里将火力发电厂震害指数取值范围与破坏等级对应关系参考采用美国的做法,见表5(应用技术委员会,1991)。这一关系有别于我国建筑设施的震害指数与破坏等级的对应关系。将表2、4中火力发电厂震害指数期望值和分布方差代入式(9)、式(10)中可计算得到参数aj、bj,计算结果见表6。
表5 火力发电厂震害指数区间与破坏等级对应关系
Tab.5 The corresponding relationship between the intervals of seismic damage indexes and seismic damage levels of the thermal power plant表6 不同烈度下火力发电厂Beta分布的概率密度分布拟合参数
Tab.6 The fitting parameter aj and bj of probability density distribution of the Beta distribution of the thermal power plant将表6中火力发电厂拟合参数aj、bj值代入式(11),得到不同地震烈度下火力发电厂的分布的概率密度分布曲线(图3)。由图3可以看出,低烈度区的火力发电厂的震害指数的概率密度值在震害指数值较小的区域比较大。随着震害指数值的增大,概率密度值迅速减小,说明在低烈度区火力发电厂的破坏主要为轻微破坏。随着烈度的增大,火力发电厂的震害指数概率密度值在震害指数较大的范围内逐渐增长,说明在高烈度区火力发电厂开始出现较大破坏等级的震害。
图3 不同地震烈度下火力发电厂震害指数的概率密度分布
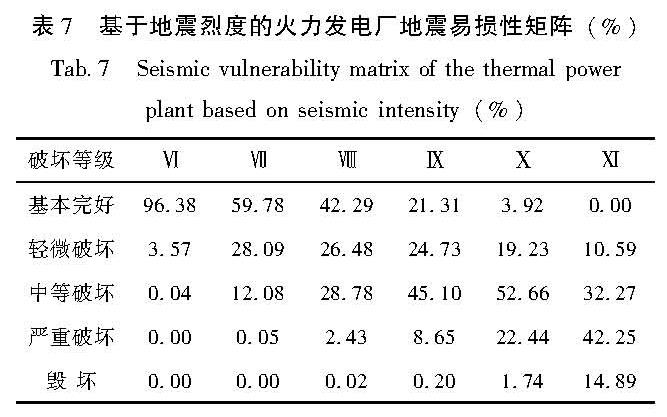
Fig.3 Probability density distribution of the seismic damage index of the thermal power plant subjected to seismic intensities在Beta分布的概率密度分布函数基础上,利用式(12)计算获得不同烈度下火力发电厂整体破坏的地震易损性矩阵,见表7。由表7可见,当地震烈度为Ⅵ度时,火力发电厂基本未发生破坏; 当地震烈度为Ⅶ度和Ⅷ度时,火力发电厂开始出现轻微破坏和中等破坏,破坏等级较低; 当地震烈度为Ⅹ度时,火力发电厂发生中等破坏的破坏概率最高,部分火电厂可能发生严重破坏; 当地震烈度Ⅺ度时,火力发电厂破坏相对严重,破坏等级主要为严重破坏,毁坏的概率约为15%。
表7 基于地震烈度的火力发电厂地震易损性矩阵(%)
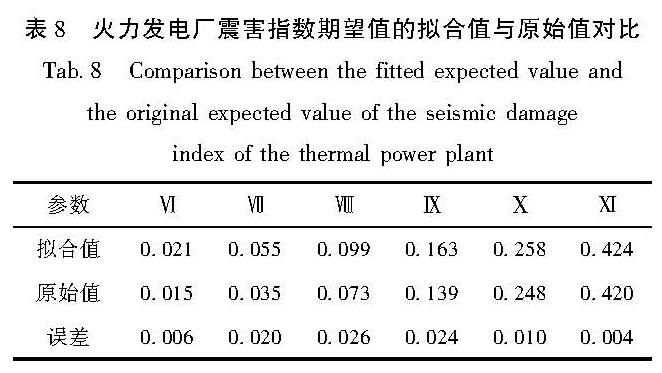
Tab.7 Seismic vulnerability matrix of the thermal power plant based on seismic intensity(%)基于本文方法拟合获得的火力发电厂地震易损性矩阵,计算得到不同地震烈度下火力发电厂震害指数期望值。由表8可见,对比使用Beta分布函数拟合获得的震害指数期望值与美国ATC-25报告中的原始期望值,在不同地震烈度下,震害指数期望值的拟合误差均低于0.03,说明拟合的易损性矩阵在反算震害指数期望值时不存在系统偏差,使用Beta分布函数拟合火力发电厂地震易损性矩阵拟合效果较好。
4 基于峰值加速度的火力发电厂地震易损性曲线拟合
由于地震烈度是由房屋结构的破坏、人的感觉以及地表破坏的表观现象等[HJ2.3mm]因素来评定的,它并不是一个物理量,因此烈度的评定结果存在一定不确定性。随着防震减灾研究的发展,不论是地震动强度观测、建构筑物的抗震设计或地震易损性评定,都大量使用地震动峰值加速度来表示地震动强度。根据地震烈度与地震动峰值加速度的基本对应关系,本文采用对数正态分布函数将基于烈度的地震易损性矩阵转化为基于地震动峰值加速度的地震易损性矩阵。
使用对数正态分布函数拟合地震易损性曲线的方法在过往研究中得到了广泛的应用(陈波等,2018; Yamazaki et al,2000)。为了获得火力发电厂在不同地震动峰值加速度下的详细破坏与损失情况,本文基于拟合得到的地震易损性矩阵,采用双参数对数正态累积分布函数对火力发电厂进行不同破坏等级下的地震易损性曲线拟合,函数表达式为:
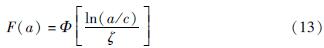
式中:F(a)为火力发电厂达到某破坏等级的超越概率; a为地震动峰值加速度; Φ为标准正态分布函数; c和ζ分别为易损性函数的中位值和对数标准差。火力发电厂破坏等级超越概率为:

式中:fij为j烈度下在i破坏等级的超越概率值; pij为j烈度下发生i破坏等级的概率值。
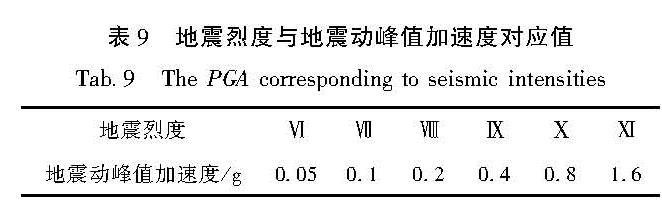
本文根据《建筑抗震设计规范》(GB 50011―2010)中地震烈度与地震动峰值加速度之间的对应关系,将火力发电厂地震易损性矩阵的输入参数由地震烈度转换为地震动峰值加速度,见表9。根据表7和表9,利用式(14),计算得到以地震动峰值加速度为输入参数的火力发电厂超越概率矩阵,见表 10。
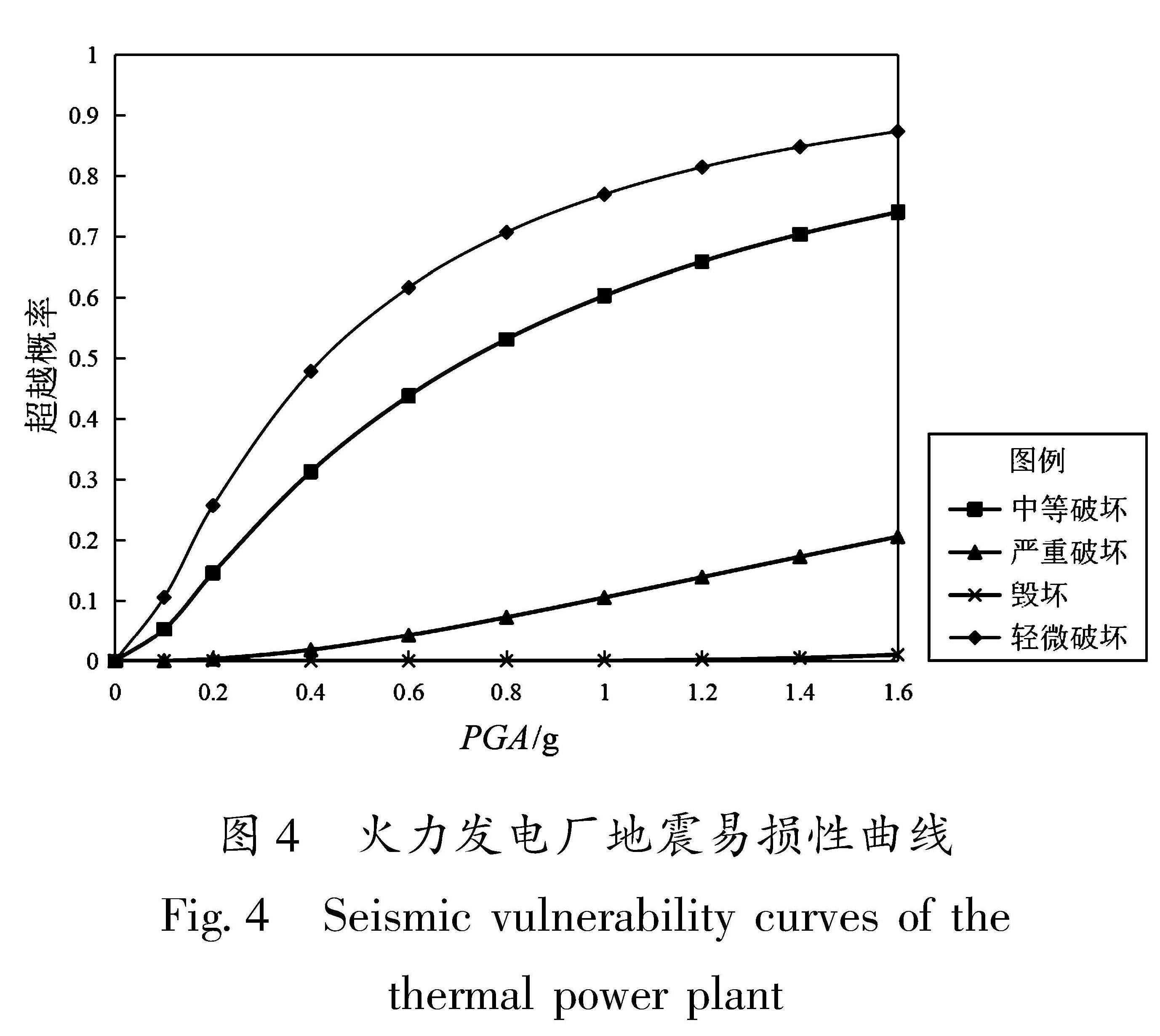
根据表 10和式(13)可计算得到火力发电厂的地震易损性函数曲线,即各破坏等级的超越概率曲线,如图4所示。拟合得到的各个破坏等级的超越概率函数曲线的中位值参数值(c)与对数标准差参数值(ζ)见表 11。
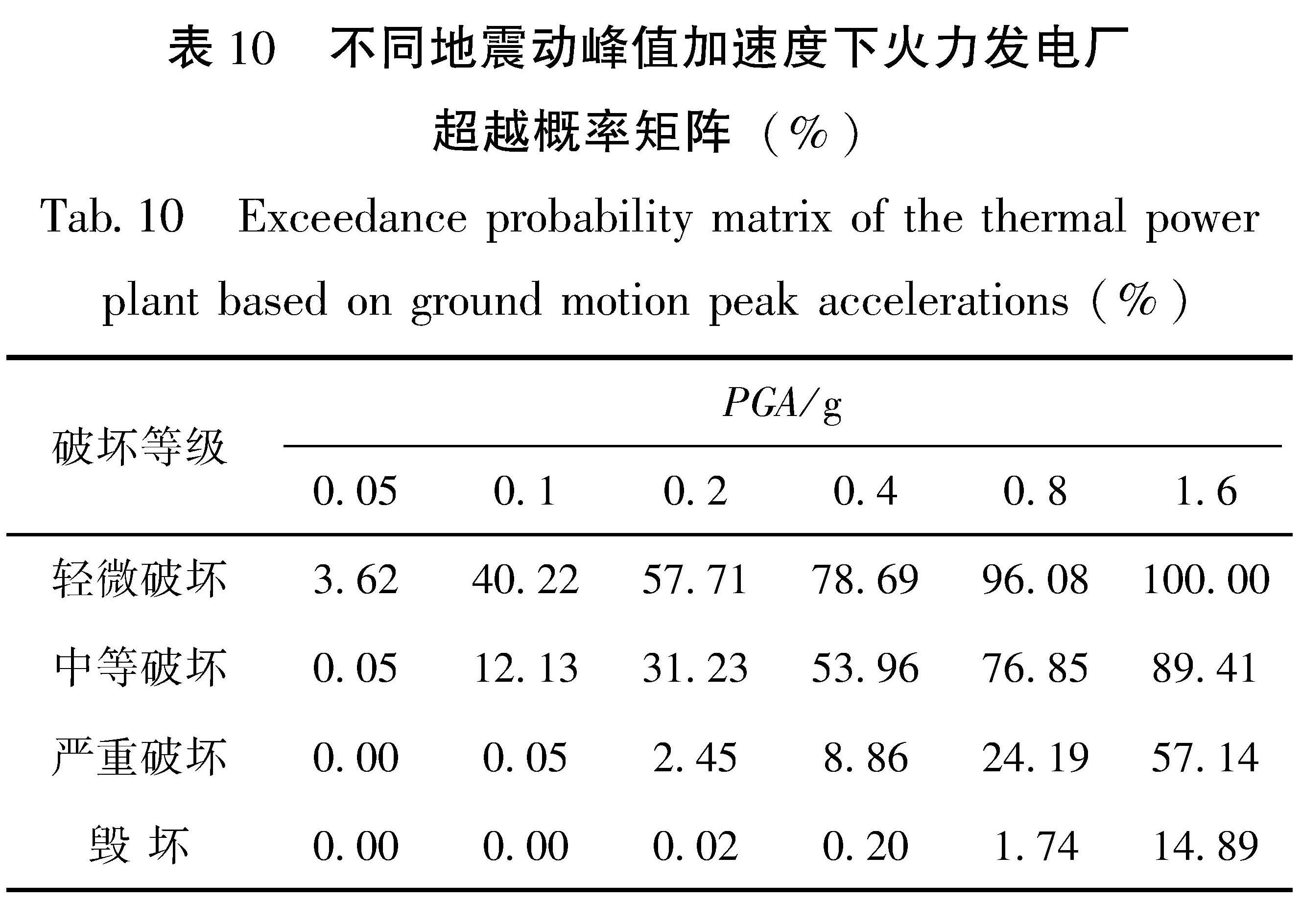
表 10 不同地震动峰值加速度下火力发电厂超越概率矩阵(%)
Tab.10 Exceedance probability matrix of the thermal power plant based on ground motion peak accelerations(%)表 11 火力发电厂地震易损性函数的中位值与对数标准差
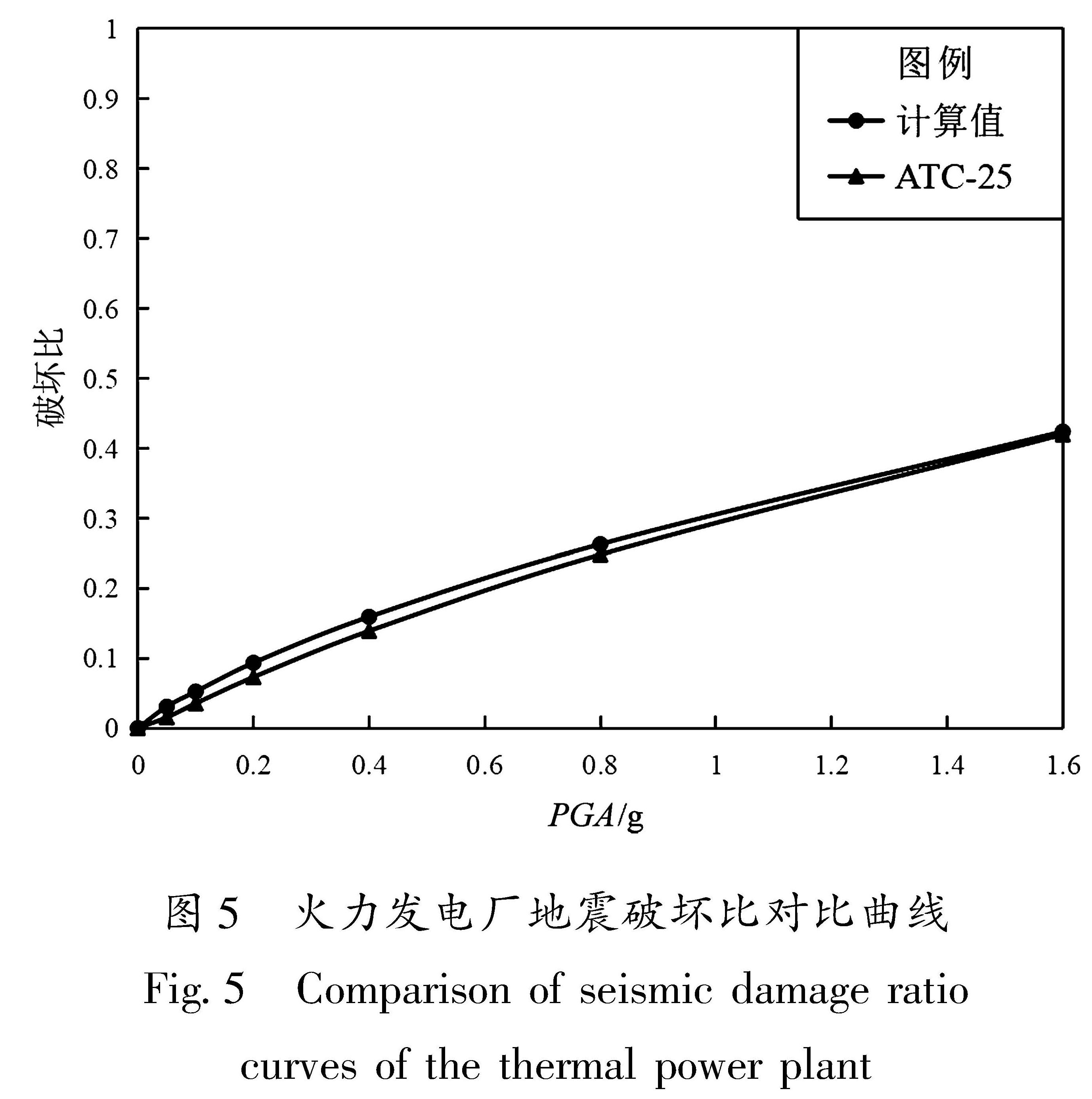
Tab.11 Median values and logarithmic standard deviation of seismic vulnerability function of the thermal power plant根据拟合得到的火力发电厂地震易损性曲线,可以计算得到不同地震动峰值加速度下的火力发电厂破坏比曲线。将ATC-25报告中火力发电厂破坏比-烈度的关系根据表9中烈度与地震动峰值加速度对应关系转换为破坏比-地震动峰值加速度的对应关系,也可得到相应的火力发电厂破坏比曲线。本文方法计算得到的火力发电厂破坏比和ATC-25报告中火力发电厂破坏比的对比图如图5所示。
由图5可知,本文方法计算得到的火力发电厂破坏比值与ATC-25报告相比,虽然数值稍偏大, 但是两者差别较小,并且随着地震动峰值加速度的增大,二者趋于相同。该对比结果虽然不能证明易损性曲线是正确的,但能够很好地说明使用本文建立的地震易损性曲线计算给定地震动强度下火力发电厂破坏比没有偏离原来的数值,即没有偏离ATC-25报告中的结果。
5 地震易损性的适用性讨论
ATC-25报告中火电厂破坏比曲线适用于美国广泛存在的普通火力发电厂,抗震设防水平上没有特别说明。美国的火力发电厂大都是以天然气和燃煤做为燃料的发电厂,其厂房多数为钢结构,部分为钢筋混凝土结构。我国的发电厂抗震设计标准基本是参考美、日等国的设防标准,火力发电厂的房屋结构类型以及燃料种类与美国相同,抗震设防水平与美国相比虽然有差别但不是很大。因此,本文计算方法得到的火力发电厂易损性研究结果亦适用于中国普通的以燃煤和天然气作为燃料的火力发电厂。
本文以ATC-25报告中的火力发电厂破坏比值为期望值,借助变电站的地震破坏比的离散性参数来构建火力发电厂地震易损性曲线,之所以采用该方法,关键原因在于实际地震中,火力发电厂震害样本很少,不能通过统计的方法直接得到发电厂易损性。因此,构建的易损性曲线不可能通过我国某一两个实际震害的例子来完全验证火电厂易损性曲线的期望值与离散性的合理性。
1978年唐山7.8级地震造成陡河火电厂钢筋混凝土框排架主厂房部分倒塌,带来电力供应中断(刘恢先,1986)。自此以后,我国学者对火力发电厂钢筋混凝土框排架结构开始进行了深入的分析研究,并制订了《火力发电厂土建结构设计规定》(DL 5022—93)等相应行业规程。唐山地震由于年代久远,当时发电厂的抗震能力已经不能反映我国现在火力发电厂抗震能力的真实水平。
近十几年来,我国发生的破坏性地震中,震灾区存在火电厂破坏的案例很少,如2008年汶川MS8.0地震中,江油火力发电厂造成了严重破坏。江油火力发电厂是西南地区最大的火力发电厂之一,建成于1958年。江油火力发电厂是川西地区重要电源支撑点,汶川地震时在运行的有2×330 MW燃煤发电机组和2×300 MW燃煤发电机组。其中2×300 MW机组(#33、#34机)于2005年建成并投入使用。建构筑物的抗震设防烈度为Ⅶ度,设计所依据的规范为《建筑抗震设计规范》(GB 50011—2001)。
汶川地震发生后,江油市火力发电厂厂址评定的地震烈度为Ⅷ度或稍强,根据ATC-25报告的推算式,其破坏比期望值在0.2以下。由于33号汽机房圈梁非完全性闭合,地震时外侧柱外闪较大,致使33号汽机房网架屋盖塌落(图6),将汽机组砸坏,这也成为电厂停运的最主要的原因之一。另外,由于电厂建设年代较早,抗震设防水平较低,厂区内行政办公楼、工程公司办公楼、综合楼、档案楼、生产楼、锅炉车间办公楼、化学车间办公楼、厂大门、物资库房等建筑出现较严重震害现象,多数成为危楼。2×330 MW汽机房楼层柱体根部混凝土也有脱落和钢筋外漏、混凝土牛腿压碎的现象。由于上述原因,实际震害较推算结果更为严重一些。如果去除以上因素,综合目前我国抗震设防情况,本文构建的地震易损性还是能够为我国的火电厂提供参考的。
6 结论
本文提出了一种火力发电厂地震易损性计算方法。通过ATC-25报告中火力发电厂的研究成果和汶川地震变电站的地震易损性矩阵,获得了火力发电厂整体破坏情况的震害指数期望值和方差; 使用Beta分布的概率密度函数拟合了不同地震烈度下火力发电厂的地震易损性矩阵; 最后使用标准对数正态分布的累积函数式,拟合得到了火力发电厂的地震易损性曲线,确定了基于地震动峰值加速度的火力发电厂地震易损性矩阵。利用该方法计算得到火力发电厂的破坏比与ATC-25报告结果接近,满足预期要求。
本文方法思路简明、易于实现,对火力发电厂地震灾害损失风险分析,实际操作性强。由于火力发电厂实际震害资料较少,进行火力发电厂地震易损性矩阵拟合所使用的破坏比-地震烈度关系曲线以及离散性参数,仍需将来通过实证和理论做进一步研究。
-
陈波,温增平,赵文哲.2018.基于地震动参数的房屋震害矩阵曲线化分析方法[J].地震研究,41(4):613-621.
- 胡聿贤.2006.地震工程学[M].北京:地震出版社.
- 刘恢先.1986.唐山大地震震害(第二册)[M].北京:地震出版社.
- 刘如山,胡少卿,邬玉斌,等.2009.基于地震动参数的结构易损性表达方法研究[J].地震工程与工程振动,29(6):102-107.
- 刘如山,毛晨曦,郭恩栋,等.2021.生命线系统易损性分析模型和数据库[R].哈尔滨:中国地震局工程力学研究所.
- 刘如山,张中近,熊明攀,等.2017.基于设施易损性的变电站地震经济损失快速评估[J].应用基础与工程科学学报,25(3):604-614.
- 马玉宏,赵桂峰,陈小飞,等.2015.村镇建筑基于性态抗震设防的地震保险费率厘定[J].地震研究,38(3):461-466.
- 尹之潜.1996.地震灾害及损失预测方法[M].北京:地震出版社.
- 应用技术委员会.1991.加利福尼亚未来地震的损失估计[M].曹新玲,毛国敏,金学申,等,译.北京:地震出版社.
- 张治勇,刘殿魁,孙柏涛.1999.火力发电厂抗震研究概况[J].世界地震工程,15(1):34-40.
- 郑山锁,汪靖,贺金川,等.2020.变电站主接线系统地震易损性分析[J].华中科技大学学报(自然科学版),48(3):98-103.
- 周长东,王朋国,田苗旺,等.2017.多维地震下钢筋混凝土双曲线冷却塔结构易损性分析[J].振动与冲击,36(23):106-113.
- Ang A H-S,Tang H.2007.Probability concepts in engineering:emphasis on applications to civil and environmental engineering[M].John Wiley & Sons Inc.
- ATC.1991.ATC-25 Seismic vulnerability and impact of disruption of lifelines in the conterminous United States[R].Advanced Technology Council.
- Dai K S,Li B W,Wang J Z,et al.2018.Optimal probability-based partial mass isolation of elevated coal scuttle in thermal power plant building[J].Structural Design of Tall and Special Buildings,27(11):e1477.
- Liu R S,Tian D Y.2020.Study on analogy calculation method for seismic vulnerability of earth-wood structure houses[J].Mathematical Problems in Engineering,(6):1-10.
- Mohammadi R,Tehrani A.2014.An investigation on seismic behavior of three interconnected pieces of substation equipment[J].IEEE Transactions on Power Delivery,29(4):1613-1620.
- Wang J Z,Dai K H,Yin Y X,et al.2018.Seismic performance-based design and risk analysis of thermal power plant building with consideration of vertical and mass irregularities[J].Engineering Structures,164:51-57.
- Yamazaki F,Motomura H,Hamada T.2000.Damage assessment of expressway networks in Japan based on seismic monitoring[C].Auckland,New Zealand:12th World Conference on Earthquake Engineering.
- GB 50011—2010,建筑抗震设计规范[S].
- DL 5022—93,火力发电厂土建结构设计规定[S].