基金项目:国家自然科学基金项目(51978434)资助.
(Key Laboratory of Structure Engineering of Jiangsu Province,Suzhou University of Science and Technology,Suzhou 215009,Jiangsu,China)
the spectral element method; focal depth; dip angle of the basin; impedance ratio; dimensionless frequency
DOI: 10.20015/j.cnki.ISSN1000-0666.2022.0049
备注
基金项目:国家自然科学基金项目(51978434)资助.
引言
国内外多次大地震的震害经验和相关研究表明,沉积盆地对其内部的地震动有显著的放大效应,进而导致盆地内的灾害更加严重,如1994年美国北岭地震中的洛杉矶盆地(Pitarka,Irikura,1996)和2002年台湾花莲近海地震中的台北盆地(Chen,2003)。因此,针对盆地地震放大作用,地震工程研究者开展了大量的研究。Kawase和Aki(1989)认为,在1985年墨西哥地震中,在墨西哥城观察到的极长地震动持时可能是由软表面层与城市下方深盆结构的强烈相互作用造成的。Kawase(1996)对1995年日本神户地震的研究表明,一个中等强度的地震即可引起盆地内部极具破坏性的强地震动。
诸多研究表明盆地倾角、震源深度、盆地内外介质阻抗比(于彦彦等,2020)等参数对地震放大作用有较显著影响。刘启方等(2013,2020)利用三维施甸盆地模型及川滇地区的地壳速度结构,研究得到盆地内覆盖层厚的区域地震动强度大于覆盖层薄的区域,并采用谱元法模拟了1556年华县地震时渭河盆地0.02~0.5 Hz地震波的传播过程,发现盆地的深厚土层对于4 s以上的地震动有着明显的放大作用。禹乐等(2020)采用谱元法及PML边界条件,研究了内置点源下盆地倾角对地表地震动时、频域放大特征的影响。刘中宪等(2017)基于谱元法和动力学震源模型研究了盆地内外介质的波速比对地表地震动时程和峰值的影响。李雪强(2011)建立了一系列具有不同倾角、不同沉积层厚度、不同介质阻抗比的理想盆地模型,并利用波动有限元数值模拟方法,研究了以上因素对盆地的影响。丁海平等(2018)利用谱元法,通过分析盆地模型与均匀半空间模型中观测点的速度时程、峰值和放大系数,研究了盆地倾角、盆地深度对盆地地震效应的影响。但以往对于盆地内部地震动放大效应的研究多采用场地外单一平面体波入射或面波入射(陈学良等,2011; 张建经等,2014; 郭明珠等,2004),而实际入射到盆地的地震波则是体波和面波兼有。且以往采用谱元法模拟二维盆地的模型大多研究单一参数对盆地效应的影响,模拟工况较为单一。因此,本文基于谱元法,采用4种不同倾角盆地模型,研究了不同震源深度下走滑地震非平面波入射时,二维盆地的放大规律,分析了盆地边缘放大的峰值及其位置与无量纲频率、阻抗比和盆地倾角的关系。
1 计算模型及方法
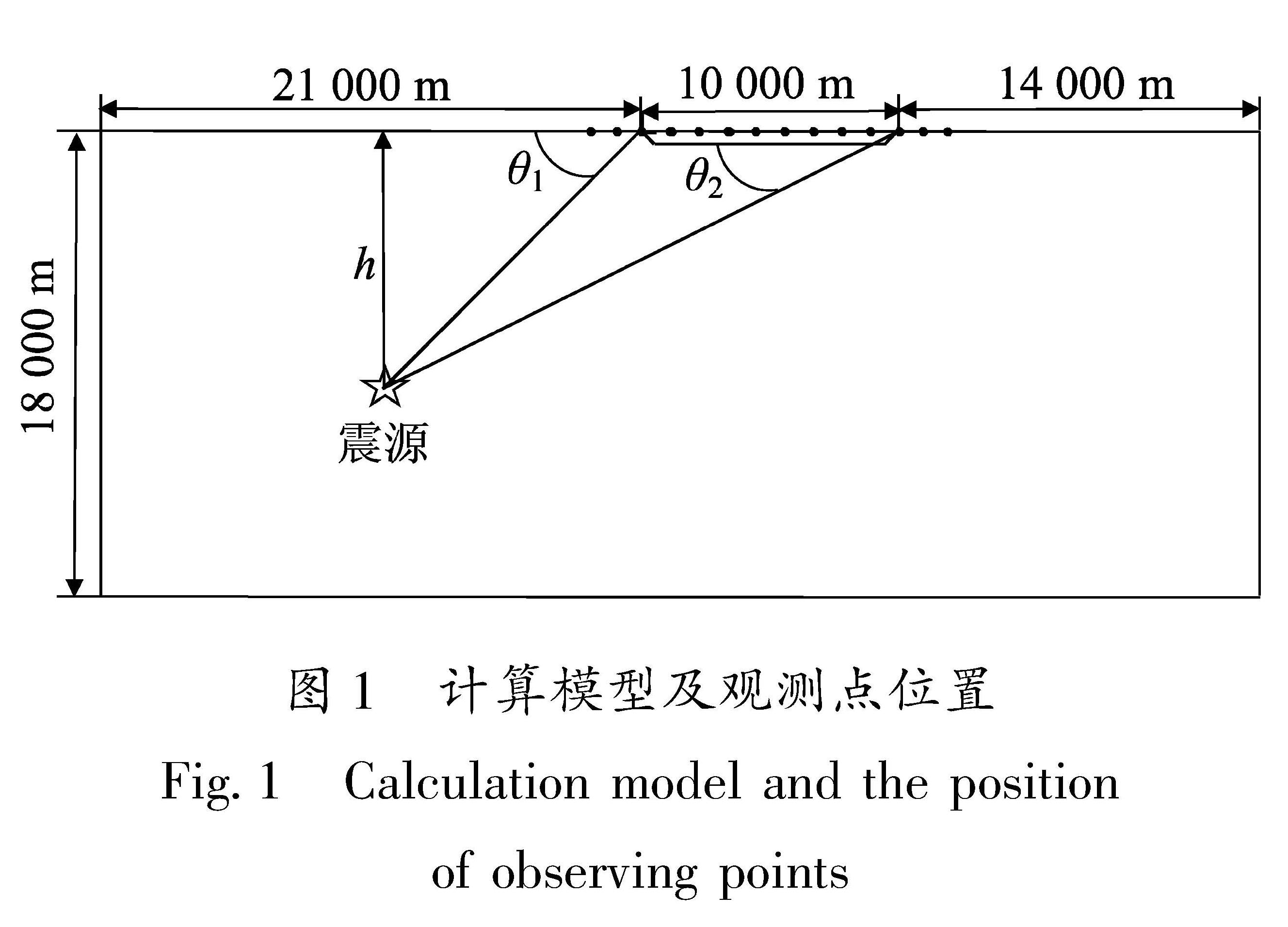
1.1 计算模型采用梯形盆地模型,盆地角度分别取15°、30°、45°和60°。计算模型长度方向为45 km,深度方向为18 km,如图1所示。盆地长10 km,深0.5 km,在盆地内部及盆地左右两侧2 km处每隔50 m布置一个观测点,共281个等间距观测点。因观测点过多,图1中每隔1 km显示一个观测点。
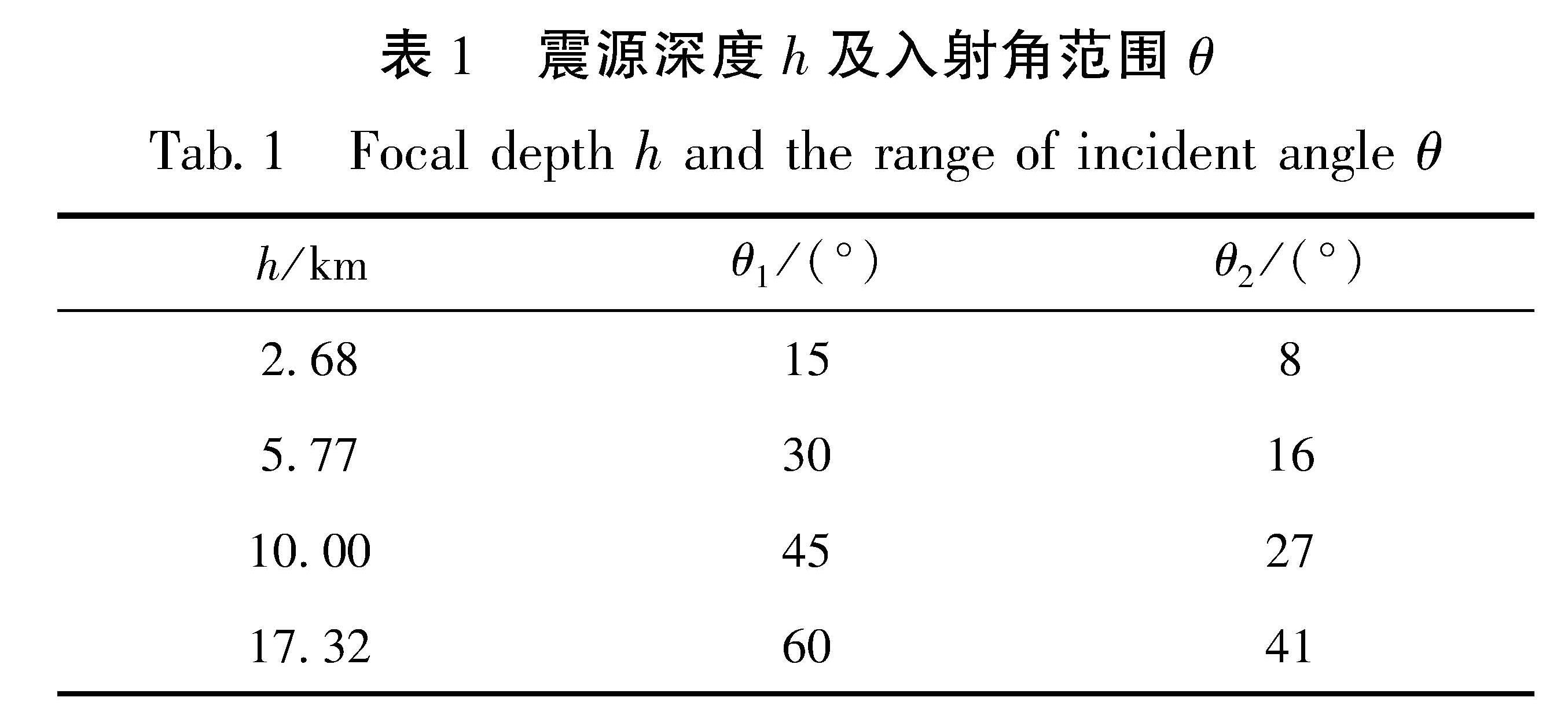
为了分析不同震源对应的不同方向入射波的影响,取4个不同的震源,震源深度分别为2.68、5.77、10.00和17.32 km。θ1和θ2代表不同震源下盆地入射波的角度范围,见表1。盆地内外的介质参数见表2,βr、ρr和Qr分别表示盆地外基岩的剪切波速、密度和品质因子,βs、ρs 和Qs则为盆地内相应参数。本文取盆地内外剪切波速分别为400 m/s和1 500 m/s,盆地内外介质的阻抗比为3.75。
1.2 计算方法目前模拟地震波在沉积盆地中传播的方法主要有限差分法、有限元法、边界元法以及谱方法。近年来,随着 Komatitsch 和 Vilotte(1999)将谱元法推广到地震波场的模拟并推出适用于二维和三维问题的谱元程序 SPECFEM2D 及 SPECFEM3D,其作为一种高精度(廖树超等,2018)的数值方法得到越来越广泛的应用(严珍珍等,2009; Komatitsch,2012)。
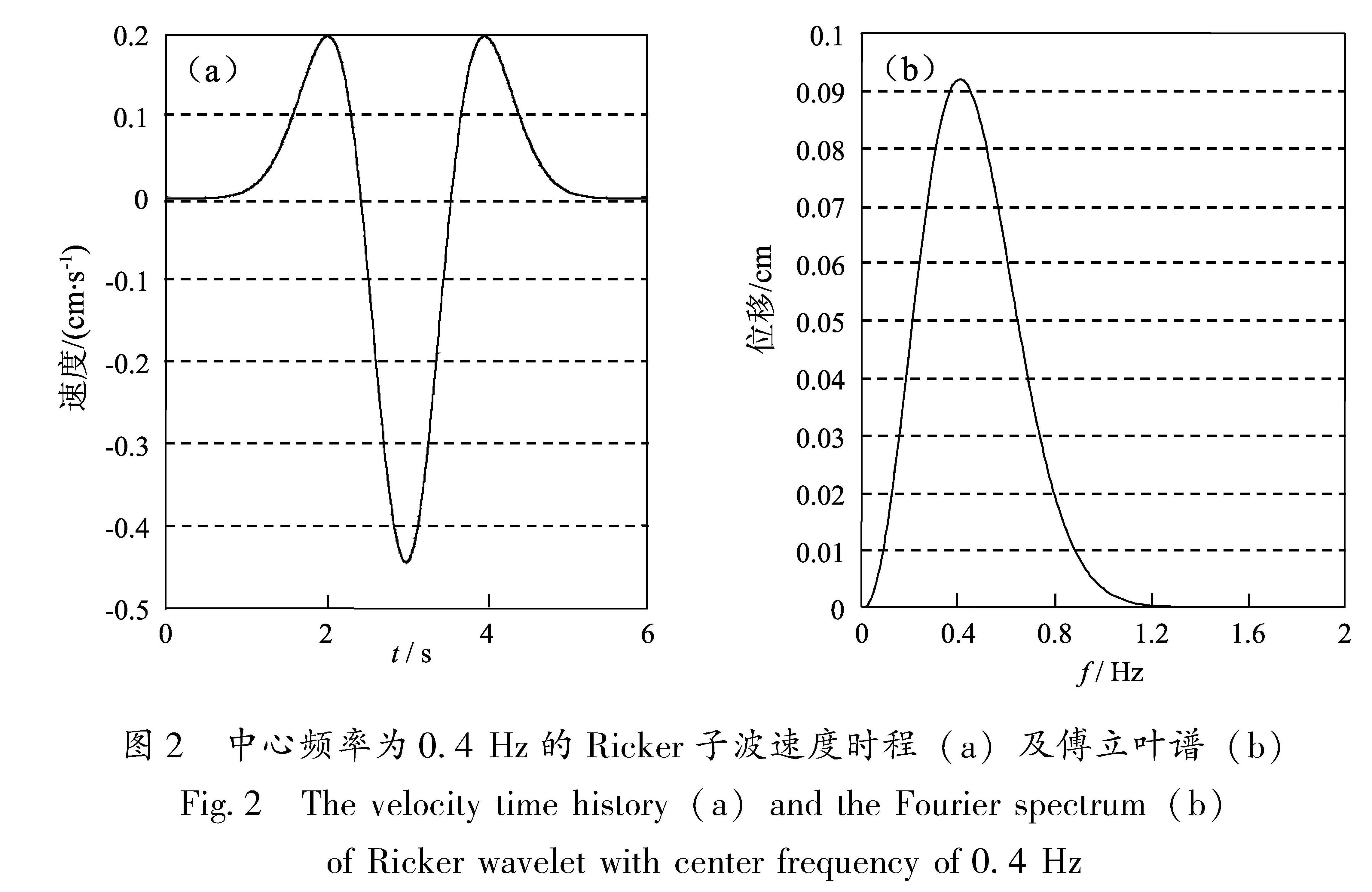
本文采用二维谱元程序SPECFEM2D进行计算,盆地内、外网格尺寸分别为40 m和80 m。模拟时间步长为0.001 s,共计模拟40 000步。本文采取4阶谱元格式,模拟计算频率至η=4。震源取MW=4.0的点源,走向90°、倾向45°、滑动角0°,地震矩张量中除Mxx为1.26×1015 dyne?cm外,其余Mzz=Mxz=0。震源时间函数采用Ricker子波,图2给出了中心频率为0.4 Hz的Ricker子波速度时程及傅立叶谱。
本文采用无量纲频率分析盆地的放大与几何形状、盆地内外介质阻抗比和输入角度的关系。无量纲频率η代表盆地的深度和入射Ricker子波中心频率对应的波长之比,定义为:
η=h/λ
λ=βs×f0 (1)
式中:h为盆地深度; λ 为波长; f0为Ricker子波主频。本文采用不同中心频率Ricker子波的震源时间函数,分析不同η的影响。本文用到的参数为:η=0.125、0.25、0.5、1、2、4; 盆地倾角=15°、30°、45°、60°; 阻抗比=3.75。
2 数据分析
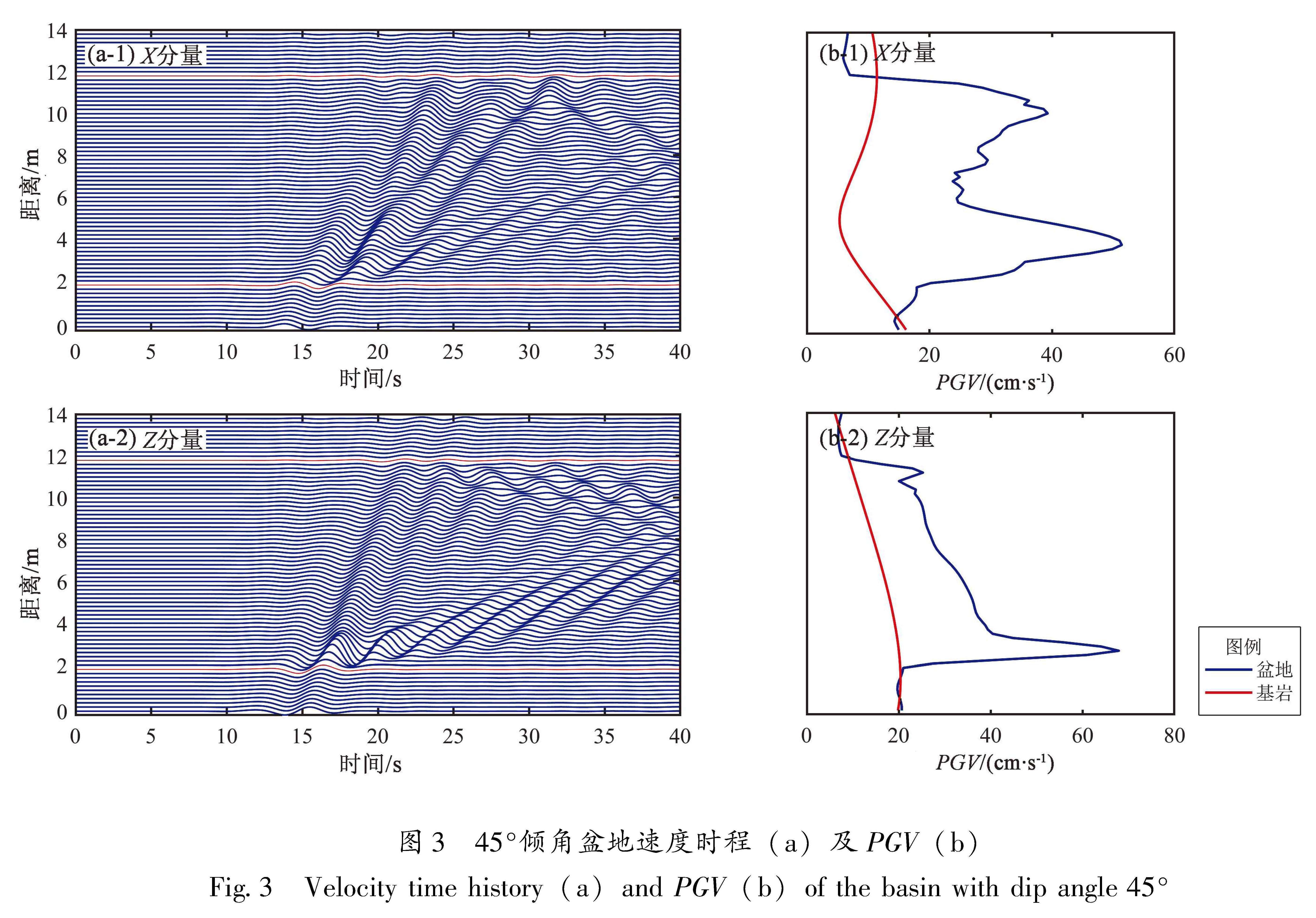
由于采用Ricker子波作为震源时间函数,激发的地震波主要位于中心频率附近,因此本文采用同一无量纲频率下,分别计算盆地模型和基岩半空间模型的各点的速度时程的峰值。图3为阻抗比3.75、η=0.25下的45°倾角盆地速度时程及PGV。从图中可以看到,P波首先进入盆地,然后是S波; 盆地内地震动持时显著增长,PGV显著增大。本文定义盆地模型和基岩半空间模型各点速度时程的峰值之比,为该无量纲频率下的放大。
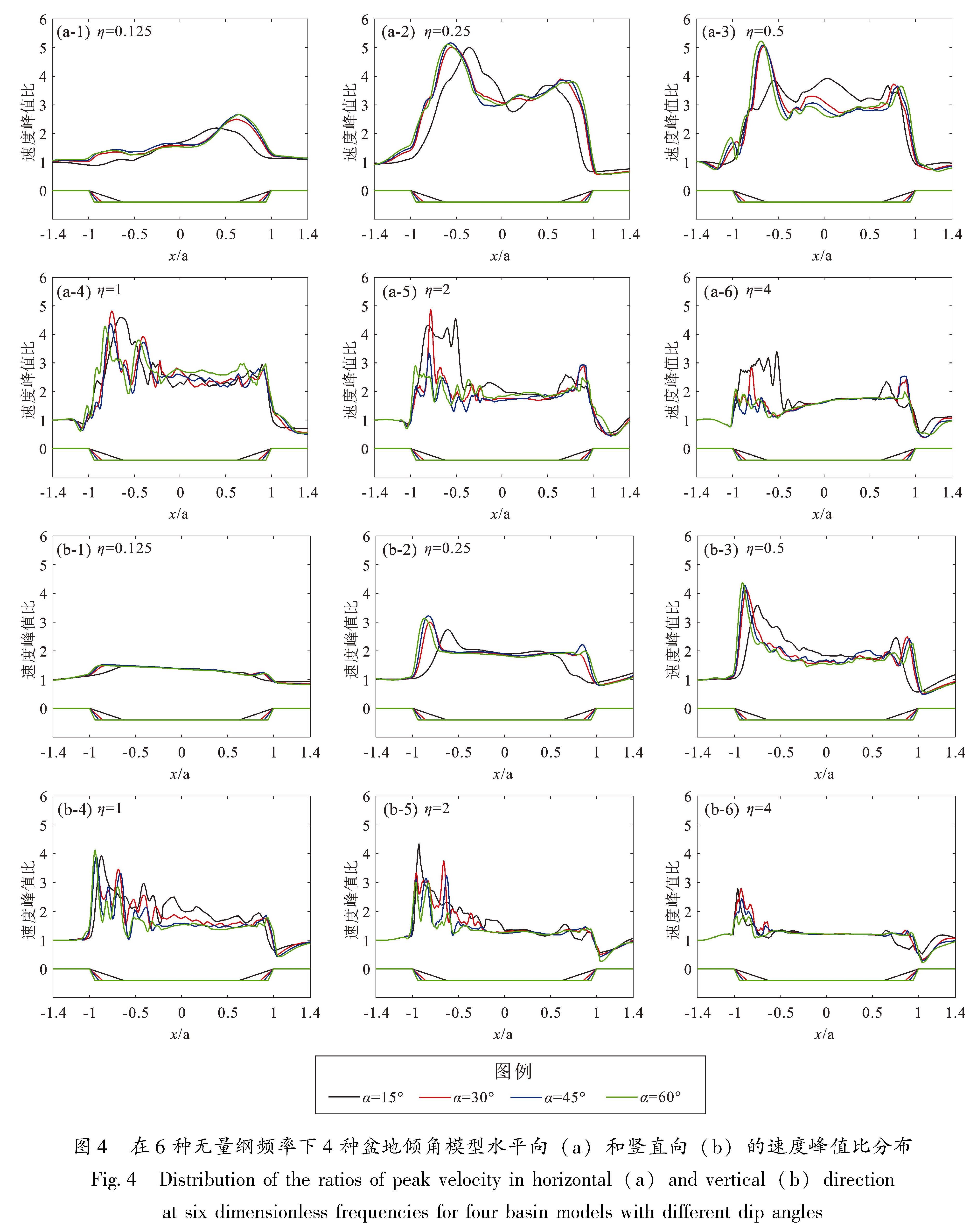
图4给出了震源深度为10 km,阻抗比为3.75时,6种无量纲频率η下,4种倾角盆地模型水平向和竖直向的盆地和基岩半空间的速度峰值比,该震源深度下,盆地入射波范围是27°~45°。笔者对图像进行归一化处理,取盆地中心点为原点,设定a为盆地宽度的一半(5 km),x为变量,在盆地最左侧即x=-1,α为盆地倾角。
由图4可见:①在水平和竖直方向,随着η的增大,速度峰值比由非常平滑转向局部振荡,特别是在盆地边缘附近。②在竖直方向,盆地边缘速度峰值也呈现较大的值。这表明盆地边缘不仅会出现强烈的横向振动,还会出现剧烈的垂直运动。③η较大时,盆地两侧边缘的地面运动变化比较剧烈,这是因为高频的入射波与盆地边缘相互作用更强,从而影响较短距离上的地面运动特征。这与Ayoubi(2020)的研究结果相同。④η增大后,15°倾角盆地模型的速度峰值比突变较大,与其它角度的盆地模型的速度峰值比形成鲜明对比,这可能是因为15°倾角盆地比其他角度的盆地有着更长的斜边。丁海平等(2018)发现盆地边缘倾角较小时,盆地边缘对地震动的放大效应更强(ricker子波中心频率为5 Hz),与本文结果一致。盆地中心区域受倾角影响相对较小,禹乐(2020)也有类似的研究成果。
图4 在6种无量纲频率下4种盆地倾角模型水平向(a)和竖直向(b)的速度峰值比分布
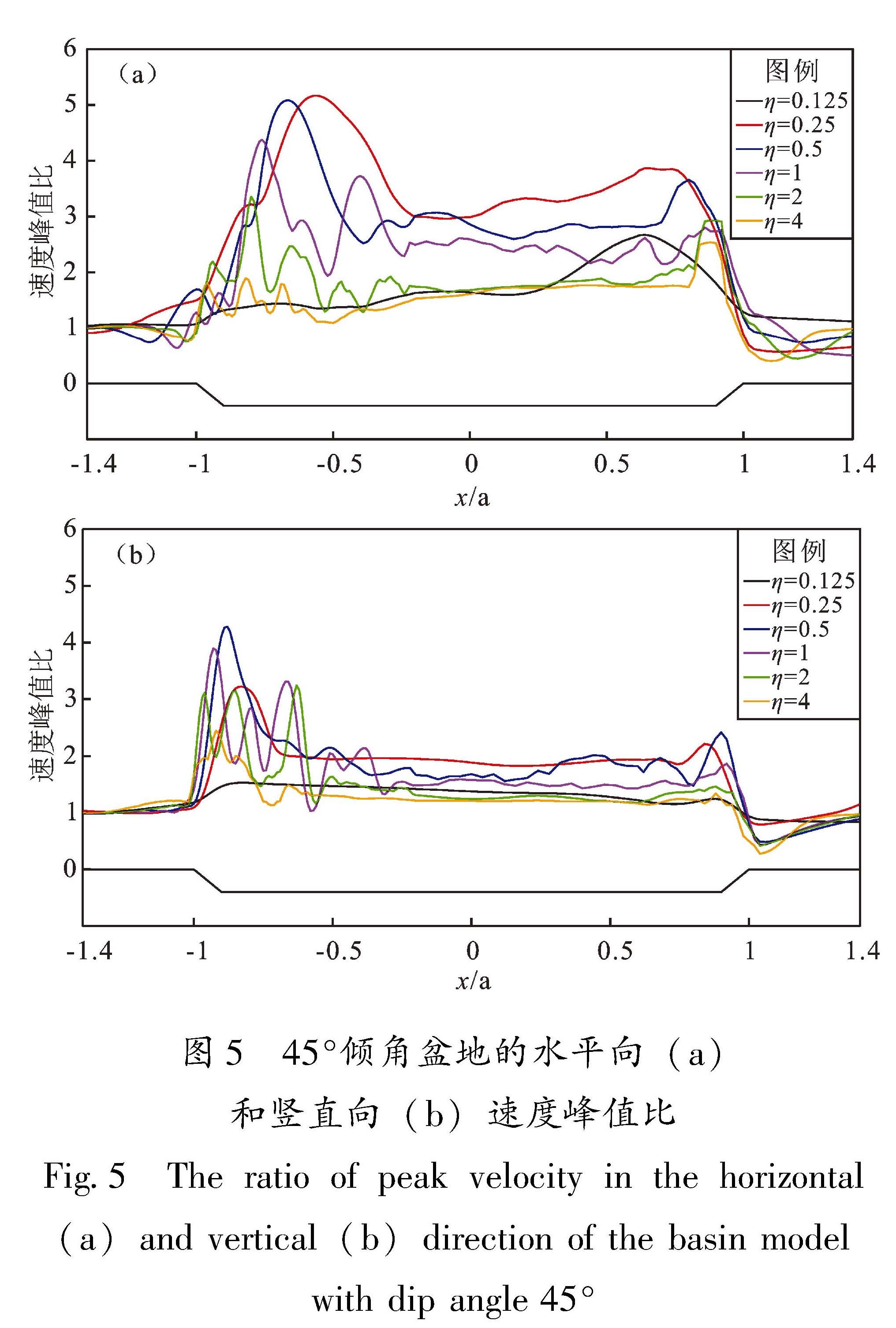
Fig.4 Distribution of the ratios of peak velocity in horizontal(a)and vertical(b)direction at six dimensionless frequencies for four basin models with different dip angles为研究不同无量纲频率在单一倾角盆地下速度峰值比的大小,图5给出阻抗比为3.75时,不同无量纲频率下45°倾角盆地水平向和竖直向的速度峰值比。由图5可见:①随着η的增大,速度峰值比在η=0.5时达到最大值,然后衰减。即当η≤0.5时,速度峰值比变大; 当η>0.5时,速度峰值比逐渐减小。②对于较低的η,入射波将盆地视为一个整体,放大很小; 随η增大,入射波与盆地局部相互作用增强,地震动也更为复杂。
图5 45°倾角盆地的水平向(a)和竖直向(b)速度峰值比
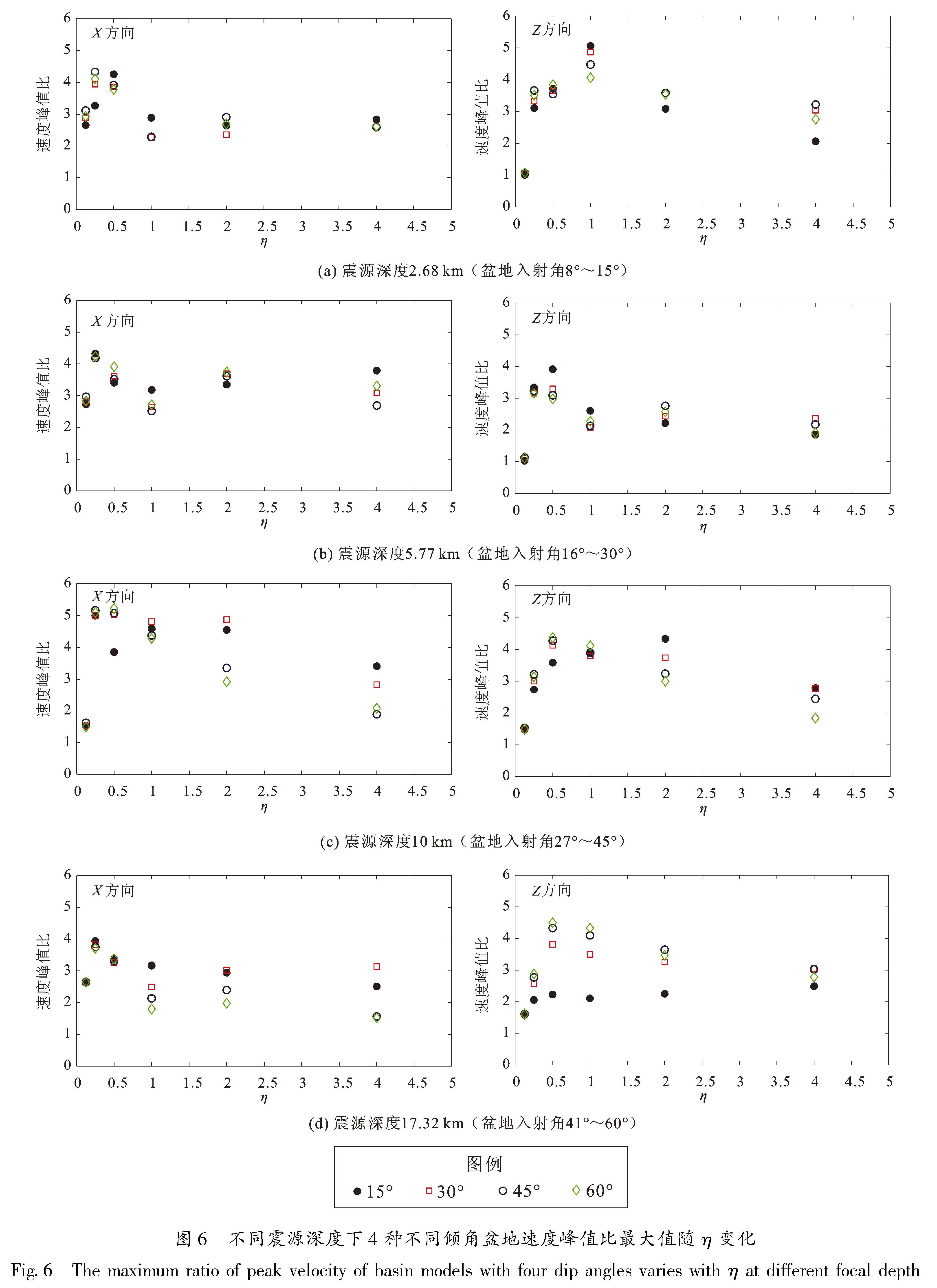
Fig.5 The ratio of peak velocity in the horizontal (a)and vertical(b)direction of the basin model with dip angle 45°为了探讨速度峰值比最大值变化的规律,图6给出了阻抗比为3.75时,不同震源深度下4种倾角盆地速度峰值比最大值随η的变化。由图6可见:①随着震源深度的增大,4种倾角盆地水平方向速度峰值比最大值逐渐增大,在震源深度为10 km时达到最大,随后减小。震源深度较浅时(2.68 km和5.77 km),4种倾角盆地水平方向速度峰值比最大值相差不大,差值始终小于1。震源深度较深时(10 km和17.32 km),4种盆地的速度峰值比最大值在η≤0.5时相差不大,在η≥1时相差很大。如图6c所示,η=2时60°倾角盆地的速度峰值比值为2.6,15°倾角盆地的值为4.5,后者约为前者的1.73倍; η=4时45°倾角盆地的速度峰值比的值为1.8,15°倾角盆地的值为3.5,后者是前者的两倍左右。②水平方向上的速度峰值比最大值为1~5.3,竖直方向为1~5。整体来看,随着η增大,水平向和竖直向速度峰值比最大值也增大,于η为0.5~1时达到最大,随后减小。
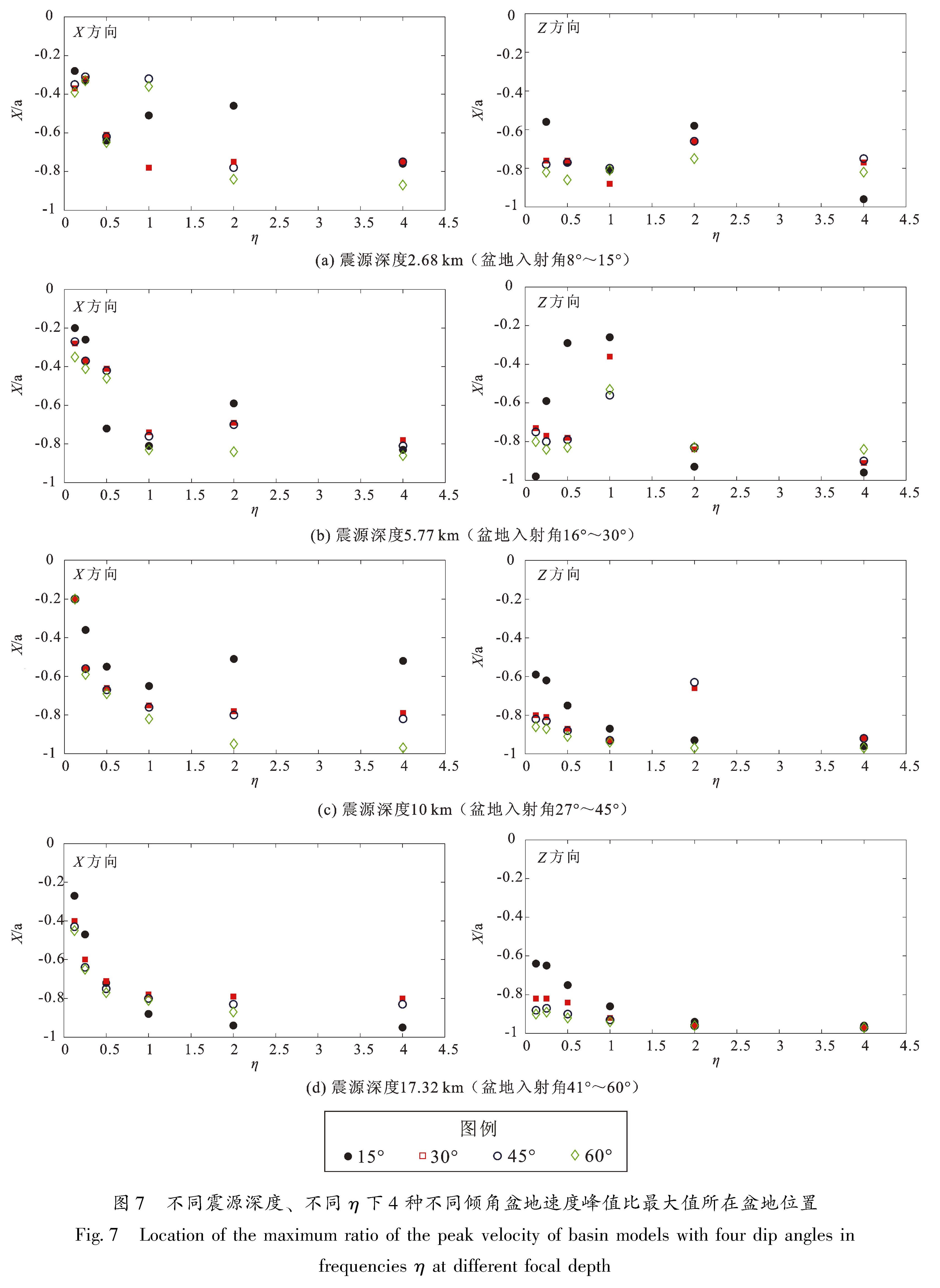
为了探讨影响速度峰值比最大值位置的因素,图7给出了阻抗比为3.75时,不同震源深度、不同η下4种不同倾角盆地速度峰值比最大值的位置。由图7可见:①同一震源深度下,随着η增大,速度峰值比的最大值的位置逐渐偏向盆地边缘。竖直方向上,当震源深度为10和17.32 km时,随着盆地倾角的增大,最大值的位置偏向盆地边缘。水平方向上,当η≥2,震源深度为2.68、5.77和10 km时,随着盆地倾角的增大,最大值的位置偏向盆地边缘。②当震源深度为2.68、5.77和10 km时,不同η下15°倾角盆地速度峰值比最大值的位置相比另外3种倾角盆地更偏向盆地中心。当震源深度为2.68 km、η=2时,15°倾角盆地的速度峰值比的最大值的位置与盆地边缘的距离是60°倾角盆地的3.7倍。当震源深度逐渐增大时,水平向和竖直向速度峰值比最大值的位置逐渐偏向盆地边缘。
图6 不同震源深度下4种不同倾角盆地速度峰值比最大值随η变化
Fig.6 The maximum ratio of peak velocity of basin models with four dip angles varies with η at different focal depth3 结论
本文基于二维谱元法,采用4种不同倾角盆地模型,研究不同震源深度走滑地震非平面波入射时,二维盆地的放大规律,分析了盆地边缘放大的最大值及其位置与无量纲频率η和盆地倾角的关系,主要得出以下结论:
(1)水平方向速度峰值比的最大值为1~5.3,竖直方向为1~5。盆地边缘处竖直方向速度峰值比也呈现较大的值,这表明盆地边缘也会出现剧烈的垂直运动。随着震源深度的增大,水平方向速度峰值比的最大值逐渐增大,在震源深度为10 km时达到最大,随后减小,水平向和竖直向速度峰值比的最大值的位置逐渐偏向盆地边缘。
(2)震源深度较浅时,4种倾角盆地在水平方向上的速度峰值比的最大值大小相差不大,差值始终小于1; 震源深度较深且η较高时(η≥1),4种倾角的盆地的速度峰值比相差很大,最大差值达到3。竖直方向上,震源深度较浅时,随着盆地倾角的增大,速度峰值比的最大值的位置偏向盆地边缘。水平方向上,震源深度较浅且η较高时,随着盆地倾角的增大,速度峰值比的最大值的位置偏向盆地边缘。
(3)同一震源深度下,η越大,速度峰值比最大值的位置也更接近盆地边缘。对于较低的η,入射波将盆地视为一个整体,放大很小。随着η的增大,入射波与盆地局部相互作用增强,放大倍数(水平向和竖直向)将明显增加。当无量纲频率到达一定值后(η≥1),放大倍数开始逐渐减小。同一震源深度下,η越大,速度峰值比最大值的位置越偏向盆地边缘。
需要说明的是,本文的结果由对特定盆地形状、尺寸、阻抗比及特定震源等的研究得出,以上因素对盆地地震响应均有显著影响,若相应参数改变,对盆地效应影响的差异性也会显现,这还需要开展进一步的研究。
-
陈学良,高孟潭,李铁飞.2011.Rayleigh面波作用下盆地场地响应特性研究[J].土木建筑与环境工程,33(S2):29-33.
- 丁海平,吕思东,于彦彦.2018.内源输入时盆地特征参数对盆地地震效应的影响[J].苏州科技大学学报(工程技术版),31(3):1-6.
- 郭明珠,谢礼立,凌贤长.2004.弹性介质面波地脉动单点谱比法研究[J].岩土工程学报,26(4):4.
- 李雪强.2011.沉积盆地地震效应研究[D].哈尔滨:中国地震局工程力学研究所.
- 廖树超,于彦彦,丁海平.2018.基于Lamb问题的谱元法和有限元法模拟精度比较[J].世界地震工程,34(3):190-198.
- 刘启方,于彦彦,章旭斌.2013.施甸盆地三维地震动研究[J].地震工程与工程振动,33(4):54-60.
- 刘启方.2020.1556年华县大地震地震动场模拟[J].自然灾害学报,29(5):3-12.
- 刘中宪,刘明珍,韩建斌.2017.近断层沉积盆地强地震动谱元模拟[J].世界地震工程,33(4):76-86.
- 严珍珍,张怀,杨长春,等.2009.汶川大地震地震波传播的谱元法数值模拟研究[J].中国科学:地球科学,39(4):393-402.
- 于彦彦,丁海平,刘启方.2020.盆地内外介质阻抗比对盆地地表地震动及次生Rayleigh面波的影响[J].岩土工程学报,42(4):667-677.
- 禹乐,于彦彦,丁海平.2020.内源作用下盆地倾角对地表地震动放大特征的影响[J].地震工程与工程振动,40(5):99-108.
- 张建经,朱传彬,张明,等.2014.地震入射角对盆地地震反应影响的数值分析[J].岩石力学与工程学报,33(S1):2720-2726.
- Ayoubi P,Mohammadi K,Asimaki D.2020.A systematic analysis of basin effects on surface ground motion[J].Soil Dynamics and Earthquake Engineering,141:106490.
- Chen K C.2003.Strong ground motion and damage in the Taipei basin from the Moho reflected seismic waves during the March 31,2002,Hualien,Taiwan earthquake[J].Geophysical Research Letters,30(11),doi:10.1029/2003GL017193,2003.
- Kawase H,Aki K.1989.A study on the response of a soft basin for incident S,P,and Rayleigh waves with special reference to the long duration observed in Mexico City[J].Bulletin of the Seismological Society of America,79(5):1361-1382.
- Kawase H.1996.The cause of the damage belt in Kobe:“the basin-edge effect,”constructive interference of the direct S-wave with the basin-induced diffracted/Rayleigh waves[J].Seismological Research Letters,67(5):25-34.
- Komatitsch D,Vilotte J P.1999.Reply to comment by E Faccioli and A Quarteroni on “The spectral element method:An efficient tool to simulate the seismic response of 2D and 3D geological structures” by D Komatitsch and J-P Vilotte[J].Bulletin of the Seismological Society of America,89(1):332-334.
- Komatitsch D.2012.Simulations of ground motion in the Los Angeles Basin based upon the spectral-element method[J].Bulletin of the Seismological Society of America,94(1):187-206.
- PitarkaA,Irikura K.1996.Basin structure effects on long-period strong motions in the San Fernando Valley and the Los Angeles Basin from the 1994 Northridge earthquake and an aftershock[J].Bulletin of the Seismological Society of America,86(1B):672107.