基金项目:国家自然科学基金(51878426)、四川省科研创新项目(2020JDGD0035)、四川省自然科学基金(2022NSFC0988)和中央高校基本科研业务费项目联合资助.
(1.四川大学 土木工程系,四川 成都 610065; 2.深地科学与工程教育部重点实验室,四川 成都 610065; 3.破坏力学与工程防灾减灾四川省重点实验室,四川 成都 610065)
(1.Department of Civil Engineering,Sichuan University,Chengdu 610065,Sichuan,China)(2.Key Laboratory of Deep Earth Science and Engineering(Sichuan University),Ministry of Education,Chengdu 610065,Sichuan,China)(3.Failure Mechanics & Engineering Disaster Prevention and Mitigation,Key Laboratory of Sichuan Province,Chengdu 610065,Sichuan,China)
seismic losses; architectural function combination; commercial buildings; the generic algorithm; risk of the structure's collapse
DOI: 10.20015/j.cnki.ISSN1000-0666.2022.0064
备注
基金项目:国家自然科学基金(51878426)、四川省科研创新项目(2020JDGD0035)、四川省自然科学基金(2022NSFC0988)和中央高校基本科研业务费项目联合资助.
引言
近年震灾报告表明,尽管人员伤亡得到有效降低,但业主方的经济损失始终居高不下(Guha-Sapir et al,2012)。现行抗震设计规范可有效保证“生命安全”这一性能目标,但地震灾害引发的直接经济损失和间接经济损失需要更多关注。为了便于投资方与业主方能够更加直观了解到自然灾害的影响并做出相关决策,地震损失风险需要通过非专业性语言和性能参数来表征,如修复费用、修复时间、倒塌风险、年预期损失等。
随着Seismic Performonce Assessment of Buildings(FEMA P58—2012)的发展以及我国《建筑抗震韧性评价标准》(2020)的施行,近年来很多学者采用新一代基于性能的地震工程理论对不同建筑结构的地震损失开展了评估工作。如石晟等(2020)依据修复费用、修复时间等指标对比了3个减震结构体系方案的抗震性能。同时,建筑内部的非结构构件损失也越发受到研究关注。叶良浩等(2020)综合考虑了地震作用下导致的医疗建筑中的建筑结构、非结构构件和内部物品的损失,发现非结构构件的优化设计与布置对降低建筑物地震损失更为关键。Reilly和Sullivan(2018)研究发现,一味地加强结构强度设计,提高结构抗倒塌能力,反而会导致部分加速度敏感型非结构构件在地震作用下造成巨大的经济损失,严重影响灾后功能恢复。田源等(2018)与曾翔等(2016)研究发现,非结构构件破坏引起的修复费用和修复时间是地震损失的主要部分。
综上所述,地震损失风险是业主方参与结构选型和建筑业态组合等决策的重要参考依据之一。目前,已有研究多是基于确定的结构设计方案对新建或既有的建筑结构开展地震损失分析,较少有通过地震损失风险分析手段协助建筑功能业态组合的方案设计。与多数已有研究不同,本文将地震损失风险分析在建筑设计阶段介入,以一栋9层建筑结构作为研究对象,采用Opensees建立分析模型,选用了22组地震动开展增量动力分析(Incremental Dynamic Analysis,IDA),结合地震危险性计算建筑倒塌风险。根据业态决策的常规基本思路,首先考虑了7种业态组合,从修复费用、修复时间、人口伤亡、损失比、预期年损失等多个指标来综合评价与对比了不同业态组合的地震损失风险。随后,发展了基于遗传算法的业态组合优化设计方法,为业主方在业态组合层面提供决策方法,也为保险方厘定保费提供决策依据。
1 评估方法
第二代基于性能的地震工程(PBEE)主要基本框架由地震危险性分析、需求分析、能力分析、损失分析4部分组成,将建筑地震损失以业主能够直观理解的指标表示。该评估方法需要获取建筑的基本信息,包括建筑结构构件布置、非结构构件布置、建筑内部物品布置等种类与数量。针对该问题,Zeng 等(2016)针对已有建筑信息不同缺失程度的建筑提出3种不同统计方法。Seismic Performonce Assessment of Buildings(FEMA P58—2012)提供了建筑在地震作用下的维修成本、维修时间、人口伤亡等损失分析方法与计算流程。地震损失主要由3部分组成,分别是建筑发生倒塌造成的损失、建筑未倒塌但无法继续使用需重建所造成的损失、建筑不倒塌且可继续使用但需要维修造成的损失。
给定地震强度下的地震经济总损失为:
E(LT|IM)=E(LC|IM)+E(LD|NC,IM)+E(LR|NC∩ND,IM) (1)
式中:LT表示建筑遭受地震灾害时总经济损失; LC表示地震灾害下建筑发生倒塌时的经济损失; LD表示地震灾害下建筑未发生倒塌但由于破坏严重需要拆除重建所带来的经济损失; LR表示地震灾害下建筑不需拆除重建可直接维修所产生的经济损失; NC表示建筑在地震灾害下未发生倒塌; ND表示建筑在地震灾害下不需拆除重建。
给定地震强度下,建筑发生倒塌时的地震经济损失可表示为建筑重置价值Cr乘以给定地震动下的倒塌概率P(Col|IM):
E(LC|IM)=P(Col|IM)·Cr (2)
给定地震动强度下,建筑不发生倒塌但需要拆除和重建的情况下的地震经济损失计算公式如下:
E(LD|IM)=P(Dem|IM)·(Cr+Cdem-Berec)=P(Dem|IM)·Cr (3)
E(LD|NC,IM)=E(LD|IM)·〔1-P(Col|IM)〕 (4)
式中:Cdem 、Berec 分别表示建筑重置成本与重置回收材料收益,在此假定建筑重置成本和重置回收材料收益相近(Hwang,Lignos,2017); P(Dem|IM)表示给定地震强度下需要拆除重建的概率。
给定地震动强度下,建筑不发生倒塌且可修复的情况下的预期地震经济损失为:
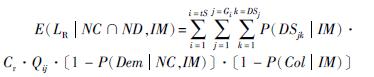 (5)
(5)式中:tS表示建筑楼层总数; Gi表示第i层的所有性能组数量总和; DSj表示第j个性能组对应的所有损伤状态的数量; Qij表示第i层第j个性能组的数量。
NEHRP Recommended Seismic Design Criteria for New Steel Moment-Frame Building(FEMA 350—2000)认为倒塌可从刚度退化和变形2个角度来判断,若结构在IDA结果曲线上的相邻两点连线斜率开始下降至弹性阶段斜率的20%或最大层间位移角(Story Drift Angle,SDR)超过1/10则认为结构发生倒塌。Ding(2006)认为2点连线斜率开始等于弹性阶段斜率的20%时的地震强度作为倒塌强度过于保守,显著低估了支撑钢框架的变形能力,建议采用弹性斜率的5%作为倒塌判据。综上,本文选择的倒塌判断准则为IDA分析得到的能力曲线中2点连线斜率下降至弹性段斜率的5%或者最大层间位移角达到1/10。
建筑是否可修需依据层间残余变形判定。任军宇等(2021)认为宜用罕遇地震水准下弹塑性时程分析的平均值,并取最大层间残余变形平均值与层间残余变形限值比较。若大于限值,则判断建筑不可修,终止建筑抗震韧性评级; 若小于或等于限值,可进行建筑抗震韧性评级。为了更合理地估计钢框架结构可修复的概率,根据Jayaram等(2012)的建议,钢框架结构的拆除概率与结构残余层间位移角(Residual Story Drift Angle,RSDR)应该服从对数正态分布,其对数均值为1.85%,对数标准差为0.3,拆除概率计算公式为:
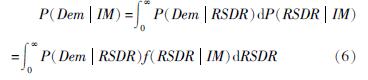
式中:P(Dem|IM)表示给定RSDR下建筑发生拆除重建的概率; P(RSDR|IM)表示给定IM下建筑结构响应超过某一RSDR的概率; f(RSDR|IM)表示给定IM下RSDR的概率密度函数。以上讨论了特定地震强度水平下的地震损失,可进一步可探讨地震风险。假定在T年内地震发生概率服从泊松分布:
Pc=1-e-λc·T (7)
则年均倒塌概率与年平均损失为:
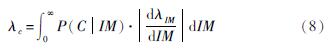
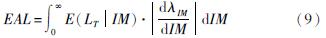
式中:λc表示年均倒塌概率; EAL表示年平均损失; λIM表示地震危险性。
2 典型商业建筑结构分析
3 考虑业态组合的损失分析
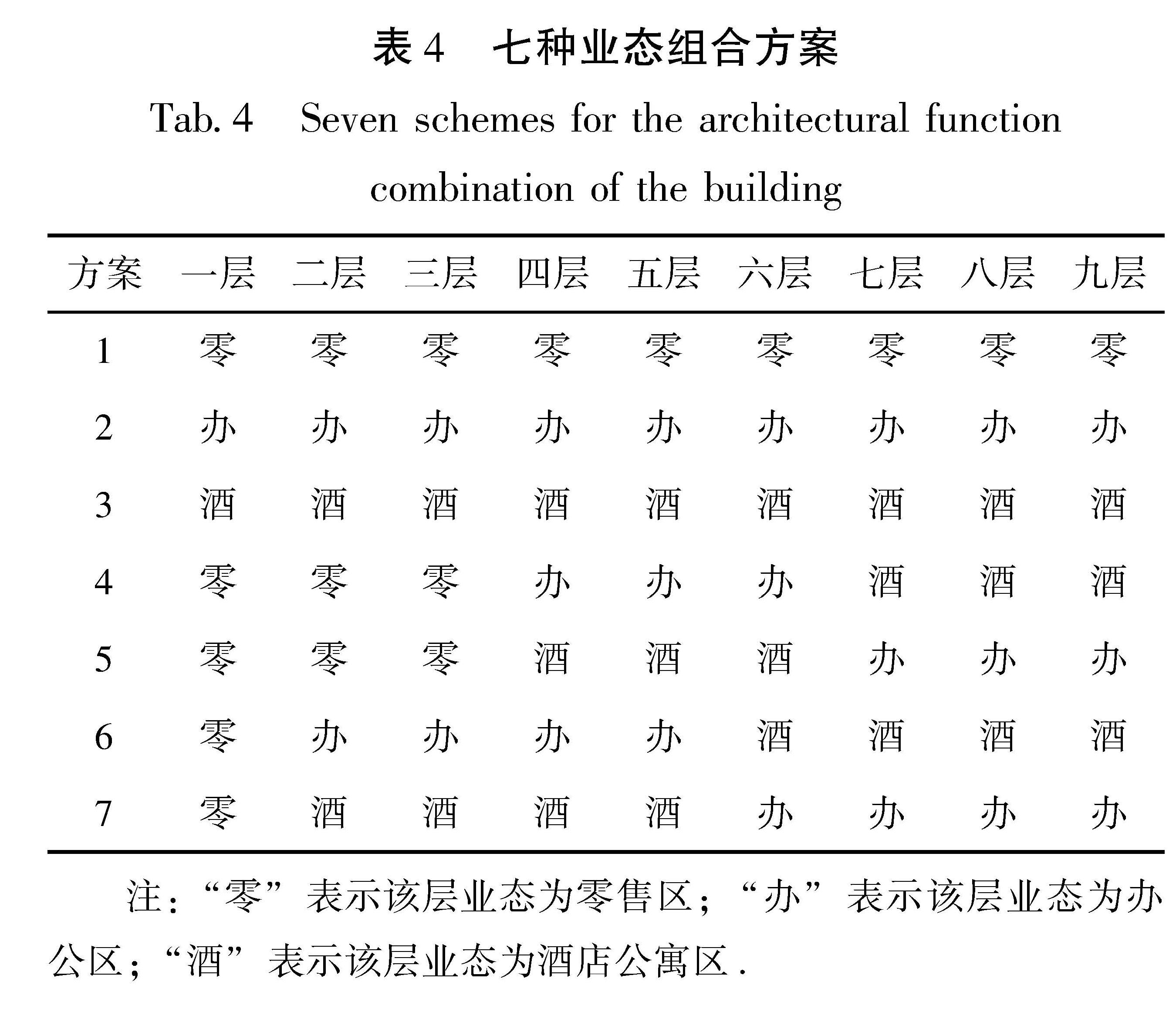
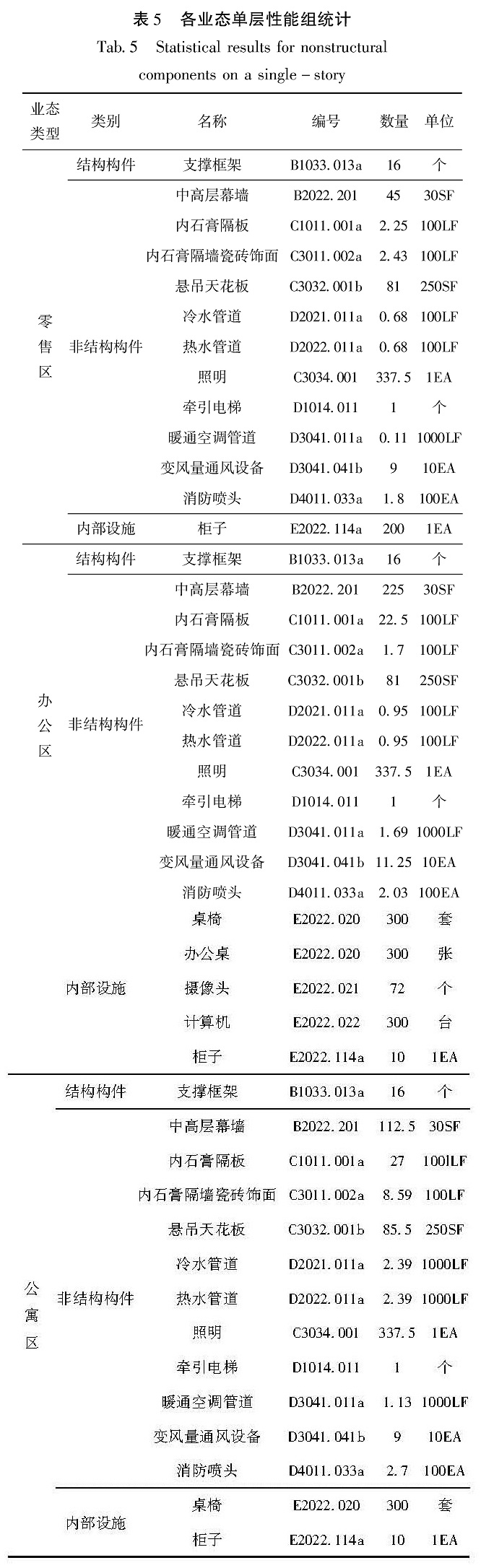
3.1 7种业态组合方案介绍本文主要是研究建筑不同业态组合方案的地震损失,业态一般是指业主方为了满足不同的营业需求而形成的建筑内部营业形态分布。Seismic Performance Assessment of Buildings(FEMA P58—2012)提供的损失预测方法需要获取建筑的基本信息,包括建筑结构构件布置、非结构构件布置、建筑内部物品布置等种类与数量。针对该问题,Zeng等(2016)针对已有建筑信息不同缺失程度的建筑提出来3种不同统计方法。本文主要以办公、零售、酒店公寓3种业态为例展开分析,以上3种业态功能区的建筑性能组类别与非结构构件性能组的数量主要通过调研与FEMA P58 PACT工具确定。考虑到实际情况中,零售(超市、商场)一般在低层,相邻楼层业态相同的情况,初步考虑业态组合方案见表4,前3个方案由单一业态构成,方案4~7由3个业态组合构成。各业态单层性能组统计情况见表5。
3.2 损伤计算调整说明已有统计表明,建筑结构构件投资占比不足20%,非结构构件和内部设施投资远高于结构构件(叶良浩,2020; O'Reilly,Calvi,2021)。目前通过统计和PACT工具估算得到的计算模型中的建筑结构部分的投资占比约为50%,这与实际不符的原因是统计中主要考虑了符合各业态功能需要的典型构件,未覆盖所有类型与数量的非结构构件和内部设施。因此,为了保证计算模型能够反映真实的建筑内部投资构成,对每个业态组合方案的非结构构件及内部设施的数量进行调整以保证建筑结构重建成本占每个业态方案下的总建筑成本的20%左右。
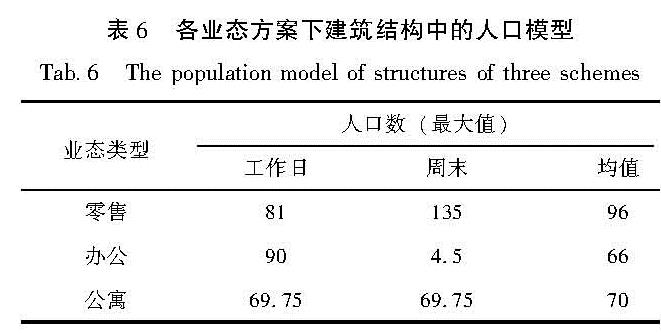
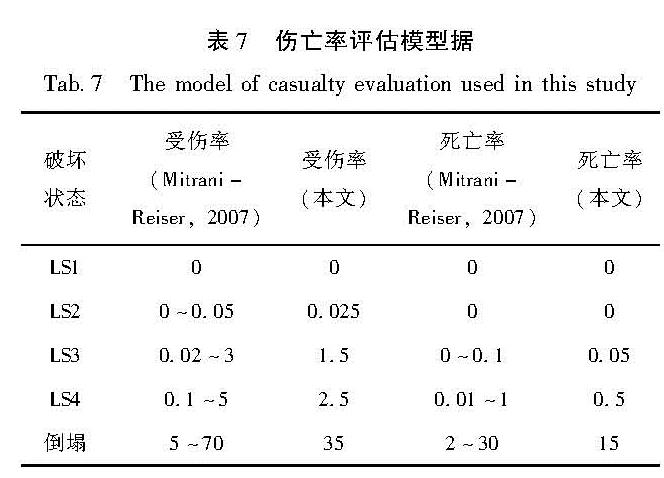
利用PACT工具提供的人口模型估计各业态方案下建筑结构中的人口数量(表6)。伤亡率是目前地震人员伤亡评估模型的重要参数(闫佳琦等,2021),采用Mitrani-Reiser(2007)提出的伤亡率模型进行人口伤亡分析(表7)。
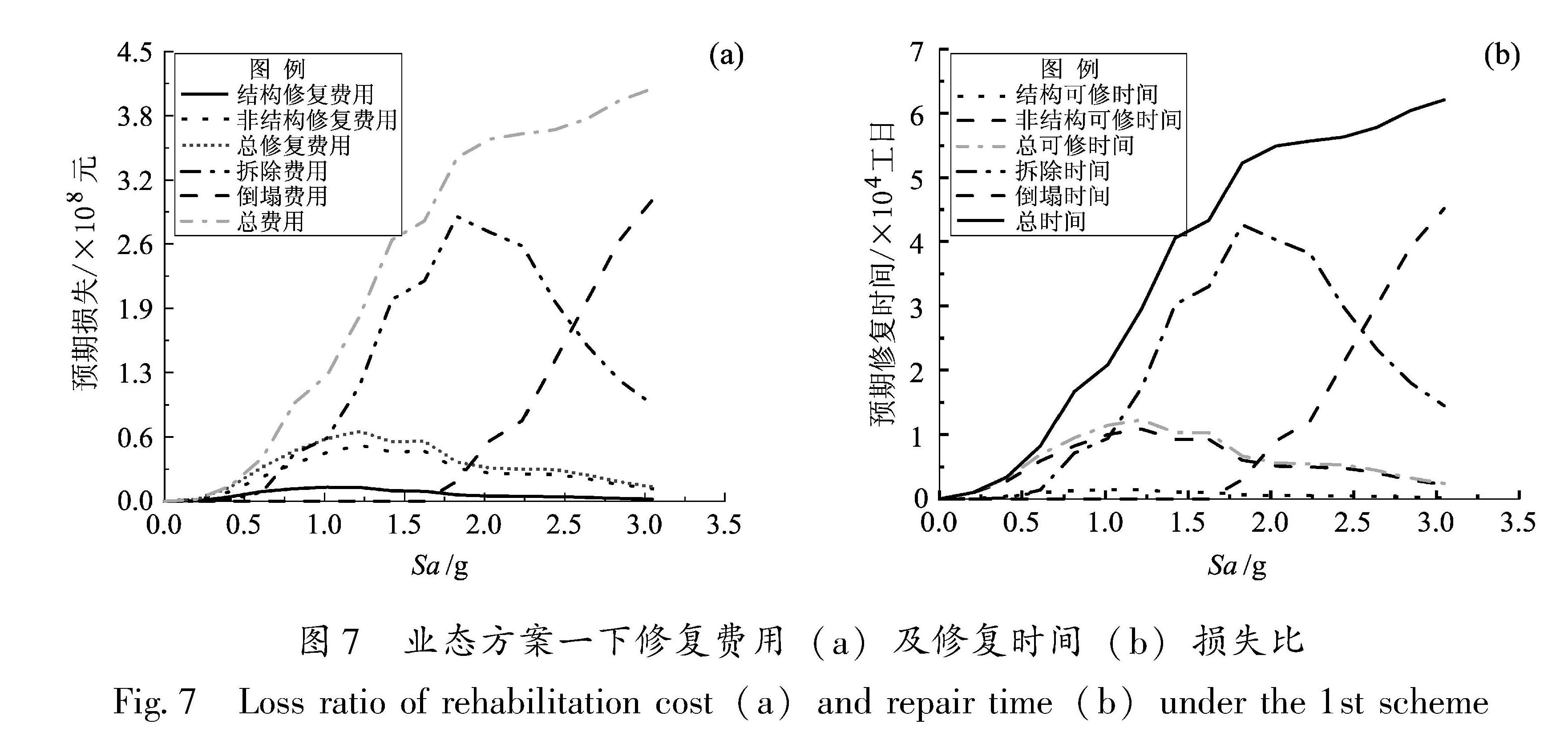
3.3 损失评估分析及比较图7是由业态组合方案一计算获得的修复费用与修复时间损失曲线,从图中可看出,两类结果的趋势类似,下述讨论都以修复费用为例展开。需要说明的是,一个工日代表一个工人一个工作日的劳动量,修复时间表征建筑修复所需的工作量。为了了解修复费用随着地震动强度增强的变化情况,将损失结果分为可修复部分总修复费用、不可修复部分拆除重建费用、倒塌部分重建费用,其中可修复部分又细分为结构修复费用和非结构修复费用。图7a中总费用包括建筑可修复部分产生的总修复费用及拆除和倒塌的置换费用。其中,总修复费用包括了建筑在可修复状态下非结构构件和结构构件的修复费用。从图7a可以发现,当Sa<0.61 g(60%Sa(T1,DBE))时,倒塌费用与拆除费用基本为0,总修复费用占建筑总费用的主导,其中非结构构件的损伤是造成结构损失的主要来源。拆除费用随着地震动强度的增强先增大然后又降低,主要是由于随着地震动强度的增强,建筑倒塌概率逐步提升。
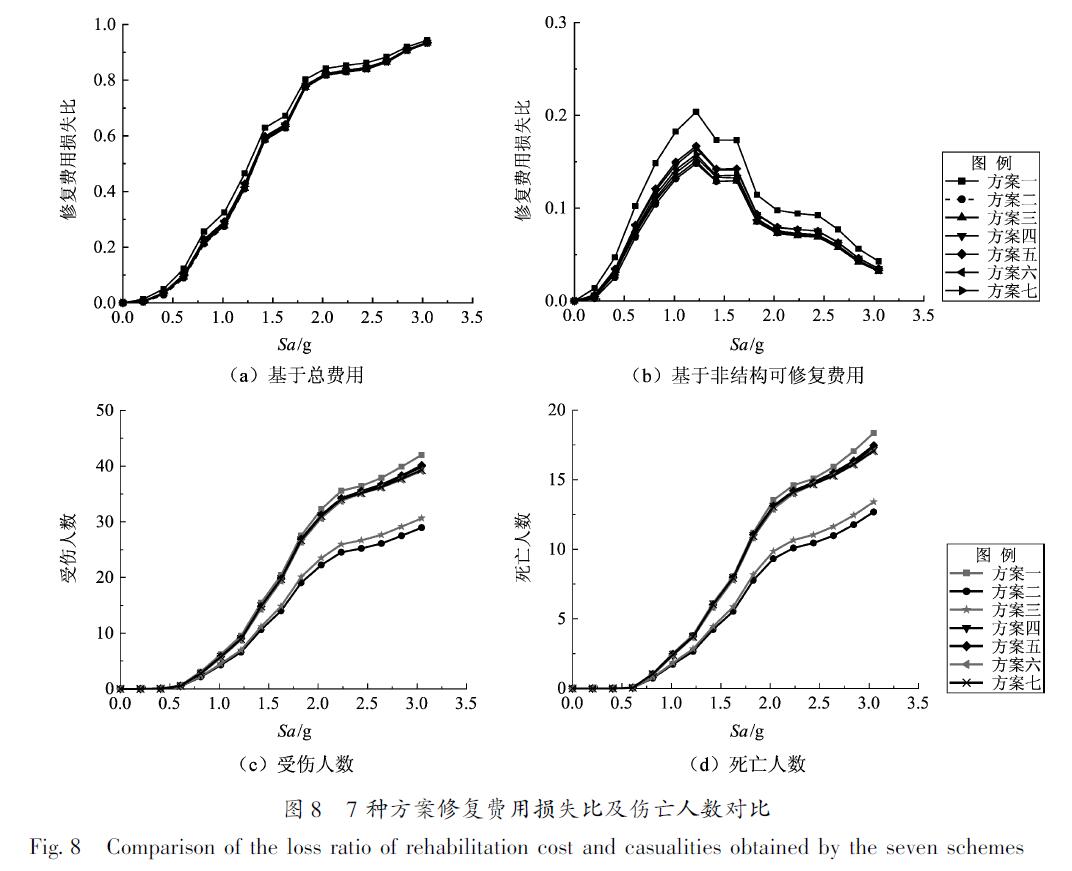
由于重建成本受建筑业态组合的影响,为了更加直观了解各业态组合方案的优劣,采用损失比进行归一化。损失比定义为预期损失与该业态组合下重建成本的比值。图8a展示了7种方案修复费用损失比,方案1(零售业态)的损失比明显高于其他方案,其他方案损失比较为接近。从图8b可以发现,方案2(商业办公业态)明显优于其他方案,各方案在设计地震强度附近的损失比存在较大差异。
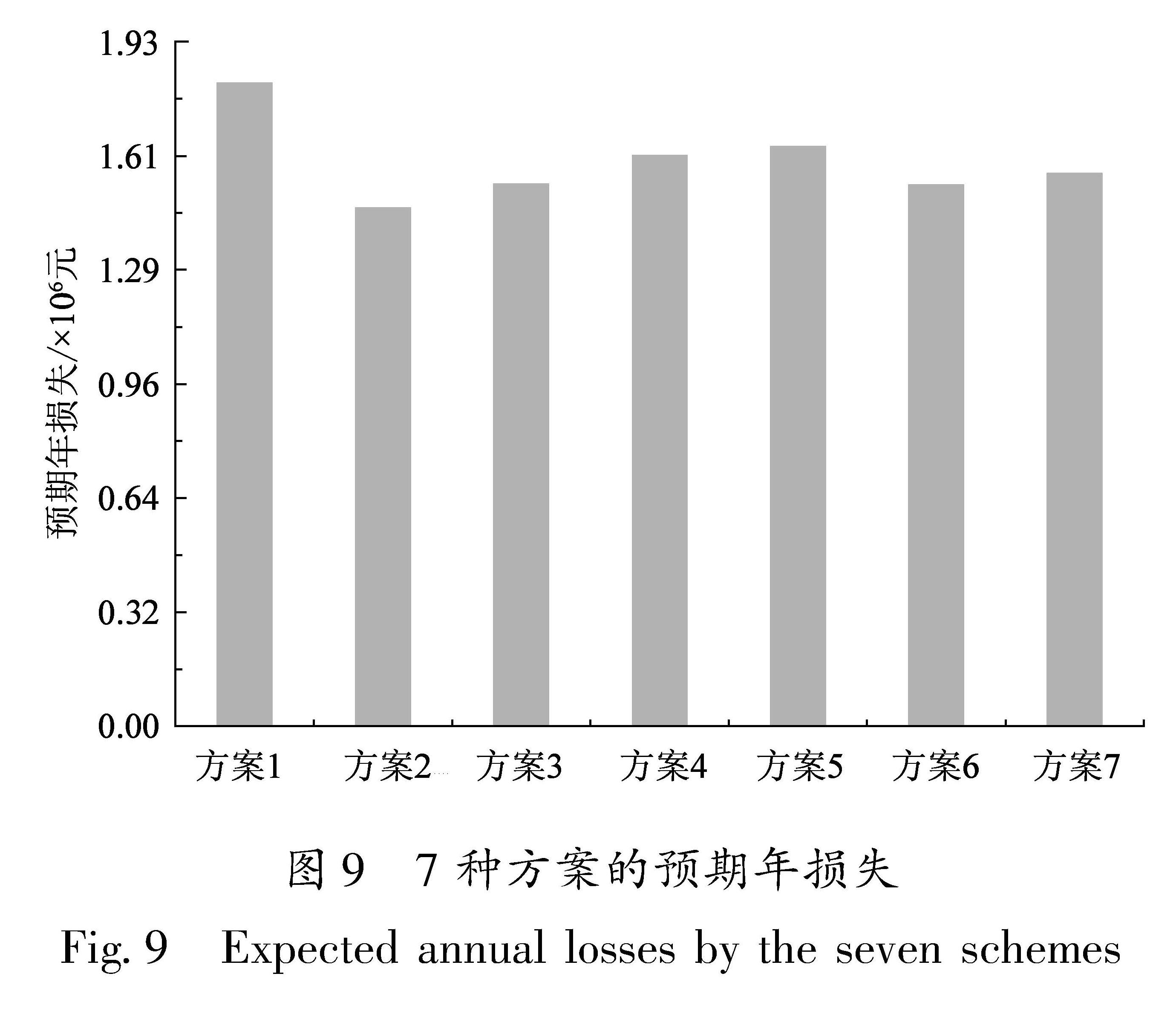
从图8c、d可以看出,方案1伤亡人数最高,方案2伤亡人数最少,方案4~7伤亡情况基本一致。图9也表明方案1的年平均损失最高,从投保角度来说,若是业主方选择方案1,需要提高在该建筑场所内办公的员工人员的意外险费用。方案2年平均损失最低,较方案1少30万,约少19.5%。方案3与方案4~6的年平均损失较为接近。
图7 业态方案一下修复费用(a)及修复时间(b)损失比
Fig.7 Loss ratio of rehabilitation cost(a)and repair time(b)under the 1st scheme图8 7种方案修复费用损失比及伤亡人数对比
Fig.8 Comparison of the loss ratio of rehabilitation cost and casualities obtained by the seven schemes4 基于遗传算法的最优业态组合决策方法
4.1 方法思路前文研究结果表明业态组合方案的差异将导致不同的地震损失,从而影响业主方的业态组合方案决策与投保费用厘定。但由于地震损失有多种指标可以考虑,每个业主方和财产承保方的关注也有所差异,为了制定更为符合业主方或财产承保方的决策方案,需把各方的主观想法考虑在决策流程中。以本文采用的9层商业建筑为例,业态组合方案不限于表4中列出的7种,在不考虑任何限制条件下,业态组合方案有39=19 683种,采用枚举法选择最优方案效率较低。
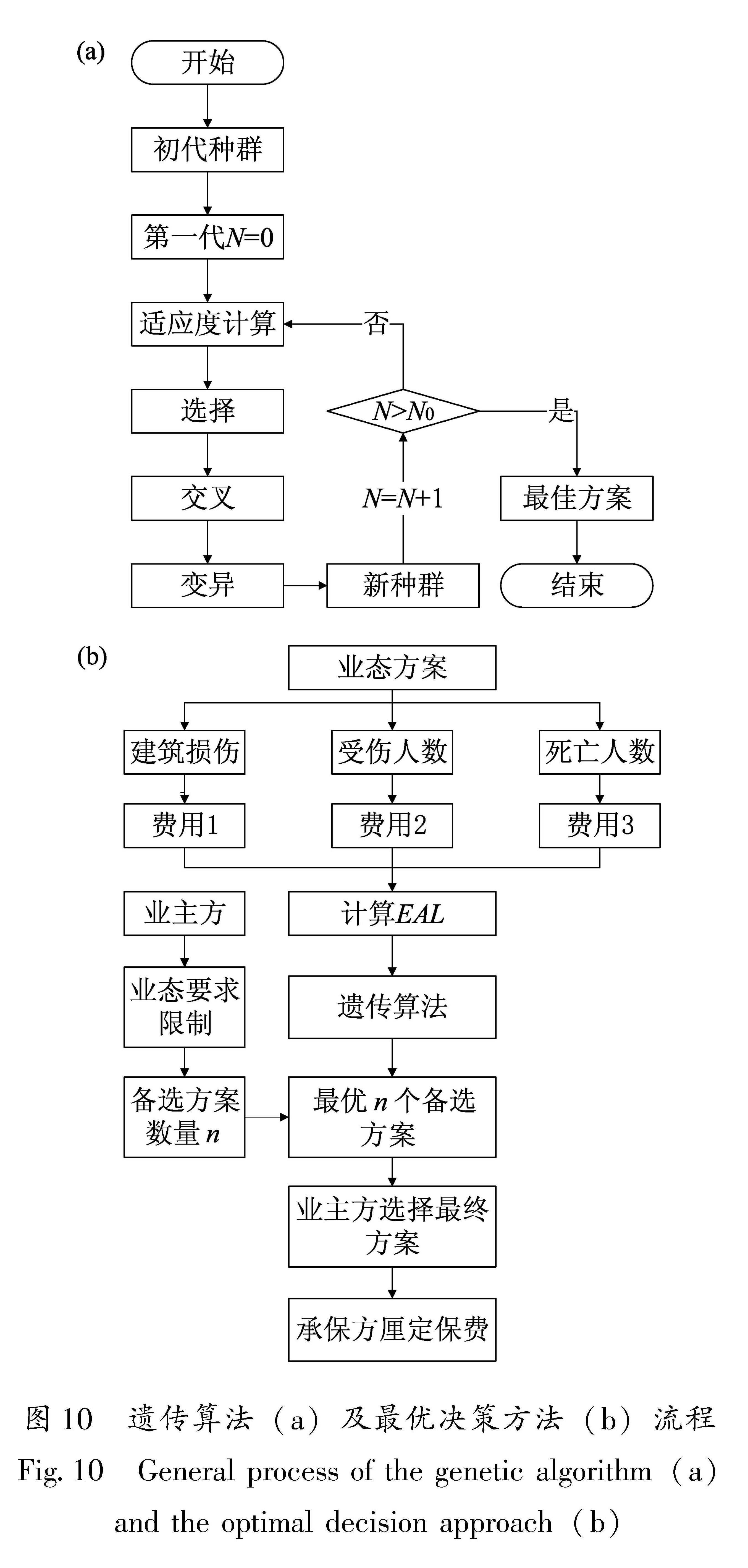
遗传算法是基于生物遗传进化的相关理论发展而来,并已应用于工程的各个领域,例如结构优化设计(Steneker et al,2020)。遗传算法的基本流程如图 10a所示,其基因遗传主要通过适应度函数来决定。为了避免适应度最高的个体由于选择、交叉、变异的随机性导致丢失,采用精英保存的策略确保最优个体能够一直遗传,并提高遗传算法的运行速度和收敛效率。对于业主方和保险方而言,年平均损失是重要决策指标,故选择其作为初步决策的适应度函数。前文所述的年平均损失仅考虑了建筑结构与非结构在地震作用下的破坏,忽略了地震下人员伤亡造成的影响。为了更全面地反映地震下的损失,有必要将人员伤亡造成的损失费用也纳入到年平均损失的计算中。
基于遗传算法的最优决策方法见图 10b。为了给业主方和保险承保方提供详细的地震损失相关信息,将地震灾害下的建筑结构与非结构构件损伤、受伤人数、死亡人数全部转化为费用,从而计算决策指标EAL。在利用遗传算法过程中,同时考虑业主方对于业态要求的限制,尊重业主方主观意愿,选出最优的n个备选方案,业主方最终在n个备选方案中做出选择,承保方根据业主方选择的最终方案厘定对应的保险费。
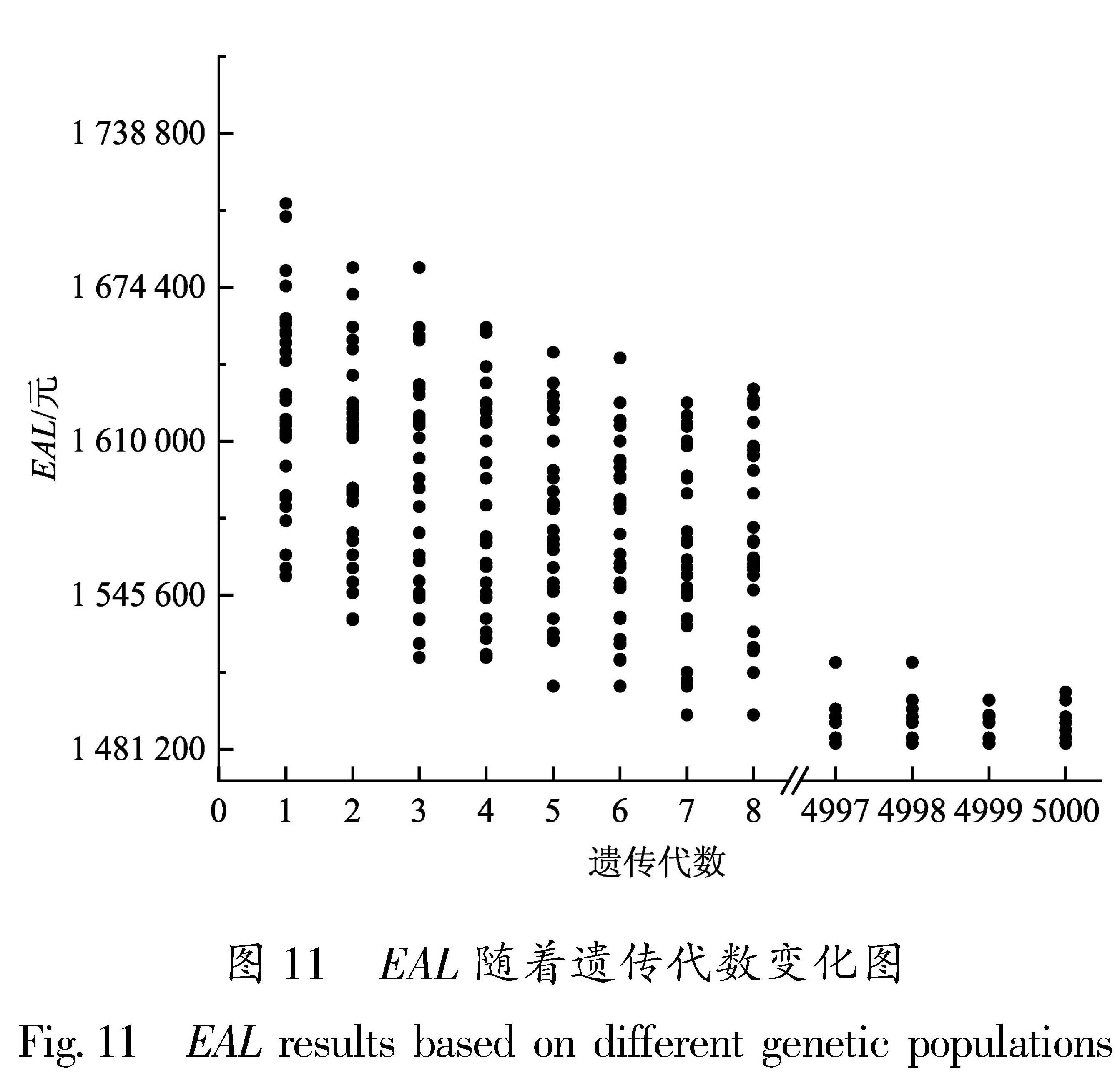
4.2 实例分析为了验证基于遗传算法的决策方法的可行性,基于前述研究展开案例分析。参考中国平安企业团体综合意外险(2021)的伤亡赔付规定,暂定单人受伤赔付10万元,单人死亡赔付60万元。初代种群个体总数,即方案数设置为30,遗传代数为5 000。基于遗传算法计算分析,记录每一代种群的年均损失(EAL),结果如图 11所示。从图中可以看出,不同业态组合的EAL差异明显,基于遗传算法的决策框架可快速求取到最优方案,避免了枚举等方法的繁杂计算。假定业主方目前对业态组合要求无限制,根据遗传算法迭代计算结果,选取了最优方案。最优方案见表8。
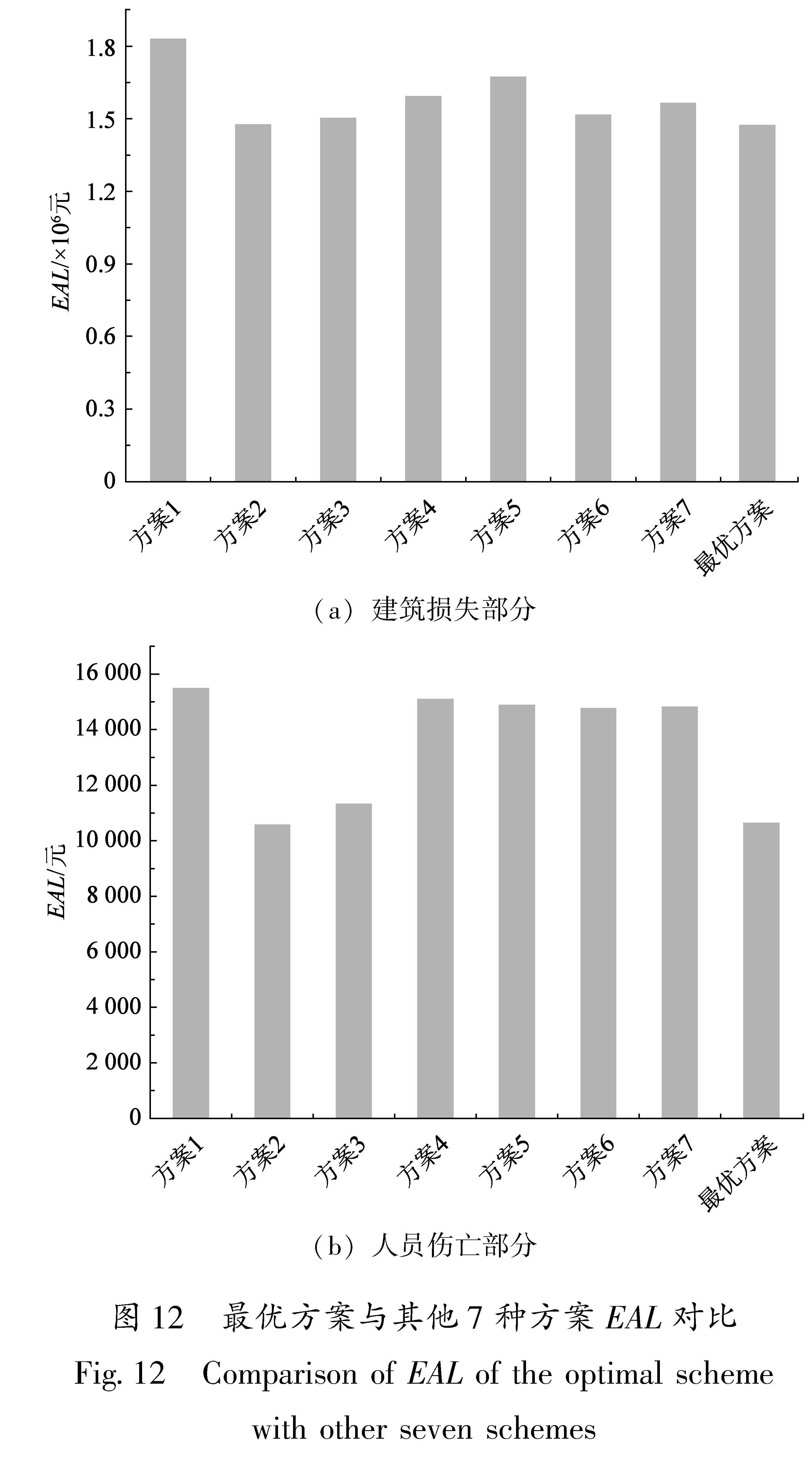
将最优方案与初始7种方案对比,建筑损失和人员伤亡分别造成的EAL对比结果如图 12所示。从图中可以发现,EAL主要由建筑结构与非结构损伤控制,人员伤亡部分的EAL相对较小。遗传算法求解的最优方案与第二种方案的年平均损失虽然较为接近,但仍少约2 448元。
5 结论
本文以一座9层钢支撑框架模型作为研究对象,基于22组地震动对算例开展IDA分析,进一步对易损性和倒塌风险进行了分析。讨论了7种业态组合方案下的地震损失,并基于遗传算法发展了考虑地震风险的最优业态组合决策方法,得到以下几点结论:
(1)当地震动强度小于60%Sa(T1,DBE)时,可修复部分修复费用是地震经济损失的主要影响因素,且非结构构件的损伤是修复费用的主要部分,也是影响不同业态方案经济损失的主要来源。考虑建筑业态差异对厘定建筑保费有实际意义。
(2)基于遗传实现最优业态组合决策方法可灵活添加限制条件,可考虑业主方对主要业态的选择偏向与布置规则等要求。经算例证实提出的基于遗传算法的决策框架可快速求取到最优方案,避免了枚举法等方法的重复计算,在实际应用中具有快速求解寻取最优建筑业态方案的优势。
(3)不同业态组合的EAL差异明显,最大相对损失差距约为20%。考虑业态组合的建筑地震损失,对业主等利益相关方的决策有参考意义。本文提出的决策方法为业主方提供了考虑地震损失风险的业态组合方案优化,同时为保险方厘定保险费用提供决策依据。
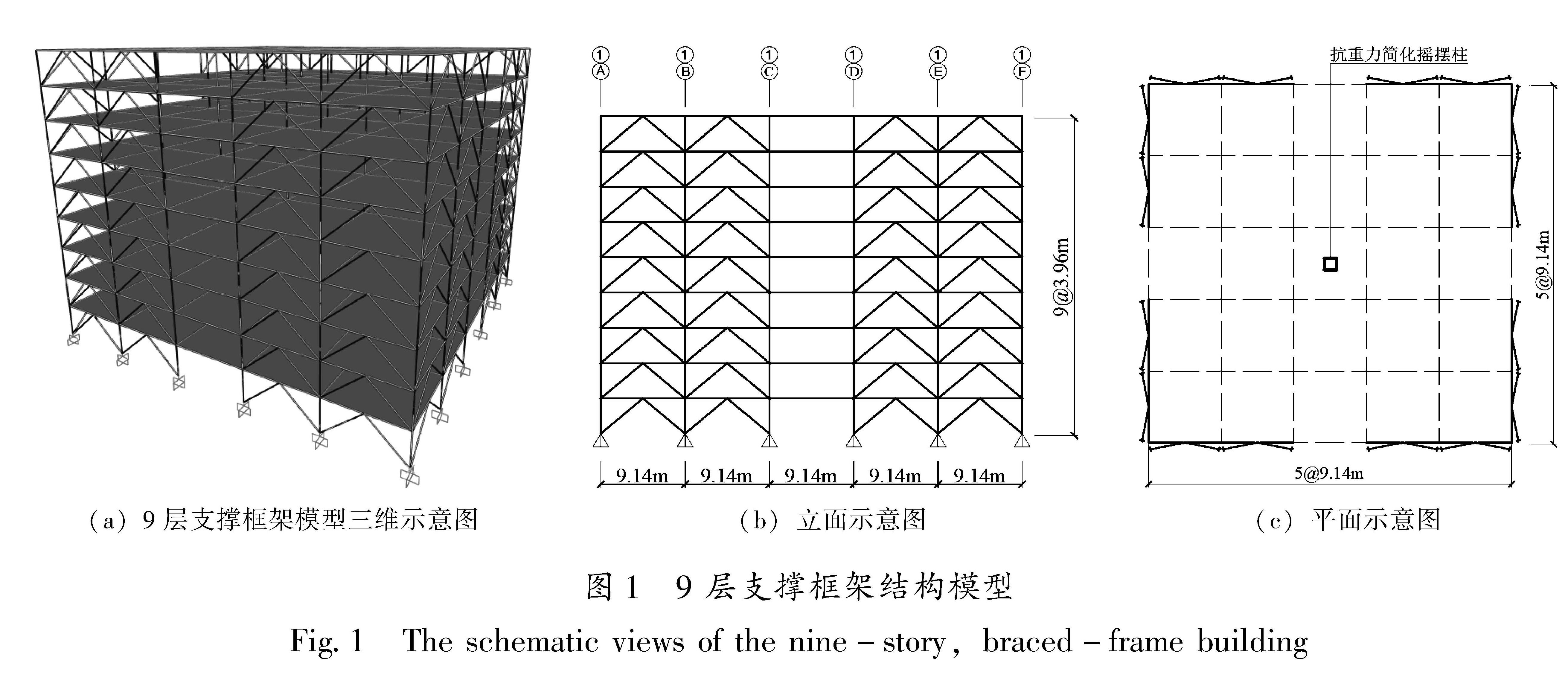
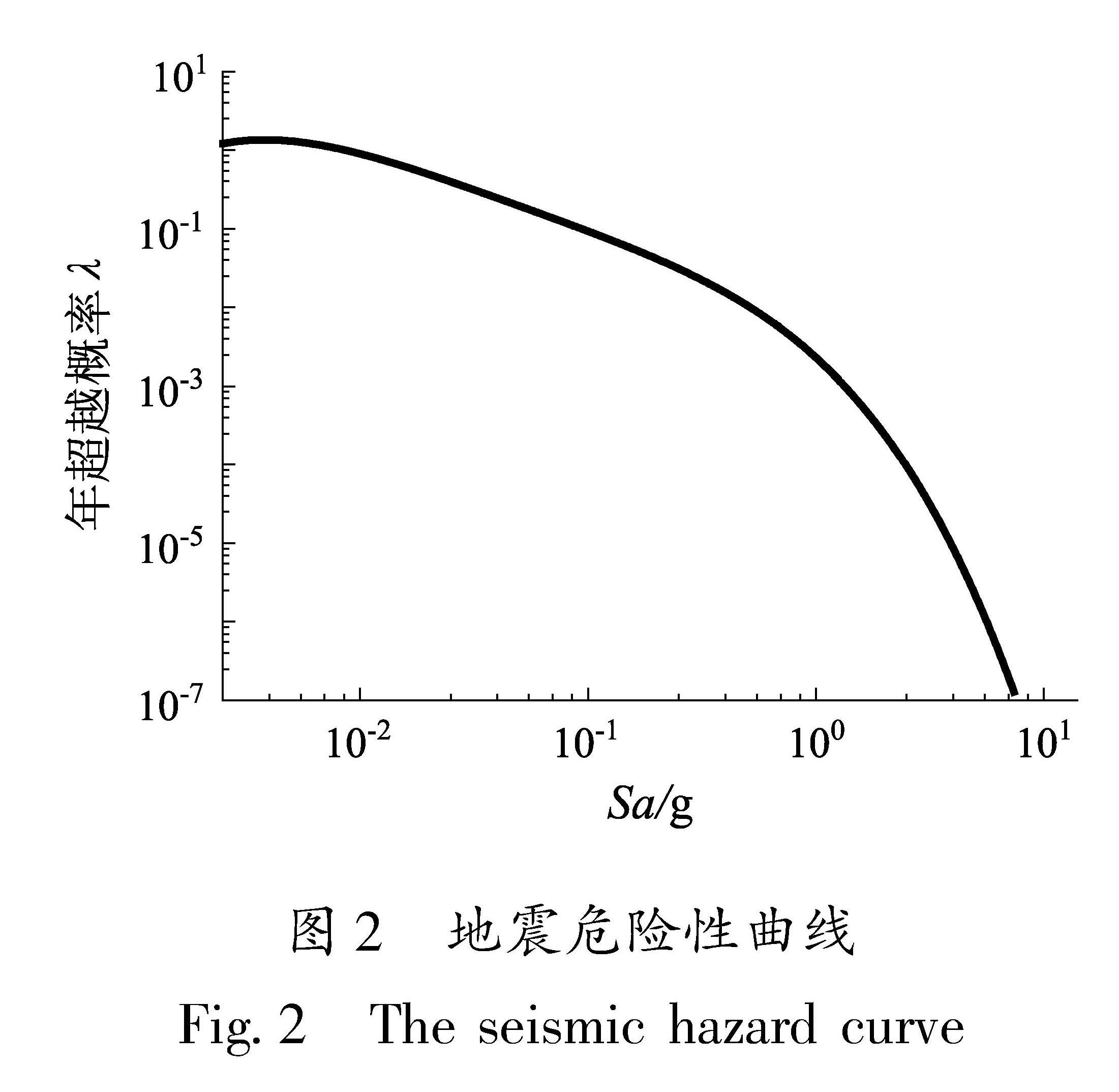
2.1 模型介绍本文研究对象为一栋位于美国加州洛杉矶高发地震地区的中心支撑框架结构,场地类别为D类,地震参数SS=2.17 g,S1=0.79 g,建筑模型如图1所示,所在场地的地震危险性见图2。该建筑共9层,每层层高相等,均为3.96 m,X、Y方向各有五跨,每跨跨度均为9.14 m。
本文采用Opensees软件建立有限元模型,梁、柱和支撑均采用基于纤维截面的梁柱单元进行模拟。梁柱单元使用Gauss-Lobatto求积规则进行每个分段内的数值积分,该单元考虑了5个积分点,以获得构件非弹性变形。动力分析中采用瑞利阻尼模型,阻尼比为3%。考虑1/1 000的初始缺陷来模拟柱和支撑平面内和平面外的屈曲行为(Wang et al,2021)。每个梁柱构件划分为2个单元,支撑构件共划分为8个单元以模拟平面外屈曲变形响应。Opensees中,Steel 02材料是单轴各向同性强化的Giuffre-Menegotto-Pinto钢材本构,可有效反映钢材受力特性,故本文钢材本构定义为Steel 02。在每个结构构件的两端指定刚性单元模拟节点刚域。支撑端部节点板采用非线性转动弹簧模拟,单元本构依据Hsiao等(2012)的建议定义。
由于该模型是一个规则对称结构,所以前两阶平动振型基本一致,第一周期为T1=0.78 s,第二周期为T2=0.77 s,第三周期为T3=0.27 s。该结构按Minimum Design Loads for Buildings And Other Structures(ASCE/SEI 7-16—2016)设计,在设计地震下(Design Based Earthquake,DBE)的结构第一周期对应的谱加速度Sa(T1,DBE)=1.02 g,最大考虑地震(Maximun Considered Earthquake,MCE)对应的谱加速度Sa(T1,MCE)=1.52 g。
2.2 不同业态组合对结构动力特性的影响不同业态组合对模型的影响主要体现在荷载分布方面。在建筑主体结构布置不发生变动的情况下,当建筑业态发生变化时,结构设计中考虑的荷载分布及荷载大小会产生细微不同。参考Minimum Design Loads for Buildings And Other Structures(ASCE/SEI 7-16—2016)与《建筑结构荷载规范》(GB 50009—2012)等相关建筑设计规范,发现零售、办公、酒店公寓的荷载差异主要体现在两个层面:一是楼面活荷载的不同; 二是隔墙分布受建筑业态不同导致的恒荷载的差异。经计算对比发现,零售、办公、酒店公寓业态下恒活荷载组合值相差较小,在分析中可按一致的组合荷载值进行计算。同时,Silva等(2020)关于分别用于公寓和办公的人字型钢框架在地震下的响应统计也得出了“业态差异对于‘人'字型钢框架的结构响应影响较小”这一结论。综上所述,为减少计算量,对于不同业态组合的模型荷载可采用统一荷载分布模式展开分析。
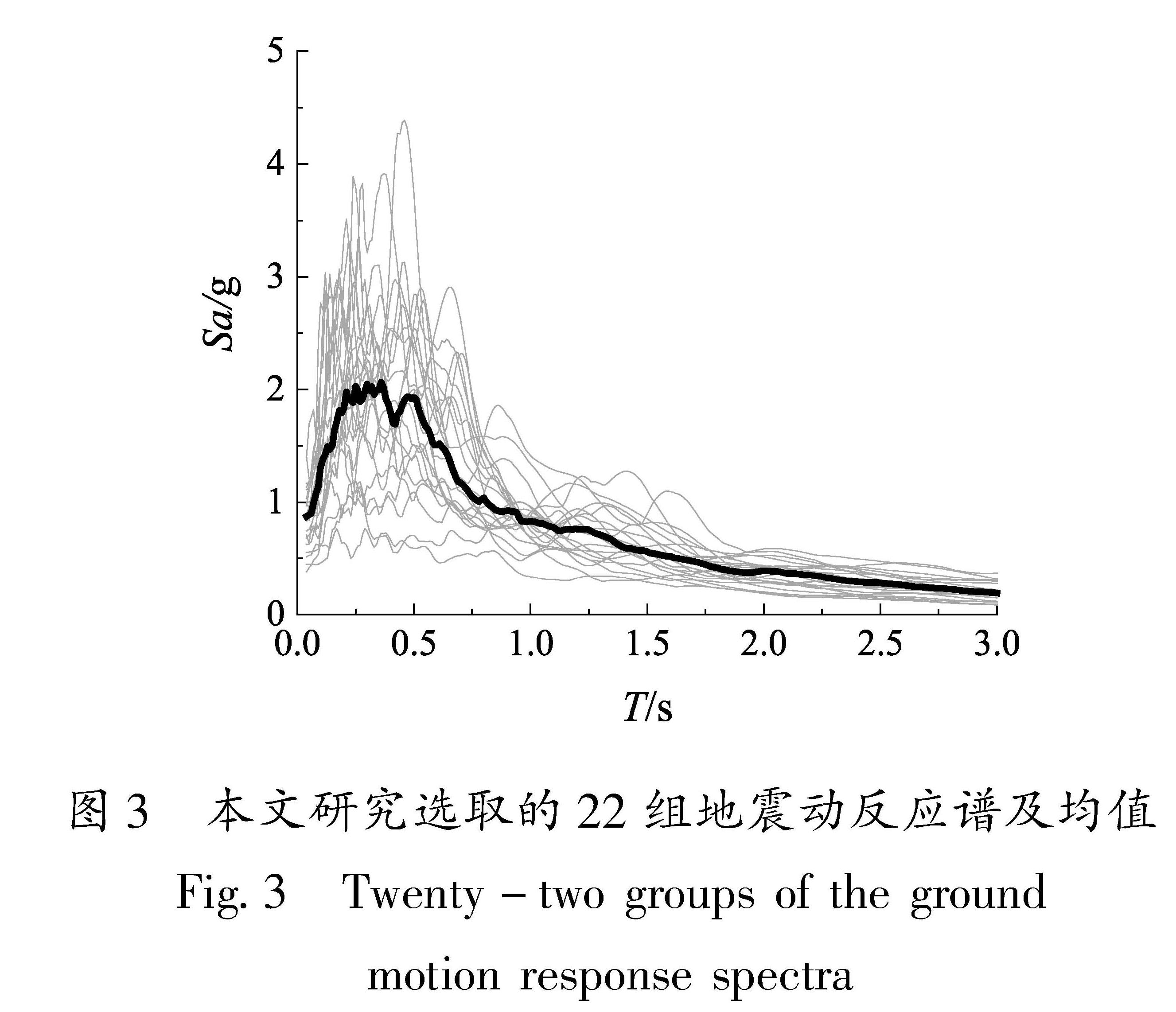
2.3 地震动选择本文采用Quantification of Building Seismic Performance Factors(FEMA P695—2009)提供的22组地震波,如图3所示。基于22组地震动开展增量动力分析(Incremental Dynamic Analysis,IDA),采用Sa(T1)作为地震动强度参数(Intensity Measures,IM)。地震动强度选择等距调幅,以设计地震动强度Sa(T1,DBE)为基准,调幅步长为设计地震动强度的20%,强度变化范围为(20%~300%)Sa(T1,DBE),共计15个工况,见表1。
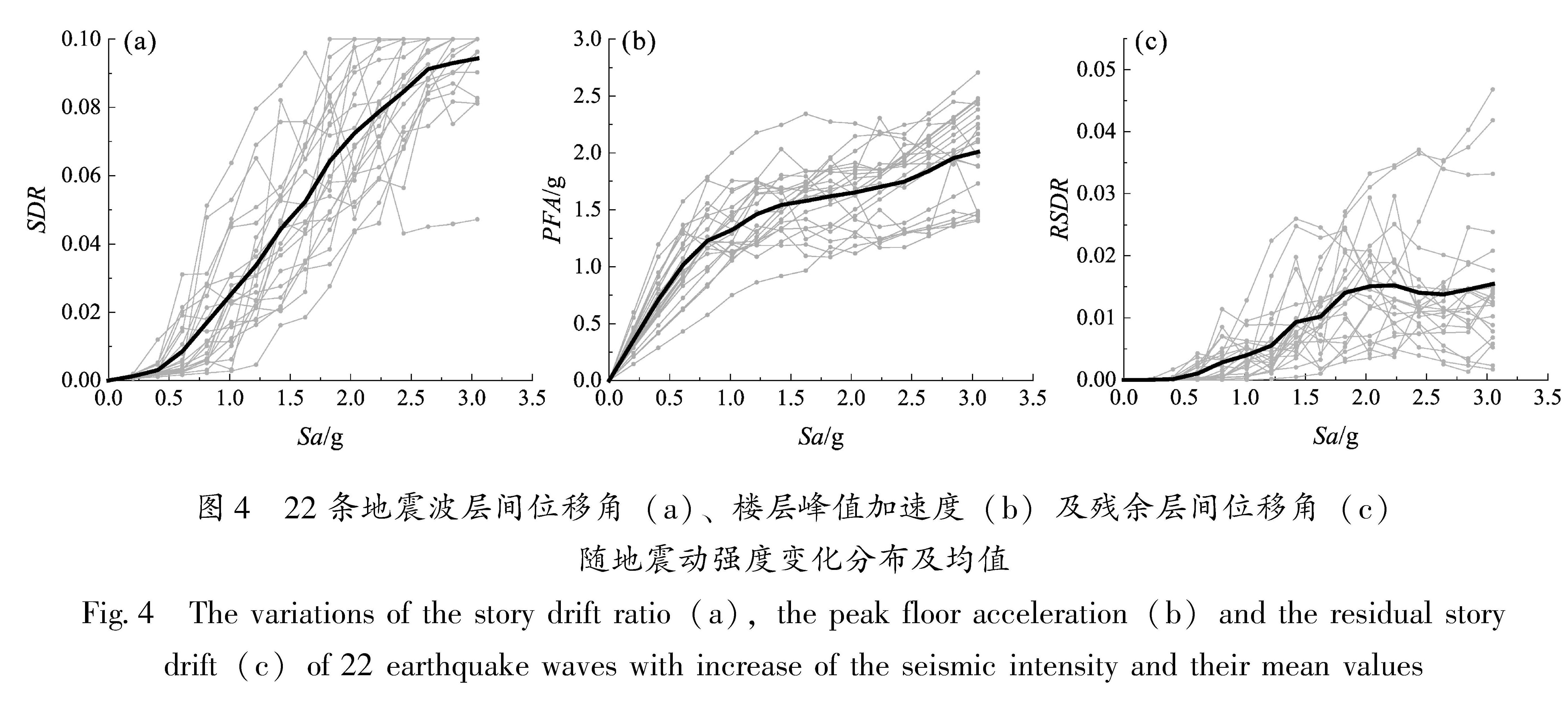
2.4 结构响应分析图4展示了22组地震动下的层间位移角、楼层峰值加速度、残余层间位移角随地震动强度增强的变化情况。从图4a可以看出,不同地震动下层间位移角响应较为离散。当Sa(T1)<0.4 g时,结构处于弹性阶段,随着地震动强度增加,层间位移角线性增大,当Sa(T1)>1.8 g时,多数工况进入倒塌状态。从图4b可以看出,当Sa(T1)<1.02 g时,结构处于线性阶段,楼层峰值加速度线性增大; 当结构进入非线性阶段,楼层峰值加速度随地震动强度变化趋于平稳。从图4c可看出,当Sa(T1)>1.8 g时,残余层间位移基本稳定,这主要由于结构在此工况下大都发生倒塌,没有发生残余位移。
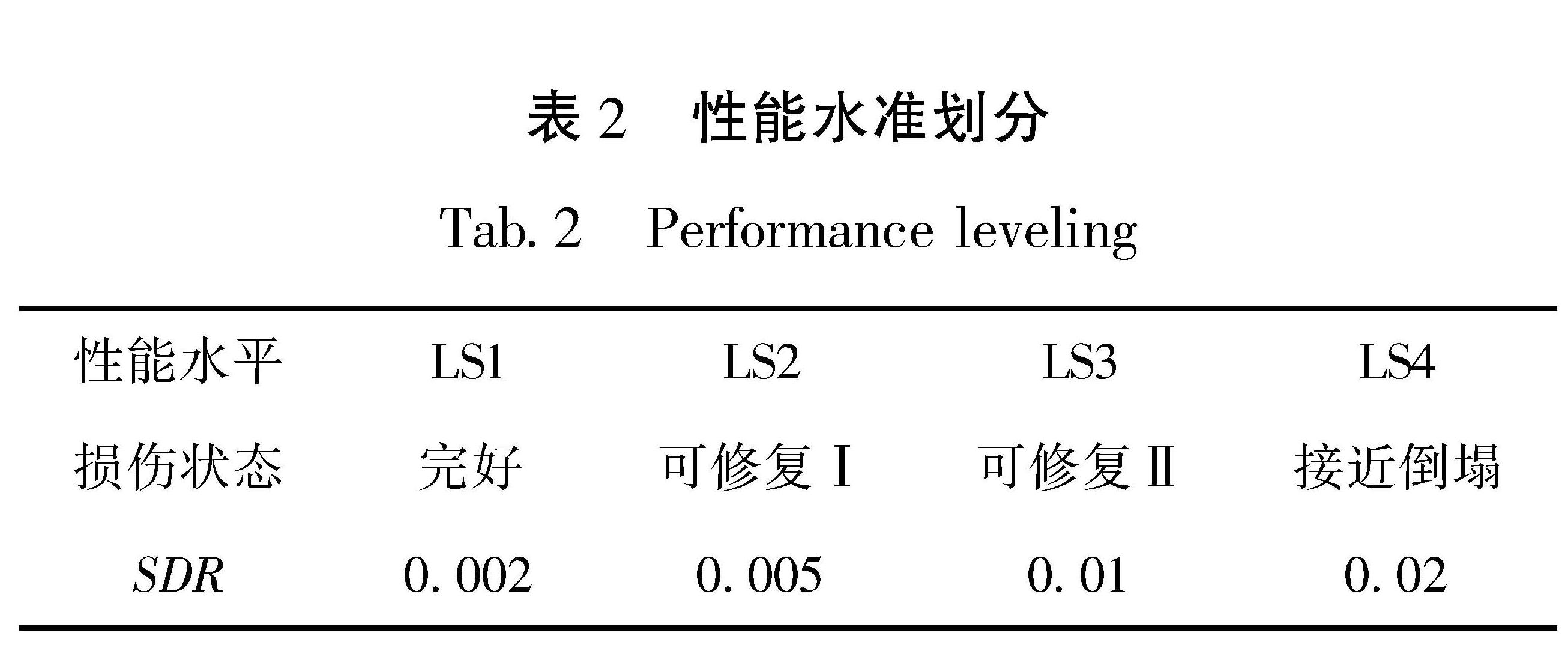
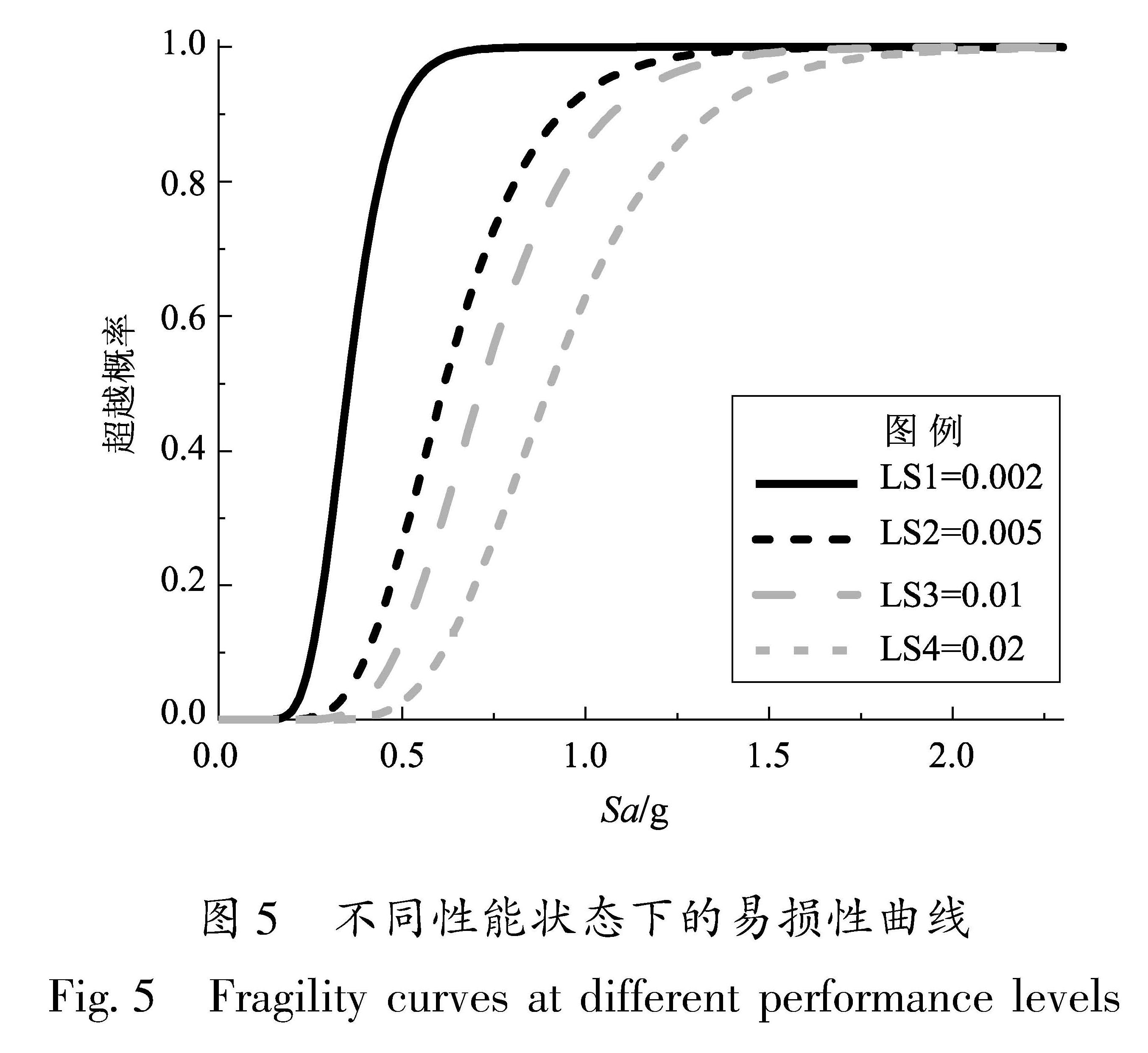
2.5 易损性与风险分析2.5.1 不同性能水平的易损性建筑结构与非结构构件的易损性函数主要依据Seismic Performance Assessment of Buildings(FEMA P58—2012)确定的,其工程需求参数在不同性能水平的限值也有明确规定。同时,为了后续准确预测地震灾害下人员伤亡,需要进一步确定钢支撑框架整体的不同性能水平划分。Huan等(2012)通过对钢支撑框架试验数据统计分析以及与各国位移角限值的比较,给出了各性能水平相对应的层间位移角建议限值。在此基础上,本文划分了性能水准,具体见表2。图5展示了通过IDA分析结果构建的不同性能水平下的易损性曲线,将用于各业态方案的人口伤亡损失分析。
2.5.2 倒塌风险分析本文选择的倒塌判断准则为IDA分析下层间位移角随地震动强度变化结果(图4a)中两点连线斜率达到弹性斜率的5%或者最大层间位移角超
过10%。倒塌裕度比(Collapse Margin Ratio,CMR)是评估结构抗倒塌能力的一个有效指标,其定义为:
CMR=(Sa(T1,PC=0.5))/(Sa(T1,MCE))=1.78(10)
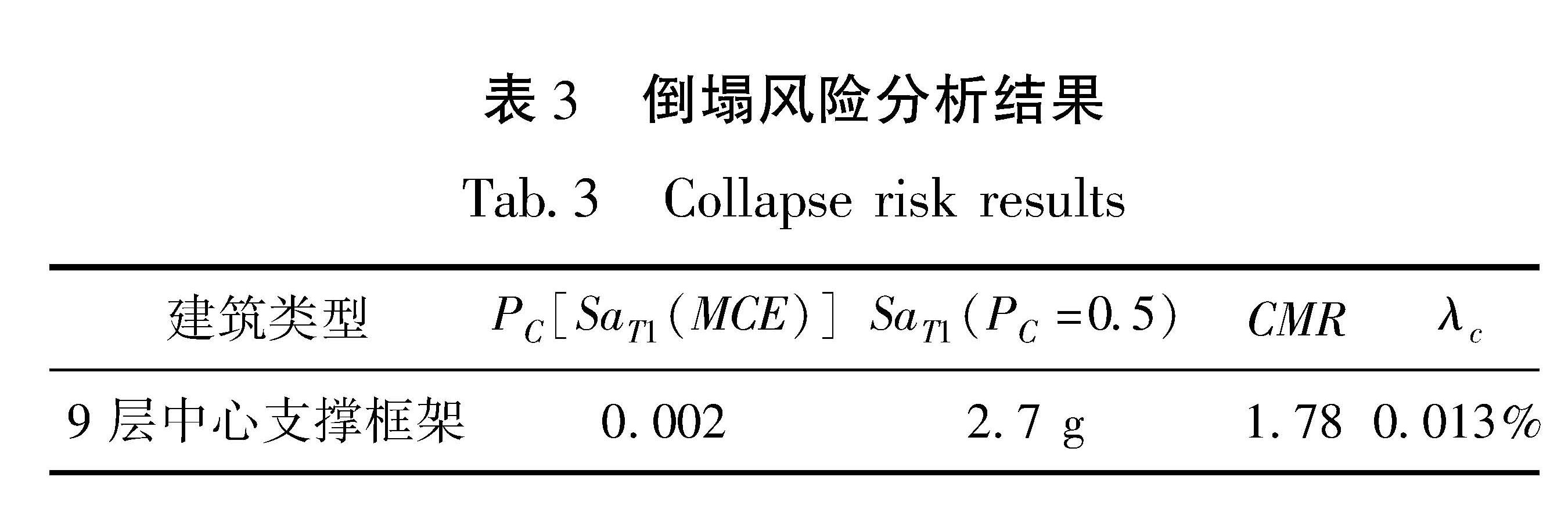
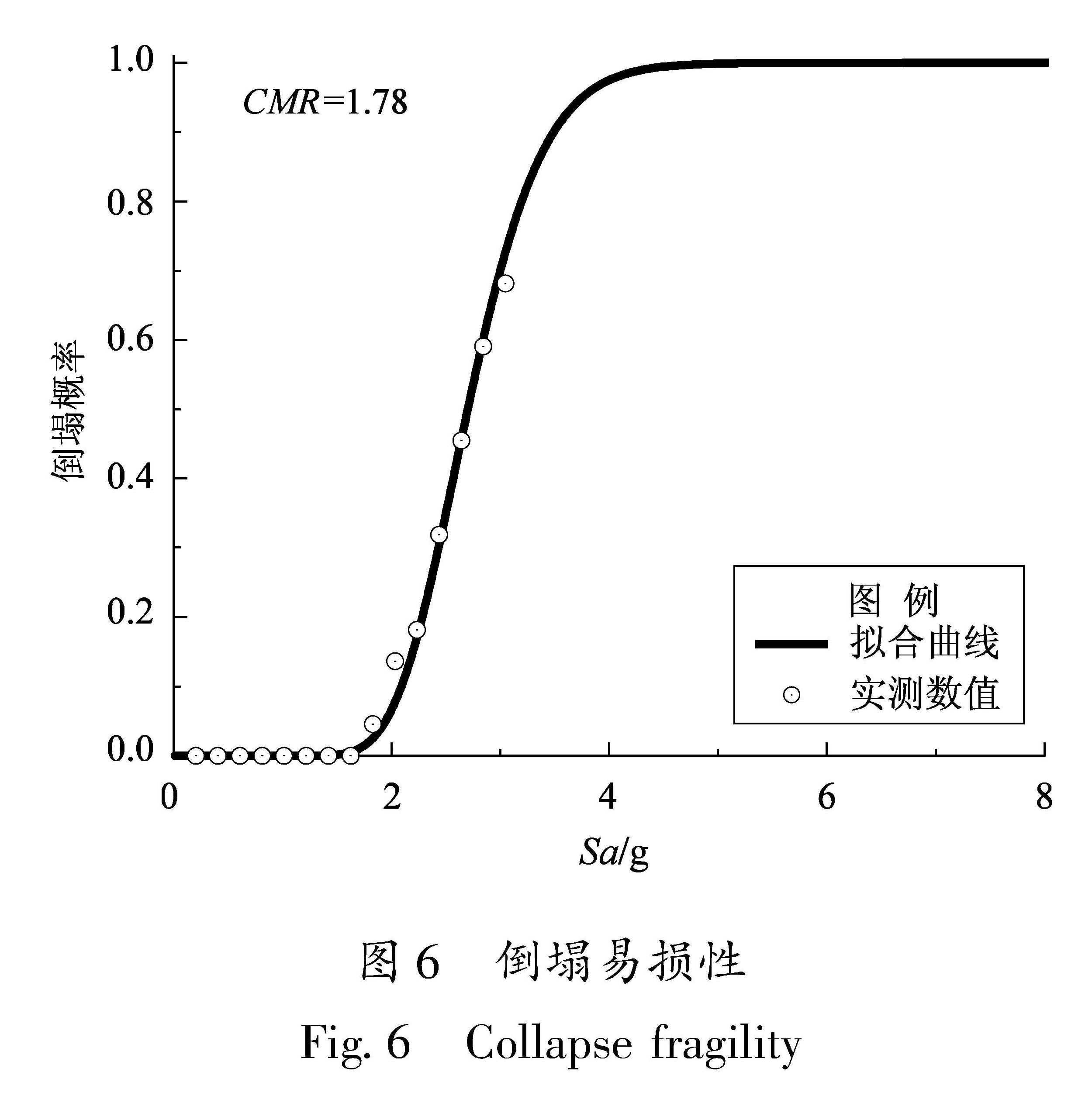
式中:Sa(T1,PC=0.5)表示倒塌超越概率为0.5时对应的谱加速度。通过公式(8)计算得到该结构50年内倒塌概率是0.64%,Minimum Design Loads for Buildings And Other Structures(ASCE/SEI 7—16)规定结构在50年内的倒塌概率要低于1%。倒塌分析统计结果见表3,倒塌曲线见图6。由此可见,该建筑设计符合要求。
- 任军宇,潘鹏,王涛,等.2021.GB/T 38591—2020《建筑抗震韧性评价标准》解读[J].建筑结构学报,42(1):48-56.
- 石晟,杜东升,王曙光,等.2020.高层钢结构不同减震加固方案的抗震韧性评估[J].土木工程学报,53(4):71-82.
- 田源,李梦珂,解琳琳,等.2018.采用新一代性能化设计方法对比典型中美高层建筑地震损失[J].建筑结构,48(4):26-33.
- 闫佳琦,陈相兆,孙柏涛.2021.地震人员伤亡评估方法及损失评估系统综述[J].工程力学,38(12):1-16.
- 叶良浩,曲哲,孙海林,等.2020.采用不同减震结构体系的医疗建筑地震经济损失评估[J].建筑结构学报,41(7):15-26.
- 曾翔,刘诗璇,许镇,等.2016.基于FEMA-P58方法的校园建筑地震经济损失预测案例分析[J].工程力学,33(S1):113-118.
- 中国平安企业团体综合意外险[EB/OL].(2021-03-01).[2021-05-26].http://baoxian.pingan.com/product/tuanyixian.shtml?WT.mc_id=TCW-BD-XZ-20210201-018018&WT.srch=1,2021.
- Ding X.2006.Redundancy in steel braced frames under seismic excitations[D].Bloominton-Normal:University of Illinois.
- Guha-Sapir D,Vos F,Below R,et al.2012.Annual disaster statistical review 2011:the numbers and trends[R].Centre for Research on the Epidemiology of Disasters(CRED).
- Hsiao P,Lehman D E,Roeder C W.2012.Improved analytical model for special concentrically braced frames[J].Journal of Constructional Steel Research,73(2012):80-94.
- Huan H X,Wen F L,Yan Q G.2012.Statistical analysis of steel frame
- structure drift angle[J].Applied Mechanics and Materials,208:1102-1108.
- Hwang S,Lignos D G.2017.Earthquake-induced loss assessment of steel frame buildings with special moment frames designed in highly seismic regions[J].Earthquake Engineering and Structural Dynamics,46(13):2141-2162.
- Jayaram N,Shome N,Rahnama M.2012.Development of earthquake vulnerability functions for tall buildings[J].Earthquake Engineering and Structural Dynamics,41(11):1495-1514.
- Mitrani-Reiser J.2007.An ounce of prevention:probabilistic loss estimation for performance-based earthquake engineering[D].Earthquake Engineering Research Laboratory.
- O'Reilly G J,Calvi G M.2021.A seismic risk classification framework for non-structural elements[J].Bulletin of Earthquake Engineering,19(13):5471-5494.
- Reilly G J,Sullivan T J.2018.Probabilistic seismic assessment and retrofit considerations for Italian RC frame buildings[J].Bulletin of earthquake engineering,16(3):1447-1485.
- Silva A,Macedo L,Monteiro R,et al.2020.Earthquake-induced loss assessment of steel buildings designed to Eurocode 8[J].Engineering Structures,208(2020):1-15.
- Steneker P,Filiatrault A,Wiebe L,et al.2020.Integrated structural-nonstructural performance-based seismic design and retrofit optimization of buildings[J].Journal of Structural Engineering,146(8):04020141.
- Wang J,Burton H V,Dai K.2021.Reliability-based assessment of percentage combination rules considering the collapse performance of special concentrically braced frames[J].Engineering Structures,226(2021):1-13.
- Zeng X,Lu X Z,Yang T Y,et al.2016.Application of the FEMA-P58 methodology for regional earthquake loss prediction[J].Natural Hazards,83(1):177-192.
- ASCE/SEI 7-16—2016,Minimum design loads for buildings and other structures[S].
- FEMA 350—2000,NEHRP recommended seismic design criteria for new steel moment-frame buildings[S].
- FEMA 695—2009,Quantification of building seismic performance factors[S].
- FEMA P58—2012,Seismic performance assessment of buildings[S].
- GB 50009—2012,建筑结构荷载规范[S].
- GB/T 38591—2020,建筑抗震韧性评价标准[S].