(1.中国地震台网中心,北京 100045; 2.中国地震局地震预测研究所,北京 100036)
(1.China Earthquake Networks Center,Beijing 100045,China)(2.Institute of Earthquake Forecasting,China Earthquake Administration,Beijing 100036,China)
earthquake sequence type; machine learning; feature; mutual information
DOI: 10.20015/j.cnki.ISSN1000-0666.2023.0034
正确的震后趋势预测,是破坏性地震发生后政府和社会最为关心的问题,是地震应急、抗震救灾和恢复重建的重要决策依据之一。震后趋势预测的目的是强余震震级估计,最主要的技术手段是地震序列类型判定。基于历史地震类比和序列参数计算的地震序列类型判定,是当前广泛采用并且还将长期发挥作用的主要余震预测方法(陈立德等,1992; 蒋海昆等,2015)。已有研究显示,不同参数对序列类型具有或多或少的分辨能力,但从严格的统计检验结果来看,单参数序列类型识别正确率并不十分理想(蒋海昆等,2006a):一是实际序列参数数值分布较为离散,即使同一类型的地震序列,也有较为离散的序列参数数值分布范围; 二是部分参数最优分类标准与主震震级、震后持续时间等因素有关; 三是单参数预测为主,不同参数对同一个序列的判定结论经常出现矛盾,因而序列类型判定较多地依赖于“统计+经验”的方法以及研究者的经验和能力。还有非常重要的一点是,当前的序列类型判定方法对多震型地震和前震几乎没有序列类型甄别能力(蒋海昆,周少辉,2020),而多震型和前震型地震又属于可能导致更严重灾害的地震序列类型。
机器学习(machine learning)是人工智能的重要组成部分,近年来以机器学习和深度学习为代表的基于大数据的人工智能技术飞速发展,通过数据驱动的技术手段,在样本分类、指标提取、综合决策等方面提供了许多新的工具,在疾病诊断、图像识别、自然语言处理、精准服务、虚拟体验等实际应用场景取得许多突破。在地震预测领域,尤其是针对固定区域、固定时间窗内可能发生地震的震级预测方面,也已有许多探索,具体可参见Mignan和Broccardo(2020)、Al Banna等(2020)、Mousavi 和Beroza(2022)以及王锦红和蒋海昆(2023)的综述。但目前专门针对序列类型判定及余震预测的机器学习研究尚不多见(王锦红,蒋海昆,2023),因而针对现有主要基于单参数、以及“统计+经验”为主的序列后续趋势预测模式存在的不足,同时考虑更多的影响因素(特征),采用人工智能等新技术对序列类型进行多因素的综合判定,是研究者始终持续探索的一条途径(韩渭宾等,1993; 蔡立冬等,1994; 周翠英等,1996; 庄昆元等,2001; 蒋海昆等,2007a; 李冬梅等,2013)。从另一个角度来看,序列类型判定从技术上属于分类问题,而“分类”正是机器学习的长项。
机器学习是利用计算机基于历史数据(经验),建立某种模型(规律),并据此预测未来的一种方法或手段(赵志勇,2018),与人类思考和经验总结过程有些类似,但它能顾及更多的情形,执行更为复杂的计算。机器学习需要基于历史数据对模型进行训练,训练的结果被用来对新数据进行预测,这个结果即模型。训练与预测是机器学习的两个过程,模型则是过程的中间输出结果。机器学习中的训练与预测可粗略对应于人类思维活动的归纳和推测,这与震后趋势预测领域当前主流的“统计+经验”的预测模式有些类似。
有监督学习是最为常见的机器学习算法,它使用标记良好的训练数据进行模型训练,目的是找到一个映射函数来映射输入变量(特征)和输出变量(标签)之间的关系。所谓标签,即样本的分类属性,在地震序列类型判定中即是常用的多震型、主余型、孤立型等序列类型。所谓特征即用于机器学习的样本的特性,以往地震序列类型判定中用到的历史地震活动、序列衰减、G-R关系等均属机器学习样本数据集中的特征类数据。监督学习包含样本数据集构建、数据集拆分、模型选择和训练、外推预测等4个主要步骤,其中样本数据集构建是机器学习最重要的基础,对诸如地震预测这一类机理不明、单项特征与标签之间关系不唯一的分类任务,如何确定训练数据集的输入特征,是机器学习数据准备的最重要工作。机器学习应用大多与大数据高度关联,各种不同模型或算法在输入的数据量达到一定量级后,都有相近的准确度 https://www.cnblogs.com/subconscious/p/4107357.html.,这也是机器学习领域推崇“数据为王”的重要原因 https://hellofuture.orange.com/en/towards-a-less-data-and-energy-intensive-ai/.。样本数量、数据质量、对实际场景的覆盖程度以及特征与标签之间的关联性,都会影响到学习和训练的效果(王东,2021)。
综上,作为机器学习模型训练的基础,本文将基于1970—2021年中国大陆地震目录和历史地震、震源机制等资料,针对序列类型判定这一目的,构建样本数据集; 讨论数据集备选特征与标签之间的统计关联特性,给出推荐的样本数据特征参数集合,构建适用于不同应用场景、具有较高预测准确性及泛化能力的序列分类模型。
依据中国地震台网统一地震目录 http://data.earthquake.cn/data/.,1970—2021年中国大陆及边邻地区(国界线外扩10 km)共记录到MS≥5.0地震1 336次,依据余震破裂范围(Wells,Coppersmith,1994)及余震活动持续时间(Lolli,Gasperini,2003)甄别并删除其中的余震。删除余震后有MS≥5.0地震902次,其中5.0～5.9级722次、6.0～6.9级153次、7.0～7.9级25次、8.0级以上地震2次。以0.5级为间隔的地震频次统计结果如表1第II行所列。地震主要分布于南北地震带、青藏地块、新疆天山地震带和西昆仑地震带,大陆东部地震主要分布于华北、东北地区。基于中国地震台网统一地震目录,采用时-空距离方法(Wells,Coppersmith,1994; Lolli,Gasperim,2003)构建MS≥5.0地震的序列目录,其中204个川滇及附近区域地震的序列目录直接采用赵小艳等人工整理的序列目录 赵小艳.2022.地震预测开放基金(2021)结题报告——“基于决策树的西南地区中强地震序列类型判定研究”.。
表1 1970—2021年中国大陆及边邻地区MS≥5.0地震基本概况
Tab.1 Statistics of the MS≥5.0 earthquakes in Chinese mainland and neighboring areas from 1970 to 2021
针对地震序列类型判定的机器学习样本数据集,序列类型即是样本标签。国外通常把地震序列类型分为主余型(mainshock-aftershock)、震群型(swarm)或多震型(multiplets/multievents)(Utsu,2002; Felzer et al,2004),着重序列显著特征的定性描述,但缺乏定量的分类标准。我国由于余震预测的实际需要,从定量的角度以序列中最大地震释放的能量Emax占全序列释放能量Etotal之比RE=Emax/Etotal进行序列类型划分(周惠兰等,1980),这种分类方式物理含义清晰,但序列活动未结束之前无法计算全序列释放的能量。另一种更为简洁的序列类型划分是基于序列最大与次大地震的震级差ΔM=M0-M1来进行(吴开统,1971),其中M0、M1分别为序列最大与次大地震的震级。上述两种序列分类方法在一定的简化假设条件下等价(蒋海昆等,2006b)。在实际序列跟踪及强余震预测中,由于难以明确判断后续类似大小地震究竟是两次(双震型)还是两次以上(震群型),因而一般把双震型、震群型合称为“多震型”(Felzer et al,2004)。因而,在我国实际地震序列类型判定工作中一般依据震级差ΔM将余震序列分为多震型(-0.6<ΔM<0.6)、主余型(0.6<ΔM<2.4)、孤立型(ΔM>2.4)3类(蒋海昆等,2006c,2015)。考虑到与当前业务工作的衔接,本文服务于机器学习序列类型判定的样本数据集标签(序列类型)仍基于序列主震与序列后续最大地震震级差ΔM=M0-M1确定。
需要说明的是,部分地震序列主震前短时间内震源区会有震级小于主震的地震发生,即前震活动。全球不同区域的研究结果显示大约10%～40%的中强以上地震伴随有前震活动(陈颙,1980; Jones,Molnar,1979; 朱传镇,王琳瑛,1989; Reasenberg,1999; 李振,王辉,2011; 薛艳等,2012),且前震检出率随地震监测能力的提升似有增加的趋势(Trugman,Ross,2019)。笼统而言,主震前短时间内震源区震级小于主震的地震均可称为前震(蒋海昆,周少辉,2020),但为与广泛使用的多震型序列(-0.6<ΔM<0.6)相区分,可约定符合ΔM≤-0.6的地震序列为前震序列。由于本文目的是为中强地震震后趋势判定构建机器学习样本数据集,目标地震(序列主震)均为M0≥5.0地震,因而即使考虑前震,所涉地震序列中符合主震M0≥5.0且震级差ΔM≤-0.6的样本集也仅有17例。由于前震型、多震型均属后续地震危险性较大的序列类型(前震型后续存在发生比主震更大地震的危险,多震型后续存在发生与主震同等大小地震的危险),加之本文前震型样本数量较少,因而合并前震序列与多震型为一类,暂且仍称为“多震型”序列。
据此,本文地震序列类型标签确定标准为:①多震型:ΔM<0.6(包含以往提及的双震型、震群型及前震序列); ②主余型:0.6≤ΔM≤2.4; ③孤立型:ΔM>2.4。
基于地震序列资料计算主震与最大余震震级差ΔM=M0-M1,依据上述地震序列标签确定标准,确定表1第II行所列902个地震的样本标签,其中181个样本由于余震区后续无余震记录而无法分辨序列类型,这些无法分辨序列类型的地震主要分布于西藏、青藏交界、新藏交界、青新交界等地震监测能力较弱的区域,还包括1999年4月8日、2002年6月29日吉林汪清2次7.2级深源地震以及该区域的几次6级深源地震。对721个可以确定序列标签(序列类型)的样本,分序列类型及不同震级区间的地震频次统计如表1第III～V行所列。总的来看多震型、主余型、孤立型分别约占15.5%、59.8%和24.7%,主余型和孤立型合计约占84.5%,与前人78%～87%的统计结果(吴开统等,1990; 蒋海昆等,2006; 苏有锦等,2014)基本一致。后续研究中将无余震记录从而无法确认序列类型的181个样本(表1第VI行)统一归并为“孤立型”,之所以如此处理,是因为它们都具有后续都无显著余震发生这一共同的特点。最终,本文数据集样本特征标签分为多震型、主余型和孤立型3类,3类样本数据集G-R关系b值分别为(0.73±0.030)、(0.77±0.046)和(1.04±0.075)(图1),可见多震型、主余型样本中不同震级地震比例基本一致,孤立型样本中低震级地震明显较多。
图1 1970—2021年中国大陆及边邻地区不同序列类型MS≥5.0地震G-R关系(阴影指示95%置信区间)
Fig.1 G-R relationships of the earthquakes with MS≥5.0 in different types of sequences in Chinese mainland and the surrounding areas from 1970 to 2021
研究显示,构造和介质不均匀性以及应力水平对地震序列类型有重要影响(Mogi,1962; Takayuki,Hirata,1987; Chen,Knopoff,1987; Ben-Zion,James,1993; Ban-Zion,Lyakhovsky et al,2005; Somerville et al,1999; 苏有锦等,1999; Yamanaka,Kikuchi,2004; Kanamori,Brodsky,2004; 蒋海昆等,2006b; Aochi,Ide,2009; Marone,Richardson,2016; 曲均浩等,2015)。迄今为止尚无完全准确、普适的序列类型判定方法,当前使用较多的主要有定性类比和定量计算两类。震后早期,序列数据尚少,一般只能基于构造及历史地震活动定性类比的方法来判断序列类型; 随着序列地震数据逐渐增多,基于地震目录的序列参数计算结果被用于序列类型判定,依据震后不同时段序列参数变化特征,对序列类型进行定性(变化趋势)或定量(参数统计指标)的判定,例如大森公式p值、h值,G-R关系b值,归一化能量熵,地震震级、频次和应变等参数的变化。
基于地震目录的统计地震学方法在当前地震序列类型判定中发挥着不可替代的作用,而基于数字地震记录的研究结果也得到越来越多的应用。例如震源机制一致性和波形相似性方法就被广泛提及(陈颙,1980; Wiemer,Wyss,2002; 王俊国,刁桂苓,2005),但不同研究者得到的认识有一定差异(崔子健等,2012; 黄浩,付虹,2014)。由于应力降与震后断层面上的剩余应力水平有关,因而应力降或视应力也被尝试用于序列类型判定(陈学忠等,2003; 钟羽云等,2004; 秦嘉政等,2005)、余震区应力水平估计及强余震预测(杜迎春,2000; Baltay et al,2011; 王培玲等,2013; 周少辉,蒋海昆,2017)。需要指出的是,尽管基于地震波的方法因其能够直接获得震源或路径信息而受到重视,但到目前为止,要给出地震序列类型的定量判据仍十分困难,难点首先在于从理论上无法给出不同类型序列“应该”具有的震源特征,仍然只能采用震例统计的方式进行分析,而这又由于已研究样本有限使得结果欠缺统计显著性(Abercrombie,1995; Ide,Beroz,2001; Allman,Shearer,2009),加之中小地震应力降或视应力等震源参数随震级变化(Dysart et al,1988; Trifu,Radulian,1989; 吴忠良等,1999; 赵翠萍等,2011; 华卫等,2012; 周少辉,蒋海昆,2017),更是带来了诸多的不确定性。因而,本文备选特征未包含基于数字地震记录计算的这些震源或介质参数。
参考现有地震序列类型判定参数和方法,用于机器学习地震序列类型判定的备选特征见表2,主要依据参数来源细分为8类44个备选特征。
表2 机器学习序列类型判定备选特征列表
Tab.2 List of alternative features for judgement of the earthquake sequence types by machine learning
(1)主震相关参数(表2特征1～3)
余震活动强度与主震大小定性正相关,因而余震活动水平与主震大小直接关联(Båth,1965; Helmstetter,Sornette,2003; alohar,2014)。序列类型具有一定的区域特征(刁守中等,1995; 王华林等,1997; 郭大庆等,1998; 蒋海昆等,2006b),结合区域及发震构造特征的历史地震活动类比,可在一定程度提供序列类型判定的参考依据。因而,开展序列类型判定备选特征选择应考虑主震空间位置即经、纬度参数的影响。
(2)主震震源机制相关参数及相对于附近区域平均应力场的偏差(表2特征4～19)
地震序列类型与构造运动或主震破裂形式有一定关系(陈颙,1980; 秦保燕,刘武英,1992; Reasenberg,1999; 苏有锦等,1999; 蒋海昆等,2006b; 张国民等,2010),因而主震震源机制相关参数(表2特征4～11)被纳入作为机器学习的备选特征。考虑导致地震破裂的应力场特征,主震附近区域平均P轴方位角、倾角及其标准差(表2特征12～15),主震P轴方位角和倾角相对于区域平均结果的偏差及离散程度(表2特征16～19)也一并纳入作为机器学习的备选特征。此处的“平均结果”来源于主震附近区域以往地震相关参数的统计,“附近区域”是以主震为圆心、以R为半径的圆域,R与震级MW相关,可粗略地认为等同于主震破裂尺度(Wells,Coppersmith,1994):
式(1)右侧加10为考虑定位误差而人为增加的一个常量(单位:km)。震级标度MS与MW之间采用下式进行粗略转换(Giacomo et al,2015):
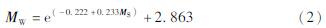
(3)主震附近区域历史地震序列类型相关参数(表2特征20～22)
基于与历史地震序列类型的定性类比,是当前最主要的序列类型判定手段之一(蒋海昆等,2015),表2第20～22行分别为主震附近半径为R的圆域范围内、震级MS≥x地震序列中,多震型、主余型及孤立型所占的比例。与主震震级相关的R由式(1)(2)计算得到,历史地震序列类型基础数据来源于当前正在实时运行并准实时更新的CAAFs系统基础数据(刘珠妹等,2019)。
(4)序列衰减相关参数(表2特征23～29)
序列衰减是余震活动的最主要特征,修改的大森公式n(t)=K(t+c)-p是对余震衰减的最经典描述,衰减系数p分布在0.6～2.5之间,均值为1.1(Utsu et al,1995; Freed,Lin,2001; Scholz,2002; Lyakhovsky et al,2005; 贾若,蒋海昆,2014)。p值与区域地壳介质状况有关(Creamer,Kisslinger,1993; Rabinowitz,Steinberg,1998; Jones,Craven,1990; 曲均浩等,2015),余震衰减还受控于应力状态(Narteau,2009)。在修改的大森公式基础上,刘正荣等(1979)、刘正荣和孔绍麟(1986)提出的 h值方法,在余震跟踪预测中发挥着重要作用。因而,本文为机器学习序列类型判定而构建的备选特征数据集中包含了大森公式相关参数的计算结果(表2特征23～29)。其中特征23为大森公式衰减系数p值; 特征24、25分别为指定时段基于修改的大森公式计算的完备震级以上的理论地震频次与 实际地震频次之差的绝对值及标准差,两者共同表征了修改的大森公式与实际地震频次变化的贴合程度; 特征26为指定时段单位时间折合震级的线性衰减速率(假定为线性衰减),特征27为折合震级线性衰减纵轴截距(ML),特征28、29分别为实际折合震级与线性衰减理论折合震级之差绝对值的平均值及标准差,三者间接表征了序列应变能释放时间衰减特征,以及理论预期相对于实际的偏差。
(5)G-R关系相关参数(表2特征30～35)
完整地震序列的震级-频度关系遵循G-R关系LogN=a-bM,比例系数b值介于0.6～1.1之间,与构造及背景应力状态有关(Utsu,2002)。G-R关系相关参数是机器学习地震预测研究中使用最为广泛的一类参数(王锦红,蒋海昆,2023)。表2特征30、31为MLE方法计算的G-R关系比例系数b值及标准差; 特征32、33为G-R关系比例系数a值及标准差(Gulia,Wiemer,2019); 特征34为基于G-R关系外推的最大余震震级,即依据b值截距方法(国家地震局科技监测司,1990; 刘正荣,1995; Shcherbakov et al,2013)估计的最大余震震级,这在当前最大余震震级预测中发挥着重要作用。已有研究显示,震后足够长时间之后,序列G-R关系外推最大余震震级逐渐趋近于真实的最大余震震级(苏有锦等,2014); 特征35为序列主震震级与G-R关系外推最大余震震级之差的绝对值。
(6)归一化能量熵(表2特征36)
归一化能量熵是描述地震序列能量分配均匀程度的一个统计量,反映了序列地震能量分配均匀程度随时间的变化(朱传镇,王琳瑛,1989; 王琳瑛,舒曦,1997)。余震序列性质判定单参数判据的统计研究显示,归一化能量熵具有相对较强的序列分类能力(蒋海昆等,2006a)。
(7)序列地震震级相关参数(表2特征37、38)
余震活动强度与主震大小定性正相关,早期一般认为主震与最大余震震级差ΔM是一个与主震震级无关的常数(平均约为1.2; Båth,1965)。进一步的研究显示,Båth定律并不严格适合所有余震序列,实际ΔM介于0～3之间,受震源机制、震源深度、序列类型、区域构造特征、断层之间相互作用等多种因素的影响(Kisslinger,Jones,1991; Helmstetter,Sornette,2003; 蒋海昆等,2006c,2015; 苏有锦等,2014; alohar,2014; Rodríguez-Pérez,Zúñiga,2016; Apostol,2021),这意味着同等强度主震的余震活动水平可以明显不同。在实际预测应用方面,Shcherbakov 等(2013)、Shcherbakov和Turcotte(2004)提出改进的Båth定律并引入推定最大余震震级对最大余震震级进行估算; 也有研究利用主震震级、余震分布尺度等参数之间的统计关系(蒋海昆等,2007c; 吕晓健等,2010)、震级差(刘蒲雄等,1996)等来对最大余震震级进行估计。基于以上研究,表2特征37、38分别为指定时段最大余震震级、序列主震与该最大余震震级差的绝对值。随震后时间的推移,特征37将趋近于序列最大余震,特征38会趋近于序列主震与序列最大余震震级差ΔM,而ΔM是序列标签的确定依据。
(8)序列地震频次相关参数(表2特征39～44)
已有研究显示,震后不同时段小震频次(王志东等,1982; 陈荣华等,1994)及应变释放(戴英华等,1990)特征一定程度上含有序列的分类信息。据此,表2特征39～41分别为震后指定时段ML≥x小震的累积频次、日均频次及相对于震后首日的归一化频次; 特征42～44分别为ML≥x小震的平均震级、平均震级标准差和折合震级,两者分别从小震频次和震级/应变释放的角度,反映指定时段余震活动的平均水平以及震级分布的离散程度。
根据前人提出的序列类型判定方法或参数,本文分8类列出44个备选特征,自特征23之后所有基于地震序列目录计算的参数中,指定时段可包含一系列震后不同的统计时段,特征20～22中x亦可取不同的震级下限,如此可得到多个组合备选特征,分别对应震后不同时段震中附近区域MS≥x地震样本中,多震型、主余型及孤立型所占的比例。同样,特征39～43中涉及的震级下限x,在保证数据基本完备的情况下也可取如ML3.0、ML3.5等多个数值。因而,以上述44个备选特征为基础,可以扩充出更多的机器学习备选特征。具体到本文,针对表1中所列902次MS≥5.0地震样本,以震后3天资料为例,计算表2所列44个参数,构建包含902个样本的机器学习样本集,每个样本包含44个备选特征。为简单起见,特征20～22仅考虑x=MS5.0的情形,即仅使用震中附近区域MS≥5.0地震多震型、主余型及孤立型所占的比例; 特征39～43中仅考虑x=ML3.0的情形。
44个备选特征中,特征23之后的序列参数计算要求一定的样本量,加之由于地震监测能力的差异,部分早期地震序列以及发生在青藏高原监测能力较低区域的地震,有些特征参数无法给出计算结果。由44个备选特征的数据缺失情况统计可见(图2),主震参数及主震附近区域历史地震相关参数的完备性相对较高,达98%; 涉及主震震源机制的相关参数,特征完备性接近70%; 涉及统计时段震级差或震级相关参数的特征,特征完备性接近60%; 修改的大森公式及G-R关系相关参数,特征完备性仅及32%。图2中108Lab2为序列标签。
图2 1970—2021年中国大陆及近邻MS≥5.0地震样本集特征缺失情况统计
Fig.2 Statistics of missing features in sample sets(MS≥5.0 earthquakes in Chinese mainland and the surrounding areas from 1970 to 2021)
机器学习算法一方面期望有尽可能多的特征用于序列分类,另一方面过高的特征维度又可能导致维度灾难的发生。对高维向量的降维处理,不仅能显著降低运算和存储开销,还有利于提高模型训练效率、提高分类效果(杨秋良等,2021)。特征降维的主要依据是特征重要性,主要有特征选择和特征抽取两大类算法,其中特征选择由于计算复杂度较低而被广泛采用(刘健,张维明,2008)。尽管诸如决策树、随机森林等机器学习算法本身就包含有相关的特征重要性评估(Breiman,2001; 赵志勇,2018),但有研究表明,机器学习模型默认的特征重要性更“偏好”连续型的类型变量,因为连续型的类型变量在树节点上更容易找到切分点,换言之更容易过拟合从而得到“好”的训练模型(Strobl et al,2007)。
本文不涉及具体的机器学习模型,仅从特征与分类标签之间相关性的角度,通过互信息方法展示和讨论上述备选特征对地震序列分类的重要性,为后续实际模型选择或训练提供参考。
在概率论和信息论中,互信息可用于表征随机变量之间的相互依赖或相关性程度,其基础是信息熵。信息熵是系统不确定性或复杂性的一种度量,早在20世纪40年代即已提出。假设随机变量X={x1,x2,…,xn}的概率分布为p(x),则X的信息熵定义为:
信息熵H(X)越大,信息量越大、系统越复杂。
若随机变量X和Y={y1,y2,…,yn}服从联合分布P(X,Y), Y的概率分布为p(y), 则X和Y的联合熵表示为(Cai et al,2018):
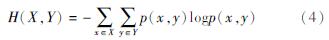
式中:H(X,Y)表示多个随机变量信息量的总和。
给定X变量的条件下,Y的不确定程度由条件熵H(X│Y)表示 https://blog.csdn.net/qq_40765537/article/details/114838485.:
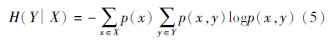
对于两个随机变量X和Y,互信息熵(简称互信息MI,Mutual Information)定义为(李欣倩等,2022)https://zhuanlan.zhihu.com/p/128091167.:
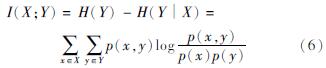
互信息值I(X; Y)用于衡量变量之间的依存关系,具体描述两组变量之间的信息共享及相互依赖程度(徐洪峰,孙振强,2019)。换言之,MI可用于确定X中所含Y的信息量,或在X已知时确定Y所减少的不确定性(李欣倩等,2022)。在机器学习特征工程中,常用MI来度量特征与标签之间的相关性强弱,即讨论特征对标签分类(categorical)的重要性。X和Y完全无关或相互独立时I(X; Y)=0; 反之I(X; Y)值越大,表示该特征与样本标签之间的相关性越强(周志华,2016)https://blog.csdn.net/weixin_46072771/article/details/106188753.。利用scikit-learn库 https://scikit-learn.org/stable/modules/generated/sklearn.feature_selection.mutual_info_classif.html.基于k最近邻居距离方法计算互信息值(Kraskov et al,2004; Ross,2014),最近邻居数取缺省值k=3。
作为地震序列类型判定的依据,特征与序列类型(标签)之间的相关性强弱,是衡量特征重要性的重要指标。图3给出特征与类型之间的互信息计算结果,从下往上为互信息值从大到小的排序,表征相关性由高到低,亦可理解为各特征对序列分类重要性由大到小的排序。由于序列资料的限制,许多样本有不同的特征缺失,图3删除了所有有特征缺失的样本,因而仅有285个样本参加计算。
图3a为未进行任何更进一步的数据预处理,是针对最原始数据的互信息计算结果。从图3a总的来看,各特征与序列类型之间相关性均不十分显著,其中特征38(主震与统计时段最大余震震级差的绝对值)与序列类型之间具有最大的关联性,互信息约为0.33; 震级相关参数(特征38、37、44)、能量熵(特征36)、历史地震序列类型(特征20)、主震震级及G-R关系外推震级相关参数(特征35)等特征互信息相对较高(MI>0.1)。除此之外,其它诸如小震频次和震级相关参数(特征43、42、28、41、25、40、39、24)、主震纬度(特征1)、G-R关系b值及相关参数(特征27、34、31、33)、震源机制相关参数(特征18、11、19、14)等特征也有较弱的分类贡献率,互信息大于0。
图3b为对不平衡样本数据进行了处理。不平衡样本是指样本数据集各类标签不均衡,例如主余型样本就远多于多震型样本。通常多数类与少数类样本比例接近100:1时可认为属于不平衡样本 https://www.cnblogs.com/kamekin/p/9824294.html.,不平衡样本对模型训练结果有一定影响。在样本总量受限的情况下,对不平衡数据集的处理主要从数据本身和算法两方面入手。由于本文不涉及具体的机器学习算法,因而主要从数据的角度进行不平衡数据处理。针对图3a数据,采用随机重采样算法 https://github.com/scikit-learn-contrib/imbalanced-learn.,从少数类样本中对特征进行随机采样,以组合构建新的(伪)样本,从而达到各分类样本数均衡的目的。不平衡数据处理之后的互信息计算结果如图3b所示。从不平衡数据处理前、后的结果对比来看(图3a、b之间的连线),除个别特征(如特征11、22、40、26、39)重要性排序有较大差异外,大多数特征的重要性排序及互信息值基本一致。这意味着,对删除特征缺失样本后的数据集,是否进行不平衡数据处理对特征分类重要性影响不大。
图3 基于互信息的机器学习特征重要性(删除特征缺失样本)
Fig.3 Sorts of feature importance based on mutual information (for data set deleting the samples with missing feature)
类似图3对含有缺失特征样本进行删除的数据处理方式,对大数据问题不会有明显影响,但对地震预测这一类小样本问题,会进一步加剧样本不足的矛盾。机器学习数据预处理算法中有许多缺失特征处理方式,图4为采用同类样本中位值对缺失特征进行补齐的结果。
具体做法是:对表2中每一个特征,首先分多震型、主余型、孤立型3类,计算该特征中位值,之后对该类样本中缺失该特征的样本,以该中位值进行补齐。例如对多震型样本的G-R关系b值(30 bVal),首先基于多震型样本中无b值缺失的样本,计算b值的中位值,进而对有b值缺失的多震型样本,用该中位值进行补齐,对主余型、孤立型样本做类似处理。如此处理的好处是,所有样本都可参与互信息计算。并且从初步结果来看,缺失特征补齐与否,对特征与类型之间的相关性有较大影响,主要体现在4个方面:
(1)缺失特征补齐之后绝大多数特征均显示与序列类型之间具有或多或少的相关性(图4),且各特征互信息值较图3所示的未进行缺失特征处理的结果有明显增大,例如特征38的互信息值就增大到0.49。
图4 基于互信息的机器学习特征重要性(以中位值补齐缺失特征)
Fig.4 Sorts of feature importance based on mutual information (for data set filling the missing feature by the median value)
(2)针对缺失特征补齐之后的样本数据,是否进行不平衡数据处理,对重要性较大特征的排序仍然影响不大。从图4具体来看,对序列分类具有较大贡献的特征的重要性排序始终比较稳定,关联性最好的特征(MI>0.2)在不平衡数据处理前、后完全一致,这些特征仍然以震级、频次相关参数为主(特征38、37、44、42、43、40、39); MI>0.1的特征相关性排序也基本一致,这些特征包括能量熵(36)、主震及G-R关系外推震级相关参数(35)、G-R关系和序列衰减相关参数(特征34、33、27、30); 此外主震破裂形式和P轴方位相关参数(特征11、15、10)、历史地震序列类型(特征21、22、23)等也有一定的序列分类能力,其MI>0.05。这种相对稳定的特征重要性排序,对后续序列类型判定机器学习模型训练非常重要。
(3)缺失特征补齐前后的特征重要性排序并不完全一致(图5),这意味着是否进行缺失特征补齐对特征重要性排序有影响。所幸的是,对序列分类重要性最大的前几个特征排序几乎完全一致,例如特征38、37、44、43、42、36、35等,而对序列类型判定真正起“驾辕”作用的,可能就是这些与序列类型相关性最强的、重要性排序比较稳定的特征。
图5 缺失特征处理方式对特征重要性排序的影响
Fig.5 Influence of the missing feature processing on feature importance sort
(4)图5红色水平条上侧与图3上部互信息等于或接近于0的区域相对应,这些特征未进行任何数据预处理之前对序列分类没有贡献。但由图5对比可见,这些先前对序列分类没有贡献的特征,在进行缺失值补齐处理之后,部分特征、尤其是序列衰减相关参数(特征23、29)、序列G-R关系相关参数(特征30、32)的互信息值排序明显提前,序列分类的贡献度明显提升; 而缺失值补齐处理前有一定序列分类能力的历史地震序列类型(特征20)、震源机制相关参数(特征18、19、14)等特征,其重要性排序在缺失值补齐之后明显降低。这意味着,恰当的数据处理方式在一定程度上会提高大多数特征的序列分类能力,但同时也可能导致部分特征的序列分类能力降低,具体如何取舍需视最终模型需求而定。
理论上总是希望特征之间彼此独立以拓展尽可能宽泛的信息来源,但实际上彼此完全独立的信息来源总是很少,特征的独立性假设往往难以达成(李欣倩等,2022)。但另一方面,机器学习中有一个重要的概念即特征间的信息交互(feature interaction)。已有研究显示,很多特征单独来看可能与标签无关,一旦组合在一起却与标签集明显相关(Jakulin,Bratko,2003)。信息交互在诸如信息推送等人工智能应用中已被广泛采用 https://zhuanlan.zhihu.com/p/384271606.。丰富特征表达、拓展可用特征数量的重要方式之一即添加原始数据的交互特征(interaction feature),例如针对线性模型不仅可以学习偏移,还可以学习斜率 https://blog.csdn.net/snail9610/article/details/105925305/.。由表2各特征参数物理含义可见,特征之间或多或少具有物理上的关联性,这从特征参数之间的树状关系(图6)亦可看出。由图6中虚线可将特征粗略划分为具有一定相关性的4个部分,自左至右第I部分是序列G-R关系及序列衰减关系相关参数,第II部分是主震及震中附近震源机制相关参数,第III部分是主震及震中附近历史地震序列类型相关参数,第IV部分是序列地震震级及频次相关参数。实际上,上述所有用于序列类型判定的备选特征,都来源于地震目录及震源机制,特征之间自然具有或多或少的相关性,但在特征组合之后仍显示出与序列标签更强的关联性。类似的特征组合方式,在机器学习地震预测中已有许多应用(Reyes et al,2013; Asencio-Cortes et al,2016,2018; Shodiq et al,2017,2018)。实际上,著名的G-R关系、修改的大森公式等都来源于地震目录,但它们又都提供了对地震序列震级-频度关系、地震序列衰减特征等的全新认识,某种程度上说,这就是信息交互的典型做法。
图6 特征参数关联性树状图 https://github.com/ResidentMario/missingno.
Fig.6 Tree diagram of the dependency of the feature parameters
基于1970—2021年中国大陆及边邻地区地震数据,参考以往研究和余震预测实践,以服务于震后序列类型判定为目的,构建基于地震观测数据的地震序列类型判定机器学习特征样本数据集。基于互信息方法,通过样本特征数据与标签之间的相关性,评估特征对序列分类的重要性,以利于构建适用于不同应用场景、具有较高预测准确
性及较强泛化能力的序列分类模型,得到以下主要认识:
(1)初步提出可用于机器学习地震序列类型判定的备选特征。参考现有地震序列类型判定参数和方法,初步提出44个可用于机器学习地震序列类型判定的备选特征,这些特征包括主震三要素相关参数、主震及附近区域震源机制相关参数、主震附近区域历史地震序列类型、序列衰减相关参数、序列G-R关系相关参数、序列能量相关参数、序列地震震级及频次相关参数等8类。以震后
3天观测数据为例,构建了包含902个样本、每个样本包含44个备选特征的机器学习样本集。根据地震序列类型设置样本“标签”,分为多震型、主余型、孤立型3类。基于对后续危险性的考虑,将前震型序列合并至多震型。902个样本中多震型、主余型、孤立型分别约占15.5%、59.8%和24.7%,其中主余型和孤立型合计为84.5%,与前人研究结果基本一致。
由于序列参数的计算要求一定的样本量,加之部分监测能力较低区域地震记录不完备,因而部分样本的部分特征参数(如G-R关系b值、序列衰减系数p值等)无法计算。总的来看,主震及主震附近区域历史地震相关参数完备性较高,约为98%,主震震源机制相关参数完备性接近70%,序列地震震级相关参数完备性接近60%,修改的大森公式及G-R关系等相关参数的完备性仅及32%。
(2)近60%的备选特征显示与序列类型之间具有一定的关联性。基于互信息方法分析特征与标签(序列分类)之间的相关性强弱,讨论各特征对序列分类的重要性。在删除缺失特征样本的情况下,有近60%的特征(26项)与序列类型之间互信息大于0,但相关性均不太强,最大互信息值仅为0.33。这些特征中,震级相关参数、能量相关参数、历史地震序列类型、主震震级及序列G-R关系外推震级相关参数等特征的互信息相对较高(MI>0.1),其它如小震频次相关参数、主震纬度、G-R关系b值及相关参数、震源机制相关参数等特征也有相对弱的序列分类能力。
(3)补齐缺失特征可明显提升特征的序列分类能力。缺失特征补齐的数据预处理方式,不但可显著增加可用的模型训练和检验样本量,更可以明显提升特征与序列分类之间的关联性。本文以中位值补齐样本缺失特征的情况下,大多数特征(42项,约占95%)显示出与序列类型之间具有或多或少的关联特性,且各特征的互信息值明显增大,最大达0.49。
(4)特征间之间的信息交互有利于提升特征的序列分类能力。信息交互是机器学习特征构建的重要手段。本文结果显示,即使实际资料中特征的独立性假设难以达成,但依据这些彼此并不完全独立的参数构建的特征,仍显示一定的特征重要性,即具有一定的序列分类能力。换言之,在机器学习数据处理过程中,即使已明确知道彼此或多或少相关的特征,也不宜一开始即完全删除。特征选择是一个复杂的过程,尽管为节省内存和运算开支,特征选取应在保留尽可能多分类信息的前提下仅保留尽可能少的特征(姜文煊等,2021),但特征之间的信息交互对特征与标签之间关联性的提升作用亦须重视,在当前机器学习仍属“黑箱”操作的前提下,最终的特征选择应以模型预测效能的综合评价结果为准。
(5)震级相关参数对序列类型判定的特征重要性相对较大。宏观来看,震级相关参数、能量相关参数、G-R关系和序列衰减相关参数、历史地震序列类型、震源机制相关参数等的特征重要性排序相对靠前,对序列分类有贡献,其中震级相关参数特征与标签之间的互信息明显较大且排序稳定。本文结果还显示一些有趣的现象,例如主震空间位置尤其是主震纬度,以及主震震源机制相对于区域应力场的偏差等参数,对序列分类似乎也具有一定的贡献率,前者实际上与此前序列类型具有一定区域特征这一认识(王华林等,1997; 蒋海昆等,2006b)相契合,后者此前研究未见提及,但这也提示我们,通过大数据或人工智能所揭示的现象或特征,有可能为地震序列分类物理本质的探寻提供思路或指引。
(6)需重点关注机器学习算法的小尺度样本数据适用性问题。需要指出的是,机器学习算法着重于大样本数据共性特征的提取和学习,其能够发挥作用的基础是大数据。事实上已有研究关注到中尺度数据集(～10K尺度样本数)的算法适用性问题(Grinsztajn et al,2022),但与此相比,用于地震预测的数据或学习样本可谓十分匮乏,加之如本文所展示的那样,不同的数据处理方式对结果还有复杂的影响,因而尽管基于机器学习的地震预测已经展现出一定的应用前景(Al Banna et al,2020; Mignan,Broccardo,2020; 王锦红,蒋海昆,2023),但就余震预测而言,机器学习是否比现有“经验+统计”的传统预测方法有更好的预测效率,有待进一步的深入探讨,各种机器学习算法对小尺度样本数据(K尺度样本数)的模型适应性问题即是当前面临的重要问题之一。
