基金项目:科技部国家重点实验室基金(SLDRCE19-B-24).
第一作者简介:刘威(1976-),副教授,博士生导师,工学博士,主要从事生命线工程防灾和韧性评价方面研究.E-mail:liuw@tongji.edu.cn.
(1.同济大学 土木工程防灾国家重点实验室,上海 200092; 2.同济大学 土木工程学院,上海 200092)
(1.State Key Laboratory of Disaster Reduction in Civil Engineering,Tongji University,Shanghai 200092,China)(2.College of Civil Engineering,Tongji University,Shanghai 200092,China)
the water distribution network; seismic resilience; the resilience index; the recovery strategy; importance
DOI: 10.20015/j.cnki.ISSN1000-0666.2023.0017
生命线工程系统是维系现代城市功能和区域经济功能的基础性工程设施系统(李杰,2005),供水管网作为其中的重要组成部分,对城市正常运转起着重要的作用。截至2020年,我国城市供水管道总长度已达到100.69万km,相比于2015年增长了41.78%(中华人民共和国住房和城乡建设部,2015,2020)。然而,与供水管网快速发展不相适应的是我国供水管网的抗震性能依然较为薄弱。1976年河北唐山7.8级地震后,市区220 km的供水管网严重受损,水源井、原水管道和二级泵站均发生破坏,给震后供水造成了巨大的困难(侯忠良,1990; 谢志平,谢宇,1996)。2008年汶川MS8.0地震后,四川省受损水厂共156个,受损管道总长度47 643 km(李宏男等,2008)。在靠近震中的都江堰市,供水管网的修复耗时长达一个半月(同济大学土木工程防灾国家重点实验室,2008)。2013年四川芦山MS7.0地震后,芦山县城镇受损管道长度达73 km,乡镇受损管道长度达800 km,受损情况较汶川地震时更为严重(叶飞等,2013)。由此可见,我国供水管网在强烈地震下往往受损严重,除管道外,供水管网中的其它构筑物也会发生破坏。供水管网破坏后的恢复会持续较长一段时间,这也影响震后恢复的整体进度。因此,供水管网抵御地震灾害影响并快速恢复的能力显得至关重要。这种能力的提升符合我国目前防灾减灾工作的需求,与当前在工程领域广泛应用的“韧性”的内涵相契合(毕熙荣等,2020)。
韧性这一概念最早起源于心理学或生态学领域(Manyena,2006)。Bruneau等(2003)最早将其引入到抗震研究领域中,并提出韧性是指减轻灾害、控制灾害发生时的影响、以尽量减少社会干扰和减轻未来地震影响的方式开展恢复活动的能力。目前,针对供排水系统、电力系统、燃气系统、交通系统和通讯系统等生命线工程系统,学者们开展了韧性分析的研究(Liu,Song,2020; 钟江荣,张令心,2020),对一些城市进行了不同角度下的韧性研究(王慧彦等,2021; 费智涛等,2020)。对于供水系统,常见的韧性分析方法包括能量法(Todini,2000; Creaco et al,2014)、图论法(Yazdani et al,2011; Herrera et al,2016)和恢复模拟法(Zhuang et al,2013; Cimellaro et al,2016)。其中恢复模拟法通过流分析仿真计算管网中的流量、水压等物理量,效果优于前2种方法。Liu等(2020)利用恢复模拟法对供水管网进行了抗震韧性分析,以绵竹管网作为案例,比较了静态重要度、基于损伤和基于距离3种策略的效果,发现均衡考虑计算效率与效果,静态重要度策略是一种很好的策略。但是该研究所建立的模型只考虑了管道,未考虑管网中其它常见组件。
动态重要度策略也被众多学者用于生命线工程系统恢复顺序的研究中,如Nurre等(2012)将待修复的组件分为多个修复组,通过多轮计算重要度确定纽约市曼哈顿下城电力系统的修复组顺序; Xu等(2019)进一步确定了多个修复组中组件的修复顺序,对谢尔比县电力系统震后恢复进行了案例分析; Gonzlez等(2016)利用该思路对谢尔比县关联基础设施系统恢复进行了分析; Han等(2020)采用动态成本效益法对供水系统的震后恢复进行了分析,但只考虑了管道和水源点,并未将泵站等组件纳入研究。鉴于此,本文给出了一套基于恢复模拟法的供水系统抗震韧性分析框架,包括管道、水厂、泵站和水塔在内的各类组件,使用动态重要度的策略给出供水系统的组件震后恢复次序,并利用1个中型管网案例对上述方法进行了说明。
为了进行供水管网抗震韧性分析,首先就需要对供水管网抗震韧性指标进行定义。Liu等(2020)从用户需求角度出发,建立了基于需求的供水管网抗震韧性指标。对于供水管网从遭遇地震到逐渐恢复完毕的整个过程,该指标 以用户节点满意度的加权平均值定义管网整体满意度并作为管网的性能指标,利用管网性能与时间轴围合区域的面积值与控制时间之比作为抗震韧性指标。
地震发生后,供水管网的性能变化如图1所示。t0时刻,地震发生,管网性能从正常运行阶段时性能下降为震后初始性能。t1时刻,过渡阶段结束,震后修复工作开始,管网性能逐渐提升。整个修复阶段持续到t2时刻修复结束为止,此时管网性能恢复到正常水平。针对上述过程,本文做出了如下假设:①在管网正常运行阶段,可能会由于用水高峰等原因,系统满意度发生波动,但波动不会太大,本文简化在此阶段管网性能为1。②在地震发生时,假设从破坏发生到管网性能下降至震后初始性能这一过程是瞬时发生的。③由于过渡阶段时间相比于总体时间较短,在分析时可忽略这一阶段。④在修复过程中出现的各种情况可能使得管网最终性能小于1,例如管网中部分组件因特殊情况无法恢复。为了简化,本文认为管网最终将恢复原状,性能可恢复到1。
管网性能以管网整体满意度SDI定义,表达式为:
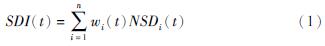
式中:SDI(t)表示t时刻的管网整体满意度; wi(t)表示用户节点i在t时刻的权重值; NSDi(t)表示用户节点i在t时刻的用户节点满意度; n为用户节点总数。管网整体满意度由所有用户节点满意度的加权平均值得出。
从用户需求的角度出发,将用户节点满意度定义为用户节点水压的满足程度,表达式为:
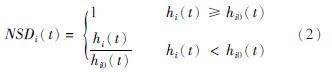
式中:hi0(t)为用户节点i在t时刻的需求水压; hi(t)为用户节点i在t时刻的实际水压。
根据上述定义,可以认为当管网性能处于正常水平时,管网整体满意度SDI=1,而当管网完全受损时,SDI=0。为了使抗震韧性指标能够反映管网性能从地震开始到修复结束全过程的变化趋势,供水管网抗震韧性指标RI定义为:
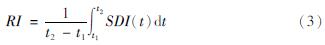
式中:t2-t1为控制时间,控制时间可以结合具体情况进行选取,但是在进行抗震韧性指标的横向对比时,控制时间需要统一。结合式(1)~(3)与图1可以发现,RI取值在0~1,且数值越大,说明系统韧性越好。
供水管网的水力分析方法有流量法和水压法两种(严煦世,赵洪宾,1986),分别以流量和水压作为未知量进行求解。本文选取水压法对供水管网进行稳态流分析。在管道未受损的情况下,管网中各个节点流入与流出的流量应当恒定相等。与常规情况相比,考虑震后管网渗漏的节点平衡方程的唯一区别就是引入了渗漏流量,此时,管网各节点流量守恒方程表达式如下:
AQP+QN+QL=0 (4)
式中:QP为管道或泵站流量向量; QN为节点流量向量,在本文为各个节点用水量; QL为节点渗漏流量向量; A为表达管网拓扑结构的管网邻接矩阵。
对于震后发生渗漏的管道,常见的处理方式是将渗漏流量平均分配到受损管道的两端节点上(Liu et al,2016)。管道渗漏流量qL的计算公式为:

式中:α为渗漏系数; μ为孔口流量系数; HL为渗漏处的水压; AL为渗漏面积; g为重力加速度。渗漏面积计算公式为:
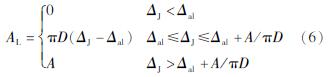
式中:D为管道直径; A为管道横截面积; ΔJ为接头变形; Δal为接头变形限值,参数的计算方法可参考Liu等(2016)研究,这里不再赘述。
地震后,管网中各类组件会发生不同程度的破坏,从而影响管网功能。为真实模拟震后管网功能状态,应考虑不同组件的破坏与管网功能的关系。本文主要考虑管道、泵站、水塔、水厂4种组件,下面将对其水力模型进行介绍。
管道水力模型可以利用管道中输送的水流流量与两端压力差之间的物理关系来给出。本文采用水力分析中广泛使用的物理关系式Hazen-Williams方程,表达式为:
QP=0.278CD2.63ΔE0.54L-0.54 (7)
式中:C为海曾威廉系数,其取值与管材及管道使用状态相关,具体取值可参考赵洪宾(2003)研究; D为管道直径; L为管道长度; ΔE为管道两端压力差。
将式(7)代入式(4),即可将管道水力分析模型引入节点守恒方程中。当管道发生渗漏时,根据式(5)计算渗漏流量并平均分配到受损管道两端节点即可。
泵站可以看作是一种特殊的管道,水流只能经由单一方向通过,并且在通过后水压会有一定程度的增加。泵站的水力模型表达式为:
QP=(h0-ΔE)0.5/B (8)
式中:h0、B为泵的性能参数; ΔE为泵站两端压力差。由于泵站最大输出功率恒定,因此当两端压力差越大时,通过泵站的流量越小; B决定了通过泵站的流量; h0决定了泵站理论上所能够产生的最大压力差。将式(8)代入式(4),即可将泵站水力分析模型引入节点守恒方程中。当泵站损毁时,水流无法从泵站通过。
水塔在供水管网中起到调节用水量的作用。当用水量较低时,水塔将储存多余的水,在用水高峰期作为补充。因此,模型中同时考虑了排水和充水模式。①在排水模式下,水塔被视为具有恒定压力的水源点,视同水厂。②在充水模式下,水塔被视为用户节点。一般来说,当白天用水量较大时,水塔处于排水模式; 夜间用水量较小时,处于充水模式。当水塔没有损坏时,判断水塔的实际压力是否满足充水模式下的需求水压。如果不满足需求水压,则认为水塔在排水模式下无法工作; 如果满足需求水压,则认为水塔在排水模式下正常工作。最后,分别计算排水和充水模式的管网满意度后,将平均值作为当前时刻的管网满意度。
在供水管网中,水厂被视为压力恒定的源点,能够在恒定压力下向供水管网供水。当水厂损毁时,认为该节点无法向供水管网中供水。
组件损伤程度直接关系到震后恢复过程,对管网韧性影响很大,因此,给出科学的组件易损性模型是韧性评价的关键一步。本文详细介绍4个组件的易损性模型。
对于管道,常常以震害率形式给出其易损性模型,并且假设管道发生一定破坏数目的概率服从泊松分布。本文采用Liu等(2020)所提出的一种基于可靠性的方法计算管道震害率。该方法首先计算管道可靠度,并通过建立管道震害率与管道可靠度的关系求解管道震害率。
供水管道常见的破坏准则为接口处变形SJ大于接口渗漏变形限值RJ。因此,求解管道可靠度的第一步就是求解管道的接口可靠度。韩阳(2002)已给出RJ服从正态分布。SJ可依据《室外给水排水和煤气热力工程抗震设计规范》(TJ 32—78)计算。Liu等(2020)认为接口处变形也服从正态分布,即可求解接口可靠度。由于一根管道会存在多个接口,为了求解管道可靠度,Liu等(2020)对此问题进行了简化处理:首先将这些接口分成一系列集合Λi(i =1,2,…,ns),其中ns是集合数; 同一组Λi中的接头具有相同的特征,如场地、生产商、环境、材料、类型和直径,因此具有很强的失效相关性。对于这些接头,认为其失效完全相关是合适的,集合Λi的可靠性Re{Λi}等于其中的最小接头可靠度,对于不同的集合,接头具有弱相关性,因此采用了失效独立假设。综上,管道可靠度Rep计算公式为:

为了将式(9)得到的管道可靠度转化为管道的震害率,就需要建立二者的关系式。Rep为管道发生0处破坏的概率,因此可以给出Rep与管道震害率RR的关系为:
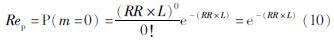
式中:L为管道长度,管道震害率RR=-ln(Rep/L)。当进行确定性分析时,将管道长度乘以震害率即可得到管道破坏数目。
水厂、泵站和水塔属于构筑物,震后破坏机理类似,因此可以用一类易损性模型来描述,这些组件在地震中遭受的损坏可用Hazus地震风险评估模型确定(FEMA,2012)将其状态分为5种类型,即未受损、轻微受损、中等受损、严重受损和完全受损,其划分主要根据分析对象各主要部件的损坏状态来确定。当部件功能的一部分损坏到定义要求的程度时,则认为该分析对象已损坏到相应的程度。这些组件不同状态的含义本文不再赘述,详见相关文献。对于不同类型的构件,相应类型的损伤概率服从以地面峰值加速度(PGA)为自变量的对数正态分布函数,表示为:

式中:P(PGA)为不同PGA下结构发生相应程度及以上损伤的概率; Φ(?)为标准正态函数; 两个参数λ、β由不同的结构类型以及对应损伤状态所决定,可查询Hazus模型获得。
本文认为组件只有2种状态,即正常状态和失效状态。对于遭受中等或更严重损坏的组件,认为其完全失去功能。对于轻微损坏或未损坏的组件,认为其功能正常。当进行确定性分析时,利用式(11)计算某组件发生中等破坏以上程度损伤的概率,若≥50%,则认为该组件在该情况下受损失效。对于受损结构的修复时间,Hazus模型以正态分布的形式给出供水管网中组件的恢复时间模型,具体参数可从FEMA(2012)中获得。当进行确定性分析时,取正态分布均值作为组件的恢复时间。
供水管网韧性提升的策略为:一是提升供水管网的抗震性能,包括对管网内各类组件加固、设置冗余等措施; 二是提升供水管网的震后恢复能力,包括合理安排组件恢复顺序、增加震后修复力量等措施。上述两种措施分别从震前和震后两个阶段提升供水管网的抗震韧性。合理安排组件恢复顺序不需要额外的人力物力投入,因此本文提出了基于重要度的策略用以指导供水管网的震后恢复,对组件恢复的合理顺序进行探讨。
地震后,组件恢复顺序对供水管网性能的恢复速度有着重要影响。对于不同的组件,其恢复后对供水管网性能改善的影响是不同的。因此,本文采用组件重要度理论来研究其影响。对于组件j,定义其静态重要度指标Is,j为:

式中:Tj为组件j修复所需时间; SDIj为组件修复后管网满意度指标; SDI0为管网震后初始满意度。组件的静态重要度越高,则其修复带来的单位时间内管网的性能提升便越高,应当予以优先修复。
之所以称其为静态重要度,主要是由于该指标基于管网损毁后的初始状态为依据进行计算,然而管网中部分组件修复后可能会使得管网性能发生变化,进而影响后续其它组件的重要度。因此,可以定义动态重要度指标Id,j(t)为:
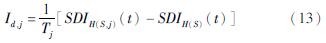
式中:SDIH(S)(t)为t时刻已修复集合S的供水管网的满意度指标; SDIH(S,j)(t)为在此基础上进一步修复组件j的管网满意度指标; Tj为组件j的修复时间。式(13)为t时刻时,s个组件所组成的集合S已经修复完毕后,未修复的组件j对应动态重要度指标的计算方法。
对于存在n个受损组件的供水管网,利用静态重要度进行分析时,需要进行n次计算; 而在利用动态重要度时,需要进行n轮计算,总计算次数为n+(n-1)+…+1=n(n+1)/2次。动态重要度虽然计算次数显著增加,但是对于考虑多种组件的供水管网而言,单纯的静态重要度指标难以反映管网性能的实时变化,不一定能够给出较好的震后恢复策略,当管网规模在一定范围内时,采用动态重要度策略有着显著的优势。
综上所述,对供水管网进行抗震韧性分析主要可以分为5个步骤:①供水管网初始化。确定各种供水管网参数,建立供水管网模型。②利用组件易损性模型判断组件受损状态。根据供水管网遭受的地震作用,使用供水管网组件的易损性模型,获得各组件的震后状态。③计算震后管网初始满意度。利用震后供水管网水力分析模型计算初始受损管网满意度。④确定受损组件的恢复顺序。使用基于重要度的恢复策略来确定受损组件的恢复顺序。⑤管网性能曲线和抗震韧性指标计算。使用基于需求的供水管网抗震韧性指标和水力分析模型,结合步骤④中确定的恢复顺序,逐天计算管网满意度,获得管网性能曲线和抗震韧性指标。通过以上5个步骤,完成了供水管网的一次地震韧性分析。
以一中型管网为例,使用本文方法对其进行抗震韧性分析。该中型管网包括了17个用户节点、25根管道、2座水厂、2座泵站和2座水塔,如图2所示。假定该管网遭受烈度为Ⅸ度(0.40 g)的地震作用。各用户节点需求水压值为10 m。各节点处于统一高度,相对高程均为0。所有管道所采用的管材均为钢筋混凝土管,各管道的管长与管径见表1,表中编号12、18的管道为泵站,无管长管径信息,在建模时被处理为一种特殊的管道。水塔日间输出水压均为20 m,夜间需求水压均为10 m,水厂对外输出水压均为20 m。各用户节点日夜需水量比 为2.5:1。2座泵站的扬程曲线参数h0=10、B=250。
水厂、泵站和水塔等构筑物的易损性模型参数取值及在Ⅸ度烈度下发生中等及以上破坏的概率见表2。由表可见,上述3类组件在该情况下发生中等以上破坏的概率均超过50%。本文在进行确定性分析时,认为上述组件在震后均受损。
根据Hazus模型,管道接口、水厂、泵站和水塔受损后修复时间服从正态分布。本文在进行确定性分析时,取其均值作为修复时间,认为管道接口的修复时间为6 h,水厂修复时间为2 d,水塔和泵站修复时间为3 d。进行韧性分析时,控制时间取值为50 d。供水管网的震后恢复一般由供水公司组织专业队伍进行,包括对不同破坏组件的维修,因此本文假设专业修复队伍能够对各类组件进行维修,不区分修复队伍的类型,并通过队伍数量对修复能力进行描述。针对该管网,维修队伍数量为1队。
表2 组件易损性模型参数取值及破坏概率
Tab.2 Parameters of fragility models for components and their failure probabilities
利用动态重要度策略,对上述情况进行分析,恢复次序及分析结果见表3,其中供水管网抗震韧性指标为0.678 9,修复耗时33 d。
为说明动态重要度策略的效果,本文利用了静态重要度策略和2种经验策略进行对比分析。由于案例中管网所有组件均损坏,对初始管网进行分析时只有修复2座水厂才会对管网性能有提升,其他组件的重要度均为0,无法进行排序,因此首先修复2座水厂,在此基础上再进行静态重要度分析,这是本文所采用的静态重要度策略。2种经验策略的总体思路都是从水源点出发,按照由近及远的原则逐个对组件进行修复,区别在于经验策略1严格按照距离进行修复,而经验策略2在水厂修复完毕后,优先修复2座泵站。根据上述策略,对于该管网中组件的具体修复次序见表3。
表3 不同策略的修复次序及抗震性能对比
Tab.3 Comparison of repair sequence and seismic performance according to different strategies
对比4种策略的抗震韧性指标与修复耗时(表3),可以发现中型管网在遭遇相同的地震情况下,由于采用了不同的恢复策略,其抗震韧性指标与恢复耗时发生了变化。其中采用动态重要度策略后,供水管网的抗震韧性指标显著高于其它3种经验策略的情况,修复耗时也略短,这说明了动态重要度策略的有效性。
4种策略下供水管网性能恢复曲线如图3所示。从图中可以发现,采取动态重要度策略后,供水管网性能恢复曲线在除了对2座水厂进行修复的时间段内,其实时性能均高于2种经验策略; 除修复水厂和前3根管道阶段,其实时性能高于静态重要度策略,并且性能恢复到1的时间也更早。在实际的震后修复中,这意味着供水管网能够更早更好地服务更多的用户节点,并且提前恢复正常运转。4种策略下的抗震韧性指标由大到小排序依次为动态重要度、静态重要度策略、经验策略1、经验策略2,其中效果最好的动态重要度策略的抗震韧性指标高于效果最差的经验策略2的抗震韧性指标16.47%。动态重要度策略下管网恢复耗时短于两种经验策略6.06%,短于静态重要度策略9.09%。静态重要度策略在考虑多种组件的管网中效果不一定很好,这是由于这些组件的功能状态受管网完好程度影响或会对管网整体性能产生较大影响。与提高管网中组件抗震性能等提高管网地震抵抗力的策略不同,通过优化供水管网的震后恢复顺序这一策略不需要对管网进行额外的投资,但可获得较为显著的效果。
图3 不同策略下供水管网性能恢复曲线
Fig.3 Curves of the performance recovery of the water distribution network corresponding to different strategies
从表3可以看出,观察动态重要度策略首先被修复的是2座水厂,它们是供水管网中的水源点,其优先级最高。泵站的修复优先级并非较高,这是因为在管网整体渗漏较为严重的情况下,水流经由管网从水厂流到泵站时,流量和压力都已经较小,泵站即使恢复也难以发挥作用,甚至由于其提高了部分节点的水压,导致管网渗漏量进一步增大,例如静态重要度策略中,在泵站1后,系统性能出现了小幅的下降。水塔的修复优先级也相对较低,这是由于水塔需要在用水低峰期先蓄水才能在用水高峰期向管网中供水,因此在管网整体破坏较为严重的情况下,水塔即使结构恢复正常,也会由于无法正常蓄水而不能正常使用并发挥功能。泵站和水塔这2类组件正常发挥功能都需要管网的破坏程度不能过于严重,因此在修复时的优先级并非较高,这也是经验策略1效果好于经验策略2的原因所在。除了上述3类组件外,观察管道的修复顺序可以发现,优先修复的管道主要是较为靠近水厂但并非与水厂直接相连的管道,如管道26、16、20、14、17、23等。随着修复工作的进行,逐渐修复距离水厂更远的管道,如13、10、6、8、3、9等管道。最终进行修复的管道大多都为紧邻水厂的管道,如24、19、22、27等管道。当管网遭受地震灾害后,管道发生多处渗漏,需要优先修复比较靠近水厂的管道使得水厂中流出的水流可以在压力与流量损失较小的情况下到达周边的用户节点,因此管道总体的修复的大原则是由近及远修复管道,但是并非是严格的按照距离修复。对于最靠近水厂的管道,由于其长度有限,因而水流流经后压力下降相对较小,且周边用户节点由于靠近水厂,节点满意度相对较高,提升幅度有限,因此其恢复次序较为靠后。
本文建立了一种供水管网抗震韧性分析框架并提出了基于重要度的恢复策略,以一中型管网为案例,对其供水管网的抗震韧性进行确定性分析,并利用动态重要度理论对供水管网的震后修复给出了建议,所得主要结论如下:
(1)动态重要度策略可以显著地提高供水管网抗震韧性指标,并缩短修复耗时。相比于效果最差的经验策略2,动态重要度策略将供水管网抗震韧性指标提高了16.47%; 修复耗时方面,比2种经验策略缩短了6.06%,比静态重要度策略缩短了9.09%。
(2)静态重要度策略在给出考虑多种组件的管网震后恢复次序时效果不一定较为理想,在应用时应当根据实际管网情况进行评估与策略的选取。
(3)从观察动态重要度策略给出的震后修复顺序可以发现,最优先修复的组件为水厂,泵站和水塔的恢复优先级不是很高。管道的恢复顺序大体遵循距离水源点由近及远的顺序,但是最为靠近水厂的管道修复优先级大多都很低。
(4)对比4种策略与动态重要度策略得到的供水管网性能恢复曲线,可以发现除最开始阶段外,动态重要度策略的供水管网震后实时性能均高于同时期的静态重要度和经验策略的性能。更高的抗震韧性指标不仅仅代表了更快完成修复,也体现了在修复过程中有着相对较高的性能,这对于震后恢复与抢险救灾工作的保障有着重要的意义。