(School of Naval Architecture,Ocean & Civil Engineering,Shanghai Jiao Tong University,Shanghai 200240,China)
the traffic system; seismic resilience; connectivity; the Dynamic Bayesian Network; Qingdao City
DOI: 10.20015/j.cnki.ISSN1000-0666.2023.0016
自然灾害难以预测且破坏性强,常导致巨大的损失。对于高度集成化的系统来说,过高的冗余资源成本是系统灾前预防的一大经济性难题。因此,灾后的缓解与恢复是应对这类灾害事件合理且经济的策略。基于此,韧性作为系统抵抗干扰、恢复原有功能/性能能力的表征,受到了交通系统防灾减灾领域学者的关注(Kim et al,2019)。
可靠性(Michael,2013; Chen et al,1999; Al-Deek,Emam,2006)、鲁棒性(Zhang et al,2013; Sakakibara et al,2004)和脆弱性(Katja,2002; Jenelius,Mattsson,2015)是交通系统防灾减灾的研究热点。可靠性反映了系统在无干扰事件下保持正常运作的能力; 鲁棒性反映了系统在干扰事件下保持正常运作的能力; 脆弱性反映了系统在干扰事件下无法保持正常运作的属性。可靠性与鲁棒性的区别在于系统有无受到干扰事件影响,而鲁棒性与脆弱性可以视为一种互补的概念。以上3种属性互有差异,但都关注系统的灾前预防阶段,缺少对系统灾后恢复阶段的考虑。而韧性是系统抵抗灾害事件干扰、恢复功能的能力,涉及自灾害发生至系统性能恢复的全过程。
目前,交通系统韧性研究主要集中在提出韧性指标并构建韧性量化评价模型。针对研究的对象与范围,韧性评价分为宏观和中微观两类。宏观评价主要考虑系统各种与韧性相关的属性与能力,如鲁棒性、适应性、维修性、可负担性等,关注系统韧性的解构,如Tang 等(2020)将鲁棒性、适应性、维修性和可负担性指标从两级(Tang et al,2019)改进为三级; 中微观评价主要研究灾后性能变化与韧性的联系,灾后网络性能包含如Wu等(2021)采用的交通出行时间和事故数、吕彪等(2020)采用的网络效率、Li和Zhou(2020)采用的路网可达性等。相比之下,宏观评价涉及的性能一般较多,但其与系统韧性的联系难以量化,无法精确评价系统韧性,适用于宏观战略规划; 中微观评价以可量化的性能指标直观地反映系统的韧性,适用于韧性具体策略的研究。
贝叶斯网络方法作为概率理论和图论相结合的产物,因其具有可直观表达变量间的关系、不确定性应对等能力,成为系统韧性研究中应用较多的图论研究方法(Kameshwar et al,2019; Mihunov,Lam,2020; Johansen,Tien,2018)。贝叶斯网络具有概率更新的能力,使用者可以将实时观测数据作为目标变量的证据,更新变量的概率值,进而实现整个网络的概率更新。然而,贝叶斯网络概率更新的能力是基于观测数据的支持,其能够更新目标变量的观测值变化,但并不能表征变量随时间变化的机理。作为贝叶斯网络的扩展,动态贝叶斯网络的优势就在于其直观表达变量时变特征的能力,增加了时间维度,以跨时间片变量间的条件概率表征变量随时间的变化。
基于韧性的内涵,目前已有许多学者考虑到韧性的时间属性,并开展了系统动态韧性的研究,如多模式公交网络(Liu et al,2022a,b)、城市交通网络(Liu et al,2022a,b; 宣功奉等,2022)等。动态贝叶斯网络符合韧性的内涵,具有研究系统动态韧性的潜力。目前,基于动态贝叶斯网络的道路交通系统韧性研究尚处于起步阶段,Kammouh等(2020)采用了宏观指标量化韧性,模型中各宏观指标间的关系以及时变特征基于专家观点,模型构建的主观性较强。基于此,本文采用中微观的、动态的指标,即交通系统抗震性能之一的连通性随时间的变化的性能曲线,应用韧性函数量化系统韧性,提出基于动态贝叶斯网络的道路交通系统抗震韧性评价模型,旨在探索动态贝叶斯网络进行系统韧性全过程分析的具体应用。
韧性函数是量化系统韧性的常用模型,其以系统性能随时间变化的曲线为基础。一般来说,一次干扰事件发生后,系统性能会经历4个阶段,即灾前阶段、抵抗/破坏阶段、恢复阶段和恢复后阶段。在整个过程中,系统的状态会经历初始稳定状态—干扰状态—恢复后稳定状态的过渡。Henry等(2012)给出了普遍的系统受干扰事件影响的性能曲线,如图1所示。
图1 干扰事件下的系统性能变化曲线
Fig.1 System performance curve in one disrupted event
在干扰事件发生前,即图1中的[t0,te]时间段,系统正常运行,处于初始稳定状态,系统正常运行水平体现了系统的可靠性; te时刻,干扰事件发生,系统受干扰事件的影响,至td时刻影响结束,系统性能此时降至最低水平,但由于自身具有一定的抗灾能力因而并未完全丧失性能,体现了系统的鲁棒性; [td,ts]时间段表示在恢复策略实施之前,系统性能保持灾后水平一段时间,时间段的长短取决于恢复策略响应的速度; ts时刻,恢复策略开始实施,系统性能逐渐上升,至tf时刻达到新的稳定水平,[ts,tf]时间段的长短取决于恢复速率,系统性能恢复至新的稳定水平体现了系统的恢复性; tf时刻开始,系统以恢复后新的稳定状态运行,新的稳定状态下系统性能可能低于、等于或高于初始稳定状态水平,一般取系统达到95%或100%初始稳定状态水平的时刻作为系统恢复结束的时间节点。
[te,tf]时间段系统性能曲线表达了系统自干扰事件发生起,抵抗干扰事件造成的负面影响,并逐渐恢复至原有或新稳定水平时性能随时间变化的特征。该时间段的性能曲线即为系统韧性量化的基础,应用韧性函数即可计算系统t时刻的韧性。韧性函数表示为系统性能曲线与横轴所围面积和系统正常运行时性能与横轴所围面积之比,表达式为:
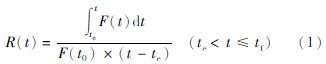
式中:R(t)为t时刻系统的韧性; F(t)为t时刻系统的性能; F(t0)为干扰事件发生前系统正常运行时的性能; te为干扰事件发生的起始时刻; tf为系统恢复95%或100%初始稳定状态水平的时刻。
在地震发生后,一个区域路网节点可以按照不同的功能划分为3类:救援要害部门、人口密集区和区域对外出入口(张洁,2013),如图2所示。在地震灾害发生后,受灾区域的道路交通系统承担的任务主要包括应急救援、物资运输和医疗救护(张洁,2013),如图3所示。应急救援
图2 地震灾害下路网节点的功能划分
Fig.2 Function division of road network nodes in an earthquake disaster
图3 道路交通系统不同抗震功能下源/汇点的组成
Fig.3 Composition of source and sink points corresponding to different seismic functions of the traffic system
指消防、公安单位对社区、商业人口密集区的救援,该系统以消防、公安单位为源点,人口密集区为汇点; 物资运输指将外来应急救援物资从区域对外出入口送达各避灾疏散场所,该系统以区域对外出入口为源点,避灾疏散场所为汇点; 医疗救护指将人口密集区受灾人员送达医院治疗,该系统以人口密集区为源点,医院为汇点。
应急救援、物资运输和医疗救护系统作为抗震功能的子系统,当3个功能均有效时,道路交通系统的抗震功能被认为是有效的。因此,子系统的连通性共同决定了道路交通系统的连通性,或者说系统抗震功能的有效性。
从图3可以看出,道路交通系统的连通性与3个抗震功能系统的连通性有关,抗震功能系统的连通性由所含源点/汇点(O点/D点)的连通性有关,O点/D点与相应OD对有关。在区域路网中,OD对的连通性与相应的路径有关,路径与路段有关。基于事件树和成功树分析,可以总结道路交通系统的连通逻辑:①路段-路径:路径上的每条路段都连通时,该条路径被认为是连通的,路段与路径的关系类似逻辑门中的与门; ②路径-OD对:OD对所含路径至少有一条是连通时,该OD对被认为是连通的,路径与OD对的关系类似逻辑门中的或门; ③OD对-OD对中的O点/D点:与O点/D点组成的OD对中至少有一对是连通时,该O点/D点被认为是连通的,O点/D点与相应的OD对的关系类似或门; ④O点/D点-抗震功能系统:抗震功能系统所含的每个O点/D点都连通时,该系统被认为是连通的,O点/D点与系统的关系类似与门; ⑤抗震功能系统-道路交通系统:道路交通系统的抗震功能分系统均连通时,该系统被认为是连通的,抗震功能系统与总系统的关系类似与门。
本文以道路交通系统的连通性随时间变化的曲线作为抗震韧性评价的基础,采用动态贝叶斯网络表征系统抗震功能的连通逻辑与路段连通性随时间的变化,输出道路交通系统的连通性时变曲线。
本文构建的贝叶斯网络中,根节点为地震节点,叶节点为道路交通系统,中间节点为路段、路径、OD对、O点/D点、抗震功能分系统节点; 根据道路交通系统的连通逻辑,为地震节点外的其它节点之间添加有向边,将与门和或门转化为条件概率表(Conditioned Probability Table,CPT),表2表示由路段1、2组成的路径的CPT,表3表示由路径1、2组成的OD对的CPT; 为地震节点与路段节点添加有向边,将不同烈度下路段的连通/中断概率填入条件概率表。基于地震烈度的先验概率与节点间的条件概率表,可以计算道路交通系统的震后连通性。以观测数据作为证据,结合先验概率表可以实现贝叶斯网络的双向推理,得到各相关节点的后验概率,更新网络各节点的概率及网络各节点状态的认知。图4的贝叶斯网络适用于评价道路交通系统抗震的鲁棒性或脆弱性。
表2 与门对应的条件概率表
Tab.2 CPT corresponding to AND Gate
表3 或门对应的条件概率表
Tab.3 CPT corresponding to OR Gate
图4 道路交通系统贝叶斯网络样例
Fig.4 Example of the Bayesian network of the traffic system
动态贝叶斯网络的构建基于时间盘。时间盘内的节点被称为时间节点,其状态随时间变化; 时间盘外的节点被称为固定节点,其状态不随时间变化。本文构建的贝叶斯网络中,地震节点的烈度不受道路抢修行为而改变,为固定节点; 其余节点的连通概率受道路抢修行为而改变,为时间节点。
为表征路段状态随时间的变化,在时间盘中添加代表道路抢修行为的恢复节点,地震节点与恢复节点的条件概率表(表4)用于确定在不同烈度下采用的恢复速率。恢复节点与路段节点、路段节点与自身添加跨时间片的边(图5),表示某时刻路段节点状态与之前时刻恢复节点与路段节点状态相关,图5中边上的数字代表跨时刻数,1代表相邻时刻。因此,在构建的动态贝叶斯网络中,路段节点具有2个条件概率表。t=0时刻的条件概率表(表5),表示震后路段的连通概率,即贝叶斯网络构建时输入的条件概率表; t=1时刻的条件概率表(表6),表示路段受上一时刻状态和恢复速率共同影响下,下一时刻的状态概率。基于地震烈度的先验概率与节点间的条件概率表,可以计算每一时刻道路交通系统的连通性,输出连通性曲线。动态贝叶斯网络也具有以观测数据为证据实现双向推理的能力。
表4 恢复节点CPT
Tab.4 CPT of nodes recovery
表5 路段节点t=0时刻CPT
Tab.5 CPT of nodes when t=0
图5 道路交通系统动态贝叶斯网络样例
Fig.5 DBN example of the traffic system
表6 路段节点t=1时刻CPT(Ⅶ度烈度下)
Tab.6 CPT of nodes when t=1(subjected to Intensity Ⅶ)
本文选取青岛市市南区八大湖、金门路、香港中路和珠海路4个街道路网作为应用实例。根据地震灾害下路网节点的功能划分(图2),从该区域路网中选取17个节点,见表7; 基于区域路网的节点,将该路网中的路段划分为42条,并转化为相应的拓扑结构图,如图6所示。
表7 区域路网节点的功能划分
Tab.7 Function division of the nodes of regional road network
图6 研究区域路网的拓扑结构图
Fig.6 Topological structure of road network in the study area
本文提出的动态贝叶斯网络模型中,灾害事件、抗震功能系统与系统节点是确定的,即地震、应急救援系统、物资运输系统、医疗救护系统和道路交通系统是确定的,而O点/D点、OD对、OD对所含的路径、路径所含的路段需要从具体的路网中提取。基于道路交通系统不同抗震功能下源/汇点的组成(图3),将表7中的路网节点划分到对应的抗震功能系统中并组成OD对。抗震功能系统中的源点即OD对中的O点,汇点即D点。对每个OD对,本文选择2条满足OD对间连通的路径(表8)。路段的连通概率如表9所示(张洁,2013),其中路段6、9、11和26上的节点7、15、14和5距离道路交叉口较近,因此在选择OD对的路径时未考虑这4条路段的连通性影响。
应急救援与物资运输系统中,每个汇点至少有一个源点与其连通时,该系统的功能被认为是有效的; 医疗救护系统中,每个源点至少有一个汇点与其连通时,该系统的功能被认为是有效的。在本实例中,应急救援系统的每个汇点只对应一个源点,无需在贝叶斯网络中添加D点; 物资运输系统的路网节点7对应4个源点,需要添加D点; 类似的,医疗救护系统的路网节点4、10、11和12分别对应2个汇点,需要添加对应的O点。变量及因果关系的确定是贝叶斯网络构建的重要基础。
表8 抗震功能分系统下的OD对及路径
Tab.8 OD pairs and routes of each subsystem
表9 不同烈度下路段的连通概率
Tab.9 Connectivity probability of roads subjected to different intensity
根据贝叶斯网络的变量与因果关系,构建道路交通系统的贝叶斯网络,如图7所示。构建的贝叶斯网络中,第一层为地震灾害节点; 第二层为路段节点,共38个,为地震灾害节点的子节点; 第三层为路径节点,共34个,为所含路段节点的子节点; 第四层为OD对节点,共17个,为所含路径节点的子节点; 第五层为O点/D点节点,分别代表路网节点4、7、10、11和12; 第六层为抗震功能系统节点,即应急救援、物资运输和医疗救护系统节点; 第七层为道路交通系统节点,是抗震功能系统节点的子节点。
基于动态贝叶斯网络建模方法,构建道路交通系统的动态贝叶斯网络,如图8所示。与图7相比,动态贝叶斯网络增加了恢复节点、地震节点与其相连的网络内的边,以及恢复节点与路段节点、路段节点与自身的跨相邻时间片的边。恢复节点用于确定不同烈度下路段的恢复速率,跨时间片的边用于表达路段连通性随时间恢复的特征。方东平等(2020)给出了不同烈度下各类交通功能完全恢复的平均时间,基于此本文设定烈度为Ⅶ、Ⅷ、Ⅸ度下的恢复速率MTTR分别为2、5 和11 d。
基于地震烈度的先验概率与变量间的条件概率,动态贝叶斯网络模型输出相应的道路交通系统连通性曲线,本文给出Ⅸ度烈度下的动态贝叶斯网络模型求解结果,道路交通系统连通性随时间变化与相应的连通性曲线如表 10和图9所示。从表 10中可以看出,在0时刻,道路交通系统的连通性受到地震灾害的影响而下降到最低水平0.774,反映了该系统的抗震鲁棒性水平。自0时刻开始,道路交通系统的连通性逐渐恢复。第13天时,道路交通系统的连通性约为0.954,超过了期望的系统震后连通性(本文取1)的95%。
表 10 Ⅸ度烈度下道路交通系统连通性与韧性的变化
Tab.10 Variation of the traffic system connectivity &resilience subjected to Intensity Ⅸ
图7 道路交通系统的贝叶斯网络
Fig.7 Bayesian network of the traffic system
根据式(1)的定义,确定t时刻系统的性能F(t)为表 10中的连通性数据,干扰事件发生前系统正常运行时的性能F(t0)为1,干扰事件发生的起始时刻te为0时刻,系统恢复95%或100%初始稳定状态水平的时刻tf为第13天。道路交通系统t时刻的韧性R(t)计算结果见表 10。从图9中可以看出,在抗震全过程中,道路交通系统的韧性随时间推移逐渐上升,趋势与连通性曲线一致。在Ⅸ度烈度下,该道路交通系统实例的最终抗震韧性水平为0.885。
本文提出了一种道路交通系统抗震韧性评价模型,该模型能够量化系统自地震发生起至性能恢复至期望水平的全过程韧性。模型以连通性随时间变化的曲线为韧性量化的基础,采用贝叶斯网络表征道路交通系统抗震功能的连通逻辑,并利用了动态贝叶斯网络直观表达变量时变特征的优势表征路段的连通性变化。以青岛市局部路网
图8 道路交通系统的动态贝叶斯网络
Fig.8 Dynamic Bayesian network of the traffic system
图9 Ⅸ度烈度下道路交通系统的连通性曲线(a)和韧性曲线(b)
Fig.9 Connectivity(a)and resilience(b)curves of the traffic system subjected to Intensity Ⅸ
为例,对Ⅸ度烈度下的道路交通系统进行了全过程抗震韧性评价,主要得出以下结论:
(1)本文提出的韧性指标可全面描述震后系统连通性退化与恢复全过程,所构建的动态贝叶斯网络能直观表征系统抗震功能的连通逻辑与变化。
(2)实例研究表明,研究区道路交通系统的连通性受到地震灾害的影响而下降到最低水平0.774,反映了该系统的抗震鲁棒性水平。在抗震全过程中,道路交通系统的韧性随时间推移逐渐上升,趋势与连通性曲线一致。在Ⅸ度烈度下,该道路交通系统实例的最终抗震韧性水平为0.885。全过程韧性评价反映了系统的抗震鲁棒性与恢复性,符合韧性的内涵,评价结果能够为系统震前预防与震后恢复策略提供参考,从而提升和改善系统韧性,达到更高的抗震减灾水平。
(3)震前预防和震后恢复策略往往离不开对路段重要度的排序研究。震前提高路段抗震能力,或震后加急修复重要路段,是提升系统抗震韧性的两个方向,特别是在震后维修资源不充足的客观条件下,路段的修复顺序影响整个交通系统的恢复效率。因此,在道路交通系统的抗震韧性评价的基础上,后续研究可基于敏感性分析与贝叶斯网络特有的证据更新能力,探索基于该模型的路段韧性重要度排序方法。
本文仅考虑了道路交通系统抗震性能中最基本的连通性的时变曲线作为抗震韧性评价的指标。但实际上,运输能力、行程时间可靠性等也属于抗震性能的范围,综合考虑多种抗震性能能够丰富和完善道路交通系统的抗震韧性评价研究。因此,后续研究可探索基于多指标的道路交通系统抗震韧性评价。
