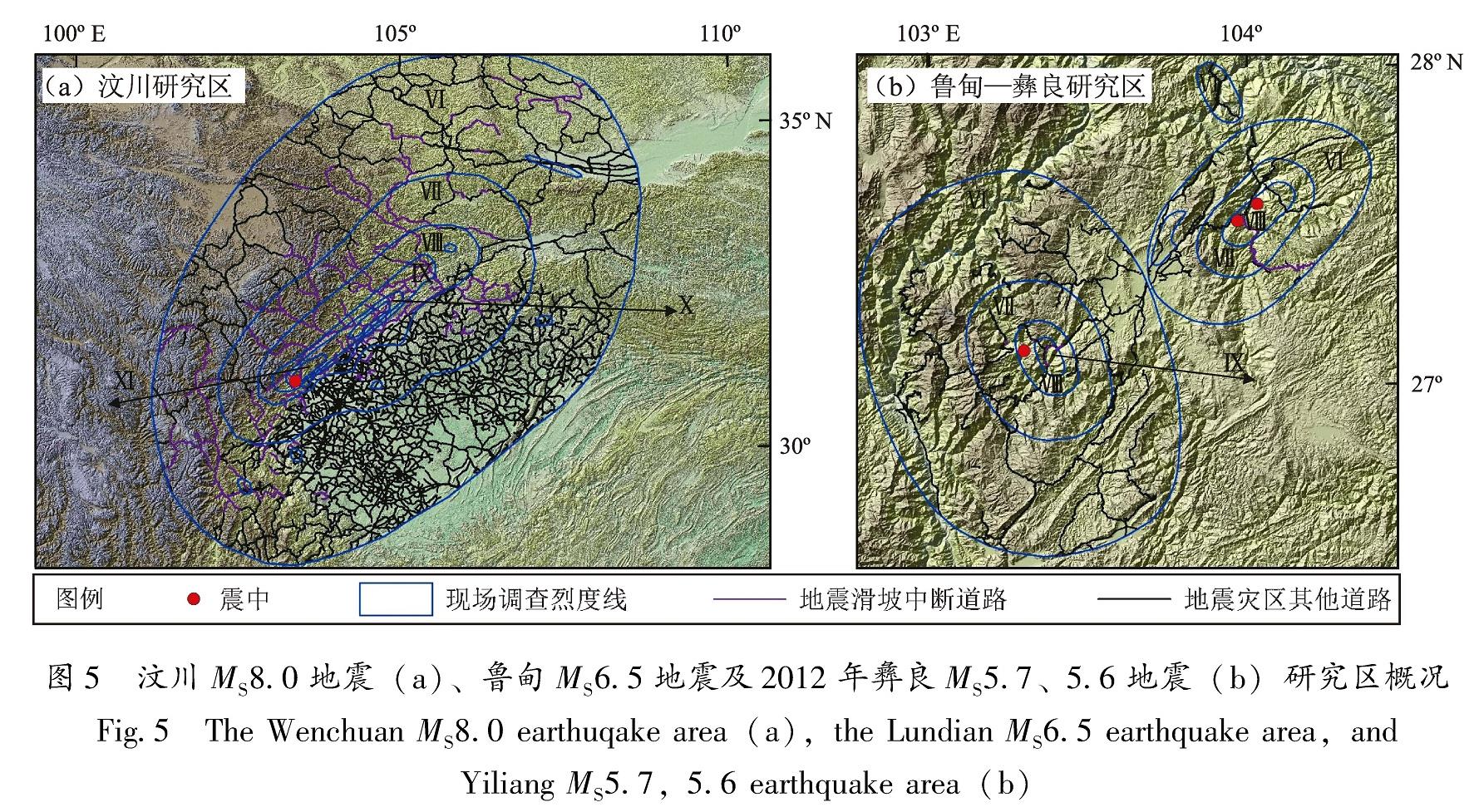
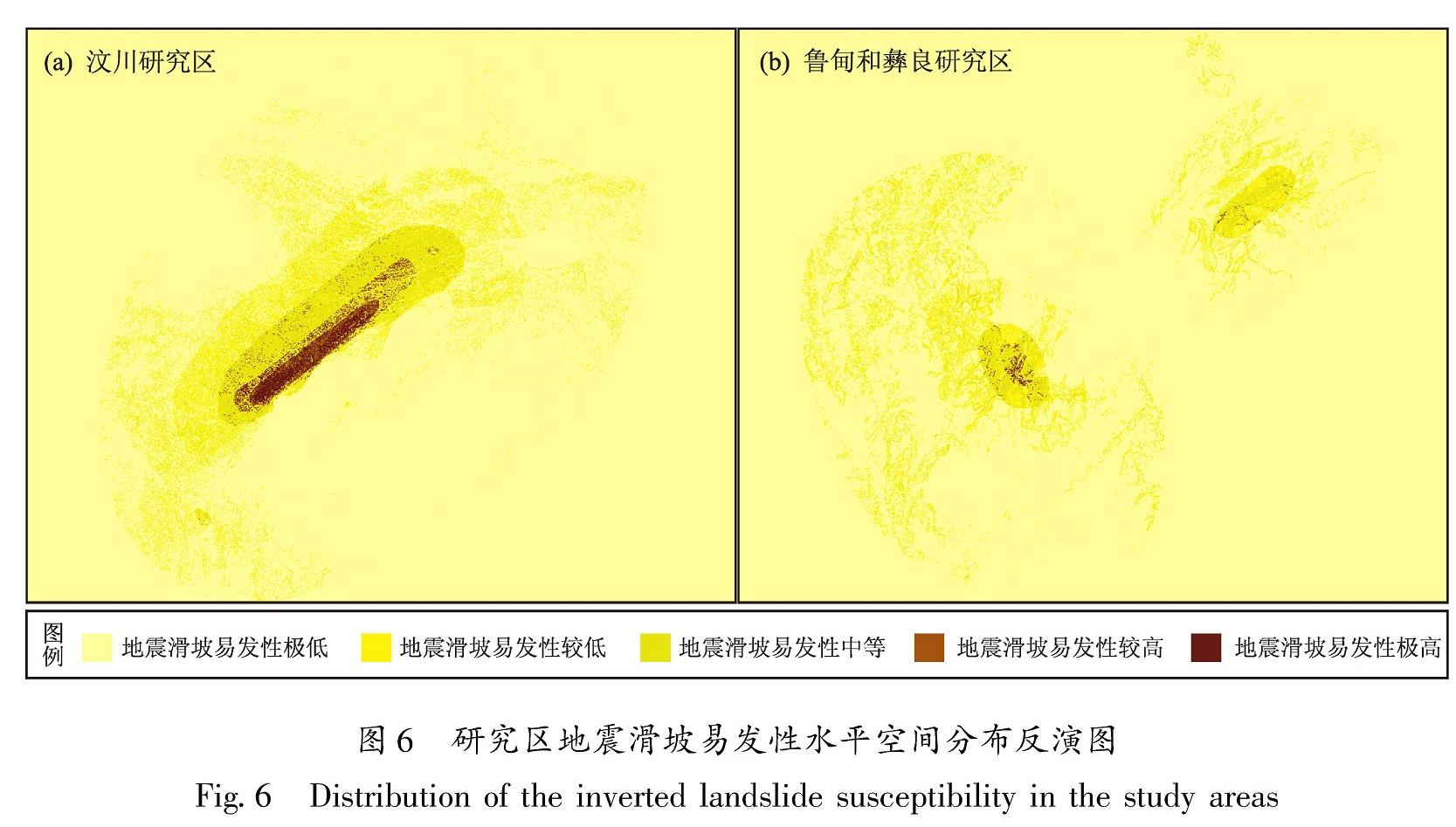
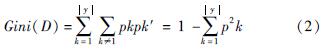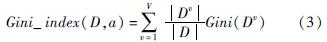2.4.1 影响地震滑坡道路中断因子分析
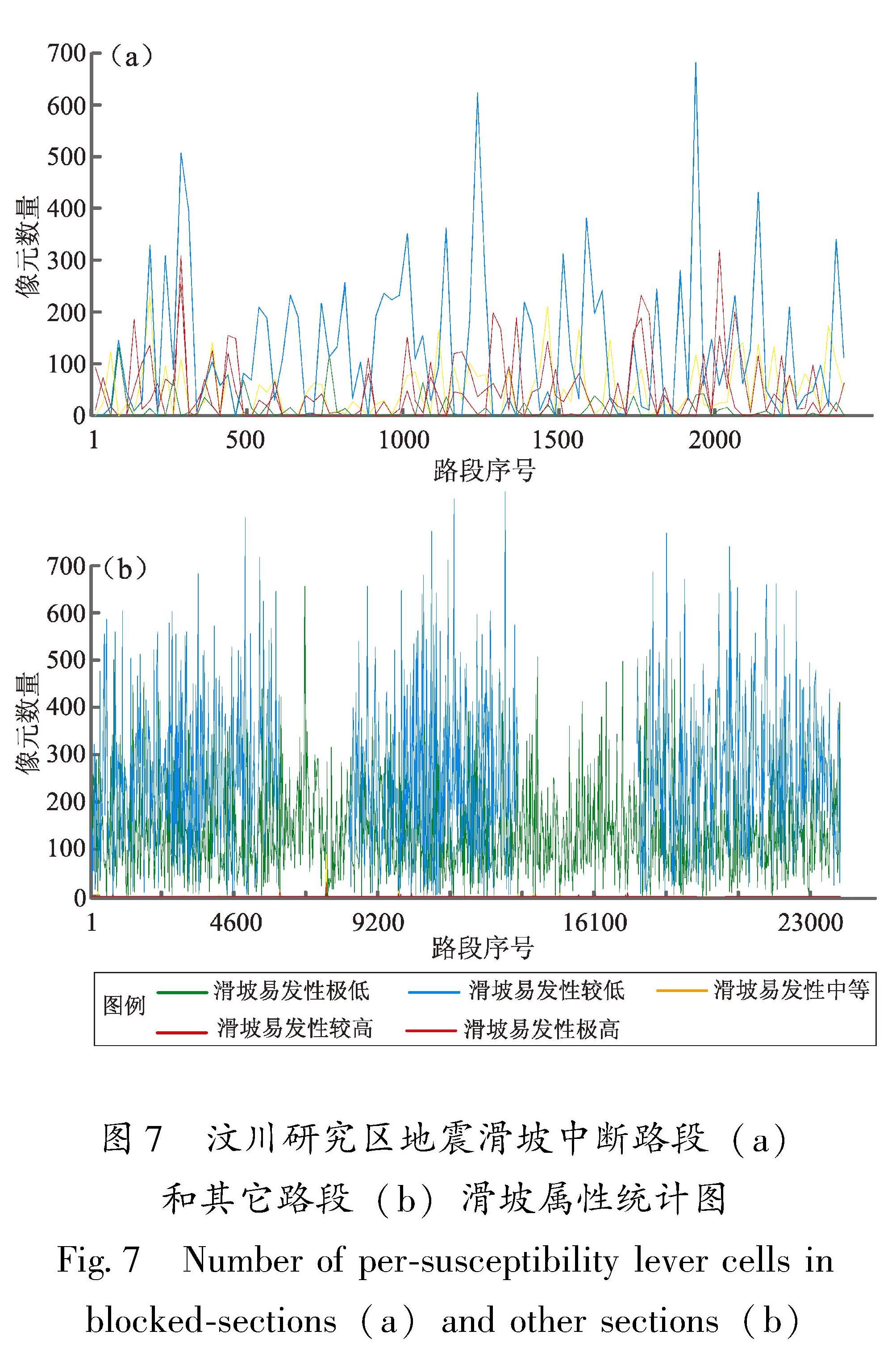
将2008年汶川地震灾区的路段分为两类:地震滑坡中断路段(定义为有风险,属性值为1)和其它路段(定义为无风险,属性值为0)。在路段分析中,只考虑了高等级公路(包括高速公路、国道、省道),其它公路没有统计在内。从汶川研究区地震滑坡中断路段和其他路段的滑坡属性统计图(图7)可以看出,中断路段两侧180 m范围内滑坡易发性极高或较高的像元数量较多,其它路段两侧滑坡易发性极高或较高的像元极少或没有,表明路段的地震滑坡属性是其中断风险的重要指标。
图7 汶川研究区地震滑坡中断路段(a)和其它路段(b)滑坡属性统计图
Fig.7 Number of per-susceptibility lever cells in blocked-sections(a)and other sections(b)
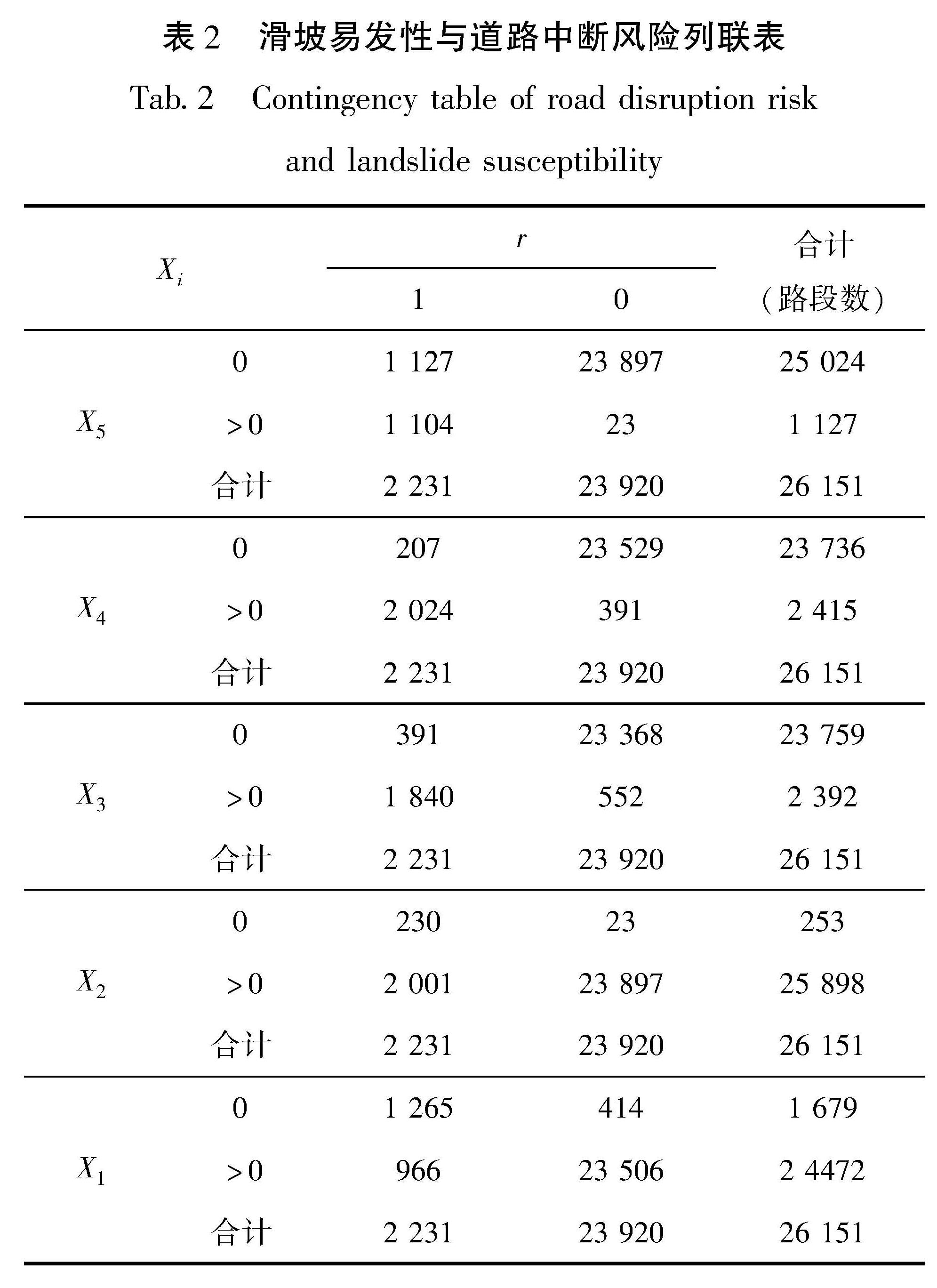
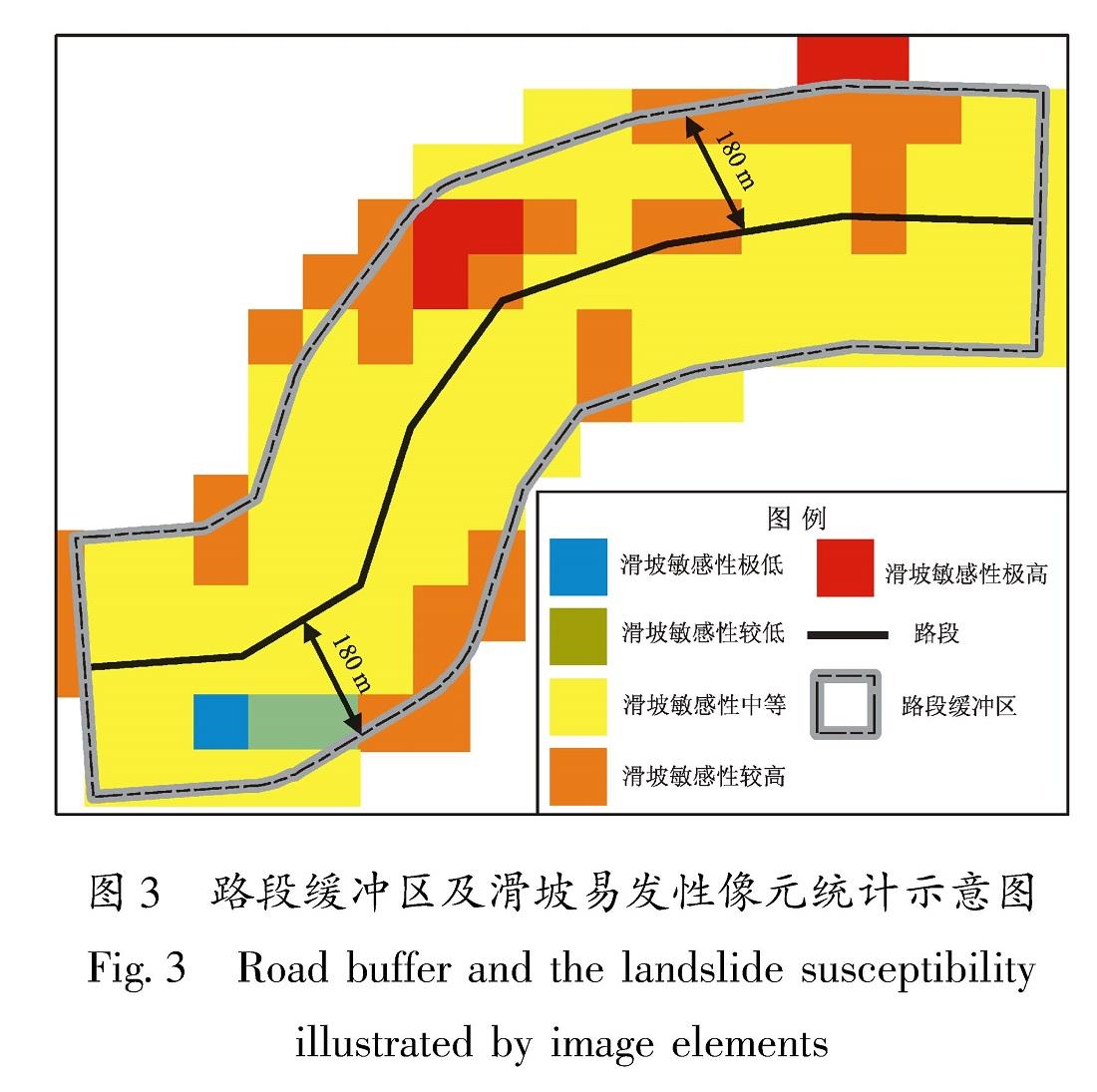
采用列联表对汶川研究区内26 151条路段的地震滑坡中断风险与滑坡属性的相关性进行分析与推断。进行列联分析时,将样本中地震滑坡中断道路的r记为1,其它路段的r记为0,把缓冲区上代表各滑坡易发性等级像元数量的X1~X5分为大于0和等于0两类,然后进行不同地震滑坡易发性水平像元数量组合与道路中断风险之间的关系分析,见表2。 对应的X1~X5分别表示路段缓冲区上地震滑坡易发性等级从极低到极高的像元数量。滑坡属性与中断风险属性对应下的数值为满足这两个条件的路段数量。用表2进行列联分析时,约定:原假设H0:Xi与r独立; 备择假设H1:Xi与r相合。X5与r的检验P值为4.831 1×10-116,相合系数为0.679 4。显著地有X5=0, 倾向于r的取值等于0; X5>0,倾向于r的取值等于1,拒绝原假设,X5与r的正相合。X4与r的检验P值为4.361×10-144,相合系数为0.859 8。显著地有X4=0,倾向于r的取值等于0; X4>0,倾向于r的取值等于1,拒绝原假设,X4与r的正相合。X3与r的检验P值为1.070 3×10-155,相合系数为0.959 1。显著地有X3=0,倾向于r的取值等于0; X3>0,r的取值倾向于等于1,拒绝原假设,X3与r的正相合。X2与r的检验P值为1.216×10-155,相合系数为-0.2915。显著地有X2=0,r的取值倾向于等于1; X2>0,r的取值倾向于等于0,拒绝原假设,X2与r的负相合。X1与r的检验P值为1.79 146×10-38,相合系数为-0.621 7。显著地有X1=0,r的取值倾向于等于1; X1>0,r的取值倾向于等于0,拒绝原假设,X1与r的负相合。
表2 滑坡易发性与道路中断风险列联表
Tab.2 Contingency table of road disruption risk and landslide susceptibility
从表2结果可以看出,路段两侧180 m范围内不同滑坡易发性等级的像元数量与路段是否因地震滑坡中断存在联系。列联分析表明可以使用路段的地震滑坡属性推断其滑坡中断风险。
2.4.2 模型参数求解
选取汶川地震灾区中的8 717条路段数据(约占汶川研究区样本数据的30%)作为训练集构建地震滑坡道路中断风险多变量决策树模型,其余的17 434条路段数据作为测试集测试模型的合理性。通常在决策时,随着划分过程的进行,我们希望决策树的分支结点所包含的样本尽可能属于同一类别,即结点的“纯度”尽可能高。基尼指数是度量样本集合纯度常用的一种指标。假定当前样本集合D中第k类样本所占的比例为pk(k=1,2,…,〖JB<1|〗y〖JB>1|〗),则D的基尼指数定义为:
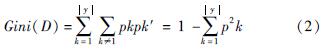
Gini(D)越小,则数据集D的纯度越高。假定离散属性a有V个可能的取值,若使用a来对样本集D进行划分,则会产生V个分支结点,其中第v个分支结点包含了D中所有在属性a上取值为av的样本记为Dv。可根据式(2)计算出Dv的基尼指数,再考虑到不同的分支结点所包含的样本数不同,各分支结点赋予权重〖JB<1|〗Dv〖JB>1|〗/〖JB<1|〗D〖JB>1|〗计算出用属性a对样本集D进行划分所获得的基尼指数(Gini_index)。采用与式(2)相同的符号表示,属性a的基尼指数定义为:
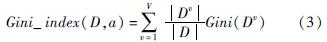
在候选属性集合A中,选择使划分后基尼指数最小的属性作为最优划分方案,即:

当Gini(D)值取最小时,通常认为对应的分类器是最佳分类。
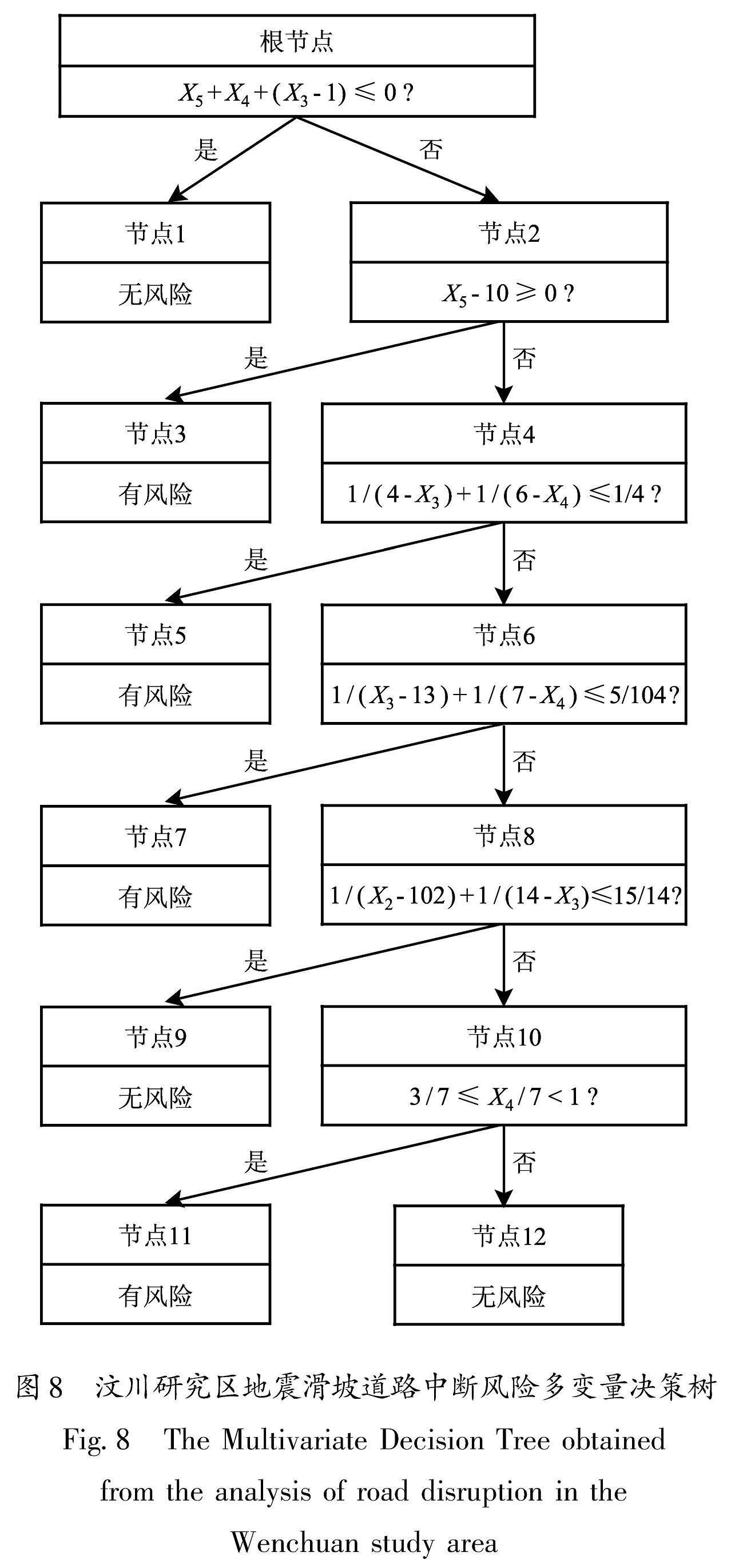
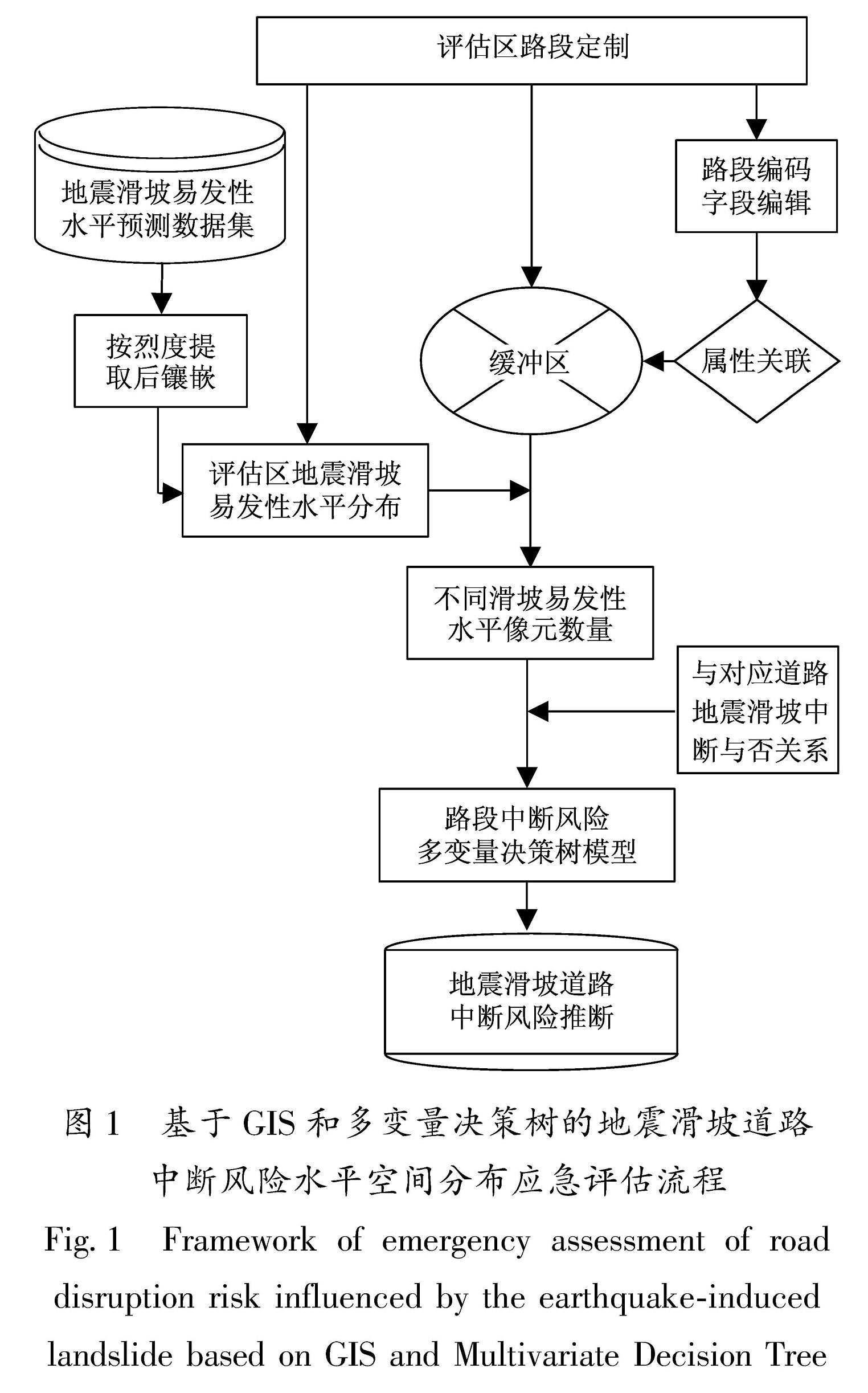
根据上述约束,采用统计软件R完成地震滑坡道路中断风险多变量决策树模型的构建,结果如图8所示。
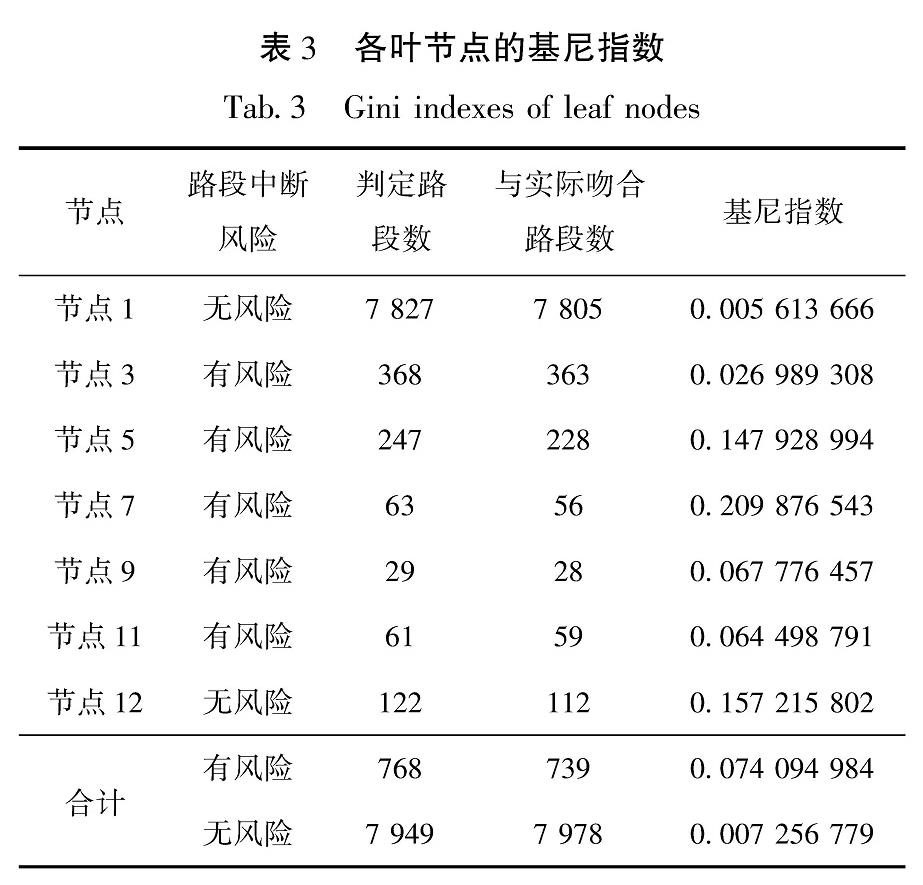
地震滑坡道路中断风险多变量决策树应急评估模型从根结点开始“生长”,建模时使用的训练样本8 717个,其中实际地震滑坡风险属性为有风险的样本739个,无风险的样本7 978个。训练样本在各叶节点上的基尼指数见表3。
图8 汶川研究区地震滑坡道路中断风险多变量决策树
Fig.8 The Multivariate Decision Tree obtained from the analysis of road disruption in the Wenchuan study area
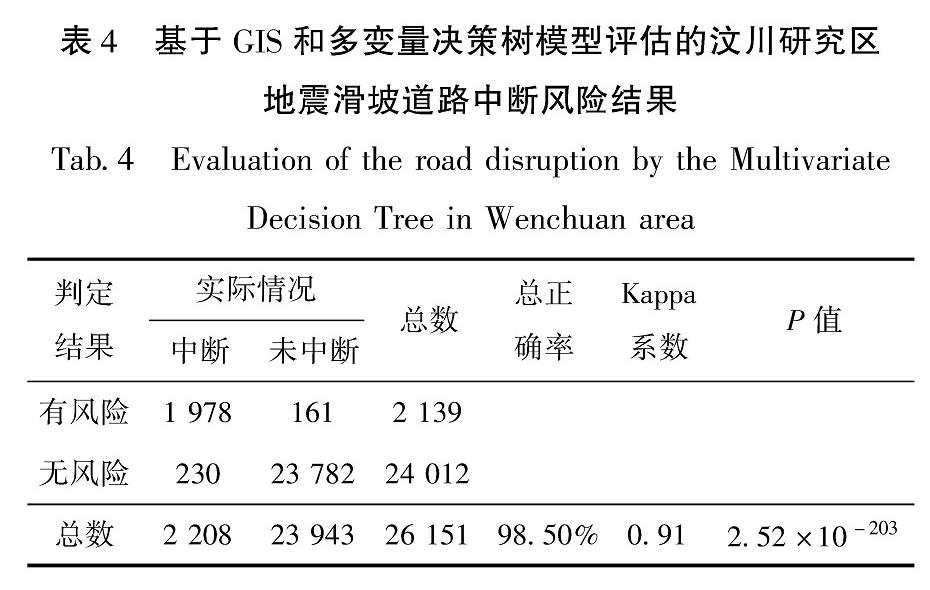
一般来说,一个模型只有通过统计学评价和一致性检验才能表明其具有科学意义。统计学上,P值为结果可信程度的一个递减指标,P值越大,样本中变量的关联越无法作为总体中各变量关联的可靠指标。Kappa系数反映的是模拟结果与实际情况的一致性程度,通行的做法是将Kappa值分为5组来表示不同级别的一致性:(0.0~0.20)为极低一致性,(0.21~0.40)为一般一致性,(0.41~0.60)为中等一致性,(0.61~0.80)为高度一致性,(0.81~1)为几乎完全一致。将通过训练集求解的模型对包括测试集在内的所有样本进行地震滑坡道路中断风险推断,然后对推断结果进行检验(表4)。汶川研究区的检验P值为2.52×10-203,远小于0.001; 总体正确率达到98.50%; Kappa系数达到0.91。对比C4.5的决策树方法研究结果,多变量决策树模型覆盖的范围更广,涵盖了Ⅵ~Ⅺ度区域,且有更高的差异显著性(更显著的统计学意义)、更高的Kappa系数(更高的一致性)和更高的总体正确率。
表3 各叶节点的基尼指数
Tab.3 Gini indexes of leaf nodes
表4 基于GIS和多变量决策树模型评估的汶川研究区地震滑坡道路中断风险结果
Tab.4 Evaluation of the road disruption by the Multivariate Decision Tree in Wenchuan area
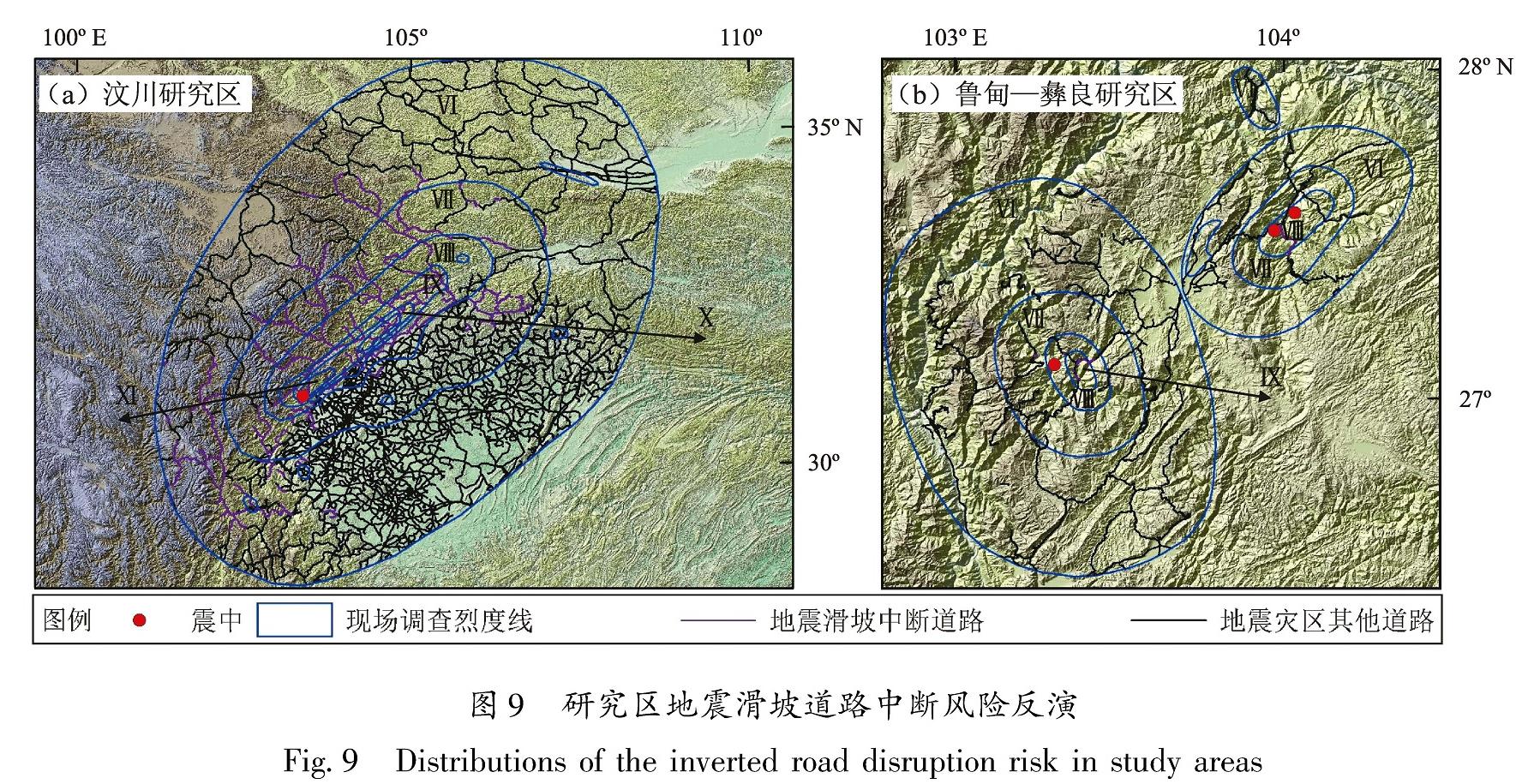
利用上述模型,基于地震后现场调查得到的地震烈度计算各路段的地震滑坡道路中断风险值,在GIS中反演研究区地震滑坡道路中断风险分布(图9a),对照实际道路中断情况(图5)发现,模型评估为有风险而实际畅通的路段主要是高烈度区的少量高速公路,而模型评估为无风险但实际却因滑坡中断的主要是低烈度区的部分省道。
图9 研究区地震滑坡道路中断风险反演
Fig.9 Distributions of the inverted road disruption risk in study areas
2.5 模型的外延适用性检验
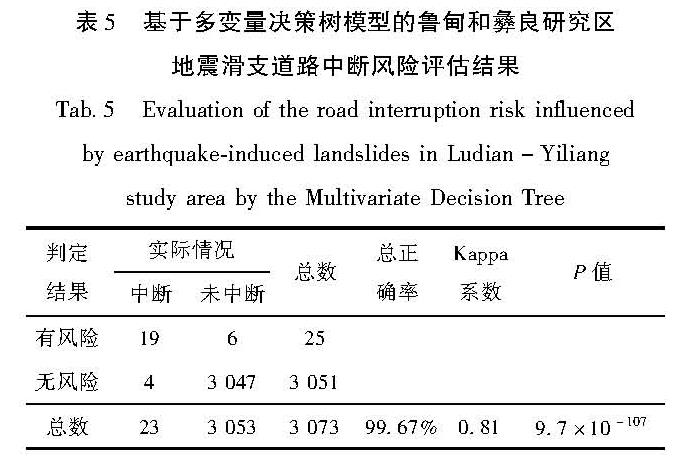
模型的外延适用性检验即在所有数据处理方法、建模指标和模型参数都不发生变化的情况下,使用在汶川研究区建立的地震滑坡道路中断风险多变量决策树应急评估模型,对云南2014年鲁甸MS6.5和2012年彝良MS5.7、5.6地震灾区的路段进行地震滑坡中断风险推断。鲁甸和彝良研究区的地震滑坡道路中断风险空间分布反演结果如图9b所示。从检验结果(表5)可以看出,鲁甸和彝良研究区的检验P值更加接近于0; 总体正确率99.67%; Kappa系数0.81,仍属于几乎完全一致性级别。这表明,用模型计算出的道路中断风险属性是路段是否因地震滑坡而中断的良好指标,在允许存在一定误差的情况下,所建立的模型可以用于地理环境相似地区的地震滑坡道路中断风险应急评估。
表5 基于多变量决策树模型的鲁甸和彝良研究区地震滑支道路中断风险评估结果
Tab.5 Evaluation of the road interruption risk influenced by earthquake-induced landslides in Ludian-Yiliang study area by the Multivariate Decision Tree

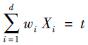 t的线分类器,其中wi是Xi属性的权重; t是该节点的分类阈值。与单变量决策树不同的是,在多变量决策树的学习目标不是为每个非叶结点寻找一个最优划分属性,而是建立一个合适的线性分类器(周志华,2016)。本文通过R软件求解地震滑坡道路中断风险多变量决策树应急评估模型构建时的wi、Xi和t的参数值。
t的线分类器,其中wi是Xi属性的权重; t是该节点的分类阈值。与单变量决策树不同的是,在多变量决策树的学习目标不是为每个非叶结点寻找一个最优划分属性,而是建立一个合适的线性分类器(周志华,2016)。本文通过R软件求解地震滑坡道路中断风险多变量决策树应急评估模型构建时的wi、Xi和t的参数值。