基金项目:中国地震局震情跟踪定向工作(2023010222).
第一作者简介:黄江培(1984-),工程师,主要从事相对重力数据采集及分析研究工作.E-mail:164909307@qq.com.
(1.云南省地震局,云南 昆明 650024; 2.弥勒县地震局,云南 弥勒 652399)
(1.Yunnan Earthquake Agency,Kunming 650224,Yunnan,China; 2.Mile Earthquake Agency,Mile 652399,Yunnan,China)
drift rate; the Bayesian estimation; mobile-gravity observation; adjustment results; Yunnan
DOI: 10.20015/j.cnki.ISSN1000-0666.2023.0060
由于地球的不可入性,高精度时变重力被视为探测地球内部密度变化的主要手段,被广泛地应用于各个科学研究领域,包括矿物探测(李小孟,曾华霖,1996)、地壳构造特征(陈石,王溪身,2015,汪健等,2015)、地下水变化特征(佘雅文等,2015)和地震研究(卢造勋等,1978; 陈运泰等,1980; 吴国华等,1995,1997; 祝意青等,2015,2018; 孙少安等,2015; 胡敏章等,2019; Xing et al,2021; 刘洪良等,2021; 黄江培等,2022)等方面。但在高精度重力获取过程中,受外部环境、仪器设备性能等影响,其数据质量成为众多学者最关心的问题之一。外部环境中的温度、气压、固体潮等影响因素目前已经有被国际学会接受的经验改正公式进行解算; 由于个体差异极大,仪器性能方面的一次项、格值系数、漂移率等特征,无法进行统一规定,只能通过仪器厂商的出厂设置、观测前的仪器标定、观测数据的似然估计综合获取。
2010年以前,中国大陆的流动重力观测网络主要采用以Lacoste(拉科斯特)和Burries(贝尔雷斯)为主的金属弹簧重力仪进行流动重力观测工作,金属弹簧型的漂移率基本为(1~3)×10-8(m·s-2)/h(邢乐林等,2010; 赵云峰等,2018),所以这个阶段主要是针对仪器一次项及格值系数的改正研究。2010年以后,CG-5型石英弹簧相对重力仪被引进并广泛应用,其采用自动倾斜补偿、高精度温度控制、电子读数等先进技术,出厂设置将格值进行了处理,参数估计中只需要考虑一次项及漂移率即可,而且在一个观测周期内,可以采用相同的一次项系数解算(郝洪涛等,2016,黄江培等,2020)。
2009年6 月,中国地震局在武汉及江西九江庐山基线场对10 台CG-5 相对重力仪进行测试,显示其静态漂移率呈较好的线性,平均静态漂移率与平均动态漂移率符合性较好,个别仪器线性漂移率较大,最大超过100×10-8(m·s-2)/h(邢乐林,李辉,2010)。通过本次标定,发现平均动态漂移率与静态线性漂移率吻合较好,认为将动态漂移进行线性化计算是可行的。但在实际工作中,CG-5相对重力仪的零点漂移并不是线性的(汪健等,2016; 杨雅慧等,2021),并且漂移率变化可达到10×10-8(m·s-2)/h(隗寿春等,2016,2017),因此在一个观测周期内将漂移率当做一个定值进行平差的方法是不恰当的。针对这种情况,学者们提出了分段平差法(隗寿春等,2016)、基于贝叶斯准则的似然估计法(Chen et al,2019)等,其中贝叶斯平差方法的有效性得到了部分学者的验证(王林海等,2020; 杨锦玲等,2021; Zheng et al,2022)。本文基于云南地区近30年的流动重力观测数据,分别采用基于传统最小二乘原理的平差方法计算线性漂移及基于贝叶斯原理的平差方法计算非线性漂移率,提出合理的相对重力仪零漂参数估计方案,以期为高精度时变重力数据处理提供参考。
相对重力仪零点漂移是指仪器零点随着弹簧的老化、弹性疲劳、测值段的突变或在运输过程中发生颠簸等因素出现的偏移,在不考虑观测误差和测点重力实际变化的情况下,可以理解为同一测点在不同时间段重复观测的差值。漂移率则是在单位时间内的零点漂移量,一般取1 h为时间单位。设观测值为g,观测时间间隔为t,漂移率v计算公式为(隗寿春等,2017):
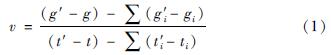
式中:g、g'、t、t'分别为测点往返观测值和观测时间; ∑(g'i-gi)和∑(t'i-ti)分别为需要计算静止漂移的测点的初测和离开时的测值和时间。式(1)可作为外业单条测线往返测量时的仪器漂移率预处理计算模型。
由于CG型号仪器不考虑二次项以上的影响,在经过固体潮、温度、气压等改正以后,仅考虑一次项系数及漂移影响即可,其误差方程可以简化为:
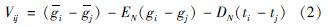
式中:Vij为段差观测值(gi-gj)的改正数; g^-i、g^-j 为i、j点平差后的重力值; ti、tj为i、j两点上的观测时刻; DN为漂移率,在整个观测周期内当做一个未知数进行求解; EN为一次项系数,可在开测前的仪器标定中获得,也可在测网全部观测完成后,利用已知的绝对重力点进行标定得出。
设观测误差、绝对重力测点观测误差及每日漂移率变化误差均服从正态分布,则有:
Ax+Dv-y~N(0,σ2)(3)
Gx+g~N(0,σ2g)(4)
Bv~N(0,σ2b)(5)
式中:x=[x1,x2,…,xp]T,为待估重力点值; v=[v1,v2,…,vp]T,为待求漂移率; y=[y1,y2,…,yp]T,为观测段差; g=[g1,g2,…,gp]T,为绝对点值; p为测点数; σ2、σ2g、σ2b分别为观测方差、绝对重力观测方差及仪器漂移率方差; A为观测矩阵,当未知重力点xi为段差yi的终点时,Aij=1,反之,对应起点时,Aij=-1,否则为0; D为所有段差观测的时间间隔,与A和段差向量y相对应; G为绝对重力矩阵,对应已知重力点值,即当相对重力观测的联测点i为已知重力点时,Gi=1,否则为0; B为二阶光滑矩阵,表示为:
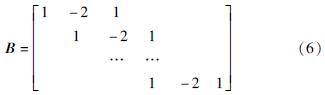
S为A、D、G和B的联合矩阵,表示为:

X为未知重力点值x和漂移率v的联合矩阵,Y为策略段差y及已知重力点值g的联合矩阵,分别表示为:

由式(7)~(8)可得:
SX=Y(9)
W为权矩阵,即方差的倒数矩阵,表示为:
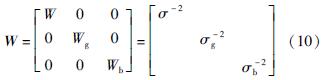
式中:Wg为已知重力点权矩阵; Wb为漂移率权矩阵,此时,该平差问题的最小二乘解求解公式为:
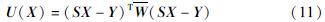
基于式(3)~(5)的先验假设条件,可以给出漂移率、绝对重力点值及相对观测段差的先验概率密度为:
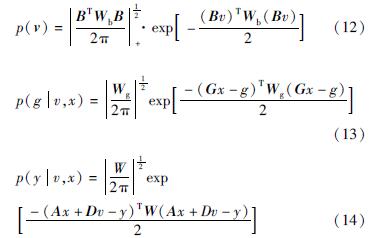
式中:“+”表示非零特征值的积。
基于贝叶斯公式,漂移率和重力点值的后验概率密度函数可表示为:
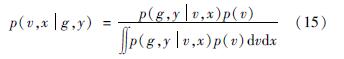
采用贝叶斯信息准则(ABIC)原理,能在模型参数复杂度(参数数量)与模型对数据集描述能力(即似然函数)之间寻求最佳平衡,通过求取ABIC最小值进行贝叶斯模型优化估计,本文所用数据采用单纯形非线性优化法加速ABIC最小化(Nelder,Mead,1965),表示为:
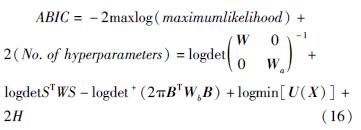
本文收集1990—2022年云南地区的流动重力观测数据,采用最小二乘平差方法(ADJ)及贝叶斯平差方法(BAY)分别计算其漂移率,统计结果见表1,表中ADJ即为整期漂移率,BAY取整期观测中每日漂移率的平均值。其中1990—2013年所用仪器为Lacoste金属弹簧相对重力仪,2014年以后采用CG-5石英弹簧相对重力仪,2014年所用数据为在仪器中设置漂移率后的观测数据,2015年以后所用数据为未进行漂移率修正的数据。从表1可见,不管使用哪种型号的仪器,通过BAY和ADJ计算的每日漂移率的平均值都非常接近。
表1 ADJ计算的漂移率与BAY计算的漂移率均值对比
Tab.1 Comparison between drift rate calculated by the ADJ method and average drift rate calculated by the BAY method
从表1中可以看出,2014年以前,仪器漂移率基本都在4×10-8(m·s-2)/h以内,两种方法计算的点值平均误差也没有明显差距; 2014年以后,CG-5相对重力仪的漂移率较大,且漂移率明显是变化的,在一个观测周期内,将漂移率当做一个定值处理是欠妥的,ADJ计算结果的点值误差基本大于BAY计算结果。
由表1可以看出,一个观测周期内,使用BAY计算的非线性漂移率的数学期望就是使用ADJ计算的线性漂移率,说明BAY计算结果是可靠的。本文以2020-03期为例,进一步分析1个测期内漂移率的变化情况,图1为2020-03期观测网示意图。
野外数据采集过程中,采用A→B→C…N…C→B→A的测线往返观测模式,一条测线往返观测时间不超过72 h,其中A→B与B→A构成一个往返测段,2020-03测期共计完成82条测线、275个测段,历时91 d。如果不考虑偶然误差,根据式(1)可以计算出每个测段及每条测线的仪器漂移率,然后根据大量的漂移率样本量,拟合出漂移率的变化趋势,如图2所示。为了与BAY计算结果对应,测段及测线编号均按照时间先后排序。
根据式(1)计算的每个测段漂移率,是将每个往返两次观测的不等差均当做漂移处理,即误差全带入,此时如果观测间隔较短,实际漂移不大,求取的漂移率中大部分是由误差引起的。2020-03期全网观测点值平均精度为8.8×10-8 m/s2,全网漂移率为26.3×10-8(m·s-2)/h。根据误差理论,一般取大于2倍误差的变化值作为有效数据,即变化大于17.6×10-8 m/s2才能视为计算的漂移率是有效的,通过与漂移率取商,得出测段观测时间间隔需达到40 min以上,才能计算有效漂移率。在实际观测中有部分测段观测间隔低于40 min,所以图2a中,存在部分离散幅度非常大的测点,可理解为观测误差大于实际漂移。图2b中采用往返测线作为计算基础,每条测线均包含2段以上测段,部分高达10多个,每个测段均是一次独立观测,偶然误差能够叠加消除一部分,计算采用的有效间隔时间也较长,所以计算的漂移率离散度明显降低。虽然测段及测线计算的结果均是将误差全带入的结果,不过当样本量较大时,通过拟合得出的趋势是准确的。从图2可以看出,CG-1170仪器的漂移率近似于线性,变化不大,但CG-1169仪器的漂移率有明显的变化趋势。图3为整网计算的使用ADJ和BAY得到的漂移率。
图2 2020-03测期所有测段(a)和测线(b)漂移率
Fig.2 Drift rate of all survey sections(a)and survey lines(b)during the 2020-03 surveying period
图3 2020-03测期使用ADJ及BAY计算得到的漂移率
Fig.3 Drift rates calculated by the ADJ method and the BAY method during the 2020-03 surveying period
从图3可以看出,BAY结果与所有测段和测线计算的漂移率变化趋势(图2)一致,其中使用BAY计算的CG5-1170仪器的漂移率从4月7日以后一直处于ADJ计算结果的上方,且差值在不断增大; 在5月17日之前,使用BAY计算的CG5-1169仪器的漂移率处于ADJ计算结果附近上下波动的状态,但是从5月18日之后,一直处于ADJ计算结果之上,并且差值也在不断增大。在ADJ平差计算时,偏离部分的有效漂移率被当做误差处理了,而BAY算法能够极大的拟合这些有效漂移率。
从表1能够发现,使用CG-5型相对重力仪后,BAY全网计算结果的平均点值精度均优于ADJ计算结果,本文采用2020-03测期数据,分析两种方法计算结果的具体点值精度情况。
从表2可以看出,在σ<5区间,BAY计算结果的点值精度明显大于ADJ计算结果; 在σ<7区间,BAY结果测点占比达到86%,ADJ测点占比为60.2%; 在σ≥9区间,BAY只有4个测点,ADJ有19个测点,所以,BAY计算方法对点值精度有优化效果。本文在空间分布上分析其优化能力如图4所示。
表2 ADJ和BAY计算的点值精度对比统计
Tab.2 Comparison of the accuracy of the point values calculated by the ADJ method and the BAY method
图4 2020-03期ADJ(a)及BAY(b)计算结果点值误差空间分布
Fig.4 Spatial distribution of the point-value error calculated by the ADJ method(a) and the BAY method(b)in the 2020-03 surveying period
结合图1和图4可以看出,ADJ计算结果点值误差主要分布在测网边缘和远离控制点的地方,特别是支线上,点值精度较差,这是符合最小二乘平差中边缘效应原理的; BAY计算结果点值误差的空间分布趋势与ADJ计算结果是一致的,但是在边缘效应上有明显的优化结果,特别是在支线的处理上,能够明显降低点值误差。
2021年云南漾濞MS6.4地震后,刘东等(2021)和黄江培等(2022)采用相同的相对重力历史数据,分别采用ADJ和BAY方法进行解算,并分别对震前相对重力变化特征进行了分析,本文对两份解算结果进行对比分析,如图5所示。由图5可以看出,两种方法计算结果采用相同的绘图范围和历史数据,并使用相同的色标。总体来看,两种方法解算的重力变化趋势是一致的,漾濞地震震中西南侧的局部区域异常不一致是两位学者对重力变化高频噪声的取舍不同所致。
从图5b可以看出,在震中附近,NW-SE方向上形成了一个弱四象限趋势,沿红河断裂带是以负变化为主。震中附近,红河断裂两侧,有正变化趋势,地震发生于零值线附近,符合学者们的部分经验结论(祝意青等,2018; 胡敏章等,2019),所以认为本次地震前相对重力变化特征分析时,基于BAY所得结果是能够有效捕捉震前异常的。
陆地高精度相对重力观测中,观测段差往返不符值中包含零点漂移及观测误差,如何恰当地区分两者一直是一个难题。在使用Lacoste仪器的年代,漂移率较小且变化也小,经典最小二乘平差方法由于计算方便,计算机语言也比较简洁,无疑是最优的平差方法。但是CG-5型相对重力仪投入使用后,其漂移率较大,且非线性漂移明显,个体差异也大。从表1可以看出,2015—2022年CG5-1169和CG5-1170仪器的漂移率有明显的下降,上下半年也有明显的差距,但是随着时间的推移,下降速率有收敛的迹象,上下半年差距也在减小。所以,从长时间来看,漂移率是变化的,且漂移率变化也是非线性的,这种情况下,把漂移率当做一个定值处理是不恰当的。而BAY能够较好地反映漂移率的变化趋势(图3、图4),并且受到光滑矩阵的约束,加强了其稳健性,部分离散度较大的漂移率对其影响并不明显。
地震重力的研究是基于高精度重力观测,研究10×10-8 m/s级的重力变化,对于云南测区这种数百千米以上的大尺度构造环境的监测,闭合时间长、仪器多、测网复杂的情况下,漂移率的变化对计算结果影响较大,更需要BAY这种能够计算非线性漂移率,并且根据仪器性能自动分配仪器权重的算法。
本文利用传统最小二乘平差方法和贝叶斯平差方法计算1990—2022年云南流动重力观测数据的漂移率,并以2021年云南漾濞MS6.4地震为例进行分析,主要得出以下结论:
(1)流动重力观测数据的测段时间间隔需要达到40 min以上,才能够计算有效漂移率。
(2)对于漂移较小且非线性变化不明显的仪器观测结果,ADJ及BAY计算结果是一样的。
(3)对于漂移较大且非线性变化的仪器观测结果,ADJ把漂移率当做一个定值进行平差,会把部分有效漂移率当做误差处理,造成计算结果点值误差增大; BAY能够计算出每日漂移率的极大似然值,较好地拟合漂移率变化趋势,具有更好的数据自洽性,计算结果点值精度能够得到明显优化。
(4)在测网边缘和远离控制点、支线等控制较弱的位置,BAY处理结果的点值精度优于DAJ。
综上所述,BAY适用于云南测区这种空间跨度大、时间周期长的测网,由于BAY需要解算的参数较多,计算机解算过程较长,对于仪器数量少、省网级的解算是值得推荐的,但是对于仪器数量多且型号不一的全国联测网的解算,由于对计算机配置要求较高,并且解算耗时较长,目前还没有学者进行过尝试,可在将来进一步研究。