基金项目:中央高校基本科研业务专项(20215105); 国家自然科学基金——地震科学联合基金项目(U1939209); 中国地震局科技星火公关项目(XH20084).
第一作者简介:李 平(1981-),教授,博士,主要从事场地效应及岩土工程抗震方面研究.E-mail:chinaliping1981@126.com.
(1.防灾科技学院,河北 三河 065201; 2.河北省地震灾害防御与风险评价重点实验室,河北 三河 065201)
(1.Institute of Disaster Prevention,Sanhe 065201,Hebei,China)(2.Key Laboratory of Earthquake Disaster Prevention and Risk Assessment of Hebei Province,Sanhe 065201,Hebei,China)
the Loess region; ground motion; PGA; the Two-step Regression method; attenuation relations
DOI: 10.20015/j.cnki.ISSN1000-0666.2023.0028
地震引发的建筑物破坏和地质灾害给人类造成了难以估计的损失。其中,我国黄土地区由于地表切割剧烈,导致冲沟、崩塌、滑坡以及泥石流等地质灾害极为发育,其震害的影响更为严重,致灾范围也更广(徐世芳,李博,2000)。如1920年宁夏海源8.5级地震,2010年青海玉树7.1级地震都导致多人遇难,倒塌房屋不计其数。黄土微结构独特的动力性质也使该地区具有极高的地震易损性,如1986年山西运城3.1~3.9级地震群,震后20天内发生了487次地震,同样引起许多房屋和黄土窑洞的变形或倒塌(王兰民,2006)。因此提高黄土地区的抗震设防水平十分必要。
地震动衰减关系是表征地震动参数随震级、距离、场地等因素变化规律的函数关系,也是震后快速预估地震动影响、地震动区划和地震危险性分析等工作的重要组成部分,对提高地区的抗震设防水平有着重要的意义(袁一凡,2012)。而地震动峰值加速度(PGA)数据更容易获取,且常被用于反映地震动强度以及对结构的影响程度,因此是研究衰减关系时的首选因素(Douglas,2004)。
受震源特性、地质特性、传播路径等因素的影响,各区域地震动衰减关系往往表现出较大的差异性,因此建立反映不同区域特点的地震动衰减关系一直是研究的热点,也是十分有意义的工作,许多学者在分区地震动衰减关系研究上取得了众多成果(Chiou et al,2010)。如汪素云等(2000)以105°E为界将中国分为东部和西部两个地区,并利用美国西部丰富的地震动数据,采用地震动与烈度转换的方法分别拟合出了我国东西部的地震动衰减关系; 周典(2019)基于我国西部地区发生的42次地震数据,对比了7个国际上通用的衰减关系,认为霍俊荣(1989)的衰减模型更符合实测数据的衰减趋势,然后对该衰减模型进行了基于残差分析的修正,让其更适合中国西部地区。但这些研究并没有针对黄土地区,无法更准确地得到黄土地区的地震动衰减规律。杨帆等(2011)基于2008年汶川MS8.0地震及其余震资料,选用霍俊荣(1989)提出的衰减模型,首次利用直接拟合的方法得到了中国黄土地区的土层PGA衰减关系,直接回归的预测误差更小,但由于汶川地震震级本身偏大,且余震的地震性质与主震不同,其衰减关系模型应用到一般黄土地区的衰减关系预测时相对偏高。鉴于此,本文基于2001—2019年我国黄土地区发生的包括主震和余震在内的共141次地震资料,对地震进行筛选、处理,并采用两步回归方法拟合出适合我国黄土地区的土层峰值加速度衰减关系。
本文选取中国地震局工程力学研究所强震动观测与工程振动中心提供的2001—2019年我国黄土地区发生的包括主震和余震在内的共141次地震的1 092条台站记录,震级范围为MS2.4~6.7,各地震震中及台站分布如图1所示,地震主要分布在祁连山、贺兰山、太行山,这些山脉都处于汾渭、银川—河套、龙门山以及六盘山—祁连山等地震带。由于主震和余震的诱发机制不同,因此本次研究不考虑余震记录。工程中的地震动往往针对自由地表,Campbell(1981)认为有明显场地效应的环境会改变自由地表的记录,因此在进行衰减关系研究时通常选择自由场地的数据。在数据筛选时,发现有些台站的两个水平向的PGA差值太大,超过了1.4倍,甚至超过了2倍(图2),将这些异常台站数据剔除。最终获得的台站信息大多为Ⅱ类场地,因此本文针对Ⅱ类土层台站进行研究。
对数据进行如下筛选:①剔除台站三个分量有缺乏的记录; ②剔除基岩场地记录; ③剔除异常台站记录; ④剔除震中距大于500 km的台站记录; ⑤剔除余震记录; ⑥剔除非自由场地记录; ⑦剔除记录到单次地震的台站数量低于3个的记录; ⑧剔除质量差的记录(Abrahamson et al,2014),最后选取到79次地震的898条台站记录,所选记录的震级—震中距分布如图3所示。震中距50 km以内的台站有313个,震中距50~100 km的台站共有202个,震中距100~200 km的台站有197个,震中距200~300 km的台站有51个,记录的均为4级以上地震动数据,震中距300~500 km的台站有33个,记录的几乎都为6级及以上地震动数据。
图1 2001—2019年黄土地区MS2.4~6.7地震和台站分布
Fig.1 Distribution of MS2.4-6.7 earthquakes from 2001 to 2019 and seismic stations in the study area
对筛选后的数据先进行基线校正处理,再进行滤波处理。周宝峰等(2012)对因果滤波器和非因果滤波器进行比较,对4种滤波器在不同阶数下的计算结果进行比较后发现,非因果滤波方式除了具有保持相位不变的特点外,也更有利于减少有用信息的损失; 同时,Butterworth滤波器在各阶数下的稳定性都最好,因此本文也采用四阶非因果Butterworth带通滤波器进行处理,滤波范围为0.1~25 Hz(Converse,Brady,1992)。将处理后的数据选取每个台站两水平向记录中PGA偏大的值用于统计分析研究。
本文采用霍俊荣(1989)提出的考虑距离饱和因素的衰减模型:
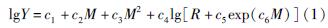
式中:Y为地震动参数,在本文中表示地震的PGA; M为震级; R为距离; c1~c6为回归系数。本文震级直接采用台站信息中提供的面波震级MS(Douglas,Benjamin,2016); 由于本次研究所选地震中只有3个6级以上地震,最大为6.7级地震,其余均为中小地震,因此距离参数直接采用震中距Repi。距离项和震级项是两个重要参数,c3反映了高频地震动随震级饱和现象,c6则反映了高频地震动随距离饱和现象。当c3,c6都为0时,衰减模型为Ⅰ型; 当c3为0,c6不为0时,衰减模型为Ⅱ型; 当c3,c6都不为零时,衰减模型为Ⅲ型。学者一般都以Ⅱ型和Ⅲ型作为衰减模型,由于样本多为中小地震,因此本文采用Ⅱ型模型进行拟合,只考虑距离的饱和因素。
本文采用Joyner和Boore(1979)提出的两步回归法。先将模型改写为:
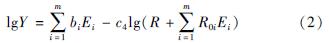
其中:
b=c1+c2M (3)
R0=c5exp(c6M) (4)
式中:将所有震级进行分档,相同震级归为同一档,分档后的总数即为m; bi,R0i为地震的影响因子; 当Y为第i个震级的地震信息时,Ei=1,否则为0。第一步,分别将各震级档的PGA和震中距代入式(2)进行回归得到bi和R0i,选取合适的c4值使回归后的函数方差之和最小; 第二步,将得到的bi和R0i(i=1,2,…,m)值分别代入式(3)、(4)进行回归,计算得到c1、c2、c5和c6。两步回归法的好处是对震级和距离进行解耦,第一步回归时只考虑距离项,不会受震级因素的影响; 第二步回归时只考虑震级项,不会受距离因素的影响。
采用处理过的强震记录数据和两步回归方法得到地震动衰减关系为:
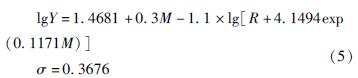
由于MS5~6.5地震的近场数据较少,因此该范围内衰减模型主要由MS3~4地震和中远场台站数据预测得出,受小震级地震和中远场台站数据影响较大。为了将各震级地震的PGA实测值与本文拟合出的PGA衰减曲线进行对比,分别选取震级为MS3.6、MS4.6、MS5.8和MS6.4地震的拟合PGA衰减曲线与实测值进行对比,如图4所示。由图可看出,各震级地震的PGA衰减曲线基本都穿过了数据中心,且除少部分点外,各震级地震的绝大多数PGA实测值都在拟合曲线的±1倍标准差以内。
图4 MS3.6(a)、MS4.6(b)、MS5.8(c)及MS6.4(d)地震的PGA衰减曲线与实测值的对比
Fig.4 Comparison between the attenuation curves and the observed PGA values of MS3.6(a),MS4.6(b),MS5.8(c)and MS6.4(d)earthquakes
为进一步评估本文模型的回归效果,图5给出了地震动残差随震级和距离的分布。残差是评价衰减关系回归结果优劣的重要指标,表示为实测PGA减去衰减关系的计算值:
εij=Yij-uij (6)
式中:Yij为实测值; uij为衰减关系预测值。
残差变量一般应服从均值为零的独立正态分布,当残差均值在零点以上时,说明模型曲线低估了实测值; 当残差均值在零点以下时,说明模型曲线高估了实测值。如图5所示,黑色点为震级或距离内的残差均值,黑色线条为相对应的误差棒,地震动残差均值随震级分布时,误差棒分布为-1~1,且均值均处在零点附近; 地震动残差均值随距离分布时,误差棒分布为-1~0.5,且每个残差均值都接近于零点,该结果表明本文模型对黄土地区的地震动衰减关系的估计相对于MS、Repi相对无偏差。
俞言祥等(2013)按Vs30的NEHRP划分标准将我国分为4个区域,基于美国西部地区地震动、烈度资料和我国烈度资料,采用转换方法建立了我国分区地震动衰减关系,MS≥6.5和MS<6.5的地震分别采用不同的衰减系数。汪素云等(2000)以105°E为界,将我国分为东部和西部地区,基于我国丰富的烈度资料,以有丰富烈度资料和强震记录的美国西部地区作为参考区进行转换得到我国地震动衰减关系。我国黄土地区分布于青藏区和中强地震区,因此将本文衰减模型与俞言祥等(2013)青藏区MS<6.5地震衰减模型和汪素云等(2000)中国西部地区衰减模型进行对比分析。
图6 本文模型与我国青藏区和中国西部地区模型对比
Fig.6 Comparison of the model proposed in this paper with the model of Qinghai-Tibet region by Yu et al(2013)and the model of Western China by Wang et al(2000)
如图6所示,整体上4个参考模型长轴衰减曲线高于短轴,俞言祥等(2013)模型的衰减曲线高于汪素云等(2000)模型和本文模型的衰减曲线,但4个参考模型在近场处的PGA均大于本文模型衰减曲线的PGA; 随后5条衰减曲线分别在4个震级档中的10 km、20 km、40 km、100 km左右处相交后,4个参考模型的衰减曲线又逐渐低于本文的衰减曲线,说明本文模型预测的黄土地区PGA随着距离的增加衰减缓慢。5个模型的衰减曲线与台站实测数据相比,在近场处,除MS3.0~4.0地震外,俞言祥等(2013)模型的长、短轴衰减模型数据均大于台站实测数据,其它衰减模型均较符合台站实测数据的衰减趋势。对于MS6~6.5地震,由于近场台站数据太少,无法对近场处衰减模型与台站实测数据进行有效比较; 当4个震级档的震中距分别大于20 km、40 km、80 km、300 km时,随着震中距的增加,4个参考模型PGA随着距离的增加均逐渐低于台站实测数据,本文模型均相对符合台站实测数据衰减趋势。同时,本文模型在各个震级范围内的标准偏差值都小于参考模型。
基于2001—2019年我国黄土地区发生的141次地震事件的1 092条台站记录,本文选取两水平向峰值加速度偏高的值作为衰减拟合的计算值,采用两步回归法拟合得到我国黄土地区水平向土层峰值加速度衰减关系。通过对本文衰减关系的分析和与其它模型的比较,得出如下结论:
(1)本文衰减关系模型的总残差均在零点附近均匀分布,各震级的绝大多数PGA实测值也分布在本文衰减模型拟合PGA曲线±1倍的标准差以内。由于本文选取的MS≥6地震只有5个,其余均为中小地震,且MS5~6.5地震震中10 km以内台站记录太少,故在近场范围的衰减结果是通过MS3~4地震以及中远场台站数据预测得到,统计回归得到的PGA衰减关系的近场趋势的影响有限。因此本文衰减模型对黄土地区中小地震在中远场的地震动衰减预测更准确。
(2)与中国西部地区、青藏区地震动衰减模型相比,本文衰减曲线在近场处明显低于参考模型的衰减曲线,但超过一定距离后逐渐高于参考模型,这与张振斌和唐丽华(2010)研究得出得出新疆地区地震动衰减关系、与汪素云等(2000)和俞言祥等(2013)地震动衰减模型结果大体一致。差异的原因是,参考模型的研究数据包含了基岩场地数据,而本文得到的黄土地区的衰减关系是由土层地表强震记录统计得到的,反映了黄土地区土层PGA衰减趋势。现有的西部地区的地震动衰减关系模型在黄土地区并不适用,有必要进一步研究适合黄土地区的地震动衰减关系。