基金项目:国家自然科学联合基金重点项目(U2239252); 中国地震局工程力学研究所基本科研业务费专项(2021EEEVL0315).
(中国地震局工程力学研究所 地震工程与工程振动重点实验室,黑龙江 哈尔滨 150080)
(Key Laboratory of Earthquake Engineering and Engineering Vibration,Institute of Engineering Mechanics,China Earthquake Administration,Harbin 150080,Heilongjiang,China)
transmission lines; seismic resilience; vulnerability; functional failure; recovery time
DOI: 10.20015/j.cnki.ISSN1000-0666.2024.0003
备注
基金项目:国家自然科学联合基金重点项目(U2239252); 中国地震局工程力学研究所基本科研业务费专项(2021EEEVL0315).
引言
地震发生后,恢复电力供应是灾区的迫切需求。随着城市抗震韧性概念的发展(翟长海等,2018),减少震后电力系统供电功能损失、加快功能恢复已经成为城市电力系统韧性建设的主要目标。输电线路是电力系统中承担从发电端到用户端传输电能的重要设施。如今大规模、跨区域、高电压输电工程发展迅速,输电线路跨越地形复杂,震后功能损失概率增加。为了减轻地震对经济的影响,亟需对输电线路抗震韧性有准确、清晰的认识。
目前国际国内关于提高城乡韧性的理念越来越深入人心,相关研究已有许多成果。Bruneau等(2003)提出韧性是系统降低破坏事件发生概率、吸收冲击并快速恢复正常运行的能力; 毕熙荣等(2020)总结了韧性量化评估的要素、韧性定量评估方法以及目前国内的韧性量化方法,指出应当结合易损性等成熟成果和待评价系统特点对韧性评估方法进行选择和改进。电力系统是重要的生命线系统,近年来其抗灾韧性也得到了学者们的重视,Reed等(2009)利用飓风破坏后的电力统计数据开展研究,认识到改善电力系统韧性对于其它生命线系统恢复至关重要。而作为电力系统的重要组成部分,输电线路抗震韧性目前以电力可靠性、连通性研究和输电杆塔结构抗震分析较多,如林均岐等(2011)利用图论进行了川西北地区电网抗震连通性和可靠性分析; 贺海磊等(2011)以2008年汶川8.0级地震中杆塔存活率作为判定损坏依据,给出了500 kV和220 kV架空线路杆塔的易损性曲线; Ouyang(2014)在评价电力系统遭受飓风灾害时,对输电线路失效因素如风速、线路周围树木种类等进行了定量考虑; 刘如山等(2013)调查了2013年芦山7.0级地震中的输电线路破坏比例,分析了破坏原因; 李宏男和白海峰(2007)分析了输电塔-线体系在不同灾害下的灾害机理,并提出了结构动力分析方法; Omar等(2018)利用32次震后停电数据,使用3种概率密度函数对电力系统停机时间进行了拟合; Ghorani等(2021)针对滑坡,提出了以各输电杆塔形成串联系统进行停电风险分析的方法。
总体而言,目前关于输电线路的抗震能力、易损性、网络可靠性的研究较多,但对震后功能损失、恢复时间相关研究较少,而在输电线路抗震韧性评价方法方面的研究则几乎为空白。鉴于此,本文从输电线路震后功能失效和恢复时间情况两个方面出发,根据实际震害资料进行统计并总结规律,建立输电线路的功能累积损失函数,进而提出输电线路抗震韧性评估计算方法,并将该方法应用于我国某地区输电线路,分析其抗震韧性。
1 功能失效函数
1.1 输电线路震害统计和破坏等级划分目前输电线路包括架空线路和埋地电缆两种类型,考虑到骨干电网架空输电线路占大多数且较易发生地震破坏,因此本文研究对象为架空输电线路,主要由杆塔与基础、导线、绝缘子、金具以及接地装置等部件组成。《架空输电线路运行规程》(DL/T 741—2019)对线路部件状态,如杆塔倾斜度、绝缘子变形破坏程度等提出了安全运行要求。
在中国地震局电力科考小组、四川电力试验研究院、国网四川省电力公司搜集的2008年汶川8.0级地震震害统计资料(刘如山等,2010)中,输电线路遭受地震破坏的类型主要包括:堡坎裂缝、垮塌、基础滑坡,杆塔裂缝、倾斜、倒塌,塔材变形和导线断股、绝缘子倾斜等,其中堡坎基础相关震害比例很大(谢华飞,2011)。堡坎基础的破坏可能导致杆塔产生裂缝、倾斜、倒塌、塔材变形等问题,从而增大了线路断电的风险,在其破坏数量较多时会与其它震害同时出现,但不会直接导致断电。因此堡坎基础破坏对线路输电功能影响较小,属于线路轻微破坏的情况,震后对此类破坏通常采取监视运行、临时加固等方法以保持线路继续工作。对于杆塔裂缝、倾斜、倒塌等直接影响线路工作状态的震害,需要采取塔身调正、更换部件等措施以恢复正常功能。所以在整理震害资料、判断线路功能时,通常以杆塔破坏为主,堡坎基础破坏为辅。
《生命线工程地震破坏等级划分》(GB/T 24336—2009)中规定,以每10 km杆塔破损数作为评定指标,将输电线路整体破坏等级分为5级:基本完好、轻微破坏、中等破坏、严重破坏和毁坏。本文直接使用该标准的基本规定,并根据实际震害统计情况,把堡坎基础破坏增补到评定指标中:在无杆塔破损时,线路杆塔的堡坎基础破坏数多于总堡坎基础数的5%,线路破坏等级提升一级至轻微破坏,见表1。
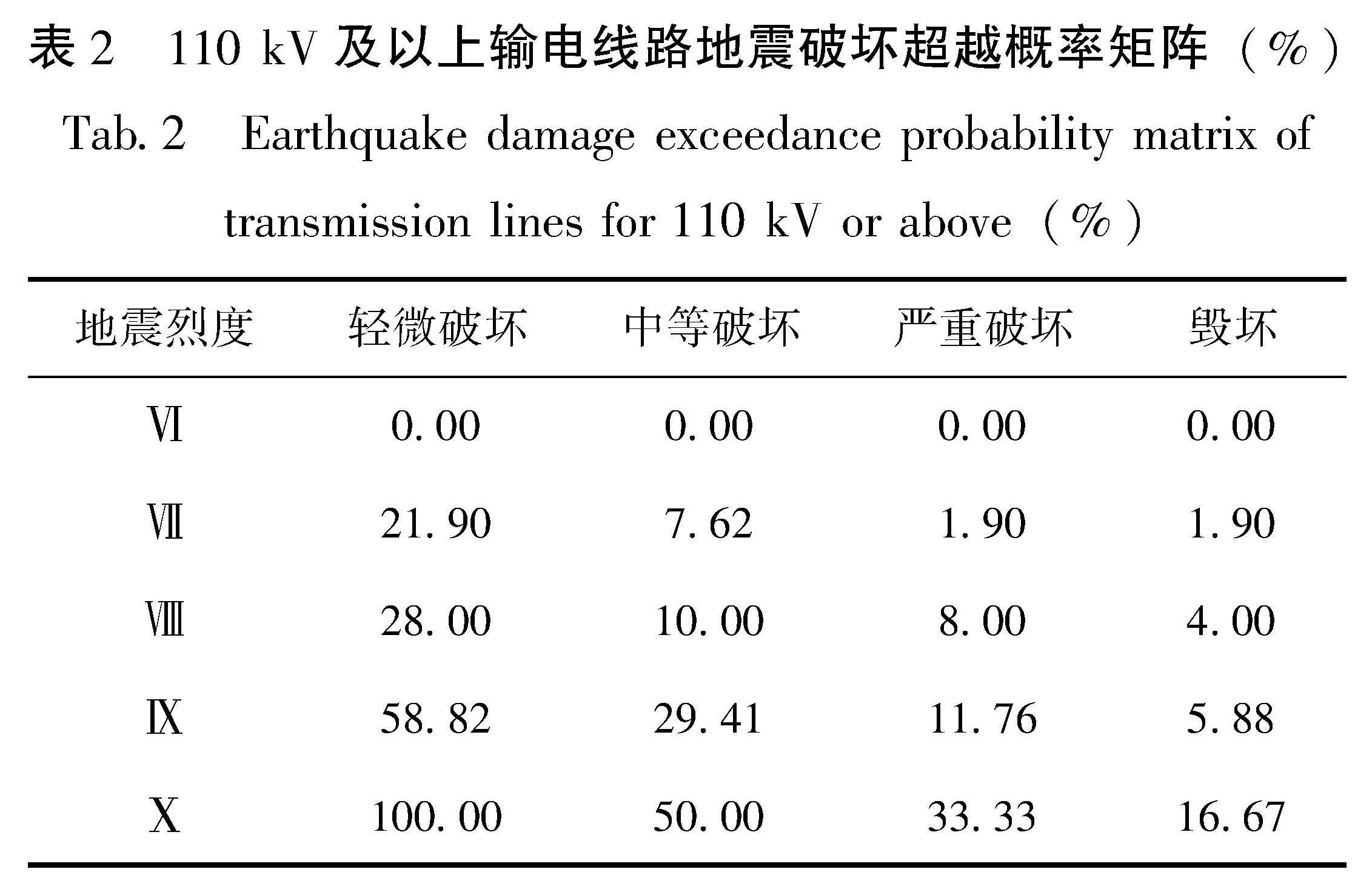
1.2 输电线路易损性曲线的拟合本文收集了2008年汶川8.0级地震后绵阳、阿坝、成都、广元和德阳5个地区共173条110 kV及以上输电线路、78条35 kV输电线路具体破坏信息,并结合破坏等级评定指标对其进行统计,分别得到两种输电线路地震破坏的超越概率矩阵,分别见表2、图3。
地震易损性曲线一般采用对数正态分布描述,本文参考HAZUS-MH技术手册(FEMA,2013)中配电网易损性曲线,使用双参数对数正态分布函数,对地震烈度与不同破坏等级的超越概率的关系进行了曲线拟合,具体公式如下:
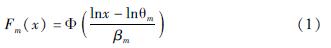
表2 110 kV及以上输电线路地震破坏超越概率矩阵(%)
Tab.2 Earthquake damage exceedance probability matrix oftransmission lines for 110 kV or above(%)表3 35 kV输电线路地震破坏超越概率矩阵(%)
Tab.3 Earthquake damage exceedance probability matrix of 35 kV transmission lines(%)式中:Fm(x)为地震烈度达到x时,输电线路到达某一破坏等级m的概率; m是破坏等级,包括轻微破坏、中等破坏、严重破坏和毁坏; Φ为标准累积正态分布函数; θm为中位数; βm为对数标准差。
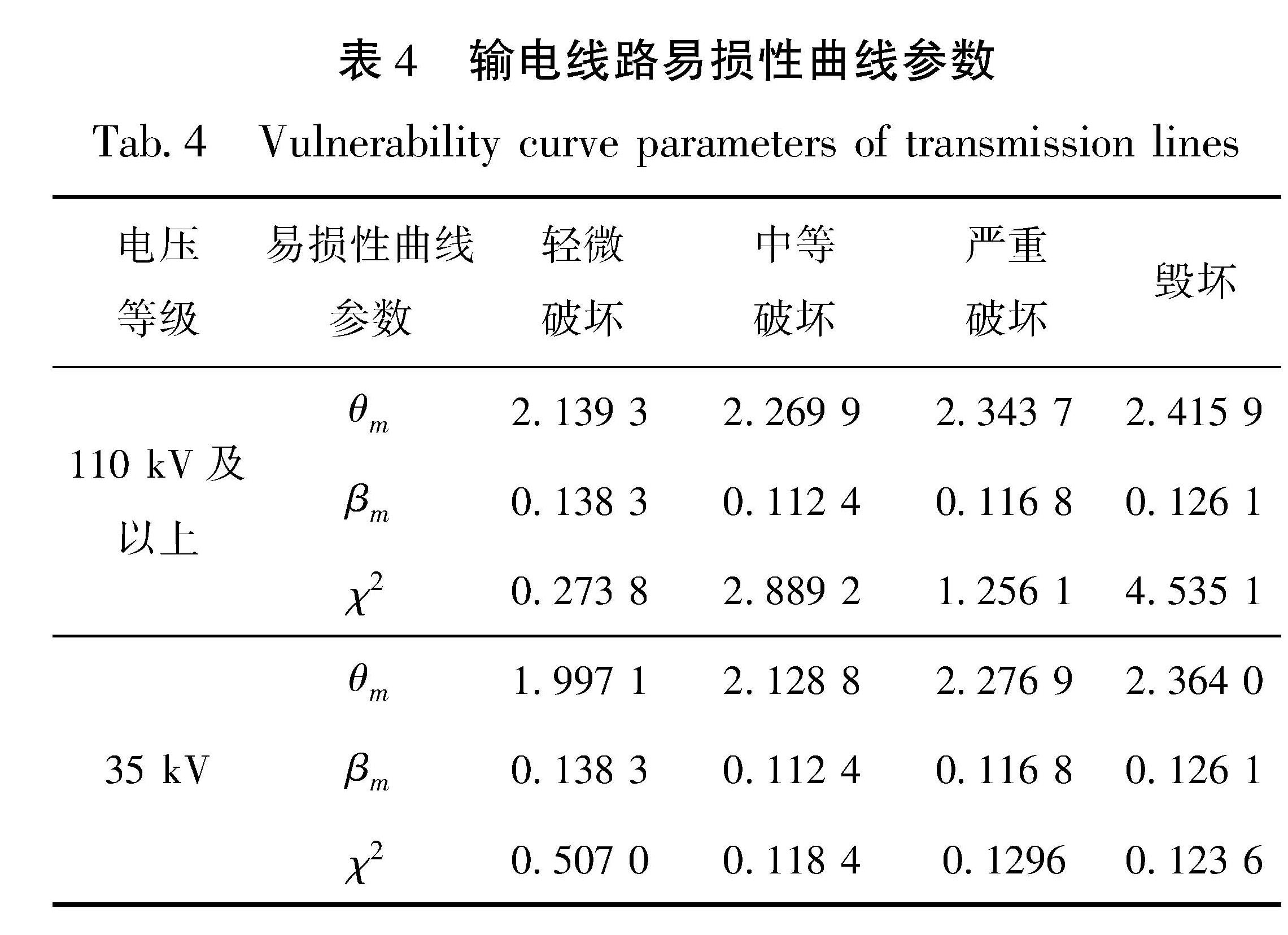
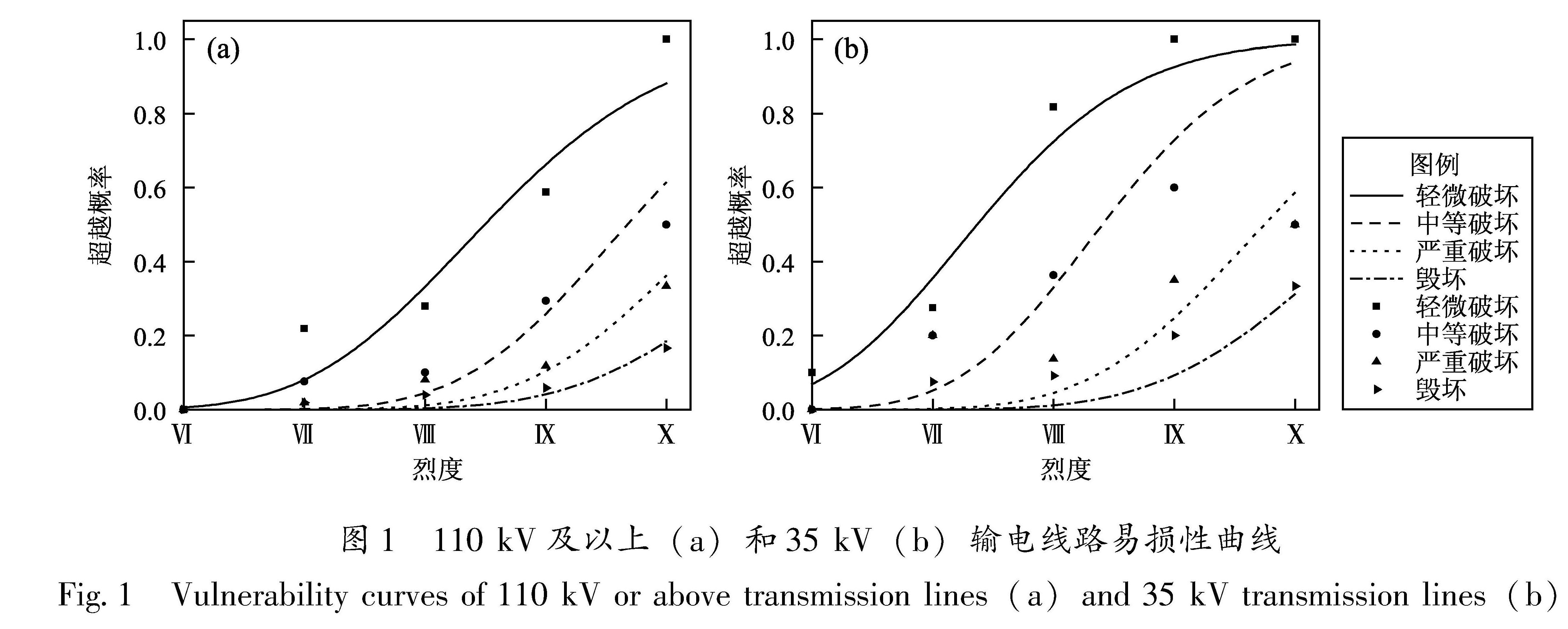
根据式(1),拟合得到110 kV及以上和35 kV的架空输电线路地震易损性曲线,如图1所示,其双参数对数曲线的参数见表4。由图可知,110 kV及以上的输电线路的抗震能力要高于35 kV输电线路。本文采用χ2分布对曲线进行拟合优度检验,自由度取观测烈度组数减1取为4,取95%置信率查卡方分布临界值(Pearson,1992)可得临界值为9.487 7,计算后χ2均小于临界值,通过检验。
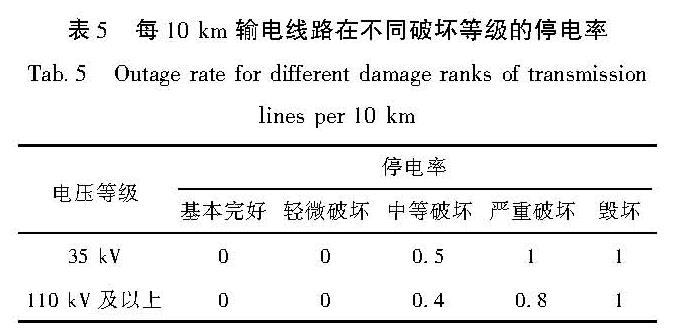
1.3 输电线路功能失效判定以及失效函数震后输电线路是否停电,除了取决于自身受到的破坏程度,还与其上下游变电站、发电厂等电网节点的受损情况有关,本文只讨论由输电线路自身破坏导致的停电情况。汶川地震后输电线路停电率与破坏等级的统计关系见表5。从表5可以看出,在基本完好、轻微破坏等级时,输电线路功能受到影响较小,基本处于完全正常工作状态; 在中等破坏等级时,输电线路处于危险状态需要检修,有的输电线路处于停电状态,有的输电线路未停电,仍处于继续供电状态; 在严重破坏和毁坏等级时,输电线路功能受到影响较大,基本处于无法工作状态。汶川地震震害调查资料显示,部分110 kV及以上线路在严重破坏时仍可在监视情况下运行; 相比110 kV及以上线路,35 kV线路的设备抗震能力较差。因此建立评估模型时,对于输电线路功能失效发生率和破坏等级之间的对应关系,直接采用表5的统计结果。
根据输电线路易损性拟合结果以及其在不同破坏等级的停电率,可以判断具体的某条输电线路震后功能失效情况。设线路长度为L(单位:km),电压等级为i=1、2,包括35 kV和110 kV及以上2个等级。首先将线路划分为10 km的单元(不足10 km按10 km计,四舍五入取整),得到单元数γ为:
γ=round(L/10) (2)
山区不良地质条件以及放大效应导致山区输电线路的损失远大于平原地区。张中近(2017)分析了山区和平原地区的输电线路破坏情况,结合美国ATC-25报告(ATC,1991),取0.2作为平原地区相比山区的易损性曲线折减系数。本文1.2节的易损性统计结果适用于山区和丘陵地形环境,再加入地形折减系数α1,α1在地形为山地时取1,平原时取0.2,每个10 km单元输电线路的停电率计算公式如下:

式中:Pn为输电线路第n个单元长度的停电率; j为单元所处烈度区; k=1、2、3、4、5,分别代表5种破坏等级; Pijk为线路在i电压等级j烈度处于k破坏等级的概率,由表4参数获得; Qk为破坏等级对应的停电概率,按照表5数据获得。
单条输电线路是各单元串联系统,其中某一单元失效则整体停电,所以一条线路功能失效率函数表达式为:
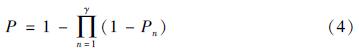
式中:P为输电线路功能失效率; γ为输电线路中单元长度个数。
2 恢复时间函数
4 输电线路抗震韧性计算实例
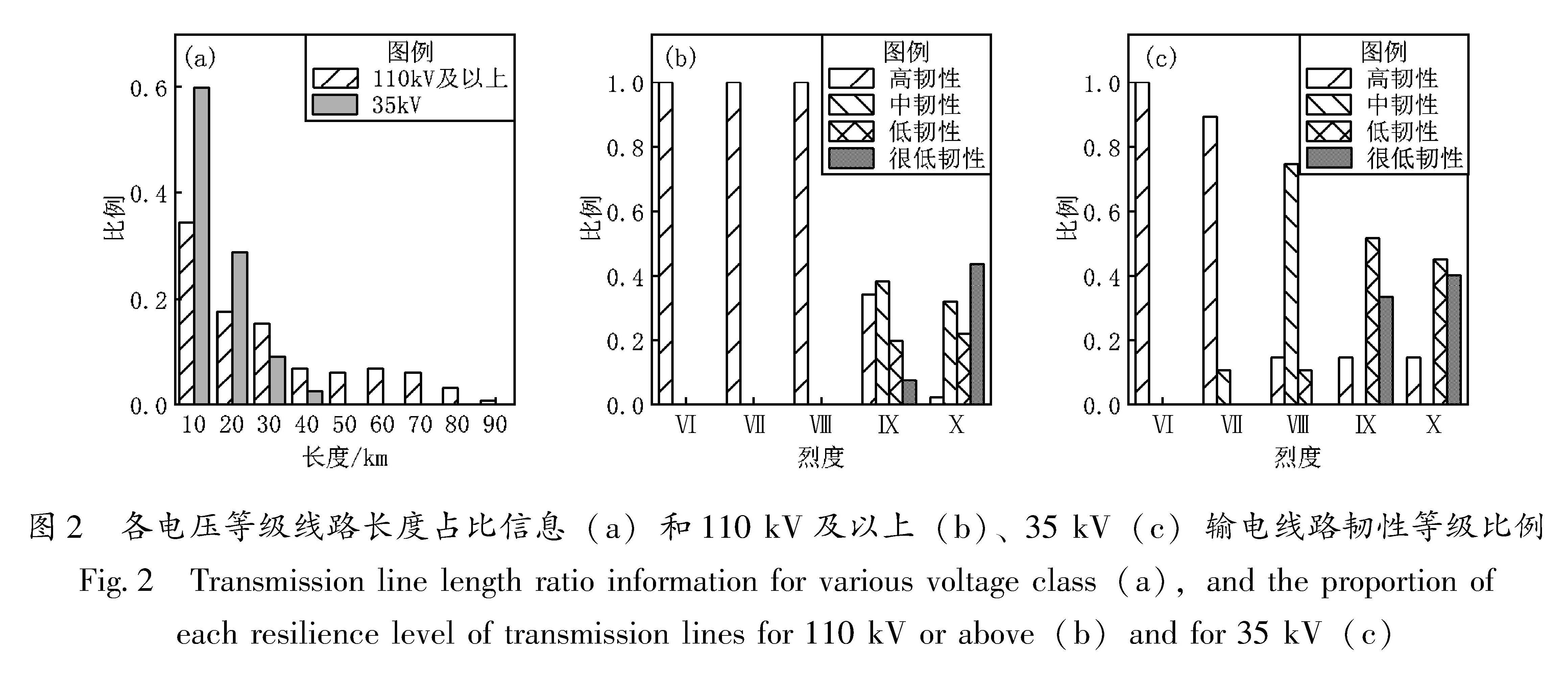
4.1 基本情况本文选取我国某地区输电线路,使用本文方法对其抗震韧性进行试算。研究地区地形较为复杂,区域内多为山地,平原面积较少。根据该地区输电线路的长度、地形等资料,按电压等级对其划分,共计有122条35 kV线路,总长度1 567 km,其中山地线路96条,长度1 430 km,平原部分线路26条,长度137 km; 131条110 kV及以上线路,总长度3 709 km,其中山地线路115条,长度3 413 km,平原线路16条,长度296 km,按单条线路长度分类占比如图2a所示。
4.2 结果与讨论研究地区110 kV及以上和35 kV等级的输电线路处于不同韧性等级输电线路数量占比如图2b、c所示。由图可见,110 kV及以上输电线路在Ⅷ度及以下时为高韧性水平,高于Ⅸ度时,中、低韧性水平占比增多,在Ⅹ度时韧性水平很低的输电线路数量占比大量上升; 35 kV输电线路在低于Ⅶ度时基本为高韧性水平,而在Ⅷ度时,中等韧性水平占绝大多数,在Ⅸ度及Ⅹ度时基本处于低和很低韧性水平。小于Ⅷ度烈度时,各电压等级的输电线路损失很少,而在高烈度下损失较多,总体上35 kV比110 kV及以上线路损失更多,该结果与以往评价输电线路震后损失结果(谢强,2008)相近。
5 结论
本文基于2008年汶川8.0级地震后5个受灾地区的输电线路震害资料,分析了输电线路的物理破坏现象与输电线路功能损失、恢复时间的关系,分别建立了输电线路的功能失效函数和恢复时间函数,然后结合韧性定义给出了输电线路功能损失累积函数,在此基础上构造了输电线路的韧性指数函数,进行了韧性水平等级划分,确立了韧性指数与韧性等级的对应关系,提出了以电压等级、长度、地形地貌为参数的输电线路抗震韧性计算方法。使用该方法对我国某地区输电线路进行试算,计算结果与以往对输电线路震害情况的定性判断基本相符,同时验证了山地地区在低烈度时损失较轻、在高烈度时损失较重的基本规律。
输电线路的电压等级、长度、地形是影响其震后功能最重要的3个影响因素,且容易收集,因此本文建立的韧性评价方法易于使用和推广,操作性强,但应当指出的是,该方法本质上是一种静态分析方法,对于具体的恢复过程和其它影响功能损失的因素、机理等需进一步研究,评估模型的参数取值也有待于更多地震案例的统计来支持。在韧性水平等级划分上,本文提出的划分方法可供一般部门和用户参考,实际应用中,不同用户可根据自身特殊需求进行个性化分级。
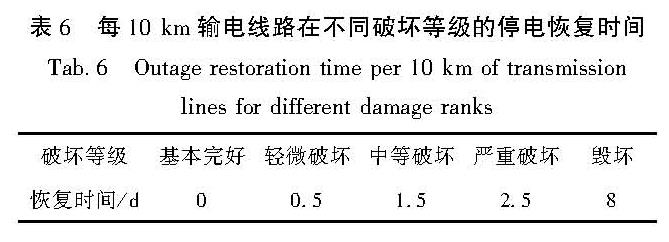
2.1 恢复时间统计分析输电线路与变电站的破坏情况和恢复运行时间统计往往是联结在一起的,这对独立分析输电线路破坏与停电恢复时间的对应关系造成一定困难。本文通过整理汶川地震中输电线路的破坏统计资料及恢复时间统计资料的交集,去除交集中有可能与两端发电厂、变电站停运时间相关的数据,得到220、110和35 kV三个电压等级相对独立的线路停运时间数据,并对输电线路做10 km长度的归一化处理后再进行统计。从震害数据分析中看到,在轻微破坏等级时,大部分输电线路当天即可恢复; 在中等破坏等级时,输电线路恢复时间在1~4 d不等; 而在严重破坏和毁坏等级时,输电线路受随机性影响较大。影响不同线路恢复的因素较多,如线路重要程度、地形、恢复策略和恢复资源等。结合统计情况和破坏等级定义,本文给出每10 km输电线路在不同破坏等级停电后恢复用时的平均值,见表6。
2.2 恢复时间函数要得到整条输电线路恢复时间,首先要依据式(2)计算输电线路的10 km长度的单元个数,然后每个单元的停电时间为:

式中:Tn0为山地条件下某线路第n个10 km单元的停电时间; tk为k破坏等级下的停电恢复时间,由表6获得。
电压等级线路、电气设备均相同时,不同地形的造价差异体现了输电线路建设的难易程度,也可以认为是线路恢复的难易程度。张中近(2017)在整理了国家电网输变电工程不同等级通用造价册后,得到了不同地形的造价差异,由此将结果归一化处理后得到地形修正系数α2,取值见表7,因此考虑地形恢复难度的时间Tn表示为:
Tn=α2Tn0 (6)
输电线路修复时间与长度呈线性相关,则一条输电线路总体恢复时间T应为全体单元的恢复时间之和:

表7 地形修正系数α2
Tab.7 Terrain reduction coefficient α23.1 功能失效累积损失函数的构建对于抗震韧性的衡量方法研究,最早由Bruneau等(2003)提出了系统功能损失在时间上的积分作为韧性衡量指标,利用三角形面积的积分表示韧性损失; Ouyang等(2012)则将系统震后功能曲线划分为3个阶段,比韧性三角形增加了功能下降阶段,利用梯形面积积分表述韧性损失。输电线路的韧性取决于功能失效和恢复速度,越容易停电、恢复时间越久则韧性越差,而停电和通电具有瞬时性,修复完成后即刻恢复功能,而不像其它系统具有逐步恢复的过程。因此本文选择矩形功能恢复曲线来计算输电线路功能失效累积损失:
RL=P×T (8)
式中:RL为输电线路的功能失效累积损失; P为功能失效率,由式(4)计算得出; T为恢复时间,由式(7)计算得出。
3.2 韧性水平划分功能累积损失RL是一个停电时间的期望,单位是d。划分输电线路不同韧性水平等级,应当综合考虑输电线路功能损失、恢复速度以及用户的可接受程度。根据国家电网有限公司供电服务“十项承诺”的规定,城镇地区应在报修后3 h内恢复供电,本文将此时间定为城镇地区用户正常用电期间可接受的停电时间,并由此作为输电线路韧性水平高与中的划分界限。在汶川地震震害统计结果中发现,输电线路恢复时间大于8 d,线路破坏严重,其中一些线路属于重建状态,可认为其已完全丧失恢复能力。结合统计的恢复时间,本文给出输电线路韧性水平等级划分标准,见表8。为了方便与其它电力系统韧性成果进行横向对比,本文将RL进行对数归一化后得到类似震害指数的韧性指数为:
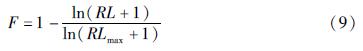
式中:RLmax为8 d,当RL≥RLmax时,取RL=RLmax。
针对不同地震烈度情况,得到的输电线路韧性水平等级也不同。在实际工作中,判断输电线路是否满足当地韧性需求,需要结合用户需求,预先设定需求韧性水平后与计算结果进行比较。
- 毕熙荣,冀昆,宗成才,等.2020.工程抗震韧性定量评估方法研究进展综述[J].地震研究,43(3):417-430.
- Bi X R,Ji K,Zong C C,et al.2020.Review on advances in quantitative evaluation methods for engineering seismic resilience[J].Journal of Seismological Research,43(3):417-430.(in Chinese)
- 贺海磊,郭剑波,谢强.2011.电气设备的地震灾害易损性分析[J].电网技术,35(4):25-28.
- He H L,Guo J B,Xie Q.2011.Vulnerability analysis of power equipments caused by earthquake disaster[J].Power System Technology,35(4):25-28.(in Chinese)
- 李宏男,白海峰.2007.高压输电塔-线体系抗灾研究的现状与发展趋势[J].土木工程学报,40(2):39-46.
- Li H N,Bai H F.2007.State-of-the-art review on studies of disater resistance of high-voltage transmission tower-line systems[J].China Civil Engineering Journal,40(2):39-46.(in Chinese)
- 林均岐,陈永盛,刘金龙.2011.电力系统震后网络连通性研究[J].地震工程与工程振动,31(6):181-185.
- Lin J Q,Chen Y S,Liu J L.2011.Study on post-earthquake connectivity of electric power systems[J].Journal of Earthquake Engineering and Engineering Vibration,31(6):181-185.(in Chinese)
- 刘如山,刘金龙,颜冬启,等.2013.芦山7.0级地震电力设施震害调查分析[J].自然灾害学报,22(5):83-90.
- Liu R S,Liu J L,Yan D Q,et al.2013.Seismic damage investigation and analysis of electric power system in Lushan MS7.0 Earthquake[J].Journal of Natural Disasters,22(5):83-90.(in Chinese)
- 刘如山,张美晶,邬玉斌,等.2010.汶川地震四川电网震害及功能失效研究[J].应用基础与工程科学学报,18(S1):200-211.
- Liu R S,Zhang M J,Wu Y B,et al.2010.Damage and failure study of Sichuan electric power grid in Wenchuan earthquake[J].Journal of Basic Science and Engineering,18(S1):200-211.(in Chinese)
- 谢华飞.2011.地震灾害对电网的损毁性评估技术研究[D].杭州:浙江大学.[LL]Xie H F.2011.Research on damage assessment to electrical grid caused by earthquake[D].Hangzhou:Zhejiang University.(in Chinese)
- 谢强.2008.电力系统的地震灾害研究现状与应急响应[J].电力建设,29(8):1-6.
- Xie Q.2008.State-of-the-art of seismic disaster research and emergency response of electric power system[J].Electric Power Construction,29(8):1-6.(in Chinese)
- 翟长海,刘文,谢礼立.2018.城市抗震韧性评估研究进展[J].建筑结构学报,39(9):1-9.
- Zhai C H,Liu W,Xie L L.2018.Progress of research on city seismic resilience evaluation[J].Journal of Building Structures,39(9):1-9.(in Chinese)
- 张中近.2017.电力设施地震经济损失快速评估[D].哈尔滨:中国地震局工程力学研究所.
- Zhang Z J.2017.Rapid evaluation of electric power facility economic loss caused by earthquake[D].Harbin:Institute of Engineering Mechanics.(in Chinese)
- DL/T 741—2019,架空输电线路运行规程[S].
- DL/T 741—2019,Operating code for overhead transmission line[S].(in Chinese)
- GB/T 24336—2009,生命线工程地震破坏等级划分[S].
- GB/T 24336—2009,Classification of earthquake damage to lifeline engineering[S].(in Chinese)
- ATC.1991.ATC25 Seismic vulnerability and impact of disruption of lifelines in the conterminous United States[R].Advanced Technology Council.
- Bruneau M,Chang S E,Eguchi R T,et al.2003.A framework to quantitatively assess and enhance the seismic resilience of communities[J].Earthquake spectra,19(4):733-752.
- FEMA.2013.Multi-hazard loss estimation methodology,earthquake model,Hazus-MH 2.1,technical manual[R].Washington D C,USA.
- Ghorani R,Fattaheian-Dehkordi S,Farrokhi M,et al.2021.Modeling and quantification of power system resilience to natural hazards:A case of landslide[J].IEEE Access,9:80300-80309.
- Omar K,Paolo C G,Mahin S A.2018.Downtime estimation and analysis of lifelines after an earthquake[J].Engineering Structures,173:393-403.
- Ouyang M.2014.Review on modeling and simulation of interdependent critical infrastructure systems[J].Reliability Engineering & System Safety,121(1):43-60.
- Ouyang M,Dueñas-Osorio L,Min X.2012.A three-stage resilience analysis framework for urban infrastructure systems[J].Structural Safety,36-37:23-31.
- Pearson K.1992.On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling[M]//Springer Series in Statistics,11-28.
- Reed D A,Kapur K C,Christie R D.2009.Methodology for assessing the resilience of networked infrastructure[J].IEEE Systems Journal,3(2):174-180.