基金项目:黑龙江省重点研发计划项目(GA22C001); 国家重点研发计划课题(2019YFC1509301).
(1.中国地震局工程力学研究所 地震工程与工程振动重点实验室,黑龙江 哈尔滨 150080; 2.地震灾害防治应急管理部重点实验室,黑龙江 哈尔滨 150080)
(1.Key Laboratory of Earthquake Engineering and Engineering Vibration,Institute of Engineering Mechanics,China Earthquake Administration,Harbin 150080,Heilongjiang,China)(2.Key Laboratory of Earthquake Disaster Mitigation,Ministry of Emergency Management,Harbin 150080,Heilongjiang,China)
buried pipeline; infinite element; boundary condition; finite element analysis; pipe-soil interaction
DOI: 10.20015/j.cnki.ISSN1000-0666.2024.0006
备注
基金项目:黑龙江省重点研发计划项目(GA22C001); 国家重点研发计划课题(2019YFC1509301).
引言
埋地管线纵横交错、长距离延伸、互相关联,构成管线与管网。埋地管线在历次大地震中都有不同程度的震害,甚至会引发次生灾害,给国计民生带来重大损失。由于其隐蔽性和复杂性,管网破坏后在短期内修复困难,严重影响震后基础设施功能恢复的进程。由于埋地管线和管网的抗震试验受条件限制,其研究范围和成果有限,采用数值模拟的方法进行分析既能提升效率,又能节约成本,对整套地下管网的地震反应性状的研究或抗震设计都大有助益。
埋地管线在地震波作用下的反应分析最早由Newmark和Hall(1975)提出,Kennedy等(1977)在Newmark管道模型假定的基础上进行改进,提出了二维弹性地基梁模型。这2种常用的方法都是将管道周围的土体对管道的作用简化为一系列土弹簧的作用,计算精度难以满足要求。鉴于此,笔者将埋地管线及周围土体从半无限空间中取出作为一个整体进行研究,但面临3个需要重点考虑的问题:①地震动如何输入?②土体的截断面如何设置人工边界条件?③管线周围的土体取值范围如何确定?
人工边界早期的处理方法是避开边界问题。如果人工边界至研究对象的距离L≥[SX(]cT[]2[SX)],其中c为无限域介质的最大波速,T为地震动持续时间,则结构反应在0≤t≤T将不受边界的影响,但是这种处理方法计算效率极低,有时甚至低到无法计算的程度。考虑管线-土体相互作用的埋地管线地震反应数值模拟通常只能人为截取足够大的有限域来模拟实际的半无限空间,此时截断面必须设置合理的人工边界,再配合波动输入方法来消除地震波在截断面上的反射,诸多学者曾对此开展了深入研究。考虑其计算精度、计算效率以及在通用有限元软件中的兼容性,应用较为广泛的人工边界有黏性边界、黏弹性边界、无限元边界和远置自由边界等。其中无限元最早由Ungless(1973)提出,经过Bettess等(1977,1984),Zhang和Zhao(1987)的改进和发展,无限元已经从一维发展到三维,从单向映射扩展到了多向映射。无限元的主要特点为:①局部坐标系中的有限域到整体坐标系中的无限域的映射。即局部坐标趋近于1时,相应整体坐标趋向无穷大,从而实现计算范围趋于无穷远点; ②无限域上位移衰减过程的描述。即局部坐标趋近于1时,位移趋近零,从而实现无限远处位移为零的边界条件,无限元具有较强的鲁棒性,其与有限元方法的协调性较好,计算效率和精度都较高。本文利用ABAQUS软件提供的丰富的无限单元库(石亦平,周玉蓉,2006; 庄茁,2009),在模型截断面的侧边界和底边界采用三维动力无限元边界模拟半无限空间,在非一致地震波激励下对埋地管线的动力响应进行了数值分析,确定了管线周围土体的取值范围。
1 非一致激励下动力无限元边界上的地震动输入方法
1.1 ABAQUS动力无限元基本理论ABAQUS动力无限元边界以Lysmer和Kuhlemeyer(1969)的动力响应理论为基础,由平面体波垂直入射边界的运动方程进行推导,包含以下基本假设:①有限域边界区动力反应很小,边界区介质在线弹性范围内响应; ②无限单元区域介质满足理想线弹性体假定。则质点运动微分方程可表示为:

式中:ρ为介质密度;
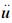 为质点加速度矢量; σ为质点应力; x为质点坐标矢量。
为质点加速度矢量; σ为质点应力; x为质点坐标矢量。根据理想线弹性体假定,由广义胡克定律可知,质点的应力应变关系可用张量表示为:
σij=λεkkδij+2Gεij (2)
式中:εkk为边界面质点的应变分量; λ和G为拉梅常数,
 ; E为介质的弹性模量; v为介质的泊松比。
; E为介质的弹性模量; v为介质的泊松比。根据无限单元区域介质理想弹性体的小变形假定,边界面上任意一点的应变可表示为:
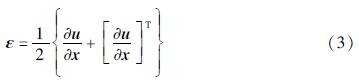
由式(1)~(3)可得质点运动方程为:

沿x轴传播的平面波可表示为:
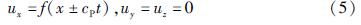
式中:ux=f(x-cPt)代表沿x轴正方向传播的波; ux=f(x+cPt)代表沿x轴负方向传播的波。将式(5)代入式(4),可得P波波速为:

同理可得S波波速为:

为了吸收从有限域反射回边界上的反射波,无限单元内置了分布阻尼,其表达式为:

现通过一维平面纵波ux=f1(x-cPt), uy=uz=0垂直入射自由边界的形式求解分布阻尼系数dP,如果其在边界面上完全反射,则应满足应力为零的自由边界条件,此时反射波可表示为:
ux=f2(x-cPt), uy=uz=0 (9)
根据本节设定的2个基本假设,边界面上的力和位移均满足叠加原理,边界面上的位移、应力和质点振动速度可表示为:
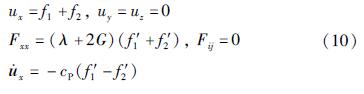
式中:f1',f2'分别为入射波和反射波的速度; Fxx为边界面上某一质点在x方向的合应力。
无限元边界相当于在自由边界面上施加了分布阻尼,根据力的平衡原理有:入射波应力矢量+入射波引发的边界阻尼力+反射波应力矢量+反射波引发的边界阻尼力=0,即:
(λ+2G-dPcP)f1'+(λ+2G+dPcP)f2'=0 (11)
如果边界面上的反射波被完全吸收,则只需要合理选取阻尼系数dP的取值,使反射波f2=0(f2'=0),此时P波入射时无限元边界的阻尼系数表示为:

同理可得S波入射时无限元边界的阻尼系数为:
dS=ρcS (13)
1.2 地震动输入的波动法从震源出发的地震波,经过在地壳中复杂介质的多次折射、反射,很难确定其入射方向。在整个传播过程中,地震波的幅值、频谱组成及其传播和振动的方向都在不断改变,且其各个频率分量的传播速度也不相同。地震波中所包含的体波、面波也随到达的时间不同而不断改变。目前尚难区分在地表记录到的地震动加速度波形中的各个波型,但场址地表某点的地震动加速度总是可以分解成相互正交的3个分量,通常取为沿地表2个水平方向和垂直于地表的竖直方向。总体上,由于地壳介质的密度由地表向下随地层深度变深而逐渐增大,根据波在不同介质中传播的折射和反射定律,由地壳深部向地表传播的地震波,其入射方向将逐渐变为接近垂直水平地表的竖向方向。对于研究对象为地表以下十几米到几十米的地下结构,可以认为地震波在其底面垂直入射。因此,本文地震动的输入方法均假定地震波从有限域的底边界垂直入射(胡聿贤,2006; 赵武胜等,2010)。
刘晶波等(2005,2006)和杜修力(2006)通过把近域地基作为半无限空间自由场地基的子结构,推导出了入射地震波作用下的边界相互作用力P的一般公式为:

式中:n为边界外法向方向余弦向量; A为边界节点的影响面积; K、C为边界上的等效刚度和阻尼系数。
谷音等(2007),杜修力等(2009)和赵建峰等(2007)通过对局部波场进行分解,结合波传播的物理规律,推导出了适用于应力型人工边界的各个边界面的等效地震荷载公式。对于无限元边界,K=0,当S波入射时,C=DS=ρcS; 当P波入射时,C=DP=ρcP。假设直角坐标的x-y面平行于底边界,z轴竖直向上,P波和S波在底边界竖直入射(S波沿x轴向振动),位移时程分别为uP(t)和uS(t),则有限元-无限元耦合模型边界上应输入的P波等效节点力σ(t)为:
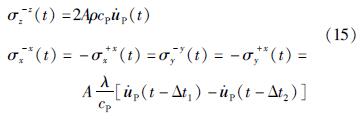
S波等效节点力σ(t)为:
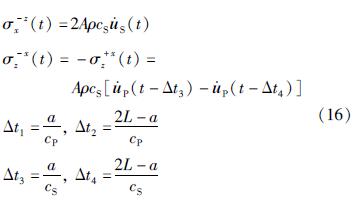
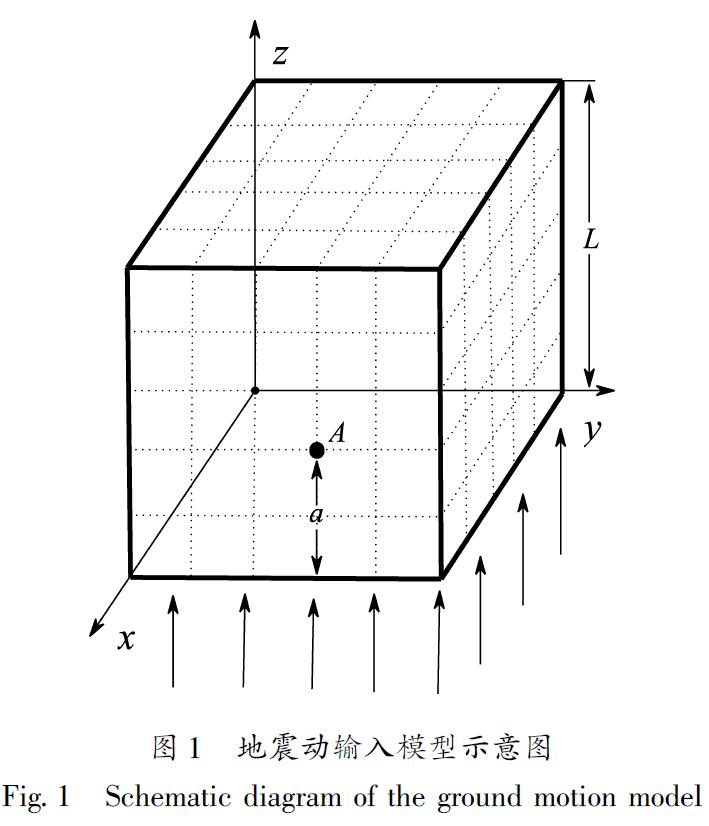
式中:等效节点力的下标为分量方向,上标为节点所在人工边界的外法线方向,与坐标轴相同为正,反之为负; Δt1和Δt2分别为入射P波和地表反射P波的时间延迟; Δt3和Δt4为入射S波和地表反射S波的时间延迟。如图1所示,a为节点到底边界的距离,L为底边界到地表的距离。动力计算时可将给出的地震动通过式(15)(16)转化为节点力,像面荷载一样以节点力的形式进行施加。
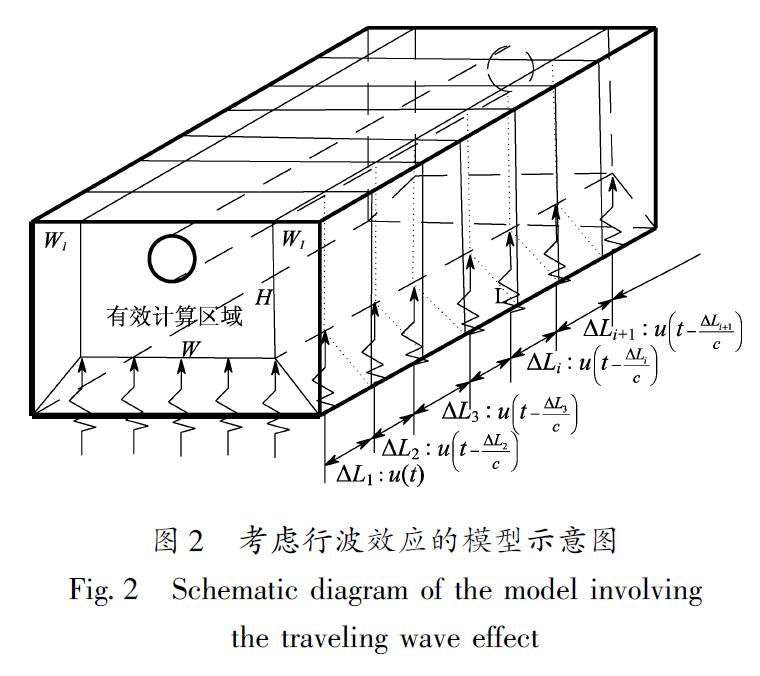
1.3 基于波动法的非一致激励问题现阶段对空间地震动传播规律的研究以行波效应为主,基岩面上不同位置的地震激励是不同步的(图2)。假设行波传播方向与管道铺设方向相同,基底各点受到的地震激励存在相位差Δt,即地震波从基底一点传到相邻的下一点所用的时间为:

式中:ΔL为相邻地震动入射点的距离; c为地震波水平方向的视波速。
如果模型底边界任一地震动入射点i在t时刻的地震加速度为
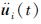 , 则与其相邻点i+1所对应的地震加速度为:
, 则与其相邻点i+1所对应的地震加速度为: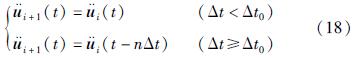
式中:Δt0为最小时间间隔,取值与输入地震动记录的时间步长有关。实际输入的地震动是一系列离散的点,其采样率一般为Δt0=0.005或0.01 s,为了保证各点输入地震动的时间标准与原记录保持一致,以ΔLi=cΔt0为单位对模型在沿着地震动传播方向上进行等间隔分段,各段ΔLi内采用一致输入,相邻段ΔLi和ΔLi+1在时间上相差Δt0。
2 模型设计
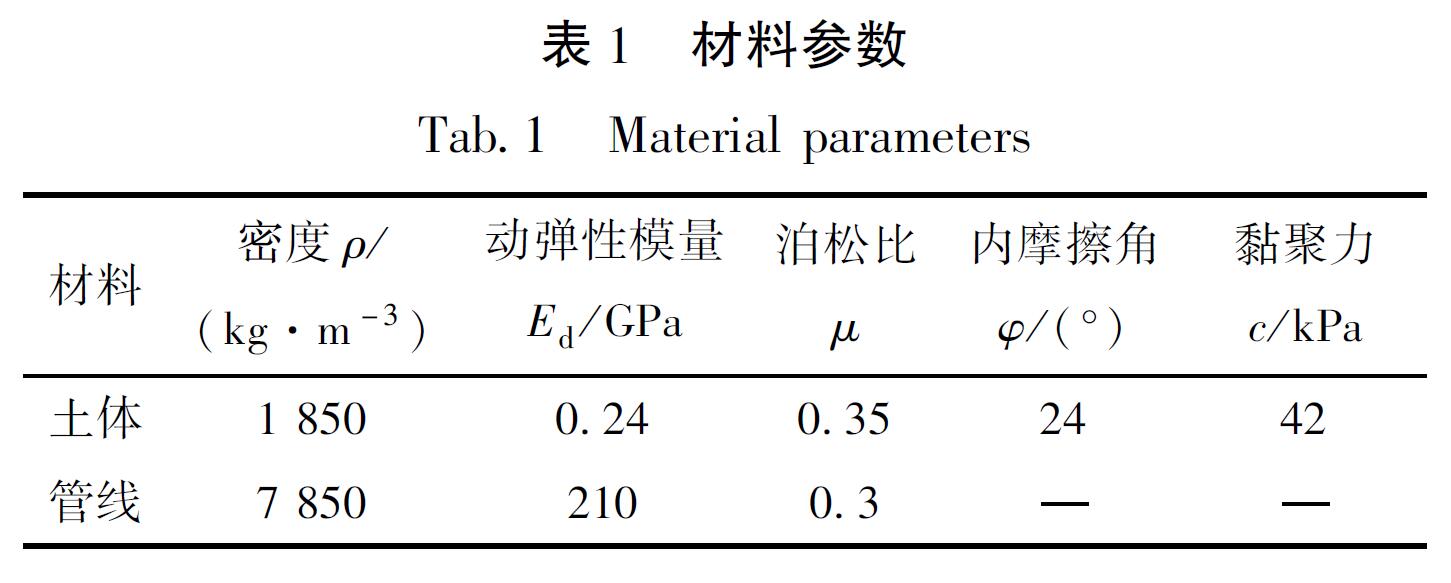
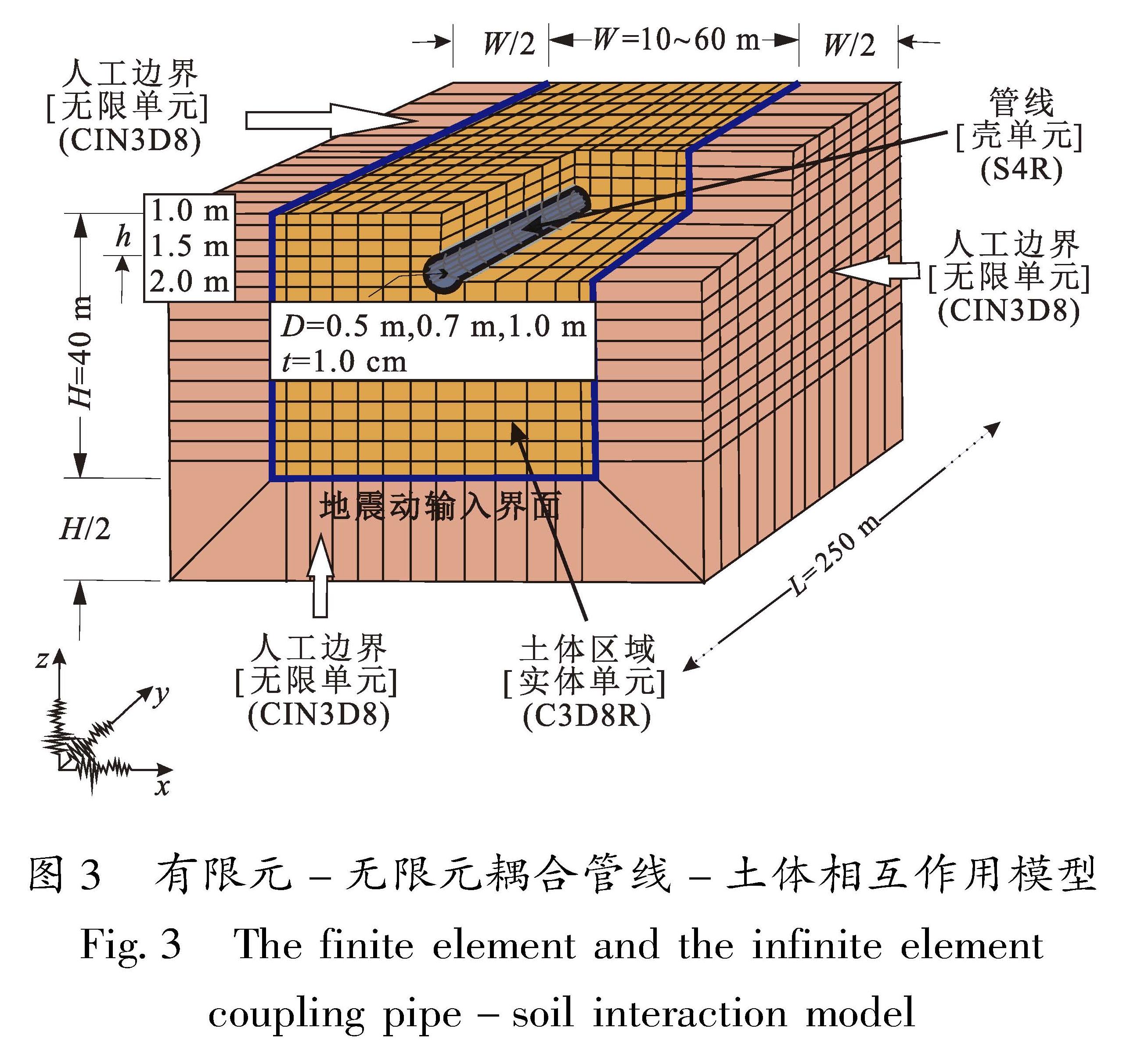
2.1 基本参数本文研究长地下埋设管线,管线由预制铸铁管构成,管材选用X42铸铁管,轴向设计拉伸曲线采用Ramberg-Osgood方程(Ramberg,Osgood,1943)拟合,具体参数见表1。三维土体的等效有限域计算尺寸为有效宽度W,土层厚度H,管线分布长度L,土体的本构模型采用线性Drucker-Prager(D-P)模型。考虑管线-土体接触区域的应力集中现象,对管线附近的土体离散网格局部加密,三维土体自由场计算模型如图3所示。
2.2 管线-土体相互作用效应在管线-土体的相互作用分析中,由于管线和土体刚度存在较大差异,在地震波作用下,管线和土体的交界面上可能发生明显的相对剪切滑移,为了考虑这种复杂的相互作用效应,在管线-土体交界面上通过设置接触单元进行模拟。该单元在交界面的法向方向采用硬接触,即只考虑土体对管道的压应力,忽略土体对管道的拉应力; 在交界面的切向方向采用库伦摩擦准则计算管线-土体之间的摩擦力为:
τ=μ×P (19)
P=WBbD (20)
图3 有限元-无限元耦合管线-土体相互作用模型
Fig.3 The finite element and the infinite elementcoupling pipe-soil interaction model式中:P为两接触面上的法向压应力; W为土的比重; D为管径; Bb为管沟顶部宽度; μ为管线-土体之间的摩擦系数,根据《工程地质手册(第四版)》(常士骠,张苏民,2007),μ取0.5。当接触面上的切向剪切应力小于摩擦力时,接触面沿切向不发生相对滑移; 反之,接触面沿切向发生相对滑移。
2.3 边界条件在模型截断面设置动力无限元边界,模型的侧边界和底边界采用三维动力无限元边界模拟半无限空间,采用CIN3D8单元离散; 由于整个模型属细长结构,根据圣维南原理的局部效应,端部截断面对管线中间段的受力影响较小,故两端边界采用远置滑动自由边界,即仅约束界面的y、z方向自由度,不约束x方向自由度。具体设置见表2。
2.4 地震动输入原则《油气输送管道线路工程抗震技术规范》(GB/T 50470—2017)指出,根据大量震害统计资料,一般场地的地下直埋管道地震动峰值加速度(PGA)大于或等于0.3 g时才开始破坏。为了安全起见,PGA≥0.2 g时,地下直埋管道应进行抗拉伸和抗压缩验算。已有研究表明,PGA随地面下的深度的增加逐渐衰减,但具体的衰减规律尚未达成共识。《苏联地震区建筑设计规范》(СНИПⅡ-A 12-69)中规定,地面下100 m深处设计地震加速度可取为地面的50%; 《印度标准:结构抗震设计规范》(IS:1893—1984)规定,地面下30 m深处设计地震加速度可减少50%; 冈本舜三(1978)建议在地下几十米深处的设计地震加速度可取为地面的1/2~1/3; 《油气输送管道线路工程抗震技术规范》(GB/T 50470—2017)建议地下50 m深处的设计地震加速度值取为地面的50%,以上按内插法取用。本文地震动以自由表面的PGA(0.2、0.3、0.4、0.5 g)为基准,y方向输入时考虑地震波的行波效应,x、z方向一致输入。加速度最大值按照1(y方向):0.85(x方向):0.65(z方向)对其调幅,再按照《油气输送管道线路工程抗震技术规范》(GB/T 50470—2017)的建议在基底输入面折减。
3 埋地管线周围土体计算范围取值
管线周围土体截取足够大的方盒形有限域、同时在边界上施加相应的近似约束边界条件模拟无限域时,对“足够大”的界定令人困扰:区域较小对数值计算规模的控制很有利,但理论上会带来较大误差; 区域较大能减小理论误差,但数值计算规模将以级数倍增加。目前对各类人工边界计算区域合理取值的讨论较少,无限元边界的位置问题的研究还是空白,以下对埋地管线的有限土体计算区域取值问题进行讨论。
3.1 有效计算深度H场地土层对地震动有放大效应。已有研究表明,埋地管线的破坏率随着场地覆盖层厚度的增加而升高,但覆盖层厚度超出一定范围后破坏率变化不大。在土层的地震反应分析中,如果以实际基岩面作为地震动输入面,覆盖层厚度会变得很大,这在一般工程计算中难以实现。因此本文不在实际基岩面输入地震波,而是采用在土层的假想基岩面处输入地震波的方式计算土层的动力反应。工程中常按以下原则确定假想基岩面:①假想基岩面以下各层岩土的剪切波速均不小于500 m/s; ②当地面5 m以下存在剪切波速大于其上部各土层剪切波速2.5倍的土层,且该层及下卧各层岩土的剪切波速均不小于400 m/s时,可取该土层顶面为假想基岩面。表3给出了假想基岩面按土层剪切波速和场地覆盖层厚度划分的类别。埋地管线所处地质环境多以Ⅱ类场地为主,本文的有效计算深度H取40 m,涵盖大多数管线所处的地质环境。
3.2 有效计算长度LL的取值范围与实际的场址条件有关,其大小至少应反映地震动的主要特性,综合考虑采用以下方法确定L的最小限值:①求解输入地震动的Fourier振幅谱的峰值振幅对应的周期T; ②求解假想基岩面处土层的剪切波速VS; ③计算该地震动在场地土层中的传播波长:λ=TVS; ④L应至少包含一个地震动卓越周期段的波长,据此取L≥λ。本文选取EI-Centro地震波,峰值振幅对应的周期为0.42 s,VS范围为219.20~489.80 m/s,则L≥205.714 m。
3.3 有效计算宽度W有效计算宽度W的取值对地震波的反射和散射效应非常敏感,取值过小可能导致巨大误差,取值过大计算量成倍增加、计算效率较低。为了确定W的合理范围,本文建立三维精细化模型。为了得到具有规律性的一般结论,对土体模型作如下简化:土体采用线弹性本构模型; 在竖向范围内不考虑土层的差异性。
实际上,土体进入塑性变形之后对管线的作用力减小,在该假设下由于未考虑塑性变形,计算结果是偏于安全的。本文以埋深1.5 m、管壁厚t=8 mm的埋地管道为例,其土体范围竖向深度H=40 m、纵向长度L=250 m,分析其有效计算宽度W的取值。选取不同的管径D,截取不同的土层宽度W,采用动力无限元边界在模型底边界输入4条不同的地震动,将其PGA调幅为0.2、0.3、0.4和0.5 g,比较分析模型中部截面管道顶部的最大轴向应变ε的变化规律。
从不同管径D、宽度W的管线峰值应变ε变化图(图4a)对比发现,当PGA一定时,管道截面的ε随着D的增大呈明显的减小趋势; 当D一定时,管道截面的ε随着PGA的增大呈增大趋势,并且增幅越来越大,但其曲线的整体走势基本保持一致; 管道截面的ε随着W的增大逐渐降低直至趋于稳定。当W取值较小时,边界效应对核心计算区的影响较大,随着W的逐渐增大,其影响越来越小。这是由于当W取值较小时,无限元边界不能完全吸收反射波,边界反射波对计算区域有较大的影响,不可忽略; 当W逐渐增大时,反射波对计算区域的影响逐渐减弱。
为了进一步分析W的取值对核心计算区域的影响,本文采用W=40 m(D=0.5,0.7 m)、W=60 m(D=1.0 m)时的管线中部截面某一节点处的轴向峰值应变ε0作为基准值,讨论不同PGA取值下管线中部截面的轴向峰值应变ε的相对误差随有效计算宽度W的变化情况。其相对误差可表示为:
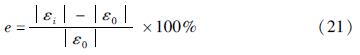
式中:εi(i=10~60)为不同有效计算宽度W的管线中部截面同一节点处的轴向峰值应变。
分析图4b可知:相对误差随着W的增大而减小,但不同PGA对计算结果的收敛速度影响不大,最终都能收敛到精确解。当D=0.5 m、W≥20 m时,或者当D=0.7 m、W>25 m时,相对误差均可以控制在5%以内; 当D=1.0 m、W≥40 m时,相对误差可以控制在5%以内; 当W取值足够大时,相对误差就会足够小。图4的分析结果表明:W与D有较大关联,不同的D对W的取值较敏感。当W=40D时,管体的ε明显趋于稳定,相对误差均在5%以内,此时可以认为W=40D时可消除边界反射波对计算区域的影响。
4 结论
本文阐述了无限元基本理论,建立了管线-土体相互作用的三维动力有限元-无限元耦合模型,提出了一种考虑非一致激励时无限元边界面上地震动的输入方法,分析了在地震波作用下埋地管线的动力响应,研究了模型中土体有效计算区域的取值问题,通过多种工况的对比分析,得到了如下结论:
(1)按照土层剪切波速和覆盖层厚度划分的假想基岩面作为地震动输入界面,此时土层的有效深度取值为H=40 m,可涵盖管线所处的大多数地质环境,具体取值根据管线所处场地的类别决定,一般情况下H=30~60 m。
(2)有效计算长度L的取值与考虑的实际地震波有很大关系,L应至少包含一个地震动的卓越周期段的波长,才可基本反应地震动的时空差异性。
(3)有效计算宽度W与管线的直径D有很大关联,W的取值随着管径的增大而增大,通过多工况的对比分析,W=40D时可消除边界反射波对计算区域的影响。
限于文章篇幅,本文以管线周围土体匀质作为基本假设,未考虑管沟形状和回填砂土的影响。未来,将考虑管线周围土体的差异性和管沟形状的不同对管线地震响应进开展一步研究。
- 常士骠,张苏民.2007.工程地质手册(第四版)[M].北京:中国建筑工业出版社.
- Chang S B,Zhang S M.2007.Engineering geology handbook(4th Edition)[M].Beijing:China Architecture & Building Press.(in Chinese)
- 杜修力,赵密,王进廷.2006.近场波动模拟的人工应力边界条件[J].力学学报,38(1):49-56.
- Du X L,Zhao M,Wang J T.2006.A stress artificial boundary in FEA for near-field wave problem[J].Chinese Journal of Theoretical and Applied Mechanics,38(1):49-56.(in Chinese)
- 杜修力.2009.工程波动理论与方法[M].北京:科学出版社.
- Du X L.2009.Theories and methods of wave motion for engineering[M].Beijing:Science Press.(in Chinese)
- 冈本舜三.1978.抗震工程学[M].北京:中国建筑工业出版社.
- Okamoto S.1978.Aseismic engineering[M].Beijing:China Architecture & Building Press.(in Chinese)
- 谷音,刘晶波,杜义欣.2007.三维一致黏弹性人工边界及黏弹性边界单元[J].工程力学,24(12):31-37.
- Gu Y,Liu J B,Du Y X.2007.3D Consistent viscous-spring artificial boundary and viscous-spring boundary element.[J].Engineering Mechanics,24(12):31-37.(in Chinese)
- 胡聿贤.2006.地震工程学(第2版)[M].北京:地震出版社.
- Hu Y X.2006.Earthquake engineering(2nd Edition)[M].Beijing:Seismological Press.(in Chinese)
- 刘晶波,古音,杜义欣.2006.一致黏弹性人工边界及黏弹性边界单元[J].岩土工程学报,28(9):1070-1075.
- Liu J B,Gu Y,Du Y X.2006.Consistent viscous-spring artificial boundary and viscous-spring boundary element[J].Chinese Journal of Geotechnical Engineering,28(9):1070-1075.(in Chinese)
- 刘晶波,王振宇,杜修力,等.2005.波动问题中的三维时域黏弹性人工边界[J].工程力学,22(6):46-51.
- Liu J B,Wang Z Y,Du X L.2005.Three-dimensional visco-elastic artificial boundaries in time domain for wave motion problems[J].Engineering Mechanics,22(6):46-51.(in Chinese)
- 石亦平,周玉蓉.2006.ABAQUS有限元分析实例详解[M]北京:机械工业出版社.
- Shi Y P,Zhou Y R.2006.Detailed explanation of ABAQUS finite element analysis example[M].Beijing:China Machine Press.(in Chinese)
- 赵建峰,杜修力,韩强,等.2007.外源波动问题数值模拟的一种实现方式[J].工程力学,24(4):52-58.
- Zhao J F,Du X L,Han Q,et al.2007.An approach to numerical simulation for external source wave motion[J].Engineering Mechanics,24(4):52-58.(in Chinese)
- 赵武胜,陈卫忠,黄胜,等.2010.地下结构抗震分析中地震动输入方法研究[J].土木工程学报.43(S1):554-559.
- Zhao W S,Chen W Z,Huang S,et al.2010.Research on method of seismic motion input in aseismic analysis for underground structure[J].China Civil Engineering Journal,43(S1):554-559.(in Chinese)
- 庄茁.2009.基于ABAQUS的有限元分析和应用[M]北京:清华大学出版社.
- Zhuang Z.2009.Finite element analysis and application based on ABAQUS[M].Beijing:Tsinghua University Press.(in Chinese)
- CHИПⅡ-A 12-69,苏联地震区建筑设计规范[S].
- CHИПⅡ-A 12-69,Building design code for earthquake area in USSR[S].(in Chinese)
- GB/T 50470—2017,油气输送管道线路工程抗震技术规范[S].
- GB/T 50470—2017,Seismic technical code for oil and gas transmission pipeline engineering[S].(in Chinese)
- GB 50011—2010,建筑抗震设计规范[S].
- GB 50011—2010,Code for seismic design of buildings[S].(in Chinese)
- IS:1893—1984(2003),印度标准:结构抗震设计规范[S].
- IS:1893—1984(2003),Indian standard:Criteria for earthquake resistant design of structures[S].(in Chinese)
- Bettess P,Eemson C,Chiam T C.1984.A new mapped infinite element for exterior wave problems[M].New York:John Wiley & Sons.
- Bettess P,Zienkiewicz.1977.Diffraction and refraction of surface waves using finite and infinite elements[J].International Journal for Numerical Methods in Engineering,11(6):1271-1290.
- Kennedy R P,Chow A W,William R A.1977.Fault movement effects on buried oil pipeline[J].Journal of Transportation Engineering,ASCE,103(6):617-633.
- Lysmer J,Kuhlemeyer R L.1969.Finite dynamic model for infinite media[J].Journal of Engineering Mechanics,ASCE,95(4):859-877.
- Newmark N M,Hall W J.1975.Pipeline design to resist large fault displacement[C]//Earthquake Engineering Research Institute.Proceedings of US National Conference on Earthquake Engineering,416-425.
- Ramberg W,Osgood W R.1943.Description of stress-strain curves by three parameters[R].National Advisory Committee For Aeronautics,Washington D C,Technical Note No.902.
- Ungless R F.1973.An infinite finite element[D].Vancouver:the University of British Columbia.
- Zhang C H,Zhao C B.1987.Coupling method of finite and infinite elements for strip foundation wave problems[J].Earthquake Engineering and Structural Dynamics,15(7):839-851.