基金项目:中国地震局工程力学研究所基本科研业务费专项项目(2021EEEVL0301); 国家自然科学基金(51878631).
(1.中国地震局工程力学研究所 地震工程与工程振动重点实验室,黑龙江 哈尔滨 150080; 2.地震灾害防治应急管理部重点实验室,黑龙江 哈尔滨 150080)
(1.Key Laboratory of Earthquake Engineering and Engineering Vibration,Institute of Engineering Mechanics,China Earthquake Administration,Harbin 150080,Heilongjiang,China)(2.Key Laboratory of Earthquake Disaster Mitigation,Ministry of Emergency Management,Harbin 150080,Heilongjiang,China)
long-span,deck CFST arch bridge; nonlinear structural response analysis; performance group; seismic resilience index; seismic resilience rating
DOI: 10.20015/j.cnki.ISSN1000-0666.2024.0029
备注
基金项目:中国地震局工程力学研究所基本科研业务费专项项目(2021EEEVL0301); 国家自然科学基金(51878631).
引言
近年来,高速交通网络特别是在其中占据着重要地位的高速桥梁迅速建设。大跨拱桥作为重要的生命线工程之一易受地震影响,一旦发生较大的地震损伤,不仅会造成人民生命财产的巨额损失,还会给正常的交通运输行业以及灾区救援工作造成极大的压力,因此针对桥梁结构进行地震损失评估以及抗震韧性提升是十分必要的。
目前国内外学者对桥梁的地震损失评估开展了一些工作,如张强(2014)以层次分析法和模糊数学为基础提出了一种混凝土简支梁桥震害快速评定方法,实现从宏观上快速评估桥梁地震损失; 许圣(2015)以一座公路RC连续梁桥为例进行地震易损性分析和经济损失估计; 刘洋(2018)考虑了桥梁震后修复方法的差异并定义性能组,对3种中小跨径钢-混凝土组合结构桥梁的直接经济损失和维修时间等抗震韧性指标进行了评估,结果显示改进横梁构造能够改善钢-混组合梁桥的震后损伤状态并能提高其抗震韧性; 冯莉等(2020)以一座高速铁路连续梁桥为研究对象,运用全概率基于性能地震工程(Performance Based Earthquake Engineering,PBEE)方法计算该桥梁全生命周期内的地震经济损失,发现该高铁连续梁桥在整个设计周期内发生轻微损伤及中等损伤的概率较大,且选用不同的折现率对结构全周期地震损失成本的影响较大; 杨国俊等(2022)选择一座三跨RC连续梁桥为研究对象,发现3种修复函数对修复时间、目标功能和耽搁时间等韧性指标的敏感程度有显著差异; Ghosh和Padgett(2011)基于非齐次泊松过程考虑腐蚀退化的影响,以两座不同类型的公路桥梁为例,基于时间进行地震经济损失评估,结果表明通过明确考虑桥梁构件退化的影响所估计的地震经济损失显著偏高,构件的相对贡献会发生变化并因桥梁类型而异,且老化桥梁的损失估计往 往比原始桥梁对工程需求参数(Engineering Demand Parameter,EDP)更敏感; Li等(2020)对采用4种形状记忆合金限制器改装的隔震简支公路梁桥进行了直接经济损失和生命周期损失的评估,结果表明该类隔震装置对桥梁的长期地震损失有显著影响; Giouvanidis和Dong(2020)采用PBEE方法对单摇摆柱桥梁进行了基于地震场景的抗震韧性评价,结果表明与固定基座结构相比,摇摆类桥梁结构的地震损失显著减小并在所有超越概率的地震危险场景下均能保持很好的韧性,对摇摆柱的长细比稍作修改便可显著降低地震损失。
2012年美国FEMA和ATC部门共同提出了FEMA P-58建筑抗震性能评估理论(FEMA,2018),通过引入全概率PBEE方法对维修成本、维修时间和人员伤亡等损失结果进行量化,进而指导结构的性能设计; 2021年我国正式实施《建筑抗震韧性评价标准》(GB/T 38591—2020),将维修成本、维修时间和人员伤亡作为韧性指标用于我国建筑结构的抗震韧性评估。目前,国内对桥梁结构的地震损失评估多基于经验统计方法,而PBEE方法主要应用于普通建筑结构,应用于桥梁结构的研究较少且大多停留在经济损失评估层面上。上承式CFST拱桥由于其刚度大、强度高的特点被广泛应用于大跨桥梁建设中,是高速公路桥梁的优选之一。鉴于此,本文以一座大跨度上承式CFST拱桥为研究对象进行抗震韧性评估,定义易损性组和性能组,评估该结构在不同地震动强度下的各抗震韧性指标,并评定其抗震韧性等级。
1 桥梁模型
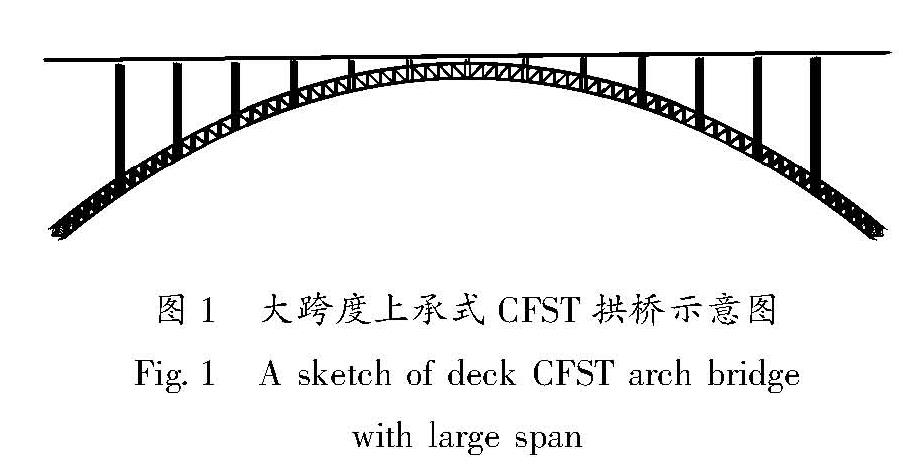
以我国西南地区某实体大桥为基础,按照《桥梁抗震设计规范》(JTG/T 2231-01—2020),设计了一座大跨度上承式CFST拱桥作为研究对象,结构所在场地类别为II类,设防烈度为Ⅷ度(PGA=0.2 g),设计地震分组为第2组。根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)第3.1.2条规定,桥梁抗震设防类别为A类。桥梁净跨320 m,矢跨比为1/4.2,桥面宽为25.5 m,双向四车道; 主拱圈、斜竖杆以及拱上立柱等主体部分构件为钢管混凝土材料,腹杆和剪力撑等构件为空钢管; 桥面结构形式采用预制混凝土板梁,盖梁为钢筋混凝土构件。利用Midas/Civil软件建立该结构的有限元模型,共有3 126个节点,5 318个单元,整体构造如图1所示。
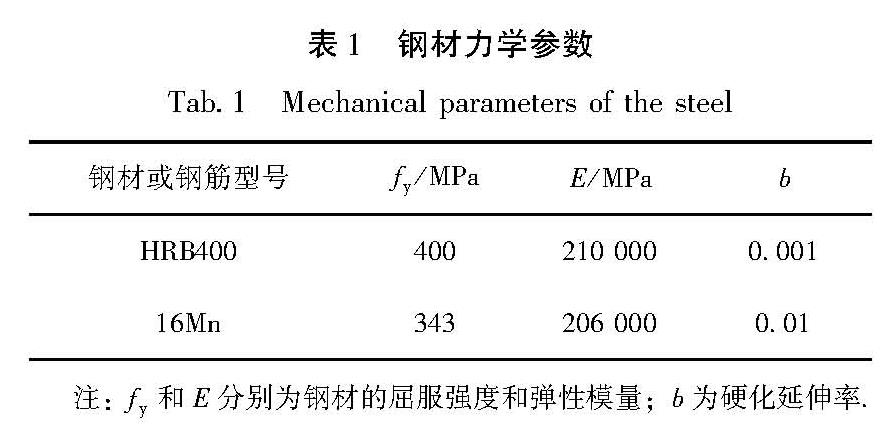
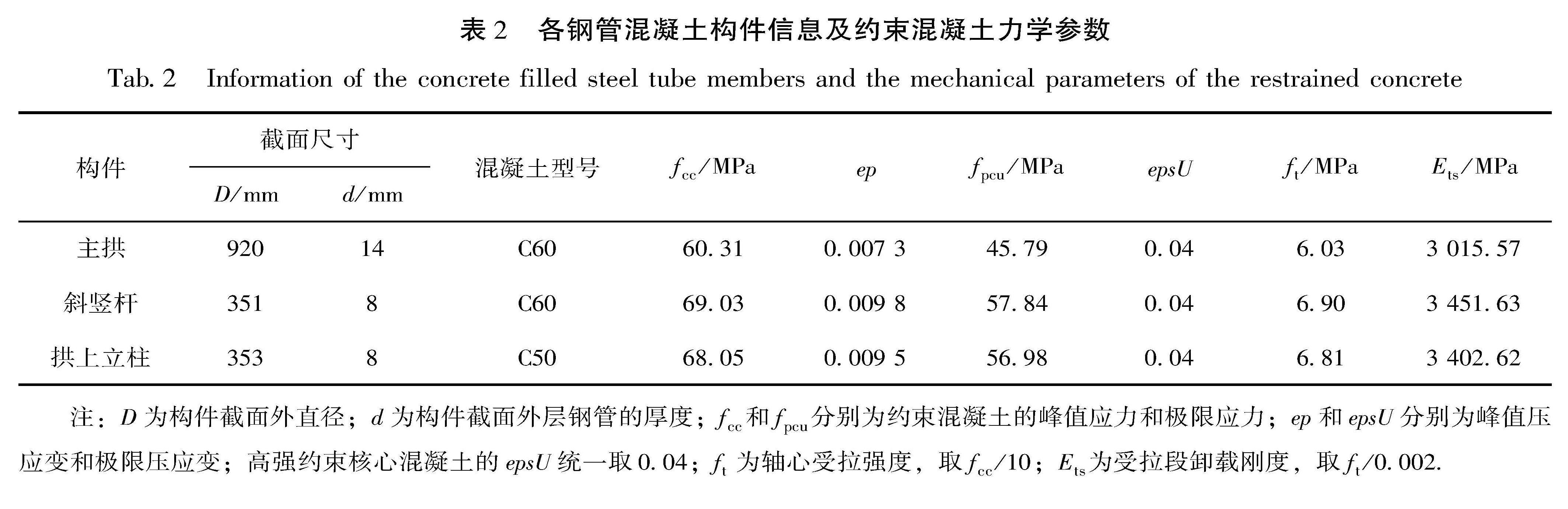
全桥所有构件均采用梁单元模拟,通过考虑材料的本构关系和划分纤维截面来设置纤维模型,钢材和混凝土的型号从《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)和《公路桥涵钢结构及木结构设计规范》(JTG D64—2015)中选取,钢管混凝土构件以及空钢管构件均采用16Mn钢材,其他构件所用钢筋采用HRB400级,钢材的本构关系采用双折线模型,对应的力学参数见表1。由于钢管的约束作用,需考虑钢管对核心混凝土应变和轴压强度的提高作用,约束混凝土本构关系采用Mander模型(陈建伟等,2015)模拟,各钢管混凝土构件的材料型号、截面尺寸以及约束混凝土的各项力学参数见表2。
表2 各钢管混凝土构件信息及约束混凝土力学参数
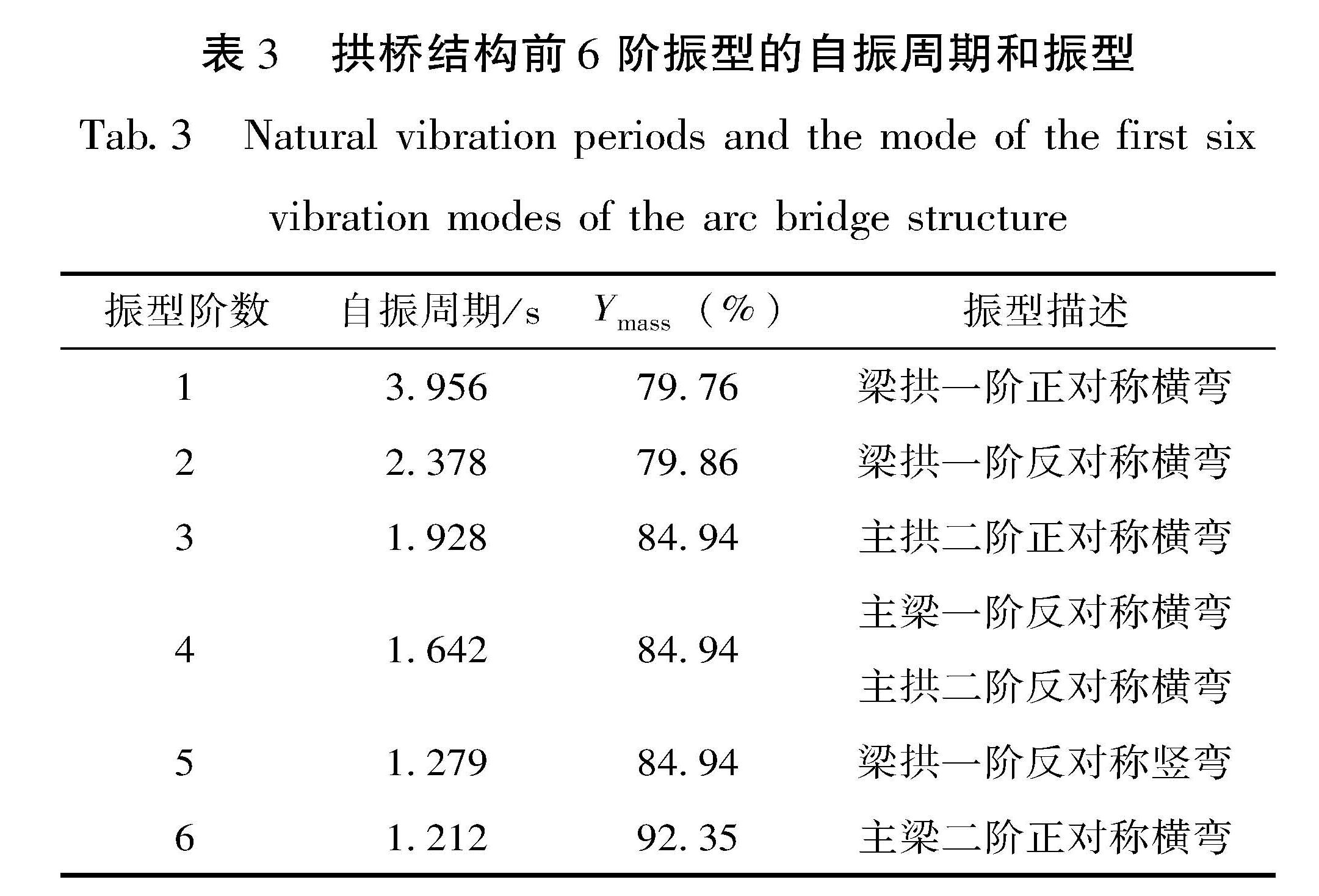
Tab.2 Information of the concrete filled steel tube members and the mechanical parameters of the restrained concrete拱脚与基础连接处固结,拱上立柱和主拱连接处为刚性连接,桥面两端处参照实际结构的处理方式,释放6个自由度中其中2个转动方向的自由度。对结构施加3%的瑞利阻尼并进行模态分析,选取前6阶振型的主要信息列于表3,对应的各阶振型如图2所示,通过分析结构的基本动力特性可以验证该拱桥结构有限元模型建立的准确性。
2 结构响应分析和易损性分析
3 抗震韧性评估
4 结论
本文以一座大跨度上承式CFST拱桥为研究对象进行了基于不同地震动强度作用下的抗震韧性评估,并完成在不同地震动强度作用下各抗震韧性指标的地震损失评估,并评定结构的抗震韧性等级,主要得到以下结论:
(1)对一座大跨度上承式CFST拱桥结构进行非线性结构响应分析,发现立柱桥墩这种结构响应较大的钢管混凝土构件,混凝土材料总是先于钢材达到较高的损伤状态; 本文针对拱桥结构不同类型的构件分别从材料本构和宏观变形的角度采用了不同的EDP,抗震韧性评估结果验证了这一方法的可行性。
(2)在地震动强度较小时,非结构构件的损失占比较大,但随着地震动强度的增大占比逐渐减小,结构构件的情况正好相反; 结构构件的维修费用和维修时间组成主要来源于立柱桥墩,非结构构件的损失组成中管线类构件占比最高。
(3)结构构件对大跨度上承式CFST拱桥结构的抗震韧性有较大的影响,是造成结构地震损失的主要因素,对抗震韧性的影响突出体现在维修时间上,特别是在强地震作用下。
(4)拱桥结构抗震韧性评级为一星,其中维修时间是影响其综合抗震韧性等级的关键指标,可作为防灾决策的依据。维修时间指标对大跨度上承式CFST拱桥结构整体的抗震韧性更为重要,在实现震后桥面通行功能的快速恢复时较为关键。为提高此类结构的综合抗震韧性,建议其抗震韧性设计可重点从对维修时间影响较大的结构构件方面入手。
- 陈建伟,边瑾靓,苏幼坡,等.2015.应用OpenSEES模拟方钢管混凝土柱的抗震性能[J].世界地震工程,31(3):71-77.
- Chen J W,Bian J L,Su Y P,et al.2015.Application of OpenSEES on calculating lateral force-displacement hysteretic curves of concrete-filled rectangular steel tubular columns[J].World Earthquake Engineering,31(3):71-77.(in Chinese)
- 冯莉,樊燕燕,李子奇,等.2020.高速铁路连续梁桥全寿命周期概率地震损失分析[J].铁道科学与工程学报,17(4):815-822.
- Feng L,Fan Y Y,Li Z Q,et al.2020.Probabilistic whole life cycle seismic loss analysis of high-speed railway continuous girder bridge[J].Journal of Railway Science and Engineering,17(4):815-822.(in Chinese)
- 李小珍,刘鸣,杨得海,等.2020.大跨度上承式钢桁架拱桥的地震损伤演化模拟[J].西南交通大学学报,55(6):1207-1214,1223.
- Li X Z,Liu M,Yang D H,et al.2020.Seismic damage evolution simulation of long-span deck steel truss arch bridge[J].Journal of Southwest Jiaotong University,55(6):1207-1214,1223.(in Chinese)
- 刘洋.2018.基于混合易损性与功能损失的钢-混组合梁桥地震风险与韧性评估[D].哈尔滨:哈尔滨工业大学.
- Liu Y.2018.Seismic risk and resilience assessment of steel-concrete composite girder bridges based on hybrid fragility and functionality loss[D].Harbin:Harbin Institute of Technology.(in Chinese)
- 乔保娟,肖从真,杨志勇.2023.基于构件损伤状态的复杂建筑抗震韧性评价方法研究[J/OL].工程力学,40(11):21-30.
- Qiao B J,Xiao C Z,Yang Z Y.2023.Research on seismic resilience assessment method of complex buildings based on component damage states[J/OL].Engineering Mechanics,40(11):21-30.(in Chinese)
- 许圣.2015.钢筋混凝土公路连续梁桥地震风险与抗震可恢复性分析[D].哈尔滨:哈尔滨工业大学.
- Xu S.2015.Seismic risk and resilience analysis of RC continuous-girder highway bridges[D].Harbin:Harbin Institute of Technology.(in Chinese)
- 杨国俊,田里,杜永峰,等.2022.基于修复函数的连续梁桥抗震韧性因素及改进评估研究[J].土木工程学报,55(S1):219-226.
- Yang G J,Tian L,Du Y F,et al.2022.Research on seismic resilience factors and improved evaluation of continuous beam bridges based on recovery function[J].China Civil Engineering Journal,55(S1):219-226.(in Chinese)
- 张强.2014.大震后铁路混凝土简支梁桥灾害损失评估研究[D].北京:北京交通大学.
- Zhang Q.2014.Seismic damage assessment of railway simply supported bridges after large earthquake[D].Beijing:Beijing Jiaotong University.(in Chinese)
- 周长东,田苗旺,张许,等.2017.考虑多维地震作用的高耸钢筋混凝土烟囱结构易损性分析[J].土木工程学报,50(3):54-64.
- Zhang C D,Tian M W,Zhang X,et al.2017.Seismic fragility analysis for high-rise RC chimney considering multi-dimensional seismic actions[J].China Civil Engineering Journal,50(3):54-64.(in Chinese)
- GB/T 38591—2020,建筑抗震韧性评价标准[S].
- GB/T 38591—2020,Standard for seismic resilience assessment of buildings[S].(in Chinese)
- GB 18306—2015,中国地震动参数区划图[S].
- GB 18306—2015,Seismic ground motion parameters zonation map of China[S].(in Chinese)
- JTG 3362—2018,公路钢筋混凝土及预应力混凝土桥涵设计规范[S].
- JTG 3362—2018,Code for design of highway reinforced concrete and prestressed concrete bridges and culverts[S].(in Chinese)
- JTG/T 2231-01—2020,公路桥梁抗震设计规范[S].
- JTG/T 2231-01—2020,Design specification for seismic design of highway bridges[S].(in Chinese)
- JTG D64—2015,公路桥涵钢结构及木结构设计规范[S].
- JTG D64—2015,Design specification for steel structure and timberwork of bridges and culverts in highways[S].(in Chinese)
- California Department of Transportation.2002.Guide specifications for seismic design of steel bridges[S].
- FEMA.2018.Seismic performance assessment of buildings:Volume 1-Methodology,Second Edition:FEMA P-58[R].Washington D C,UAS.
- Ghosh J,Padgett J E.2011.Probabilistic seismic loss assessment of aging bridges using a component-level cost estimation approach[J].Earthquake Engineering & Structural Dynamics,40(15):1743-1761.
- Giouvanidis A I,Dong Y.2020.Seismic loss and resilience assessment of single-column rocking bridges[J].Bulletin of earthquake engineering,18(9):4481-4513.
- Li S,Hedayati D F,Wang J,et al.2020.Performance-based seismic loss assessment of isolated simply-supported highway bridges retrofitted with different shape memory alloy cable restrainers in a life-cycle context[J].Journal of Intelligent Material Systems and Structures,31(8):1053-1075.
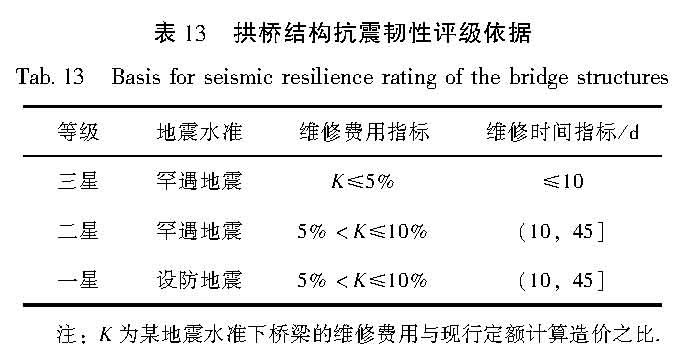
对该拱桥进行抗震韧性评价,在不同地震动强度下评估各抗震韧性指标并评定其抗震韧性等级。在评估结构地震损失和进行韧性评级时,桥梁结构与普通建筑结构的相关理论有所不同:桥梁结构的实际修复工作不考虑沿高度方向(层间)的并行性,考虑到其修复逻辑的差异性,维修时间指标的计算方法和评级依据需单独研究; 与建筑结构人员大量聚集且长时间居住的特点不同,常见的桥梁结构以桥面交通为主要功能,故本文对桥梁结构的抗震韧性评估暂不选用人员伤亡指标; 维修费用指标的计算和评级参考《建筑抗震韧性评价标准》(GB/T 38591—2020)。
3.1 桥梁的性能模型3.1.1 基本信息主桥面长为320 m,拱高63.2 m,桥面可通行总面积为3 360 m2。我国西南地区大跨拱桥平均造价最低在6 000元/m2以上,按现行定额计算取8 000 元/m2,预计全桥总造价约为2 680 万元,建筑重建需要拆迁,拆迁会使重建费用增长20%~30%(FEMA,2018),综合考虑该桥梁的重置成本为3 200万元。查询经验性的大型施工单位工期计算标准,结合实际地形影响,估计结构的重置时间为320 d; 设损失阈值为重建费用的45%,地震作用下的修复费用超过该阈值时建议重建。
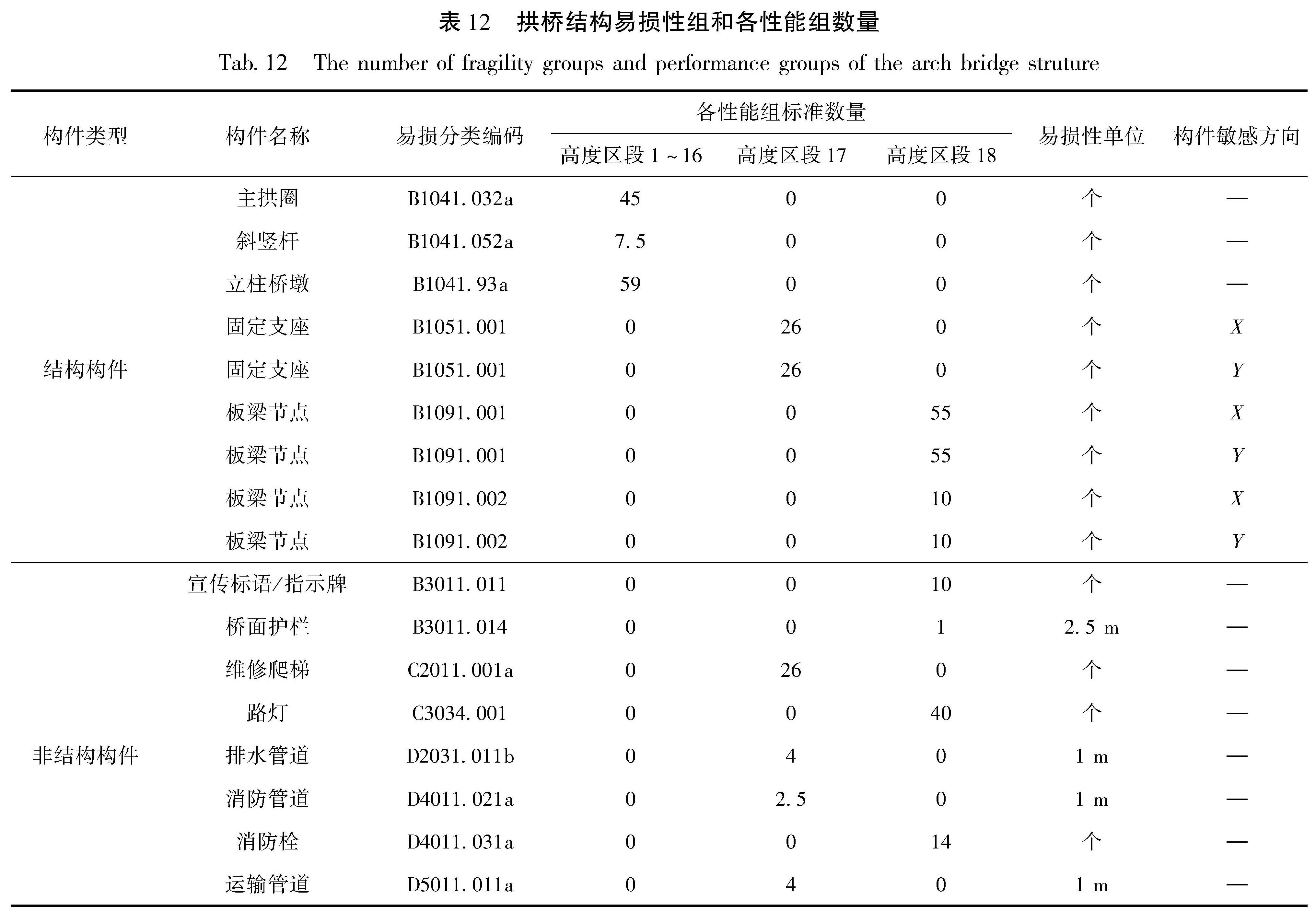
3.1.2 易损性组和性能组性能组是将具有相同需求参数的易损性构件进行细分,其划分依据主要是EDP大小和方向性的差异。由于加速度沿高度也是变化的,所以位于不同高度水平的加速度敏感型构件应归为不同的性能组。将本文的拱桥结构按修复顺序沿高度从下到上分为若干不同的高度区段,桥梁下部结构(主拱圈和桥墩高度部分)按每4 m为一个高度区段,盖梁、上部结构高度部分可分别作为一个高度区段,从下往上分别编号为1~18; 使用μΔ和μθ作为EDP的结构构件要考虑的方向性,加速度敏感型非结构构件的加速度与方向独立。易损性组以及各性能组的数量见表 12。
3.2 地震损失评估地震损失评估使用蒙特卡洛抽样方法(MC方法),也叫统计试验方法,这是一种基于“随机数”的计算方法,通常解决一些数值方法难以计算的问题。从弹塑性时程分析结果中提取所需要的EDP,结合构件易损性信息利用MC方法评估结构的地震损失,将各指标的评估结果数据进行对数正态分布拟合即可得到结构在某一地震损失水准下的概率分布曲线,其中蒙特卡洛模拟的独立重复次数不少于1 000次。将结构各构件划分为结构构件W1、楼梯W2、围护构件W3、宣传标语/指示牌W4、路灯W5、管线类构件W6、消防栓W7共7个部分,以便统计整理时较为直观地展示不同使用功能的构件的损失评估结果。
表 12 拱桥结构易损性组和各性能组数量
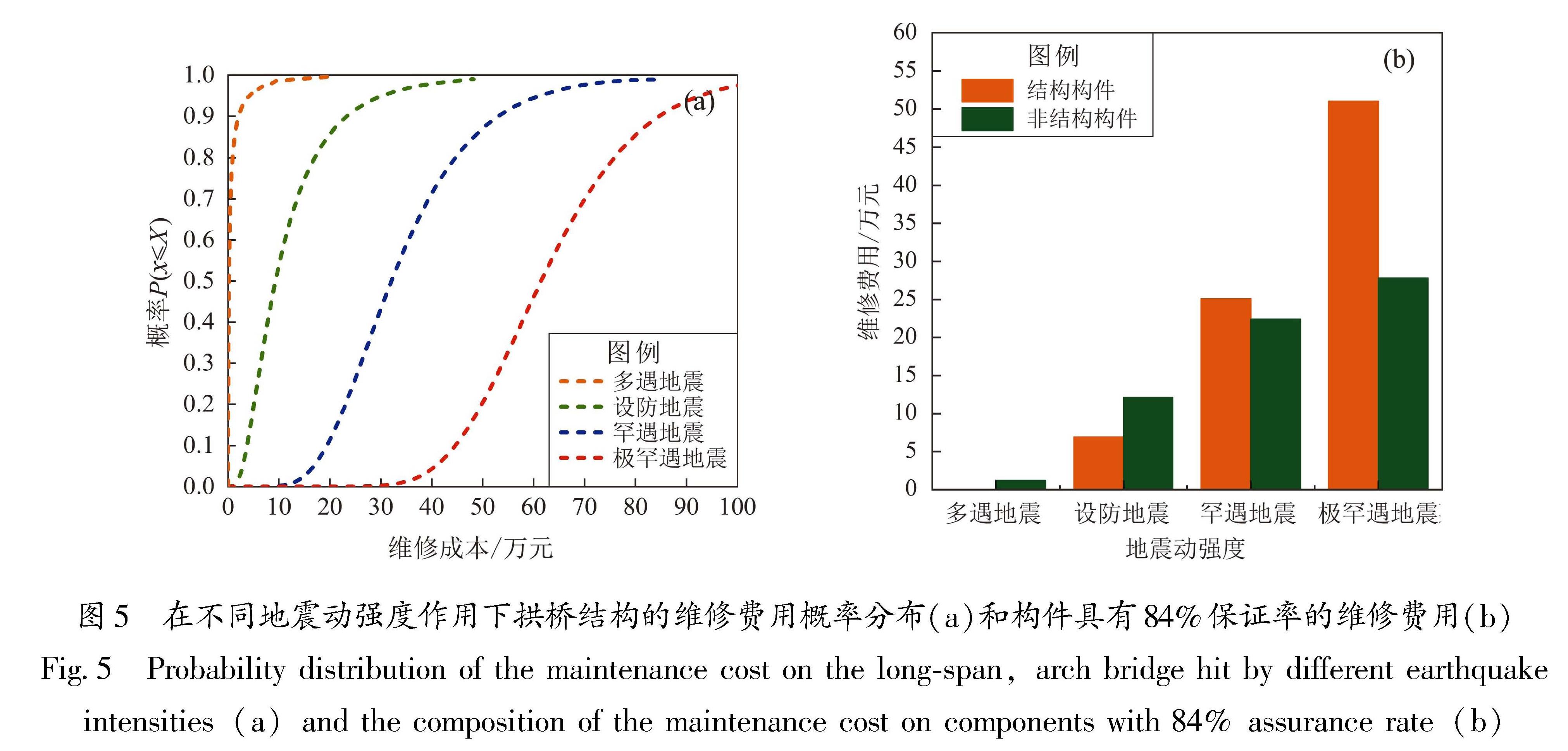
Tab.12 The number of fragility groups and performance groups of the arch bridge struture图5 在不同地震动强度作用下拱桥结构的维修费用概率分布(a)和构件具有84%保证率的维修费用(b)
Fig.5 Probability distribution of the maintenance cost on the long-span,arch bridge hit by different earthquake intensities(a)and the composition of the maintenance cost on components with 84% assurance rate(b)结构在4种地震动强度水平下84%保证率对应的修复费用分别为1.2万、19.03万、47.5万和78.78万元,其中有关结构构件的修复费用依次为0万、6.91万、25.1万和51.0万元,可以发现:①地震动强度的增大会使大跨度上承式CFST拱桥结构的维修费用以及结构构件部分的维修费用快速增加,且地震动强度越大增长速度越快; ②在不同地震动强度下非结构构件和结构构件的维修费用所占比重区分明显。
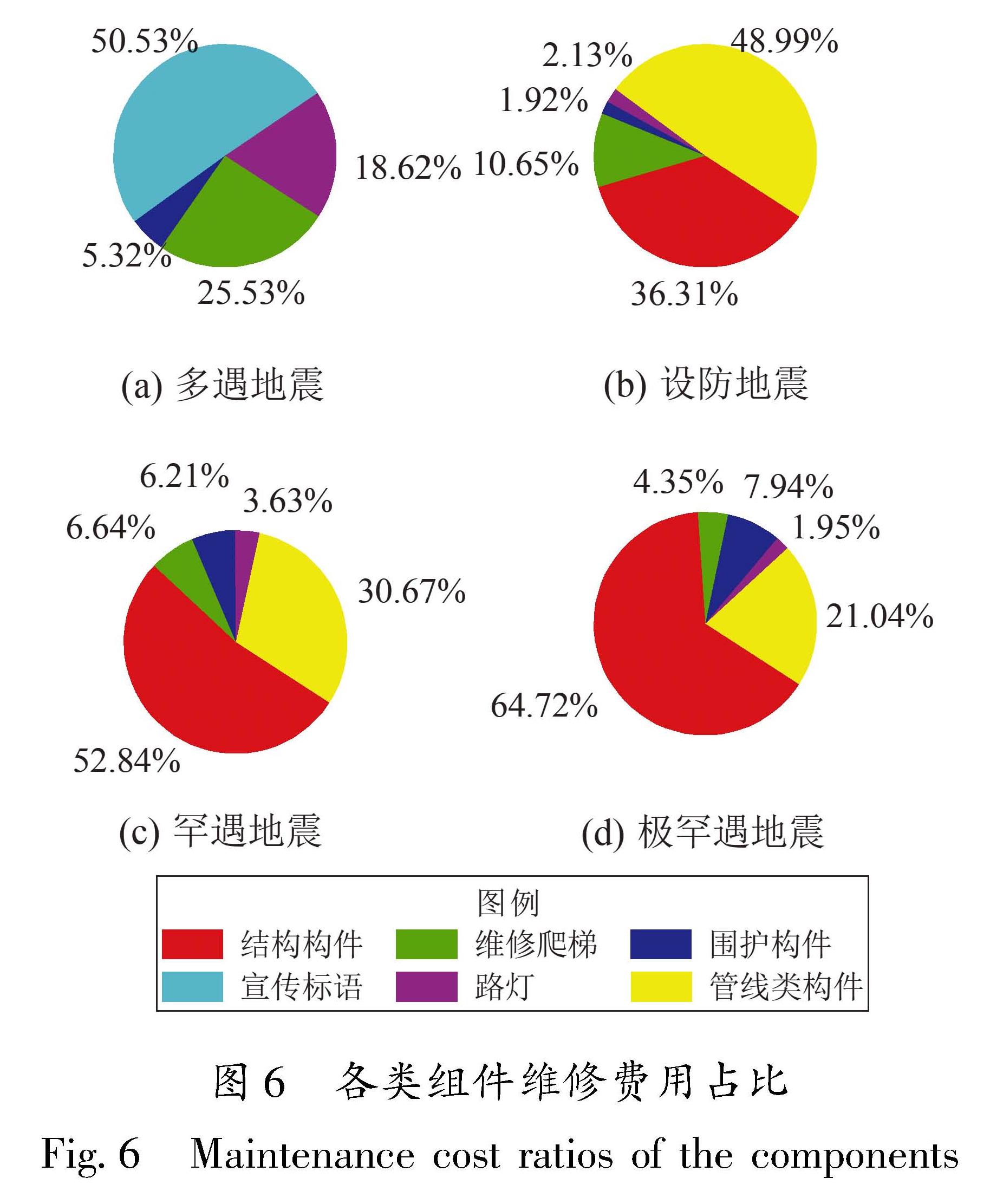
非结构构件的维修费用最先出现,多遇地震下拱桥结构的维修费用全部来源于路灯、宣传标语指示牌等易破坏的非结构构件,数值较小可忽略不计; 结构构件的维修费用从设防地震开始出现且占比逐渐增大,在设防地震下占比约为1/3,罕遇和极罕遇地震下分别达到1/2和2/3,是造成结构地震经济损失的主要因素。结构构件的维修费用主要来源是立柱桥和支座等结构响应较大的构件,其中桥墩在所有构件中占比最大,其次是固定支座,相较之下桥面的板梁节点不易损伤但由于其数量较多,因此总体损失占比略小于固定支座; 非结构构件的维修费用中,管线类构件虽损伤阈值较高但因其成本高所以维修费用同样较高,从设防地震开始损失占比一直最大,围护构件的维修费用次之但占比增长较快,其余非结构构件占比较小。
大多数非结构构件相较于结构构件更易破坏,在遭遇较高的地震动强度之前就已达到较严重的损伤状态,因此其维修费用在遭遇罕遇地震之后增长缓慢; 结构构件在多遇地震时不易损伤,遭遇设防地震甚至罕遇地震之后才对应出现较为明显的维修费用,且地震动强度越大结构构件的损伤状态越严重,维修费用及所占比重就越高。因此非结构构件的地震经济损失在小震时占比较大,但随地震动强度的增大占比逐渐减小,而结构构件的经济损失情况刚好相反。
3.2.2 维修时间评估美国FEMA P-58规范(FEMA,2018)和《建筑抗震韧性评价标准》(GB/T 38591—2020)均适用于常见建筑结构的韧性评价,两者对于维修时间指标的计算是基于房屋建筑层间并行修复的假定,不同楼层的修复工作可同时展开,而桥梁的上下部结构作为一个整体在施工流程和修复工作中有较为明确的先后顺序,需要依次进行。因此本文的拱桥结构假定沿高度串行修复,修复区段即3.1.2节中划分的若干高度区段,同一高度区段的构件修复可分为两个阶段,第一阶段包括楼梯和结构构件修复,第二阶段为其余非结构构件的修复,后者可同时进行。相较之下,本文采用的修复方式所得的维修时间更符合实际情况,桥梁结构的维修时间计算公式如下:
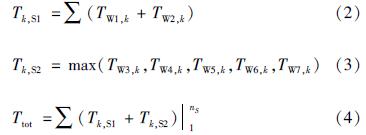
式中:Tk,S1为第k个修复区段完成第一段修复工作需要的修复时间,单位为d; Tk,S2为第k个修复区段完成第二段修复工作需要的修复时间,单位为d; Ttot为桥梁维修时间,即该拱桥完成全部功能性修复工作所需要的维修时间,单位为d; nS为沿高度划分的修复区段数,对于本文拱桥结构,nS=18。
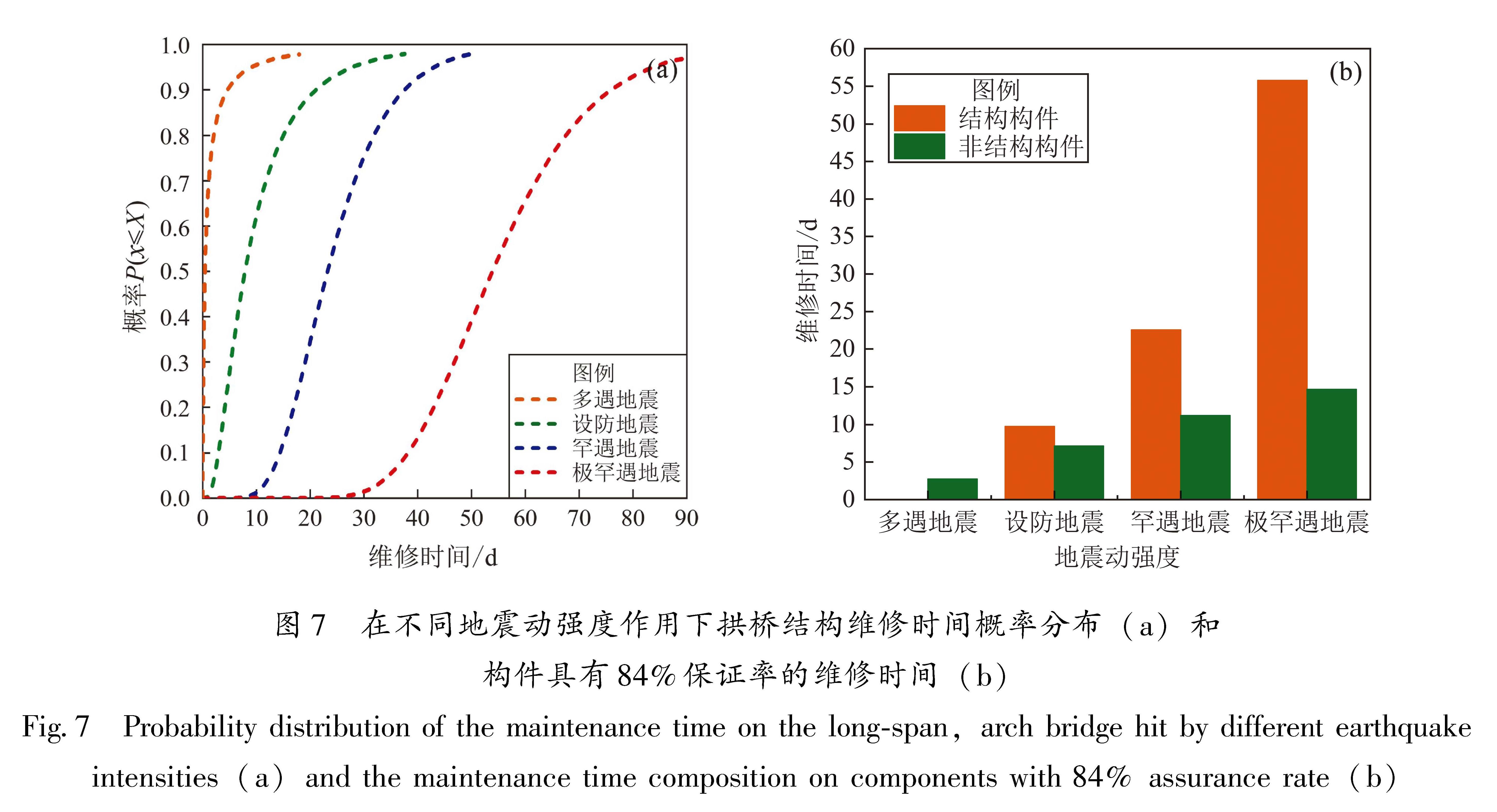
对于维修时间,使用蒙特卡洛方法模拟得到的评估结果如图7、8所示,其中图7a为该拱桥结构在不同地震动强度作用下维修时间的概率分布,图7b为各地震动强度作用下结构构件和非结构构件具有84%保证率的维修时间,图8为部分修复工作并行开展的非结构构件的维修时间所占比重,图中只能展示其中占比最大的一组)。
拱桥结构在各地震动强度下对应具有84%保证率的维修时间分别为2.73、16.88、33.75和70.43 d,其中有关结构构件的维修时间依次为9.74、22.53和55.79 d,可以看出结构整体和
结构构件部分的维修时间均随地震动强度的增大而迅速增加,且增长速度越来越快。
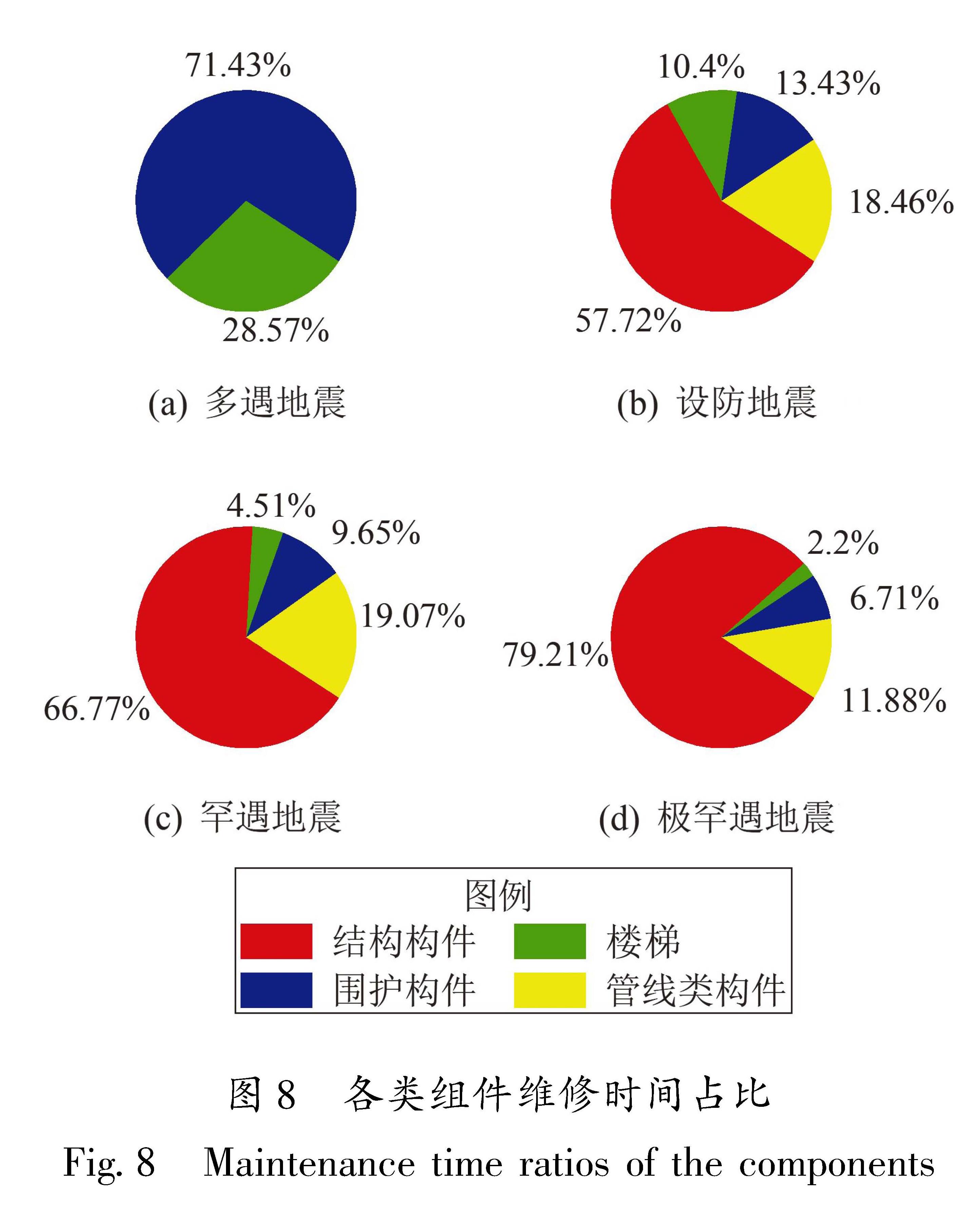
多遇地震下拱桥结构的维修时间平均为0.42 d,由少部分易损坏的非结构构件组成,此时结构经过很短的时间便可修复完成继续投入使用。结构构件在设防地震下就开始出现很高的维修时间占比,之后一直保持较高的增长,在设防地震、罕遇地震和极罕遇地震下的维修时间占比分别约
图7 在不同地震动强度作用下拱桥结构维修时间概率分布(a)和构件具有84%保证率的维修时间(b)
Fig.7 Probability distribution of the maintenance time on the long-span,arch bridge hit by different earthquakeintensities(a)and the maintenance time composition on components with 84% assurance rate(b)为3/5、2/3和4/5,这是因为地震动强度越大,结构构件破坏越严重。地震过程中大量结构构件的损伤是结构整体维修时间的主要来源,可见结构构件对该结构地震损失的贡献,在维修时间指标上更加突出,特别是在强地震作用下。
各结构构件中桥墩、支座和桥面节点等的维修时间较多,其中立柱桥墩的维修时间及占比最大,板梁由于节点较多、修复工作量大所以维修时间多于支座; 各主要的非结构构件中,管道类构件的维修时间在各地震动强度作用下的占比均为最高,其他组的维修时间占比较小且均匀。宣传标语/指示牌成本低、更换快,消防栓不易损伤,此类构件在各地震动强度作用下的维修费用和维修时间占比都很小,可以忽略,因此未全部在地震损失评估结果图中标注。
由上述分析结果得到:结构构件的破坏是影响大跨度上承式CFST拱桥结构维修费用和维修时间的最主要因素,结构构件对该结构的抗震韧性有较大的影响。在同高度的非结构构件同时修复的情况下,排水管道、消防管道等各管线类组件的维修时间依然很高,因此在进行管线类所在高度区段的修复工作时,决策者可适当增加维修人员数量。
3.3 抗震韧性评级因为大跨度上承式CFST拱桥结构与建筑结构在结构类型、使用功能以及修复逻辑等方面区别明显,在抗震韧性评估流程中部分评价指标的选用依据和计算方法差异较大,所以两者对应的评级依据应当不同,针对桥梁结构应专门研究:一方面大跨拱桥构件沿高度串行修复方式得到的结构维修时间明显比高度相同、工程量相近的考虑层间修复并行性的普通建筑结构卡得多,所以对桥梁结构维修时间指标的评级标准可适当放宽; 另一方面考虑到交通功能是桥梁的主要功能,本文拱桥结构的抗震韧性评价未增加人员伤亡指标,导致采用剩余的评价指标对结构综合抗震韧性等级的影响权重会有所变化,且为保证震后桥面快速恢复通行,桥梁实际维修时间的控制标准又不能过大。由于各结构类型的结构维修费用的计算原理基本一致,是否考虑修复工作的并行性对于维修费用评估结果影响不大,故桥梁维修费用指标的评级依据参照《建筑抗震韧性评价标准》(GB/T 38591—2020)。本文借鉴了我国标准中对评级方法的定义同时综合考虑以上因素,最后针对该拱桥结构各抗震韧性指标的评级依据见表 13,取所有评价指标的最低等级作为该结构的抗震韧性等级。[KH*2D]
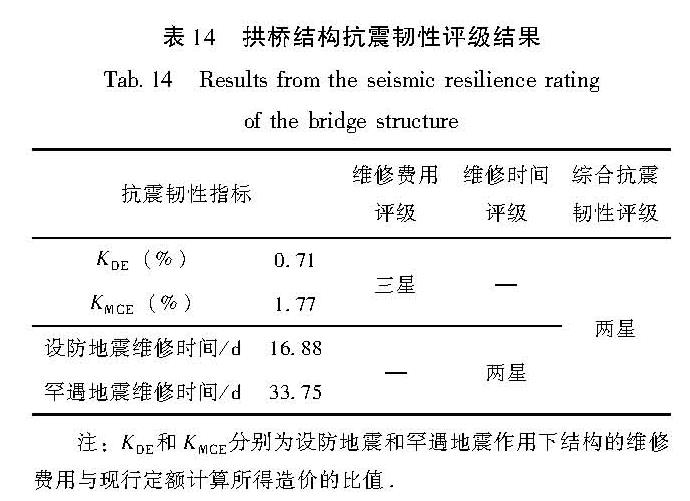
对3.2节中由1 000次蒙特卡洛模拟得到的维修费用和维修时间指标等地震损失结果进行总结,按具有84%保证率的对数正态拟合值为依据分别评定各个抗震韧性指标的等级,最后对该结构进行综合抗震韧性评级,评级结果见表 14。
大跨度上承式CFST拱桥结构抗震韧性评级为一星,其中维修时间是抗震韧性指标中的短板,是影响该结构抗震韧性等级的关键指标,可为防灾决策提供依据。在不考虑人员伤亡的前提下(按现行规范或标准设计的建筑结构其人员伤亡评估结果一般极小),一些内部含有较多昂贵的机器设备等非结构构件的建筑结构可能要求设备具备较高的抗震韧性,以尽可能降低结构的维修费用; 而该类拱桥通常是重要的生命线工程,实现结构的震后快速修复以保证交通运输和灾区援建工作的正常运行较为关键,由于应用途径和设备组成等差异,其结构构件无论是数量、造价还是施工时间都远超非结构构件,其对维修费用和维修时间评估结果的影响权重都比后者大,同时考虑到维修时间指标是该类拱桥结构抗震韧性评级的关键,因此此类结构抗震韧性的提升主要依赖于结构构件抗震性能的提升,通过提高结构在维修时间方面的韧性,从而达到提高其综合抗震韧性的目的。
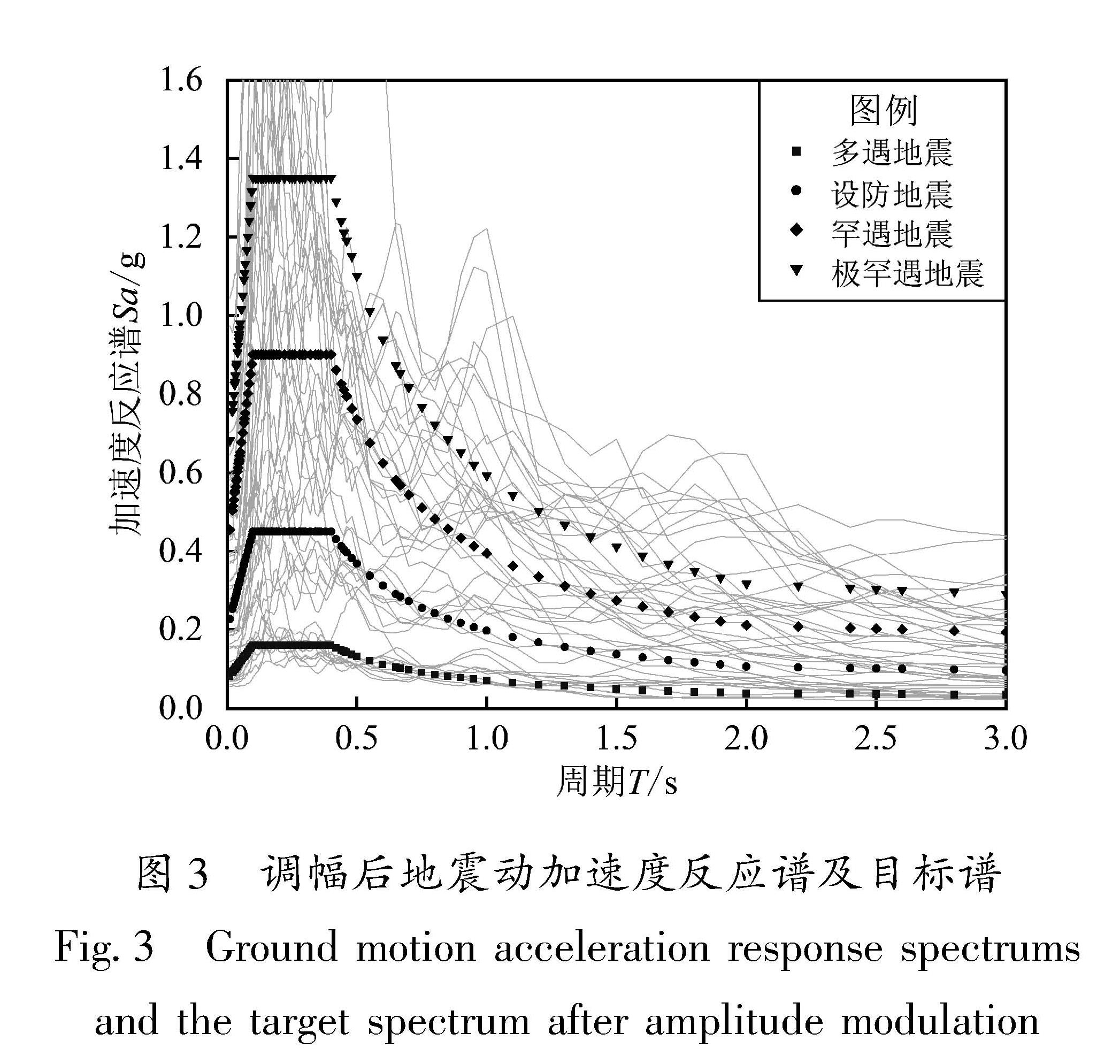
2.1 地震动的选取与调幅桥址处的分区特征周期从《中国地震动参数区划图》(GB 18306—2015)中得到,结合结构设防等级和其他场地信息,根据《桥梁抗震设计规范》(JTG/T 2231-01—2020)得到该桥梁结构的规范设计反应谱,以上述规范谱作为目标谱,从太平洋地震工程研究中心(PEER)网站上共筛选出18条地震动记录,其具体信息见表4。
为得到合理的结构响应中值和标准差,选取过程中应以谱形匹配为原则,在结构主要周期段进行匹配,Tmax取基本周期T1的两倍,Tmin取0.2TX1和0.2TY1中的较小值(FEMA,2018),由于该结构的高阶振型对EDP有较大贡献,Tmin应取足够小。地震动强度指标选用谱加速度Sa(T1),采用单点调幅法将地震动记录分别调至多遇地震Sa(T1)=0.16 g、设防地震Sa(T1)=0.45 g、罕遇地震Sa(T1)=0.9 g和极罕遇地震Sa(T1)=1.35 g这4个强度水平下,所用目标谱及地震动调幅后的加速度反应谱如图3所示。
2.2 结构响应分析和EDP的选取输入X、Y和竖向的三维地震动,分别在多遇地震、设防地震、罕遇地震和极罕遇地震强度水平下对结构进行非线性结构响应分析。分析结果表明:在多遇和设防地震下,桥体下部的主拱圈及附属构件绝大多数处于线弹性状态,而立柱桥墩以及支座处延性较大,在罕遇和极罕遇地震下进入弹塑性状态,位移响应较大的关键构件主要位于跨中附近,且Y方向(横桥向)的响应远大于X方向(顺桥向),应变较大的地方多集中在立柱桥墩顶部以及支座处; 桥墩顶部加速度与位移的结果相反,最大加速度响应主要体现在顺桥向,在4个地震动强度下拱桥结构X方向的平均最大绝对加速度分别为0.187、0.513、0.939和1.116 g。
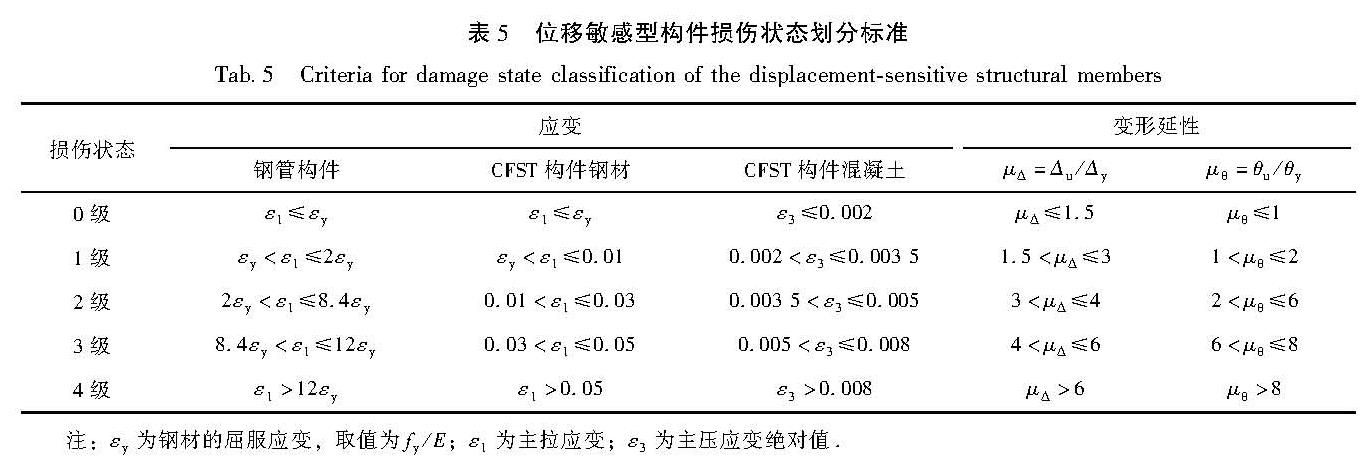
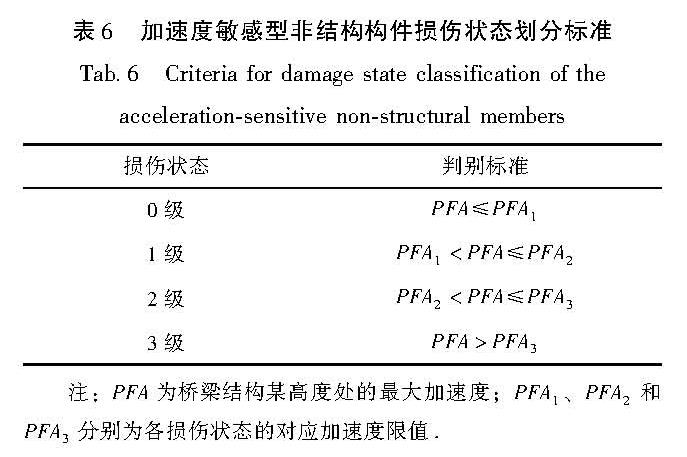
对于大跨度上承式CFST拱桥这种高阶振型贡献率较大的不规则复杂结构,从材料本构层次采用构件截面最大应变ε作为结构需求参数更加精确(乔保娟等,2022)。由于结构构件种类较多且考虑桥梁通行功能的影响,增加位移延性系数μΔ和转角延性系数μθ这2个宏观指标。钢管混凝土构件的EDP采用最大应变,固定支座采用μΔ,桥面处板梁节点采用μθ。以上EDP与变形或位移有关的结构构件可统称为位移敏感型构件,其损伤状态分为5级,分别为完好(0级)、轻微损伤(1级)、轻度损伤(2级)、中度损伤(3级)和严重损伤(4级),对应的划分标准见表5(李小珍等,2020; California Department of Transportation,2002)。钢管混凝土构件的截面最大应变原则上应对钢材和混凝土分别考虑,但对于某些结构响应较大的构件,混凝土总是比钢材先达到较高的损伤状态,所以可只将混凝土的最大应变列为需求参数。非结构构件常用的EDP有峰值加速度、峰值速度等,本文中桥梁的路灯、维修爬梯等非结构构件大都为加速度敏感型,故其需求参数均采用最大加速度,损伤状态分为4级,分别为完好(0级)、轻度损伤(1级)、中度损伤(2级)和严重损伤(3级),对应划分标准见表6。
表5 位移敏感型构件损伤状态划分标准
Tab.5 Criteria for damage state classification of the displacement-sensitive structural members2.3 结构易损性分析2.3.1 易损性分组将全桥所有构件划分成有代表性的有限组别,分组计算地震损失,每个易损性组对应唯一的需求参数,组内的所有构件具备相同的构件易损性函数和相似的损伤状态。除去对地震损失评估影响不大的牢固构件,该拱桥结构参与易损性分组的共有14种构件,其中有6种结构构件和8种非结构构件,最终划分得到13个易损性组。各类构件的易损分类编码含义如下:B10代表结构构件; B30和C代表位于上部结构(桥面)的非结构构件; D代表非结构构件中的消防设施和管道类构件。
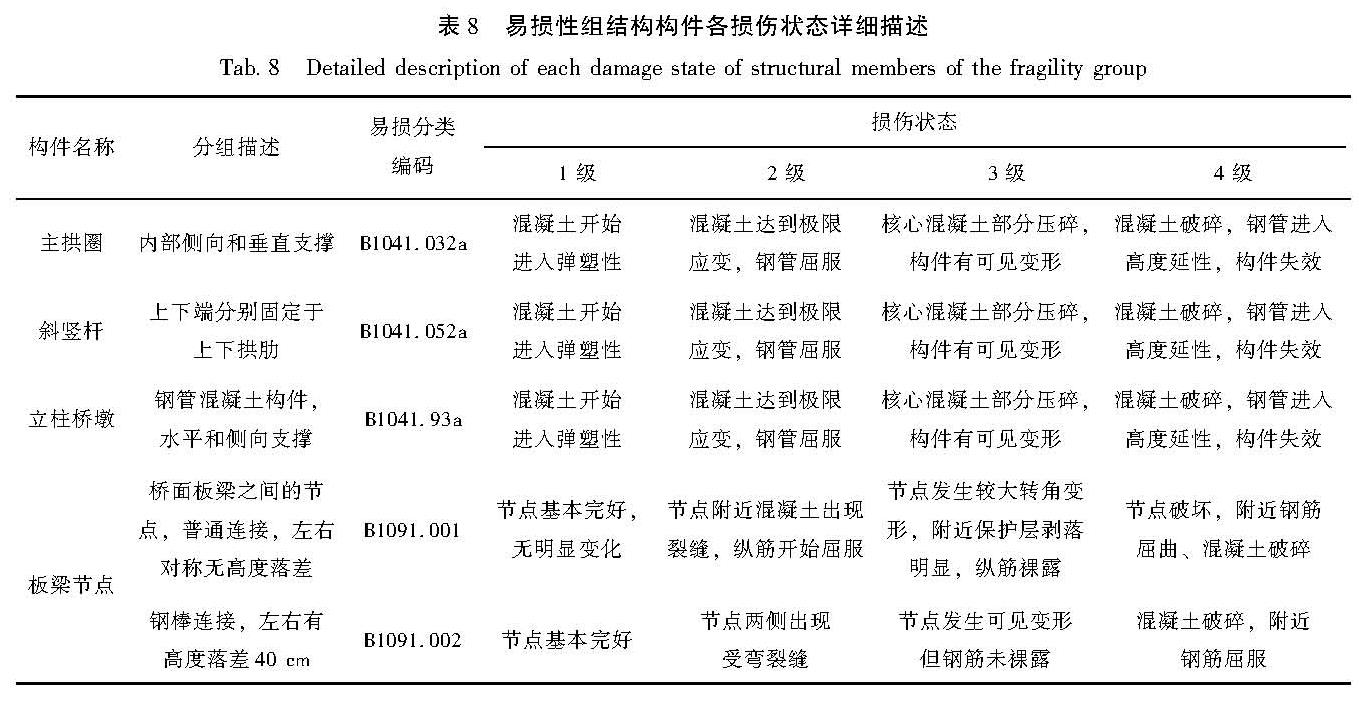
主拱构件和斜竖杆构件的易损性函数完全相同,具有相同的损伤状态和维修方案,且最终作为一个装配体在施工上有一定的联系,可划分到同一个易损性组中。分组后对于每个易损性组细化损伤状态,以固定支座B1051.001为例,其各级损伤状态如下:1级为支座发生轻微损伤,支座的大部分处于线弹性状态,局部发生屈服,总体处于有限延性状态(0≤μ<1.5),无需修复或仅需要极短的修复时间,对修复费用的影响微小,可忽略不计; 2级为支座屈服,总体处于适度延性状态(1.5≤μ<3),需要部分维修或更换,造成更大的修复费用和更长的修复时间; 3级为支座进入高度延性状态,发生可见大位移,μ为4~6甚至更大,需要立即更换,要求很高的修复费用和很长的修复时间; 4级为支座完全破坏。其余易损性组构件的各损伤状态详见表7、图8。
2.3.2 构件易损性函数构件易损性函数是在给定需求下构件发生某种损伤状态的条件概率分布,假设服从对数正态分布,同一易损性组里的每个损伤状态的易损性曲线由2个易损性参数需求中位值θ和对数标准差β确定,可表示为:
Fi(D)=Φ(ln(D/θi)/βi) (1)
式中:Fi(D)为第i个损伤状态的易损性函数; θi和βi分别为对应的需求中值和对数标准差。
表7 易损性组非结构构件各损伤状态详细描述
Tab.7 Detailed description of each damage state of non-structural members of the fragility group表8 易损性组结构构件各损伤状态详细描述
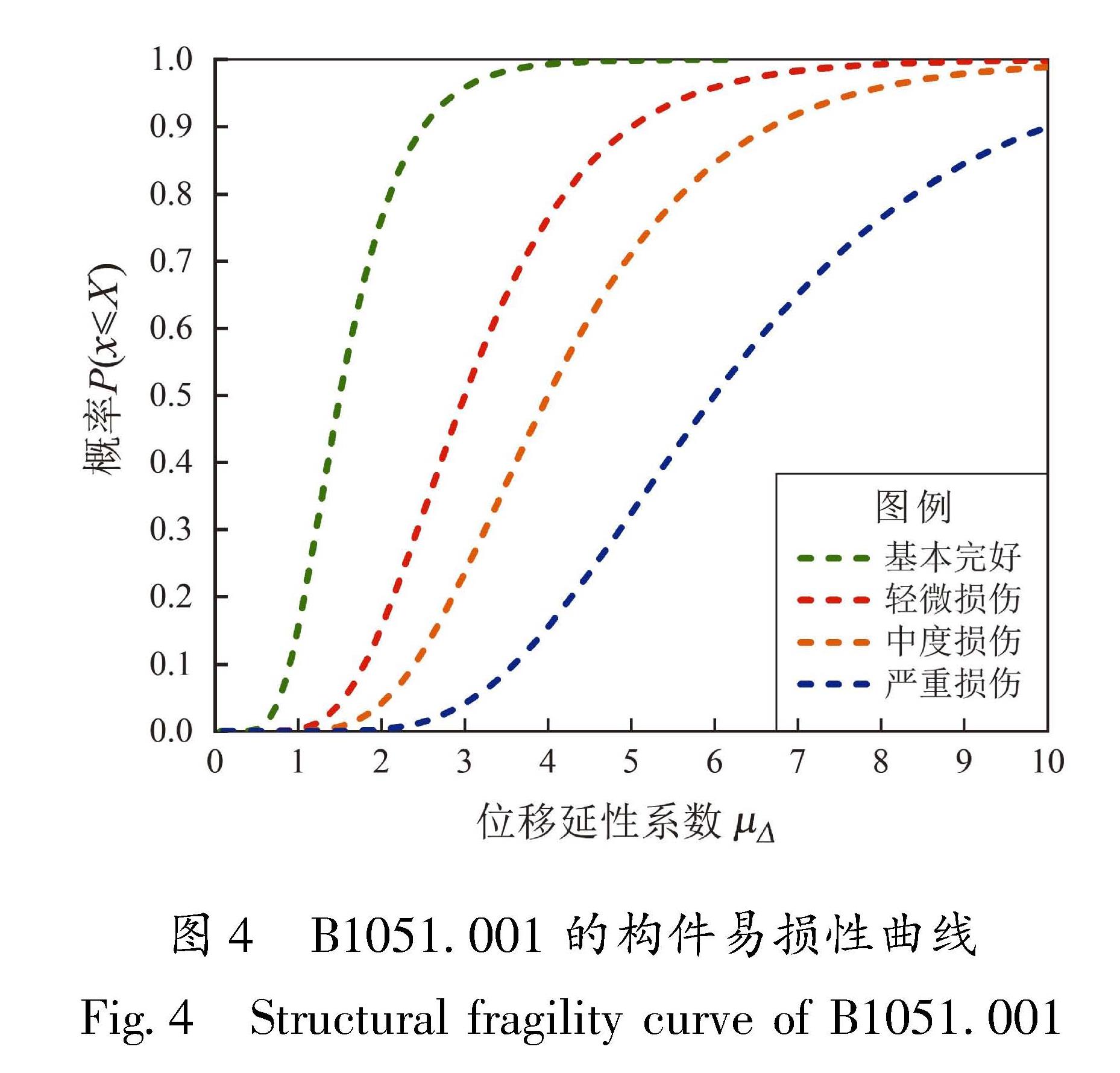
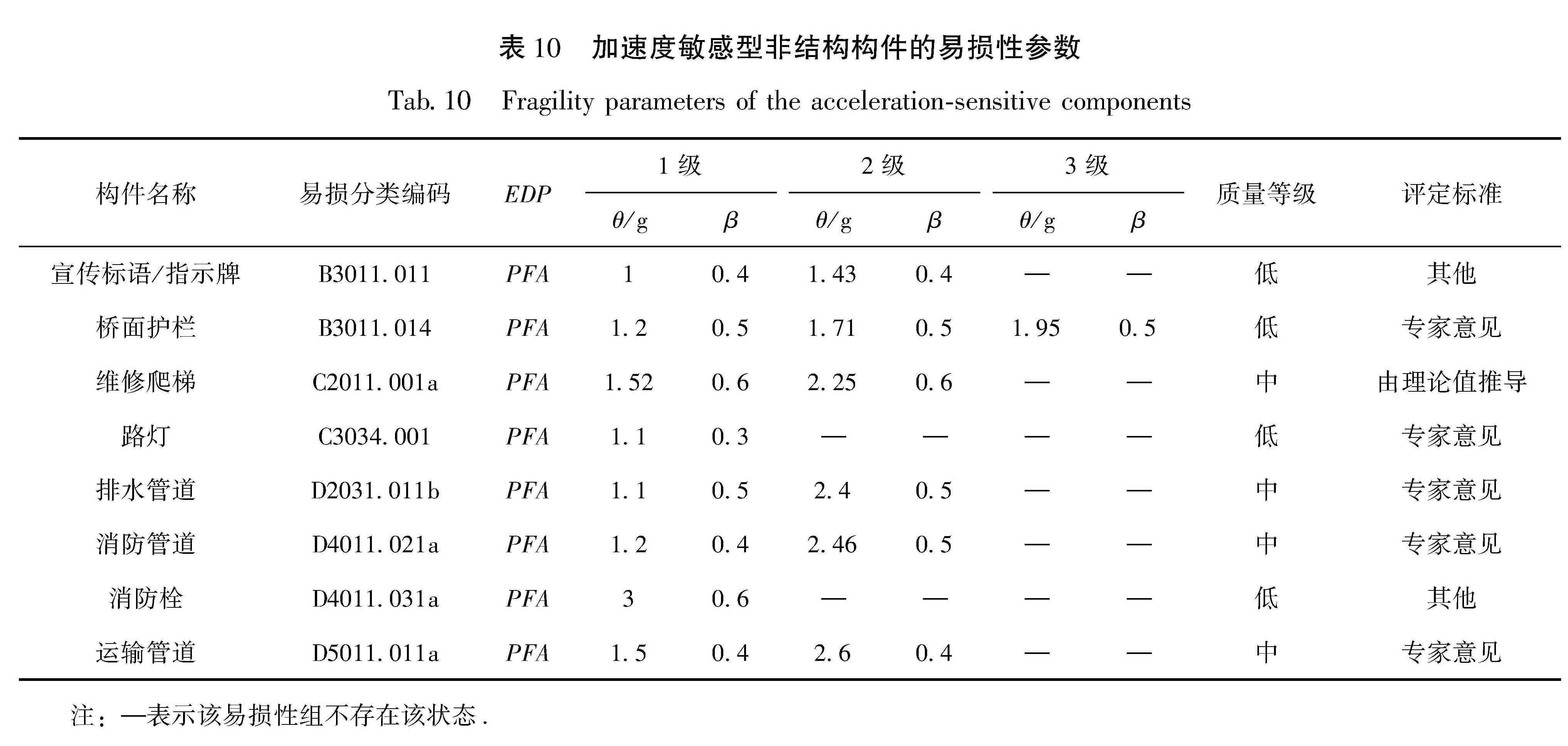
Tab.8 Detailed description of each damage state of structural members of the fragility group《建筑抗震韧性评价标准》(GB/T 38591—2020)和FEMA(2018)提供了多种建立构件易损性函数的方法:①通过试验或破坏性地震后的数据采集、分析等建立; ②对于没有可获得的数据,可采取专家基于工程经验提供的有关意见建立; ③基于计算的易损性,使用理论值进行推导。本文参考《建筑抗震韧性评价标准》(GB/T 38591—2020)推荐的方法对该拱桥各主要构件易损性函数的θ和β进行量化,并对易损性函数进行了分析和总结:对于位移敏感型结构构件,其易损性参数可参照表5或根据结构响应时程分析得到的构件最大应变或转角确定; 对于加速度敏感型非结构构件,根据结构响应时程分析得到的结构某高度处最大加速度按表6确定或按上述规范提供的其他方法确定,B1051.001的构件易损性曲线如图4所示。其余各构件损伤状态的易损性参数列于表9、10,非结构构件相较于结构构件更易损伤,其损伤状态数量可能出现较少的情况。
分析总结得到易损性函数的θ和β等具体参数后,参考FEMA(2018)定义各易损性组中构件易损性函数的质量等级水平,质量等级分为高、中和低,具体划分方法和评定依据见表 11。由于易损性数据库的局限性,对于定义的易损性组,各组内易损性参数的质量等级水平各有高低。本文得到的构件易损性参数θ≥0.2且β≤0.6,位移敏感型结构构件EDP对应的损伤状态的划分标准及易损性信息来源于大量试验或震害后的数据统计,此类易损性组总结得到的易损性信息的合理性和可靠度较高,其质量等级可定为高; 对于加速度敏感型的非结构构件,主要是基于计算的易损性或有行内从业经验的专家意见得到的结果,部分组别的结果有待后续验证和完善,此类易损性组的质量等级可能较低。