基金项目:国家自然科学基金资助项目(51978337); 中国水利水电科学研究院开放研究基金(IWHR-SKL-202216).
(1.南京航空航天大学 航空学院,江苏 南京 210016; 2.南京航空航天大学 民航学院,江苏 南京 210016; 3.中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室,北京 100048)
(1.College of Aeronautics,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,Jiangsu,China)(2.College of Civil Aviation,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,Jiangsu,China)(3.State Key Laboratory of Simulation and Regulation of Water Cycle in River Basin,China Instituteof Water Resources and Hydropower Research,Beijing 100048,China)
concrete arch dam; generalized saturated porous media; sediment; water-sediment-dam-foundation system of the reservoir; seismic response analysis
DOI: 10.20015/j.cnki.ISSN1000-0666.2024.0009
备注
基金项目:国家自然科学基金资助项目(51978337); 中国水利水电科学研究院开放研究基金(IWHR-SKL-202216).
引言
为满足不断增长的能源需求,并实现“碳达峰、碳中和”的战略目标,我国目前正积极开展大坝水库建设。我国丰富的水资源大多集中在西部陡峭河谷中,其地形、地质条件适宜修建移民淹地相对较少而调节性能较好的混凝土高拱坝,其中已建成且完成初期蓄水、高294.5 m的小湾混凝土双曲拱坝是目前世界上最高的拱坝。但我国强震多发区也集中在西部地区,因此我国高坝大库的安全面临着严峻的考验。由于地形环境复杂,混凝土拱坝的地震响应受到各种因素的影响(陈厚群,2017; 张楚汉等,2016; Chopra,2012),这些因素包括但不限于:①库水的动水压力及其可压缩性; ②半无限域坝基的辐射阻尼效应; ③因常年运行而在库水底部堆积的积淤砂层的能量吸收效应; ④库水-坝体-坝基相互作用; ⑤坝体和坝基的非线性效应以及坝体与坝基的接触非线性效应。
库水的动水压力对地震响应的影响不容忽视。早在20世纪30年代,Westergaard(1933)就采用附加水动力的形式研究了库水和坝体之间的相互作用,对后来的动水压力的研究产生了深远的影响; Nath(1982)的研究表明当拱坝的形状近似于圆形时,库水可压缩性的影响可以忽略不计; 而Fok等(1987)认为库水可压缩性的影响受无限域库水与坝体自振频率比值的影响; 王进廷(2001)研究发现可压缩库水对坝体反应有明显的影响,尤其是在垂直地震动作用时,库水自振频率对应的作用于坝体的动水压力反应十分显著。库水底部沉积的淤砂层同样对坝体的地震响应有一定的影响。大量研究表明沉积物可压缩性对大坝响应具有非常重要的作用。完全饱和的沉积物的效果比较有限,[HJ2mm]而部分饱和的沉积物效果比较明显(Domnguez et al,1997; 王进廷等,2003,2006,2007)。综上所述,混凝土的地震响应分析需要综合考虑库水、淤砂层、坝体、坝基的耦合效应。
库水-淤砂层-坝体-坝基体系的地震响应分析涉及到流体、饱和多孔介质、固体介质的动力耦合作用。早期发展了波函数开展结合解析方法求解耦合问题(Liaw,Chopra,1974; Fenves,Chopra,1984; Wang et al,2018),但是由于解析方法局限于规则情形的土体边界,一定程度上限制了其推广应用。随着大型水坝的建设需求增加,以及计算机的迅速普及,极大地推动了数值分析方法的发展。按照求解域可将数值分析手段划分为频域法和时域法,频域法一般采用子结构法(Tan,Chopra,1995; 林皋,2017),将整个系统分为库水、坝体、坝基3个子结构,求解频域动水压力及地基阻抗矩阵实现耦合。该方法比较成熟,但其本质上基于线性叠加原理,原则上只能分析线性问题以及可以等效线性化的弱非线性问题,在分析强非线性和接触非线性方面存在不足。相较而言,时域法可以合理处理各种非线性问题,对于耦合问题可以直接整体求解(涂劲等,2018; Lokke,Chopra,2019),也可以分区并行求解(Farhat,Roux,1991; Felippa et al,2001; Zhao et al,2003; Chen et al,2022),具有一定优势,在各类工程结构的抗震安全方面应用得比较广泛。
陈少林等(2019a,b)对多介质耦合问题作了统一处理,提出了广义饱和多孔介质的观点,将流体和固体分别看作孔隙率为0和1的广义饱和多孔介质,发展了流体-饱和多孔介质-固体的统一计算框架,并将其应用于海洋工程结构的波动散射问题。对于库水-淤砂层-坝体-坝基体系的复杂耦合问题,同样可以作相似处理,将其视为坝体在复杂环境中的波动散射问题,其地震响应分析包含两个方面:①不包含主体结构的自由场分析; ②包含主体结构的耦合动力分析。其中,自由场分析目前主要采用两类方法,一是传递矩阵法(Thomson,1950; Haskell,1953),该方法基于水平成层基岩场地,直接考虑了无穷远边界条件,在频域内进行求解,计算效率较高,并被推广至饱和土情形的水平成层场地(赵宇昕,陈少林,2016),但该方法无法应用于不规则场地; 另一类是有限元数值方法,该方法需要采用人工边界条件,可用于解决不规则的场地剖面,但目前大多进行了简化处理,一般不考虑库水和淤砂层的影响。为了明确复杂的峡谷地形下的地震动输入,对大坝地震响应做出更加准确可靠的预测,需要考虑库水和淤砂层,计算不规则峡谷地形的自由场。
本文考虑库水动水压力及其可压缩性,将淤砂层视为饱和多孔介质,研究库水-淤砂层-坝体-坝基体系耦合作用下的地震响应规律。以小湾拱坝为研究对象,根据坝体结构在脉冲波及地震波作用下的响应结果,探讨了淤砂层对结果的影响。
1 基本原理
对混凝土拱坝的地震响应分析涉及到库水-淤砂层-坝体-坝基体系的耦合分析,其物理模型主要由3部分组成:①混凝土坝体; ②与坝体相邻的不规则有界坝基和远离坝体的半无限地基; ③与坝体相邻的不规则形状的库水区域和上游截面一致的均匀水库。考虑半无限库水以及半无限地基环境时,库水-淤砂层-坝体-坝基体系是一种开放性系统(图1),此时,对混凝土拱坝的地震响应分析可以视为半无限域的波动散射问题,即为给定地震波由半无限基岩入射时,由坝体引起的波动散射问题。
开放系统的波动散射问题可以分解为自由场体系和有界的耦合体系(有界的库水-淤砂层-坝体-坝基体系)的求解。自由场体系用于解决为无限域坝基或库水设定人工边界时的输入问题。当混凝土坝体蓄水后,自由场体系包含人工边界外(Γr:库水人工边界、Γf:坝基人工边界)的半无限域坝基区域Ω+f及半无限库水区域Ω+r。该系统的自由场解可根据地形采用水平成层基岩的传递矩阵法(Thomson,1950; Haskell,1953)、饱和多孔介质的传递矩阵法(赵宇昕,陈少林,2016)或广义饱和土的二维有限元法(陈少林等,2021)等进行计算。求出自由场体系的自由场后,可将自由场视为参考场,作为有界耦合系统的波动输入,计算耦合系统的地震响应。本文采用透射边界作为人工边界,用广义饱和多孔介质描述库水-淤砂层-坝体-坝基体系的内部区域,然后通过广义饱和土的统一计算框架进行计算分析,最终得到考虑库水-淤砂层-坝体-坝基耦合效应的地震响应。
图1 库水-淤砂层-坝体-坝基体系的波动散射问题分解
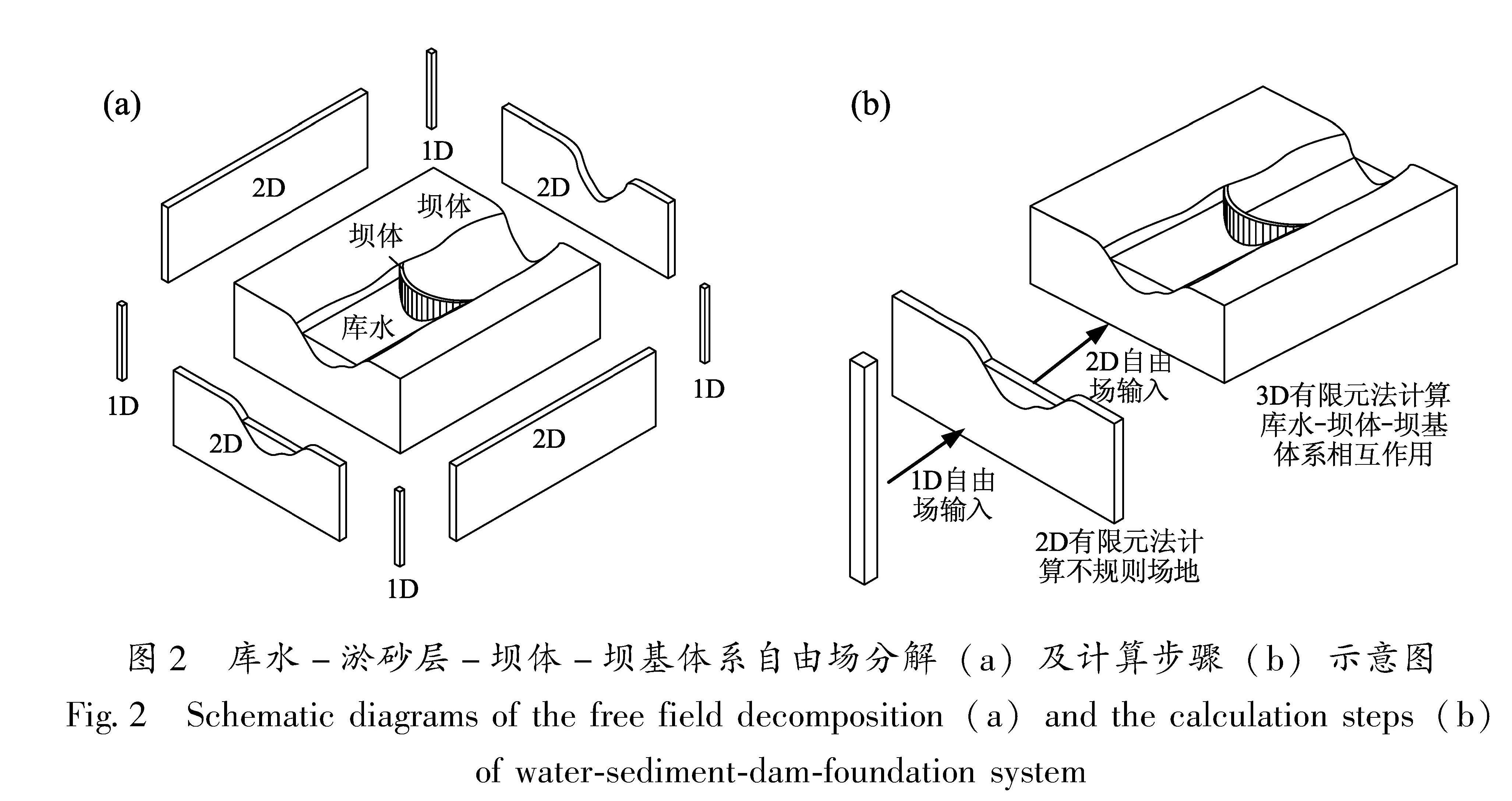
Fig.1 Decomposition of wave scattering for water-sediment-dam-foundation system1.1 三维不规则场地的自由场计算方法对于截面一致的重力坝,可以将模型简化为二维模型,对水坝上游和下游分别采用传递矩阵法计算自由场响应。然而,拱坝的截面并不一致,而且通常水坝体系所在的场地为不规则的峡谷地形,因此无法简化为二维模型,求解自由场仍然是一大难题。本文给出了三维峡谷地形下,库水-淤砂层-坝体-坝基体系自由场的求解方法。假设人工边界的选取足够远以至于自由场区域的4个角远离峡谷地形,可以被看作水平成层场地,将需要计算自由场响应的三维不规则场地边界区域分解为左、后、右、前、底5个二维平面,如图2a所示。利用二维有限元计算左、后、右、前面的自由场响应作为系统侧面的参考场,以地震波入射场作为系统底面的参考场,采用透射人工边界为坝体波动散射问题提供地震动输入。理论上,该方法在地震波垂直入射下是行之有效的。具体的步骤如图2b所示,可以概括为:①利用传递矩阵法求解计算区域4个角的一维自由场响应,由于计算区域选取足够远,因此4个角的基岩层可以假设满足水平成层假定; ②以步骤①求得的一维自由场响应作为输入,利用二维库水-淤砂层-坝基体系有限元程序,结合透射人工边界计算4个侧面的地震响应; ③以4个侧面的地震响应以及底部入射场作为参考场,为库水-淤砂层-坝体-坝基体系地震响应提供地震动输入。
1.2 库水-淤砂层-坝体-坝基体系分析方法对库水-淤砂层-坝体-坝基体系进行地震响应分析,涉及到库水、饱和土、基岩(和坝体)3种介质的相互耦合。采用陈少林等(2019a,b)提出的广义饱和多孔介质统一计算框架,该方法将3种介质看作一种广义饱和多孔介质,避免了多种求解器之间的复杂耦合; 人工边界采用透射边界,具有精度高、易实现的优点。利用集中质量显式有限元法对库水-淤砂层-坝体-坝基体系进行时间离散和空间离散,可得内部任意节点的固、液相位移递推公式为:
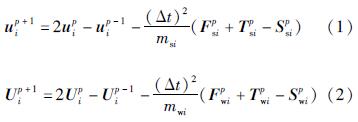
式中:ui、Ui分别为固相和液相位移矢量; msi、mwi分别为集中在节点上的固、液相质量; Fsi、Fwi分别为集中在节点上的固、液相本构力矢量; Tsi、Twi分别为集中在节点上的固、液相黏性阻力矢量; Ssi、Swi分别为作用在节点上的固、液相界面力矢量,当节点为一般内部节点时,界面力为零。
界面力通过在界面处设置节点对(第一种介质中的节点和第二种介质中的节点k)进行求解。由于界面力在切线方向的不连续性,可将界面力分解为法向和切向部分,先求解法向部分的界面力,再求解切向部分的界面力。以节点i为例,其固、液相法向界面力可表示为:
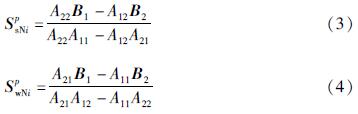
式中:
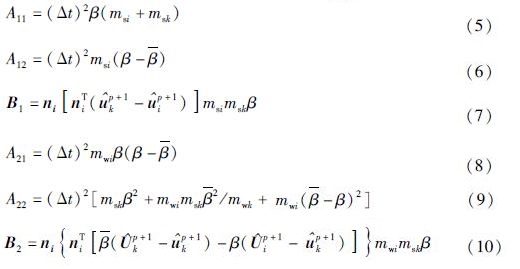
式中:β和
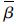 分别为第一种介质和第二种介质的孔隙率; ni为界面点的法向量;
分别为第一种介质和第二种介质的孔隙率; ni为界面点的法向量; 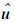 和
和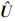 分别是不考虑界面力时得到的固、液相位移矢量,其表达式为:
分别是不考虑界面力时得到的固、液相位移矢量,其表达式为:
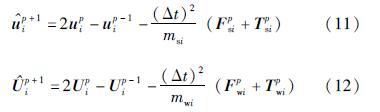
同理,可求得节点的法向界面力
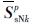 和
和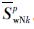 。由于液相不承受剪应力,所以液相的切向界面力为0,而固相的切向界面力可根据固相位移连续条件求解:
。由于液相不承受剪应力,所以液相的切向界面力为0,而固相的切向界面力可根据固相位移连续条件求解: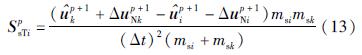
同理,可求得节点k的切向界面力
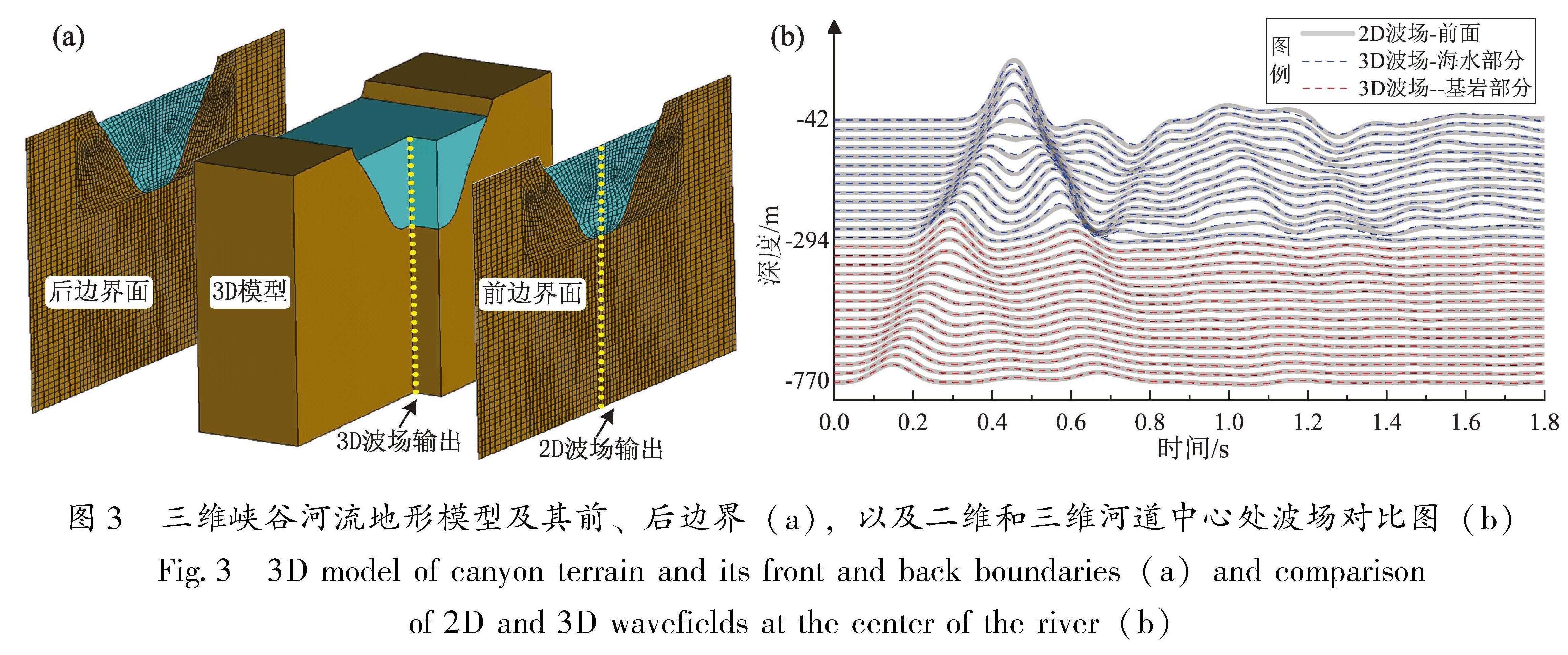
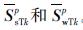 。最后,按式(1)(2)求得界面点的位移响应。
。最后,按式(1)(2)求得界面点的位移响应。为了验证本文提出的三维不规则自由场计算方法以及库水-淤砂层-坝体-坝基体系分析方法的有效性,以横截面一致的峡谷河流地形为例,建立有限元模型(图3a),计算其在脉冲波输入下的响应。首先计算模型的前、后边界面的二维有限元结果,然后利用本文的自由场计算方法为三维峡谷河流模型提供输入,并利用库水-淤砂层-坝体-坝基体系耦合计算方法计算三维模型的响应。由于该模型在顺河流方向的横截面是不变的,因此理论上其二维和三维计算结果应该保持一致。本文分别选取了二维和三维模型在河道中心位置处沿竖直方向的30个连续观测点,绘制了河道中心位置处的波场图,如图3b所示,结果表明:二维和三维有限元的波场在基岩部分完全重合,在海水部分略有出入,但是差别很小。因此,上述算例在一定程度上验证了本文的不规则地形自由场计算方法的有效性,以及库水-淤砂层-坝体-坝基体系耦合分析方法的正确性。对于没有河流的峡谷地形模型验证可以参考陈少林等(2021)的研究。
2 小湾拱坝地震响应分析研究
2.1 小湾拱坝的力学参数及有限元模型小湾水电站作为国家“西电东送”战略的标志性工程,是我国最有代表性的水利水电枢纽工程之一,其主要建筑物是一座大型的抛物线型混凝土双曲拱坝。本文以该混凝土双曲拱坝为研究对象,建立库水-淤砂层-坝体-坝基体系有限元耦合模型。小湾水电站双曲拱坝最大坝高为294 m,坝顶到坝底拱冠梁厚度不断变化,坝顶和坝底拱冠梁厚度分别为12 m和73 m,厚高比为0.248。坝顶中心线弦长为798 m,宽高比为2.71,为计算方便,对小湾拱坝的部分构件进行合理简化。
考虑半无限基岩以及半无限库水对坝体地震响应的影响,采用人工边界截取计算域,本文所用数值模型坝基范围为:左右拱端、上下游坝面各延伸1倍坝高左右,坝底向下延伸1.5倍坝高左右,有限元模型计算区域的尺寸为横河向1 200 m,顺河向600 m,竖直向770 m。同时,建立了与实际工程常遇水位相当的库水模型。整体模型如图4a所示,采用笛卡尔坐标系,以上游坝顶拱圈中点为坐标原点,横河向为X轴,沿河向为Y轴,竖直向为Z轴。
用八节点六面体的实体单元对库水-淤砂层-坝体-坝基体系进行空间离散,由于坝体形状不规则并且尺寸差异过大,所以坝体及其附近库水和坝基的单元为不规则单元,并且单元尺寸较小,而远离坝体的坝基单元为规则六面体单元,考虑到波动精度的要求,单元尺寸需要满足ΔX<λmin/10,因此单元尺寸不能过大。经计算,本文的单元尺寸限制在18 m以内,库水-淤砂层-坝体-坝基的整体有限元离散模型如图4b所示,坝体有限元模型及其观测点如图4c所示。
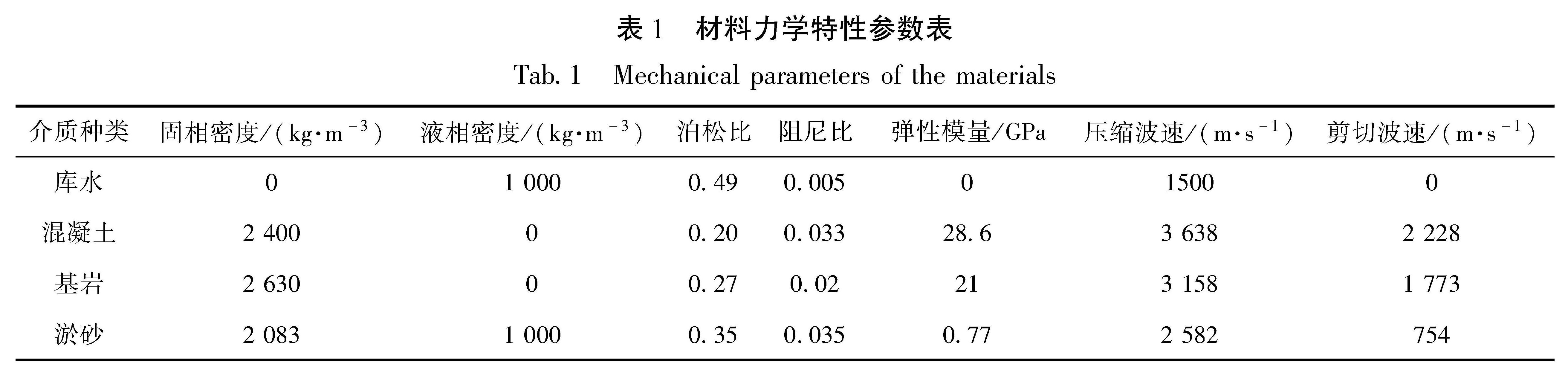
根据小湾拱坝的设计和施工资料,坝体混凝土静弹性模量为22 GPa,动弹性模量为28.6 GPa,泊松比为0.2,容重为2 400 kg/m3。小湾拱坝坝基包含多种岩石,但考虑到实际建模和数值计算的简便性,建模时坝基考虑为均质各向同性弹性介质。水坝体系中坝体混凝土、库水、淤沙以及坝基岩石的主要材料参数见表1。
图4 小湾拱坝计算模型(a)、库水-淤砂层-坝体-坝基有限元模型(b)及坝体有限元模型及观测点(c)
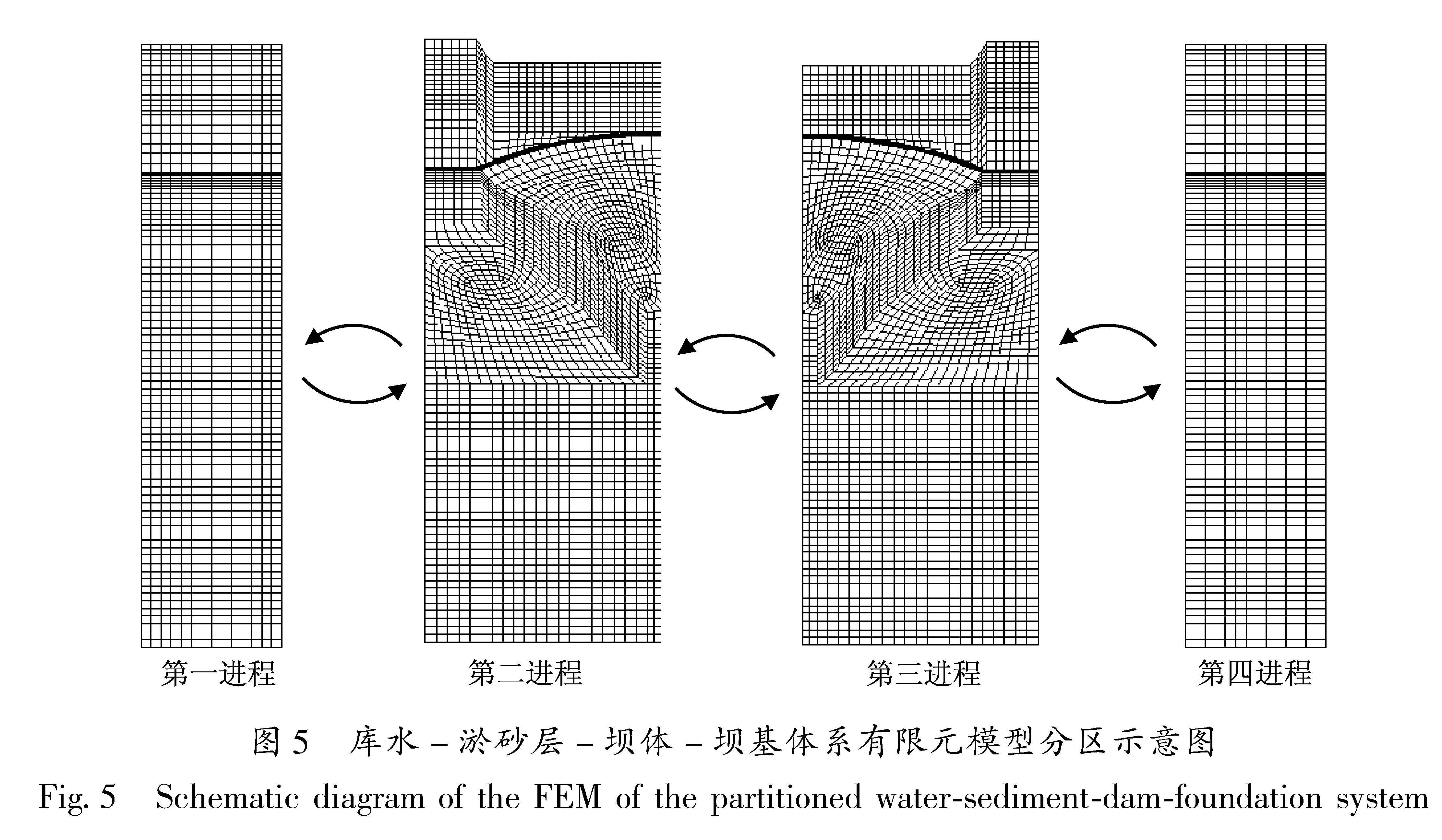
Fig.4 Computational model of Xiaowan Dam(a),FEM of reservoir-sediment-dam-foundation(b)and FEM of the dam and its observation points(c)[KH*2D]整体计算模型各方向尺寸较大,离散的单元和节点数量较多,约有16万个单元、18万个节点,因此对计算机内存提出了很高的要求。为降低内存需求,提高计算效率,对整体模型进行分区并行处理。将整体模型沿横河向划分为4个区域,如图5所示,每个区域为一个进程,每个进程独立计算,而进程间的消息传递采用MPI标准协议进行,通过分区界面点传递节点力和节点位移实现整体耦合,可大大提高计算效率(陈少林等,2017)。
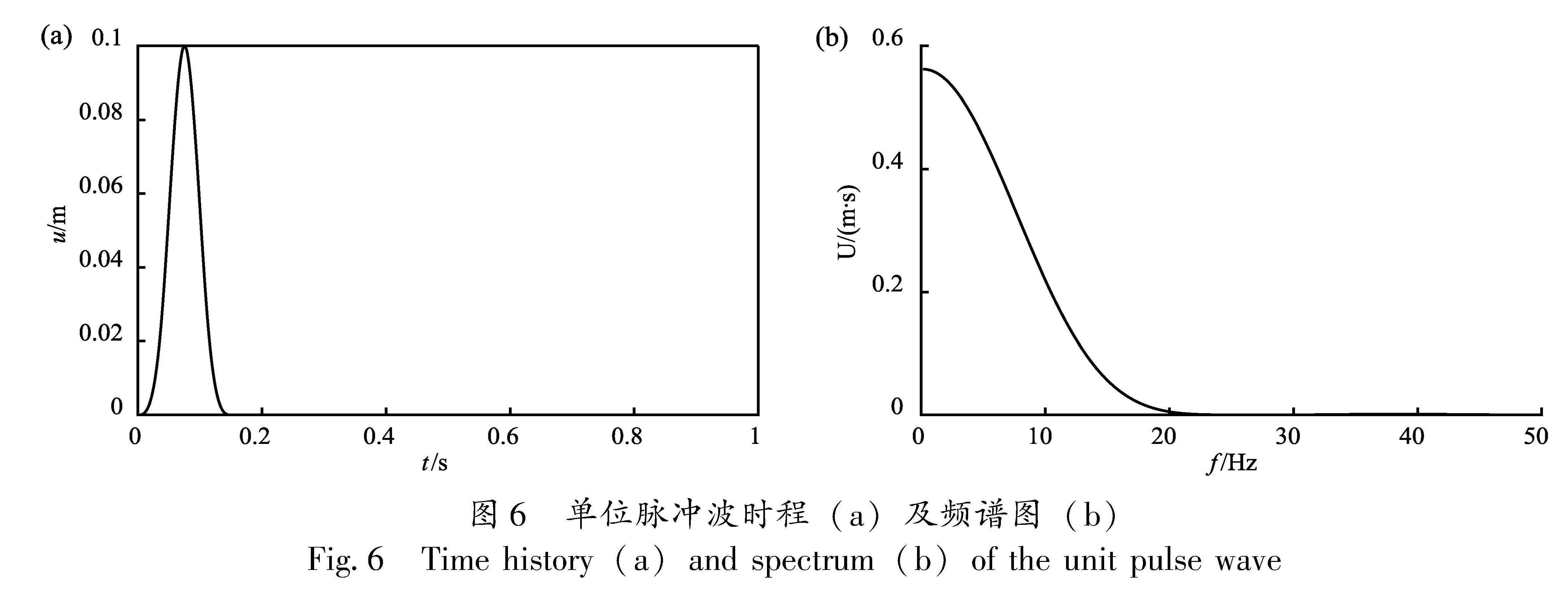
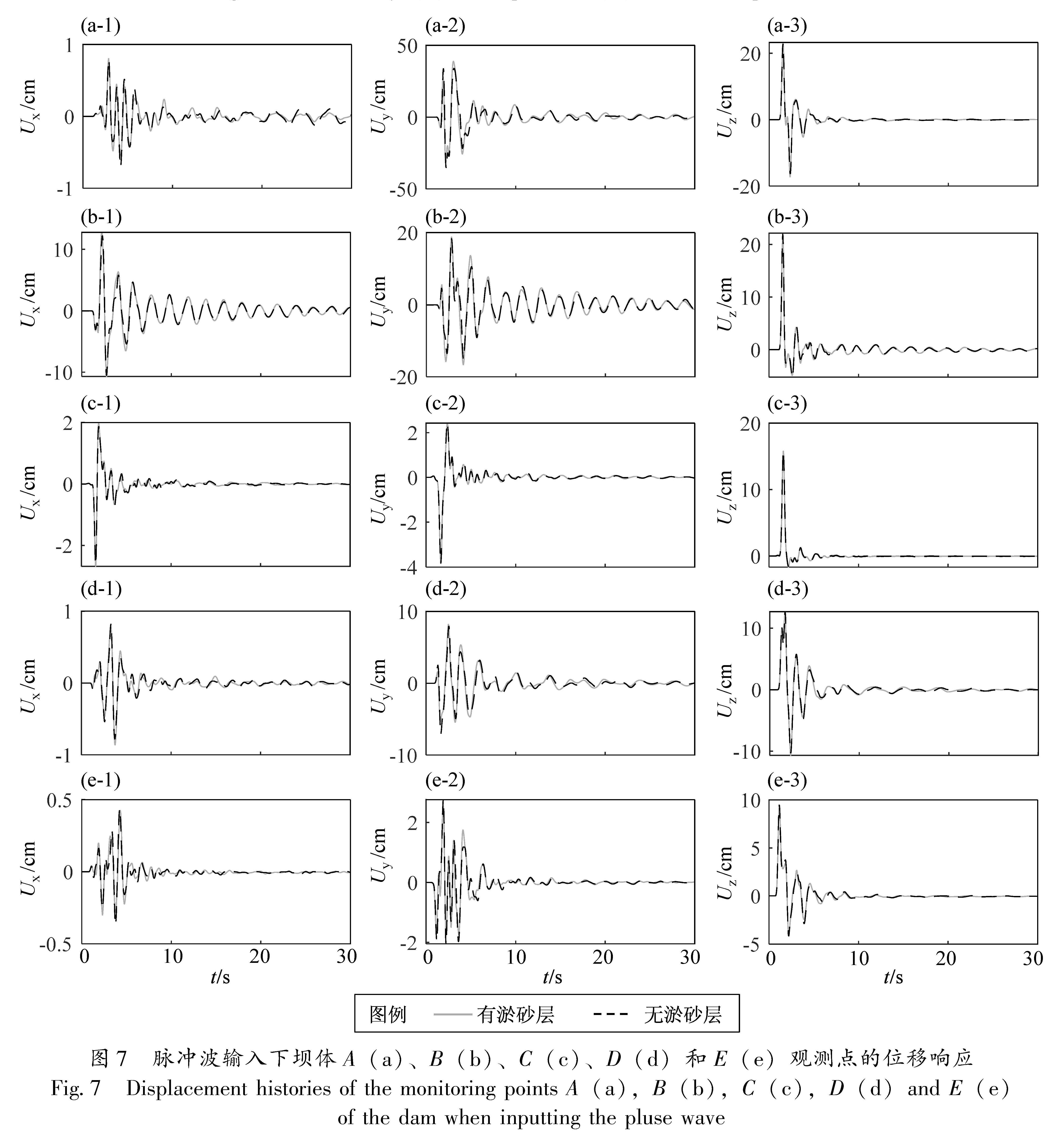
2.2 脉冲波输入下坝体响应分析本文首先以脉冲波作为输入,对坝体进行响应分析。脉冲波相较于地震波,有更高的频谱信息,可以更好地进行坝体频响分析。本文以单位P波脉冲作为输入,分别计算了考虑库水淤砂层和不考虑淤砂层时坝体的响应结果。在考虑库水淤砂层时,将库水底部厚度约为28 m的水替换为孔隙率为0.35的饱和多孔介质,淤沙层与坝基直接相接。单位脉冲宽度为0.15 s,时间步距为0.000 1 s,计算步数为65 536步,单位脉冲波前1 s的时程图及频谱信息如图6所示。坝体各观测点在有淤砂层和无淤砂层情形下的计算结果对比如图7所示。
对比各观测点的位移响应峰值及时程曲线,可以发现坝体响应的一般规律为:①各方向的位移峰值都在坝体顶部中心处最大(A点),位移峰值沿着拱圈方向(A-B-C)和拱冠梁方向(A-D-E)逐渐减小。②由于拱坝具有弯曲且壁薄的特点,加之库水震荡效应,坝体顶部中心点的顺河向位移甚至超过了主方向位移。整体位移规律与拱坝的主振型相匹配。
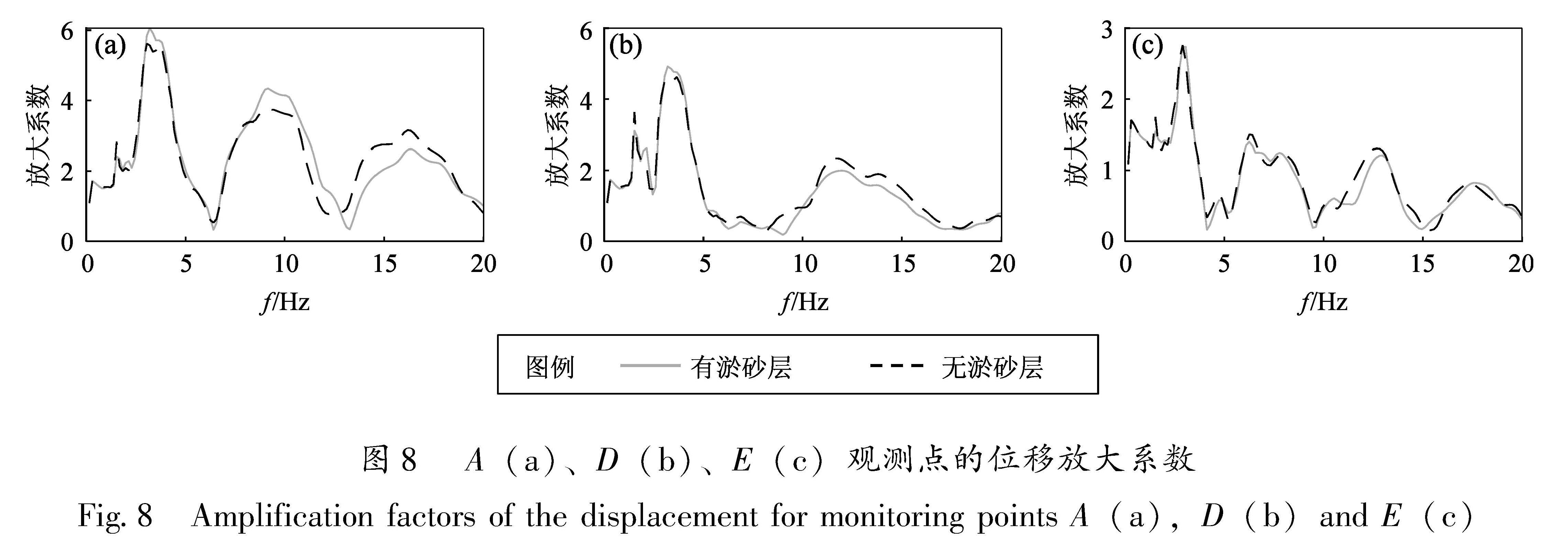
对比考虑淤砂层与不考虑淤砂层的响应结果可以发现,淤砂层对坝体响应影响较小,主要影响体现在各方向的位移峰值上。在输入主方向上(竖直方向),考虑淤砂层时,A、B、C三点的位移峰值仅仅分别放大了2%、1%和0.1%,与无淤砂层情形相比差别不大。如图8所示,对比分析拱冠梁上3个点(A、D、E)的频率放大系数,可以发现淤砂层主要增加了较低频段的放大系数,减小了较高频段的放大系数。
图7 脉冲波输入下坝体A(a)、B(b)、C(c)、D(d)和E(e)观测点的位移响应
Fig.7 Displacement histories of the monitoring points A(a),B(b),C(c),D(d)and E(e)of the dam when inputting the pluse wave2.3 地震波输入下坝体响应分析本文根据《水工建筑物抗震设计规范》(GB 51247—2018)的相关规定选取地震波,其中场地属于I类场地,Tg为0.2 s,βmax为2.5。对于基本烈度为Ⅵ及以上的区域,坝高超过200 m的工程应该按照专门的以概率理论为基础的地震危险性分析成果确定设计地震动加速度。根据小湾拱坝坝址区地质条件和《中国地震动参数区划图》(GB 18306—2015),可以确定小湾拱坝所在区域的基本地震烈度为Ⅷ度,小湾拱坝的设防烈度为Ⅸ度。根据地震危险性分析结果(陈厚群等,2012),其基岩水平向设计地震加速度为0.308 g,竖向设计地震动加速度取水平方向的2/3,为0.205 g。从美国太平洋地震中心数据库(PEER)选取30条与反应谱相吻合的天然地震动记录数据(图9a),对上述30条地震波进行分析,最终选择了与目标设计谱平均误差相差最小的2008年IWT010监测站记录到的Iwate_Japan地震波。由于数据库中记录的地震波长达一百多秒,若以完整的地震动记录作为输入,计算时间过长,且该条地震波记录中有很多较为平缓甚至平静的阶段。因此选取比较有代表性的一段30 s的地震波,调整其地震动峰值加速度,作为小湾拱坝的地震动输入,其加速度、速度及位移时程如图9b所示。
图9 目标设计谱与选取地震波反应谱(a)及 Iwate_Japan地震记录(b)
Fig.9 Target design spectrum and response spectrums of records(a)and Iwate_Japan seismic records(b)为探究在峡谷地形下,小湾拱坝的地震响应规律以及库水底部淤砂层对结果的影响,以Iwate_Japan地震波作为输入(暂时仅考虑垂直入射的压缩波),分别对小湾拱坝进行了考虑淤砂层和不考虑淤砂层时的地震模拟。鉴于传播过程中计算模型对弹性波的放大作用,将输入波折减1/2作为实际输入,通过本文理论及Fortran程序进行动力有限元模拟,获取了各观测点的位移响应曲线(图 10),并提取响应过程中的最大主应力和最小主应力,不考虑和考虑淤砂层时的上游坝面和下游坝面的最大和最小主应力包络如图 11所示,图中正值代表拉应力,负值代表压应力。
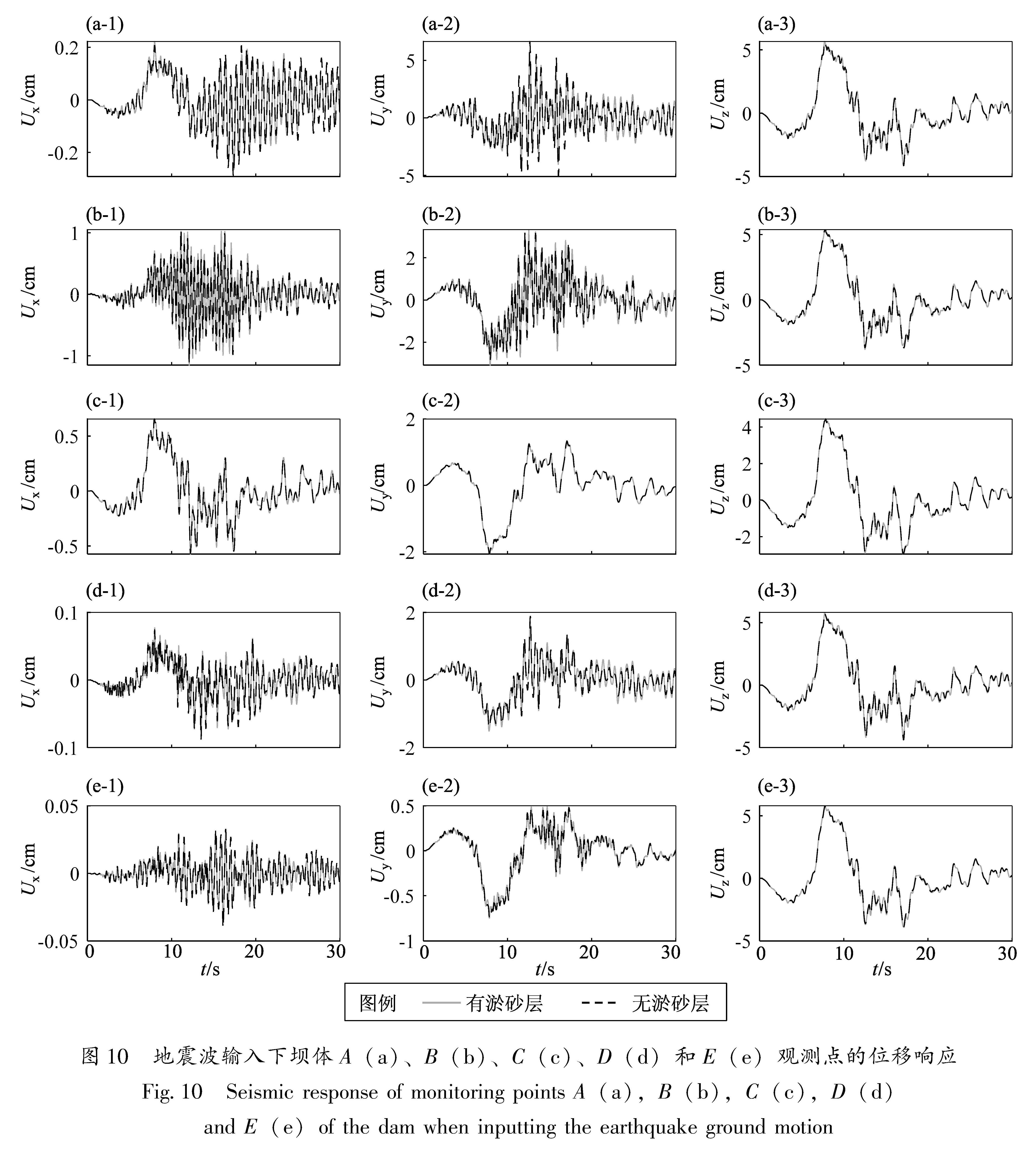
图 10 地震波输入下坝体A(a)、B(b)、C(c)、D(d)和E(e)观测点的位移响应
Fig.10 Seismic response of monitoring points A(a),B(b),C(c),D(d)and E(e)of the dam when inputting the earthquake ground motion从图 10可以看出,坝体各点主方向位移峰值相比地震波输入放大了约1.5倍。而由于拱坝薄壁的特点,坝体在顺河向方向位移较大,尤其是坝体顶部中心点,峰值大小甚至超过了主方向的位移峰值。对比有淤砂层与无淤砂层的计算结果可以看出,淤砂层对坝体的位移响应影响比较小,仅仅改变了各点的部分峰值大小,且离坝体顶部中心处越远,影响越小。
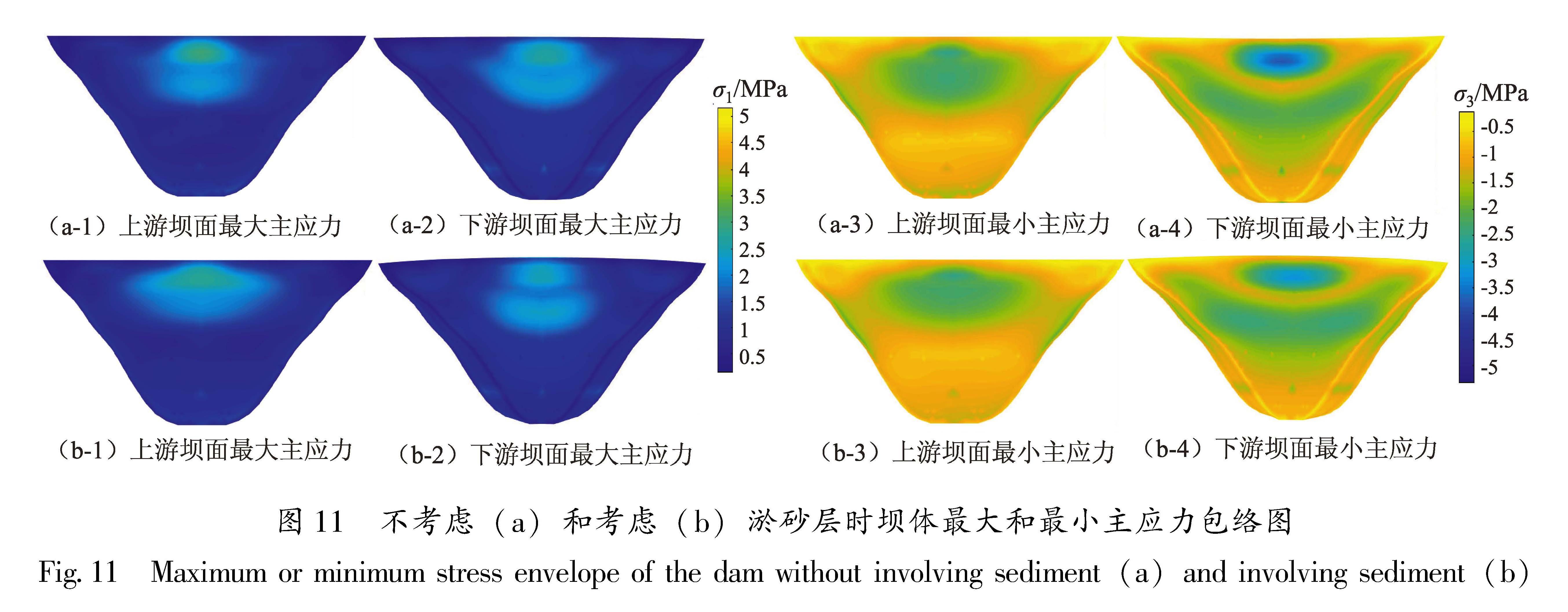
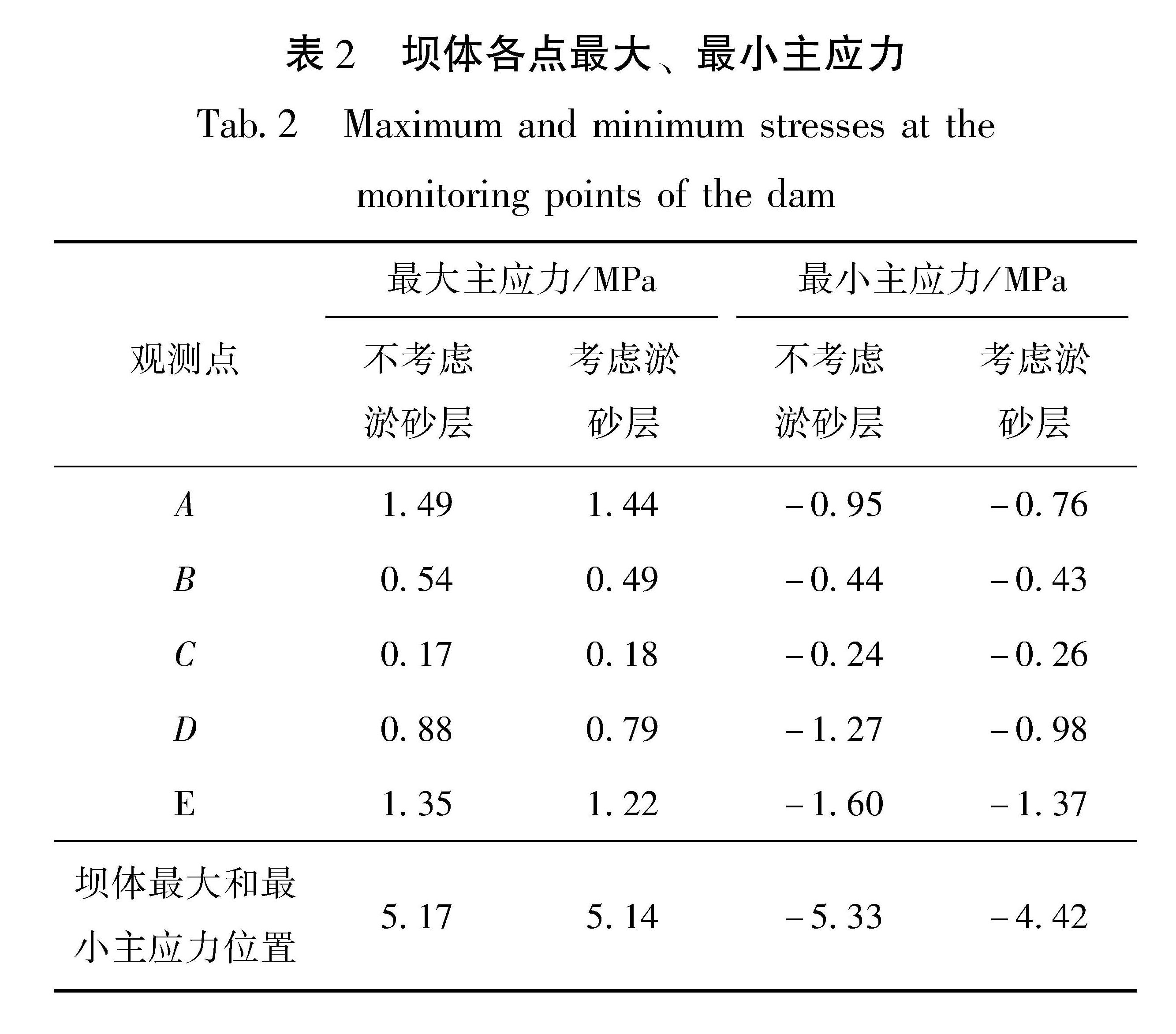
通过分析上游坝面和下游坝面在地震过程中的最大主应力和最小主应力包络图(图 11)可以发现,无论是否考虑淤砂层,坝体在地震过程中承受较大拉、压应力的位置均处于坝体顶部中心区域附近,这是因为坝体顶部中心区域较为薄弱,容易受地震作用而产生晃动。而淤砂层的影响对坝体最大主应力的改变并不显著,总的来说,考虑淤砂层的影响会轻微减小坝体受到的拉、压应力。由表2可见,考虑淤砂层后,坝体大部分观测点的最大及最小主应力都略微减小了,其主要原因可能是淤砂层对地震作用的能量吸收效应。在下游坝面的边缘处均出现了贯穿的细条状的异常分布,其原因可能是:坝体四周边缘处直接接触山体及地基,在地震动作用及上游库水的动水压力作用下,出现了应力集中现象,局部产生了较大的主应力。
图 11 不考虑(a)和考虑(b)淤砂层时坝体最大和最小主应力包络图
Fig.11 Maximum or minimum stress envelope of the dam without involving sediment(a)and involving sediment(b)综上所述,小湾拱坝在地震波作用下,较大位移及较大拉、压应力均出现在水坝顶部中心区域,地震安全设计时应该注意这些部位,而淤砂层对坝体地震响应影响比较小,稍微减小了坝体顶部区域最大主应力。
3 结论
本文以小湾拱坝为研究对象,考虑库水、淤沙层、坝体、坝基的耦合效应,建立了库水-淤砂层-坝体-坝基体系的动力分析算法,并编制了分区并行的有限元程序,分别以脉冲波和地震波作为输入,对小湾拱坝进行动力响应分析,探讨了小湾拱坝的动力响应特性,以及淤砂层对拱坝地震响应的影响,主要得出了以下结论:
(1)地震过程中,由于拱坝的拱形设计及上游动水压力的作用,坝体顶部中心区域会出现较大的位移峰值,尤其是顺河方向,位移峰值甚至超过了输入的主方向。总体上,位移峰值呈现从坝体顶部中心区域向坝体边缘区域逐渐减小的规律。
(2)地震波输入下,坝体顶部中心区域会承受较大的拉、压应力,在抗震安全设计时应该重点关注这个部位。从结果看,设计地震荷载作用下,小湾混凝土拱坝承受的拉、压应力并没有超过混凝土的动态抗压强度和动态抗拉强度,符合设计规范的要求。
(3)库水底部淤砂层对坝体的位移及应力影响不大。从脉冲结果的频响关系可以看出淤砂层会放大低频段的响应,减小较高频段的响应,而对于像地震波这种低频成分较多的输入,淤砂层会略微降低坝体的最大主应力。
- 陈厚群,吴胜兴,党发宁,等.2012.高拱坝抗震安全[M].北京:中国电力出版社.
- Chen H Q,Wu S X,Dang F N,et al.2012.Seismic safety of high arch concrete dam[M].Beijing:China Electric Power Press.(in Chinese)
- 陈厚群.2017.高混凝土坝抗震设计面临的挑战[J].水电与抽水蓄能,3(2):1-13,49.
- Chen H Q.2017.Challenge confronted in seismic design of high concrete dams[J].Hydropower and Pumped Storage,3(2):1-13,49.(in Chinese)
- 陈少林,程书林,柯小飞.2019b.海洋地震工程流固耦合问题统一计算框架——不规则界面情形[J].力学学报,51(5):1517-1529.
- Chen S L,Cheng S L,Ke X F.2019b.A unified computational framework for fluid:Solid coupling in marine earthquake engineering:irregular interface case[J].Chinese Journal of Theoretical and Applied Mechanics,51(5):1517-1529.(in Chinese)
- 陈少林,柯小飞,张洪翔.2019a.海洋地震工程中流固耦合问题统一计算框架[J].力学学报,51(2):594-606.
- Chen S L,Ke X F,Zhang H X.2019a.A unified computational framework for fluid-solid coupling in marine earthquake engineering[J].Chinese Journal of Theoretical and Applied Mechanics,51(2):594-606.(in Chinese)
- 陈少林,王俊泉,刘启方,等.2017.基于显-隐式格式的三维时域土-结相互作用分析的异步并行算法[J].中国科学:技术科学,47(12):1321-1330.
- Chen S L,Wang J Q,Liu Q F,et al.2017.An asynchronous parallel algorithm for soil-junction interaction analysis in three-dimensional time domain based on explicit-implicit format[J].Science China:Technological Sciences,47(12):1321-1330.(in Chinese)
- 陈少林,伍锐,张娇,等.2021.地形和土-结相互作用效应对三维跨峡谷桥梁地震响应的影响分析[J].力学学报,53(6):1781-1794.
- Chen S L,Wu R,Zhang J,et al.2021.Topography and soil-structure interaction effects on the seismic response of three-dimensional canyon-crossing bridge[J].Chinese Journal of Theoretical and Applied Mechanics,53(6):1781-1794.(in Chinese)
- 林皋.2017.大坝抗震与安全分析[J].水电与抽水蓄能,3(2):14-27.
- Lin G.2017.Seismic analysis and safety evaluation of large dams[J].China Electric Power Press,3(2):14-27.(in Chinese)
- 涂劲,廖建新,李德玉,等.2018.高拱坝-地基系统整体稳定强震破坏机理研究[J].水电与抽水蓄能,4(2):49-55.
- Tu J,Liao J X,Li D Y,et al.2018.Study on the failure mechanism of integral stability of the high arch dam-foundation system under strong earthquake[J].China Electric Power Press,4(2):49-55.(in Chinese)
- 王进廷,杜修力,张楚汉.2003.重力坝-库水-淤砂-地基系统动力分析的时域显式有限元模型[J].清华大学学报(自然科学版),43(8):1112-1115.
- Wang J T,Du X L,Zhang C H.2003.Time-domain explicit finite element model for dynamic analysis of gravity dam-reservoir water-silt-foundation system[J].Journal of Tsinghua University(Science and Technology),43(8):1112-1115.(in Chinese)
- 王进廷,唐庆,杜修力.2006.库底饱和淤积砂层对高拱坝地震反应的影响研究[J].水力发电学报,(2):11-15.
- Wang J T,Tang Q,Du X L.2006.Analysis of the saturated sediment effect on the seismic response of high arch dams[J].Journal of hydroelectric engineering,(2):11-15.(in Chinese)
- 王进廷,唐庆,杜修力.2007.库底非饱和淤砂层对高拱坝地震反应的影响[J].水利水电科技进展,(2):22-25.
- Wang J T,Tang Q,Du X L.2007.Effect of unsaturated sediment layer on seis mic responses of high arch dams[J].Advances in Science and Technology of Water Resources,(2):22-25.(in Chinese)
- 王进廷.2001.高混凝土坝-可压缩库水-淤砂-地基系统的地震反应分析研究[D].北京:中国水利水电科学研究院.
- Wang J T.2001.The analyses of seismic response of high concrete dam-compressible water-sediment-foundation systems[D].Institute of Water Conservancy and Hydroelectric Power Research.(in Chinese)
- 张楚汉,金峰,王进廷,等.2016.高混凝土坝抗震安全评价的关键问题与研究进展[J].水利学报,47(3):253-264.
- Zhang C H,Jin F,Wang J T,et al.2016.Key issues and developments on seismic safety evaluation of high concrete dams[J].Journal of Hydraulic Engineering,47(3):253-264.(in Chinese)
- 赵宇昕,陈少林.2016.关于传递矩阵法分析饱和成层介质响应问题的讨论[J].力学学报,48(5):1145-1158.
- Zhao Y X,Chen S L.2016.Discussion on the matrix propagator method to analyze the response of saturated layered media[J].Chinese Journal of Theoretical and Applied Mechanics,48(5):1145-1158.(in Chinese)
- GB 18306—2015,中国地震动参数区划图[S].
- GB 18306—2015,Seismic ground motion parameter zonation map of China[S].(in Chinese)
- GB 51247—2018,水工建筑物抗震设计规范.
- GB 51247—2018,Specifications for seismic design of hydraulic structures[S].(in Chinese)
- Chen S L,Lyu H,Zhou G L.2022.Partitioned analysis of soil-structure interaction for Nuclear Island Buildings[J].Earthquake Engineering & Structural Dynamics,51(3):1-28.
- Chopra A K.2012.Earthquake analysis of arch dams:Factors to be considered[J].Journal of Structural Engineering,138(2):205-214.
- Domnguez J,Gallego R,Japn B R.1997.Effects of porous sediments on seismic response of concrete gravity dams[J].Journal of Engineering Mechanics,123(4):302-311.
- Farhat C,Roux F X.1991.A method of finite element tearing and interconnecting and its parallel solution algorithm[J].International Journal for Numerical Methods in Engineering,32(6):1205-1227.
- Felippa C A,Park K C,Farhat C.2001.Partitioned analysis of coupled mechanical systems[J].Computer Methods in Applied Mechanics and Engineering,190(24):3247-3270.
- Fenves G,Chopra A K.1984.Earthquake analysis of concrete gravity dams including reservoir bottom absorption and dam-water-foundation rock interaction[J].Earthquake Engineering and Structural Dynamics,12(5):663-680.
- Fok,Ka-lun,Chopra A K.1987.Water compressibility in earthquake response of arch dams[J].Journal of Structural Engineering,113(5):958-975.
- [JP3]Haskell N A.1953.The dispersion of surface waves on multilayered media[J].Bulletin of the Seismological Society of America,43(1):17-34.
- Liaw C Y,Chopra A K.1974.Dynamics of towers surrounded by water[J].Earthquake Engineering and Structural Dynamics,3(1):33-49.
- Lokke A,Chopra A K.2019.Direct finite element method for nonlinear earthquake analysis of concrete dams:Simplification,modeling,and practical application[J].Earthquake Engineering & Structural Dynamics,48(7):818-842.
- Nath B.1982.Natural frequencies of arch dam reservoir systems-by a mapping finite element method[J].Earthquake Engineering & Structural Dynamics,10(5):719-734.
- Tan H C,Chopra A K.1995.Earthquake analysis of arch dams including dam-water-foundation rock interaction[J].Earthquake Engineering & Structural Dynamics,24(11):1453-1474.
- Thomson W T.1950.Transmission of elastic waves through a stratified solid media[J].Journal of Applied Physics,21(2):89-93.
- Wang P G,Zhao M,Du X L,et al.2018.Analytical solution and simplified formula for earthquake induced hydrodynamic pressure on elliptical hollow cylinders in water[J].Ocean Engineering,148(15):149-160.
- Westergaard H M.1933.Water pressures on dams during earthquakes[J].Transactions of the American Society of Civil Engineers(Trans Asce),98(2):418-432.
- Zhao C G,Li W H,Wang J T.2003.An explicit finite element method for dynamic analysis in three-medium coupling system and its application[J].Acta Seismological Sinica,16(3):272-282.

![图4 小湾拱坝计算模型(a)、库水-淤砂层-坝体-坝基有限元模型(b)及坝体有限元模型及观测点(c)<br/>Fig.4 Computational model of Xiaowan Dam(a),FEM of reservoir-sediment-dam-foundation(b)and FEM of the dam and its observation points(c)[KH*2D]](2024年01期/pic70.jpg)