收稿日期:2023-07-01
基金项目:辽宁省教育厅项目(LJKZ0336).
基金项目:辽宁省教育厅项目(LJKZ0336).
隧道侧穿箱基框架结构体系振动台试验及数值模拟
(1.辽宁工程技术大学 土木工程学院,辽宁 阜新 123000; 2.北京工业大学 城市与工程安全减灾教育部重点实验室,北京 100124)
Shaking Table Test and Numerical Simulation of Tunnel Side-crossing Box Foundation Frame Structure System
LU Shasha1,BAI Xiaoxiao1,ZHANG Yanan1,MENG Wei1,YUAN Di1,XU Hong2
(1.College of Civil Engineering,Liaoning Technical University,Fuxin 123000,Liaoning,China)(2.Key Laboratory of Urban and Engineering Safety and Disaster Reduction,Ministry of Education,Beijing University of Technology,Beijing 100124,China)
underground tunnels; box-foundation frame structure; shaking-table test; numerical simulation; dynamic response
DOI: 10.20015/j.cnki.ISSN1000-0666.2024.0033
备注
摘要
全文
图/表
参考文献
以郑州市轨道交通7号线侧穿箱基框架结构工程为背景,开展了室内振动台缩尺模型试验,并借助有限元软件ABAQUS对不同工况进行数值建模,将振动台试验和数值模拟结果进行对比,验证数值模拟结果的可靠性。基于验证后的模型,分析隧道侧穿箱基框架结构体系的动力响应特性。结果表明:①隧道或箱基框架结构的存在均会降低整个体系的自振频率; ②箱基框架结构的存在会降低隧道结构的加速度响应,同时减弱隧道结构所受到的弯矩,而对其所受剪力的影响不大; ③隧道结构的存在会减弱箱基框架结构的加速度响应和位移响应。箱室的存在会改变地震波的传播路径,且当箱基框架结构高于三层时,楼板加速度响应随楼层高度的增大更明显。
In this paper,based on a side-crossing,box-foundation frame structure of the project of Line 7 urban rail traffic in Zhengzhou city,a scaled model test on the indoor shaking table is carried out.With the help of the finite element software ABAQUS,the numerical modeling for different working conditions is done,and the results from the shaking table test are compared with the results from the numerical analysis to verify the results from the shaking table test.Then,based on the validated model,the seismic response characteristics of the side-crossing,box-foundation frame structure of the tunnel side is studied.The results show that:① The tunnel or box-foundation frame structure will reduce the natural frequency of the whole system; ② The box-foundation frame structure will reduce the acceleration response of the tunnel structure,weaken the bending moment of the tunnel structure,but it has little effect on its sheer force of the structure itself; ③ The tunnel structure will weaken the acceleration response and displacement response of the box-foundation frame structure.The box will change the propagation path of the seismic wave,and when the box-foundation frame structure is more than three stories,the acceleration response of the floor becomes more obvious with the increase of the number of the floors.
引言
随着城市地下空间的开发利用和既有地下结构的扩展改造,地下结构近距离穿越地表建筑的工程越来越多,如莞惠城际隧道下穿密集建筑区(李铮等,2015)、武汉轨道7号线纸坊大街站侧穿7层居民楼(何如,2019)。这类建筑工程不仅实现了城市空间立体式的开发,也极大地满足了人们的生活需求。此外,由于超限高层建筑的大量崛起,箱型基础也得到推广使用。但地震学家对1995年日本阪神地震后考察发现,很多地下结构(包括箱型基础)均受到不同程度的破坏(于翔,2002),因此人们开始加强了对箱基框架结构抗震性能的研究。
地下结构、土体和地上结构间的相互作用形成了一个复杂的体系。Ghergu和Ionescu(2009)、Semblat等(2008)将地表结构与邻近地下结构的相互作用称为地下结构的城市效应,这种城市效应会明显改变地震波的传播方式,从而导致地表输入的地震动不同于自由场。目前已有许多学者对地上结构、地基土以及邻近地下结构所组成的复杂相互作用体系进行了研究,如Guo等(2013)采用广义层间位移谱法研究得出建筑物自身动力特性和建筑物与车站的间距是地铁车站对地表建筑物响应的关键影响因素; 王国波等(2014)通过建立下穿隧道-土-地表邻近框架结构体系二维数值模型,分析得出下穿隧道对地表框架结构的地震响应影响有限,而地表结构的存在对隧道结构地震响应的影响很小; 程业等(2022)基于室内振动台模型试验,对不同地震动作用下的结构-土-结构相互作用(SSSI)体系和土-结构相互作用(SSI)体系动力响应进行对比得出,SSSI体系的结构变形反应最大可达到SSI体系变形反应的1.267倍。我国针对上部结构-基础-土相互作用体系较为全面的研究最早是由李培振等(2002)、陈跃庆等(2001)通过室内模型试验实现的。此后,许多学者也对该体系展开了深入研究,尚守平等(2006)通过野外大比例结构模型动力试验,研究了土与箱基及框架结构间的动力相互作用; 王国波等(2022)基于试验探讨了基础类型与地震动特性对场地土以及结构自身地震响应的影响,认为地表结构的存在放大了地表加速度响应,且具有一定埋深箱型基础的地震响应大于浅埋独立基础。
综上可见,近年来关于地下结构-土体-地上结构相互作用体系动力响应方面的研究已取得了重要进展,但着重考虑隧道侧穿箱基框架结构体系地震响应的相关研究还较少,本文以郑州市轨道交通7号线侧穿箱基框架结构工程为背景,采用振动台试验和数值模拟相结合的研究方法,探究地震作用下隧道侧穿箱基框架结构体系的动力响应规律。
1 工程概况
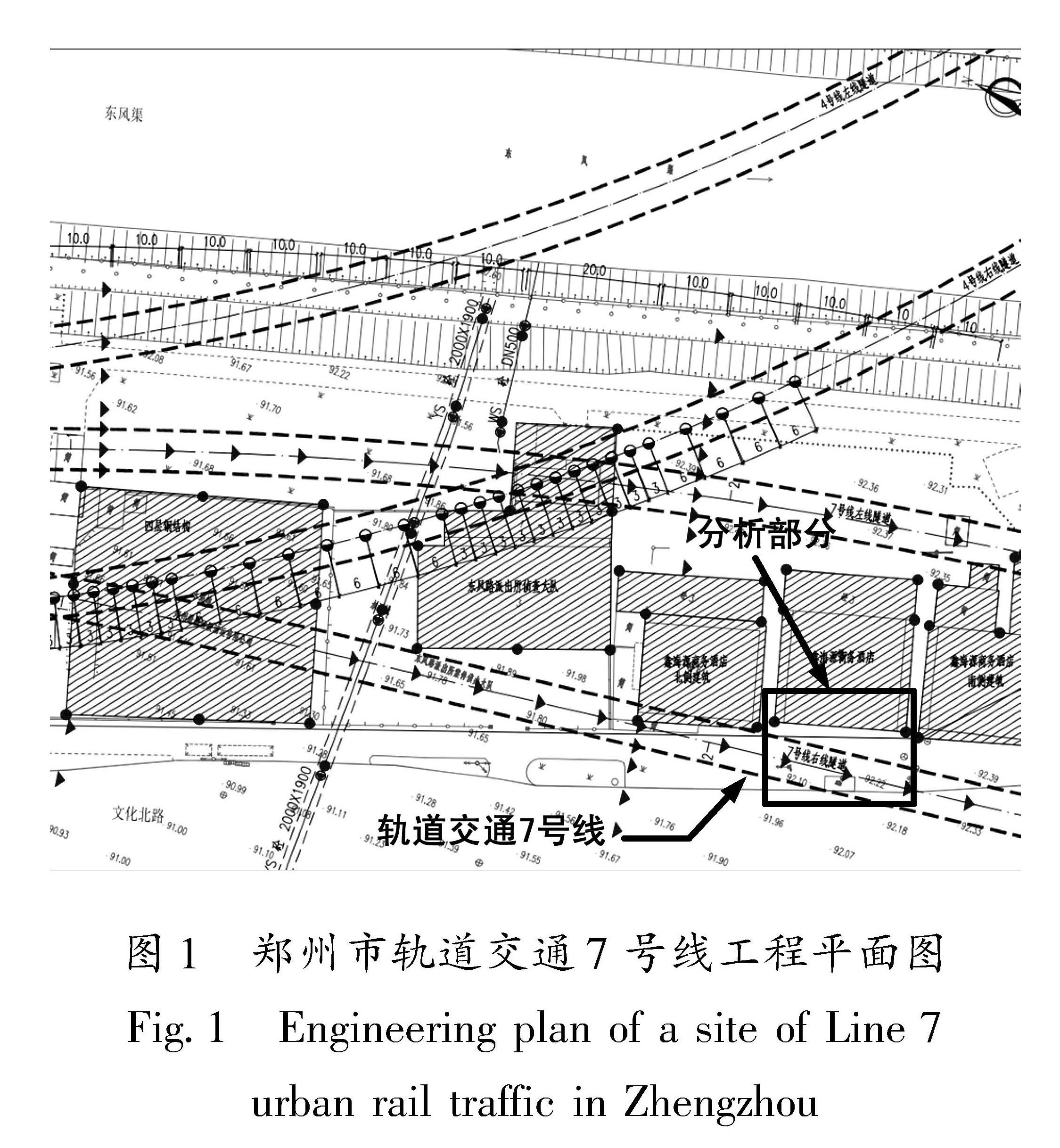
郑州市轨道交通7号线张家村站—陈砦站区间盾构段起止里程为DK7+004.996～DK7+909.478,长度为904.482单线延米,线路出张家村站后侧穿鑫海源商务酒店建筑群以及众多市政管线后到达陈砦站北端头,工程平面布局如图1所示。工程区间场地地面标高约为91.17～92.21 m,区间隧道覆土厚度约为7.0～13.6 m。据本场地钻探55.0 m深度范围内揭露,结合郑州市区域地质资料,本工点场地地层自上而下依次由杂填土、黏质粉土、粉质黏土、粉砂、细砂等构成。场地内未发现如塌陷、岩溶、滑坡、地面沉降、地裂缝等不良地质作用。
图1 郑州市轨道交通7号线工程平面图
Fig.1 Engineering plan of a site of Line 7urban rail traffic in Zhengzhou2 振动台试验设计
2.1 振动台及模型箱试验所用振动台台面尺寸为3 m×3 m,工作频率范围为0.1～50 Hz,最大承载力为10 t。振动台上放置2 m×2 m×1.5 m的刚性模型箱,其侧壁由3 mm厚钢板焊接而成。在模型箱四周采用40 mm×40 mm×3 mm矩形方钢管进行支撑,以防止其在振动过程中发生侧向倒塌而失稳。试验时在模型箱四周侧壁内衬200 mm厚的聚苯乙烯泡沫塑料板以消减边界效应,同时铺设聚氯乙烯薄膜来减小试验误差。在模型箱底部铺设一层碎石以增大模型土与箱底的摩擦,防止模型土与模型箱底在激励过程中发生相对滑移。试验所用振动台及模型箱如图2所示。
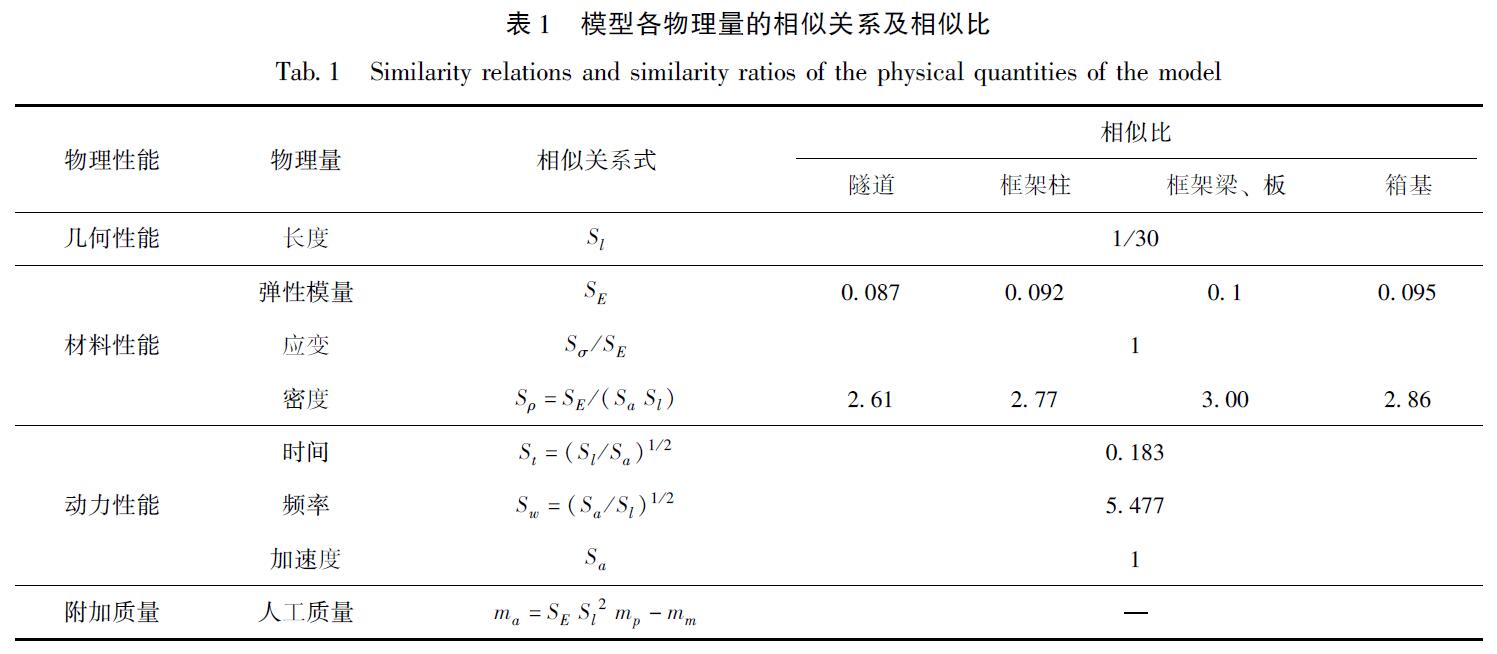
2.2 相似关系根据Bukingham-π定理,以长度、弹性模量、加速度为基本物理量,根据相似条件间的关系可初步确定其他相似关系(Moncarz,1981; Krawinkler,Moncarz,1981)。综合考虑试验设备基本参数(主要包括模型几何尺寸、振动台的承载能力)以及模型箱边界效应的影响,首先确定几何相似比为1/30。为了避免无法区分在强震作用下土体非线性和结构非线性引起的场地反应变化的区别,试验中仅考虑土体非线性的影响(程业,2022),模型结构均选用线弹性较好的有机玻璃,经力学性能试验测得有机玻璃的弹性模量为3 GPa。实际工程中地下隧道原型结构采用C50混凝土,箱基框架原型结构中梁、板均采用C30混凝土,柱与箱室分别采用C40、C35混凝土,故根据相似关系即可计算求得模型体系各物理量的相似关系及相似比,结果见表1。考虑到实际工程中原型结构和缩尺模型在同一个重力场,故加速度相似比选取为1。[FL)][JZ][XC路沙沙2A.TIF; %90%90] [XC路沙沙2B.TIF; %90%90]
图2 试验所用振动台(a)及模型箱(b)
Fig.2 The shaking table(a)and the test box(b)used for the test表1 模型各物理量的相似关系及相似比
Tab.1 Similarity relations and similarity ratios of the physical quantities of the model
2.3 模型结构及模型土试验箱基框架结构原型为六层双向单跨钢筋混凝土框架。框架纵向和横向跨度分别为6 m、8.4 m,1层楼层高为4.5 m,2～6层楼层高均为3.6 m,楼层柱的横截面尺寸为0.6 m×0.6 m,楼板层厚度为0.12 m,整体箱型基础高度为6.15 m。试验中隧道结构原型为外直径6.20 m,内直径5.50 m的盾构隧道,拱顶埋深为12.77 m。根据几何相似比即可确定试验模型结构尺寸。本试验主要目的是进行规律性探索,为便于后续对试验结果进行对比分析,试验中将隧道结构简化为均质圆形隧道,不考虑盾构隧道管片间的接头特性,箱基框架结构及隧道结构如图3所示。计算模型配重时,首先由原型结构质量按相似常数计算得到模型理论所需质量,然后减去模型质量,即可得到模型对应楼层所需配重(Chen et al,2015)。经计算求得,箱基框架模型总配重为50.52 kg,隧道模型总配重为60 kg。
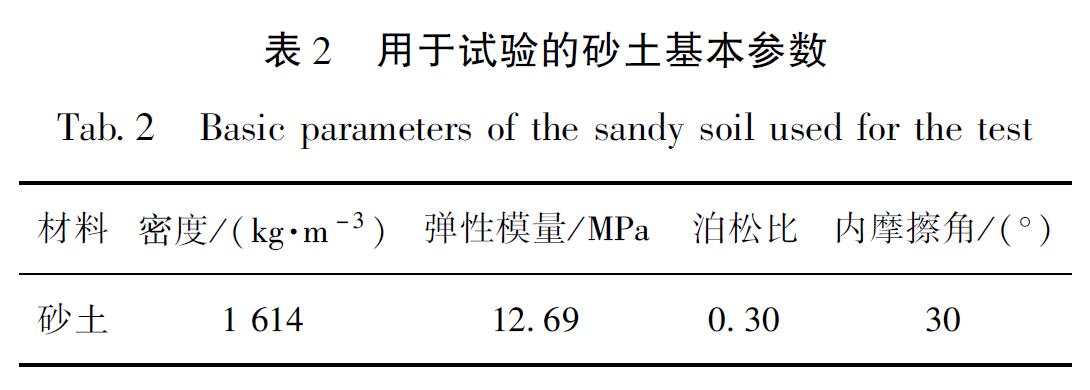
试验所选用的模型土为砂土,除去在振动方向两端箱壁泡沫板占据的尺寸及其沿高度方向预留尺寸,模型箱内土体尺寸为1.6 m×1.6 m×1.3 m。试验前需对砂土进行干燥和筛分处理,并测定砂土的物理特性及力学参数,结果见表2。
表2 用于试验的砂土基本参数
Tab.2 Basic parameters of the sandy soil used for the test
图3 箱基框架姑构(a) 和隧道结构(b)
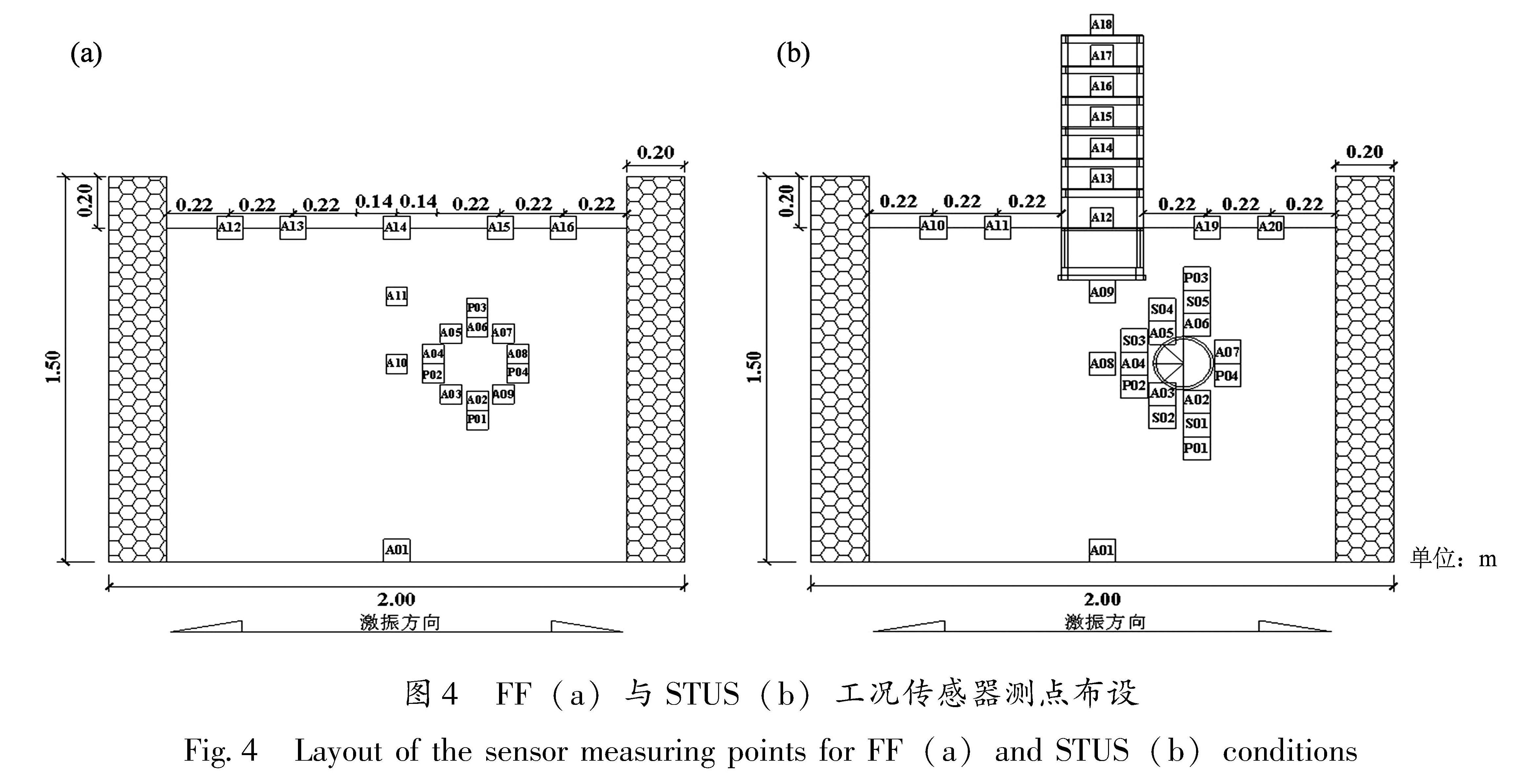
Fig.3 The box-base frame structure(a) and the tunnel structure( b)2.4 试验工况及加载顺序结合实际工程及试验目的,本文设计4组工况:自由场(FF)、砂土-隧道结构(ST)、砂土-箱基框架结构(SUS)、砂土-隧道-箱基框架结构(STUS)。本次振动台试验中所使用的传感器有:加速度传感器、电阻应变片及土压力传感器,分别用A、P、S表示加速度、土压力以及应变,数字表示传感器标号。图4所示为FF与STUS工况试验传感器测点布设图。
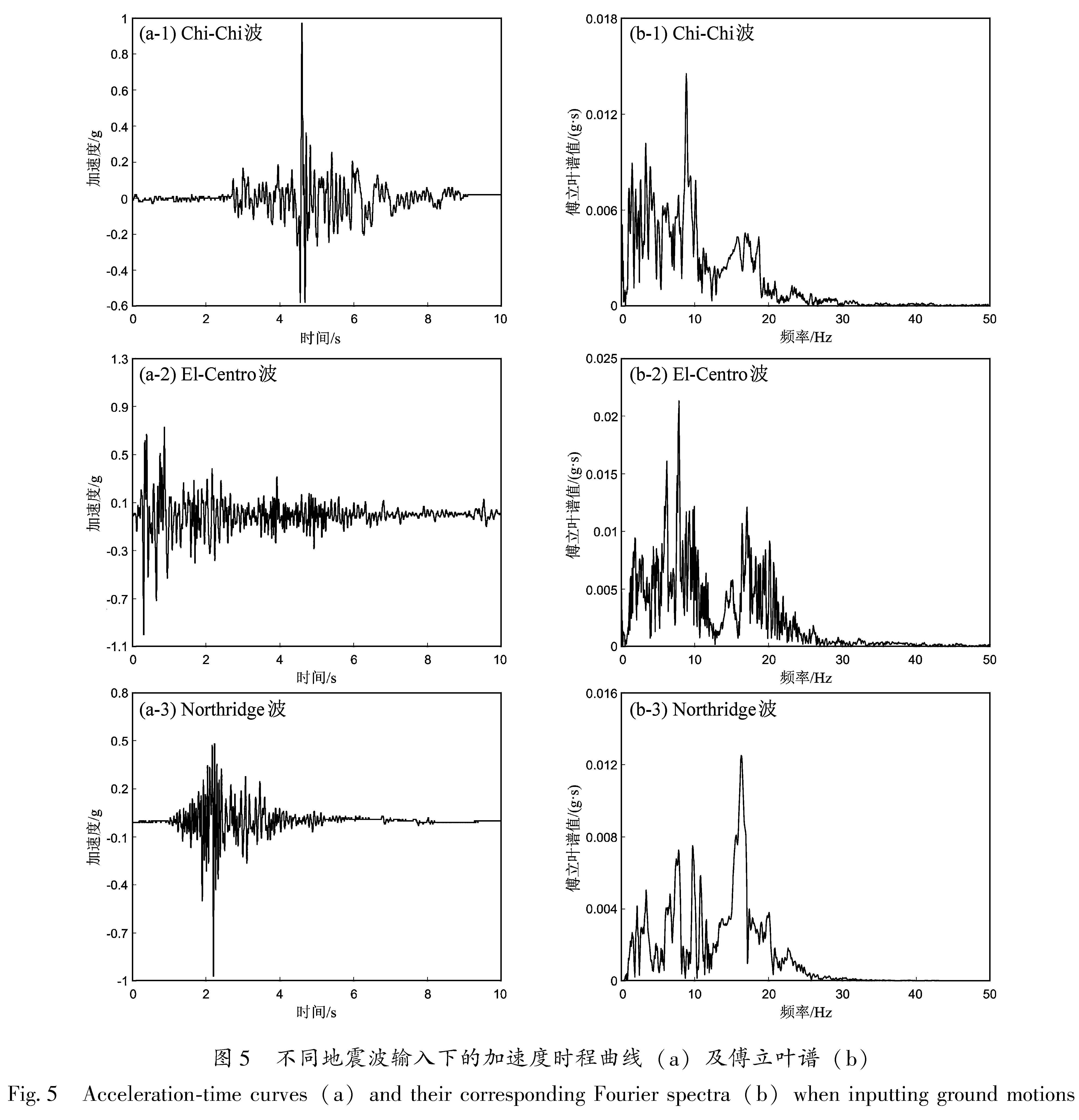
试验中选用3种不同地震波(Chi-Chi波、El-Centro波、Northridge波)作为振动台试验的输入波。根据相似比进行时间缩尺,得到振动台台面输入的地震波加速度时程曲线(PGA=0.1 g),并进行傅立叶变换得到其对应的频谱图(图5)。从图5b可以看出,Chi-Chi波、El-Centro波、Northridge波具有不同的卓越频率和能量频段,卓越频率分别为8.85、7.87和16.29 Hz,试验中将这3种地震波的加速度峰值分别调整为0.1、0.2和0.3 g,并采取阶梯式进行逐级加载。在每一级峰值加载前后均需采用0.1 g的白噪声扫频,且试验结束后需对试验结果进行滤波和基线校正(Lu et al,2022)。
图4 FF(a)与STUS(b)工况传感器测点布设
Fig.4 Layout of the sensor measuring points for FF(a)and STUS(b)conditions
图5 不同地震波输入下的加速度时程曲线(a)及傅立叶谱(b)
Fig.5 Acceleration-time curves(a)and their corresponding Fourier spectra(b)when inputting ground motions2.5 模型箱边界效应验证在试验之前,首先对刚性模型箱的边界效应进行了合理性验证。为了能够定量地研究模型场地的边界效应问题,本文利用Chen等(2010)和陈红娟等(2016)提出的2-范数偏差法对模型箱的边界效应进行评价,其公式为:
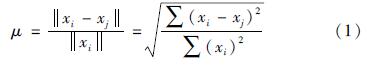
式中:xi为基准信号:xj为对比信号,xi和xj可直接取时程或频谱信号; μ为2-范数偏差,μ在统计的意义上是均方逼近的概念,反映两个信号的差异,若两个信号的μ值等于零,说明两个信号完全相同。
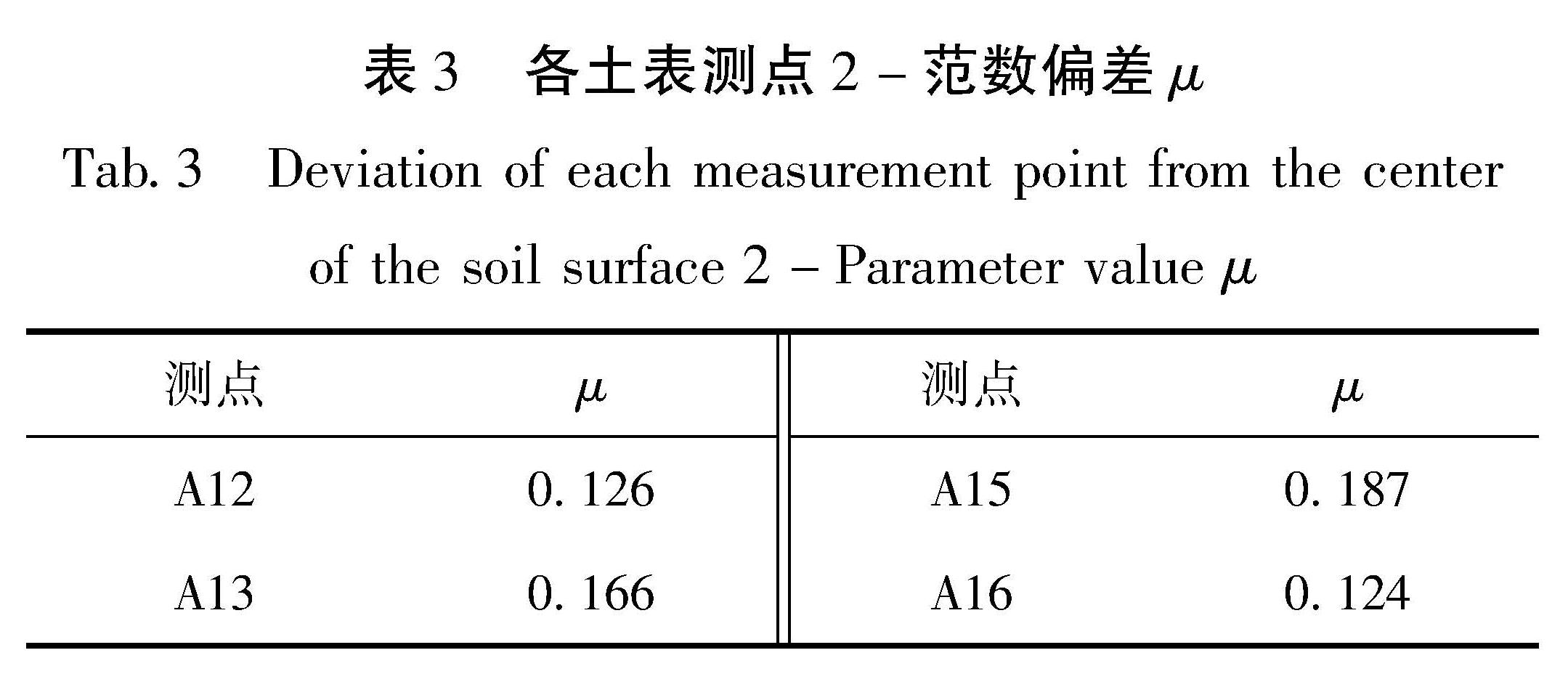
本文以自由场工况下Chi-Chi波(PGA=0.1 g)水平X向输入为例,取土表测点A12、A13、A15、A16(图4a)记录的加速度时程数据,根据式(1)求得土表各测点的加速度响应μ值,结果见表3。表中各测点的μ值均在0.1～0.2,几乎接近于零,表明本试验中模型箱边界效应处理良好(张涛等,2018)。[HJ2mm]
表3 各土表测点2-范数偏差μ
Tab.3 Deviation of each measurement point from the centerof the soil surface 2-Parameter value μ
3 数值模拟及结果验证
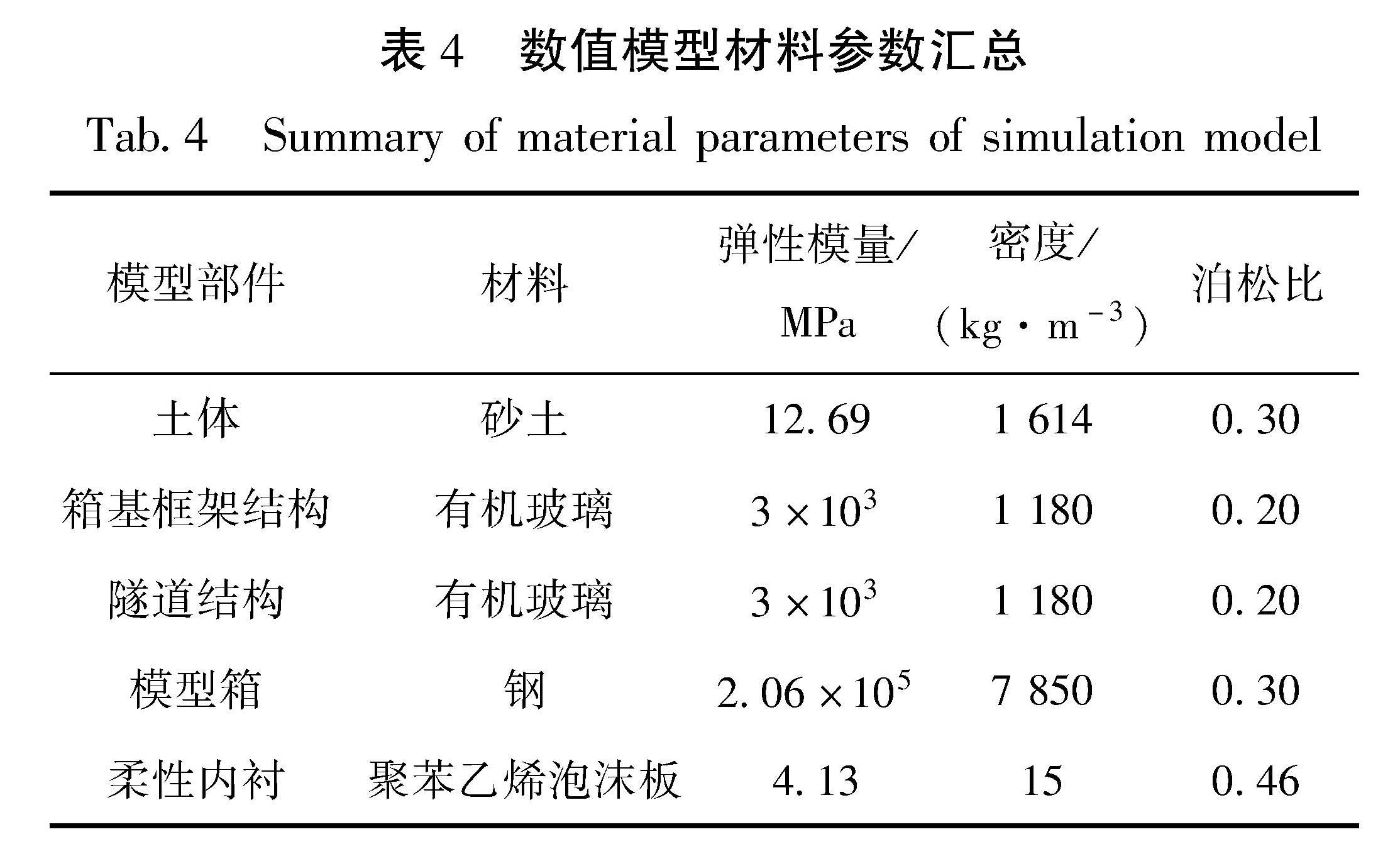
3.1 缩尺模型建立在进行数值建模的过程中,为保证模拟结果的准确性,数值模型采用的材料参数与试验一致,见表4。为提升数值模拟的运算效率,建模时仅考虑质量阻尼系数的影响(雷浩,2021),并设置阻尼比为0.05(邹德高等,2011)。
表4 数值模型材料参数汇总
Tab.4 Summary of material parameters of simulation model
由于试验中模型箱的底部视为刚性边界,且本试验仅对水平X向输入地震动进行研究,故对数值模型进行模态分析时,需同时限制模型箱X、Y、Z方向的自由度; 在进行瞬态分析时,只需解除X向约束,并将地震动从数值模型底部边界输入(赵东旭,2022)。在STUS体系模型的建立中,对箱基框架结构及隧道结构与其配重块间的接触均采用绑定约束。此外,数值模型单元网格的划分也尤为重要。根据Kuhlemeyer和Lysmer(1973)提出的要求,有限单元网格的尺寸大小Δl应满足:
式中:fmax为地震波的最大频率; 模型土剪切波速vS为56.8 m/s。
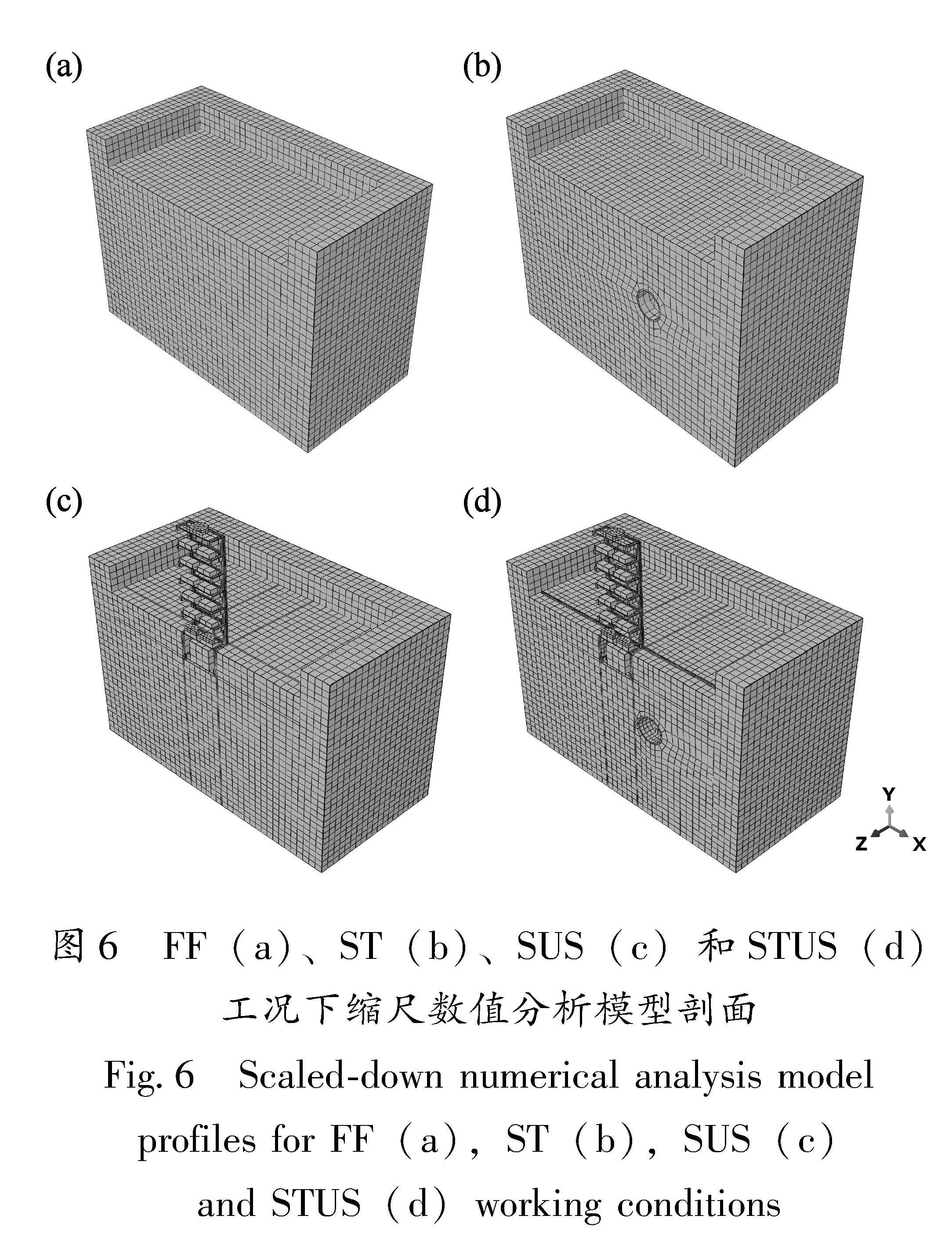
经计算,在保证模拟结果精度的前提下,选取单元尺寸为0.05 m。为尽可能地表示体系的特性、提高计算精度及效率,本文采用八节点线性六面体实体单元(C3D8)对所有部件进行模拟,4种工况下缩尺数值分析模型剖面如图6所示。
图6 FF(a)、ST(b)、SUS(c)和STUS(d)工况下缩尺数值分析模型剖面
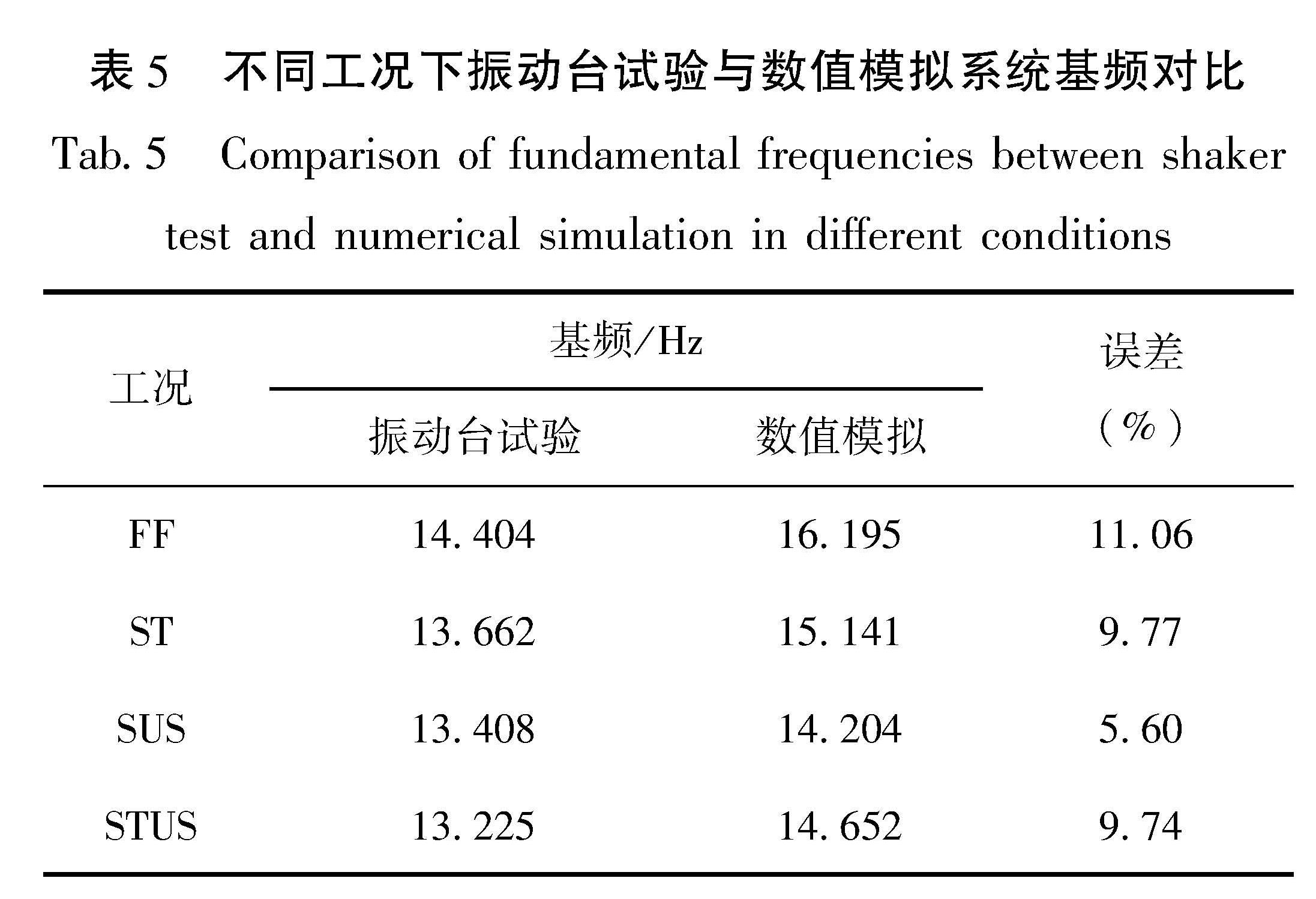
Fig.6 Scaled-down numerical analysis modelprofiles for FF(a),ST(b),SUS(c)and STUS(d)working conditions3.2 结果对比与验证模态响应是土-结构相互作用分析中的重要动力特性,表5为不同工况下振动台试验与数值模拟的基频对比情况。从表中对比发现,振动台试验与数值模拟得到的体系基频相差不大,两者误差均在10%左右。隧道结构与箱基框架结构单独存在时均会降低整个体系的自振频率,但二者同时存在时与单一结构的频率相差不大。
表5 不同工况下振动台试验与数值模拟系统基频对比
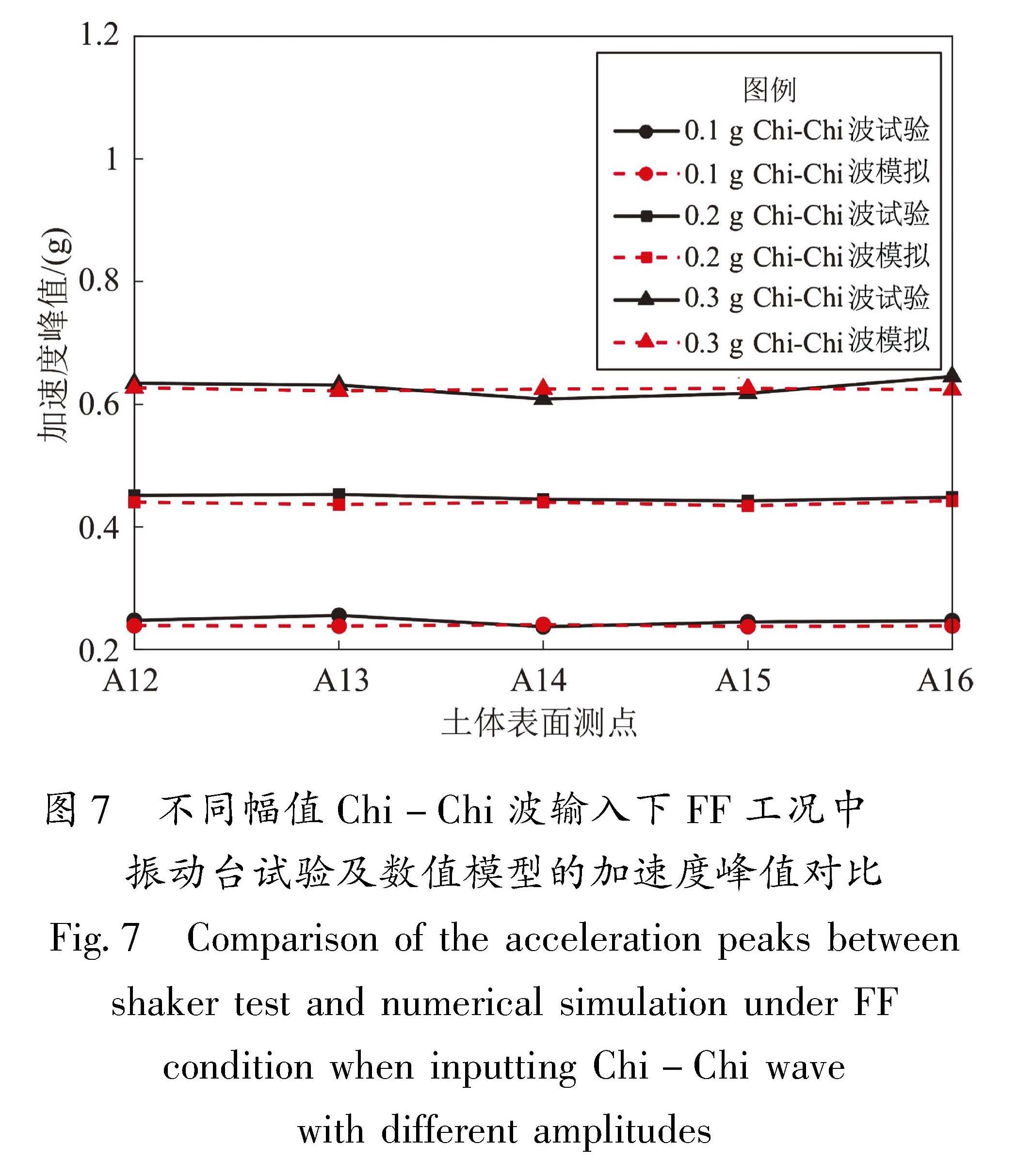
Tab.5 Comparison of fundamental frequencies between shaker test and numerical simulation in different conditions
以不同幅值Chi-Chi波输入下的FF工况为例,对土表测点的加速度峰值的振动台试验及数值模拟结果(图7)进行对比分析。由图7可以看出:①不同幅值Chi-Chi波输入下,试验与模拟结果相差不大,且随地震动幅值的增大,地表加速度响应随之增大。②在同一幅值地震动输入下,地表不同测点处的加速度峰值差异很小,地表加速度几乎一致,数值模拟结果尤为显著,这表明本文所建立的数值模型对场地边界的处理效果是可靠的。
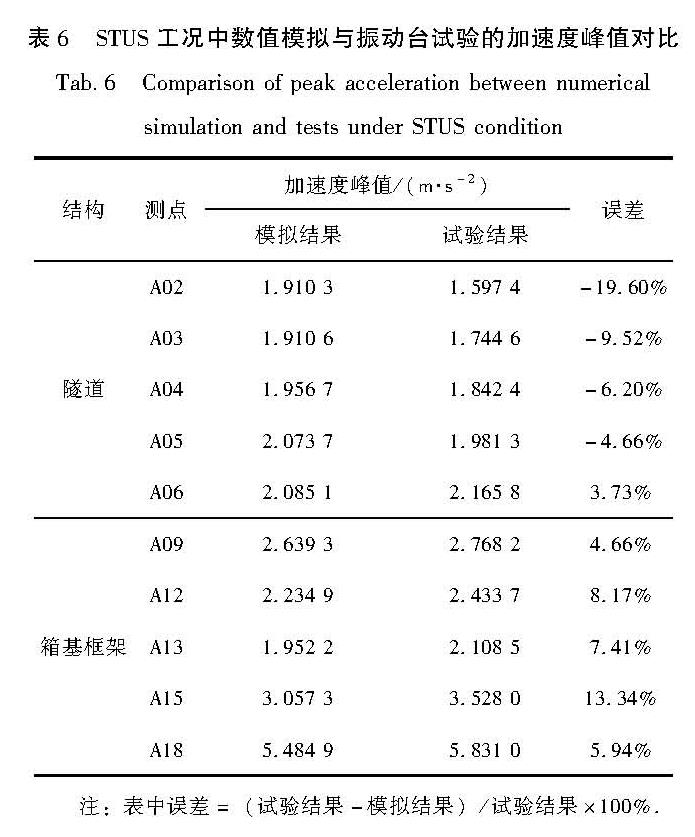
限于文章篇幅,本文选取加速度峰值为0.1 g的Chi-Chi波输入下STUS工况中隧道及箱基框架结构上的部分测点加速度峰值的数值模拟与振动台试验结果(表6)进行对比验证。由表6可知:振动台试验与数值模拟结果的误差均在20%范围内(路沙沙等,2023),这表明试验与模拟结果的吻合程度较好,数值模拟结果具有可靠性。
图7 不同幅值Chi-Chi波输入下FF工况中振动台试验及数值模型的加速度峰值对比
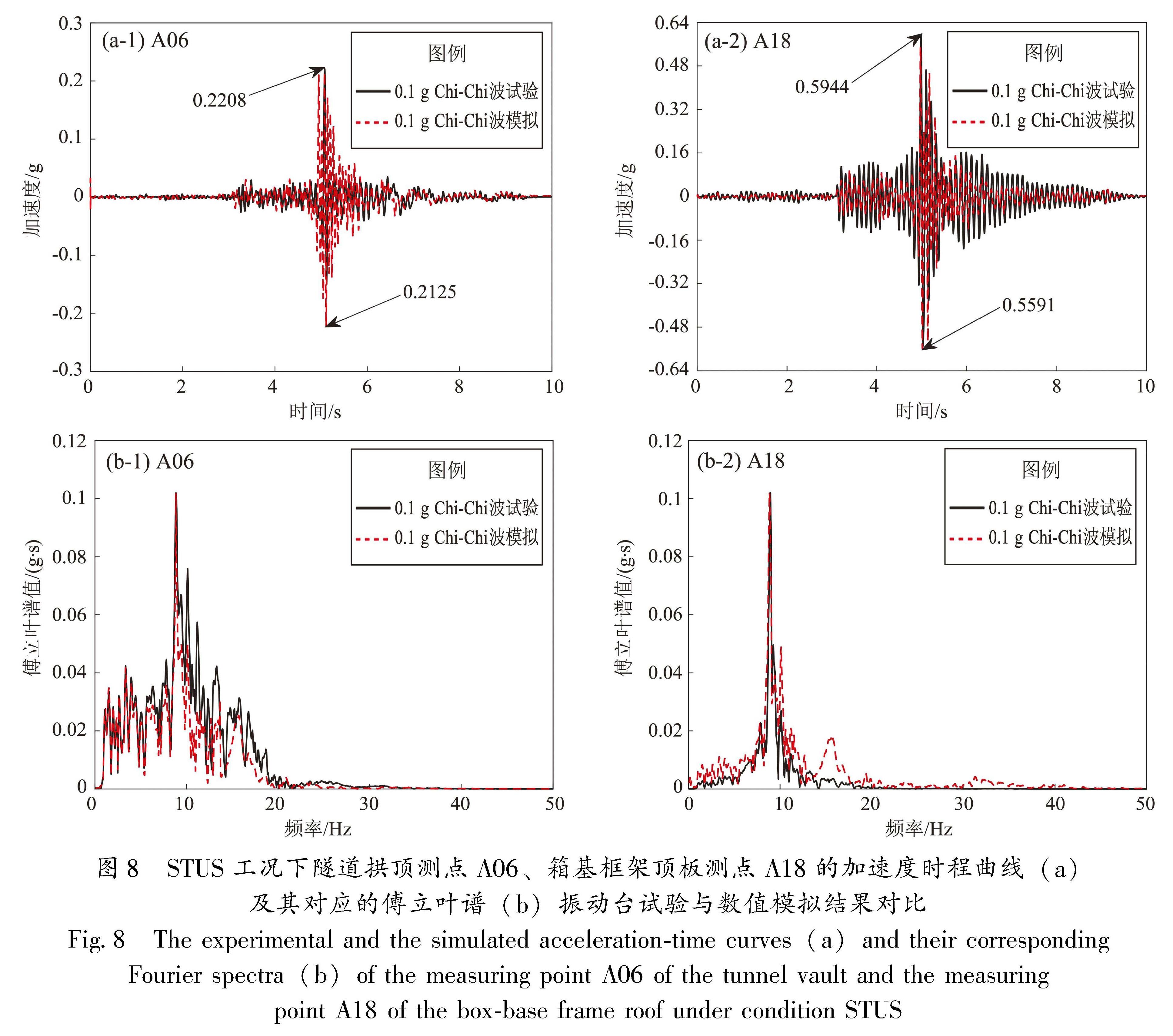
Fig.7 Comparison of the acceleration peaks between shaker test and numerical simulation under FF condition when inputting Chi-Chi wave with different amplitudes
图8 STUS工况下隧道拱顶测点A06、箱基框架顶板测点A18的加速度时程曲线(a)及其对应的傅立叶谱(b)振动台试验与数值模拟结果对比
Fig.8 The experimental and the simulated acceleration-time curves(a)and their corresponding Fourier spectra(b)of the measuring point A06 of the tunnel vault and the measuring point A18 of the box-base frame roof under condition STUS为进一步验证数值模拟结果的准确性,图8绘制了隧道结构拱顶测点A06与箱基框架顶板测点A18的加速度时程曲线及其对应的傅立叶谱。为便于对比,此处对各测点的傅立叶频谱图作归一化处理。从图8a可见,试验与数值模拟的隧道及箱基框架结构测点的加速度时程曲线拟合效果较好。从图8b可见,试验与模拟结果的频率成分存在较小的差异,其原因可能是由于对土体模型的简化与振动台老化造成的。前者可能起到滤波作用,后者可能产生一些与地震动混合的高频干扰噪声(王彤辉等,2023)。
综上可得,振动台试验与模拟结果的体系基频接近,且峰值加速度差异均在可接受误差范围内。从部分测点的加速度时程及傅立叶谱对比来看,也足以验证本文数值模拟结果的可靠性。
表6 STUS工况中数值模拟与振动台试验的加速度峰值对比
Tab.6 Comparison of peak acceleration between numericalsimulation and tests under STUS condition
4 动力响应分析
5 结论
本文通过振动台缩尺模型试验,借助有限元软件ABAQUS对不同工况进行了数值建模,并对试验与模拟结果进行了对比验证。基于验证后的模型,通过将STUS工况与其余工况的数值模拟结果进行对比,初步探讨了隧道侧穿箱基框架结构体系的动力响应规律,得到如下主要结论:
(1)隧道或箱基框架结构的存在均会降低整个体系的自振频率。
(2)隧道结构的加速度峰值随输入地震波幅值增大而增大,且在不同类型、不同幅值地震波输入下,隧道结构拱顶加速度峰值总大于拱腰,拱腰加速度峰值总大于拱底; 箱基框架结构的存在会降低隧道结构的加速度响应。
(3)隧道结构的弯矩与剪力均随输入地震波幅值增大而增大; 箱基框架结构的存在会减弱隧道结构所受到的弯矩,而对隧道结构所受剪力的影响不大。
(4)箱基的存在会改变地震波的传播路径,从而使得箱基框架一层加速度峰值减小; 当箱基框架结构高于三层时,随楼层高度的增大,楼板峰值加速度响应越显著。
(5)箱基框架结构的放大系数随地震波幅值的增大而减小; 隧道结构的存在会减弱箱基框架结构的加速度响应和位移响应。
上述结论中场地土、隧道及箱基框架结构的动力响应规律均以郑州市轨道交通7号线侧穿箱基框架结构实际工程背景为前提,研究结果可为类似建筑工程的抗震设计提供相关理论依据。根据本文研究结果,隧道、土、箱基框架结构之间存在着复杂且不可忽略的动力相互作用。因此,后续有必要通过建立三维精细化足尺模型对该体系进行原工况的深入分析和研究。
- 陈红娟,李小军,闫维明,等.2016.锯末混合土场地模型振动台试验研究[J].岩土工程学报,39(11):2068-2077.
- Chen H J,Li X J,Yan W M,et al.2016.Experimental study on model shaking table for sawdust mixed soil site[J].Journal of Geotechnical Engineering,39(11):2068-2077.(in Chinese)
- 陈跃庆,吕西林,李培振,等.2001.分层土-基础-高层框架结构相互作用体系振动台模型试验研究[J].地震工程与工程振动,21(3):104-112.
- Chen Y Q,Lyu X L,Li P Z,et al.2001.Shaking table modeling of layered soil-foundation-high-rise frame structure interaction system[J].Earthquake Engineering and Engineering Vibration,21(3):104-112.(in Chinese)
- 程业,潘旦光,陈清军,等.2022.地下空间结构对邻近地上结构地震反应影响振动台实验[J].工程力学,39(1):91-99.
- Cheng Y,Pan D G,Chen Q J,et al.2022.Shaking table experiments on the effect of underground space structures on the seismic response of neighboring above-ground structures[J].Engineering Mechanics,39(1):91-99.(in Chinese)
- 程业.2022.地下结构-土-地上结构振动台试验及理论分析[D].北京:北京科技大学.
- Cheng Y.2022.Underground structure-soil-above-ground structure shaking table test and theoretical analysis[D].Beijing:University of Science and Technology Beijing.(in Chinese)
- 何如.2019.下穿隧道爆破作用下建筑结构的动力响应特征研究[D].北京:中国地质大学.
- He R.2019.Characterization of dynamic response of building structures under blasting action in underpass tunnels[D].Beijing:China University of Geosciences.(in Chinese)
- 雷浩.2021.小净距立体交叉隧道动力响应特征及变形破坏模式研究[D].兰州:兰州交通大学.
- Lei H.2021.Research on the dynamic response characteristics and deformation damage mode of small-clearance three-dimensional intersection tunnel[D].Lanzhou:Lanzhou Jiaotong University.(in Chinese)
- [HJ2mm]李培振,吕西林,陈波,等.2002.均匀土-箱基-结构相互作用体系的计算分析[J].地震工程与工程振动,22(5):115-121.
- Li P Z,Lyu X L,Chen B,et al.2002.Computational analysis of homogeneous soil-box foundation-structure interaction system[J].Earthquake Engineering and Engineering Vibration,22(5):115-121.(in Chinese)
- 李铮,汪波,骆耀文,等.2015.城市隧道下穿密集建筑区静、动力响应特征分析[J].铁道科学与工程学报,12(2):384-392.
- Li Z,Wang B,Luo Y W,et al.2015.Analysis of static and dynamic response characteristics of urban tunnels passing through dense building areas[J].Journal of Railway Scienence and Engineering,12(2):384-392.(in Chinese)
- 路沙沙,赵东旭,白举科,等.2023.隧道-土-桥桩相互作用体系振动台试验与数值模拟研究[J/OL].(2022-08-26)[2023-07-01].振动工程学报,1-15.https://kns.cnki.net/kcms2/article/abstract?v=3uoqIhG8 C45S0n9fL2suRadTyEVl2pW9UrhTDCdPD 65g9wpxZRZJbNaOC2NxwcizgjBVuW2iE1yUzTlVzJlaMCgkg2n1DED 1&uniplatform=NZKPT.
- Lu S S,Zhao D X,Bai J K,et al.2023.Study on shaking table test and numerical simulation of tunnel-soil-bridge pile interaction system[J/OL].(2022-08-26)[2023-07-01].Journal of Vibration Engineering,1-15.https://kns.cnki.net/kcms2/article/abstract?v=3uoqIhG8C45S0n9fL2suRadTyEVl2pW9UrhTDCdPD65g9wpxZR ZJbNaOC2NxwcizgjBVuW2iE1yUzTlVzJlaMCgkg2n1DED1&uniplatf orm=NZKPT.(in Chinese)
- 尚守平,朱志辉,吴方伯.2006.土-箱基-框架结构动力相互作用大比例模型野外试验研究[J].工程力学,23(10):118-124.
- Shang S P,Zhu Z H,Wu F B.2006.Field experimental study on large scale modeling of dynamic interaction of soil-box foundation-frame structure[J].Engineering Mechanics,23(10):118-124.(in Chinese)
- 王国波,王垚,孙富学,等.2022.基础类型对框架结构及场地土地震响应影响试验研究[J].世界地震工程,38(2):96-109.
- Wang G B,Wang Y,Sun F X,et al.2022.Experimental study on the effect of foundation type on the seismic response of framed structures and site land[J].World Earthquake Engineering,38(2):96-109.(in Chinese)
- 王国波,于艳丽,何卫.2014.下穿隧道-土-地表邻近框架结构相互作用体系地震响应初步分析[J].岩土工程学报,36(2):334-338.
- Wang G B,Yu Y L,He W.2014.Preliminary analysis of seismic response of underpass tunnel-soil-surface neighboring frame structure interaction system[J].Journal of Geotechnical Engineering,36(2):334-338.(in Chinese)
- 王彤辉,李小军,陈红娟,等.2023.场地-隧道-地上建筑结构体系地震响应的振动台试验[J].防灾减灾工程学报,43(4):742-751.
- Wang T H,Li X J,Chen H J,et al.2023.Shaking table tests on the seismic response of site-tunnel-above-ground building structural systems[J].Journal of Pisaster Prevention and Mitigation Engineering,43(4):742-751.(in Chinese)
- 于翔.2002.地下建筑结构应充分考虑抗震问题——1995年阪神地震破坏的启示[J].工程抗震,4(4):17-20.
- Yu X.2002.Seismic Resistance of underground building structures should be fully considered:Revelation of the damage caused by the 1995 Hanshin Earthquake[J].Engineering Seismic Resistance,4(4):17-20.(in Chinese)
- 赵东旭.2022.桥桩-土体-隧道相互作用体系地震响应研究[D].阜新:辽宁工程技术大学.
- Zhao D X.2022.Research on seismic response of bridge pile-soil-tunnel interaction system[D].Fuxin:Liaoning University of Engineering and Technology.(in Chinese)
- 邹德高,徐斌,孔宪京.2011.瑞利阻尼系数确定方法对高土石坝地震反应的影响研究[J].岩土力学,32(3):797-803.
- Zou D G,Xu B,Kong X J.2011.Study on the effect of Rayleigh damping coefficient determination method on seismic response of high earth-rock dams[J].Geotechnics,32(3):797-803.(in Chinese)
- 张涛,高波,范凯祥,等.2018.地震作用下振动台试验刚性模型箱侧壁柔性材料研究[J].岩石力学与工程学报,37(10):2415-2424.
- Zhang T,Gao B,Fan K X,et al.2018.Research on flexible materials for the sidewall of rigid model box of shaking table test under seismic action[J].Journal of Rock Mechanics and Engineering,37(10):2415-2424.(in Chinese)
- Chen G,Chen S,Qi C,et al.2015.Shaking table tests on a three-arch type subway station structure in a liquefiable soil[J].Bulletin of Earthquake Engineering,13(6):1675-1701.
- Chen J,Shi X,Li J.2010.Shaking table test of utility tunnel under non-uniform earthquake wave excitation[J].Soil Dynamics and Earthquake Engineering,30(11):1400-1416.
- Ghergu M,Ionescu I R.2009.Structure-soil-structure coupling in seismic excitation and “city effect”[J].International Journal of Engineering Science,47(3):342-354.
- Guo J,Chen J,Bobet A.2013.Influence of a subway station on the inter-story drift ratio of adjacent surface structures[J].Tunnelling and Underground Space Technology,35:8-19.
- Krawinkler H,Moncarz P D.1981.Theory and application of experimental model analysis in earthquake engineering[J].NASA STI/Recon Technical Report N,82:18430.
- Kuhlemeyer R L,Lysmer J.1973.Finite element method accuracy for wave propagation problems[J].Journal of the Soil Mechanics and Foundations Division,99(5):421-427.
- Lu S S,Xu H,Wang L G,et al.2022.Effect of flexibility ratio on seismic response of rectangular tunnels in sand:Experimental and numerical investigation[J].Soil Dynamics and Earthquake Engineering,157:107256.
- Miao Y,Zhong Y,Ruan B,et al.2020.Seismic response of a subway station in soft soil considering the structure-soil-structure interaction[J].Tunnelling and Underground Space Technology,106:103629.
- Moncarz P D.1981.Theory and application of experimental model analysis in earthquake engineering[M].Stanford:Stanford University.
- Semblat J F,Kham M,Bard P Y.2008.Seismic-wave propagation in alluvial basins and influence of site-city interaction[J].Bulletin of the Seismological Society of America,98(6):2665-2678.
基于验证后的数值模型,以不同幅值Chi-Chi波、El-Centro波输入为例,将STUS工况与其余工况的数值模拟结果进行对比,分析探讨隧道侧穿箱基框架结构体系的动力响应规律。
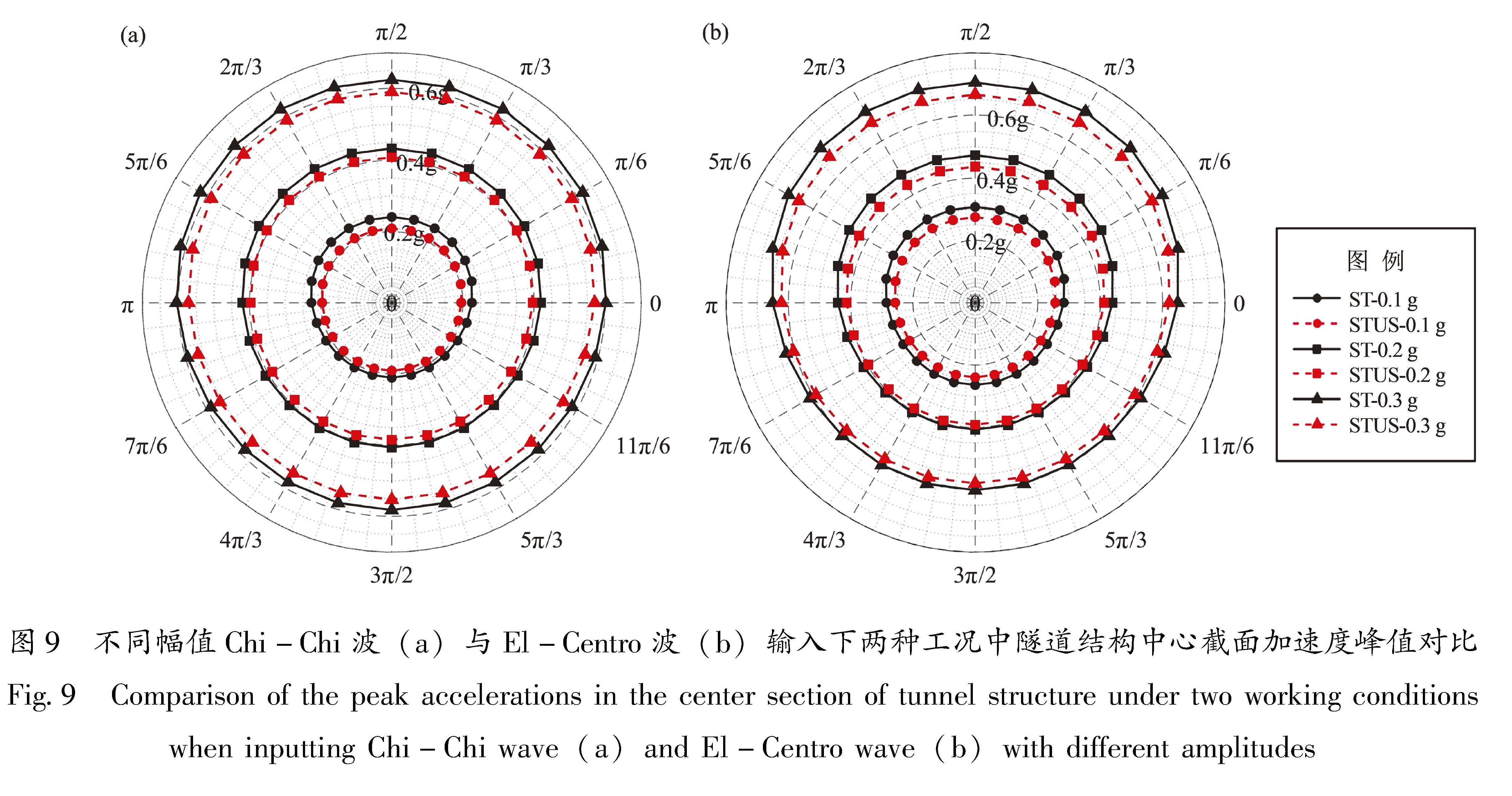
4.1 隧道结构动力响应分析4.1.1 加速度响应通过对比ST与STUS工况中隧道结构的加速度响应结果,分析隧道侧穿箱基框架结构体系中隧道结构的加速度响应规律。为了能够直观展示隧道衬砌表面测点加速度峰值的变化,采用极坐标法来描述隧道不同部位的加速度峰值变化。图9为不同幅值Chi-Chi波与El-Centro波输入下ST和STUS工况中隧道结构中心截面处的加速度峰值,图中π为接近箱基框架结构一侧的隧道拱腰位置。由图可以看出,输入Chi-Chi波与El-Centro波时,ST和STUS工况中的隧道结构由拱底到拱顶均表现出基本相同的规律,即隧道拱顶加速度峰值大于拱腰,隧道拱腰加速度峰值大于拱底,且输入El-Centro波时隧道加速度峰值略大于输入Chi-Chi波时的隧道加速度峰值。对比两种工况可知,ST工况的隧道加速度响应大于STUS工况,这说明箱基框架结构的存在会降低隧道结构的加速度响应。
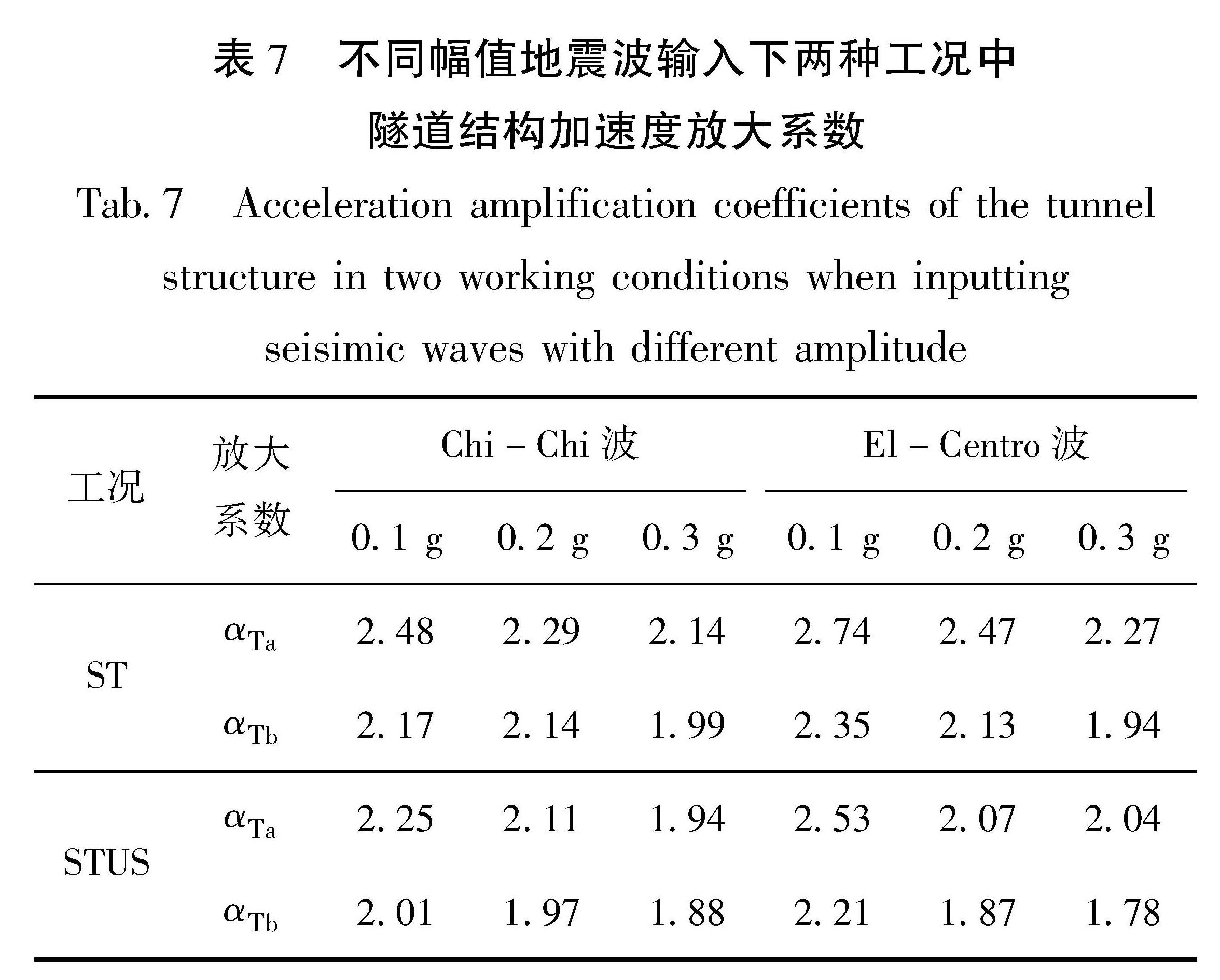
为进一步分析ST和STUS工况中隧道结构的地震响应规律,定义隧道加速度放大系数αΤa为隧道拱顶加速度峰值与输入波的加速度峰值之比,αΤb为隧道拱底加速度峰值与输入波的加速度峰值之比。
表7给出了在不同幅值Chi-Chi波与El-Centro波输入下ST和STVS工况中隧道拱顶、拱底的加速度放大系数变化。从表7可以发现,在ST和STUS工况中αΤa始终大于αΤb,且αΤa/αΤb的比值均在1.0～2.0,这表明从基底输入地震波时,隧道拱顶的加速度峰值大于隧道拱底。比较两种工况不难发现,在不同幅值地震波输入下,两种工况隧道结构加速度放大系数均随输入地震波幅值的增大而减小,这是因为当输入地震波幅值较小时,土体基本上处于弹性状态,而随着输入地震波幅值的增大,土体进入塑性表现出一定的非线性,耗散了部分地震动能量(Miao et al,2020); 在同一幅值同种地震波输入下,ST工况的加速度放大系数均大于STUS工况,这也进一步验证了箱基框架结构的存在降低了隧道的加速度响应的结论,故其放大系数小于单一隧道的放大系数。
图9 不同幅值Chi-Chi波(a)与El-Centro波(b)输入下两种工况中隧道结构中心截面加速度峰值对比
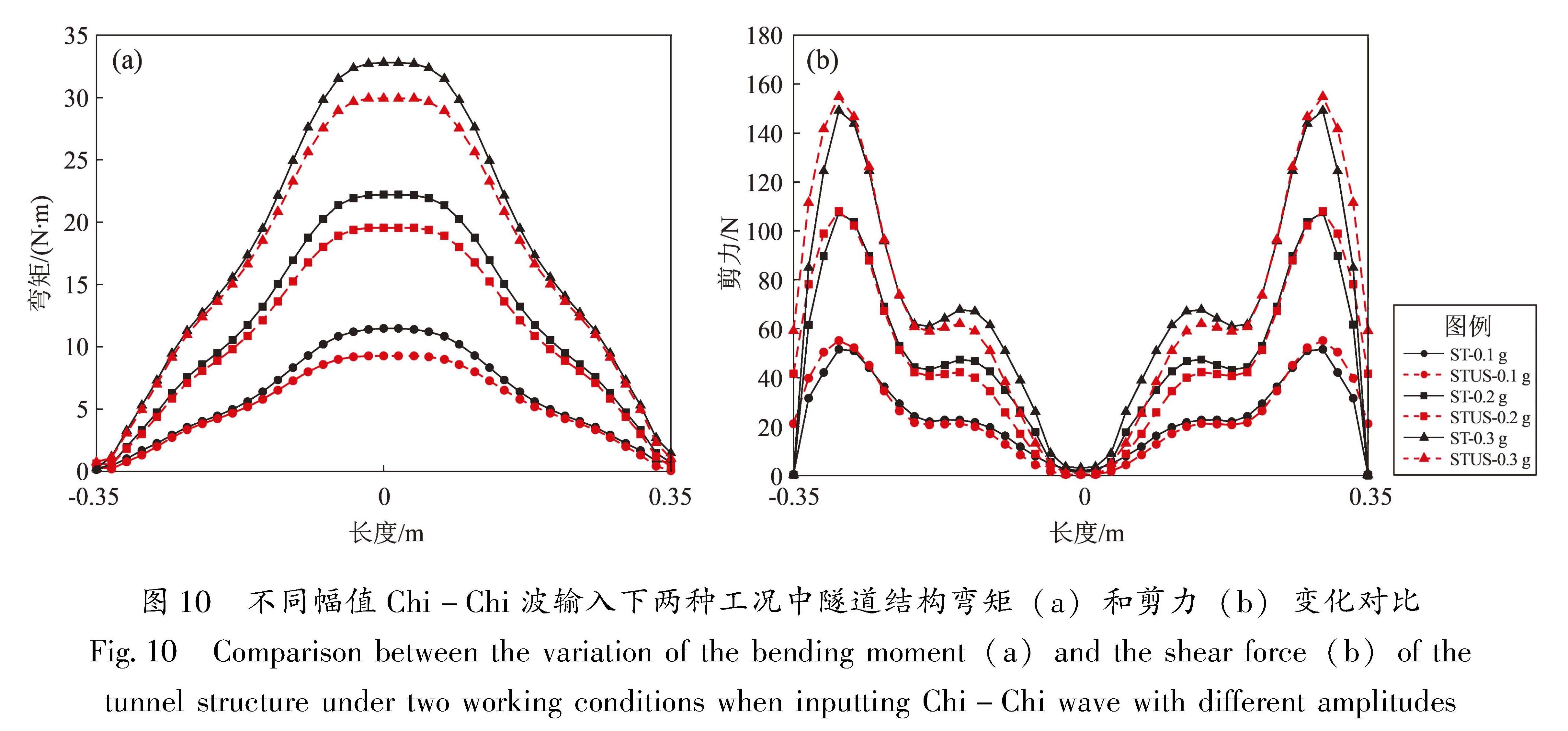
Fig.9 Comparison of the peak accelerations in the center section of tunnel structure under two working conditions when inputting Chi-Chi wave(a)and El-Centro wave(b)with different amplitudes表7 不同幅值地震波输入下两种工况中隧道结构加速度放大系数
Tab.7 Acceleration amplification coefficients of the tunnel structure in two working conditions when inputting seisimic waves with different amplitude
4.1.2 内力响应本节主要对ST与STUS工况中隧道的内力响应结果进行对比分析。图 10为不同幅值Chi-Chi波输入下ST和STUS工况中隧道结构弯矩、剪力变化对比。由图可以发现,在ST与STUS工况中隧道结构的弯矩与剪力曲线变化趋势基本一致,且均随着输入地震动幅值的增大而增大。ST工况中隧道结构的弯矩在不同幅值地震动输入下均大于STUS工况,这表明箱基框架结构的存在会减弱隧道结构所受到的弯矩,而两种工况的剪力相差并不大,这表明箱基框架结构的存在对隧道结构所受剪力的影响不大。
图 10 不同幅值Chi-Chi波输入下两种工况中隧道结构弯矩(a)和剪力(b)变化对比
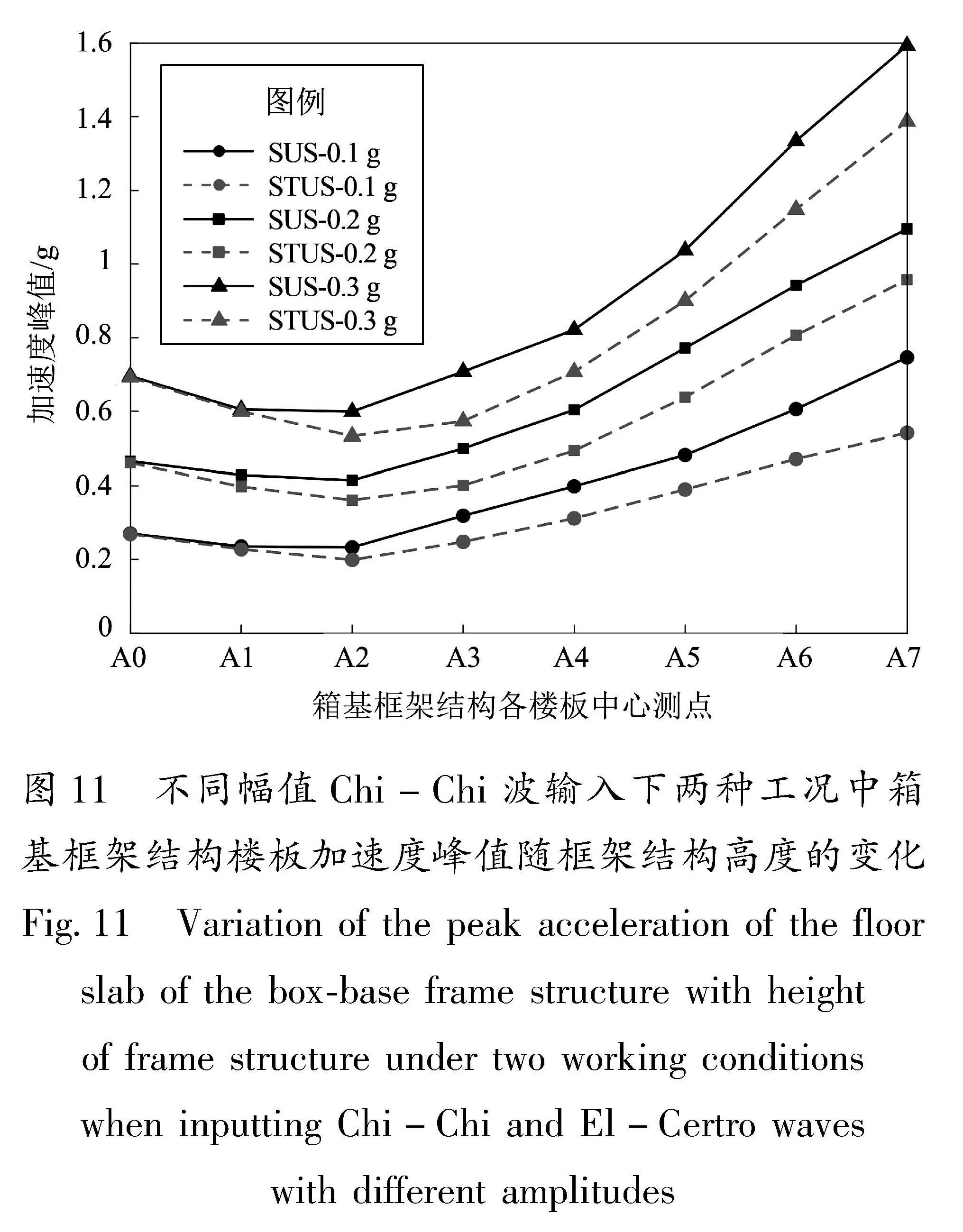
Fig.10 Comparison between the variation of the bending moment(a)and the shear force(b)of thetunnel structure under two working conditions when inputting Chi-Chi wave with different amplitudes4.2 箱基框架结构动力响应分析4.2.1 加速度响应为便于表达箱基框架结构各层楼板的加速度响应结果,记A0为箱基基础底板中心测点,A1～A6依次为箱基框架地上1～6层楼底板中心测点,A7为框架顶板中心测点。图 11为不同幅值Chi-Chi波输入下SUS和STUS工况中箱基框架结构楼板加速度峰值随框架结构高度的变化。由图可以发现:①在不同幅值Chi-Chi波输入下,SUS与STUS工况均出现箱基框架结构楼板加速度峰值随框架结构高度的增加呈现先减小后增大的趋势,其中在A2处的楼板加速度峰值最小,当楼层高于3层时,箱基框架结构的加速度响应更明显。一楼底板(A1)的加速度峰值均小于箱基基础底板(A0),造成这一现象的原因是箱基的存在会改变地震波的传播路径,地震波在箱室内多次折射,耗散了部分能量,从而降低了A1处的加速度峰值。②随着输入地震波幅值的增大,两种工况中箱基框架结构楼板的加速度峰值均增大,且在同一幅值下,SUS工况中箱基框架结构的加速度响应较STUS工况更显著。这表明隧道结构的存在会降低箱基框架结构的加速度响应。
图 11 不同幅值Chi-Chi波输入下两种工况中箱基框架结构楼板加速度峰值随框架结构高度的变化
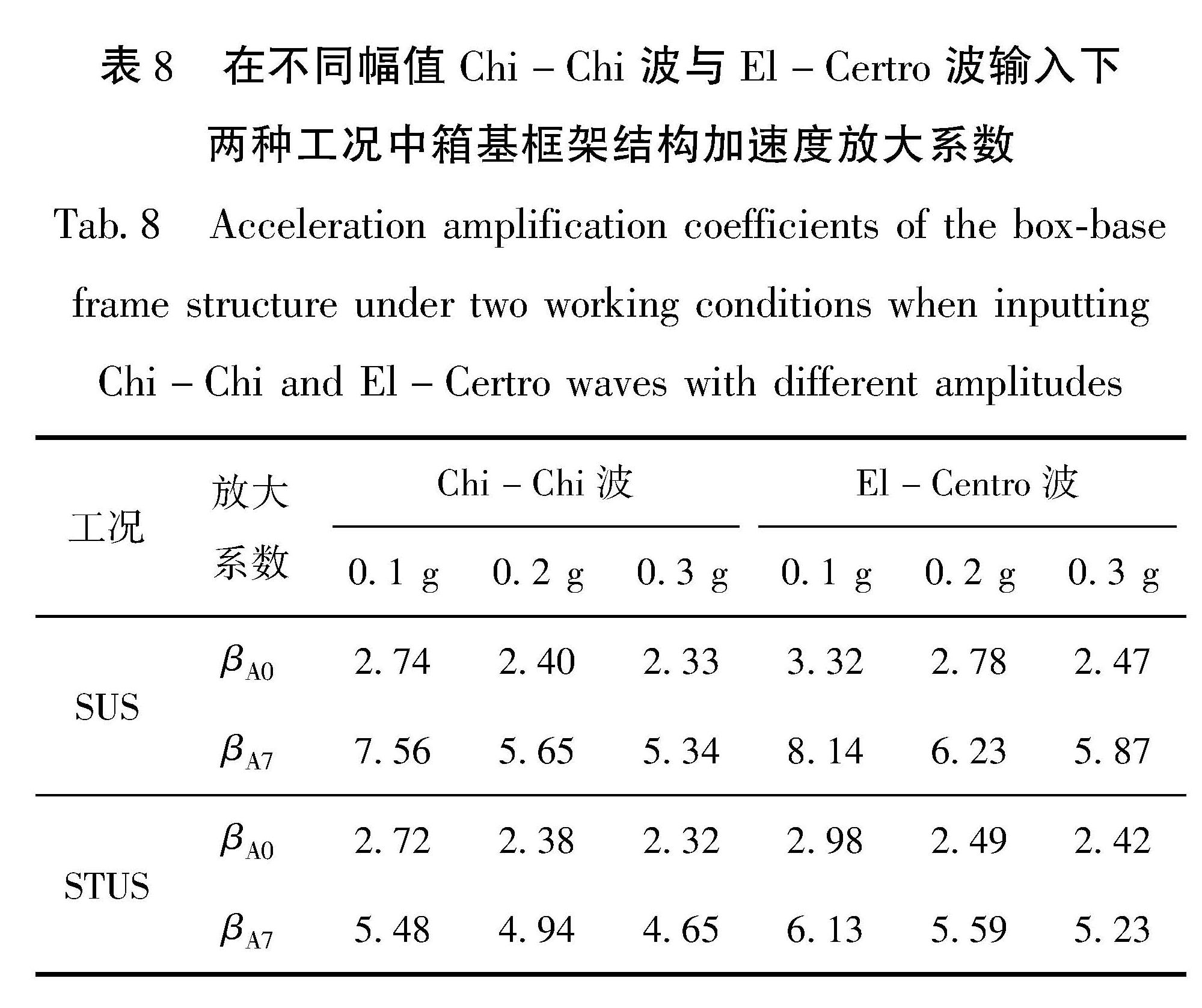
Fig.11 Variation of the peak acceleration of the floor slab of the box-base frame structure with height of frame structure under two working conditionswhen inputting Chi-Chi and El-Certro waveswith different amplitudes为进一步分析SUS和STUS工况中箱基框架结构的加速度响应规律,定义箱基框架结构的加速度放大系数βA7为框架顶板中心加速度峰值与输入波的加速度峰值之比,βA0为箱基基础底板中心加速度峰值与输入波的加速度峰值之比。在不同幅值Chi-Chi波与El-Centro波输入下两种工况中箱基框架结构加速度放大系数变化,见表8。从表中可以发现,在不同幅值地震波输入下,两种工况箱基框架结构加速度放大系数均随输入地震波幅值的增大而减小; 在同一幅值同种地震波输入下,SUS工况中箱基框架结构放大系数βA7、βA0均大于STUS工况。El-Centro波作用下两种工况箱基框架结构的加速度响应比Chi-Chi波作用下更激烈。造成这种现象的原因是SUS和STUS工况的体系基频位于El-Centro波傅立叶谱的主要成分区间内,体系容易产生共振,使得地震响应更为激烈。
表8 在不同幅值Chi-Chi波与El-Certro波输入下两种工况中箱基框架结构加速度放大系数
Tab.8 Acceleration amplification coefficients of the box-baseframe structure under two working conditions when inputtingChi-Chi and El-Certro waves with different amplitudes
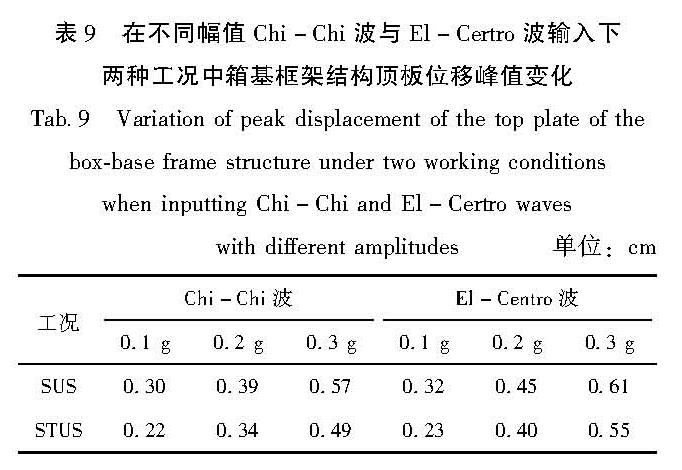
4.2.2 位移响应表9为在不同幅值Chi-Chi波与El-Centro波输入下SUS与STUS工况中箱基框架结构顶板位移峰值的变化。从表中可以发现,在不同幅值地震波输入下,两种工况箱基框架结构顶板位移峰值均随输入地震波幅值增大而增大; 在同一幅值同种地震波输入下,SUS工况中箱基框架结构顶板位移峰值均大于STUS工况,且El-Centro波作用下的位移响应比Chi-Chi波作用下更显著。这表明隧道结构的存在会降低箱基框架结构的位移响应。
表9 在不同幅值Chi-Chi波与El-Certro波输入下两种工况中箱基框架结构顶板位移峰值变化
Tab.9 Variation of peak displacement of the top plate of thebox-base frame structure under two working conditionswhen inputting Chi-Chi and El-Certro waves with different amplitudes
