基金项目:山东省自然科学基金项目(ZR2020ME246; ZR2022ME029).
(1.青岛理工大学 土木工程学院,山东 青岛 266520; 2.山东建筑大学 土木工程学院,山东 济南 250101; 3.青岛中建联合集团有限公司,山东 青岛 266100; 4.青岛市博物馆,山东 青岛 266061)
(1.College of Civil Engineering,Qingdao University of Technology,Qingdao 266520,Shandong,China)(2.College of Civil Engineering,Shandong Jianzhu University,Jinan 250101,Shandong,China)(3.Qingdao Zhongjian Combination Group Co.,Ltd.,Qingdao 266100,Shandong,China)(4.Qingdao Museum,Qingdao 266061,Shandong,China)
RC frame structure; the artificial neural network; seismic response; analysis of the parameter sensitivity
DOI: 10.20015/j.cnki.ISSN1000-0666.2024.0004
备注
基金项目:山东省自然科学基金项目(ZR2020ME246; ZR2022ME029).
引言
地震灾害引起的建筑结构破坏可能导致严重的经济损失和大量的人员伤亡。现代概率地震风险评估旨在估计用于灾害风险管理和风险意识的风险量化指标(Yoshikaw,Goda,2014),这些风险指标包括经济损失程度和人员伤亡人数等(Dolce et al,2021)。在这个背景下,研究人员通常采用基于性能的地震工程评估方法(Cornell,Krawinkler,2000)计算超过给定损失水平的年平均频率,其中包含了结构损伤、结构响应和地震动强度等变量,变量之间的关系通常通过脆弱性和易损性研究确定(Yepes et al,2016)。
近年来,科研人员对地震动强度与结构响应之间的关系进行了大量的调查研究,增量动力分析法(Incremental Dynamic Analysis,IDA)、云图法以及多条带分析法等相继被提出(Vamvatsikos,Cornell,2002; Jalayer,Cornell,2009; Jalayer et al,2015)。研究表明,以峰值地面加速度(Peak Ground Acceleration,PGA)为代表的常用地震动强度指标有诸多局限性和不足(Baker,Cornell,2005)。为解决这些问题,已有学者提出了更高阶的地震动强度指标,如地震动整体持时强度(Arias Iintensity,Ia)(Arias,1970)以及平均谱加速度(Average Spectral Acceleration,AvgSa)(Kohrangi et al,2016a)等。然而,地震动强度和结构响应之间具有很强的非线性关系(Kohrangi et al,2016b),通常需要进行大量的弹塑性时程分析进行确定,评估效率低下。因此,如何通过其它途经避开时程分析中耗时耗力的过程,使结构响应的预测更为快速有效,一直是地震工程领域亟待解决的问题。
近年来,机器学习得到了土木工程研究人员的重视,在现代地震工程中引入机器学习算法可以改进传统的分析方法,能够快速准确地解决复杂的工程问题(Lu et al,2012)。通常情况下,机器学习算法的优点是能够基于经验或模拟的数据对研究对象之间的潜在和非线性关系进行检测(Bishop,2006)。目前机器学习算法中的人工神经网络模型在多个学科研究领域中应用广泛,具有优秀的数据学习能力,用于检测特征参数与目标参数之间的非线性关系,建立较为准确的数学关系模型。在人工神经网络的结构响应预测应用方面,Morfidis和Kostinakis(2018)使用弹塑性时程分析方法,构建了RC框架结构样本数据库并训练人工神经网络,测试表明模型对结构最大层间位移角的预测结果具有较好的精确度。Kim等(2020)开发了一种概率深度学习神经网络,使用多种输入变量预测单自由度系统的最大水平位移; Oh等(2020)开发了基于人工地震动记录训练的人工神经网络钢筋混凝土结构的地震响应预测模型,同时考虑频域的影响,使模型的预测性能得到了提升。
尽管上述研究在结构响应预测方面取得了重要进展,但多数研究在选择地震动记录时未考虑结构所在场地的地震危险性,导致地震动的不确定性影响较大。本文在考虑场址地震危险性的前提下,研究实现人工神经网络模型对不同楼层数RC框架结构地震响应的合理预测; 以四川雅安地区为目标场地,设计低层、多层和小高层共3个典型RC框架结构作为研究对象,基于条件均值谱选取地震动记录作为输入,通过弹塑性时程分析搭建结构响应的样本数据库; 将地震动强度信息和结构信息作为特征参数,使用训练人工神经网络模型以预测3个RC框架结构的地震响应,并采用平均影响值(Mean Impact Value,MIV)算法对各个特征参数进行敏感性分析。
1 RC框架结构模型设计
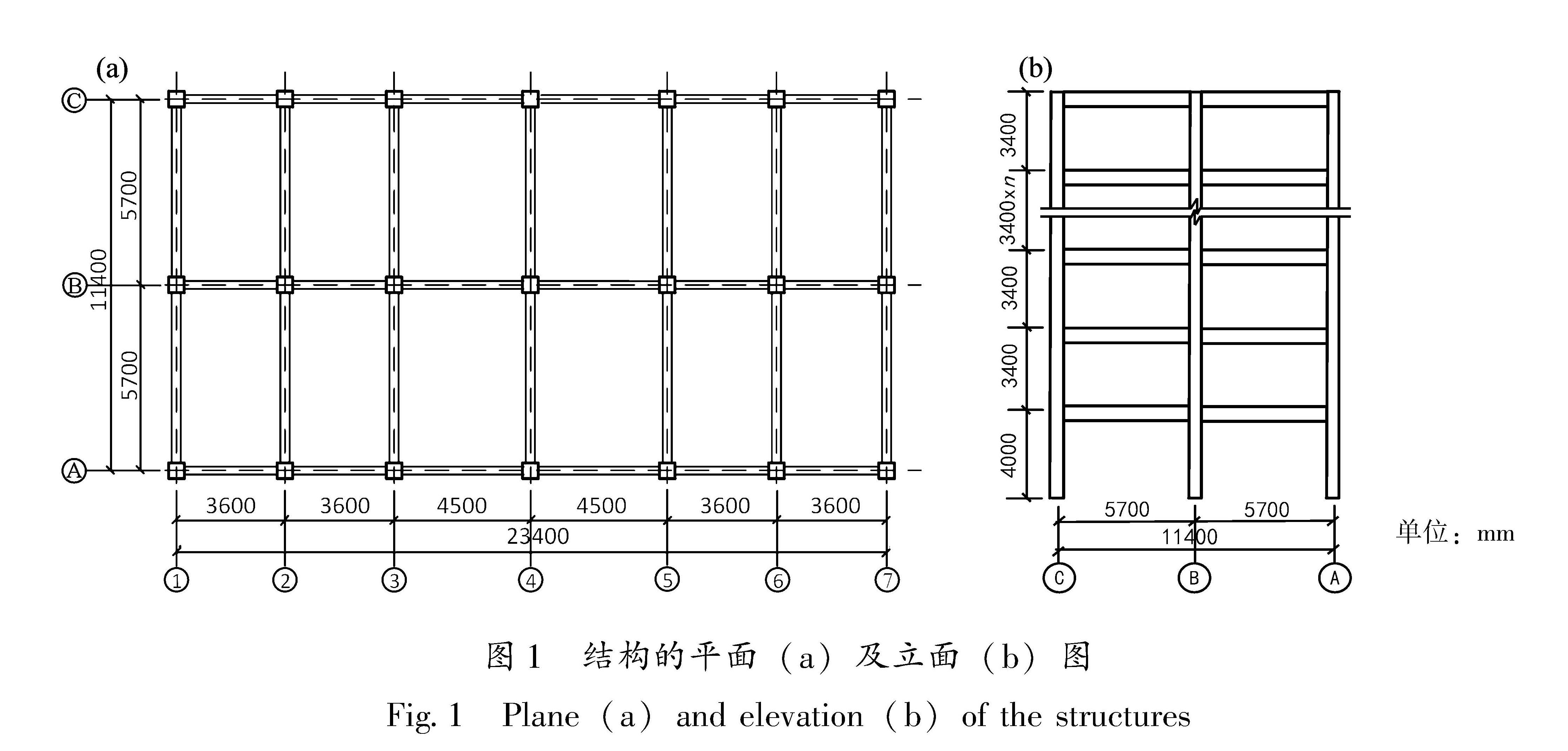
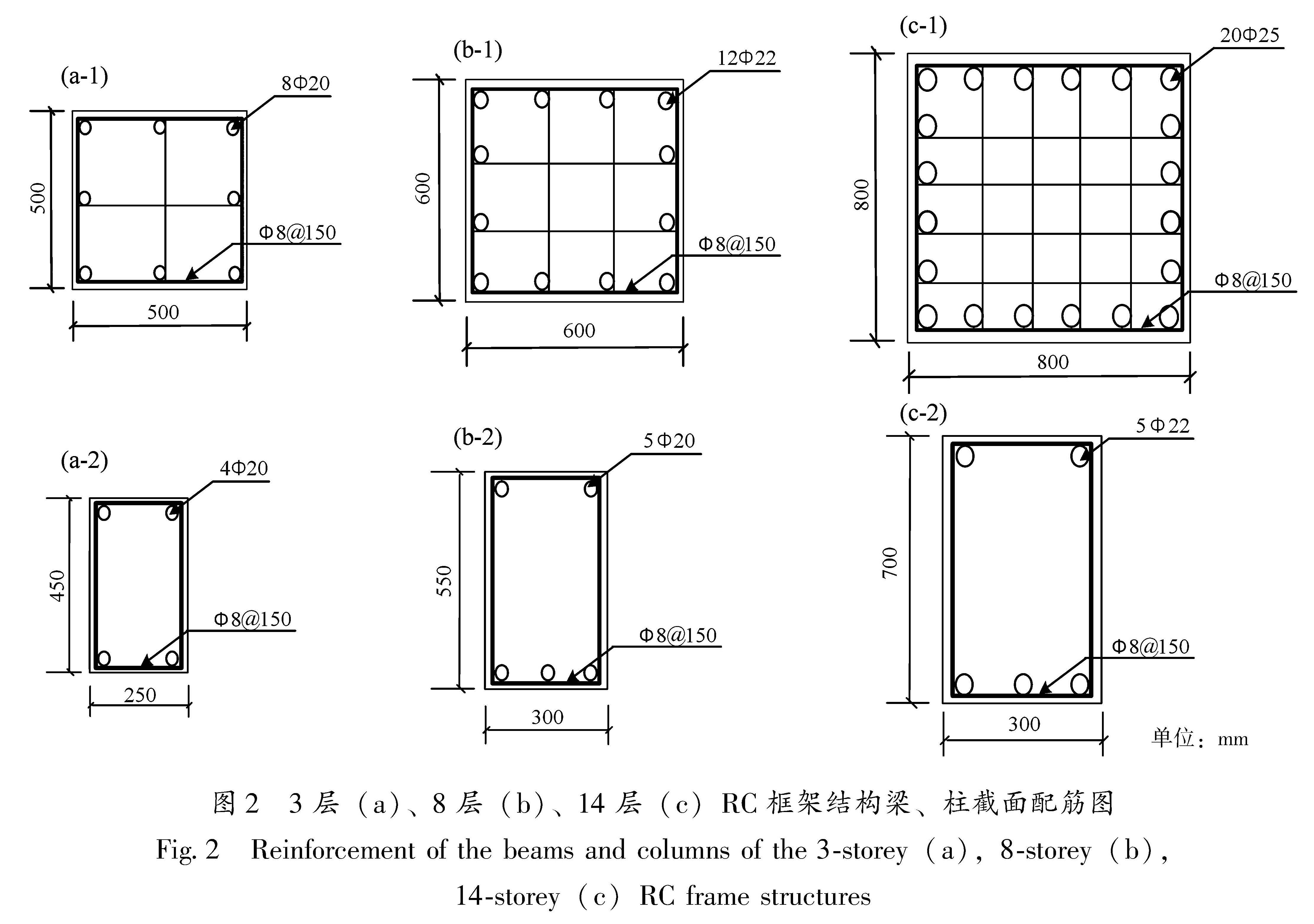
1.1 参数设计及建模方法本文按照《建筑抗震设计规范》(GB 50011—2010)、《混凝土结构设计规范》(GB 50010—2010)和《高层建筑混凝土结构技术规程》(JGJ 3—2010)设计了3层、8层和14层共3个RC框架结构作为算例结构。3层结构采用C30混凝土,8层结构采用C35混凝土,14层结构采用C40混凝土。3个框架结构中的梁、柱纵筋采用HRB400,箍筋采用HPB235。结构底层层高为4 000 mm,其余层层高均为3 400 mm。设计基本风压为0.3 kN/m2,楼板厚120 mm,标准层活载为2.0 kN/m2,恒载为4.0 kN/m2; 屋面层活载为2.0 kN/m2,恒载为4.5 kN/m2。选取以四川雅安市(30°N,103°E)为中心的周边250 km区域作为算例场地,抗震设防烈度为Ⅶ度(0.1 g),设计地震分组为第二组,设计场地类别为Ⅰ类,场地特征周期为0.30 s,抗震设防类别为丙类。结构平面图与立面图如图1所示,主要构件截面配筋如图2所示。
图2 3层(a)、8层(b)、14层(c)RC框架结构梁、柱截面配筋图
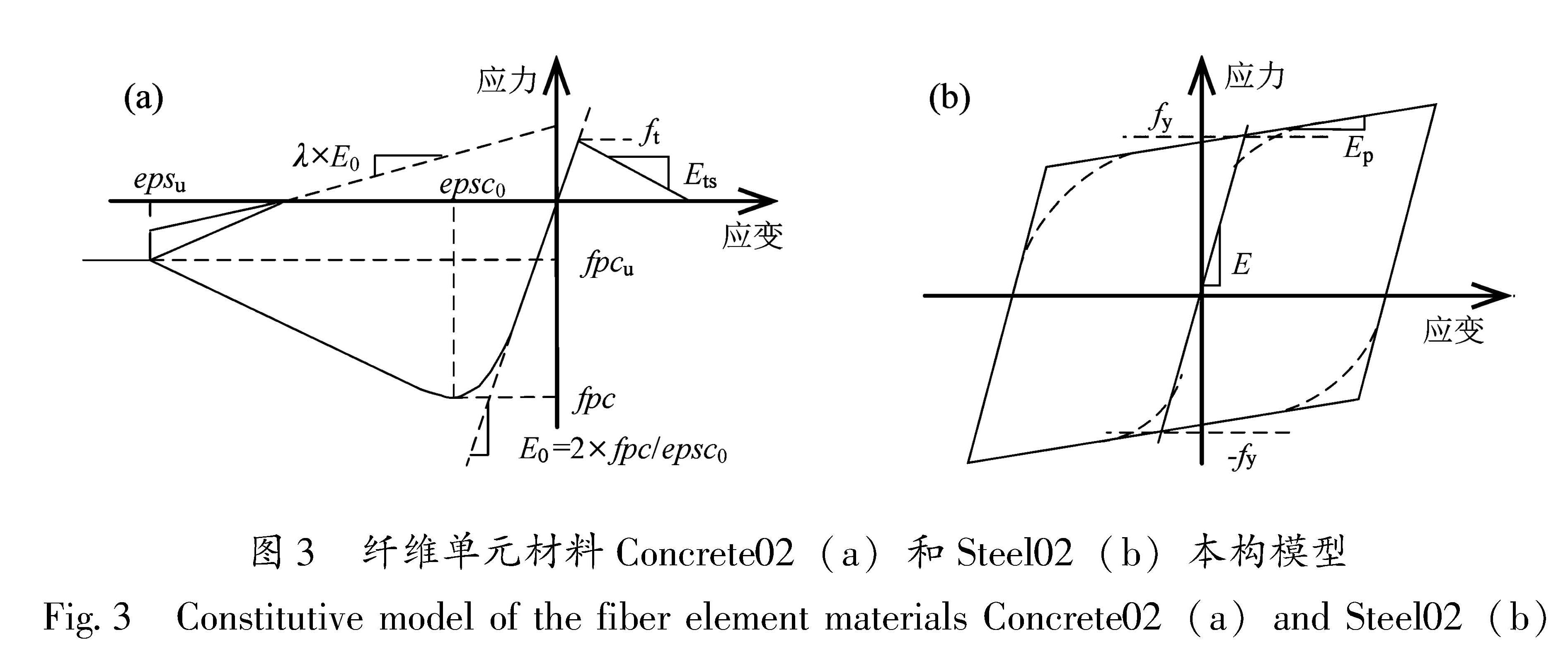
Fig.2 Reinforcement of the beams and columns of the 3-storey(a),8-storey(b),14-storey(c)RC frame structures基于OpenSEES开源软件平台建立RC框架结构有限元模型。框架梁、柱的建立采用基于柔度的纤维单元,同时考虑了结构的P-Δ效应。定义纤维单元截面时,区分框架柱、梁混凝土的核心区与保护层,其中混凝土核心区考虑箍筋的约束作用,其在保护层混凝土本构参数的基础上乘以增幅系数K=1.2,故不再定义箍筋的纤维截面。纤维单元混凝土采用Concrete02本构模型,钢筋采用Steel02本构模型,如图3所示,图中,epsu为极限应变,λ为卸载斜率比值,E0为初始刚度,epsc0为受压应变,ft为抗拉强度,fpcu为极限抗压强度,fpc为抗压强度,fy为屈服强度,E为受拉刚度,Ep为塑性刚度,Ets为受拉刚度。本构模型参数值按照《混凝土结构设计规范》(GB 50010—2010)计算获得。
1.2 有限元模型标定为标定本文建立的RC框架结构有限元模型的正确性,以一榀RC框架-剪力墙结构拟静力试验(许卫晓等,2021)作为对照。纤维单元混凝土采用Concrete02本构模型,壳单元混凝土采用PlaneStressUserMamaterial本构模型,纤维单元钢筋和壳单元钢筋均采用Steel02本构模型。
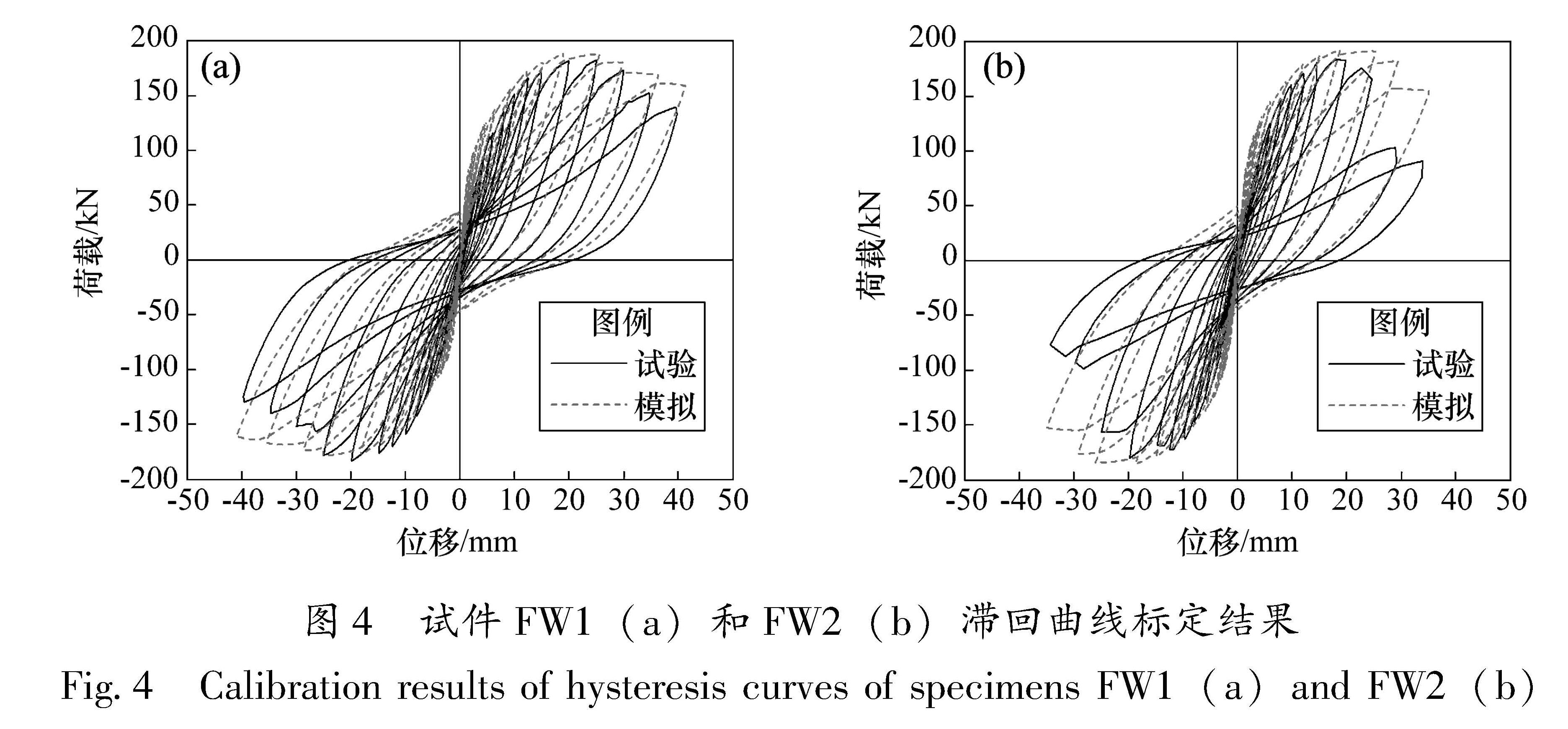
将有限元模型计算获得的第一圈滞回曲线与对照试验实测结果进行对比验证,标定结果如图4所示。根据滞回曲线标定结果,可以得出对于两个试验试件FW1、FW2,有限元模拟计算的峰值荷载与对照试验得到的峰值荷载基本相同,误差均在10%以内,说明有限元模拟与对照试验的标定情况较好,因此可以采用上述OpenSEES建模方法对3个RC框架结构的地震响应进行模拟。
2 地震动记录选取及增量动力分析
本文基于条件均值谱选取地震动记录,综合考虑了结构自身属性以及结构所在场地的地震危险性。计算主方向(Y轴)3个RC框架结构的自振周期,并在此方向输入地震动记录进行增量动力分析。对于低层和多层结构,一般根据结构的一阶自振周期进行条件均值谱的构建,但对于具有长周期特征的高层结构,则需要考虑多阶振型效应,故选取两阶振型建立包络条件均值谱(温瑞智等,2021)。3层、8层和14层RC框架结构的T1分别为0.519、1.025和1.470 s,14层RC框架结构的T2为0.476 s。条件均值谱的构建公式如下(Baker,2011):
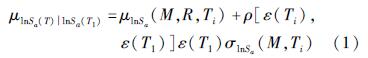
式中:μlnS[HT4.5]a(M,R,Ti)为在(M,R)的条件下,任意Ti的加速度反应谱对数值; ρ[ε(Ti),ε(T1)]为Ti与T1对应的标准差系数之间的相关系数矩阵; ε(Ti)的计算公式如下:
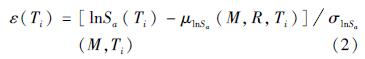
式中:lnSa(Ti)为Ti周期点对应的加速度反应谱对数值; σlnS[HT4.5]a(M,Ti)为Ti周期点对应的加速度反应谱的对数标准差。
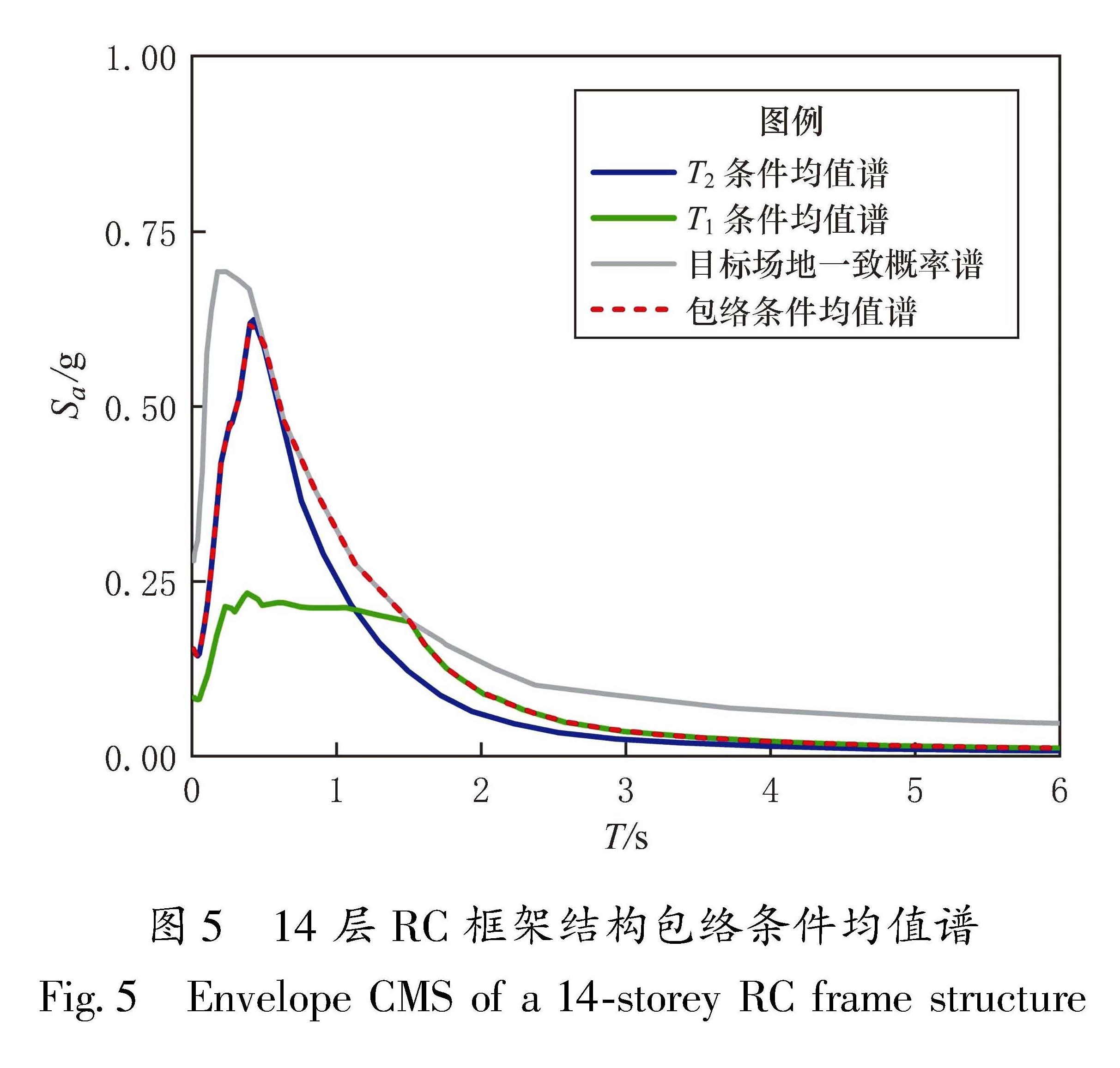
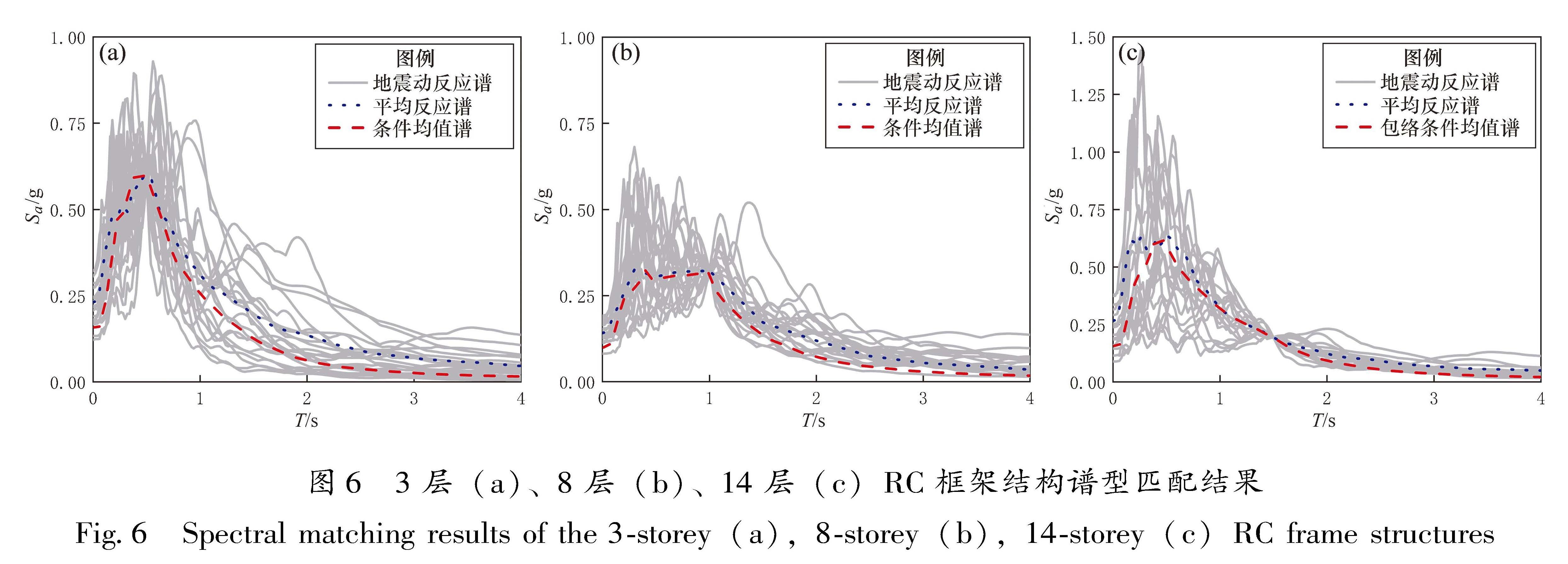
结合雅安地区场地安全性评价报告(温瑞智等,2021)得到的一致概率谱,根据中国概率地震危险性分析(Probabilistic Seismic Hazard Analysis,PSHA)在50年超越概率2%下的解耦方法(冀昆等,2016)以及中国西南地区衰减关系(霍俊荣,1989),按照式(1)构建3层和8层RC框架结构一阶自振周期T1所对应的条件均值谱(Conditional Mean Spectrum,CMS)。对于包络条件均值谱,其由14层RC框架结构T2对应的CMS前段,UHS的T1~T2段以及T1对应的CMS后段构成(温瑞智等,2021),构建的包络条件均值谱如图5所示。将条件均值谱作为目标谱, 根据雅安地区的地震场地信息(温瑞智等,2021),基于结构T1周期点在PEER NGA-WEST2数据库中筛选地震动记录,最终3个结构分别选取了30条地震动记录,作为后续增量动力分析的输入。3个结构一阶自振周期下的谱型匹配结果如图6所示。
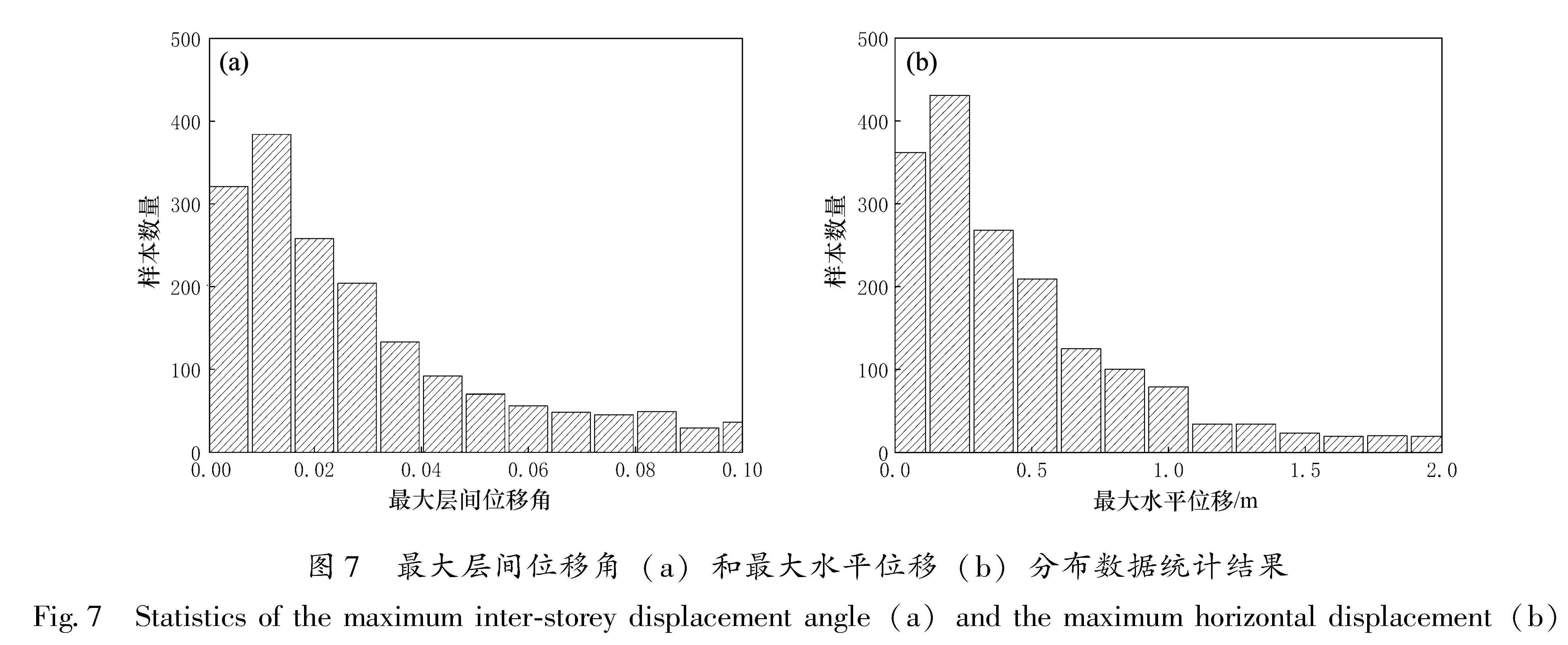
由于结构构件损伤主要表现为变形,因此本文选择最大层间位移角和最大水平位移两个常用的结构位移响应指标,作为弹塑性时程分析的输出。为了取得多个地震强度下的结构响应,以Sa(T1,5%)作为地震强度调幅指标,地震动记录调幅采用IDA中的等步长法,调幅步长取0.1 g,将90条地震动记录分别由0.1 g调整到2.0 g输入到3个RC框架结构中进行增量动力分析。基于IDA方法计算的1 800组数据结果,对各个结构响应分别进行数据分布统计,如图7所示。
图6 3层(a)、8层(b)、14层(c)RC框架结构谱型匹配结果
Fig.6 Spectral matching results of the 3-storey(a),8-storey(b),14-storey(c)RC frame structures3 基于人工神经网络的结构响应预测
结构响应预测属于有监督学习中的回归问题,而人工神经网络(Haykin,2009)能够在通用近似定理的基础上,近似表示任何有限空间中的连续函数(Wang,2020)。
反向传播(Back Propagation,BP)算法是一种训练人工神经网络的经典算法,通常与梯度下降法组合应用。BP算法通过计算神经网络中所有权重损失函数的梯度大小,再反馈到梯度下降法来更新权重,从而实现损失函数的最小化。基于此,本文使用了最典型的基于BP算法的多层前馈神经网络,该神经网络由执行代数运算的神经元组成,并以连续层的形式组织模型,同时通过BP算法训练模型实现结构响应的合理预测。神经元的运算过程如下:
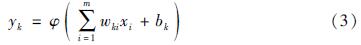
式中:yk为输出信息; xi为输入信息; 权重值wki为上一层输入信息的乘数,其定义了连续层的每个神经元k; 偏差值bk是添加到输入信息加权总和与激活函数φ的值,后者定义了神经元的输出信息。
3.1 参数选择及数据预处理地震动整体持时强度(Ia)以及平均谱加速度(AvgSa)均属于高阶地震动强度指标。地震动整体持时强度通常适用于各种周期的结构(Arias,1970),计算公式如下:
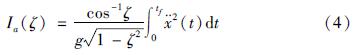
式中:ζ为阻尼比; g为重力加速度; tf为地震动的总持续时间; [AKx¨](t)为地震加速度时程。
平均谱加速度定义为(0.2~1.5)T1周期范围内10个加速度反应谱值的几何平均值(Kohrangi et al,2016a),其自然对数表达式为:
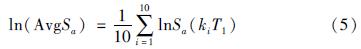
式中:ki为在[0.2,1.5]中均匀取值的常数,总共为10个。
综合考虑地震动强度指标的特性以及结构信息对地震响应的影响性,神经网络的特征参数最终选择在地震工程领域应用广泛的峰值地面加速度(PGA)、峰值地面速度(Peak Ground Velocity,PGV)、峰值地面位移(Peak Ground Displacement,PGD)和一阶周期谱加速度Sa(T</sub>1)等地震动强度信息,具有很好的充分性及有效性的地震动整体持时强度Ia、平均谱加速度AvgSa等地震动强度信息以及结构总高、柱尺寸(Y轴)、柱配筋率(纵筋)和梁高等结构信息; 输出参数选择增量动力分析中使用的2个典型结构响应指标,即最大层间位移角和最大水平位移。特征参数及输出参数选择结果见表1。
由于人工神经网络自身的训练特性,结构响应的准确预测需要大量的样本数据作为支撑。基于上文IDA数据结果搭建人工神经网络模型的样本数据库,为保证神经网络训练的可靠度,必须对样本数据进行预处理,将其值域按下式统一缩放到[0,1]:
x'i=xi/xmax (6)
式中:x'i为预处理后的数值; xi为原始样本数值; xmax为参数样本数值的最大值。[FL)][KH-1]
3.2 神经网络模型设计将预处理后的数据随机等分为10个子集,9个子集作为训练数据集,1个子集作为测试数据集。训练集采用了Picard和Cook(1984)提出的交叉验证方法确定模型的超参数,本文采用十折交叉验证法(Harirchian et al,2020)。交叉验证
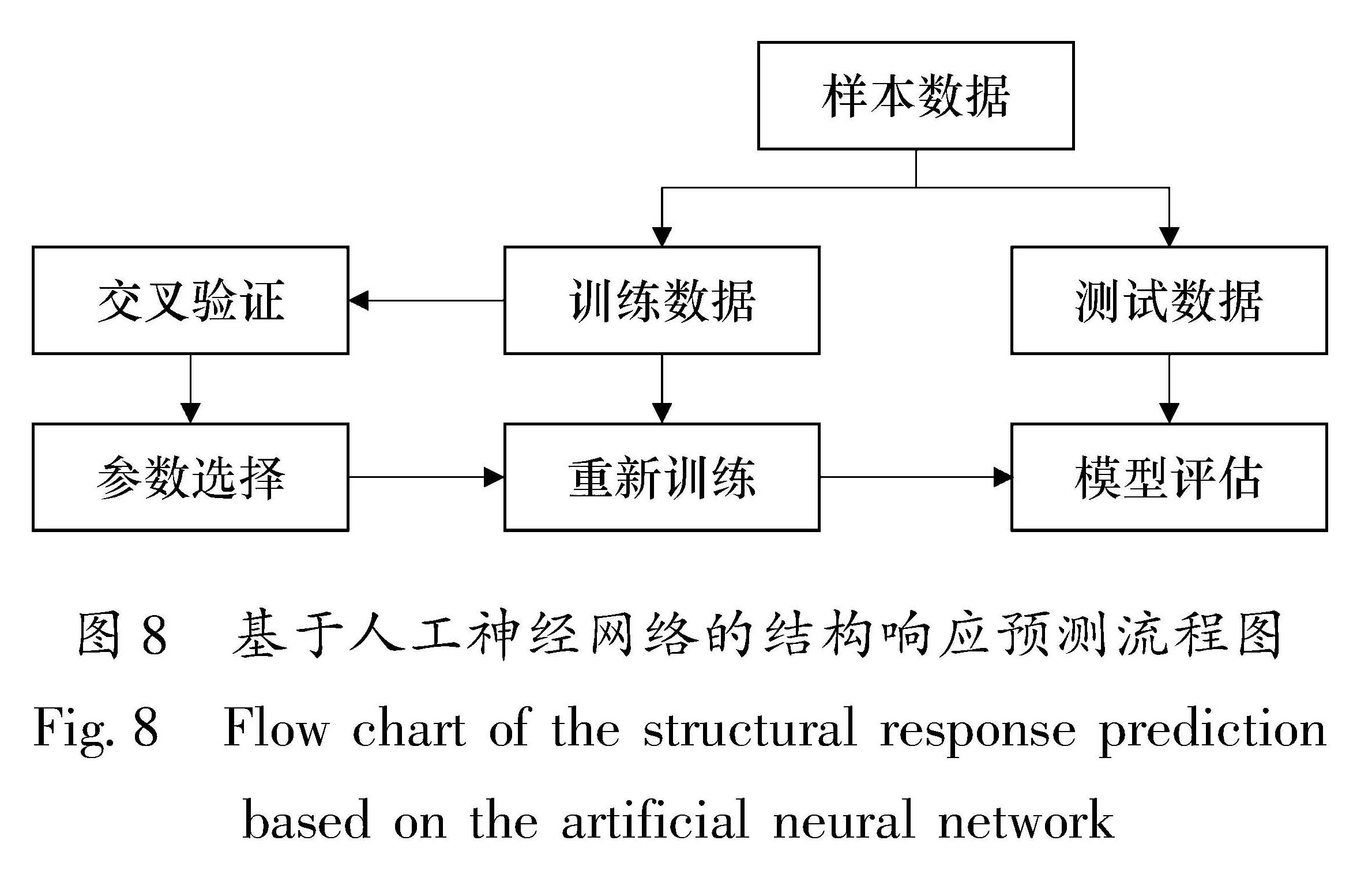
方法对数据集进行多次划分,并对评估指标取平均值,其能够消除小于以万计的数据集单次划分不平衡而造成的不良影响(Harrington,2018; Xu,Goodacre,2018)。图8为基于人工神经网络的结构响应预测流程图。
图8 基于人工神经网络的结构响应预测流程图
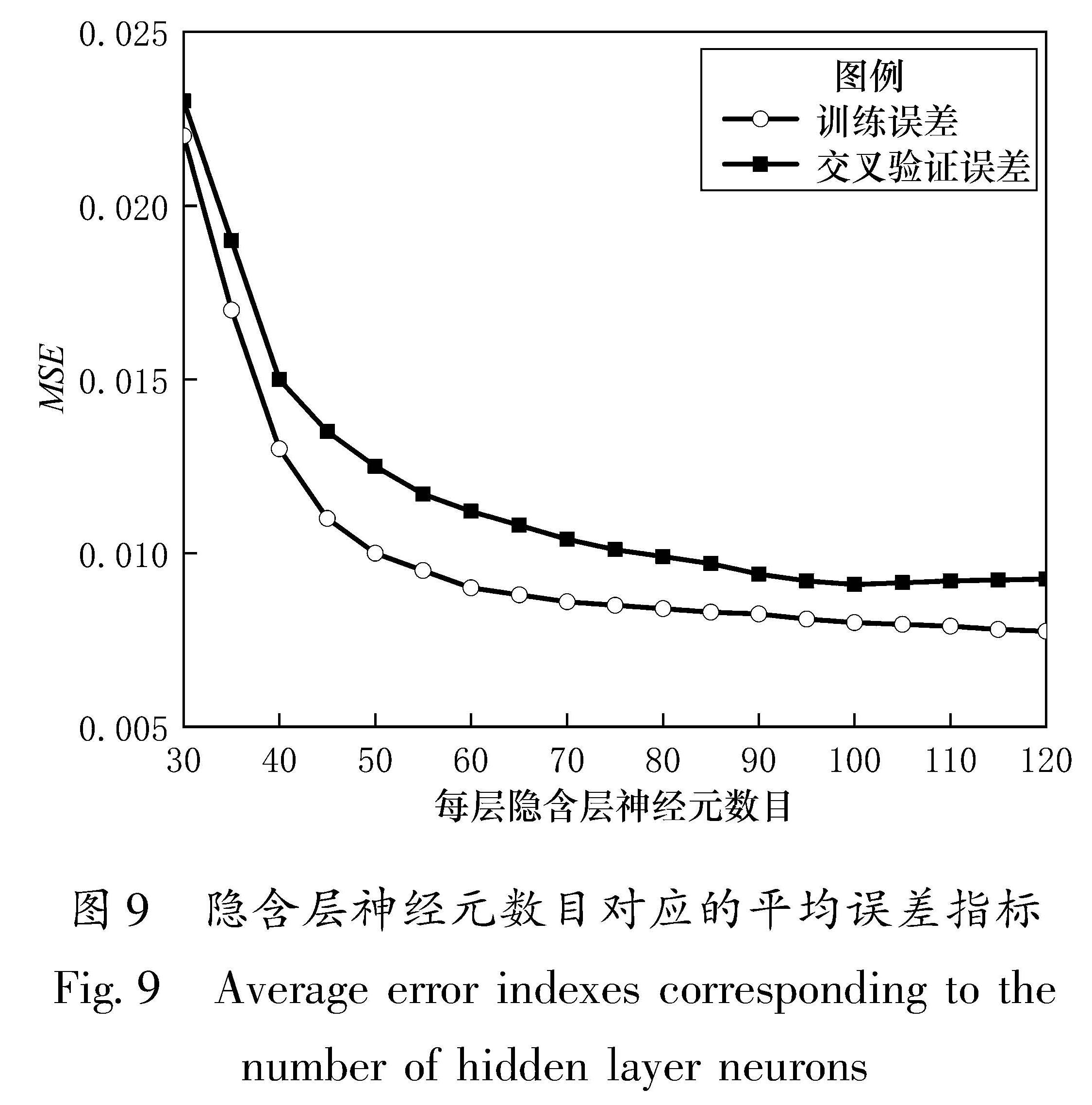
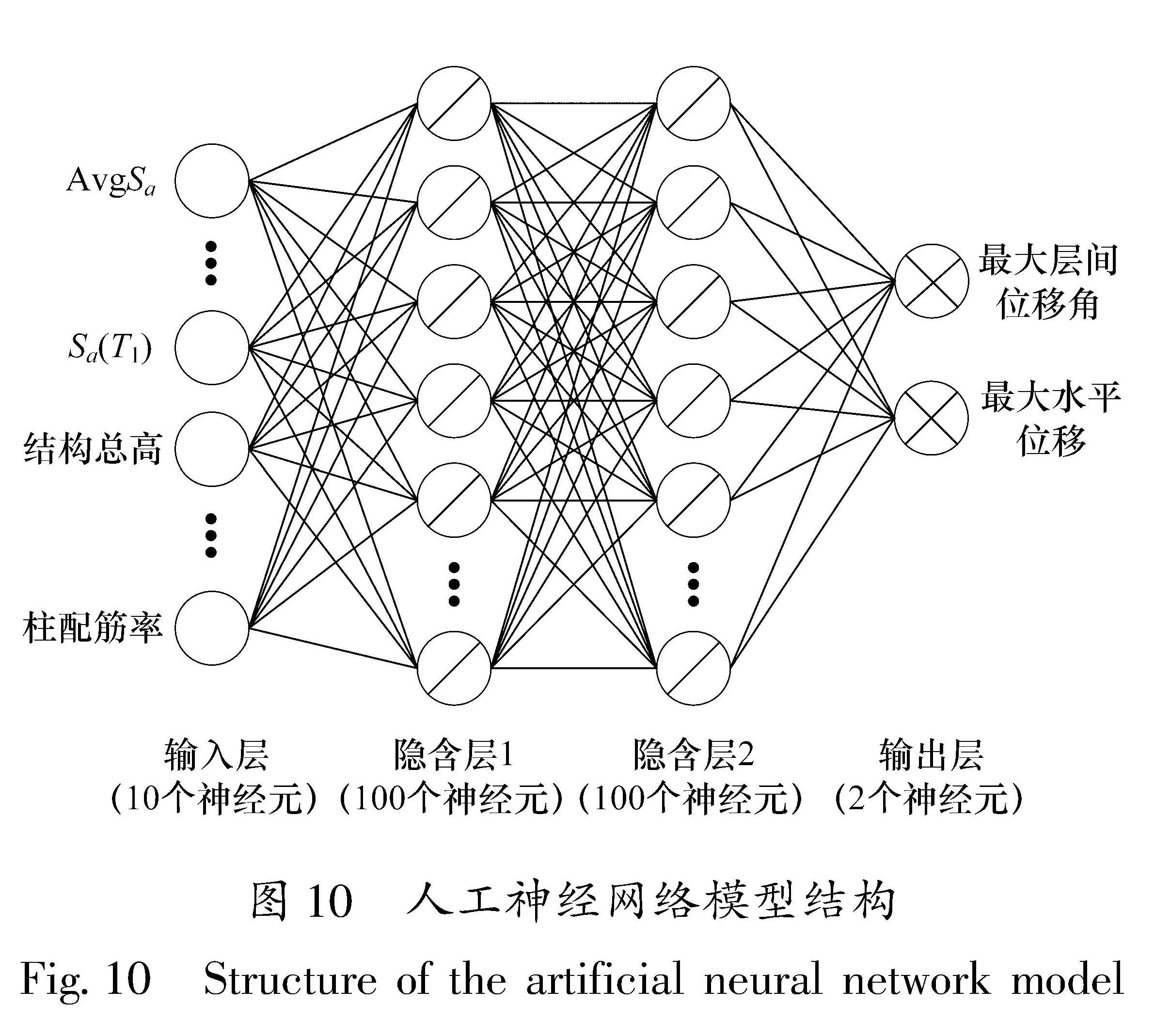
Fig.8 Flow chart of the structural response predictionbased on the artificial neural network使用基于Python环境的Tensorflow开源软件(Abadi et al,2016a)对神经网络模型进行设计。激活函数采用ReLU函数,其优势为计算效率高,且能有效防止过拟合现象的产生; 优化算法采用Adam优化器,其同时具有RMSProp和AdaGrad的优势,是目前神经网络模型优化的最好选择之一(Ruder,2017); 损失函数采用均方误差(Mean-square Error,MSE),这是数据回归问题中最常用的选择。对于模型隐含层及其神经元的数量,设计采用2层隐含层,每层隐含层包含100个神经元。Karsoliya(2012)研究表明,1~2层隐含层可以解决工程领域中任何非线性问题(Morfidis et al,2018; Wang et al,2018)。模型采用3层隐藏层时开始出现过拟合现象,Boger和Guterman(1997)建议在误差允许的条件下建立最简单的神经网络模型,因此最终选择2层隐含层。本文采用试错法(Sheela,Deepa,2013)选择隐含层的神经元数量,不同隐含层神经元个数所对应的平均误差指标如图9所示,结果表明每个隐含层设置100个神经元的情况下交叉验证误差最小,而超过105个神经元时交叉验证误差上升明显,说明产生了过拟合现象。最终建立的神经网络模型如图 10所示。
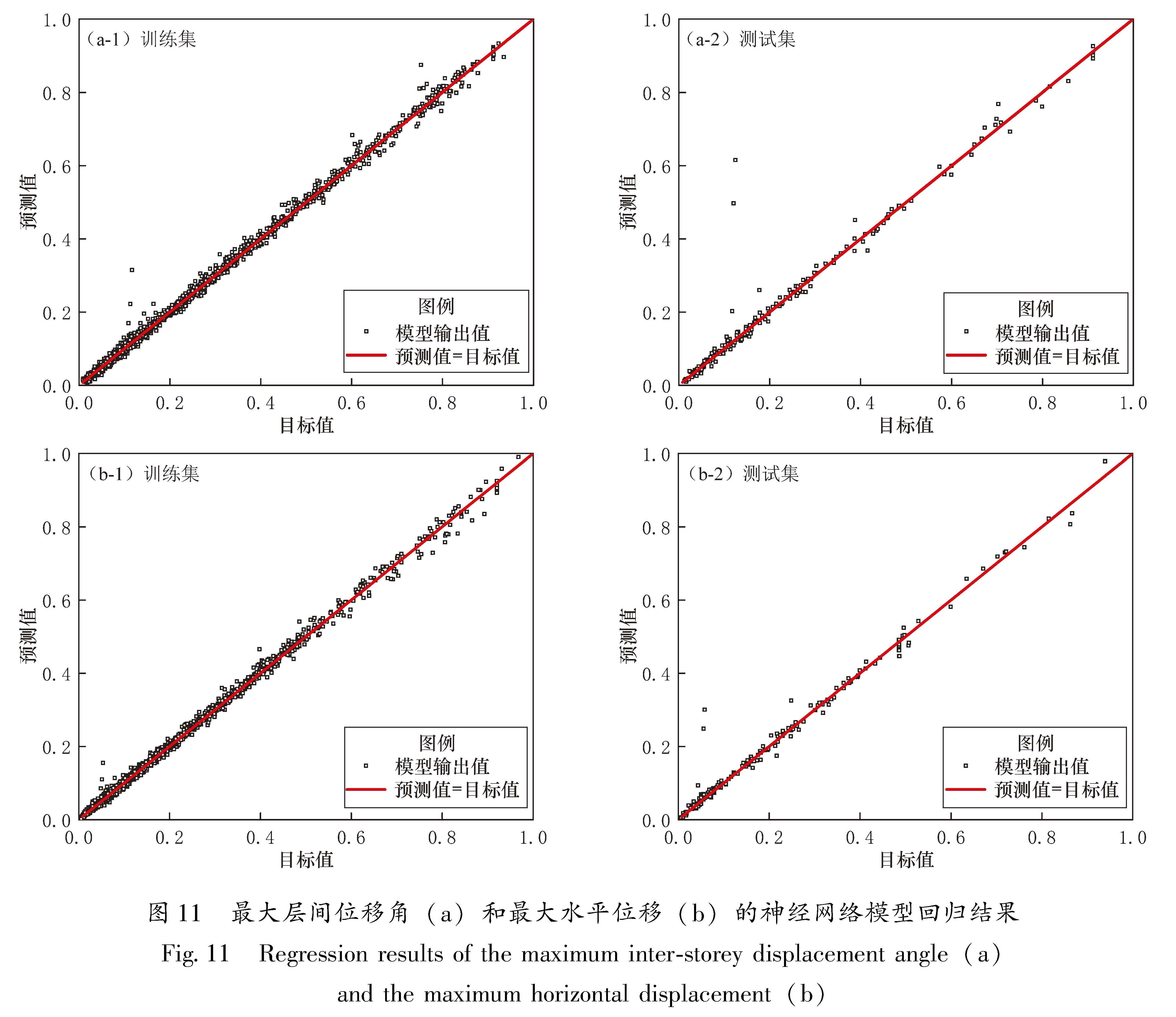
3.3 神经网络评估结果重新训练模型后,使用测试数据集对该模型的泛化能力进行评估,所得回归结果如图 11所示。结果表明,神经网络模型对两个结构响应指标的预测结果均较为稳定,训练集和测试集的大部分散点分布距离红线较近,仅有个别散点出现较明显的偏差。
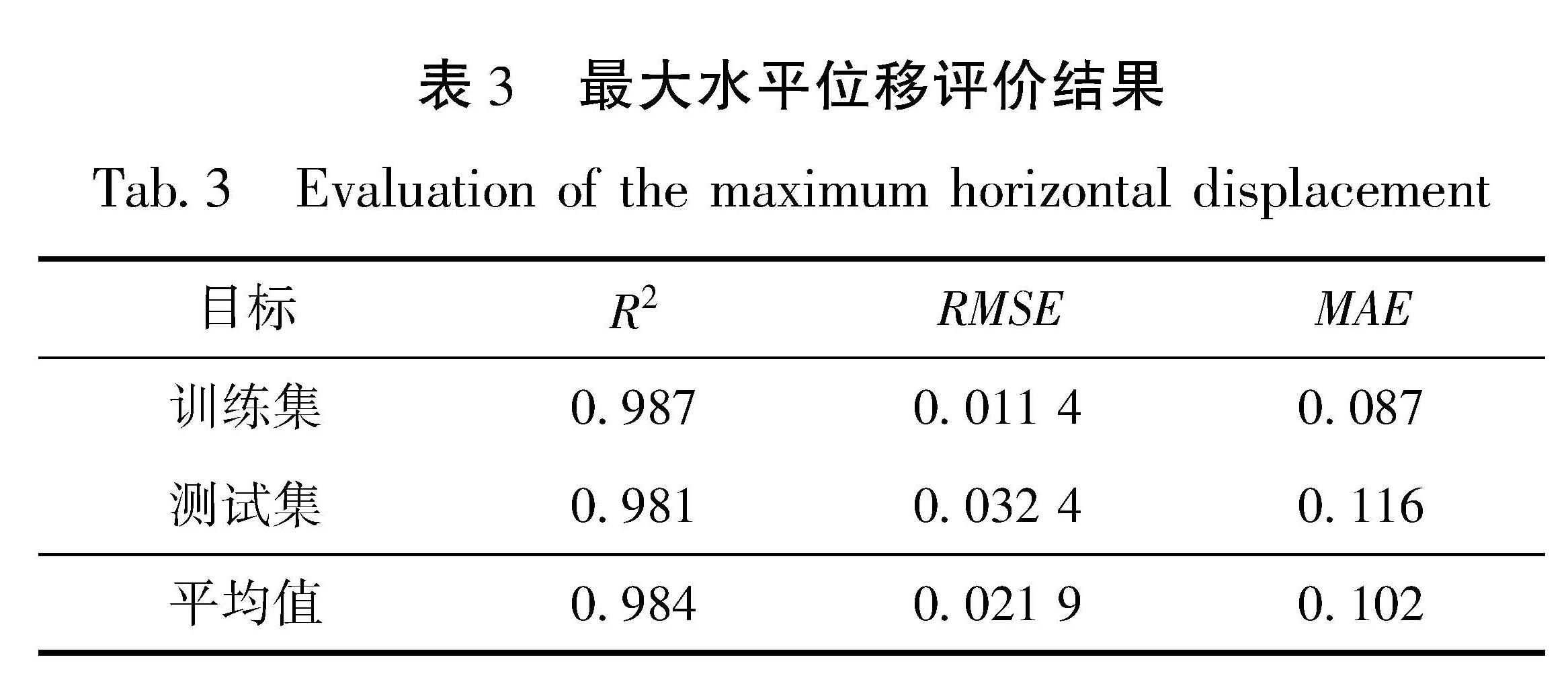
在此基础上,使用决定系数(R</sup>2)、均方根误差(Root Mean Square Error,RMSE)和平均绝对 [JZ][XC赵煜东9.TIF; %100%100]
误差(Mean Absolute Error,MAE)3个回归评价指标对模型的预测能力实现进一步量化评估,各个评价指标的计算公式如下:
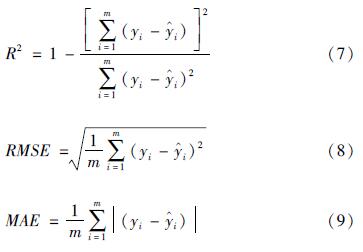
式中:m为预测次数; y为目标值;
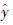 为模型预测值。
为模型预测值。图 11 最大层间位移角(a)和最大水平位移(b)的神经网络模型回归结果
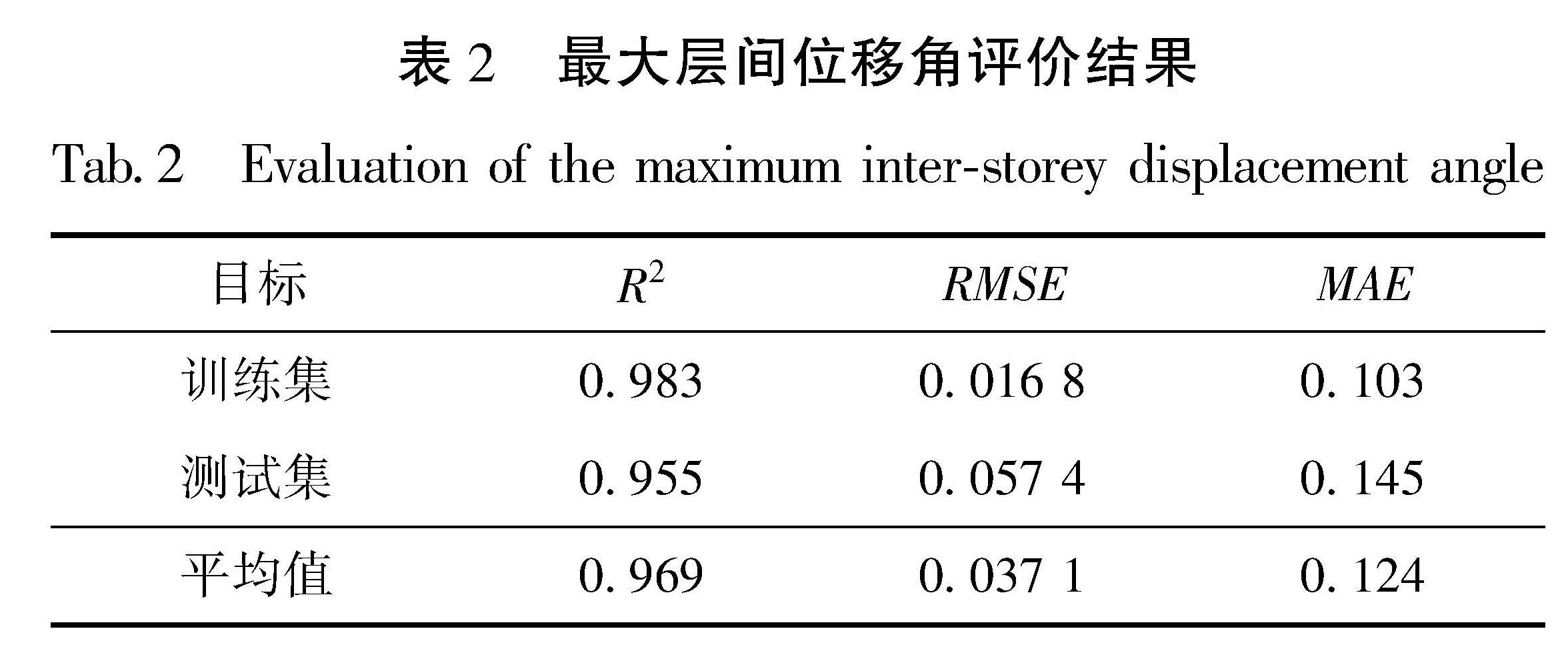
Fig.11 Regression results of the maximum inter-storey displacement angle(a)and the maximum horizontal displacement(b)对于2个结构响应指标,神经网络模型在训练集和测试集上的评价结果详见表2、图3。由表2、3可知,用于训练和测试的神经网络模型的R2均较高,表明使用增量动力分析与神经网络预测得到的结果之间具有较强的相关性; 神经网络模型在训练集以及测试集上的RMSE和MAE均较低,说明模型的预测结果与目标值之间的误差较小。神经网络模型能较好地拟合特征参数与结构响应之间的非线性关系,其对测试集的预测结果与增量动力分析计算结果基本一致,说明模型在解决回归问题时表现良好,泛化能力较强,建立的关系合理可靠。
4 神经网络模型的参数敏感性分析
为进一步理解神经网络模型的数据关系,揭示特征参数与模型预测值的内在规律,采用MIV敏感性分析法(崔智全等,2013)计算地震动强度信息和结构信息对不同结构响应指标的敏感性系数,获取各个特征参数对模型预测值的影响大小。
4.1 MIV分析算法原理特征参数xj对于模型预测值yj的MIV分析过程如下:假设神经网络模型的特征参数为a个,模型预测值为b个,则第i个样本数据的特征参数向量为xi =[xi1,xi2,…,xia],模型预测值向量为yi =[yi1,yi2,…,yib]。假设共有n个样本数据,将所有样本数据的原始值进行统一的上升(式中用序号①表示)和下降(式中用序号②表示)调幅,本文取10%的扰动幅度,得到2组有n个样本数据的新集合为:
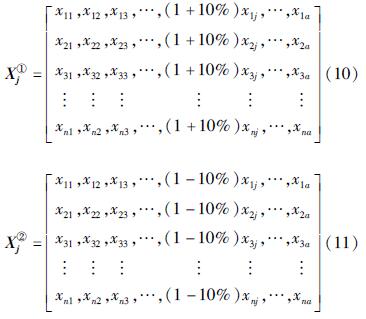
将2组新集合分别输入神经网络模型,获取特征参数xj调幅处理后分别对应的模型预测值矩阵为:
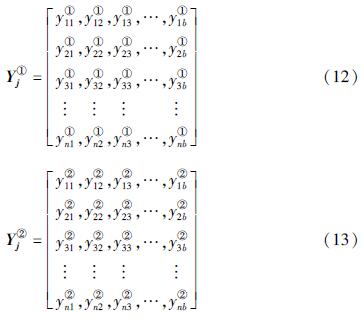
将2个模型预测值矩阵作差,获取样本数据在特征参数xj调幅后对各个模型预测值的影响矩阵。取影响矩阵按列求和后的平均值,即可得到特征参数对模型预测值的平均MIV值为:
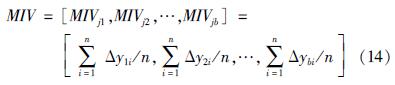
式中:MIVjb为特征参数xj对模型预测值yb的平均影响值。若MIV值为正说明特征参数与模型预测值的关系为正相关; 若MIV值为负说明特征参数与模型预测值的关系为负相关。
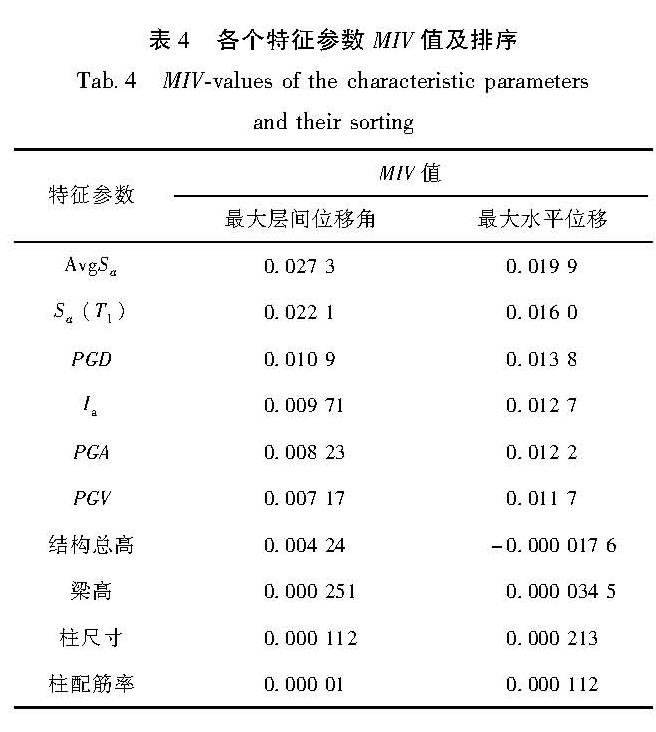
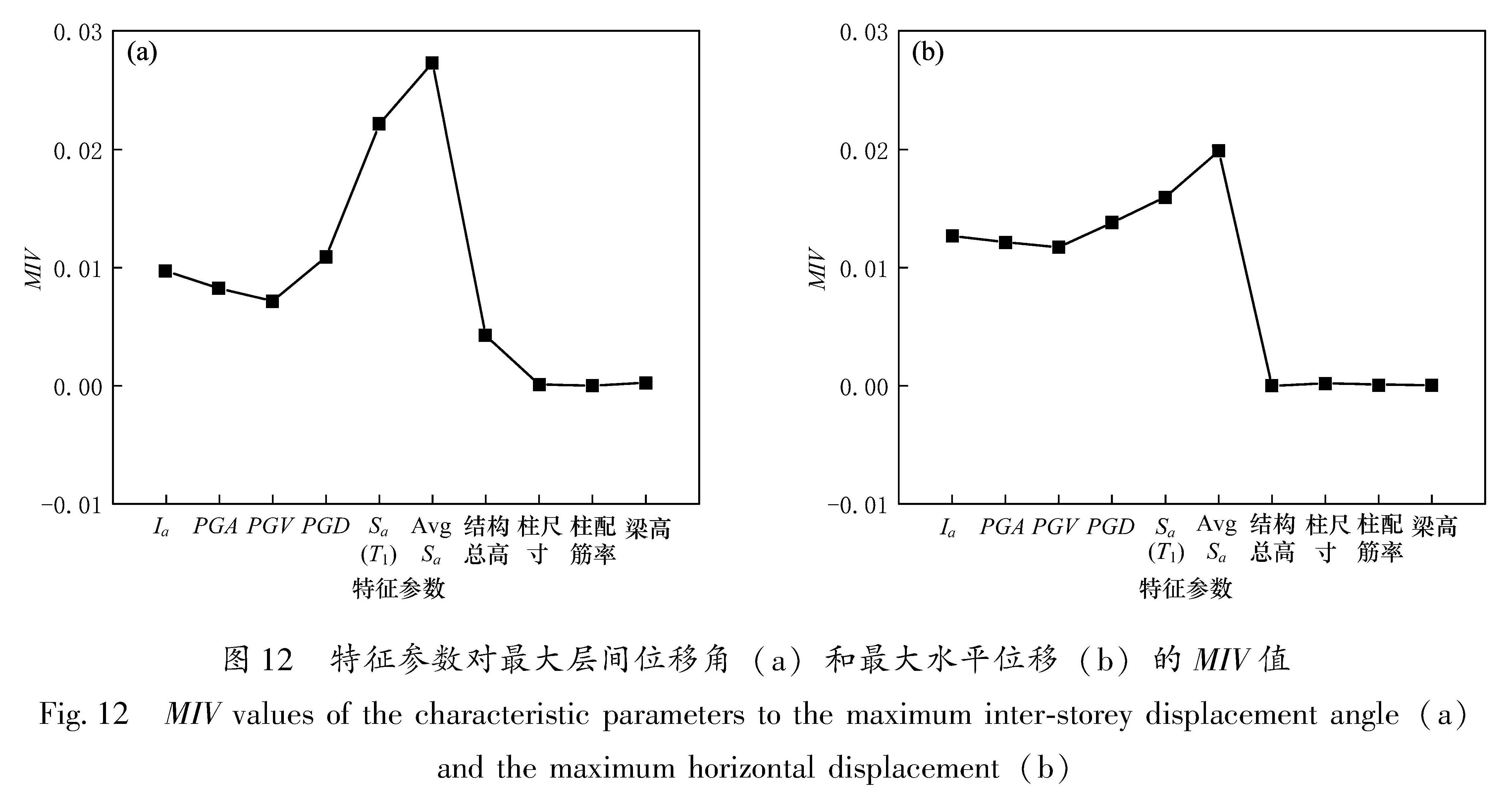
4.2 BP神经网络的MIV敏感性分析根据MIV算法原理,分别计算10个特征参数的敏感性系数,各个特征参数对于最大层间位移角和最大水平位移的MIV值如图 12所示,并基于MIV值对各个特征参数从大到小进行排序,见表4。由于最大层间位移角与最大水平位移是类似的变形参数,故地震动强度信息对这2个结构响应指标影响均较大,而对结构信息的影响普遍很小。这是因为地震动强度的增加是RC框架结构产生塑性变化的主要因素,当结构发展为塑性后,地震动强度的微小增加就可能使结构产生严重的损伤。由表4可知,针对2个结构响应指标影响最大的特征参数均为AvgSa,为(0.2~1.5)T1范围内10个加速度反应谱的几何平均值,其振动周期范围涵盖了结构从弹性状态到接近倒塌的塑形状态的整个过程,是比Sa(T1)更高阶的地震动强度指标。参数敏感性分析为特征参数的筛选提供了依据,重点考虑敏感值较大的地震动强度信息,可以提高神经网络模型的数据利用效率。
5 结论
本文以3个典型RC框架结构为研究算例,提出一种基于人工神经网络的RC框架结构地震响应预测方法,综合考虑了目标场地的地震危险性以及多种输入参数的影响,得出以下主要结论:
(1)人工神经网络模型建立了特征参数与RC框架结构地震响应之间较为合理的数学关系,采用十折交叉验证法设计的神经网络模型在回归分析中表现良好,模型测试阶段的决定系数R2均达到了0.95以上,体现了较好的泛化性能,具有较好的工程应用前景。
(2)参数敏感性分析揭示了神经网络模型的内在规律,获取了各个特征参数对模型预测值的影响大小,使模型更易于理解操作。地震动强度信息相较于结构信息对结构地震响应预测值的影响较大,且综合考虑结构动力特性的平均谱加速度AvgSa指标对于结构位移响应指标均有最高的MIV值,重点考虑平均影响值较大的地震动强度信息,可以提高神经网络模型的数据利用效率。
本文主要研究了以变形为主要指标的RC框架结构构件损伤模式,故提出的方法可以用于以变形为评估指标的地震易损性分析中。后续将进一步开展对非结构构件响应预测方法的相关研究。
- 崔智全,付旭云,钟诗胜,等.2013.小波网络平均影响值的航空发动机自变量筛选[J].计算机集成制造系统,19(12):3062-3067.
- Cui Z Q,Fu X Y,Zhong S S,et al.2013.Independent variable selection of aero-engine based on average influence value of wavelet network[J].Computer Integrated Manufacturing Systems,19(12):3062-3067.(in Chinese)
- 霍俊荣.1989.近场强地面运动衰减规律的研究[D].哈尔滨:中国地震局工程力学研究所.
- Huo J R.1989.Study on attenuation law of near field strong ground motion[D].Harbin:Institute of Engineering Mechanics,China Earthquake Administration.(in Chinese)
- 冀昆,温瑞智,任叶飞.2016.中国地震安全性评价中天然强震记录选取[J].哈尔滨工业大学学报,48(12):183-188.
- Ji K,Wen R Z,Ren Y F.2016.Selection of natural strong earthquake records in seismic safety evaluation of China[J].Journal of Harbin Institute of Technology,48(12):183-188.(in Chinese)
- 温瑞智,冀昆,任叶飞.2021.工程地震动输入—从传统抗震设防到韧性提升[M].北京:地震出版社.
- Wen R Z,Ji K,Ren Y F.2021.Engineering ground motion input:From traditional seismic fortification to toughness improvement[M].Beijing:Seismological Press.(in Chinese)
- 许卫晓,程扬,杨伟松,等.2021.RC框架—抗震墙并联结构体系拟静力试验[J].吉林大学学报(工学版),51(1):268-277.
- Xu W X,Cheng Y,Yang W S,et al.2021.Quasi-static test of RC frame-shear wall dual structure system[J].Journal of Jilin University(Engineering and Technology Edition),51(1):268-277.(in Chinese)
- GB 50010—2010,混凝土结构设计规范[S].
- GB 50010—2010,Code for design of concrete structures[S].(in Chinese)
- GB 50011—2010,建筑抗震设计规范[S].
- GB 50011—2010,Code for seismic design of buildings[S].(in Chinese)
- JGJ 3—2010,高层建筑混凝土结构技术规程[S].
- JGJ 3—2010,Technical specification for concrete structures of high-rise building[S].(in Chinese)
- Abadi M,Agarwal A,Barham P,et al.2016a.TensorFlow:Large-scale machine learning on heterogeneous distributed systems[J/OL].e-prints arXiv,(2016-03-14)[2023-02-22].https://arxiv.org/pdf/1603.04467.pdf.
- Abadi M,Agarwal A,Barham P,et al.2016b.Tensorflow:large-scale machine learning on heterogeneous distributed systems[R].CoRR,doi:10.48550/arXiv.1603.04467.
- Arias A.1970.A measure of earthquake intensity in seismic design for nuclear power plants[M].Cambridge:MA MIT Press.
- Baker J W,Cornell C A.2005.A vector-valued ground motion intensity measure consisting of spectral acceleration and epsilon[J].Earthquake Engineering and Structural Dynamic,34(10):1193-1217.
- Baker J W.2011.Conditional mean spectrum:tool for ground-motion selection[J].Journal of Structural Engineering,137(3):322-331.
- Bishop C M.2006.Pattern recognition and machine learning[M].New York:Springer.
- Boger Z,Guterman H.1997.Knowledge extraction from artificial neural network models[J].Computational Cybernetics and Simulation,62(4):3030-3035.
- Cornell C A,Krawinkler H.2000.Progress and challenges in seismic performance assessment[J].PEER Center News,3(2):1-3.
- Dolce M,Prota A,Borzi B,et al.2021.Seismic risk assessment of residential buildings in Italy[J].Bulletin of Earthquake Engineering,(19):2999-3032.
- Harirchian E,Lahmer T,Rasulzade S.2020.Earthquake hazard safety assessment of existing buildings using optimized multi-layer perceptron neural network[J].Energies,13(8):2060.
- Harrington P.2018.Multiple versus single set validation of multivariate models to avoid mistakes[J].Critical Reviews in Analytical Chemistry,48(1):33-46.
- Haykin S.2009.Neural networks and learning machines[M].New Jersey,United States:Pearson.
- Jalayer F,Cornell C A.2009.Alternative non-linear demand estimation methods for probability-based seismic assessments[J].Earthquake Engineering and Structural Dynamic,38(8):951-972.
- Jalayer F,De R R,Manfredi G.2015.Bayesian Cloud analysis:efficient structural fragility assessment using linear regression[J].Bulletin of Earthquake Engineering,13(4):1183-1203.
- Karsoliya S.2012.Approximating number of hidden layer neurons in multiple hidden layer BPNN architecture[J].International Journal of Engineering Trends and Technology,3(6):714-717.
- Kim T,Song J,Kwon O S.2020.Probabilistic evaluation of seismic responses using deep learning method[J].Structural Safety,84(4):131-139.
- Kohrangi M,Bazzurro P,Vamvatsikos D.2016a.Vector and scalar IMs in structural response estimation,part I:Hazard analysis[J].Earthquake Spectra,32(3):1507-1524.
- Kohrangi M,Vamvatsikos D,Bazzurro P.2016b.Implications of intensity measure selection for seismic loss assessment of 3-D buildings[J].Earthquake Spectra,32(4):2167-2189.
- Lu P Z,Chen S Y,Zheng Y J.2012.Artificial intelligence in civil engineering[J].Mathematical Problems in Engineering,(11):1-22.
- Morfidis K,Kostinakis K.2018.Approaches to the rapid seismic damage prediction of RC buildings using artificial neural networks[J].Engineering Structures,165(15):120-141.
- Oh B W,Glisic B,Park S W,et al.2020.Neural network-based seismic response prediction model for building structures using artificial earthquakes[J].Journal of Sound and Vibration,468:109-115.
- Picard R R,Cook R D.1984.Cross-validation of regression models[J].Journal of American Statistical Association,79(387):575-583.
- Ruder S.2017.An overview of gradient descent optimization algorithms[J/OL].e-prints arXiv,(2017-06-15)[2023-02-22].https://arxiv.org/pdf/1609.04747.pdf.
- Sheela K,Deepa S N.2013.Review on methods to fix number of hidden neurons in neural networks[J].Mathematical Problems in Engineering,(6):1-11.
- Vamvatsikos D,Cornell C A.2002.Incremental dynamic analysis[J].Earthquake Engineering and Structural Dynamic,31(3):491-514.
- Wang Z Y,Pedroni N,Zentner I,et al.2018.Seismic fragility analysis with artificial neural networks:application to nuclear power plant equipment[J].Engineering Structure,162:213-225.
- Wang Z.2020.Abstract universal approximation for neural networks[D].New York:Cornell University.
- Xu Y,Goodacre R.2018.On splitting training and validation set:a comparative study of cross-validation,bootstrap and systematic sampling for estimating the generalization performance of supervised learning[J].Journal of Analysis and Testing,2(3):249-262.
- Yepes E C,Silva V,Rossetto T,et al.2016.The global earthquake model physical vulnerability database[J].Earthquake Spectral,32(4):2567-2585.
- Yoshikaw A H,Goda K.2014.Financial seismic risk analysis of building portfolios[J].Natural Hazards Review,15(2):112-120.