基金项目:国家重点研发计划项目(2021YFC3000703、2021YFC3000602); 地震科技星火计划项目(XH202302).
第一作者简介:江宁波(1996-),助理工程师,主要从事地震学应用等方面的研究.E-mail:Jiangnb2016@foxmail.com.
通信作者简介:吴微微(1982-),正高级工程师,主要从事地震监测、数字地震学应用等方面的研究.E-mail:673065247@qq.com.
(Sichuan Earthquake Agency,Chengdu 610044,Sichuan,China)
the Lijiang MS7.0 earthquake; the Lushan MS7.0 earthquake; cross-fault observation; earthquake-case review; meta-instable characteristics; Sichuan-Yunnan area
DOI: 10.20015/j.cnki.ISSN1000-0666.2024.0025
构造块体的相对运动通常会导致断裂系统处于长期应力积累状态,积累的应力在地震发生过程中得到释放。地震期间绝对应力的时空变化一般不能直接确定,但是剪切应力的相对降低可以通过断层尺度和滑动幅度来估计。地震前后断层上的初始剪应力与最终剪应力之差定义为震源应力降,它是地震破裂期间总滑移的函数(Brune,1970,Madariaga,1976),也是描述震源尺度特征的基本参数之一。
应力降的大小和总滑移与破裂尺度之比成正比,由于震源物理尺寸通常无法直接观测,一般需要从地震记录中获得震源参数的信息。一种方法是对震级和地震破裂面积或辐射能量的估计值进行比较,使用标度关系估算应力降的具体值。另一种方法是通过假设一个震源模型(Brune,1970; Madariaga,1976),通过估计震源谱的拐角频率来推导应力降(Abercrombie,1995)。拐角频率通常定义为震源谱高、低频段的渐近线的交点所对应的频率(安艺敬一,理查兹,1986),地震矩相同时高频辐射波所含的高频成分随拐角频率的增大而丰富。第一种方法中“小地震的应力降如何随地震尺度变化”的认识仍然存在争议,与由观测资料得到的结果之间有较多矛盾,一些观点认为小地震的应力降随地震尺度增大而增加(Hardebeck,1997),另一些则认为小地震的应力降基本上保持不变(Abercrombie,1995),也有研究发现重复地震的应力降随时间推移存在系统性变化(Marone et al,1995)。第二种方法先是将地震记录反卷积为震源、场地和路径效应的函数,在扣除地震波沿传播路径的衰减和场地作用的影响后,对断层几何结构和地震破裂过程进行简化假设(例如将断层假设为Brune圆盘模型),再根据震源谱的地震矩和拐角频率来计算应力降。在计算过程中,震源物理尺度的简化假设、理论模型的有效性、路径效应的修正、观测中的不确定性以及频率域震源参数的确定(如拐角频率的测定),都对应力降有影响,因此很难对不同研究进行比较,特别是以绝对值公布的应力降估计值。在观测资料不够理想的情况下,通过震源谱高频衰减常数间接得到关于应力降的标度特征,或者对整个数据集采用一致的处理参数和模型假设,并使用大量应力降计算结果的中位估计值或相对变化来进行讨论分析,也许能够间接得到较为稳健和可靠的定性结论。
地震应力降定义为地震前、后断层面上平均剪应力之差,表示地震时断层面上所释放的应力。设震前断层面上的静态初始剪切应力为σ1,震后断层面上的最终剪切应力为σ2,则静态应力降为:
Δσ=σ1-σ2(1)
平均应力为:

与静态应力降对应的动态应力降则较为复杂。当地震破裂开始扩展后,该点的应力逐渐增加至岩石所能承受的水平应力σs时,该点发生破裂。对于未发生破裂的区域,σs为材料或岩石的剪切破裂强度,对于已经破裂的区域,依靠静摩擦应力挤压在一起的断层两盘,就是σs最大静止摩擦应力。当发生滑动后,应力从σs下降到动摩擦应力σf并在滑动期间动摩擦应力σf保持不变,随着整个断层面上的破裂过程停止,应力便由动摩擦应力σf过渡到最终应力σ2,其过程如图1所示(Yamashita,1976)。
剪切破裂强度或最大静摩擦应力σs与动摩擦应力σf之差,称为有效应力σe:
σe=σs-σf(3)
在Brune(1970)圆盘模型中,假定剪切破裂同时发生并且σ1=σs,则有效应力σe即为动态应力降Δσd:
Δσd≈σe=σ1-σf(4)
Brune(1970)圆盘模型是较为常见的应力下调模式,还存在应力上调模式(Savage,Wood,1971; Kanamori,Rivera,2006)。如图2所示,应力上调模式为当断层上发生滑移时,运动受到的阻力为摩擦应力σf,发生破裂瞬间,断层滑移受动态应力降Δσd的驱动,随着滑移的进行,驱动力减小,最后摩擦应力超过驱动应力,滑移减速,最终断层在小于摩擦应力的最终应力σ2处锁定(Savage,Wood,1971)。
在利用标度关系估计应力降的方法中(Kanamori,Anderson,1975; Andrews,1986),假定地震时长度为L的断层发生的平均位移量为D^-,依据Hooke定律可估计整个断层上的应力降为:

式中:μ是弹性剪切模量(摩擦系数); 平均位移量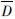 可由地震矩M0表示为:
可由地震矩M0表示为:

式中:c为断层形状参数,c=L/W; L、W分别指断层的长和宽,则
Δσ≈cM0/L3(7)
或写为:
Δσ≈cM0/LA(8)
式中:A为断层面积。
由式(7)、(8)可见,地震应力降与地震平均位移量、断层尺度和地震矩有关。
在实际中,震源破裂特征的确定十分困难。通常是假设一个理论破裂模型来计算应力降,然后根据计算模型取不同的几何系数c和断层特征长度L(Kanamori,Anderson,1975)。对于大地震,在断层走向方向的破裂尺度可达数十至数百千米,但在深度方向上受限于震源深度,一般采用L×W矩形模型,取c=2/π,则应力降Δσ表示为:

对于无限长倾滑断层模型,c=4(λ+μ)/π(λ+2μ),λ是拉梅常数。对于震级较小的地震,常采用Brune(1970)圆盘破裂模型,即假设地震破裂发生在具有均匀应力降和恒定破裂速度的圆形断层面上。通常c=7π/16,L取圆盘半径r,应力降表示为:
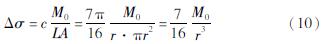
对于破裂半径r的获取,地震学上可以通过远场地震记录来反演震源破裂过程,由频率域的拐角频率fc间接获得震源物理尺度信息(Aki,Richards,1980; Kanamori,Brodsky,2004),表示为:

式中:β是震源附近剪切波速度。则式(10)改写为:

式中:k是常数,取决于使用的模型类型来关联拐角频率fc和震源破裂半径r的关系。
在Brune(1970)模型中,k=(2.34)/(2π)=0.37; 在Madariaga(1976)模型中,k=0.21(Shearer et al,2006; Allmann,2009); 在Sato和Hirasawa(1973)中,k取决于震源破裂速度(Cotton,2013)。
根据式(12)得到的Δσ与fc的立方成正比,因此应力降Δσ对fc的误差非常敏感,即使断层模型接近实际断层,fc微小的观测误差也会降低Δσ的可靠性,这也是由传统地震学方法给出地震应力值的局限性所在。
在全球尺度的研究中,全球地震应力降值集中在0.1~100 MPa。Kanamori和Anderson(1975)对1923—1968年全球6级以上地震的研究结果显示,地震应力降范围在0.1~10 MPa,平均值为6 MPa。Purcaru和Berckhemer(1978)对1857—1976年全球7级以上大地震的研究显示,地震应力降的范围在2~13 MPa。Allmann等(2009)对1900—2007年全球2 000个5级以上的地震研究表明,地震应力降范围为0.3~50 MPa,中位数为4 MPa。对于特殊区域,如第四纪火山区,地震应力降范围为0.1~40 MPa(Harrington et al,2015)。赵翠萍等(2011)认为中国大陆大部分地区的中小地震的应力范围为0.1~20 MPa,且绝大多数小于10 MPa。
整体而言,应力降对特定因素的依赖性比较弱,在局部尺度(单个地震序列内或局部小区域构造条件下),这种依赖性可能非常强。对于影响应力降的因素,学者们从地震矩、震源深度、震源机制解、构造块体、断层性质等诸多方面开展了研究,但目前仍有许多认识尚未统一。
目前关于地震应力降存在一个有争议问题,即它与地震矩M0之间是否存在相关性。Aki(1967)首次提出了地震的自相似性,即震源力学的尺度不变性。有研究认为矩震级为1018~1023 N·m的地震,地震矩与破裂尺度成幂律关系,应力降近似于常数(Hanks,1977; McGarr,1984; Abercrombie,1995; Ide,Beroza,2001; Allmann et al,2007,2009)。
但是关于微小地震的应力降与地震矩的关系具有争议。赵翠萍等(2011)认为中国大陆大部分地区的中小地震释放的应力降随震级增大而增大,不遵循常数应力降或分段模型。Mayeda和Walter(1996)指出小地震的应力降Δσ随地震矩M0按Δσ∝M0.250的规律增加, Hardebeck和Hauksson(1997)也观测到类似的小地震应力降随地震矩的增减而增减的现象,这样的观测结果可能意味着地震并非自相似。其他研究认为较小震级事件的非自相似性是由与高频衰减有关的偏差(Anderson,1986; Abercrombie,1995; Ide et al,2003),或者是因为数据带宽的限制(Hough,1996; Ide,Beroza,2001)造成的。
Abercrombie和Leary(1993)、Abercrombie(2015)、Allmann和Shearer(2007)认为小地震应力降与地震矩没有明显关系。有研究认为大震级地震的破裂过程和动力学机制与小震级地震存在差异(Moyer et al,2018),因此应力降随震级的变化存在多重标度特征,如Atkinson(2004)研究指出美国东北和加拿大东南地区较大地震的应力降接近常数,较小地震的应力降则随地震矩的增加而增加。
构造系统的差异也对地震应力降有影响,不同构造系统的应力降统计结果如图3所示。一般认为大洋转换断层具有最高的应力降,(Allmann et al,2007,Williams et al,2019)。其他构造类型中,板块内部地震释放的应力降高于板块边界的地震(Kanamori,Anderson,1975; Allmann et al,2007,2009; Seno,2014),主要是因为板块内的断层滑移速率、滑移尺度以及地震断层尺度显著小于板块边界(Scholz et al,1986),而岩石的摩擦强度与滑移速率呈负相关,与地震重复周期呈正相关(Dieterich,1972; Goldsby et al,2011)。相比于板间地震,板内地震一般重复周期更长,滑移速率更低,所以板块内部断层有更高的摩擦强度,也产生了更高的应力水平(Sykes,Sbar,1973)。Bilek和Lay(1999)研究指出板块边界的低应力降与俯冲区刚度较低有重要联系。基于构造区的研究认为板间地震满足常数应力降模型(Constant Stress Drop,CSD),即应力降不随地震大小而变化; 而板块内部的地震应力降则满足增加应力降模型(Increasing Stress Drop,ISD),即应力降随地震增大而增大(Nuttli,1983)。
在应力降与断层类型的相关性研究中,Anderson(1905)断层理论认为逆断层的剪切应力最高,正断层的剪切应力最低(McGarr,2002)。Satoh(2006)利用日本强震记录估算168次震源深度≤60 km、4.4≤MW≤6.9地震的应力降,发现逆断层地震的应力降是走滑断层地震的2倍,而走滑断层的应力降是正断层地震的2倍。Hauksson(2015)分析美国南加州约60 000次地震的应力降值,发现高应力降主要分布在加利福尼亚州东部Ridgecrest附近和San Andreas断层系统内的断层附近、低应力降则主要分布在张性区域。Boyd等(2017)使用谱比法估算美国大陆及邻区的地震应力降,发现美国东部(Eastern United States,简称EUS)少数构造地震的平均应力降(2.6~36 MPa)大约是美国西部(Western Unted States,简称WUS)构造地震平均应力降(1.0~7.9 MPa)的3倍,是中部废水注入区(Central United States,简称CUS)平均应力降(0.6~5.6 MPa)的5倍,其中EUS地震往往是较深的逆冲事件,而WUS地震往往较浅且震源机制解类型较多,CUS地震倾向于浅层、具有走滑和正断层性质。但也有不同的认识,如Allmann和Shearer(2009)利用1990—2007年约2 000次mb≥5.5的地震研究全球的应力降变化,通过确定每个地震的矩张量,在-1(正断层)—0(走滑断层)—1(逆断层)的范围内研究应力降与震源机制解的相关性,结果表明应力降中值与震源机制解有明显依赖,其中走滑地震显示出最高应力降中值(约10 MPa),而正断层和逆断层地震具有较低的应力降中值(约2~3 MPa),其结果如图4所示。
图4 应力降与震源机制的变化关系(修改自Allmann和Shearer,2009)
Fig.4 The relationship between stress drop and the source mechanism(modified from Allmann and Shearer,2009)
除断层类型外,断层的其他参数也可能导致应力降的局部变化,如平均构造滑移率、主要岩石的矿物学组成等。Goebel等(2015)分析了美国加利福尼亚南部San Gorgonio地区小震级地震的震源参数,指出由于San Andreas断层系统的作用导致该区域发生地壳变形、以及沿众多走滑和逆冲断层的不均匀滑动,中小地震应力降沿San Gorgonio山口的较高、远离San Gorgonio山口较低,表现出与地质滑动速率近负相关的变化特征。Goebel等(2018)的研究表明应力场的非均匀性和应变局部变化对应力降的影响很大,更局部化的断层和均匀的应力场有利于形成较低的应力降,在分析了2000—2014年6 000多个地震事件的应力降后,指出San Gorgonio Pass区域内局部断层段上较低的加载速率会导致较高的应力降值,而Ventura盆地内较高的加载速率则可能导致较低的应力降值。
也有研究指出应力降与断层性质、主震滑移间没有明显关系。如Zhang等(2022)利用高分辨率钻孔网络数据,基于频谱分解和改进的叠加方法,估算了2001—2016年美国加利福尼亚州Parkfield地区San Andreas断层上4 551次地震(0≤M≤4.0)的应力降,指出高频钻孔记录获得的地震应力降在时间上变化较小,在空间上表现为复杂而稳定的空间分布特征,表明局部介质特性可能控制应力降的空间各向异性,而断层滑动的性质、2004年6.0级主震的滑移对应力降没有产生明显影响。
Abercrombie等(2021)综合分析了美国加利福尼亚州、内华达州、堪萨斯州和俄克拉何马州12项研究中50 000多次0≤M≤5地震的震源谱值,探讨应力降与震源深度的相关性。研究表明,在所有震级地震中,频谱中的高频分量都会随地震震源深度的增加而系统性增加,在未对震源深度相关的衰减进行校正的情况下,应力降、破裂速度都会随震源深度增加而系统性增加; 当增加经验的、依赖于震源深度的衰减校正后,应力降对震源深度的依赖性会系统性降低。因此,无论是在频域还是时域,对于应力降的分析都应考虑震源深度的影响。
一些研究认为应力降与震源深度的依赖性可能与浅层地壳中剪切波的速度变化相关(Allmann,Shearer,2007),也可能与俯冲带内部的刚度变化相关(Bilek,Lay,1998)。Allmann和Shearer(2009)研究了全球范围内的应力降值,发现应力降中值随震源深度的变化不大。但在对比不同区域结果时,发现某些区域的应力降中值随震源深度增加而显著增大(如东南亚的爪哇俯冲带)。Hardebeck和Aron(2009)研究了美国旧金山湾东部钻孔记录1.0≤M≤4.2地震的应力降,发现应力降随震源深度的增加而增大,其中1~7 km深度的应力降中值约为5 MPa,7~13 km深度的压力降中值约为10 MPa,而13 km以上深度的压力降中值约为50 MPa。
Uchide 等(2014)研究了2011年日本Tohoku-oki地震前的3.0≤MW≤4.5小地震的应力降值,指出在30~60 km的震源深度内应力降随震源深度明显增加,但更浅和更深地震的应力降则并没有表现出与震源深度的明显相关性。Trugman(2020)研究了2000—2019年发生在美国加利福尼亚州Ridgecrest地区的地震序列,约11 000个的数据结果表明该区域的地震应力降随震源深度的增加大致呈对数增长关系。Yenier和 Atkinson(2015a,b)在美国西部和中东部的两项研究表明,当震源深度较浅时,应力降随震源深度成正相关,但超过一定深度后应力降与震源深度的变化无明显相关性,但在震级较大的地震中,应力降随震源深度增加的趋势会减弱。
对于应力降与热流之间的相关性,一些学者也开展了研究。从理论上看,热流越高,摩擦力越小。但Caporali等(2011)对意大利地区静态应力降的研究表明,只有2个区域内应力降与热流表现出相关性,其他研究区并没有得到验证。而Oth(2013)对1996—2011年日本3 964次2.7≤MW≤7.9地震应力降变化的研究表明,日本地壳内的地震应力降与热流之间具有显著相关性,本州地区的低应力降与高热流区具有较好的空间相关性,九州地区的平均应力降虽然较高,但其横向变化与热流变化之间也存在关联。Goebel(2013)计算了美国南加州60 000多次地震的应力降,发现应力降与热流相关,热流区会导致系统性的应力降低值。Hauksson(2015)分析了美国南加州约60 000次地震的应力降值,认为热流控制着应力降的变化,在中低热流区内,应力降随热流的增加而增加,相反的,在薄地壳中的高热流下,应力降则随着热流的增加而系统地减小。
由拐角频率计算得到的应力降往往是单次地震的平均应力降值,不能很好地反映地震滑动断层面上的应力变化分布。对频谱拐角频率的分析主要针对中小地震,在地震谱估算应力降的计算过程中也存在许多假设,如破裂区形状和平均破裂速度,所以也难以对不同的研究进行比较(Allmann,Shearer,2009)。对于这些问题,近年来也有学者提出改进方法。
GNSS、InSAR等高分辨率空间测量技术可以较为精确地记录到同震位错/位移量,并应用于位错模型的反演(Ji et al,2004; 张勇等,2008; 刘刚等,2015),进而计算断层面上的应力精细变化。
窦甜甜等(2021)利用地震学和大地测量数据等反演得到震源位错模型,提出从弹性力学角度计算断层面上的地震应力降分布,并将该方法应用于2004年Parkfield MW6.0地震应力降的计算。其物理原理是根据地震发生时地震波频谱或断层破裂产生的形变和位移来估算地震释放的应力,从而计算地震发生前后断层面上平均剪应力的变化。该方法的理论依据是从力学角度出发,基于Okada(1992)给出的半无限空间各向同性均匀介质中位错引起的地表和地球内部位移场及应变场的表达式,计算断层错动所引起的断层面上的剪应力变化。其计算过程首先是根据位错模型在断层走向和深度方向上划分出密集网格; 再采用Sato等(1972)半无限空间解析解程序得到每个网格节点的剪应力变化值,选取靠近断层的包络面上的应力变化来近似表示滑动断层上的结果,分别计算沿断层面上每个子断层错动对所有网格的影响; 最后将这些影响叠加,得到整个断层面上的应力变化分布。
对于5级以上的地震,破裂通常发生在非圆形断层区域并具有非均匀的滑动,不满足Brune(1970)圆盘模型的假设条件,因此需采用不同的滑动模型。Causse等(2013)计算了21次5.7≤MW≤7.7大地震、31个滑动模型下的平均应力降值,指出有限元破裂模型可为研究应力降空间分布提供重要信息,其计算偏差远小于应力降的平均偏差。Shao等(2012)引入“加权平均应力降”来减少在选择有效断层区时的不确定性:均匀破裂条件下,加权平均应力降与断层表面某一区域的平均应力降相等; 当非均匀破裂时,由于应力分布与滑动分布相关,具有高同震滑动的断层区通常也是高应力降地震事件的分布区,则加权平均应力降大于断层表面的平均应力降(Shao et al,2012; Noda,2013)。
使用加权平均应力降有两个优势:首先它是断层滑动参数的函数,对凹凸体的应力更为敏感,而凹凸体通常也是可能产生较大滑移量的区域; 其次它相当于视可用能量与地震潜在能量之比的2倍,对于分析地震释放能量具有重要意义(Shao et al,2012; Noda,2013),因此加权平均应力降也被称为基于能量的平均同震应力降(Noda,2013)。
同震应力降可以通过有限断层滑动模型来反演(Causse,2013),但常规的有限断层反演方法不能直接估算出断层上的应力变化。Adams等(2016)开发了非线性有限断层反演程序,在平均应力降接近预定值(即目标应力降)的情况下,搜索与地震观测数据和/或大地测量数据相匹配的解,将基于能量的平均同震应力降的不确定性与合成地震波形和观测地震波形之间的不匹配直接联系起来,并使用不同的目标应力降进行反演以获得最优解。Adams等(2016)将该方法应用于2014年Rat Islands MW7.9地震的应力降计算。
研究表明,大震前后的应力降变化与地震活动的强弱有关(Chinnery,1964; Richardson et al,1979; Baltay et al,2011),一些研究认为震后余震的应力降比大地震发生前的地震应力降大,另一些研究则指出余震的应力降会随时间或其他因素而发生变化。
华卫等(2009)研究指出,在汶川地震序列1 070次ML≥3.0地震的地震矩与震级之间表现出较好的线性关系,应力降和视应力的大小与震级大小有关,汶川余震序列的应力降总体上随时间衰减,预示着主震发生后整个余震区应力降呈逐渐衰减的状态。Trugman(2020)对美国加利福尼亚州Ridgecrest地震序列的研究表明,余震应力降往往比主震前的地震应力降更高,这可能是因为余震的震源深度更深; 余震应力降的空间分布模式与M7.1主震的滑移相关,主震破裂区的西北端终止于长期的应力降低值区。Kemna等(2021)研究了意大利中部多断层破裂下地震序列的静态应力降的时空分布,包括3次MW≥5.9的地震和95 000多次0.5≤M≤6.5余震,发现大震后MW≥5.9余震的应力降值明显增加,并且发生在主震破裂区周围早期余震的应力降相对较高,这些高应力降事件也与断层的复杂程度有关。Yamada 等(2021)分析了2003—2018年日本Tohoku地区东北部1 142次4.4≤MW≤5.0地震的应力降,发现在2011年Tohoku地震期间,位于主震滑移区边缘的小地震具有较高的应力降值,表明这些区域具有较高的摩擦强度,并抑制了2011年Tohoku大地震的同震滑移; 而Tohoku地震后,一些地区的小地震的应力降开始降低,表明这些地区的摩擦强度有所下降,与丰富的余震活动比较吻合,因此可以通过小地震的应力降来监测俯冲板块的摩擦特性。
更多的研究则认为,前震和余震的应力降受控于不同的因素,如区域构造的复杂程度、主震滑移等。Dalguer等(2002)计算了2000年日本Tottori地震期间的应力降变化,指出大部分前震和余震都位于应力降的负值区,前震期间凹凸体起屏障作用、前震仅分布在断层中部与凹凸体相邻的局部区域,主震后凹凸体周围的应力增加并引发了大部分余震。Pennington等(2021)比较了美国俄克拉荷马州Prague地区MW5.7地震序列、MW4.8前震和MW4.8余震的震源参数,指出虽然不同方法计算的应力降绝对值差异较大,但其时空变化模式则趋于一致,并且余震应力降受控于断层方向和距主震滑移面的距离,其中断层方向会影响沿断层分布的地震应力降,最大主震引起的滑动也会影响随后发生的地震应力降。Ruhl 等(2021)研究了美国Mogul地区4 373次地震应力降,表明具有最高应力降值的前震事件发生在主震的破裂带内,并在地震活动空隙边缘成核、集中在断裂带的复杂区域附近(即走向/倾角变化); 前震和余震活动期间,低应力降区没有发生变化,意味着应力降受控于固有的单个断层性质以及同震和/或地震滑移的潜在区域(即地震活动空隙),而不受余震序列时空变化的影响; 在前震序列的扩散阶段,应力降随着与主震断裂起始点距离的增加而增加; 断层外余震的平均应力降明显低于主震断裂带沿线的余震应力降。
也有研究指出,应力降与余震数量之间也存在相关性。Wetzler 等(2016)研究了过去25年环太平洋大型逆冲区内MW≥7.0地震的余震序列及其震源参数变化指出:高应力降的逆冲型地震所产生的余震数量,小于同等震级下的低应力降事件的余震数; 而在相似的同震破裂面积下,余震数则随着应力降和辐射能量的增加而增加,表明震源破裂过程对余震数有显著影响。
吴微微等(2015,2017)和Wu等(2020,2023)分别以次级块体、交会断裂、特殊震源区和强震影响区为研究对象,分析了不同断裂形态和复杂断裂交会背景下的地震危险性,形成综合测震学参数和断裂构造形态的震情跟踪思路。其研究指出,在不同的构造单元上断裂形态和应力分配具有不同的特征,特别是在四川三岔口地区(鲜水河断裂、龙门山断裂与安宁河断裂的交会区),相同震级的地震,其震源应力降表现出沿鲜水河断裂向安宁河断裂逐渐增大的趋势,这也许表明着安宁河断裂上石棉以北附近现今正处于相对高的应力积累。
2009—2013年,与非常规油气开采相关的诱发地震导致美国中东部的地震活动率显著增加(Ellsworth,2013)。这些地震被认为是由地下孔隙弹性压力变化所导致,其成核过程可能是受废水处理、强化地热刺激或者水力压裂的作用。一般来说,诱发地震被认为是由构造应力驱动的,其发生时间因流体注入而提前(Huang et al,2017)。由于震源深度较浅,诱发事件的地震危险性更为显著。为了建立诱发地震事件的震级预测关系,识别诱发地震与构造地震之间的物理差异或相似性,Dahm等(2012)提出3种方法:基于物理的概率模型、基于统计的地震活动模型和震源参数方法。
研究表明应力降等震源参数可能为诱发地震研究提供直接证据(Chen,Shearer,2011; Goertz-Allmann et al,2011; Sumy et al,2017)。对于诱发地震的应力降值,一种观点认为诱发地震产生的应力降比天然地震低。Hough等(2014)研究了美国地质调查局的地面观测数据,发现根据地面震动强度估计的震级比观测报告给出的仪器震级低0.4~1.3个震级单位,认为这是由较低的应力降或震源附近的低品质因子Q值造成的,并指出美国中部和东部诱发地震的应力降比同一地区的构造事件低2~10倍。Hough等(2016)对比美国中东部诱发地震的应力降与加利福尼亚州构造地震的应力降也得到类似的结论。Boyd等(2017)用谱比法估算了美国各地区的震源参数,获得了60个震群1 121次3级以上地震的应力降值,发现美国中部潜在诱发地震的应力降比西部构造地震低2倍、比东部构造地震低6倍,这些诱发地震的震源深度往往较浅,并伴随有数量较多的前震。与深部构造事件相比,在相同的震动频率和震级下,浅层诱发地震可能会增加震中10 km范围内的地面震动强度和地震风险,但其较低的应力降值也在一定程度上降低了诱发地震及其余震产生的高频震动危险。Sumy等(2017)使用标准Brune震源谱模型计算了2011年Prague MW5.7地震余震序列的震源特性,计算了87次MW1.83~3.51地震的地震矩和拐角频率,结果表明:应力降范围在0.005~4.8 MPa,中值为0.2 MPa,比美国东部典型的板内地震应力降(>10 MPa)低一个数量级,应力降随地震矩增大而增大,与震源深度、震级具有微弱的相关性,与注水井距离没有明显关联。
然而并非所有研究都认为诱发地震的应力降较低。诱发地震具有不同的类型和性质,除废水回注外,采矿、爆破、人为作业后的塌陷都可能引起地震活动,如孤立型中强震、时空丛集的浅源地震、慢地震和慢滑移事件、持续时间较长的弱地震活动以及发震模式和余震特征发生显著变化的地震事件等(Dahm et al,2012)。一些研究表明,水库和采矿诱发事件的应力降与天然地震类似,与水力压裂有关的诱发地震的应力降也被认为与构造地震相近。Goertz-Allmann等(2011)分析了瑞士地热现场1 000次诱发地震的应力降变化,观察到MW0~3.0地震的应力降范围为0.1~100 MPa,与震级的关联性不大,但与孔隙压力扰动最大的地区与注入点的距离显著相关。Clerc等(2016)使用谱比方法计算加拿大Crooked Lake附近诱发地震的静态应力降,其中MW3.0~4.0地震的应力降在11~93 MPa,与加拿大其他区域构造地震相近,与震级、深度、注水井距离没有明显关联。Ruhl等(2017)估算了美国内华达州Mogul地区148次震源深度小于6 km的浅层地震的应力降值,发现应力降沿主震断层面的时空变化较为明显,这些浅层的、可能受控于流体驱动作用的地震事件,其应力降值并没有系统性的低于构造地震的应力降值(4 MPa)。Wu等(2018)计算了俄克拉荷马州4个注水诱发地震序列中201次地震的转角频率和应力降,发现3次MW>5的主震应力降较高,每个序列中大多数前震和余震的应力降值较低,应力降与深度、时间的没有明显关联性。
还有一些观点认为应力降与他因素有关。如注水引起的流体压力变化导致有效正应力变化(Goertz-Allmann et al,2011; Lenglin et al,2014; Moyer et al,2018); 由于孔隙压力的扰动,应力降也存在随距注水井的距离增加而增大的现象(Kwiatek et al,2014; Yu et al,2020)。
火山系统中的地震活动和地表变形可以反映与火山活动有关的地球物理变化,研究火山区的应力降变化有助于了解火山喷发各个时期物理过程的变化。喷发前,伴随着岩浆上升,火山口内外岩浆和热液流体加压,火山口发生膨胀,可能导致应力集中和地壳孔隙压力扰动(Cabanis et al,2020; Sparks,2003)。在喷发期间,岩浆下降,火山口的收缩可能会打开裂缝并改变地壳的力学性质(Brenguier et al,2016; Donaldson et al,2017)。这些过程表明,火山喷发的循环过程会驱动地壳形状和强度发生变化(Carrier et al,2015; Lamb et al,2017)。因此,通过监测火山口变形过程中的应力降值可以分析喷发行为对断裂带条件和地壳强度的影响,进而了解火山所处的周期阶段(Harringto et al,2015)。
1999年10月9日,意大利那不勒斯附近的维苏威火山中央锥下发生了3.6级地震。该地震是自该火山上一次喷发(1944年)以来发生的最高震级地震。Del Pezzo 等(2004)利用震前29年至震后2年的地震数据反演了地震震源谱,并指出应力降的最值取决于地震事件的震源深度和震级大小。应力降值最高(高达100 MPa)的地震事件也是有记录以来震级最大的地震,发生在火山下方2.3 km深处的碳酸盐基底顶部附近,也是有记录以来震源深度最深的事件; 应力降值较低(最低为0.1 MPa)的地震,其震源深度较浅,且发生在火山内部。
Oth(2013)研究了1996年5月至2011年10月在日本各地发生的3 964次2.7≤MW≤7.9地震的应力降变化,包括12个特定主要序列的事件,统一处理后的数据集对日本群岛的横向应力释放进行了稳健量化。结果表明,日本本州地区的低应力降集中发生在第四纪火山附近,火山活动导致的地壳温度升高和流体的存在可能增加了孔隙流体压力,从而降低了有效正应力。
Moyer等(2020)使用海底地震数据和经验格林函数谱比法获得了火山口环形断层上、与海底火山喷发相关的423次1.6≤MW≤3.6地震的应力降。位于火山口内和沿火山口布设的海底地震仪很好地记录了2015年4月至5月胡安·德富卡洋脊上水下火山喷发期间的地震活动。研究发现,火山喷发前的膨胀期的应力降均值(6.4 MPa)比火山喷发后的释放期的应力降均值(3.2 MPa)高2倍,推测应力降下降一方面是由于火山喷发会导致地壳强度降低所导致,另一方面可能与火山口岩石的普遍破裂相关。
在地震工程领域,强震动是造成建筑结构破坏的重要原因,强震动时间序列研究可以为抗震设防、大型建筑物非线性分析、灾害损失评估等提供理论依据。目前人工合成地震主要有确定性方法、随机方法和宽频带混合模拟法等(Wang et al,2015),其中随机方法中的随机有限断层模拟方法在计算地震动时,可以从应力降求得重要参数拐角频率。
随机有限断层模型是以随机点源模型为基础,随机点源模型最早由Boore(1983,2003)提出。这种方法将震源看作1个点源,将震源谱E、路径传递函数P、场地传递函数G以及地震动转换函数I的乘积作为一个场地的地震动响应谱,即:
Y(M0, R, f)=E(M0, f)·P(R, f)·G(f)·I(f)(13)
式中:M0为地震矩; f为频率; R为震中距。
根据Brune(1970,1971)的震源模型,震源谱可以表示为:
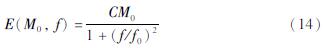
式中:C为比例系数,与频率无关; f0为拐角频率,表示为:

式中:β为震源附近的剪切波速。由上述推导关系可见,应力降在点源随机地震动模拟方面是重要的输入参数。
由于点源模型没有考虑断层的几何形状和尺度,所以不适用于大震近场地震动的模拟。Beresnev和Atkinson(1997,1998)基于点源模型建立了基于静力学拐角频率的随机有限断层模型,该方法将断层破裂面分解为有限个子断层(Hartzell,1978),并将每个子断层视为点源进行模拟,并将得到的加速度时间序列按照一定的时间延迟在时域中叠加形成,由于模型中每个子源需要多次破裂才能保证整个地震的地震矩能量守恒,所以模型高度依赖子断层的大小,对中小地震的模拟效果较差。Motazedian和Atkinson(2005)为了弥补静力学拐角频率不能合成近场地震动的缺陷,对有限断层模型进行了改造,建立了动力学拐角频率的概念,其表达式为:
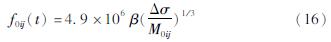
式中:f0ij为表示第ij个子断层的拐角频率; M0ij表示第ij个子断层产生的地震矩。动力学拐角频率认为每个子单元的拐角频率各不相同,且会随破裂面的延伸而逐渐减小,动力学拐角频率的最小值为静力学拐角频率。这种方法也更符合地震动的特性。之后,Boorn(2009)对随机有限断层法做了进一步的改进,使其发展为近场地震动模拟中最常用的方法,也是目前最有效的方法之一。Dang等(2020)进一步改进了拐角频率的计算方法,将断层破裂速度参数代替了剪切波速度参数,并计算了2017年九寨沟MS7.0地震后的地震动。
通过对震源特性的分析也能深入了解地震破裂过程及其与活动断裂带的地球物理和应力特征的关系。地震应力降的可变性也是地震危险性评估的基本问题,这是因为观测到的高频振动强度被认为是与应力降呈正相关的(Hanks,McGuire,1981; Boore,1983)。Trugman和Shearer(2018)认为5级以上地震的地震动中值受动态震源参数的控制(如Brune模型下的应力降值),通过研究2002—2016年旧金山湾地区5 297次地震的峰值地面加速度(PGA)和动态应力降之间的关系,发现每个事件的PGA误差与动态应力降之间存在随震级增加而增大的明显相关性,并且主震的应力降和PGA高于同等震级的余震事件。Baltay等(2019)利用中强地震的动态破裂模型研究了断裂能量和应力降之间的标度特性,发现断层平均应力降随地震烈度的增加而增加,断层平均(或最大)破裂随着震级的增加而增大,并指出破裂能量与应力强度因子的比例似乎对地震破裂是否扩展至地表很敏感,表明随着破裂扩展并到达地表,大地震消耗更多的破裂能量。
在特殊的研究区域,也有不同的认识。Wu等(2018)对美国俄克拉何马州诱发地震的研究指出,该区域较强的断层非均匀性和地下流体的影响造成应力降在空间分布上的巨大差异,这种变化不支持在地震动预测模型中使用低应力降来评估美国中东部诱发地震的地震危险性。
目前地震应力降已在天然地震、诱发地震、火山地震、地震动模拟等领域得到了重要的应用。地震应力降作为重要的震源参数,可以反映发生地震的断层性质,直接关系到强地面运动和震源物理学中的基本问题。同时,由于多种复杂因素的影响,应力降的测量也具有挑战性,特别是对于小地震,由于介质特性变化、数据限制、统计样本以及计算方法差异等因素的影响,应力降估计可能包含很多不确定性,不同的研究可以获得相同地震的不同应力降值,导致不同的解释。研究表明,通过对数据限制(例如频率带宽)和介质特性的适当矫正,可以减少应力降估算中的离散性,并降低其对深度、震级等的依赖。在讨论应力降结果时,仍然建议使用大量地震进行多种方法的交叉验证,并对不同构造区、不同的地震序列进行分别讨论。