基金项目:国家自然科学基金(41972251).
第一作者简介:刘 伟(1998-),硕士研究生在读,主要从事地下水对气压和固体潮的响应研究.E-mail:1635474420@qq.com.
通信作者简介:史浙明(1988-),教授,主要从事地下水方面的研究.E-mail:szm@cugb.edu.cn.
(1.中国地质大学(北京)水资源与环境学院,北京 100083; 2.山东省国土空间生态修复中心,山东 济南 250014)
(1.School of Water Resources and Environment,China University of Geosciences,Beijing 100083,China)(2.Shandong Land and Space Ecological Restoration Center,Jinan 250014,Shandong,China)
stress field; the grid-trial method; the grid-search method; confidence interval; Hunan region
DOI: 10.20015/j.cnki.ISSN1000-0666.2024.0010
地下水位的动态变化研究对于准确获取地下水流动特性、提高水资源的评估利用效率和识别近地表污染物迁移规律等方面具有重要的意义。具有周期性变化的自然应力,如气压、固体潮和地震波等,作用于井孔和含水层,会导致井水位产生相应的动态变化(张昭栋等,1988,1989)。大量的观测表明,大多数井孔均可记录到大气压力所引起的地下水位波动(张昭栋等,1986),虽然波动幅度较小,但若未考虑气压变化的影响,将可能导致在估计地下水力梯度的大小和方向时产生错误,也可能会掩盖降雨、地震等自然现象引起的应力变化,尤其是在抽水试验后期,气压变化对水位的影响更是不容忽视的(Rasmussen,Crawford,1997; Spane,2002; Toll,Rasmussen,2007)。因此,地下水位的气压效应在探究地下水的运动规律,识别地壳中的应力、应变信息时发挥着积极的作用。
为了描述井水位变化与气压变化之间的定量关系,Jacob(1940)最早提出了气压效率(Barometric Efficiency,BE)的概念,表示为单位气压变化所引起井水位的变化。研究表明,气压效率与含水层的孔隙度、储水系数等参数密切相关(Burbey,Zhang,2010; Acworth et al,2017; Rau et al,2022),基于气压效率可以探索有利于地震前兆信号识别的方法(殷积涛,汪成民,1988)。气压效率是进行地下水位对气压响应校正的关键参数,准确获取气压效率对于提高地下水位观测精度具有重要意义(Cook et al,2017; Turnadge et al,2019)。因此,研究气压效率的计算方法及其时间演化特征是地震地下流体研究工作中重要的一环。前人对气压效率的计算方法进行了大量的讨论和研究,目前常用的有时域法(Clark,1967; Rasmussen,Crawford,1997; Rahi,2010)、频域法(Rojstaczer,1988; Quilty,Roeloffs,1991; Acworth,Brain,2008; Acworth et al,2016)及图像法(Gonthier,2007)等。然而,不同的计算方法往往具有不同的适用条件和已知量,且计算的结果也可能存在一定的差异。所以,综合对比各种计算方法的特点和适用性对于合理选择气压效率计算方法具有重要意义。
本文选取云南高大井为研究对象,对比了4种方法计算的气压效率BE值,并分析了这些计算方法的差异性以及优缺点,以期为判断含水层相对承压性、井水位影响因素的校正、识别非饱和带的气动扩散以及探测地震地下水前兆信息等方面提供参考。
地下水位由大气压力扰动而产生的变化被称为地下水位的气压效应(Jacob,1940)。对于承压含水层而言(图1),空气中的气压P0同时作用于承压含水层的井孔和周围的地面上。当气压变化时,由于井孔与大气相通,气压的变化值ΔP0全部作用于井孔内的水体,井孔内的水位会瞬间出现变化。而气压变化ΔP0通过承压层瞬时传递到承压层和含水层之间的界面,该作用力一部分由含水层孔隙压力ΔP承担,另一部分由含水层固体骨架的有效应力Δσ承担。从而导致井孔内的水和含水层孔隙水之间产生了压力差(ΔP1=ΔP0-ΔP),这种压力差的变化将导致井内水位的波动(Weeks,1979)。当气压升高时,井水流入含水层,水位降低; 而当气压降低时,含水层中的水流出井,水位升高,即井水位的变化与气压的变化呈负相关的关系。
图1 承压含水层井孔气压效应示意图
Fig.1 Schematic diagram of the wellbore barometric pressure effect in the confined aquifer
传统意义上,用水位变化与气压变化的比值来描述水位和气压之间的关系,即气压效率,可表示为(Rasmussen,Crawford,1997):
BE=-(ΔW)/(ΔB)(1)
式中:ΔW为气压作用下的水位变化量(单位:mm); ΔB为气压的变化量(为方便计算,气压单位转化为等效水柱高度,单位:mm)。BE值是衡量井水位气压效应的一个重要指标,范围在0~1,其值越大,表明气压作用于地下水位的效果越显著; 反之,则越弱。
气压引起地下水动态变化的机理十分复杂,BE值还会受到井水位观测方式、含水层岩性、含水层埋藏深度等因素的影响。并且BE值不是一个恒定的常量,其数值会随着气压的周期性改变而改变,采用不同计算方法得到的BE值也会有所不同(车用太等,1990)。
本文选取位于云南省玉溪市通海县高大乡的地震地下水观测井为研究对象。该井成井日期为1999年6月,井深201.4 m,观测段深度为166~194 m,属于承压井,其岩性及钻孔结构如图2所示。高大井为静水位观测井,水位观测始于2001年6月,选用LN-3数字式水位仪,分辨率为1 mm,采样率为1 min,观测环境无明显干扰。辅助项气压观测始于2011年12月,记录的水位和气压数据连续性较好,有利于进行井水位气压效应的分析。
本文收集了2019年2月1日至2020年7月28日高大井水位(指水位埋深)与气压的分钟值数据,其时间序列如图3所示。从图3a可以看出,井水位有着明显的波峰波谷的动态变化特征,并且在1 d内出现了两次波峰和波谷,但总体年际变化规律呈下降趋势,说明井水位还可能受到降水、气候等长期因素的影响。所以,在分析井水位的气压效应时需要去除其它因素如趋势性成分、固体潮效应等的影响。
从2019年5月3—4日高大井的水位埋深和气压变化关系图(图4)可以看出,该井具有明显的气压效应现象。井水位对气压的响应有以下2个特征:①井水位波动与气压波动的方向基本相反,即气压升高,实际井水位降低; 气压降低,实际井水位升高。②井水位变化滞后于气压变化,且滞后时间不固定,大约在30~210 min。
图3 2019年2月—2020年7月高大井水位(a)和气压(b)时间序列图
Fig.3 Time series of water level(a)and barometric pressure(b)in Gaoda Well from February 2019 to July 2020
针对高大井的水位和气压数据,本文选择Clark方法、Rahi方法、回归反卷积法、Acworth方法计算其气压效率,并对不同方法和计算结果进行对比分析。
Clark(1967)利用观测到的气压变化Δb和水位变化Δh,以恒定的时间增量来确定气压效率BE值。如对于相同时间序列的气压和水位数据,从时间ti-1到ti,对大气压力的变化值(Δbi)和水位的变化值(Δhi)进行逐步累加:
Δbi=bi-bi-1(2)
Δhi=hi-hi-1(3)
index=Δbi·Δhi(4)
式中:bi和hi为ti时刻的气压和水位; bi-1和hi-1为ti-1时刻的气压和水位; index为ti时刻气压变化值Δbi和水位变化值Δhi的乘积。
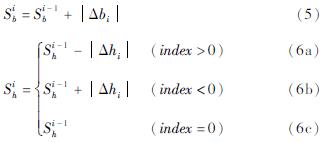
式中:Sib和Sih为ti时刻的气压变化之和和水位变化之和; Si-1b和Si-1h为ti-1时刻的气压变化之和和水位变化之和。
气压效率表示为:

式中:Snb为气压变化总和,即∑Δb; Snh为水位变化总和,即∑Δh。
由式(2)~(4)可知,当气压或者水位上升时,Clark方法将其中一个赋值为正的符号,并且有如下的规则:①当Δbi=0时,ti时刻的∑Δh等于ti-1时刻的∑Δh(式6c); ②当Δbi和Δhi符号相反时,ti时刻的∑Δh等于ti-1时刻的∑Δh加上Δhi的绝对值(式6b); ③当Δbi和Δhi符号相同时,ti时刻的∑Δh等于ti-1时刻的∑Δh减去Δhi的绝对值(式6a); ④∑Δb为所有Δb的绝对值之和(式5)。上述4条规则是为了将大气压力与其它引起水位变化的因素分开。因此,在利用Clark方法计算时,首先将气压与水位数据按照公式(2)(3)求得气压变化值Δb和水位变化值Δh,并判断Δb和Δh的符号(式4),然后根据符号的正负对气压变化值和水位变化值分别进行累加(式5~6),随着时刻ti的增加重复上述步骤(式2~6),即可得到气压变化总和Snb和水位变化总和Snh,然后作二者的散点图进行回归分析,所得的回归线的斜率即为气压效率BE。
本文选取2019年2月1日至2020年7月28日高大井采样率为1 h的气压与水位数据,对其去除线性趋势后使用Clark方法计算,得到气压变化量之和以及水位变化量之和,结果如图5a所示。从图中可见,使用Clark方法计算得到的高大井的BE值为0.439 5。Snb和Snh的散点在回归线的周围波动,表明气压效率不是一个常数,而是一个随时间不断变化的值。因此,截取不同时段的气压和水位数据进行计算并取平均值能够提高结果的准确性,同时也可获取气压效率BE值的变化情况。
由于Clark方法不能有效地消除固体潮效应的影响,会导致气压效率的高估、低估甚至产生负值问题(Hsieh et al,1987; Hobbs,Fourie,2000; Merritt,2004),因此,Rahi(2010)提出了一种新的计算方法,即调整了水位变化总和∑Δha和气压变化总和∑Δba的计算方法,规则如下:①当Δbi和Δhi符号相反且|Δhi|<|Δbi|时,|Δbi|和ti-1时刻的∑Δba相加得到ti时刻的∑Δba(式8a),|Δhi|和ti-1时刻的∑Δha相加得到ti时刻的∑Δha(式9a); ②当不满足条件①时,Δb和Δh不计入各自的总和(式8b、9b)。
从时间步长(ti)开始,根据公式(2)~(4)计算气压(bi)和水位(hi)的变化值并按照以下方法调整了气压和水位变化的总和:
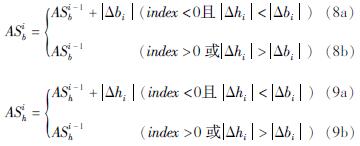
式中:ASib和ASih为ti时刻的气压变化之和和水位变化之和; ASi-1b和ASi-1h为ti-1时刻的气压变化之和和水位变化之和。
气压效率表示为:
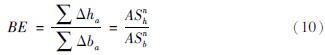
式中:ASnb为气压变化总和,即∑Δba; ASnh为水位变化总和,即∑Δha。
Rahi方法与Clark方法的不同之处在于,将水位数据添加到总和∑Δha之前对其进行了2次测试。第一次为符号测试,第二次是当数据点符合符号测试时,它将接受幅值测试(式9a)。Rahi方法使用与水位数据相同的滤波方法来处理气压数据(式8a),而Clark方法仅使用符号测试(式6)来处理数据。Rahi(2010)指出,Clark方法设计的目的是添加与潮汐相关的任何水位变化,这些变化与气压波动同相,并且该方法减去与大气压力变化不同相的潮汐引起的水位变化。其中与气压相关的S2和K1潮汐分量大部分时间与大气压力变化同相,而与固体潮相关的M2和O1潮汐分量则在同相和异相之间连续交替。Clark(1967)也指出,∑Δh与∑Δb的关系图并不总是一条直线,当非大气压力因素引起的水位波动与大气压力同相时,水位波动将得到增强; 而当它们异相时,水位波动就会被舍弃。因此,Clark方法计算气压效率时可能会高估、低估甚至产生负值,这取决于主导因素:同相或异相。
同样使用Rahi方法对高大井去除线性趋势后的水位和气压数据进行计算得到一系列水位变化总和∑Δha和气压变化总和∑Δba,并进行回归分析,得到高大井的BE值为0.496 8,如图5b所示。
本文通过Clark方法计算的BE值小于Rahi方法计算的结果,说明在该计算时间段内,高大井大部分时间内引起水位波动的潮汐变化与大气压力变化异相,使得Clark方法低估了BE值。
许多研究表明,由于非饱和带的厚度以及气体扩散的影响,气压作用于地面时会导致井内水位的变化滞后于气压的变化。对于这种气压响应的滞后效应,Rasmussen和Crawford(1997)提出可以利用气压响应函数(Barometric Response Function,BRF)来描述井水位气压响应随时间的变化,主要利用回归反卷积的方法估算井中气压变化和水位变化之间的滞后响应,其回归方程为:
H(t)=β0+β1t+Δμ0B(t)+Δμ1B(t-1)+…+ΔμnB(t-n)(11)
式中:H(t)为时间步长t的总水位; β0为回归截距; β1为线性趋势系数; Δμi为拟合气压响应系数; B(t-i)为滞后0~n时观测到的气压; n为最大时滞。
气压效率可以表示为水位随时间对气压阶跃变化的响应,即自施加荷载以来时间的函数。若不考虑降雨、蒸散发等其它因素,气压响应函数(BRF)可用以下卷积的方式来表示(Butler et al,2011):
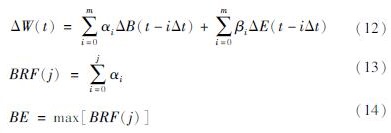
式中:ΔW(t)为去除线性趋势后t时的水位变化值; i为滞后时间; m为最大滞后时间; αi和βi为滞后i时的大气压力和固体潮的单位脉冲; ΔB(t-iΔt)为(t-iΔt)时的气压变化值; ΔE(t-iΔt)为(t-iΔt)时的固体潮变化值; j为观测时间。
利用回归反卷积的方法可以去除固体潮效应对井水位的影响。通过对井水位和气压波动之间的函数进行拟合,可获得高大井在采样间隔为1 min时的气压响应函数(图6)。从图6可知,高大井的初始响应的气压效率BE值为0.024 2,长期响应的最大BE值为0.617 4,对应的滞后时间为3.58 h。因此,利用回归反卷积法估算得到高大井的BE值为0.617 4。从图6还可以发现,其气压响应随着滞后时间不断增大且逐渐达到稳定,表现出延迟响应,据此可以判断高大井所在的含水层为承压含水层(Rasmussen,Crawford,1997)。
Acworth和Brain(2008)采用傅立叶变换的方法对水位、气压和潮汐数据进行频域分析,得到潮汐分量K1、M2和S2波的振幅值,然后根据K1或S2潮汐分量的振幅比来估计气压效率。本文定义地下水(水位)为GW,固体潮为ET,大气压为AT。
Acworth和Brain(2008)的方法基于以下原理:在地下水位信号中频率为1.932 4 cpd(MET2)的信号,只受固体潮影响; 在地下水位中频率为2 cpd(SGW2)的信号同时包含了固体潮和气压的作用。为了将这2个因素从SGW2中分离开来,认为固体潮的SET2/MET2的比值是一个常数,由于MGW2不会受到气压信号的干扰,因此可以将MGW2乘以SET2/MET2来预测SGW2中的固体潮分量。然而,Acworth和Brain(2008)的方法忽略了当2个相同频率的谐波信号叠加时产生振幅和相位与原来的谐波不同的新谐波(谐波加法定理),如2 cpd的固体潮SET2和大气潮SAT2(各个分量说明见表1)。也就是说,具有相同频率但振幅和相位不同的驱动因素共同作用时,引起可预测的振幅和相位的地下水波动信号。
Acworth等(2016)为了准确量化固体潮分量对地下水位的影响,并准确校正固体潮汐信号中的SET2分量,提出了利用大气波动信号中的SAT2和固体潮汐信号中的MET2之间的相位差进行固体潮振幅的校正,气压效率的计算公式为:
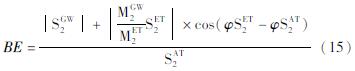
式中:S2波和M2波的振幅以及相位均可以通过快速傅立叶变换得到。
将高大井水位、气压和Tsoft程序计算得到的理论固体潮数据进行快速傅立叶变换,可得到其水位、气压和理论固体潮的频谱图(图7)。从图中可以得到水位(GW)、气压(AT)、理论固体潮(ET)的S2波和M2波的振幅值,SET2和SAT2的相位则可以通过计算对应复数的幅角得到。使用Acworth方法计算得到的各个分量结果见表1,最终可得高大井的气压效率BE值为0.665 4。
本文采用4种方法计算了高大井的气压效率BE值,其中Clark方法、Rahi方法和回归反卷积法为时域方法,Acworth方法为频域方法,4种方法都具有各自的优缺点及其适用性。如Clark方法主要基于气压和水位变化值的累加来进行计算,并假定BE值是一个稳定的常数。该方法的优点是操作简单方便,但是没有考虑水位随气压变化的时间滞后,且未能消除固体潮效应等其他非大气压力因素的影响,所以可能会高估、低估甚至产生负的BE值。Rahi方法在Clark方法的基础上对水位数据进行了符号测试和幅值测试,避免了产生负BE值的问题,其优点同样是操作简单方便,缺点是没有考虑时间滞后的影响。回归反卷积法考虑了井水位随气压变化的滞后响应并且去除了固体潮效应的影响,可以清晰地获得BE值随滞后时间的变化特征。然而,该方法容易受到降水、蒸散发等信号的干扰,当含水层所在地区的降水量较多、蒸发量较大时,该方法并不适用。Acworth方法考虑了固体潮信号,通过傅立叶分析的方法考虑了气压和固体潮之间的相位差,客观量化了考虑可压缩条件下的地下水储水系数的计算。该方法的结果受水位变化的影响较小,且不会被多个相近频率的潮汐分量所干扰,是目前唯一一种避免了降水、蒸散发等信号干扰的方法。但是M2潮汐分量仅在承压和半承压含水层中才能观测到,所以该方法仅适用于承压和半承压含水层(Turnadge et al,2019)。
综上,在分析井水位气压效应时,若要快捷、方便地获取BE值及其变化情况,可以截取不同时段的气压和水位数据使用Clark方法、Rahi方法进行计算; 若要研究BE值随时间滞后的变化情况、判断含水层的承压性以及去除固体潮效应对井水位的影响,可以选择回归反卷积的方法; 若要综合考虑各种因素对井水位的影响并精确计算BE值,Acworh方法最为稳健。总之,决定使用哪种方法通常取决于方法的适用性、存在何种解释模型、数据的完整性以及数据分析者对结果的熟悉程度(Kennel,2020)。
本文对使用4种方法计算得到的BE值取平均作为高大井的最终气压效率,见表2。
本文以云南高大井为研究对象,基于4种方法计算了其气压效率BE值,并对4种方法及其计算结果进行了比较和分析,主要得到以下结论:
(1)基于Clark方法、Rahi方法、回归反卷积法及Acworth方法获得的BE值分别为0.439 5、0.496 8、0.617 4、0.665 4,平均BE值为0.554 8。
(2)对比4种方法发现:Clark方法计算简单方便,但是没有考虑时间滞后和固体潮效应的影响,且可能存在高估、低估甚至产生负BE值的问题; Rahi方法在Clark方法的基础上对水位数据进行了符号测试和幅值测试,避免了产生负BE值的问题,但没有考虑时间滞后的影响; 回归反卷积法考虑了井水位随气压变化的滞后响应,但是易受降水、蒸散发等信号的影响; Acworth方法考虑了固体潮信号并且避免了降水、蒸散发等信号的干扰,但是该方法仅适用于承压和半承压含水层中。
(3)在实际工作中,要合理选择气压效率计算方法,如使用Clark方法和Rahi方法截取不同时段的气压和水位数据可以初步快捷、方便地获取BE值及其变化情况; 使用回归反卷积的方法可以研究BE值随时间滞后的变化情况、判断含水层的承压性以及去除固体潮效应对井水位的影响; 若要综合考虑各种因素对井水位的影响并精确计算气压效率的值,Acworh方法则最为稳健。