基金项目:上海佘山地球物理国家野外科学观测研究站开放基金(SSOP202101).
第一作者简介:钱晓东(1965-),副研究员,主要从事地震预测预报工作.E-mail:qxd13@163.com.
通信作者简介:贺素歌(1987-),工程师,主要从事地震活动性和地震综合预测工作.E-mail:724198867@qq.com.
(1.云南省地震局,云南 昆明 650224; 2.上海佘山地球物理国家野外科学观测研究站,上海 200062)
(1.Yunnan Earthquake Agency,Kunming 650224,Yunnan,China)(2.Shanghai Sheshan National Geophysical Observatory, Shanghai 200062,China)
drift rate; the Bayesian estimation; mobile-gravity observation; adjustment results; Yunnan
DOI: 10.20015/j.cnki.ISSN1000-0666.2024.0015
概率增益模型最早是为综合各种前兆异常提出来的,其基本思想是,如果同时观测到几项相互独立的前兆异常,地震发生的概率将比只有单个异常时高。概率增益模型可以综合多种前兆信息,求出各前兆异常存在的条件下地震发生的概率,给出客观定量的概率值,从而对特定地区强震危险性进行定量预测。Utsu(1977)首先提出多元前兆异常概率计算公式,Aki(1981)采用贝叶斯理论也推导出了同样的公式,提出了概率增益模型,并以计算得到的概率为依据,将地震监视区分成Ⅰ~Ⅵ级报警级别,按不同级别进行加强监视、短期预报、临震预报等级别报警。之后,国内外诸多地震科技工作者从不同方面进行了概率增益模型研究和应用(Utsu,1984; Aki,1984; Kenji,Akio,1990; 金学申等,1997; 梅世蓉等,1993; 张天中等,1998,1999; 王晓青等,2000; 邱雪强,沈繁銮,2004; 蒋长胜等,2017; 邓世广等,2019; 王芃等,2019; 马永等,2021; 郑建常等,2022; 郭文峰等,2022)。目前,概率增益模型研究常用于地震的中长期预测领域,而在中短期预测方面的研究成果不多。张天中等(1998,1999)用此方法进行了地震短期预测探索,利用1998年1月10日张北M6.2地震前出现的3项异常指标,计算得到概率增益达32倍,发震概率为58%,给出的异常涵盖地震活动背景,中期、短期异常发展过程,并认为根据中短期异常来估算很高的发震概率是不现实的,重要的是要有足够的概率增益。云南是一个多震省份,具有较多的地震中短期预测实践和验证机会,在对地震时间、地点和震级三要素的预测中,目前还找不到一种能对三要素中任何单一要素进行有效预测的方法,结合长、中、短期指标的综合预测方法,是地震预测发展的基础。本文利用概率增益预测模型方法,尝试创建基于时间概率增益的云南地区及邻区强震中短期预测综合预测方法。
在多个独立地震前兆A1,A2,A3,…,An同时存在时,该区一个震级大于等于M的地震发生的概率为(Utsu,1979):
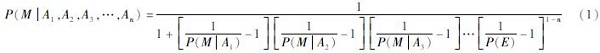
式中:P(M|A1), P(M|A2), P(M|A3),…,P(M|An)分别是地震前兆A1,A2,A3,…,An出现时发生M级以上地震的条件概率; P(E)为同一地区发生M级以上地震的无条件概率,亦称发震自然概率或背景概率。
Aki(1981)采用贝叶斯理论也导出了式(1),并且提出当P(E)及P(M|A1), P(M|A2), P(M|A3),…,P(M|An)很小时,式(1)可简化为:
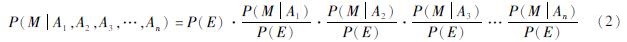
或
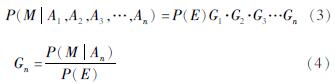
式中:Gn为各地震前兆An的概率增益,P(M)称作综合概率,也称为量化增益概率。
在一定区域内出现某些地震前兆异常时,可以求得各个地震前兆的条件概率P(M|A1), P(M|A2), P(M|A3),…,P(M|An),震级大于等于M的地震的无条件概率P(E)可由该区历史地震资料估算,进而可计算出概率增益G1,G2,…,Gn,再从式(3)求出该区在各地震前兆存在的条件下,震级大于等于M的地震发生的条件概率,以此来定量判定地震发生的可能性。
根据历史资料统计,在足够长的时期内,若地震前兆A1,A2,…,An分别出现N1,N2,…,Nn次,各地震前兆出现时分别对应地震ri次,则各个地震前兆出现时发生地震的条件概率为:
P(M|Ai)=(ri)/(Ni)(5)
式中:i为地震前兆数,i=1,2,…,n。
从式(5)可看出,各个地震前兆出现时发生地震的条件概率P(M|Ai)实际上是地震的对应率,计算时,要求每项地震前兆不能只有个别震例,要有统计意义上的认识,在没有考虑漏报的情况下,对应率越高,P(M|Ai)越大; 虚报越低,P(M|Ai)也越大。这种减少虚报、容忍漏报的特征对于预报人员是适当的(吴忠良,1998)。
若地震发生为泊松过程,地震平均发生率为v,背景概率可表示为(钱晓东等,2020):
P(E)=1-exp(-v)(6)
式中:地震发生率v=N0/T; T为研究时间长度; N0为在时间T内的地震总数。
在利用概率增益模型时,尽可能要求各项地震前兆相互独立,否则虽然可以估算地震前兆的概率增益,但是可能出现综合概率大于1的情况,使得对地震危险性的评估偏大,增大虚报的概率。
云南地区及邻区M≥6.0地震的发生时间分布是不均匀的,具有明显的平静-丛集特征,有约42%的地震其时间间隔小于0.5 a,地震丛集发生后,往往会出现长时间的平静,如图1所示。当M≥6.0地震平静时间较长时,则发震的危险性较高,但不能确切知道发震时间,无法进行中短期预测,需要其它手段来辅助,例如若同时出现M≥5.0地震平静异常,则用M≥5.0、M≥6.0地震平静两项指标显然要比仅用M≥6.0地震平静一项指标的预测信度要高。若在出现M≥5.0、M≥6.0地震平静异常后,又出现中等地震频度增高、能量释放增加,甚至在一些敏感点上出现窗口地震,由于每一项异常对云南地区及邻区M≥6.0地震的发生都有各自的预测意义和预测概率,因此,在这些异常同时出现后进行预测比仅用某项异常进行预测的信度要高,即最终发生地震的概率是各分项概率的叠加,这即是概率增益的思想,也是本文的基本思路。
(1)云南地区及邻区6级地震平静
1905—2022年,云南地区及邻区发生M≥6.0地震94次,地震发生率v=0.83次/a,将时间长度T换算为月,代入式(6)可得P(M)=0.069,地震的平均间隔时间为1.21 a,如图2所示。当云南地区及邻区M≥6.0地震时间间隔Δt达到2.0 a时,认为6级地震出现平静异常,可以作出黄色预警(苏有锦,李忠华,2011),发震自然概率达到70%。统计不同时间间隔的地震数量可知,Δt≥2.0 a的地震共22次,占地震总数的23%,其中,Δt≥2.5 a的地震有11次。在6级地震平静达到2.0 a时对未来半年地震危险性作出预测,条件概率为(22-11)/22=50%,研究总时间为118 a,预报占时为11 a,R值为0.41,R0值为0.23,由于R>R0,因此用云南地区及邻区6级地震平静对未来半年6级地震有预测意义。
图2 1905—2015年云南地区及邻区M≥6.0地震时间间隔Δt(a)及频次N(b)统计
Fig.2 Time interval Δt(a)curve and frequency N(b)statistics of M≥6.0 earthquakes in Yunnan region during 1905-2015
(2)云南地区及邻区5级地震平静
云南地区及邻区M≥5.0地震平均年发生率v=3次/a,地震的平均时间间隔Δt为0.33 a(或120 d),当云南地区及邻区5级地震时间间隔达到200 d时,认为5级地震出现平静异常,可作出地震预警(钱晓东等,2009)。由于Δt≥200 d以后的打破地震85%为5级地震,因此可以将5级打破地震的时间作为预测未来半年将发生6级地震的起始时间。图3给出了云南地区及邻区M≥5.0地震时间间隔随时间变化及频次统计。分析可知,1960—2022年的62 a间,云南地区及邻区出现5级地震时间间隔Δt≥200 d(约0.55 a)的情况共31次,平静打破后在半年内发生M≥6.0地震共有13次,对应率为13/31= 0.42,研究总时间为62 a,预报占时为15.5 a,R值为0.18,R0值为0.17,由于R>R0,因此云南地区及邻区5级地震平静对未来6级地震具有预测意义。
图3 1960—2020年云南地区及邻区M≥5.0地震时间间隔Δt(a)及频次N(b)统计
Fig.3 Statistics of time interval Δt(a)and frequency N(b)of M≥5.0 earthquakes in Yunnan region during 1960-2020
(3)云南地区及邻区4级地震平静
云南地区及邻区平均每月约发生2次ML≥4.0地震,若4级地震的时间间隔大于90 d(约0.25 a),则认为出现4级地震平静异常,图4给出了云南地区及邻区ML≥4.0地震时间间隔随时间变化及频次统计。分析可知,1965年来绝大多数4级地震平静由4级地震打破(27/32=84%),打破平静后半年发生6级以上地震的震例占比为22/38=58%。1965年以来云南地区及邻区共发生M≥6.0地震46次,报对22次,漏报24次,预报占时19 a,研究总时长57 a,R值为22/46-19/57= 0.15,R0值为0.10,能通过预报效能检验。
(4)云南地区及邻区4级地震活跃
图5给出2002—2022年云南地区及邻区ML≥4.0地震半年频度随时间变化曲线。从图中可见,当频次≥15时,云南地区及邻区4级地震活动开始活跃。1965—2022年频次≥15次的情况共29次,其中18次在其后半年发生M≥6.0地震,对应率为62%。期间云南地区及邻区共发生M≥6.0地震37次,漏报19次,预报占时为14.5 a,研究总时长为57 a,R值为0.23,R0值为0.16,通过预报效能检验。
图4 1965—2020年云南地区及邻区ML≥4.0地震时间间隔Δt(a)及频次N(b)统计
Fig.4 Statistics of time interval Δt(a)and frequency N(b)of ML≥4.0 earthquakes in Yunnan region during 1965-2020
图5 2002—2022年云南地区及邻区ML≥4地震频次随时间变化(窗长:6个月,步长:1天)
Fig.5 Frequency of ML≥4.0 earthquakes varying with time in Yunnan region during 1965-2022(window length:6 months,step length:1 day)
(5)云南地区及邻区3级地震活跃
图6给出了1997—2022年云南地区及邻区ML≥3.0地震3个月频度与M≥6.0地震的关系。从图中可以看到,云南地区及邻区ML≥3.0地震频度N≥60次的情况共出现过14次,其中有9次在地震频度出现异常后3个月内发生了M≥6.0地震,对应率为0.64。图中仅标出报对地震,未标出漏报地震(6次),预报占时3.5 a,研究时长25 a,R值为0.50,R0值为0.27,可见云南地区及邻区3级地震频度对未来3个月短期6级地震具有预报意义。
图6 1997—2022年云南地区及邻区ML≥3.0地震频次随时间变化(窗长:3个月,步长:1个月)
Fig.6 Frequency of ML≥3.0 earthquakes varying with time in Yunnan region during 1997-2022(window length:3 months,step length:1 month)
(6)地震活动度
地震活动度是描述地震活动性强弱的定量指标,它综合考虑了地震频次、平均震级或平均释放能量、最大震级以及地震空间分布的集中度及其记忆效应。谷继成和魏富成(1987)应用模糊数学概念,在只考虑地震频次、平均释放能量和最大震级3个因素时,给出地震活动度的计算公式为:
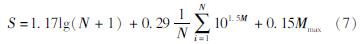
式中:N为地震总数; M为震级; Mmax为最大震级。
图7给出了1997—2022年云南地区及邻区中小地震活动度S随时间的变化,步长为1 d,震级ML≥2.5,图中曲线为原始地震活动度S值经小波分析后的结果,图中标出了该期间发生在云南地区及邻区的所有M≥6.0地震。地震活动度是地震频度和地震释放能量的综合反映,能更客观地反映一定地区的地震活动水平。从图7中可以明显看到地震活动度S的高低起伏现象明显,强震不会发生于谷底,共出现高值异常14次,报对9次,半年对应率为64%,在此期间云南地区及邻区共发生M≥6.0地震16次,报对12次,漏报4次,预报占时为7 a,研究总时长为25 a,R值为0.47,R0值为0.27,能通过预报效能检验。
图7 1997—2022年云南地区及邻区地震活动度S时间分布
Fig.7 Active degree S of M≥6.0 earthquakes varying with time in Yunnan region during 1997-2022
表1为云南地区及邻区6级地震指标所用资料参数及预测效果,从预测判据来看,主要监测地震活动平静和活跃两种异常状态,分别使用平静时间和频次参数。主要预测云南地区及邻区半年内发生M≥6.0地震三要素。从预测效果来看,所用6个指标对应率绝大部分大于0.5,指标均能通过R值检验。
概率增益:从对6个单项指标的分析可知,云南地区及邻区6级地震月背景发震概率P(E)=0.069。对于6级地震平静指标,在Δt≥2.0 a的条件下,未来半年发震的条件概率为P(M)=43%,由于不能确定在6个月当中哪个月发生地震,可将发震的可能性平均到每月,P(M)/6=0.072,据式(4)得到概率增益G1=1.04。同理可得云南地区及邻区5级地震平静的概率增益为1.01。
对于云南地区及邻区4级地震平静指标,1905—2022年云南省内共发生M≥6.0地震61次,地震发生率v=0.55次/a,地震的平均间隔时间为1.87 a,即云南省内6级地震月背景概率P(E)为0.046,每月的条件概率为0.58/6=0.097,计算得到概率增益为2.1。对于云南地区及邻区4级地震活跃指标,月背景概率为0.069,月条件概率为0.62/6=0.103,概率增益为1.5。对于云南地区及邻区3级地震活跃指标,6级地震的月背景概率为0.069,指标月条件概率为0.64/3=0.213,概率增益为3.09。对于云南地区及邻区地震活动度指标,6级地震的月背景概率为0.069,月条件概率为0.64/6=0.107,概率增益为1.6。
表2给出了各个单项指标的预报效能ΔR和概率增益。从预报效能来看,只要ΔR>0即认为该项指标有预报意义,且ΔR越大预报效果越好。由表2可见(表中ΔR=R-R0),3级地震活跃指标、地震活动度和6级地震平静指标这3项指标预报效果较好,4级地震活跃指标要好于4级地震平静指标。从概率增益来看,作为6级强震的中短期预测,5级、6级地震平静指标的概率增益并不高(均小于1.5),3级地震活跃指标概率增益最高(G3=3.09),4级地震平静、4级地震活跃和地震活动度S概率增益介于1.5~2.1。据式(3)可知,当Gn>1.0时,P(M)大于背景发震概率,单项Gn越大则P(M)越高,因此,在实际工作中应该寻找条件概率较高的单项指标。
综合概率:将整个研究时间段t划分为n段,考察每小段时间内异常出现情况。由于已知每个单项指标异常出现的时间,可根据式(3)计算每小段各分项指标的综合概率Pi,综合概率P为各分项指标概率Pi的叠加,以一定步长滑动可求出整个时间段t的P值。图8给出了1997—2022年云南地区及邻区综合概率P随时间变化曲线,红、黄、绿分别表示红色预警、黄色预警和安全。P异常阀值取20%、30%,P值小于20%为安全; P值为20%~30%黄色预警,表示云南地区及邻区未来存在发生M≥6.0地震的可能; P值大于30%为红色预警,预测未来半年云南地区及邻区将发生M≥6.0地震。图9给出了云南地区及邻区M≥6.0地震P值在不同预测时间的预报效能检验R值及相应的R0值,可以看到,预测时间大于0.43 a(约157 d)以后,R值大于R0值,因此本文综合概率指标具有预报意义。
图8 1997—2022年云南地区及邻区地震综合概率P值随时间变化
Fig.8 Synthetic probability P-value of earthquakes varying with time in Yunnan during 1997-2022
图9 云南地区及邻区M≥6.0地震综合概率P值的预报效能R值检验
Fig.9 R-value test of prediction efficiency of synthetic probability P-value of earthquakes in Yunnan region
从本文所选取的云南地区及邻区6项6级地震预测指标的预报效能来看(表2),R值均大于R0值,表明这些指标均具有预报意义,把这些指标与综合概率P得到的预报效能进行对比分析发现,综合概率指标的R值为0.45,大于6项单项指标中的4项,即综合指标的预报效能比大多数(4/6=67%)单项指标要好。由于各单项指标主要表示的是平静或活跃某单一方面的地震活动状态,而强震发生前地震活动平静或活跃均会出现,如何选用指标不容易把握,而综合概率P能有效地将地震活动平静和活跃进行融合,其预报效能比单一指标要高。
(1)单项指标的选择。综合概率P即增益概率是各个单项对背景概率的贡献和增益的综合反映,其结果与单项指标的选择直接有关。选择单项指标需要注意两个方面,一是要认真研究每个单项指标的条件概率,即当指标出现后发生地震的概率,不能只有个别震例。还要对每条曲线原始资料进行可信度分析,对测震观测目录资料要统一震级标度、去除余震,对前兆观测资料要去除环境干扰。单项资料要有明确的物理意义,预测效能的提高、干扰的排除和异常判定标准的制定等都依赖于对预测方法的物理意义的理解程度。另一方面,对各单项指标要进行独立性分析,但地震前兆的独立性判定有时是困难的,当地震前兆的独立性不完全清楚时,可以从曲线参数的公式来源和曲线趋势的相似性来考察(程万正,1999)。单项资料不宜过多,更不能是参数的罗列,要以预测思想为基础。
(2)加大强震短期指标研究力度。目前已总结的云南地区及邻区强震(尤其是6、7级强震)预测指标中,大多数预测时间在半年以上,具有统计意义的3个月及其以内的指标较少,并且随着预测区域的缩小,短期预测指标更少,在震前想要同时找到多种地震前兆异常是比较困难的,因此要加大强震短期指标研究力度并进行持续跟踪,尤其是小区域指标研发。只有在强震短期指标研究达到一定水平以后,才能制定出跨越长、中、短期不同时间尺度一体化的综合预测方案。
(3)预测地震类型。大量岩石破裂实验表明(余怀忠等,2004; 蒋海昆等,2009),岩石破裂前应变能会出现加速释放过程,这种现象与地震前出现的能量加速释放、中小地震活跃现象相似。此外,大地震前还会出现能量释放减速或匀速、中小地震平静的现象。钱晓东等(2015)对云南地区及邻区强震前中小地震活动特征的研究表明,强震前中小地震活动具有加速特征的约占70%,减速或匀速特征占30%,可见云南地区及邻区震前中小地震活跃的情况占大多数,此为本文选择地震发生模式为平静-活跃的原因。另外,大震前中小地震活跃模型在预测上具有不唯一性,目前大量震例研究认为强震前中小地震活动会普遍出现加速现象,但是,是否只要出现中小地震活动加速就一定会发生大地震(即是否具有唯一性),这方面的研究进展相对较慢,对其进行深入研究探索也是我们今后长期要面临的研究课题。
(4)综合概率P的阈值。综合概率P值需要达到多大才能发布预警信息?综合概率P的大小与所预测地震的时、空、强有关。从时间预测来看,假设预测未来1 a发生1次强震的概率为1,是一次高概率预测结果,对于1次在1 a内必定要发生的事件,由于无法判定会在哪一个月发生,根据最大熵原理(钱晓东等,2009),事件发生的概率必然满足等概率才能使熵最大,因此认为一年内的每个月发生的可能性是相同的,即为1/12=0.08,可见一次中长期预测的高概率事件转换为短期预测就变为低概率事件。对于云南地区及邻区强震短期预测来说,由于背景概率较低,震前对应率高且相互独立的地震前兆中短期异常同时出现的项数不会太多,因而综合概率P的阈值不会太高。
(5)建立各预测方法的预警概率水平。对各种地震预测方法进行较为严格的统计检验,依靠某地区相对较长时间的地震前兆资料,对多个目标地震进行检验分析以说明异常与地震之间存在某种关系,对所采取的各种方法要持续跟踪检验,在不断的预测实践中调整异常判定准则,完善预测方法,建立适合当地实际的各级预警指标体系。美国加州帕克菲尔德地震预报实验场把向公众发布预警的水平定为3天A、B、C、D 4个级别(Bakun,Lindh,1985),3天的发震概率阈值分别为37%、11%、2.8%、0.68%,根据不同预警级别制定相应对策。2005年5月18日,美国地质调查局(USGS)宣布,开放了一个可显示加州地区未来24 h内发生地震概率的公共网站,以地图的形式向人们展示地震发生概率的变化,这项研究成果主要得益于该地区较好的实时地震监测台网和对这一地区地震发生率有较为深入的研究(Hanna et al,2005)。可见,地震预报面向社会公共服务概率预测是重要手段,近年来我国在这方面进行了有益的探索(苏有锦,李忠华,2011; 陈丽丽等,2019; 邬方梅,2021)。
本文基于概率增益模型的基本原理,结合对云南地区及邻区M≥6.0地震发生规律的认识,给出了强震中短期预测思路和单项预测指标方法的选择。选用总结出的6种地震学预测方法,分别计算了每一种地震前兆异常出现时发生地震的条件概率,在此基础上给出1997—2022年云南地区及邻区M≥6.0地震未来中短期发震的综合概率指标,结果表明综合概率P对预测未来半年云南地区及邻区M≥6.0强震能通过R值检验; 取P异常阈值为20%、30%,可对强震进行不同级别预警,P值小于20%为安全,P值为20%~30%为黄色预警,表示云南地区及邻区未来存在发生M≥6.0地震的可能性; P值大于30%为红色预警,表示未来半年云南地区及邻区将发生M≥6.0地震。