本文选择2018年8月—2022年7月乌鲁木齐、喀什、且末3个地磁基准台的地磁场7要素月均值(包含主磁场和岩石圈磁场)观测数据(红浅和乌什台只有4个要素数据质量较好,故此处不选择),计算了台站观测值和CGGM模型计算值的差值并分析其随时间的变化关系,如图2所示。由图2可见,要素D、H、X、Y的曲线均呈上升趋势,这表明台站观测的月变化(后月观测值减去前月观测值)速率SV_观测要大于模型计算的月变化(后月计算值减去前月计算值)速率SV_模型; 相反,要素I的曲线呈下降趋势,这表明SV_观测要小于SV_模型; 要素Z、F除乌鲁木齐台呈上升趋势外,均呈现出先上升、后下降的趋势。

对台站观测值与CGGM模型计算值差值的时间序列按月进行拟合,其中一阶拟合多项式的一次项系数,即为2018年8月—2022年7月的SV_观测和SV_模型差值的平均值; 从拟合多项式的一次项系数来看,磁偏角D最大为0.086 88(')/月(乌鲁木齐台),磁倾角I最大为-0.048 73(')/月(且末台),其它5个要素中最大的是且末台水平分量H,一次项系数为0.891 4 nT/月。

图2b、c中,喀什台和且末台的Z、F要素呈现出先上升、后下降的趋势,对其时间序列按月进行了二阶拟合,二阶拟合多项式的形式为抛物线y=ax²+bx+c,其一阶导数y'=2ax+b即为2018年8月—2022年7月第x个月SV_观测和SV_模型的差值。二阶拟合结果显示,a均为负值,抛物线开口向下,SV_观测和SV_模型的差值从2018年8月的正值(SV_观测>SV_模型)逐步减小到2022年7月的负值(SV_观测<SV_模型),抛物线的顶点处为0(SV_观测=SV_模型)。其中,喀什台Z要素SV_观测和SV_模型差值的月变化范围是0.980～-1.609 nT,F要素为1.038～-0.905 nT; 且末台Z要素SV_观测和SV_模型差值的月变化范围为1.476～-1.525 nT,F要素为1.626～-0.732 nT。

为了进一步分析图2中喀什台和且末台Z、F要素先上升、后下降变化的原因,绘制了2018年8月—2022年7月2个台站观测值和CGGM模型计算值时序曲线,如图3所示。为了便于比较,对模型计算值进行了平移处理,使台站观测值和模型计算值在2018年8月的起点保持一致。从图3可以看出,模型计算值的时序变化比较稳定,而台站观测值时序曲线具有转折现象,表明台站观测值和模型计算值差值从上升到下降的变化趋势是由台站观测值数据的转折造成的。

图2 3个基准站观测值与CGGM模型计算值差值的特征变化
Fig.2 Characteristic changes of the difference between the observed values at three stations and the calculated values through CGGM model

图3 喀什台(a)和且末台(b)观测值(红线)与CGGM模型计算值(黑线)的特征变化
Fig.3 Characteristic changes of the observed values(red line)at Kashgar station(a)and Qiemo station(b) and the calculated values(black line)through CGGM model

为了进一步比较台站观测值和CGGM模型的关系,笔者计算了2018年8月—2022年7月乌鲁木齐台、喀什台和且末台3个基准站观测值和模型计算值的均方根误差RMSE及其差值的标准偏差σ,计算公式如下:

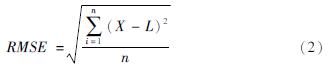
式中:X表示台站观测值; L表示模型计算值; n为统计期间的月数。

式中:Δ_i表示台站观测月均值与模型计算月均值的差值; 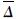表示Δ_i的平均值; n为统计期间的月数。

RMSE可以反映模型计算值与台站观测值的偏离程度,因为台站观测值由主磁场和岩石圈磁场构成,而模型描述的是主磁场,所以RMSE主要来源于岩石圈磁场,其次来源于模型的描述能力,即球谐函数模型本身的误差,该误差主要来源于忽略岩石圈磁场和外源场以及球谐级数的截断(王亶文,2003)。 表1计算结果还显示同一要素不同台站间的RMSE差别较大:D变化范围为2.4'～15.1',H变化范围为37.2～66.1 nT,Z变化范围为91.2～279.2 nT,F变化范围为91.8～221.6 nT,I变化范围为0.9'～11.2',X变化范围为36.3～66.9 nT,Y变化范围是18.5～115.2 nT。造成这种差别的主要原因是不同台站所处位置地下电性结构不同引起的岩石圈磁场的不均匀分布,

表1 3个基准站观测值与CGGM模型计算值的均方根误差及其差值的标准偏差
Tab.1 Root mean square error and standard deviation of difference between three stations' observed values and the calculated values through CGGM model

其次是不同台站的观测环境、仪器和人员不同产生的误差(常宜峰等,2014; 高明国,康国发,2010; 聂琳娟等,2017)。

本文通过标准偏差σ来研究台站观测值和模型计算值差值的离散程度。从表1可以看出,各台站D和I的σ范围为0.8'～1.2'和0.4'～0.8',强度分量(H、Z、F、X、Y)的σ均在13.1 nT以内。总体来看,各台站相同要素的差值σ相差不大,表明台站观测值与CGGM模型计算值的差值比较稳定,一致性较好。

王亶文(2003)对IGRF模型在中国大陆地区的误差进行了分析,选取我国大陆岩石圈磁异常较小的29个台站,对1998年地磁场总强度F的台站实测值和模型计算值,进行了年均值的差值分析,得到差值范围为-305.0～435.6 nT(主要是由台站实测值中岩石圈磁场和外源场的不均匀分布引起),均方根误差为146.9 nT,得出中国大陆地区IGRF误差略大于全球平均水平(90 nT)(Burdelnaya et al,1999)。为了考察CGGM模型的精度情况,本文通过CGGM模型和IGRF13模型分别计算了2019—2021年地磁场总强度F的均值,与新疆地区5个台站实测的2019—2021年F均值进行差值计算,结果见表2。

表2 台站实测F值与模型计算F值差值及其均方根误差
Tab.2 The difference between the F-values observed at the stations and the total geomagnetic intensity F calculated through CGGM model and their root mean square error

综合5个台站的差值和RMSE来看,IGRF13模型略优于CGGM模型,两个模型与实测值差值相差最小的是乌鲁木齐台,为11.34 nT; 最大为乌什台,为42.27 nT; 两个模型与实测值的RMSE相差26.7 nT。IGRF13模型是由包括CGGM模型在内的15个模型计算得到的,更多的卫星数据、地面观测数据和更长的数据序列使得IGRF13模型的精度略高于CGGM模型,但相对于5万多nT的磁感应强度来说其差别可忽略不计,说明CGGM模型的精度是可靠的,随着“张衡一号”地震电磁卫星数据的增多,CGGM模型的计算精度还会进一步提升。

由于台站观测值中包含了岩石圈磁场的成分,对台站观测月均值和模型计算月均值进行逐月相减,剩余部分即为台站观测主磁场和模型计算主磁场的逐月变化量,对其进行比较可以更加直观地分析CGGM模型计算的精度。本文选取2018年8月—2022年7月乌鲁木齐、喀什、且末3个地磁基准站的地磁场7要素月均值和乌什、红浅2个地磁基本站相对记录的D、H、Z、F月均值观测数据,对台站观测和模型计算的逐月变化量计算RMSE及其差值的σ(表3),这里的RMSE描述的是模型计算与台站观测主磁场的逐月变化量的偏离程度。表3计算结果显示,各台站D和I的RMSE变化范围为0.18'～0.41',H变化范围为4.61～5.10 nT,Z为2.24～2.68 nT,F为2.15～2.47 nT,X为4.89～5.24 nT,Y为1.42～1.80 nT。整体来看,各台站观测和CGGM模型计算的逐月变化量差值非常小,说明CGGM模型计算值和台站观测值具有比较好的一致性。从逐月变化量差值的σ结果可以看出,各台站相同要素的σ很小并且相差不大,表明逐月变化量差值离散程度较低,即CGGM模型计算值的稳定性较好。

对台站观测数据提取静日子夜均值,能够最大程度剔除其中的外源变化磁场成分,但还是会有很小一部分剩余的电离层磁场叠加在台站观测

表3 台站观测值与CGGM模型计算值逐月变化量的均方根误差及其差值的标准偏差
Tab.3 The mean square root error and standard deviation of the difference between the values observed at stations and the values calculated through CGGM model month by month

数据中。刘学旺等(2018)利用TIG-GCM模式计算电离层电流及夜间电离层磁场发现,磁平静时期中低纬(50°N～50°S)地区夜间电离层磁场的量级为几个nT,高纬度地区可达几十nT,且磁场的南北向分量和径向分量基本大于东西向分量。以乌鲁木齐台、喀什台、且末台的X、Y、Z三个要素为例,分析观测值和模型计算值逐月变化量随时间的变化特征,如图4所示。总体来看,台站观测值逐月变化量的变化幅度较模型计算值大几个nT,台站观测值逐月变化量X、Z要素的变化幅度大于Y要素,说明静日子夜均值剔除台站观测数据外源变化场是不完全的,台站观测值逐月变化量中会有几个nT的剩余电离层磁场叠加其中,使得台站观测值逐月变化量的变化幅度大于模型计算值,台站观测值逐月变化量序列的离散程度增大,否则,表3中逐月变化量差值的标准偏差会小很多。分析其原因,首先是台站观测值中剩余电离层磁场的矢量叠加具有随机性,其次是绝对观测中人员的观测误差也具有一定的随机性。

图4 3个基准站站观测值(红线)与CGGM模型计算值(黑线)逐月变化量的特征变化
Fig.4 Characteristic changes of the monthly variation of the calculated values through the CGGM model and the observed values at the stations