基金项目:国家自然科学基金项目(51978434).
第一作者简介:苏闻浩(1998-),硕士研究生在读,主要从事地震工程研究工作.E-mail:18862633233@163.com.
通信作者简介:刘启方(1969-),研究员,博士生导师,主要从事地震工程研究工作.E-mail:Qifang_liu@126.com.
(苏州科技大学 江苏省结构工程重点实验室,江苏 苏州 215009)
(Suzhou University of Science and Technology,Key Laboratory of Structure Engineering of Jiangsu Province,Suzhou 215009,Jiangsu,China)
pulse-like ground motion; frame-shear structure; buckling restrained braces; damping performance
DOI: 10.20015/j.cnki.ISSN1000-0666.2024.0016
场地非线性研究是地震工程领域的重要课题之一,它对近断层地震动模拟、地震动预测方程的建立、震害评估等都具有重要的理论意义和工程应用价值。早期的研究表明,场地非线性反应阈值介于100~200 cm/s2(Beresnev,Wen,1996),近期的研究则表明场地非线性反应阈值低于该值,如Rubinstein(2011)通过美国加州地震动记录研究发现地震动强度达到35 cm/s2时就能观察到场地非线性反应; 一些学者基于日本KiK-Net台网的地震动观测数据证实了非线性场地反应普遍存在于中等强度的地震动中,如Ghofrani等(2013)估计的49个台阵的场地非线性反应阈值介于40~150 cm/s2; Wu等(2010)估计的6个KiK-Net台阵的场地非线性反应阈值介于20~80 cm/s2; Regnier等(2013)估计的36个KiK-Net台阵的场地非线性反应阈值介于20~500 cm/s2。
近年来,有大量的研究表明神经网络在处理复杂回归预测问题时有较好表现,且在处理地震动预测问题时具有优势(Derras et al,2014; 万永革,李鸿吉,1995),基于数据驱动的人工神经网络可以在不构建具体函数关系式的前提下直接构建端到端的预测模型,如Kerb和Ting(2005)基于多层前馈神经网络,利用30个台站的历史地震记录,估算了高速铁路系统车站的峰值加速度; Alavi和Gandomi(2011)将人工神经网络和模拟退火算法相结合,使用震级、震中距、场地等效剪切波速和断层机制来预测地面峰值加速度、峰值速度和峰值位移; Dhanya和Raghukanth(2017)基于人工神经网络构建了一个适用于浅源地震的地震动参数预测模型,利用震级、震中距、场地剪切波速VS30和震源机制这4个参数预测地面峰值速度、加速度和5%的阻尼谱加速度。
场地非线性所导致的场地等效剪切波速的下降是场地分析中的重要问题,目前的研究中多使用传统回归的方法来回归单个台站的变化曲线,该方法仅能反映特定台站的情况且无法应用于部分数据量较少的台站,存在一定的局限性。本文建立了一个BP神经网络预测模型,用来预测在地震动作用下,场地的剪切波速下降情况并判断产生非线性变化的大致区间。
日本KiK-net台网具有较为完整的场地信息和大量的井上井下地震动信息,站井的深度分布介于100~2 500 m。本文搜集整理了KiK-net台网观测到的地表与井下地震动记录。考虑到大震发生后场地的剪切波速会在短期内快速恢复到90%以上并呈现出长期缓慢恢复的性质(苗雨等,2018),因此对PGA>500 cm/s2地震后100 d内的数据进行删减,将各地震动事件东西向及南北向作为两次独立的观测结果(董凯月,2020),最终筛选出近20年来具有完整地质资料的407个台站中的30 952条地震动记录。对数据进行基线校正和1~13 Hz滤波处理后,数据库中PGA<20 cm/s2的记录共17 584条,PGA>20 cm/s2的记录部分组成如图1所示。20 cm/s2<PGA<60 cm/s2的记录共7 910条,PGA>60 cm/s2的记录共有5 458条。本文所选地震动记录的震级与震中距散点分布如图2所示。根据美国NEHRP规范(表1),统计出每类场地地震动记录所占比例,如图3所示,图中无A类场地,B类场地所占比例为7%,E类场地所占比例最低,为2.1%,本文选取的台站以C类和D类为主。
图1 KiK-net台网PGA>20 cm/s2记录分布
Fig.1 The distribution of PGA >20 cm/s2 records
本文通过井上井下解卷积求取场地等效剪切波速(张亚沛,2019; 刘启方,陈长龙,2022)。设地表和井下加速度记录的傅立叶谱分别为U1(ω)和U2(ω),应用解卷积法首先计算系统的传递函数G(ω):
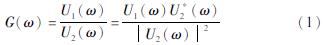
式中:*表示复共轭,分子为地表与井下加速度在频域内的互相关函数,分母为井下加速度的功率谱。为了避免分母中谱值很小引起的不稳定性,一般采用U'2(ω)对U2(ω)进行校正:
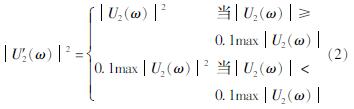
对G(ω)进行傅立叶反变换到时域g(t),即为井下脉冲输入时地表的响应。通过脉冲响应(脉冲的峰值到时)获得井下台站到地表地震波的传播时间,用该站井深度除以传播时间,计算该场地土体等效剪切波速VS。
场地等效剪切波速比VSr计算公式为:
VSr=(VS)/(VS0)(3)
式中:VS0为该场地的原始等效剪切波速值,取该场地PGA<20 cm/s2的弱震动作用下场地等效剪切波速的平均值(苗雨等,2018,2021)。
BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络。该网络模型具有函数逼近的属性,可以在不考虑输入与输出间具体函数关系的前提下,通过机器学习的方法,构建出一种输入与输出的映射,拟合任意复杂的连续函数。BP神经网络包括一个输入层、多个隐藏层和一个输出层,每一层由不同数量的人工神经元组成,网络结构如图4所示。
隐藏层中第i个神经元的输出可以写为:
yij=φ(∑wij+bj)(4)
式中:wij表示神经网络中第i层与第i-1层神经元之间的权重; bj表示神经网络中第i层第j个神经元线性层的偏置; φ表示激活函数。激活函数的类型有很多种,本文输出层采用线性激活函数linear(式5),隐藏层采用tanh激活函数(式6):
linear(x)=x(5)

目前,研究人员多以PGA来表征场地的非线性阈值(Chin,Aki,1991; Wu et al,2010; Wang et al,2019),由于该值仅能表征某次事件的峰值强度,因此本文还使用了Arias烈度(Ia)来表征某次事件整体能量大小(Benito,Herraiz,1997; Chousianitis et al,2014,2016),以及场地剪切波速VS30来表征场地情况。经过多次尝试,建立了一个包含3个输入参数(PGA、Ia、VS30)、5个隐藏神经元、1个输出参数(VSr)的BP神经网络模型,其预测过程可表示为:
VSr=f [PGA,ln(Ia),VS30](7)
式中:Ia为Arias烈度,由于其值分布范围过广,因此取其自然对数,以减小其分布范围,从而加快神经网络梯度的更新,以有效提高神经网络的收敛速度,加速模型的训练。
本文采用Adam优化算法进行神经网络模型训练,它可以根据学习环境自适应调整学习率,使得神经网络得以更快收敛,同时对初始的超参数设置不敏感,方便了神经网络的学习(Kingma,Ba,2014)。对模型预测效果的评价,本文选用MSE作为模型的损失函数(Dhanya et al,2017),使用MSE,其计算公式分别为及皮尔逊相关系数作为模型的评价指标:
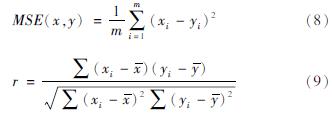
式中:xi为目标数据或记录数据; yi为预测数据; m为该批数据点总数; x^-、 y^-为该批次目标数据和预测数据的均值。
本文筛选出地震动记录较多、PGA分布较广的6个包含不同场地类型的台站作为测试台站进行图像分析及模型评价,其场地情况见表2,测试台站不参与训练。
本文使用场地非线性研究中常用的传统双曲线回归模型作为模型1,表示为:
y=1/(1+kx)(10)
式中:x为PGA; y为场地等效剪切波速比; k为回归参数。使用模型1,对6个台站的VSr关于PGA的变化做了回归分析,拟合参数见表3。通过训练所得BP神经网络模型对6个台站的VSr进行预测,模型1与神经网络模型预测结果如图5所示。由于VSr为场地等效剪切波速与弱震动作用下场地等效剪切波速均值的比值,因此比弱震动作用下场地等效剪切波速均值高的计算值会出现VSr大于1.0的结果。
表3 使用模型1得到VSr关于PGA变化的回归参数
Tab.3 Regression parameters of shear wave velocity ratios with respect to PGA variation by Model 1
由图5可见,用BP神经网络模型预测所得曲线与模型1拟合曲线整体上较为相似,两者均呈现出VSr随PGA的增大而逐渐减小的特性。在测试台站的各场地类型中,当PGA=50 cm/s2时,用BP神经网络模型得到的VSr预测值均未小于0.99; 当PGA=100 cm/s2时,各场地VSr下降幅度约为2%~3%,场地VSr开始呈现非线性变化,多数场地的非线性阈值约为50~100 cm/s2; 当PGA>100 cm/s2后,场地VSr的非线性变化较为显著。在测试台站中,对于较硬的B类场地,其PGA达到175 cm/s2左右时,场地VSr下降约5%; 对于较松软的D、E类场地,PGA达到140 cm/s2左右时,VSr即下降约5%。图中E类场地的BP神经网络预测曲线波动较大,推测是由于E类场地训练数据相对较少,训练不够充分所导致。训练得到的BP神经网络模型各层参数见表4、图5。
图5 本文所选6个台站的等效剪切波速比随PGA变化的预测曲线
Fig.5 Predicted curves of the equivalent shear wave velocity ratio of six stations changing with PGA
训练完成后,训练集的MSE为6×10-4,测试台站数据集的MSE为6.7×10-4。训练集与测试台站数据集的均方误差相似,模型整体表现良好,未出现过拟合现象。
使用BP神经网络模型及模型1计算得到6个台站的Person相关系数,结果见表6。从表中可见,BP神经网络模型对场地等效剪切波速比的预测相较于模型1,其相关系数相对较高,其预测表现均不弱于模型1,整体上有着更好的预测性能。
通常使用残差分析作为主要手段分析神经网络的性能。残差分析可以反映预测的输出与输入变量的整体性关系,可分析该网络在整个数据区间上整体预测性能的好坏(Dhanya,Raghukanth,2020)。本文将残差定义为预测值与目标值之差,如下所示:
Ri=ypred-ytarget(11)
图6展示了BP神经网络模型3个输入变量PGA、ln(Ia)和VS30对应于输出变量VSr的模型残差,图中橙色误差棒为各区间上的所有残差作均值及标准差处理。表7给出了3个输入变量在各区间的残差分布统计,由表可见,在各个区间上,该网络模型均值残差均在0附近,整体呈现出无偏特性,对于PGA及Ia较高的强震数据,可能是由于数据量较少且数据的离散度较大,因此其残差有着相对更大的标准差。VS30为120~1 270 m/s时,均有较低的均值残差及标准差,表明其在多数软硬场地中均有较好的预测性能。
表7 PGA、ln(Ia)和VS30在各区间的残差分布统计
Tab.7 Statistics of residual error distribution in each interval of PGA,ln(Ia)and VS30
图6 BP神经网络模型输入变量PGA(a)、ln(Ia)(b)和VS30(c)相对于输出变量VSr的残差
Fig.6 Residuals of the input variables PGA(a),ln(Ia)(b)and VS30(c)of the BP neural network model corresponding to the output variable VSr
对于具有明确函数形式的回归分析,每个变量的相对重要性可以从优化后得到的系数中确定。但是在BP神经网络中,由于网络本身是高度复杂的互联节点,所以想要得到其相关性较为困难。许多研究者尝试了各种技术来获得输入节点对输出的相对影响(Gevrey et al,2003),其中最简单直接的方法之一是Garson(1991)提出的基于隐藏神经元的连接权值与输入节点相关权值的划分,根据该方法,特定输出变量j的每个输入变量i的相关重要性RI为:
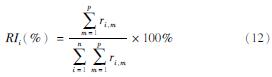
其中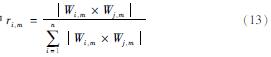
式中:Wi,m为输入层-隐藏层各神经元所对应的权值; Wj,m为隐藏层-输出层各神经元权值; n和p分别为输入参数个数及隐藏层神经元数量。
通过表4、5中的权值,将式(12)应用于BP神经网络模型上,所得到的输入参数相对输出参数VSr的相关权重如图7所示。由图7可见,PGA在该模型中所占权重较大,为该模型的主要控制参数。
图7 BP神经网络模型输入变量PGA、ln(Ia)和VS30 相对于等效剪切波速比VSr的相关权重
Fig.7 Relative importance of PGA,ln(Ia)and VS30 relative to equivalent shear wave velocity ratio VSr
控制部分输入变量不变,绘制输出变量随某一输入变量的变化关系曲线,是神经网络模型验证的常用手段。由于PGA为该网络模型的主要控制参数,而Arias烈度参数的权重较低,仅占23.3%,因此本文选取4种不同的VS30以涵盖4类场地(图8),基于模型的预测结果探讨PGA和VSr变化的关系。
图8为PGA关于VSr变化关系。由图8可见,VSr随PGA的增大有下降的趋势,PGA越大,VSr下降越快。同时,VS30越小的松软场地受PGA影响越大,下降幅度也越大。在以往的研究中普遍认为在坚硬的场地中仅会产生很小的非线性变化,但在本文中B类场地在PGA较大时仍有一定的等效剪切波速比下降,推测可能是因为数据库中B类场地数据所占比例较少,且VS30与场地整体土层情况仍有一定差异,导致该网络模型预测结果在VS30较高的场地中仍有一定程度的等效剪切波速比下降。
图8 不同场地等效剪切波速比VSr随PGA的变化
Fig.8 Variation of equivalent shear wave velocity ratio VSr with PGA in different sites
本文使用日本KiK-net台网的407个台站记录到的30 952条记录,提出了一种基于BP神经网络的场地等效剪切波速比变化预测模型。模型采用均方误差函数以及Adam优化算法,包含3个输入参数、5个隐藏神经元和1个输出参数。输入参数为加速度峰PGA、Arias烈度Ia及场地剪切波速度VS30,输出为场地等效剪切波速比VSr,得到以下结论:
(1)神经网络模型可以在不构建复杂函数回归关系的情况下,预测场地的剪切波速变化情况。本文选取的包含不同场地类型的6个台站,通过使用BP神经网络对6个台站的场地剪切波速比的预测曲线可知,BP网络模型预测曲线相对光滑,未出现过拟合现象。相较于使用最小二乘法回归所得的剪切波速比函数曲线,BP神经网络模型的相关系数较高,该神经网络模型残差对于各输入变量整体呈现出无偏特性,在大部分软硬场地中均有较好的预测性能。
(2)由BP神经网络模型预测曲线可知,PGA为50~100 cm/s2时,多数场地开始出现非线性变化,剪切波速开始发生变化; PGA>100 cm/s2时,场地发生显著的非线性变化,剪切波速开始发生较快变化。PGA达到175 cm/s2左右时,B类场地剪切波速下降5%,PGA达到约140 cm/s2时,D、E类场地剪切波速下降5%。
(3)模型敏感性分析表明,PGA在该神经网络模型中占据着较高的权重,为场地等效剪切波速比变化的最主要控制参数。该神经网络模型捕捉到场地等效剪切波速比随PGA的增大有下降的趋势,而较为松软的D、E类场地受PGA影响更大,下降的幅度也更大。
(4)在数据较少的B、E类场地中,基于数据驱动的神经网络模型存在一定的训练风险,是后续研究中需要讨论的一个关键问题。
本文使用了日本KiK-net台网提供的地震动数据,在此表示感谢。