基金项目:国家自然科学基金(地区基金)(52268028).
第一作者简介:李喜梅(1979-),副教授,博士,主要从事桥梁结构减隔震分析及振动控制研究.E-mail:mei611@163.com.
(1.兰州理工大学 西部土木工程防灾减灾教育部工程研究中心,甘肃 兰州 730050; 2.兰州理工大学防震减灾研究所,甘肃 兰州 730050; 3.中国市政工程西北设计研究院有限公司,甘肃 兰州 730050)
(1.Disaster Prevention and Mitigation Engineering Research Center of Western Civil Engineering,Lanzhou University of Technology,Lanzhou 730050,Gansu,China)(2.Institute of Earthquake Protection and Disaster Mitigation,Lanzhou University of Technology,Lanzhou 730050,Gansu,China)(3.China Municipal Engineering Northwest Design & Research Institute Co., Ltd.,Lanzhou 730050,Gansu,China)
the Luding MS6.8 earthquake; strong motion records; response spectrum; attenuation relation
DOI: 10.20015/j.cnki.ISSN1000-0666.2024.0024
各国地震工程学家和学者统计研究发现,大多数地震是以地震序列的形式发生的(何顺龙,符晓敏,2021)。序列型地震相比孤立型地震来说,对结构造成的损伤几乎呈成倍增加,且余震发生的次数越多,结构的损伤效应也会不断加剧,因此将“余震不倒”纳入抗震性能目标(刘淼鑫等,2015),在主震发生后快速研判该地震序列的类型及余震强度具有重要的减灾意义(解孟雨,孟令媛,2022)。另外,断层距作为结构抗震分析的考虑因素之一,对结构响应和地震动参数之间的相关性具有明显的影响(胡进军等,2020),而目前对不同断层区域的结构抗震性能的研究较为缺乏,但很有必要(李帅,2018)。因此,考虑断层距影响下的主余震序列对结构造成的损伤可以更全面地了解结构的抗震能力和破坏机理,从而提高结构的安全储备,这对于结构的防震减灾具有重要意义。
风险性分析是一种全面评估结构在主余震序列作用下受损状况的方法,能够综合考虑结构的易损性、危险性以及地震造成的损失。近年来,风险性分析已经成为研究热点,在地震灾害防治领域具有重要的理论和实践意义,如于晓辉等(2020)研究得出含多次余震的地震序列中具有最大峰值加速度的余震对结构起控制作用; 包旭(2020)考虑了结构的不确定性和余震致使结构增加的地震危险性; 袁万城等(2016)用云图法对比分析余震对结构的地震易损性的影响,忽略余震会高估结构的抗震能力; 王通行(2019)对比研究不同损伤指标和不同构件对易损性的影响及不同场地余震引起的超越概率最大增量; 梁岩等(2019)认为随着桥梁服役时间和地震动峰值加速度的增大,同一损伤状态的超越概率也不断增大; 黄明刚(2009)对钢混连续梁桥进行了易损性、危险性分析,在此基础上进行了风险性分析。除了以上因素,一些学者开展了关于断层距对地震易损性影响的分析,如夏长华和郭龙(2014)统计了2008年汶川8.0级地震中受损土石坝与震中距和断层距的相关性,认为大震中宜采用断层距作为现场震害评估的指标; 傅杰(2019)通过绘制易损性云图,研究了断层距对桥墩易损位置和损伤概率的影响,但桥型的针对性太强,适应性有限。综合以上研究可知,将考虑断层距的主余震序列作为评价结构震后风险性的主要因素具有重要意义,可以为工程抗震设计提供科学依据,从而提高结构的抗震性能和安全储备,有效减缓地震灾害对后期救援重建所造成的二次伤害。
本文提出一种考虑断层距的主余震序列构造方法,并构造50组主余震序列; 建立一座三跨连续梁桥的OpenSees模型进行非线性时程动力分析,依次计算和分析桥梁结构的易损性、危险性和风险性,同时,比较主余震序列和主震、设防等级以及断层距等因素对桥梁结构造成的损伤,探讨考虑余震和断层距对于评估桥梁结构震后损伤程度的影响。
重复法由Hatzigeorgiou(2010)等提出,通过调整主震峰值加速度,将主震重复一次或多次来模拟余震。尽管该方法有时会导致结果误差较大,但仍被广泛应用于余震序列构造的研究中(Lee,Foutch,2004)。
Li和Ellingwood(2010)提出将两条从不同地震事件中随机挑选的地震动进行随机组合以构造人工主余震序列,称为随机法。但余震的发生和主震有一定的相关性,因此使用此方法构造的主余震序列容易导致计算结果产生较大误差(任雪梅等,2009; 吕晓健等,2010; 朱瑞广,吕大刚,2019)。
衰减法是基于广义的大森定律(Goda,Taylor,2012)提出的,该定律认为主震与余震之间存在一定的衰减关系。因此,在衰减法中,通常将主震的震级以一定的规律作衰减来获得不同强度的余震。
对比3种主余震序列构造方法可以发现,采用重复法构造地震序列忽略了主余震序列地震动调幅前后的频谱变化,导致余震的强度大于真实情况,增量损伤附加值较大; 随机法容易低估或高估余震带来的附加损伤; 衰减法需要结合地区的地震统计规律才能构造出区域场地主余震序列的特征。
为了满足预测余震强度的真实性,本文将重复法和衰减法的优点相结合,提出考虑断层距衰减的主余震序列构造方法,给出主余震序列地震关于震级、烈度、衰减关系等的统计规律。具体步骤如下:首先,采用李喜梅等(2021)根据地震统计资料,利用震级与烈度之间的关系,结合重复法,考虑了余震的衰减变化给出余震震级与烈度的关系。其次,通过统计数据获得主余震序列震级的衰减关系(图1),根据研究对象的设防烈度,从《公路桥梁抗震设计规范》(JTGT 2231-01—2020)中选取烈度和峰值加速度。最后,已知主震的谱加速度,基于衰减法的原则,根据以断层距衡量的地震动烈度衰减关系式(1)(Joyner,Boore,1982),利用样条插值法求得每次余震的峰值加速度,获得相应的余震记录,完成主余震序列的构造。

式中:PGA表示地震动峰值加速度; Rjb是地震发生时结构距离震源断层最近处的地面直线距离; m是地震震级。
本文提出的主余震序列构造方法考虑了余震烈度衰减,综合了衰减法和重复法各自的优点,利用它能够更加合理地挑选出可以预测桥梁结构损伤的主余震序列。因此,本文排除震源深度过深的地震事件和记录不全的地震事件,从太平洋地震工程研究中心(Pacific Earthquake Engineering Research Center,PEERC)网站选取3个主余震事件的10条地震记录作为主震,见表1(表中仅列出了3个主余震事件在不同台站的信息,另外3条是相同台站选取的其他震记录),采用考虑断层距衰减的主余震序列构造方法,构造了不同断层距的50组地震记录作为余震进行后续分析,其中一组主余震序列如图2所示。
采用合适的评价标准对于定性和定量评价结构在主余震序列作用后的损伤状态和通行能力有重要影响。Park-Ang指标又称双参数损伤指标,最初由Park和Ang(1985)提出。它同时考虑了结构的变形和累计耗能,经Stone和 Taylor(1993)改进,用弯矩和曲率替代广义力和广义位移,计算结构误差更小,与实际结构有更好的一致性。Park-Ang不同损伤状态下的结构损伤指数DI表示为:
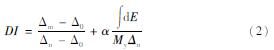
式中:DI为结构损伤指数; Δm为地震作用下结构构件的最大曲率反应,对于主余震作用的情况,取多次地震作用后构件的最大变形; Δ0为结构构件在单调荷载作用下的屈服曲率; Δn为结构构件在单调荷载作用下的极限曲率; My为结构构件在单调荷载作用下的屈服弯矩; dE为构件吸收的滞回能量,对于主余震序列情况,应取主余震地震序列作用后总的滞回耗能; α为耗能因子,根据Park(1987)研究取0.15。
根据式(2)选取DI,可合理体现余震对结构的累计损伤效应,结果见表2。
结构易损性分析,即分析在某强度的地震动作用下结构的损伤指数超过破坏状态指标的概率。在地震动强度条件下,地震需求服从对数正态分布,当结构的抗震能力与结构的地震需求均被描述为对数正态分布时,桥梁结构达到不同损伤程度的失效概率也是按对数正态分布的。设地震需求D和抗震能力C的均值为μd、μc,方差为β2d、β2c,则地震易损性分析函数可表示为:
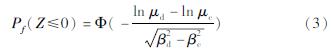
统计计算数据并进行线性回归拟合代入式(3)可判定结构在某一地震强度参数下的地震需求是否大于抗震能力。直线回归法损伤指数的线性回归拟合比较简单,且精度基本满足计算要求,因此本文选取直线回归概率线性拟合法来完成结构的易损性分析,线性拟合表达式如下:
ln(μd)=aln(IM)+ln b(4)
式中:IM表示地震动的强度; a、b是线性回归系数; 根据HAZUS99(1999)研究,以PGA为地震动强度指标时,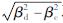 取0.5。
取0.5。
风险性分析通常包括场地危险性分析、结构易损性分析和地震损失分析3部分内容。地震风险=结构的地震危险性×地震损失。
在地震作用下,结构的地震危险性 = 结构的地震易损性×场地的危险性(任文静,2017)。桥梁的危险性是分析桥梁在遭受地震作用破坏后的承载性能和安全状态的基础,在一定程度上体现了一个地区的结构抵抗地震灾害能力的大小。地震发生后,危险性分析尤为关键,且震后较短时间内强余震发生的频率高、概率大,应引起重视。震前地震危险性评估受限于缺乏实测地震动数据、场地特征的不确定性等因素,存在一定的局限性,未考虑震后短期内场地可能发生余震的情况。本文根据危害分析的原理,提出震后的危险性分析计算方法如下:
F(S,IM)=F(S|Rjb,Rjb+ΔRjb)×F(IM)(5)
式中:F(S,IM)为结构的损伤破坏概率,即桥梁的地震危险性; F(S|Rjb,Rjb+ΔRjb)是指在Rjb和(Rjb+ΔRjb)之间桥梁发生损伤的超越概率,即桥梁的易损性,取Rjb=0,ΔRjb=20 km; F(IM)为不同地震指标下的概率密度函数。100年基准期内的场地危险性公式(任文静,2017)为:
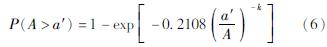
式中:A为设计基本地震峰值加速度; k为场地相关系数; a'为设防地震的峰值加速度。
本文地震损失评估的是桥梁在完好状态下遭受地震作用破坏后的损伤状态,不涉及震后救援投入费用。不考虑社会损失和交通需求,本文通过桥梁结构的经济损失比来解释不同损伤状态下结构的损伤价值。结构经济损失比是指结构在不同破坏状态下,维护或重建结构单位面积所需费用与初始造价之比,其取值参考美国地震风险评估系统(DHS,2009)所定义的损失比,见表3,其中倒塌破坏状态的损失比为2/x(x为桥梁总跨数)。
本文使用OpenSees有限元分析软件作为建模平台,以我国西北某桥梁为研究对象,该桥梁为一座跨径为26 m+27 m+24 m的连续梁桥(图3),场地条件为Ⅱ类,抗震设防烈度为Ⅷ度。主梁混凝土采用C30; 2号桥墩墩高6.65 m,3号桥墩墩高7 m,桥墩直径为1.6 m,桥墩混凝土为C30,纵筋和箍筋分别为直径28和12 mm的HRB335级钢筋; 主梁与桥墩的连接采用盆式橡胶支座JPZ(Ⅲ)。
在建模过程中,桥梁上部被简化为弹性梁柱单元,支座连接利用零长度单元模拟。考虑到支座竖向承载力较大且变形较小的特点,采用Steel01材料本构来模拟支座竖向刚度。对桥墩进行时程分析时,需考虑其弹塑性变形阶段。采用基于柔度法的弹塑性纤维梁柱单元来建立桥墩单元,核心混凝土、保护层混凝土和钢筋的材料本构分别采用Concrete02、Concrete01和Steel02模拟,使有限元模型在进行时程分析时更接近真实地震加载情况。
对算例连续梁桥的纵桥向进行时程分析,选用改进的Park-Ang损伤指标为评估标准,对在主震作用下的连续梁桥桥墩进行增量动力分析方法(Incremental Dynamic Analysis,IDA)分析,绘制损伤指数与地震峰值加速度的对数散点回归线(图4),线性拟合式为:
ln(DI)=2.946ln(PGA)-0.31775(7)
根据不同的损伤状态指标将式(7)代入式(3)中,得到主震作用下结构在不同损伤状态下的超越概率,绘制连续梁桥桥墩在不同峰值加速度下的易损性曲线(图5)。由图5可以看出,在遭遇罕遇地震(PGA=0.4 g)时,结构轻微损伤概率为5%,而在遭遇特罕遇地震(PGA=0.58 g)时,结构发生倒塌的概率低于1%,符合我国基于性能要求的抗震设防目标。
图4 主震作用下连续梁桥桥墩的损伤指数与PGA的回归分析
Fig.4 Regression analysis between DI and PGA of the bridge piers subjected to the main shock
把不同设防标准的地震动代入式(1),得到不同断层距下桥墩的地震动峰值加速度衰减曲线(图6),对比设防地震动波形和1999年中国台湾集集7.6级大地震记录可以看出,它们的衰减变化趋势较为吻合。将图6的数据代入式(3)中,求出不同断层距下结构损伤状态的超越概率,以罕遇地震为例,结果如图7所示。由图7可以看出,遭遇罕遇地震时,震中区内桥梁桥墩发生轻微破坏的超越概率为7.7%,中度破坏的概率0.55%。在震中10 km范围内桥墩结构遭受轻微破坏概率较高,严重破坏概率小于0.01%。
图6 不同断层距下桥墩的地震动加速度衰减曲线
Fig.6 Attenuation of the ground motion acceleration at different fault distances
我国《破坏性地震应急条例》(中华人民共和国国务院,1995)第22条规定:“震后应急期一般为10日”,因此,本文以主震发生后第10日发生的余震对结构造成的累积损伤为研究对象,采用式(8)进行回归拟合:
ln(DI)=2.946ln(PGA)+0.55673(8)
结合不同断层距下桥墩的地震动加速度衰减规律(图6),分析研究多遇地震、罕遇地震与特罕遇地震作用下结构损伤指数随断层距的变化规律,结果如图8所示。由图8可以看出,在地震作用下结构的损伤指数随断层距的增大而减小,断层距增大到30 km后,结构的损伤指数几乎减小到0; 损伤指数随设防地震等级的提高而增大,在近断层条件下,设防地震等级地震动峰值加速度PGA由0.2 g增大到0.58 g,则损伤指数增大20倍。
结合在遭遇多遇地震、罕遇地震、特罕遇地震3种不同设防等级地震作用时结构的损伤指数(图8)、超越概率公式(式3),以及损伤指标(表2),分别计算这3种设防等级的地震作用下桥梁发生轻微破坏、中度破坏、严重破坏和倒塌破坏的超越概率,研究其在不同断层距下的变化规律,结果如图9所示。
由图9可见,在多遇地震作用下桥梁不易发生破坏; 在罕遇地震作用下桥梁有发生中度破坏的可能; 在特罕遇地震作用下震中20 km范围内的桥梁有发生损伤破坏的可能,震中10 km范围内桥梁发生严重破坏和倒塌破坏的概率较高,地震震级逐级增大导致桥梁发生轻微破坏的概率提高了1.2×104倍,发生倒塌破坏的概率提高了4.2×1013倍。对比图7和图9b可得出,余震的发生会导致桥梁的损伤程度提高10倍以上。
算例桥梁处于Ⅷ度抗震设防区,所以设计基本峰值加速度取0.2 g,场地相关系数取6.87,设防地震的峰值加速度取0.1~1.0 g,代入式(5)可以求出不同设防地震所对应的超越概率。以损伤超越概率为纵坐标,以设防地震峰值加速度为横坐标,绘制算例桥梁场地的地震危险性曲线图(图 10)。
结构的地震危险性=结构的地震易损性×场地危险性。在图 10中分别取多遇地震(PGA=0.2 g)、罕遇地震(PGA=0.4 g)和特罕遇地震(PGA=0.58 g)对应的超越概率,将其代入图9的易损性曲线中,就可得到桥墩在遭受不同等级地震作用时发生轻微破坏、中度破坏、严重破坏和倒塌破坏的危险性概率,如图 11所示。
由《公路工程结构可靠度设计统一标准》(GB/T 50283—1999)可知,本算例桥梁的可靠度指标为1.3×10-6。由图 11可以看出,在遭遇罕遇地震时桥墩发生轻微破坏和中度破坏的危险性最高,且均大于可靠度指标1.3×10-6。严重破坏及倒塌破坏的最危险情况是在遭遇特罕遇地震时,发生严重破坏的危险性也大于可靠度指标,发生倒塌破坏的危险性小于规范给出的可靠度指标,相对于其它3种破坏,倒塌破坏最不易发生; 在震中10 km范围内结构在主余震序列作用下发生破坏的危险性最高。
本文提出一种考虑断层距衰减的主余震序列构造方法,以一座三跨连续梁桥为例,分析其主要抗震构件——桥墩在主余震序列作用下发生损伤破坏的易损性、危险性及风险性,得出以下结论:
(1)相比仅考虑主震作用,主余震序列作用下,余震会导致结构的累积损伤提高10倍以上。因此,进行桥梁抗震能力设计时应充分考虑余震的影响。
(2)将设防地震等级由多遇地震提高到特罕遇地震时,桥梁发生倒塌破坏的概率提高了4.2×1013倍。因此,提高设防地震等级对于结构抗震设计具有重要的应用价值。
(3)断层距10 km范围内的结构在遭受主余震序列作用时,发生破坏的危险性最高。在特罕遇地震作用下,当断层距从10 km减小到5 km时,结构破坏的危险性从轻微破坏提升到倒塌破坏。
建议在震后救援和恢复重建时,在主震震中10 km范围内,要及时对受损结构进行加固以减小余震造成二次损伤。同时,还要定制安全系数较高的救援方案,以防止结构发生严重的倒塌破坏,避免造成二次伤亡。