(1.云南省地震局,云南 昆明 650224; 2.中国地震台网中心,北京 100045)
(1.Yunnan Earthquake Agency,Kunming 650224,Yunnan,China;2.China Earthquake Networks Center,Beijing 100045,China)
earthquake sequence type; machine learning; characteristic parameters; decision tree
DOI: 10.20015/j.cnki.ISSN1000-0666.2024.0039
中国地震预报研究始于对1966年邢台7.2 级地震序列的认识。中国地震预报取得的首次突破是1975年海城7.3级地震的成功预报,这得益于对序列前震活动特征的把握(蒋海昆等,2015)。1966年以来,我国对地震序列的类型、划分方法、空间特征及成因已取得了相对统一的认识和成果,这些成果在中强地震序列趋势判定、强余震预测等工作中发挥了重要作用(吴开统等,1990; 周翠英等,1996; 蒋海昆等,2006b; 苏有锦等,2014)。
一次大地震发生后,公众和决策者最关心的问题是“这是一个主震还是一个更大地震的前震?”。目前研究主要基于对历史地震的统计,以此来讨论大概率下地震序列是否会正常衰减,或者在小概率下某次地震为前震序列的可能(Gulia,Wiemer,2019)。快速、准确的震后趋势判定是地震应急、抗震救灾、恢复重建等工作的重要决策依据,对稳定公众紧张情绪、维护社会稳定具有重要指导意义(蒋海昆等,2015)。因此,迫切的现实需求和仍处于探索阶段的震后趋势研判水平之间的矛盾,给科研人员带来巨大的挑战和机遇。
近年来,国内外对震后快速研判技术系统及相关产品开展了大量研究。自2018年8月开始,美国国家现代地震监测系统ANSS对美国境内显著地震事件进行余震概率预测,并在其2017—2027年战略规划设想中开展作为国家层面的余震预报,对全国重大地震之后不同时间周期(数小时、数天、数月和数年)的余震可能性进行例行通报,以提高公众意识,完善备震工作,并通知应急管理部门(U.S.Geological Survey,2017)。中国地震台网中心主导研发的震后趋势判定技术系统(Automatic Aftershock Forecasting,简称CAAFs)于2018年投入应用,初步实现了自动触发的震后早期趋势研判及相关报告的流程化产出。8个月的试运行统计数据显示,自动产出结果与地震实际情况吻合程度略好于人工研判结果(刘珠妹等,2019; Liu et al,2023),该系统在中国地震系统得到了广泛的应用。
近年来,随着人工智能技术的飞速发展,其在地震预测领域也得到了广泛应用。通过对大量观测数据的学习,发现其特征规律,利用数据建立、训练模型,对未来地震可能性开展预测,这不仅可以深化对地震机理的理解认识,还可在地震孕育机理尚不清楚的情况下提高地震预测的准确性(隗永刚,蒋长胜,2021; 蒋海昆,王锦红等,2023)。目前,机器学习在地震预测领域的研究,相对集中在利用若干特征参数对区域地震进行预测(Corbi et al,2019; Hulbert et al,2019; Asim et al,2020)。对于地震序列的研究则相对集中在余震地点的预测。DeVries等(2018)使用深度学习方法进行余震发生位置的预测,在无需事先假设主震破裂方向的条件下,该方法明显优于利用静态库仑破裂应力变化预测余震发生位置的方法,也优于基于统计地震学两大经典定律(G-R关系、修正的大森公式)给出的对地震强度和发震时间的预测(Panakkat,Adeli,2007; Martínez-Álvarez et al,2013; Asencio-Cortés et al,2016,2018)。
现阶段,国内外利用人工智能进行地震序列类型和后续强余震的研究尚不多见,这可能是因为许多研究者认为前震、主震和余震乃至震群均为“回顾性”的称谓,它们在物理本质和统计属性上难以区分,只有在地震序列完成之后才能被确认(Jordan et al,2011; 蒋长胜等,2013)。在我国,余震预测是地震工作者的一项重要职责,震后趋势判定对地震应急、抗震救灾、安定社会发挥着至关重要的作用(蒋海昆等,2015)。已有研究结果显示,很多特征参数对震后余震预测及地震序列特征判定均有一定的效果(蒋海昆,王锦红,2023),但在震后时间紧、任务重的情况下,如何从冗杂繁多的参数中,挑选出最有用的参数,是本文试图解决的问题。
本文收集整理了1966年以来川滇地区5级以上地震序列,根据震后趋势判定相关业务规定和实际工作需求,构建震后0 h至5 d共10个时间尺度的特征参数数据集,采用决策树模型对特征参数的重要性进行研究。
本文收集整理了1966—2021年川滇及其附近区域(21°～35°N,97.5～106°E)范围内5级以上地震序列,去除余震序列中5级以上余震,并将多震型地震算为1次事件,共得到5级以上地震序列225组,其中5.0～5.9级地震序列180组,6.0～6.9级地震序列33组,7.0～7.9级地震序列11组,8.0级以上地震序列1组,最大为2008年5月12日四川汶川8.0级地震序列。为保证结果统一,对于采用ML震级标度的地震序列,根据公式MS=1.13ML-1.08换算为MS震级(刘瑞丰等,2015)。
根据地震序列类型震级差分类定义(蒋海昆等,2006a),采用序列主震与后续最大地震震级差ΔM=M0-M1,将序列类型划分为多震型、主余型和孤立型,并以此作为机器学习序列类型判定的样本标签:ΔM<0.6为多震型序列,包括震群型和双震型序列; 0.6≤ΔM<2.5为主余型序列,包括主余型和前震-主震-余震型序列; ΔM≥2.5为孤立型序列。
1966—2021年川滇地区地震序列空间分布如图1所示。由图1可见,地震序列类型空间分布具有一定的区域特征:多震型相对集中在滇西的下关和姚安、腾冲—保山块体的龙陵、澜沧等地,滇东的鲁甸、川滇交界的盐源、川西巴塘、川东马边、川东北松潘—龙门山断裂带的松潘等地也有多震型地震发生; 鲜水河—安宁河—小江地震带及金沙江—红河地震带以主余型地震序列活动为主。
图1 1966—2021年川滇地区地震序列类型分布
Fig.1 Distribution of the earthquake sequence types in Sichuan-Yunnan region from 1966 to 2021
表1给出了不同范围内的主震震级的序列类型统计结果,由表1可见,主余型序列所占比例最大,约占全部序列的50%,多震型和孤立型序列各占25%; 主余型和孤立型序列合计约占75%,略低于前人78%～87%的统计结果(吴开统等,1990; 蒋海昆等,2006a; 苏有锦等,2014),表明川滇地区多震型地震的比例相对较高,具有独特的区域特征; 孤立型序列所占比例则随着主震震级升高而降低,无 7 级以上的孤立型序列,主震震级最大的孤立型序列为1981年四川道孚6.9级地震序列; 6级以上地震多震型序列比例相对较高,这与全国(蒋海昆等,2007a)及南北带中段(祁玉萍等,2021)的统计结果有一定差异,这可能是由于云南多震型序列的6、7级地震序列相对较多。
表1 不同主震震级的序列类型统计
Tab.1 The earthquake sequence types classified according to the magnitude of the main shock
图2 川滇地区不同主震震级范围序列类型统计图
Fig.2 The earthquake sequence types classified according to the magnitude of the main shock in Sichuan-Yunnan region
监督学习的输入是学习样本的特征集合和样本标签。特征工程是机器学习地震预测的最关键环节。对地震预测这类机理不明、单项特征与标签之间关系不唯一的分类任务,如何确定训练样本数据集的输入特征,是机器学习数据准备的最重要工作(蒋海昆,王锦红,2023)。
在地震序列特征研究方面,有3个重要的统计定律:①地震序列的频度-震级关系遵从G-R关系; ②地震序列的频度随时间的衰减遵从修正的大森公式; ③地震序列的主震与最大余震的震级差D遵从巴特定律。
国内外学者以这3个定律为基础,对地震序列的时、空、强分布特征开展了大量的研究(Ben-Zion,Rice,1993; Ben-Zion,Lyakhovsky,2006; 蒋海昆等,2006c,2007b; 崔子健等,2012; 黄浩,付虹,2014)。其中,对地震序列的判定多是从序列本身及其频次和能量的演化特征着手,进行定性(变化趋势)或半定量(参数统计指标)的判定(蒋海昆等,2007c),但在震后早期阶段,由于序列数据少,大多只能通过对比该地区长期地震活动的特点来判断序列类型,并在此基础上建立基于震例类比的震后趋势早期判定技术系统(刘珠妹等,2019)。震后随着时间的推移,地震目录和地震波形数据积累会越来越多,可用于序列类型判定资料和方法也越来越多。
本文参考现有地震序列类型判定参数和方法,其中一些特征和方法选择机器学习地震序列类型判定的备选特征,主要包括主震、主震震源机制、主震附近区域历史地震序列类型占比、指定时段序列衰减、指定时段G-R关系、指定时段归一化能量熵、指定时段最大余震震级、指定时段小震频次及震级共8类相关参数(蒋海昆,王锦红,2023)。此外,刘正荣和孔绍麟(1986)通过对多次地震序列的h值进行震后分时计算,成功地判定出这些地震序列的类型,并预报了序列中的最大余震震级,因此本文采用了h值这一特征参数,根据其定义,将其归类为指定时段序列衰减相关参数。
震后不同时间段数据集的构建及其划分,主要是依据震后趋势判定相关业务规定和实际工作需求来进行,如在显著地震发生后30 min内,产出震后快速研判意见,震后2 h内,产出震后首次会商意见。此外,根据《地震现场工作管理规定》 中国地震局.2013.地震现场工作管理规定(中震救函〔2013〕42号).等文件中给出的相关时间节点及震后趋势判定经验,和震后首次、震后1～3 d、4～7 d等多个会商时段工作需求,最终构建了震后0 h、1 h、2 h、3 h、6 h、12 h、18 h、1 d、3 d、5 d共10个时间尺度的特征参数数据集。
川滇地区225个地震序列样本备选特征参数缺失情况如图3所示。图中主震(浅绿色)及主震附近区域历史地震序列类型(粉红色)参数完备性相对较高,达100%。少部分地区由于历史上并没有6级地震发生,因此45M6.0Ty1、46M6.0Ty2、47M6.0Ty3这3个特征参数完备性略低,为91%; 主震震源机制相关参数(浅灰色)的特征完备性为76%。
震后,随着时间的延长,地震序列的数据逐渐增多,基于地震目录的序列参数计算结果被用于序列类型判定,因此震后1 h至5 d的数据集特征参数不断增加,其中1～18 h增加了不同时间段的折合震级、最大余震震级、震级差。1～5 d数据集还增加了满足计算样本条件的大森公式p值、h值,G-R关系b值、归一化能量熵等。随着时间的推移,指定时段最大余震震级相关参数(土黄色)的完备性略有增加,约为80%左右; 指定时段序列衰减(绿色)、G-R关系(蓝色)、归一化能量熵(棕色)等参数由于对计算样本量和监测能力有一定要求,完备性较低,约为60%(图3)。图3中108Lab2(黑色)为序列标签。
所谓的不均衡数据集,是指数据集中各类别的样本量极不均衡。通常多数类与少数类样本比例明显大于1:1时,可认为属于不均衡样本。基于不均衡样本训练的模型,会倾向于受到多数样本类别的控制。为尽可能避免此类影响,一般要从数据或算法的角度,对不均衡数据进行处理。在不同类别样本占比不是特别悬殊的情况下,可以考虑随机采样方法。本文构建的225个地震序列的特征参数中,主余型序列样本数量最多,为113个,占50%,孤立型和震群型所占比例相当,均为25%,可见虽然样本数据不均衡,但比列并不特别悬殊,可以用随机采样中的过采样,从少数类样本中对特征进行随机采样,以组合构建新的样本,从而使样本数据均衡 柚子皮.2020.不平衡数据的机器学习.https://blog.csdn.net/pipisorry/article/details/78091626.。
此外,应使用交叉验证来开展模型评价。交叉验证中,通过多次划分,大大降低了由某一次随机划分带来的偶然性,通过多次划分、多次训练,模型也能遇到各种各样的数据,从而提高其泛化能力,以确保不会出现过拟合现象 Kamekin.2018.不平衡数据集的处理.https://www.cnblogs.com/kamekin/p/9824294.html.。
图3 1966—2021年川滇地区M≥5.0地震震后3天样本集特征缺失情况统计(不同颜色代表特征参数的不同类别)
Fig.3 Statistics of missing features of the sample sets 3 days after the M≥5.0 main shocks in Sichuan-Yunnan region from 1966 to 2021(Different colors represent different categories)
一般来说,未经处理的原始数据中通常会存在缺失值、离群值等,因此在建模训练之前需要对缺失值进行处理。如图3所示,川滇地区仅225个小数据样本,数据缺失会进一步加剧样本不足的问题。缺失值处理有删除、统计值填充、统一值填充、前后值均值填充、插值法填充、建模预测填充等多种方法 Phoenix Studio.2020.特征工程之缺失值处理.https://blog.csdn.net/weixin_41503009/article/details/105550244.。在统计值填充方法中,“统计值”可选择平均值、中位数、众数、最大值、最小值等,具体使用哪一种统计值要具体问题具体分析。根据本文特征参数数据样本特点,笔者采用同类样本中位值对缺失特征进行补齐。
具体做法是:对每一个特征参数,分别计算多震型、主余型、孤立型特征中位值,之后对该类样本中缺失该特征的样本,以该中位值进行补齐。例如对主余型样本的归一化能量熵(101Entropy), 基于172个无Entropy值缺失的样本,计算其中位值,进而对有Entropy值缺失的主余型样本,用该中位值进行补齐。对多震型、孤立型样本也做类似计算处理。对所有缺失特征进行中位值补齐之后,所有样本都可参与模型训练。结果显示,缺失特征补齐的数据预处理方式,不但可显著增加可用样本量,更可以明显提升特征与序列分类之间的关联性(蒋海昆,王锦红,2023)。
在机器学习中,人们通常将原始数据按照比例分割为训练集和测试集。训练集用于训练模型,如通过利用训练集中数据,训练拟合一些参数来建立分类模型; 测试集用来评价模型好坏,测试集不参与模型训练,主要用于测试已训练好的模型的准确能力等,但不能作为与调参、选择特征等算法相关选择的依据。
本文采用train_test_split函数将数据矩阵随机划分为训练子集和测试子集。采用震后0 h数据集,计算了训练集、测试集取不同比例值时决策树预测正确的样本率。图4给出了比例值为0.2、0.25和0.3时,决策树模型给出的训练集和测试集预测正确的样本率随决策树最大拟合深度的变化图。
结果显示,决策树最大拟合深度为1～10时,训练集预测正确率随决策树最大拟合深度逐渐增大,在最大拟合深度达到10以后,正确率相对稳定,且取不同比例值对训练集预测正确率影响较小,但对测试集影响较大,最大拟合深度取0.25比例值,测试集的预测正确率相对较高。这表明,在本文构建的225个样本中,当测试集占整个数据集的25%时,模型预测正确的样本率最高。
特征选择旨在通过去除不相关、冗余或嘈杂的特征,从原始特征中选择一小部分相关特征,以减少算力和存储消耗并简化模型,以便于实际应用过程中的特征构建。
对于地震预测问题,目前尚难有足够的认识去判断特征与目标之间、特征与特征之间的相关性。这种情况下需要依靠数学或工程上的方法来更好地进行特征选择,常见的方法有过滤法、包裹法、嵌入法等,其中过滤法按照发散性或者相关性对各特征进行评分。设定阈值或者待选择阈值的个数特征选择,常用的有方差选择法、相关性选择法、特征重要性选择法、互信息选择法、卡方检验选择法 微尘-黄含驰.2022.特征选择——详尽综述.https://zhuanlan.zhihu.com/p/514845162.。
图4 测试数据取不同比例值时决策树预测正确的样本率
Fig.4 Correct sample rate of decision tree prediction when taking different proportional values for test data
本文特征选择处理流程如图5所示。图中互信息可用于表征随机变量之间的相互依赖或相关性程度(蒋海昆,王锦红,2023),而卡方检验表征的是统计样本的实际观测值与理论推断值之间的偏离程度。实际观测值与理论推断值之间的偏离程度决定卡方值的大小,卡方值越大表明二者偏差程度越大,反之二者偏差越小。若两个值完全相等,卡方值就为0,表明两者完全符合。
图5 特征选择处理流程示意图
Fig.5 The feature selection process
决策树为基于实例的归纳学习方法,它能从给定的无序的训练样本中,提炼出树型的分类模型,即从一系列具有众多特征和标签的数据中总结出决策规则,并用树状图的结构呈现这些规则。
与其它机器学习分类算法相比较,决策树分类算法相对简单,只要训练样本集能够使用特征向量和类别进行表示,就可以考虑构造决策树分类算法。预测分类算法的复杂度只与决策树的层数有关,数据处理效率高,适合于实时分类的场景。史翔宇(2021)利用包括震级-频度分布类参数、地震频度类参数、地震能量类参数和综合类参数等11个特征参数作为机器学习模型的输入变量,选择了广义线性模型(GLM)、基于决策树的随机森林模型(RF)、梯度提升机模型(GBM)和深度神经网络模型(DNN)共4种机器学习算法构建地震预测模型,结果表明,基于决策树的随机森林模型具有最好的预测效果。
决策树的两个重要参数为特征选择标准criterion和决策树最大深度max_depth。决策树需要找出最佳节点和最佳的分枝方法,衡量这个“最佳”的指标叫做“不纯度”。通常来说,“不纯度”越低,决策树对训练集的拟合越好。criterion参数正是用来决定不纯度的计算方法 数据小斑马.2019.决策树③——决策树参数介绍,对其参数设置有两种选择,即信息熵Entropy和基尼系数Gini:
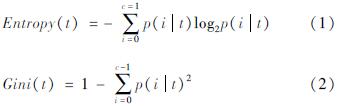
式中:t代表给定的节点; i代表标签的任意分类; p(i〖JB<1|〗t)代表标签分类i在结点t上所占的比例。
基尼系数反映了从数据集中随机抽取两个样本,其类别标记不一致的概率。信息熵对“不纯度”更加敏感、惩罚最强。在实际使用中二者的效果基本相同,但信息熵的计算比基尼系数更为复杂。另外,因为信息熵对“不纯度”更加敏感,所以将其作为指标时,决策树的生长会更加“精细”,因此对于高维数据或者噪音很多的数据,信息熵很容易过拟合,而基尼系数在这种情况下效果往往比较好,因此本文决策树的criterion参数设置使用基尼系数。
采用震后0 h和3 d数据集,计算决策树模型给出的训练集和测试集预测正确率随决策树最大拟合深度的变化(图6)。由图6可见,决策树最大拟合深度为1～10 h,训练集预测正确率随决策树最大拟合深度逐渐增大,10以后相对稳定。因此本文决策树最大拟合深度max_depth设置为10,可确保模型预测正确率尽可能高且避免过度拟合。
在机器学习领域,通常用多个参数从不同的角度对预测模型的优劣进行综合评价,而不是用准确率或其它单个指标。例如某医学算法,其预测某种疾病的准确率为99.9%,但这种疾病本身的发病率只有0.1%,换言之,即使不使用模型预测,直接判断所有人都不得这种疾病的准确率也能达到99.9%。因此,对于极度偏斜的数据(例如某种疾病患者和健康人数量差别特别大),仅用准确率等简单参数评价分类模型的好坏是有局限性的 Miracle.2021.机器学习——混淆矩阵(Confusion Matrix).https://blog.csdn.net/qq_39276337/article/details/119632707.。地震序列类型判定也存在类似问题,由于后续无更大地震的主余型和孤立型序列合计比例比较高,无需预测而直接判定后续不会发生更大地震可能的准确率平均可达80%左右(蒋海昆,2015)。据此,本文通过混淆矩阵定义更多的衡量指标以科学客观评价模型预测效能。
图6 震后0 h(a)和震后3 d(b)数据集决策树预测正确样本率随深度的变化
Fig.6 The change of correct sample rate with depth in decision tree prediction of 0-hour(a) and 3-day(b)datasets
对于本文涉及的三类地震序列(多震型、主余型、孤立型),混淆矩阵类似于一个3×3表格,用来记录分类器的预测结果,其中矩阵的行表示真实值、列表示预测值,结果有4种:TP、TN、FN、FP。首字母T或F分别代表预测结果是否符合事实(True或False),第二个字母N或P代表预测结果(Negative或Positive),具体描述见表2。
表2 混淆矩阵参数及其意义描述
Tab.2 Parameters of a confusion matrix and their meaning
基于混淆矩阵即可计算评价指标,本文主要使用准确率Accuracy、查准率Precision、查全率Recall三个指标,其计算公式如下:
准确率表示所有预测正确(包括正类和负类)的样本占总样本的比例,代表整体的预测准确程度; 查准率为正确预测为正的样本占全部预测为正的样本比例,代表对正样本结果中的预测准确程度; 查全率为正确预测为正的样本占全部实际为正的样本比例,代表实际为正的样本中被预测为正样本的概率。
表3给出了震后0 h数据集选择不同比例特征参数时的混淆矩阵及评价指标计算结果。在实际地震序列预测中,由于主余型序列自然概率较高,因而其预测的自然命中率也相对较高。多震型序列自然概率较低,且社会的恐震情绪会影响和干扰预测研究人员的决策,故在实际工作中几乎很少、也很难做出多震型序列的预测。因此在模型中,研究人员相对更看重多震型预测的查全率和查准率。
表3 震后0 h数据集的不同比例特征参数的混淆矩阵参数
Tab.3 A confusion matrix's parameters with different proportional features in the 0-hour dataset
由表3可知,对于多震型序列,特征参数选择率在10%～50%时,查全率总体较低(0.65～0.69); 特征参数选择率在60%以上时,Recall_C1查全率在0.80以上。对于多震型序列,其漏报的危害性更大,因此研究人员希望其查全率尽可能高。综合分析认为,在建立震后0 h数据集的震后预测模型时,选择60%的特征参数为最优解,此时的混淆矩阵如图7所示。
经过地震序列数据收集、特征参数处理、数据特征工程构建、决策树模型参数设置后,采用混淆矩阵对模型预测结果进行评价,就可以得到决策树模型给出的特征参数重要性。
图8为决策树模型给出的0 h数据集特征参数重要性。从特征参数类别来看,其重要性排序“主震附近区域历史地震序列类型占比”优于“主震震源机制相关参数”优于“主震相关参数”,其中,最重要的参数为40M5.0Ty1,显著高于其它特征参数。40M5.0Ty1为震中附近指定范围内M≥5.0历史地震序列类型为震群型的比例,这与震后首次会商做震后趋势预测时,常用的震中附近历史地震序列类型统计的思路一致(蒋海昆等,2015; 刘珠妹等,2019; Liu et al,2023)。
图7 震后0 h数据集中选择60%特征 参数的混淆矩阵
Fig.7 Confusion matrix for selecting 60% feature parameters in the 0-hour dataset
图8 决策树模型给出的0 h数据集特征参数重要性
Fig.8 Importance of feature parameters in the 0-hour dataset given by the decision tree model
采用同样方法,用决策树模型给出震后1 h至5 d共9个数据集特征参数重要性。结果显示,震后1～6 h, 4个数据集特征重要性排序从高到低分别为:“指定时段ML≥x小震频次及震级”优于“主震震源机制相关参数” 优于“指定时段最大余震震级” 优于“主震相关参数”优于“主震附近区域历史地震序列类型占比”; 震后12 h至5 d共5个数据集,特征重要性排序为:“指定时段最大余震震级”优于“指定时段ML≥x小震频次及震级”优于“主震震源机制相关参数”优于“主震相关参数”优于“主震附近区域历史地震序列类型占比”,但“指定时段序列衰减相关参数”“指定时段G-R关系相关参数”和“指定时段归一化能量熵”重要性为0,对序列分类没有贡献。由此可见,针对川滇地区地震序列资料,除震后0 h外,“主震附近区域历史地震序列类型占比”类参数的重要性值不高,表明随着序列数据资料的增加,序列类型判断更倚重动态的序列数据资料,而不是静态的历史地震序列类型统计数据。
由于对计算样本量及其本身计算误差等多方面的影响,“序列衰减相关参数”和“G-R关系相关参数”对序列判断的贡献率极低,这非常出乎意料,因为序列参数具有明确的物理意义,可以描述地震序列频度随时间的衰减特征和G-R特征。
地震序列参数在计算科学性、区域研究系统性以及震后早期阶段序列参数的稳定性、序列参数与地质构造、地球物理特征的相关性等方面,存在一系列问题(毕金孟等,2022a)。首先,在计算科学性方面,在震后早期阶段,由于大量余震的集中发生,会明显降低主震后数小时的地震监测能力(Iwata,2008),使参与拟合的地震数目偏少,导致使用依赖地震记录完备性的参数拟合方法遇到较大困难。其次,早期序列参数的剧烈变化,反映了主震发生后震源区应力的快速调整过程,将序列参数用于震后地震序列类型快速判断、地震预测等研究时需谨慎(毕金孟,蒋长胜,2019)。
毕金孟等(2022b)研究了震后1d和30 d数据拟合p值相关性,发现其相关性弱,这是由于p值表征的是余震活动的长期衰减特性,需要较长时间的数据来精确估计,因此震后早期阶段,想要精确计算并利用其做序列类型预测十分困难。其次,受区域深部介质环境的影响,震源区的应力调整、断层愈合以及破裂特征等多方面因素,序列参数差异明显,其共性特征难以总结。
最关键的是,人们对序列参数在地震序列分类中的应用及其研究有较大争议,如宋金等(2013)研究了44 次水库地震序列的b值平均值,发现震群型序列的与主余型加孤立型序列的 b值平均值有较为显著的差异,但两者数值分布范围有部分重叠; 李忠华等(2000)计算了云南地区27个地震序列p值,发现尽管主余型序列和震群型序列的p值平均值不同,但两者取值区间有较大的重叠,不容易从 p值来区分序列类型; 蒋海昆等(2006b)针对中国大陆293次记录相对完备的地震序列,分震后不同时段进行参数计算,结果显示b值始终无序列分类能力; 中国大陆地区中强地震序列震后早期阶段ETAS 模型参数的平均统计特征显示,b值随不同区域、不同主震断层类型或不同序列类型的变化不明显,p值与主震断层类型关系不明显,不同类型序列p值有一定差异(蒋海昆等,2007c)。
因此,序列参数受计算数据、计算方法、物性特征因素方面的影响,其在序列类型预测中的应用还处于不断探索阶段。
从最重要的特征参数结果来看,震后0 h,最重要的特征参数为震中附近指定范围内M≥5.0历史地震序列类型为震群型的比例; 震后1～6 h,最重要的特征参数为不同时间段序列余震的折合震级,该参数反映指定时段余震活动震级分布的离散程度; 震后12 h至5 d,最重要的特征参数为不同时间段的震级差,这与序列近80%的最大余震发生在主震后5 d内有关(祁玉萍等,2021)。在实际的地震序列分类工作中,主震与地震序列后续最大余震震级差常用于地震序列类型的分类定义,因此模型给出的结果与地震序列类型的定义是相互印证的。
此外,主震震源机制相关参数对震后不同时段内序列预测尤为重要,这些参数表征的是主震破裂方式,以及主震附近区域平均P轴的方位、倾角及其标准差,P轴方位和倾角相对于区域平均结果的偏差及离散程度(蒋海昆,王锦红,2023)。蒋海昆等(2006)对208次地震的主震破裂滑动类型与序列类型作了统计,发现当主震破裂滑动以倾滑或逆冲为主时,序列绝大多数情况下是主余型,属于多震型的可能性很小。而川滇地区的地震序列类型研究结果显示,地震序列类型与区域构造运动形式、断层几何结构有关(苏有锦等,1999; 蒋海昆等,2006a; 皇甫岗等,2007; 祁玉萍等,2021),而地震的震源力学机制又直接受控于区域构造。因此不难理解,主震震源机制相关参数对震后序列类型预测有较高贡献度。
主震参数尤其是其纬度、震级,对序列分类似乎具有一定的贡献。从川滇地区地震序列类型空间分布来看,尽管不同区域多震型地震序列类型有较大差异,但总体而言,多震型地震相对集中发生在纬度偏低的云南地区,越往北多震型地震越少,四川松潘以北再无多震型地震(图1)。这种纬度分布特征可以用来进行粗略的序列类型预测,也可以解释主震纬度在模型中对序列分类的重要性。祁玉萍等(2021)对南北地震带中段86 次5.0级以上的地震序列统计结果显示,随着震级增大,多震型、孤立型地震所占的比例减少,而主余型地震所占的比例增加。苏有锦等(2014)对全球7级地震研究结果显示,当主震震级M≥8.2时,均为主余型; 当主震震级M≥7.8时,不存在孤立型地震。以上研究结果表明,主震震级对序列类型分辨有一定帮助。
图9给出了震后不同时段决策树模型测试集的准确率统计结果,由图可见,震后随着时间的推移,决策树模型测试集的准确率有一定的波动变化,如震后6 h,高于震后12 h和18 h,震后5 d略低于震后3 d,这可能与前文所述的特征参数选择率有关,但准确率整体呈现上升趋势,表明随着震后序列资料的增加,模型预测的准确率会不断上升,最高值为震后3 d的0.823 5,表明震后3 d可以对序列类型进行相对可靠的判断,而国内目前通行的做法就是震后3 d向公众和政府公布序列类型预测结果(蒋海昆等,2015)。
图9 震后不同时段决策树模型测试集的准确率
Fig.9 Accuracy of decision tree model test set at different periods after an earthquake
本文关注的重点是特征参数的重要性,而不是地震序列预测的准确率,对于川滇地区而言,由于主余型和孤立型地震序列在统计中占有较高的样本,某次地震发生后,即使不做任何分析,预测其为主余型和孤立型地震序列的正确率仍然高达75%(表1),但这是简单的两分类问题结果(多震型、主余型+孤立型),而按照本文的三分类结果,震后3 d准确率高达82%,可见三分类结果明显优于的两分类结果,因而对序列类型预测而言,机器学习确实比现有“经验+统计”的传统预测方法有更高的预测效率。
本文基于1966—2021年川滇地区225次5级以上地震序列数据,构建了用于机器学习地震序列类型判定的10个不同时间段的特征参数集,对特征参数的不均衡和缺失数据情况作了处理,然后采用决策树模型对特征参数的重要性进行研究,得到以下结论:
(1)从宏观上看,不同时间段特征参数重要性类别有一定差异:对于震后0 h数据集,“主震附近区域历史地震序列类型占比”优于“主震震源机制相关参数” 优于“主震相关参数”; 对于震后1～6 h数据集,“指定时段ML≥x小震频次及震级” 优于“主震震源机制相关参数” 优于“指定时段最大余震震级; 对于震后12 h至5 d数据集,“指定时段最大余震震级” 优于“指定时段ML≥x小震频次及震级” 优于“主震震源机制相关参数”。这些情况表明随着序列数据资料的增加,序列类型判断更倚重动态的序列数据资料,而不是静态的历史地震序列类型统计数据。但在没有地震序列目录的情况下,震后0 h只能依靠历史地震序列类型比例这个参数,其中5级以上地震历史序列类型对震后趋势预测判断尤为重要。
(2)“指定时段序列衰减相关参数”“指定时段G-R关系相关参数”和“指定时段归一化能量熵”对计算样本量有一定要求,在“九五”数字化地震台网改建之前,川滇地区监测能力较弱,导致部分样本的部分特征参数,如G-R关系b值、序列衰减系数p值、h值等无法计算,特征参数缺失严重,完备性较低。决策树模型显示序列参数对序列分类贡献率极低,这可能与其受其较高的计算数据要求、科学的计算方法、复杂的物性特征等因素的影响有一定的关系。尽管序列参数在序列类型预测中的应用已有一些研究成果,但整体而言尚处于早期研究阶段。
(3)模型给出的数据集在不同时段最重要的特征参数为:震后0 h,最重要的特征参数为震中附近指定范围内M≥5.0历史地震序列类型为震群型的比例; 震后1～6 h,最重要的特征参数为地震序列在不同时间段的余震的折合震级; 震后12 h至5 d,最重要的特征参数为不同时间段的震级差。模型给出的结果与实践中预报结果以及地震序列类型的定义相互印证。
(4)不同时间段数据集结果显示,主震震源机制相关参数和主震参数对地震序列的分类有较高的贡献率。地震序列类型与区域构造运动形式和断层几何结构有关。在川滇地区,多震型地震序列相对集中发生在纬度偏低的云南的部分区域,且随着地震震级增大,多震型、孤立型地震所占的比例减少。
本文通过决策树模型给出的川滇地区不同时段数据集特征参数重要性结果,可为震后早期阶段,从繁杂众多的特征参数中筛选、剔除、确定合适的参数提供一定思路,提高地震序列跟踪工作效率,满足政府、社会及公众的需求。
