基金项目:湖北省自然科学基金面上项目(2022CFB294); 国家自然科学基金青年科学项目(52208485).
第一作者简介:欧阳谦(1999-),硕士研究生在读,主要从事结构抗震与机器学习方面的交叉研究.E-mail:2411738467@qq.com.
通信作者简介:骆 欢(1988-),博士,副教授,主要从事结构抗震与机器学习方面的交叉研究.E-mail:hluo@ctgu.edu.cn.
(1.湖北省地质灾害防治工程技术研究中心,湖北 宜昌 443002; 2.三峡大学 土木与建筑学院,湖北 宜昌 443002)
(1.Hubei Geological Disaster Prevention and Control Engineering Technology Research Center,Yichang 443002,Hubei,China;2.College of Civil Engineering & Architecture,China Three Gorges University,Yichang 443002,Hubei,China)
reinforced concrete columns; lateral strength; support vector machines; salp swarm algorithm; feature selection
DOI: 10.20015/j.cnki.ISSN1000-0666.2024.0051
地震是危害性极高的自然灾害,强烈的地震会使建筑物的抗侧移承载力下降、轴向承载能力丧失、非弹性形变机制发生改变,最终导致建筑物倒塌。在钢筋混凝土(RC)框架结构中,RC柱主要承受竖向和横向荷载,是框架结构主要的抗侧力构件,其抗侧移承载力包括延性柱的抗弯承载力和非延性柱的抗剪承载力(Noroozieh,Mansouri,2019)。RC柱发生破坏时,其失效模式分为三种:弯曲破坏、剪切破坏和弯剪破坏(于晓辉等,2022)。因此,准确预测RC柱的抗侧移承载力有助于优化RC框架的抗震设计。
对于RC柱抗侧移承载力预测,国内外许多学者开展了大量的研究工作(薛亦聪等,2020; 张勤等,2014; 甘丹等,2018; Pan,Li,2012)。在非延性柱抗剪承载力的预测方面,Priestley等(1994)提出了非延性柱抗剪承载力预测模型,将所得结果与剪切破坏柱试验结果进行了比较,证明了该方法能准确预测非延性柱的抗剪承载力; 邓明科等(2018)基于桁架-拱模型对混凝土加固RC柱进行受力分析,并推导出了抗剪承载力计算公式; Sezen和Moehle(2004)基于非延性柱的试验数据提出了一种新的柱抗剪承载力预测模型,并与现有的柱抗剪承载力预测模型进行对比,结果表明,模型的预测精度有所提高。数据驱动模型也被广泛应用于预测RC柱抗剪承载力(Luo,Paal,2021; Aval et al,2017; Ketabdari et al,2020)。Kakavand等(2021)总结了现有基于力学计算公式中不同设计变量之间相互组合构成的输入变量,基于497个非延性RC柱试件构成的数据集,按照考虑和不考虑位移延性的情况分别对这些输入变量进行线性和非线性回归分析,构建了用于预测非延性RC柱抗剪承载力的数据驱动模型。在延性柱抗弯承载力的预测方面,常用的方法是矩形应力块法(Lee,Son,2000; Bae,Bayrak,2003),该方法需要估计两个参数α1和β1来构建矩形应力块。关于这些系数,《结构混凝土建筑规范要求》(ACI 318-22)与Ozbak-kaloglu和Saatcioglu(2004)的研究给出了计算方法。虽然上述预测方法已被证明具有较好的预测性能,但是它们都存在着一定的局限性,即预测延性柱抗弯承载力的模型不能用于预测非延性柱的抗剪承载力,反之亦然。
机器学习(ML)方法如支持向量机等已被证实能够很好地解决上述问题,但其无法自动识别和剔除冗余与不相关特征,不能对数据集进行降维,这会增加模型的复杂度,容易导致最终形成的预测模型出现过拟合,进而影响模型的泛化性能。为此,许多研究者在如何将特征选择与ML方法相结合的问题上开展了大量的研究工作(Guyon,Elisseeff,2003; Huang,Wang,2006)。Lin等(2008)将粒子群优化算法与支持向量机相结合,最终形成的分类模型预测精度优于网格搜索等方法。虽然上述研究成功地将特征选择与ML方法相结合,但它们均聚焦在分类问题方面,而在回归问题方面涉及较少。且RC柱抗侧移承载力预测模型的构建过程属于回归问题,导致已有方法无法直接运用。
基于以上研究结果,本文将樽海鞘优化算法(SSA)(Mirjalili et al,2017)与ML方法中的支持向量机(LS-SVM)(Suykens et al,2002)相结合,提出了樽海鞘算法优化支持向量机(SSALS-SVM)方法,收集了248个RC柱试件的试验数据,建立了一组包含延性和非延性RC柱抗侧移承载力的试验数据集。基于此数据集,分别与已有的计算模型进行了对比。
支持向量机(SVM)(Cortes,Vapnik,1995)是一种常用的监督学习方法,其数学模型是基于1范数的损失函数,这使得其训练过程需要求解复杂的二次规划问题。而LS-SVM在继承SVM优点的情况下,将二次损失函数引入SVM,并将不等式约束条件替换为等式约束条件,极大地提高了计算效率。给定一组数据集{(xi,yi)}Ni,i=1,2,……,N,其中xi∈Rn为解释变量,yi∈R为响应变量,LS-SVM通过将目标函数最小化来找出解释变量与响应变量之间存在的非线性映射关系。其数学模型为:
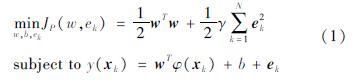
式中:e=[e1,e2,…,eN]T∈RN为误差变量; w=[w1,w2,…,wh]∈Rh和b∈RN通过使目标函数最小化得到; γ为正则化参数; 高维向量构建的矩阵φ(x)=[φ(x1),φ(x2),……,φ(xN)]T∈RN×h, 其中φ(·): Rn→Rh表示从n维到具有h维的高维度希伯特空间的映射函数; 响应或输出变量y=[y1,y2,……,yN]T∈RN。用拉格朗日乘子法将方程(1)的求解问题转换为对偶问题求解,并引进拉格朗日乘子,以构建拉格朗日函数:
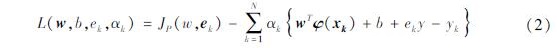
式中:α=[α1,α2,……,αN]T∈RN为拉格朗日乘子。利用Karush-Kuhn-Tucker(KKT)条件的最优性求解式(2),即分别求拉格朗日函数对w,b,ek,αk的偏导数,可得:
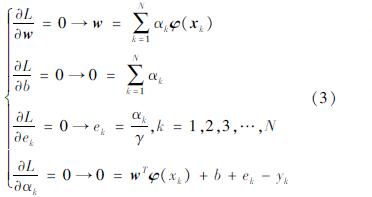
特征向量之间的内积在计算时较为复杂。为此,本文选用高斯核函数代替特征向量之间的内积,其计算模型如下:
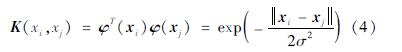
式中:σ2为核参数。LS-SVM模型的预测精度与两个超参数(σ2和γ)的取值息息相关,因此,本文引入樽海鞘优化算法(SSA)对其进行确定。此外,为了识别数据集中最能影响模型预测性能的解释变量组合(即最优特征组合),本文构建了一个控制解释变量组合的参数f,并将其作为优化参数耦合进SSA中,与前述两个超参数同时进行优化,进而形成樽海鞘算法优化支持向量机(SSALS-SVM)的数学模型。具体过程如下所述:
首先,给定f、σ2和γ 的取值范围,随机生成n个(f,σ2,γ)组合,其数学模型为:
(fi,σ2i,γi)=rand*(ub-lb)+lb,i∈(1,2,…,n) (5)
式中:f为挑选的特征数目; ub为f、σ2和γ的上界; lb为f、σ2和γ的下界; d为参数的数目。根据随机生成的f数值,随机从数据集中选取f个解释变量进行组合,作为最优特征组合的候选者。此外,σ2和γ也需要同时进行优化,因此需要建立f +2个决策变量,具体形式如图1所示。
如图1所示,Pf为随机挑选的解释变量。将σ2、γ 以及Pf输入目标函数中进行评估。对于目标函数,其建立过程如下所示:联立式(3)中的各方程式,消除方程式中的w和ek,化简可得:
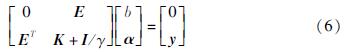
式中:E=[1,1,…,1]1×N; I为单位矩阵; K为核函数组成的核矩阵。
通过求解矩阵方程(6),可得模型参数α和b,进而可建立对偶空间下的预测模型,其表达式为:
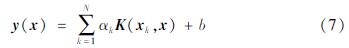
为了判断上述建立的f个解释变量是否为最优特征组合以及生成的σ2和γ值是否为最优参数,需要使用一种评估函数对通过方程(7)得到的结果进行评估。为此,本文采用均方误差(MSE)作为模型性能优劣的评估标准。其数学模型为:

因此,目标函数由方程(7)和方程(8)组成:方程(7)对结果进行预测,方程(8)对预测结果进行评估。基于已建立的目标函数,对n个(f,σ2,γ)组合进行评估,并对比n个MSE的大小,取其最小值作为本次评估的最佳适应度,对应的(f,σ2,γ)组合作为当前最优位置F。
将n个(f,σ2,γ)组合前一半设定为领导者,后一半设定为跟随者。领导者的位置跟F相关,根据F,通过一次次位置更新,不断向其靠近,位置更新公式为:
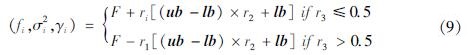
式中: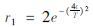 ; t表示当前迭代次数; T表示最大迭代次数; r3和r2是一个0~1的随机数,r3大于或小于0.5将决定领导者前进还是后退。跟随者的位置则与前一个个体位置相关,其数学模型为:
; t表示当前迭代次数; T表示最大迭代次数; r3和r2是一个0~1的随机数,r3大于或小于0.5将决定领导者前进还是后退。跟随者的位置则与前一个个体位置相关,其数学模型为:
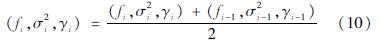
对于更新后的领导者和跟随者,其位置可能会超出设定的范围,因此需要将其重新限制到规定范围内。此外,当领导者和跟随者位置迭代更新后,需重新对其进行评估:将更新后的(f,σ2,γ)组合重新代入方程(4)、(6)和(7)中计算其预测值Ay^G1,并通过方程(8)计算其MSE。将更新后的每个(f,σ2,γ)组合的MSE与当前最佳适应度进行比较,若更新后的(f,σ2,γ)适应度优于当前最佳适应度,则以MSE更优的(f,σ2,γ)组合作为F。
重复以上步骤,直到达到最大迭代次数或适应度达到最佳(MSE=0),输出当前的F作为最优(f,σ2,γ)组合,并输出最优特征组合(P1,…,Pf),进而可得到LS-SVM预测模型的最优
形式。因此,从理论分析上看,本文提出的SSALS-SVM方法既能够优化模型的超参数σ2和γ,又能自动筛选数据中最能影响模型预测性能的解释变量x,形成最优特征组合(P1,…,Pf)。
给定一组数据集,图2描述了本文提出的SSALS-SVM的构建过程,其大致分为以下几个步骤:
①随机生成n个(f,σ2,γ)组合。
②将生成的n个(f,σ2,γ)组合输入目标函数中进行评估,以确定F。该过程需要将控制解释变量组合的参数f转化为f个解释变量构成的特征组合。
③更新领导者和跟随者的位置,并重新对更新后的(f,σ2,γ)组合进行评估。
④重复迭代,直到达到最佳适应度或最大迭代次数,输出最佳超参数组合和最优特征组合,进而得到最优LS-SVM模型。
为了评估提出的SSALS-SVM方法对RC柱抗侧移承载力预测的准确性以及泛化能力,本文搜集了248个弯曲破坏柱(延性柱)(194个)、剪切(18个)和弯曲-剪切(36个)破坏柱(非延性柱)的试验数据集,具体信息见表1。表1包含数据集中具体的26个设计变量(输入变量),以及各设计变量的平均值与标准差。
本节的主要目的是剔除无关变量,识别出既能影响延性柱抗弯承载力又能影响非延性柱抗剪承载力的设计变量,进而提高预测模型的泛化性能。为此,本文设定SSALS-SVM模型中f的取值范围为[3,10],这是因为过多或者过少的特征容易导致模型出现过拟合或欠拟合。将σ2和γ的取值范围设置为[10-6,10]和[10-6,1000 00], 这是因为σ2的取值过大时,会导致高斯核函数性能下降,而γ的取值越大,预测值与真实值的误差越小。此外,将d设置为3,种群规模设置为30,迭代次数设置为100。随机从26个设计变量中提取f个设计变量(f=3,4,…,10)
组成数据集,对每一个f值,共执行10次设计变量的随机组合。为了确立设计变量的数量对RC柱抗侧移承载力影响的不确定性,将248个试验数据按7:3划分为训练集和测试集,为了提高模型的预测精度,在训练模型的过程中采用十折交叉验证,即将训练集十等分,每次选取九份作为开发子集,剩余一份作为验证子集,并取十次训练过程的平均MSE作为此次优化的适应度。当达到最大迭代次数或最佳适应度时,输出最优特征组合及最优σ2和γ。基于输出的最优参数组合,重新建立SSALS-SVM模型,利用建立的SSALS-SVM模型预测测试集中柱的抗侧移承载力,并计算R2、RMSE和MAE,其计算公式如下:
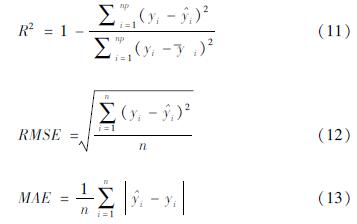
图3为不同解释变量数目f下模型预测结果的R2、RMSE、MAE箱型图。该箱型图是在f值一定时,基于10次不同的设计变量组合得到的。其中,箱型图的四分位距离越长,说明上四分位数与下四分位数之间的差异越大,即不确定性越大,进而说明该f值下,无法建立最优特征组合。
图3 筛选不同柱设计变量组合时SSALS-SVM模型的RC柱抗侧移承载力预测性能分析
Fig.3 The analysis of predictive performance for proposed SSALS-SVM model in the case of different combinations of selected features
如图3所示,当f=3时,箱型图的四分位距离最长,甚至出现异常值,这说明SSALS-SVM与下四分位数之间的差异越大,即不确定性越大,无法识别出柱设计变量的最优特征组合。随着f的取值变大,四分位距离逐渐缩小,即不确定性降低,模型的整体预测性能也在上升。当f=10时,箱型图中R2的中位值和平均值达到最大,RMSE和MAE的中位值和平均值达到最小。此时,模型的整体预测性能达到最佳且不确定性最低。
表2为不同挑选数目对应的最佳特征组合的R2、RMSE和MAE,其中,当挑选的特征数目为3时,模型性能较差,说明该数目下的特征组合不足以反映特征与响应变量之间的非线性关系。随着挑选特征数目的不断增加,当数目达到10时,模型性能达到最佳。因此,本文选取f=10时,箱型图中性能最佳所对应的设计变量组合作为最优特征组合。该组合包括轴向荷载、角部纵筋直径、中部纵筋直径、平行于加载位置处中部纵筋数量、箍筋肢数、箍筋直径、箍筋数量、箍筋面积配筋率、跨高比和轴压比。
为了充分评估SSALS-SVM模型的泛化性能,基于上一节筛选的最优特征组合,本文使用留一法交叉验证对数据集中柱的抗侧移承载力进行预测。留一法交叉验证是将248组柱试验数据划分248份,每次取1份作为测试集,剩下247份作为训练集,共执行248次计算。因此,通过使用留一法交叉验证,数据集中248个柱试件均作为测试集用于评估本文提出SSALS-SVM模型的泛化性能。使用留一法交叉验证预测的结果可根据柱破坏类型(即弯曲破坏、剪切破坏和弯曲-剪切破坏)进行划分,用于后续与传统基于力学的计算公式和数据驱动模型得到的结果进行对比,具体过程见下节。
基于上一节留一法预测的结果,本节主要用其与传统基于力学的计算公式和数据驱动模型得到的预测结果进行对比分析。对应计算模型的具体数学公式见表3,其中“AMR”指不考虑位移延性时的数据驱动模型(Kakavand et al,2021),“AMRK”指考虑位移延性时的数据驱动模型(Kakavand et al,2021)。表4为不同预测模型得到的R2、RMSE、MAE值,其中粗体值表示结果的最优值,“综合”指的是将弯曲、剪切和弯曲-剪切破坏柱的预测结果合并(即延性柱的抗弯承载力和非延性柱的抗剪承载力),用于量化模型的泛化性能。从表4和图4a中可知,ACI与OS模型预测性能较差,而相比于这两种方法,数据驱动模型预测性能有明显的提高,但SSALS-SVM模型的预测性能更加精确。从表4和图4中可知,相比于数据驱动模型,SSALS-SVM模型的R2最高提升了近28%,RMSE最高降低了近69%,MAE最高降低了近78%。对于非延性柱,SM模型预测性能优于PR模型,而数据驱动模型预测性能明显高于这两个模型,能较好地区分RC柱在地震荷载作用下的破坏模式(Luo,Paal,2018)。但是相比于数据驱动模型,SSALS-SVM模型在预测抗剪承载力时依旧表现出高预测精度,R2最高提升了近15%,RMSE最高降低了近53%,MAE最高降低了35%。
图5为轴压比、箍筋面积配筋率和跨高比在不同取值时对模型泛化性能的影响。图中,预测值与试验值比值越接近于1,则表明模型预测越准确。从图中可以看出,SSALS-SVM模型预测值与试验值比值绝大部分保持在1.0附近,这表明在本文所呈现的轴压比、箍筋面积配筋率和跨高比范围内,SSALS-SVM模型能够准确地预测延性和非延性柱的抗侧移承载力,具有较好的泛化性能。相比于其他模型,SSALS-SVM的泛化能力最高提升了近83%。
图5 关键设计变量对SSALS-SVM模型泛化性能的影响
Fig.5 Influence of key design variables on the generalization performance of proposed SSALS-SVM model
表4 各模型在不同破坏模式时的R2,RMSE,MAE值
Tab.4 R2,RMSE and MAE values for each model in the case of different failure modes
本文提出了樽海鞘算法优化支持向量机(SSALS-SVM)方法,用于剔除冗余和不相关特征。选取最具代表性、各特征之间相关性弱的特征子集,形成最优特征子集,并解决了传统的基于力学的计算公式和数据驱动模型在预测RC柱抗侧移承载力时泛化性能不足的问题。基于248个RC柱试件抗侧移承载力试验数据,分别与传统的基于力学的计算公式和数据驱动模型进行对比分析。主要结论如下:
(1)相比于传统机器学习方法,本文提出的SSALS-SVM方法能够自动识别并剔除数据集中包含的冗余和不相关特征,筛选出既能影响延性柱抗弯承载力又能影响非延性柱抗剪承载力的设计变量,降低了模型的复杂度。
(2)基于挑选的最优特征组合,与传统的基于力学的计算公式和数据驱动模型对比,本文提出的SSALS-SVM模型能够准确预测RC柱抗侧移承载力。相比于其他模型,其泛化能力最高提升了83%。
(3)在本文所呈现的轴压比、箍筋面积配筋率和跨高比范围内,SSALS-SVM模型具有较好的泛化性能。