本文构建场地土层地震动反应分析时域积分方法的基本思路如下:①选取场地土层地震反应分析的弹性半空间上覆盖非线性土层计算模型,模型中含饱和砂土层; ②建立可以考虑砂土孔压影响的土体动力本构模型,推导出相应的应力-应变关系式。本构模型构建中,以土体动态骨架曲线本构模型为基础,选取适用于非规则荷载作用下的孔压增长模型和实用的孔压与最大剪切模量及极限剪应力的关系,推导出可以考虑孔压影响的土体动力应力-应变关系式; ③采用显式中心差分方法,结合多次透射边界条件和本文建立的土体动力应力-应变关系,模拟土层模型中的波传播; ④基于Matlab平台编制相应的计算程序。

付海清等(2018)提出了计算非规则作用下孔压增长模型,并通过试验确定了公式中的各项系数。该模型认为ΔU_N受应力历史、应力强度、循环次数以及固结比4个因素的线性耦合影响,即:

ΔU_N=F₁(H)·F₂(I)·F₃(N)·F₄(K_C) (1)

式中:F₁为应力历史影响项; F₂为应力强度影响项; F₃为循环次数效应项; F₄为固结比影响项,水平自由场地固结比K_C一般为1.6,相应的F₄取值为1.0。

应力历史影响项表示振动循环开始时,孔压的增长不受应力历史影响,当场地土体完全液化时,应力历史影响项对孔压比增量的影响达到峰值,其表达式为:

F₁(H)=1-U_N (2)

应力强度影响项表示为:

式中:α为与砂土密实度相关的系数,具体取值见表1,表中C₁,C₂,C₃ 是与砂土密实度相关的系数; β₁是由埋深决定的系数,由应力折减计算公式计算得到,具体取值见表2; β₂为上覆层实际重度与有效重度的比值,需要依照场地实际情况来具体计算; A为水平加速度幅值,单位为m/s²; g为重力加速度,一般取10 m/s²。

表1 砂土密实度参数表
Tab.1 Sand compactness parameter

表2 埋深影响系数表
Tab.2 Soil depth influence coefficients

循环次级效应项表示为:

式中:e为自然常数; C₁、C₂、C₃是与砂土密实度有关的系数,具体取值见表1。

饱和砂土场地遭遇地震动作用时,孔压的增长会降低土体的最大剪切模量和抗剪强度。因此,进行场地土层地震动反应分析时,需要利用最大剪切模量及抗剪强度与孔压之间的关系对砂土体应力—应变关系进行修正。本文采用孙锐等(2018)基于动三轴试验所提出的最大剪切模量及抗剪强度修正关系,即:

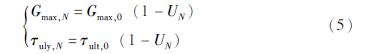
式中:G_max,N为第N-1次循环后的最大剪切模量; τ_uly,N为第N-1次循环后的极限剪应力。U_N=μ_N/σ'_V,即该层第N次循环时孔压与初始有效上覆应力的比值。

将修正关系式(5)引入动态骨架曲线应力—应变关系中,得到考虑饱和砂土孔压影响的土体动态骨架曲线应力—应变关系:

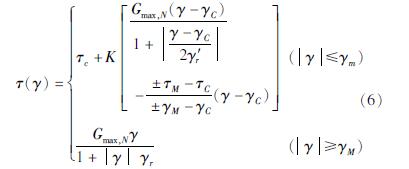
式中:K为考虑拟合试验阻尼比值的修正系数,其表达式如下:

且γ'_r和γ₀计算公式为:

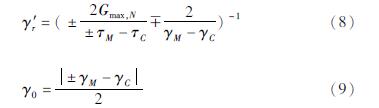
反之取“-”。

将复杂的场地模型简化为一维土层模型,定义模型中基岩、上覆土体及土体自由面皆水平成层; 定义地表水平加速度仅由基岩处的垂直向上的剪切波引起。将土层分成N个厚度为h_n的土层(n=1,…,N),且各土层的计算厚度满足:

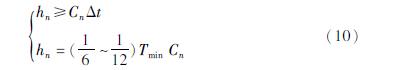
式中:C_n为第n层土层的剪切波速; T_min为输入地震动中需要考虑的频率成分的最小周期。设土体运动速度为v(z,t)、剪应力为τ(z,t)、剪应变为γ(z,t),可建立土层中介质的运动方程、变形相容方程及土体本构方程如下:

式中:ρ为土层或者基岩的密度; t为时间。采用中心差分法求解方程式(11),可以得到:

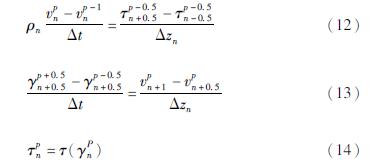
式中:

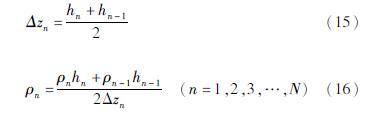
计算初始条件为:

式中:v^p_n表示p时刻第n层计算土层顶面处的速度; τ^p_n+0.5、γ^p_n+0.5分别表示在p时刻第n层计算土层中心处的剪应力及剪应变。

弹性半空间中的土体单元无法使用上述方法进行求解,需要通过设置人工边界条件来确定,本文选取多次透射边界作为模拟边界,计算公式为:

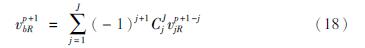
式中:J为多次透射公式的阶数; C^J_j为二阶项系数。当J=1时,多次透射边界公式即退化为一阶透射公式,即:

式中:v^p_1R是坐标为z_N的内节点在t=pΔt时刻的外行波; v^p+1_bR为人工边界在t=(p+1)Δt时刻的外行波。若已知人工边界在t=(p+1)Δt时刻的入射波场为v^p+1_bI,则人工边界在t=(p+1)Δt时刻的总场,即人工边界节点速度反应为:

使用修正后的土体动态应力-应变关系,建立时域积分方法并进行数值积分求解。在Matlab平台上编写代码,得到考虑砂土孔压影响的场地土层地震反应的时域计算程序,命名为Sand Pore Pressure One-dimensional Time Domain(以下简称SPODTD)。

本文使用美国加纳山谷岩土台阵(Garner Valley Downhole Array,简称GVDA)所观测到的地震动加速度记录和孔压变化记录,检验本文所构建的考虑砂土孔压影响的场地土层地震反应的时域计算方法的实用性和有效性,并同时与不考虑砂土孔压影响的场地土层地震反应计算结果进行比较,分析砂土孔压变化对场地地震动的影响。GVDA场地放置了4个电导压计来测量孔压变化,分别布置在地下4.0 m、6.0 m、8.5 m以及12.3 m处,分别对应模型中的第六、九、十一、十三层。并且放置了7个井下加速度计,分别位于地下6 m、15 m、22 m、50 m、150 m、220 m和500 m处。表3为GVDA场地勘测报告数据(Youd et al,2004),表4为根据GVDA场地所建立的场地土层地震反应分析模型。因GVDA场地所提供的数据中并没有提供各类砂土的动剪切模量比和阻尼比与剪应变之间的关系参数,本文计算分析中使用的是其它相应砂土类试验数据,见表5。

表3 GVDA台阵勘测报告数据
Tab.3 Data from the GVDA site survey report

表4 根据GVDA场地建立的场地土层地震反应分析模型
Tab.4 Seismic response analysis model for soil layers established based on GVDA site

表5 各类砂土的动剪切模量比和阻尼比与剪应变的关系
Tab.5 Relationship between dynamic shear modulus ratio and damping ratio values and shear strain for each soil body

选取编号为“214151344”的地震动记录作为计算分析样本,震级为5.2,震源深度为14.2 km。其地震动加速度记录(Youd et al,2004),如图1所示。根据SPODTD程序计算得到有孔压和无孔压的地表加速度时程曲线的及其相应的加速度反应谱对比,如图2所示。由图2a可知,使用SPODTD程序计算得到的地表加速度峰值略低于原始观测记录,两者地表加速度时程大致相同。由图2b可知,在长周期成分, SPODTD程序计算的加速度反应谱与实际观测记录的比较一致; 在短周期成分,计算的加速度反应谱与实际观测记录相地较小; 在T=1.0 s附近,计算的加速度反应谱相地较高。但两者的加速度反应谱曲线整体趋势较为相似,考虑到观测记录的误差,笔者认为该计算结果可以验证SPODTD程序计算结果的有效性。

图1 输入地震动加速度记录波形
Fig.1 The input ground motion curve

由模型中不同层原始观测孔压及SPODTD程序计算孔压结果(图3)可知,由程序计算得到的孔压增长曲线与观测孔压的增长趋势上基本保持一致两者,震动结束后也基本一致,因程序所使用的孔压增长模型不能考虑孔压消散的影响,所以程序计算得到的最终孔压略高于观测孔压。随着深度的增加,孔压增长也随之下降,程序计算得到的孔压增长与观测孔压的吻合度也在提升。

图2 GVDA台阵加速度原始观测曲线、SPODTD程序计算的加速度曲线(a)及其加速度反应谱(b)
Fig.2 Time-history curves of the acceleration recorded by GVDA and the acceleration calculated with SPODTD software(a)and their corresponding acceleration response spectrums(b)

为研究孔压对场地地震反应分析的影响,笔者从地震动三要素进行分析。由图1、2a可知,基岩输入地震动加速度峰值为0.49 m/s²,SPODTD程序计算的地表加速度峰值为0.70 m/s²,放大比例为143%; 不考虑孔压时,程序计算地表加速度峰值为0.73 m/s²,放大比例为149%,其结果略高于考虑孔压时的计算结果,这表明孔压的存在会略微降低地表加速度的峰值。根据括弧持时的概念,计算加速度持时,SPODTD程序计算得到的考虑孔压和不考虑孔压的地表加速度持时分别为26.99 s和26.67 s,两者基本一致,孔压的存在并没有对其造成影响; 由图2b可知,孔压存在时,加速度反应谱在短周期(T<0.3 s)出现较为明显的衰减现象; 对长周期成分,孔压的存在并没有造成明显的影响。

图3 第六(a)、 第九(b)、 第十一(c)、 第十三(d)层土层孔压原始观测孔压和SPODTD程序计算孔压
Fig.3 Original sand the calculated pore water pressures on the 6th(a), 9th(b), 11th(c), and 13th(d)soil layer

为进一步研究孔压对砂土场地地震反应分析的影响,将输入地震动分别放大0.5倍、1倍、2倍以及5倍进行计算,计算结果如图4所示。

由图4可知,SPODTD程序计算得到的有无孔压时的加速度反应谱之间存在一些差异的,主要表现在考虑砂土孔压影响的场地地表地震动中短周期成分减少,而孔压对长周期成分影响不大,这较好符合了孔压对场地地震动的影响的一般规律,因此孔压对场地地震动所产生的影响是需要考虑的。整体上,是否考虑砂土孔压影响的场地地表地震动加速度反应谱谱形整体上较相似。4种幅值地震动条件下,砂土孔压对场地地表加速度反应谱造成的影响最大差值(均取绝对值)分别为19.1%、19.9%、25.3%、25.9%,平均差值则分别为0.61%、2.20%、3.81%、7.23%; 随着地震动幅值的增大,孔压对长周期成分的影响也随之增大。但由于本文计算的算例有限,还需更多的算例来验证本文方法,产生此现象的具体原因也仍需进一步分析。

图4 0.5倍(a)、1倍(b)、2倍(c)和5倍(d)输入地震动幅值的计算结果
Fig.4 Results from the input ground motion with 0.5 times(a),1 time(b),2 times(c)and 5 times(d)amplitudes

整理不同幅值输入地震动作用下地表加速度峰值,并计算考虑有无孔压的地表加速度峰值比值,结果见表6。由表6可知,缩放倍数为0.5时,孔压的存在略微降低了幅值; 随着输入地震动幅值继续增大,孔压的存在使得地表加速度峰值出现了不同程度的增大,且SPODTD程序计算与不考虑孔压时地表加速度峰值的比值分别为101%、96%、94%以及85%。以上表明输入地震动幅值的增大以及孔压的增大,对地表加速度峰值的影响也在逐渐增大,且两者呈现正相关关系。地表加速度持时计算结果表明,孔压对其影响基本可忽略不计。

表6 不同幅值地震动作用下的地表加速度峰值
Tab.6 Peak ground acceleration subjected to different input ground motion amplitudes