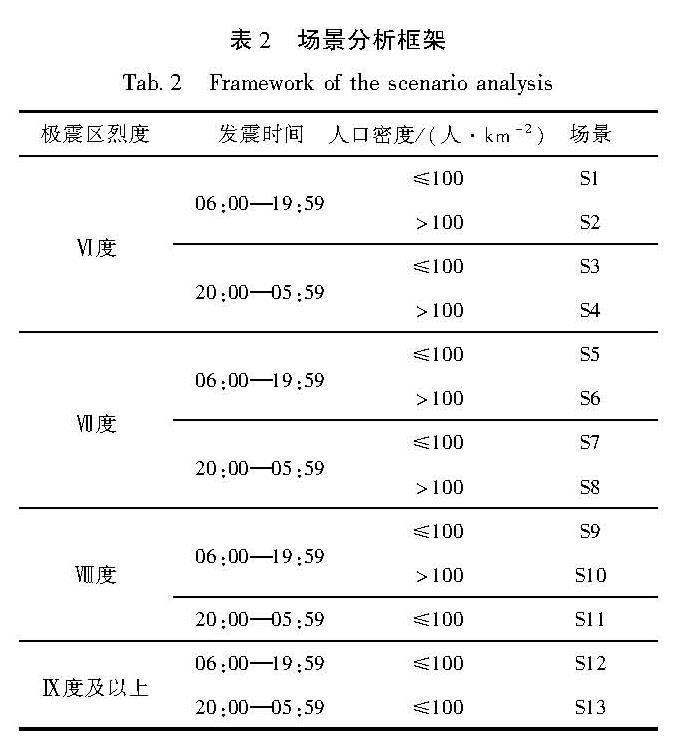
3.1 模型结果
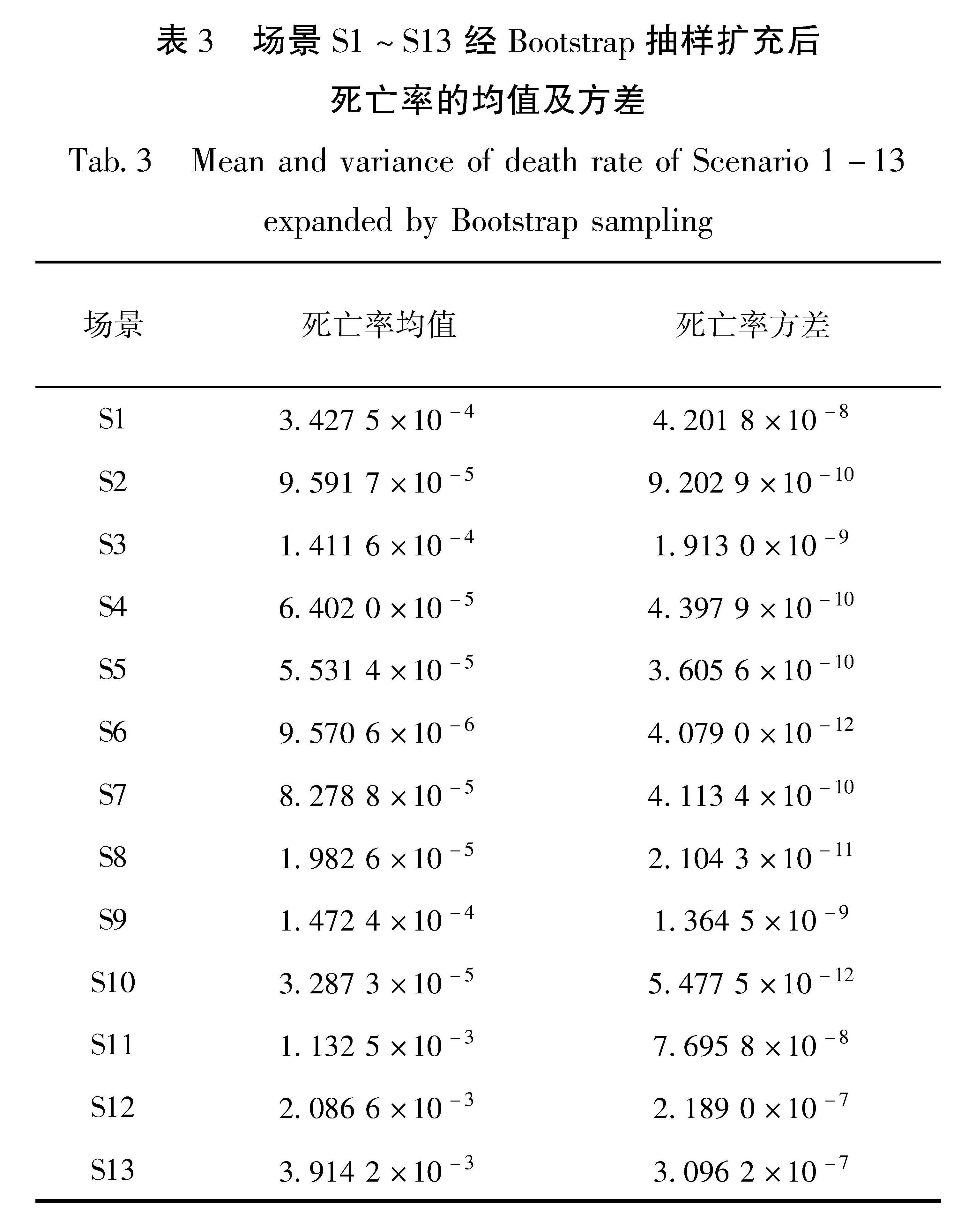
以场景S1为例,将场景S1中的死亡率通过Bootstrap抽样扩充为1 000个数据集,每个数据集中包含100个数据,再将死亡率均值x作为随机变量,拟合1 000个数据集死亡率x的频率直方图(图1),经过Bootstrap抽样扩充后各个场景死亡率x的均值、方差见表3。
图1 场景S1经过Bootstrap抽样扩充后各数据集均值x的频率直方图
Fig.1 Scenario 1 expands the frequency histogram of the mean x of each data set by Bootstrap sampling
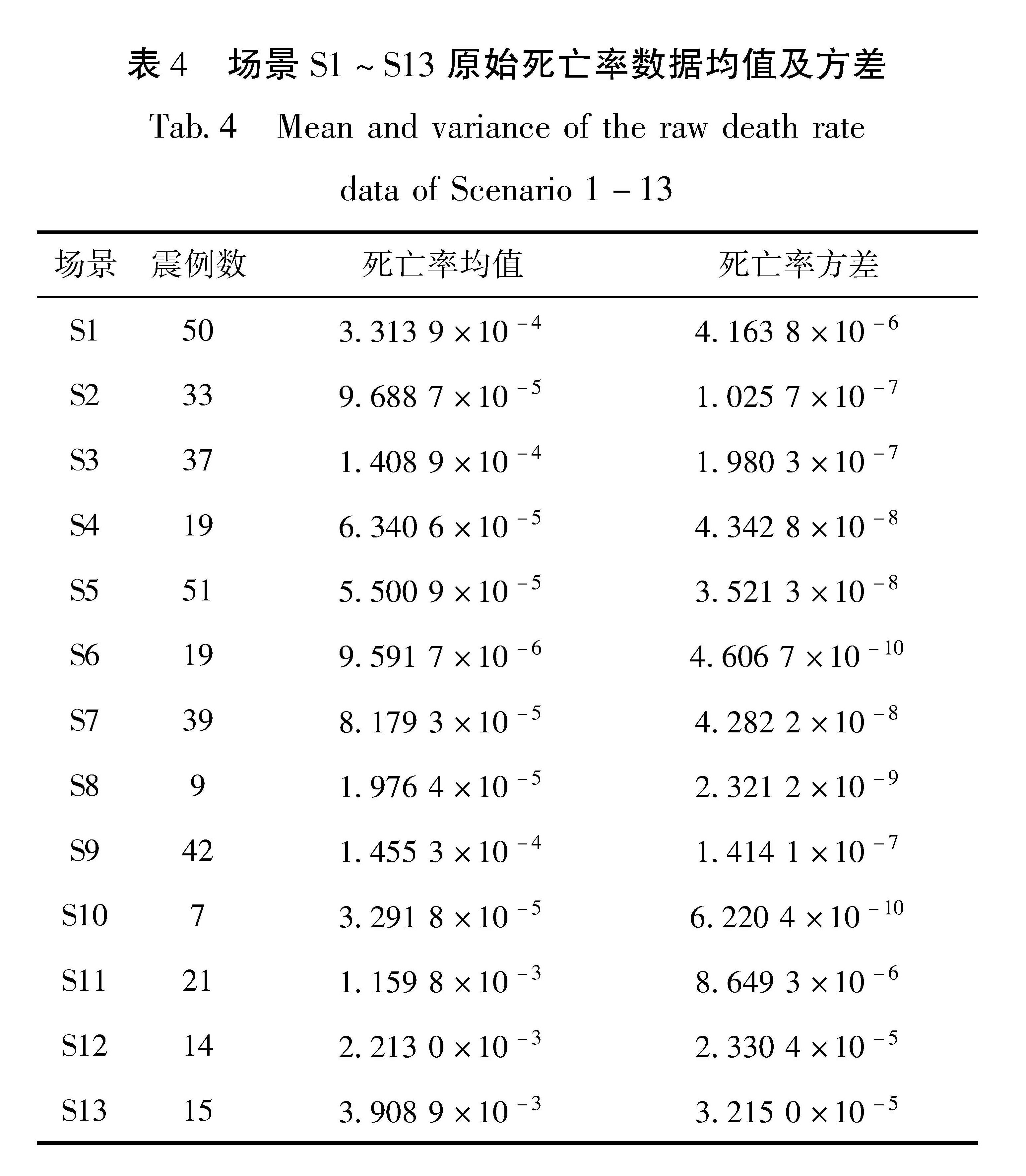
为验证Bootstrap抽样扩充后死亡率数据的可用性和可靠性,将Bootstrap抽样扩充后死亡率的均值、方差(表3)与原始死亡率数据(表4)进行对比。结果表明,Bootstrap抽样扩充后的死亡率均值与原始死亡率均值特征基本一致,表明Bootstrap抽样方法能够保持样本统计量的可靠性和精确性,不会引入明显的偏差。同时死亡率方差相较于原始数据普遍偏小,该特征说明Bootstrap抽样方法有效地减少了数据的不确定性,提高了数据的稳定性和可靠性。因此Bootstrap抽样方法扩充后的虚拟数据为后续的分析和预测工作提供可靠的基础。
表3 场景S1~S13经Bootstrap抽样扩充后死亡率的均值及方差
Tab.3 Mean and variance of death rate of Scenario 1-13 expanded by Bootstrap sampling
表4 场景S1~S13原始死亡率数据均值及方差
Tab.4 Mean and variance of the raw death rate data of Scenario 1-13
场景S1的死亡率均值服从 [FK(W][BG(][BHDWG*2,WK*2W]x[BG)W][FK)]~N(3.427 5×10-4, 4.201 4×10-8),将该正态分布作为先验分布,可得超参数μ0=3.427 5×10-4,σ20=4.201 8×10-8。为了不让先验均值和方差的影响过大,取k0=v0=1。
由于该数据集均值总体μ,σ2均未知,故采用正态—逆伽马分布N—IG(μn,kn,vn,σ2n)对其进行后验修正。根据联合后验密度公式可以求出后验参数值μn=3.571 7×10-7,σ2n=4.208 3×10-8,kn=vn=1 001,即后验正态—逆伽马分布为N—IG(3.571 7×10-7, 1 001, 1 001, 4.208 3×10-8),则该正态—逆伽马分布的联合后验密度为:
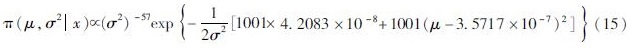
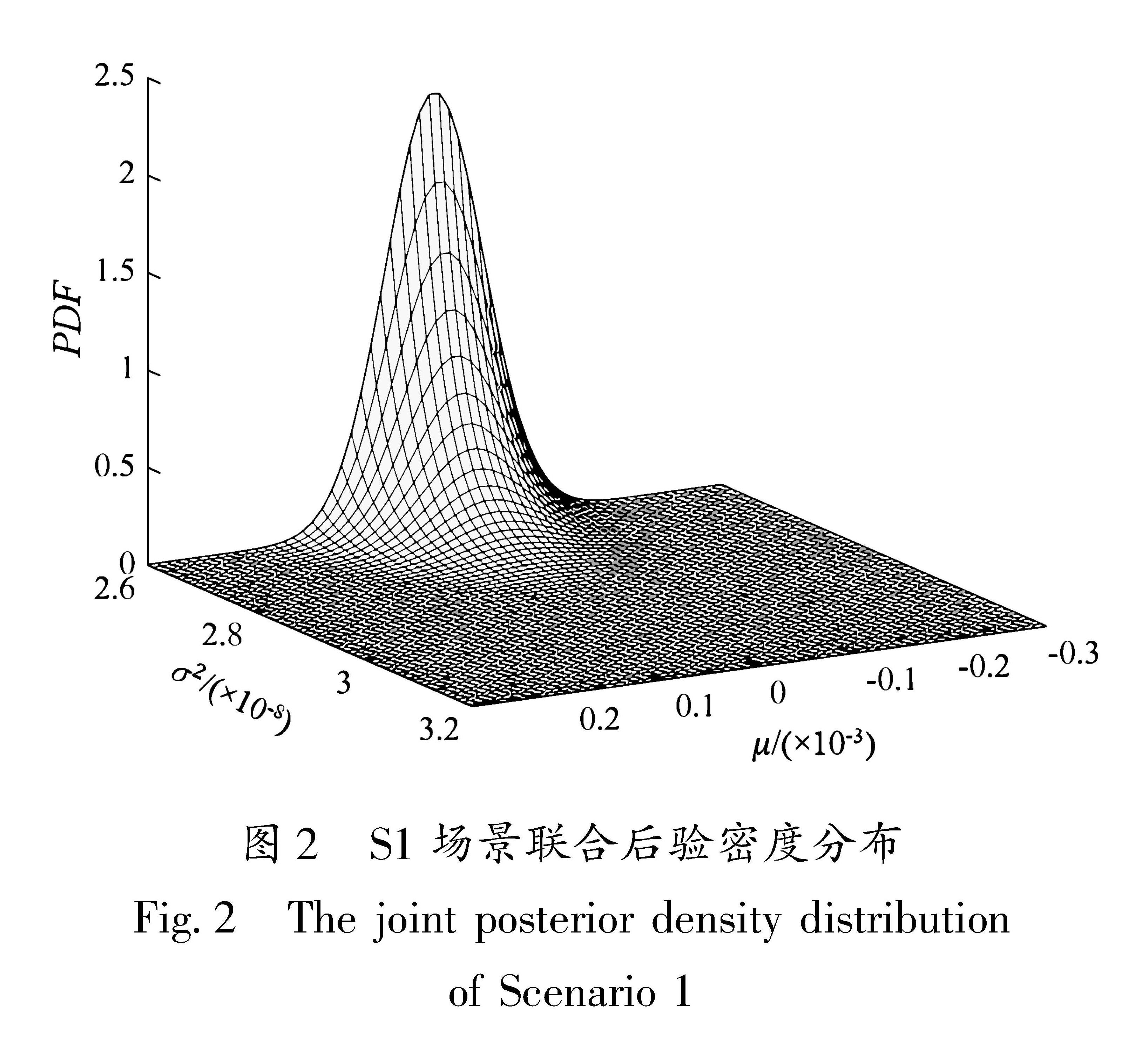
S1场景联合后分布如图2所示。由图可见,后验概率密度函数的曲面为单峰对称。根据正态近似法将其后验分布近似为正态分布,再对此正态分布进行截断分析。
图2 S1场景联合后验密度分布
Fig.2 The joint posterior density distribution of Scenario 1
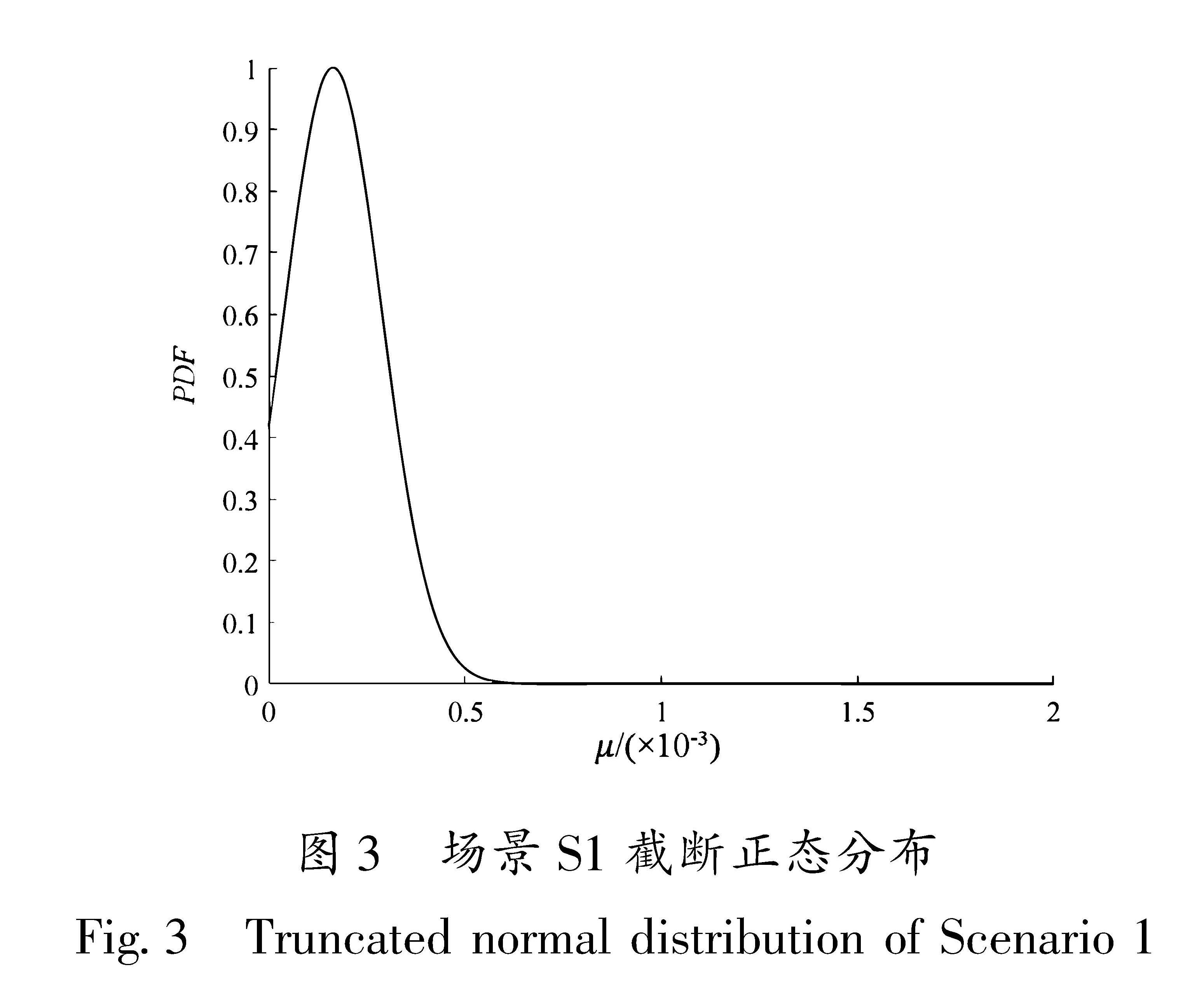
由于死亡率≥0,所以截断正态分布的范围为[0,+∞),经式(10)计算取得α=-0.001 7, β=+∞,将其带入上述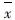 所服从的截断正态分布,可得φ(1.638 1×10-4,1.530 8×10-8,0,+∞,x ),该截断正态分布如图3所示。
所服从的截断正态分布,可得φ(1.638 1×10-4,1.530 8×10-8,0,+∞,x ),该截断正态分布如图3所示。
当该截断正态分布的逆累积分布函数为95%时,对应的死亡率为4.023 1×10-4,因此得出烈度为Ⅵ度、发震时间在白天且人口密度≤100时,95%的死亡率区间为[0,4.023 1×10-4)。
将收集的历史震例按照基础场景分级后,利用各场景下的死亡率数据结合死亡率评估模型,按照S1计算过程计算各场景下的死亡率均值以及95%的死亡率区间,见表5。由表可知,各场景下的死亡率均值及95%区间估计基本符合在极震区烈度相等并且人口密度相同的条件下,夜间的死亡率大于白天的死亡率,但在极震区烈度为Ⅵ度时,人口密度>100人/km2的死亡率均值及95%区间的上限值小于人口密度≤100人/km2的死亡率均值及95%区间的上限值。
图3 场景S1截断正态分布
Fig.3 Truncated normal distribution of Scenario 1
表5 各场景下的死亡率均值及95%死亡率区间
Tab.5 The average death rate and its 95% interval for each scenario
3.2 模型验证
模型的准确性和可靠性,需要通过实际发生的震例进行验证,随机选取中国大陆地区13次地震的人员死亡数据,将其代入本文模型得到预测人员死亡数量,并与实际死亡人数进行对比。利用表5估算各场景下的死亡率与95%死亡人数区间,结果见表6。
表6 本文模型估算的中国大陆13次地震人员死亡率和95%死亡人数区间
Tab.6 The averge death rate and its interval for 13 earthquake in Chinese Mainland evaluated by the model
由表6可见,模型总体评价效果较好,大多数震例的实际死亡人数与模型评价结果在同一数量级且被包含在区间内,评价结果较为准确。由于涉及众多不确定性因素,个别震例评估结果与实际情况存在一定出入。如模型估算的2011年云南盈江5.9级地震95%死亡人数上限值与实际死亡人数相差不大,相对来说较为合理; 而2008年四川攀枝花凉山交界6.1级地震的评估结果与实际死亡人数悬殊较大,此次地震人员伤亡较多的主要原因是大量房屋倒塌和受损(张雪飞等,2008),进而导致评估结果与实际死亡人数相差较大。
 作为随机变量, 认为地震人员死亡率均值
作为随机变量, 认为地震人员死亡率均值 服从正态分布即
服从正态分布即 ~(μ,σ2),其概率密度函数为(茆诗松等,1998):
~(μ,σ2),其概率密度函数为(茆诗松等,1998):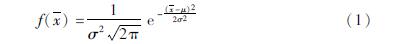
 为地震人员死亡率均值; μ、σ2均未知,确定这两个参数即可确定地震人员死亡率的概率密度函数。
为地震人员死亡率均值; μ、σ2均未知,确定这两个参数即可确定地震人员死亡率的概率密度函数。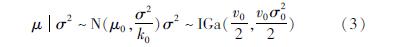
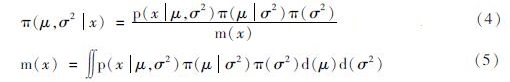
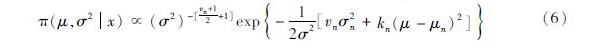
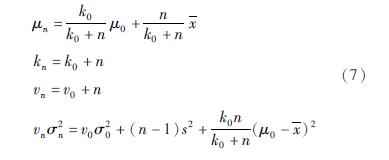
 作为随机变量构建上述地震人员伤亡的贝叶斯模型,该贝叶斯估计后验分布函数的定义域为(-∞,+∞),而根据实际情况,地震人员死亡率大于等于零,因此使用截断正态分布,对地震人员死亡率进行估计。
作为随机变量构建上述地震人员伤亡的贝叶斯模型,该贝叶斯估计后验分布函数的定义域为(-∞,+∞),而根据实际情况,地震人员死亡率大于等于零,因此使用截断正态分布,对地震人员死亡率进行估计。 ~N(μ,σ2),a、b为两个已知实数,则在a<x<b的条件下,x服从截断正态分布,该截断正态分布是通过将其范围外的值设置为0来修改原正态分布的概率密度函数,并将其范围内的值统一缩放,使其积分为1。
~N(μ,σ2),a、b为两个已知实数,则在a<x<b的条件下,x服从截断正态分布,该截断正态分布是通过将其范围外的值设置为0来修改原正态分布的概率密度函数,并将其范围内的值统一缩放,使其积分为1。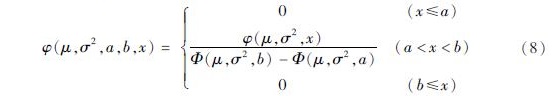
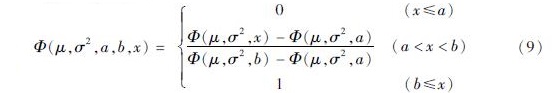

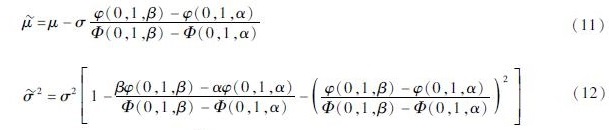

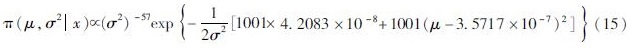
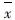 所服从的截断正态分布,可得φ(1.638 1×10-4,1.530 8×10-8,0,+∞,x ),该截断正态分布如
所服从的截断正态分布,可得φ(1.638 1×10-4,1.530 8×10-8,0,+∞,x ),该截断正态分布如