中江南塔位于四川省中江县铜鱼山的山顶,是典型的山地场地楼阁式砖石古塔。中江南塔平面形式为正八边形,共9层,坐南朝北,塔高30.2 m,塔基为金刚底座,塔基以上逐层收分,各层塔檐外挑,并设有心室。受2008年四川汶川M_S8.0地震的影响,塔身受损严重(袁建力,2018)。

本次试验研究的设备主要包括小型振动台和加速度传感器。振动台为北京波谱公司研发的型号为WS-Z30-50小型振动台,包括控制仪、传感器、功率放大器、激振器、振动台面等,振动台设备的主要技术参数见刘晓莉(2014)的研究结果。

试验的首要工作是设计试验模型的相似比。相似比一般包括几何相似比、弹性模量相似比、密度相似比及加速度相似比等。通常情况下,可以根据几何、材料及弹性模量相似比来确定其他物理量相似比(周颖,吕西林,2016)。根据振动台台面几何尺寸及台面负载确定试验模型高度为90 cm,再依据中江南塔原型结构塔高确定几何相似比S_t为1/33.5。

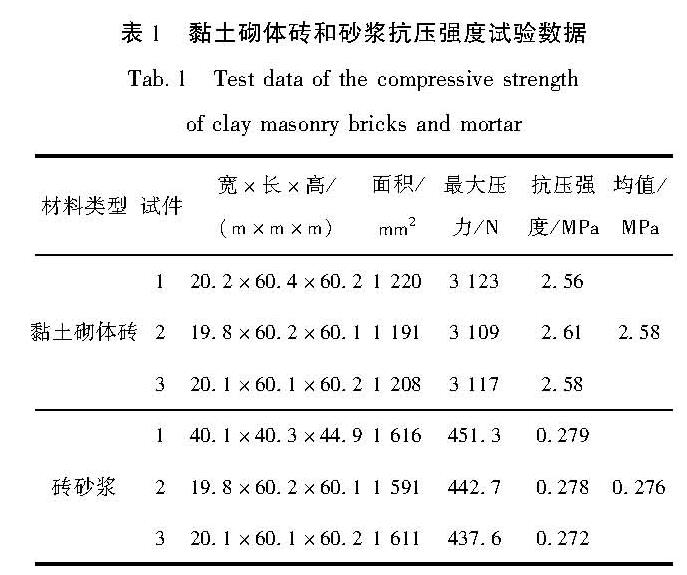
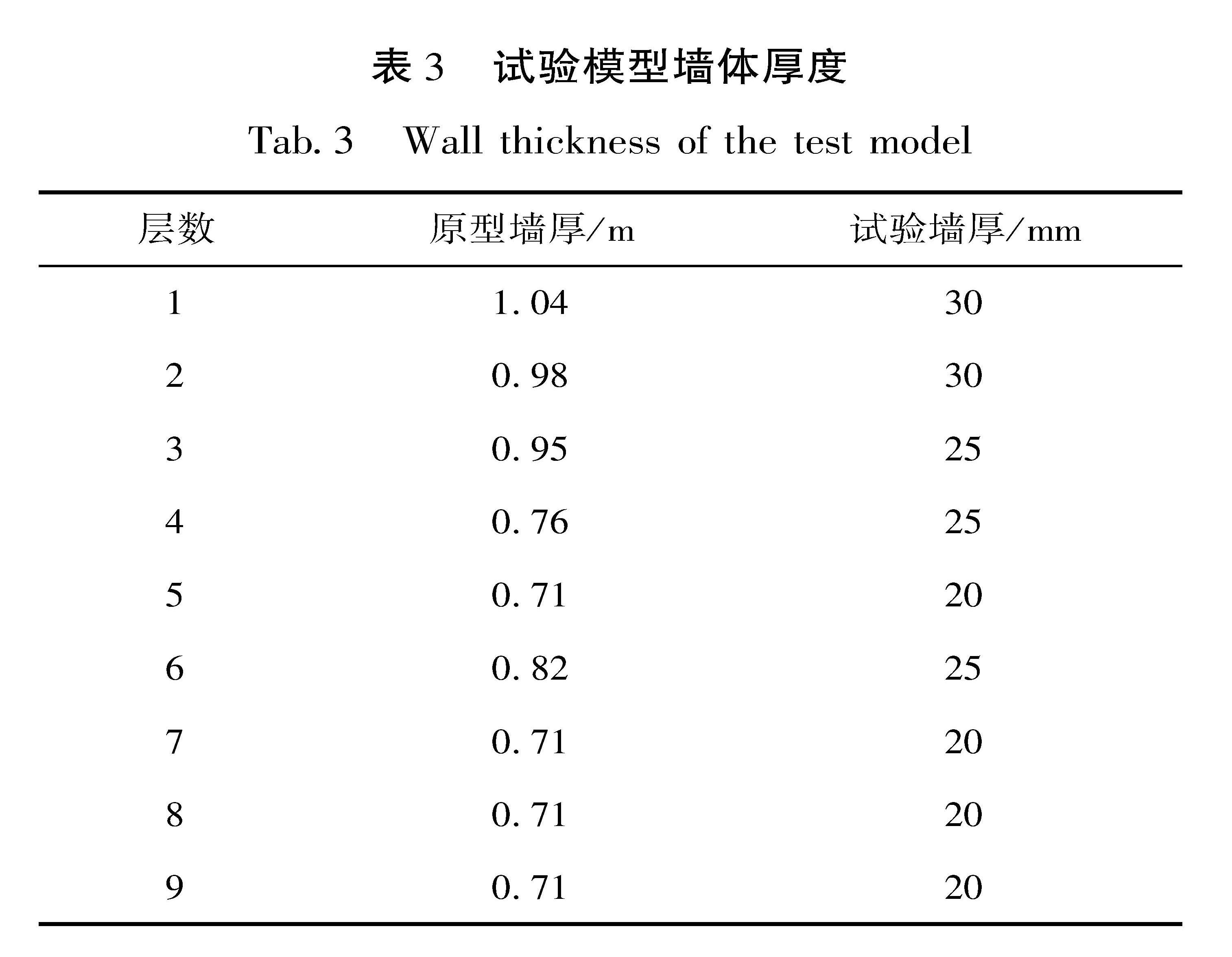
试验材料的选用是决定能否达到预期的关键。利用摩尔-库伦强度理论表征砌体材料强度,由相似比关系可知,试验砌体材料的黏结力应很小(刘晓莉,2014)。课题组最初选择石膏、烧结黏土砖及黏土与砂土混合烧结的砖块作为砌块,但是试验时无法使其发生与实际震害相似的破坏。其主要原因为模型材料的强度过大,无法满足相似比要求,致使模型在振动过程中难以破坏。而且对于同种材料,在一定范围内构件尺寸减小会导致材料强度增加,如果采用与原结构强度相近的材料,试验模型将更难破坏。因此在缩尺比较小的条件下,本文选用强度较低的替代材料,以期模型的破坏特征与实际震害相似。经多次尝试确定砌块的材料采用纯黏土,砂浆由滑石粉、腻子粉、水按照10:10:9的比例制作而成。课题组对试验所用砖块材性进行力学性能测试,结果见表1。依据材性试验和胡跃祥(2012)实测结果可确定弹性模量相似比为1/26。试验塔体材料密度测量值为2.4 g/cm³,中江南塔塔身材料密度测量值为1.8 g/cm³,由此确定密度相似比为1.33。基于上述3类物理量的相似比确定加速度相似比为0.965,进一步可获得其他物理量相似比,见表2。依据几何相似比和原型结构墙厚确定试验模型墙厚度见表3。

表1 黏土砌体砖和砂浆抗压强度试验数据
Tab.1 Test data of the compressive strength of clay masonry bricks and mortar

表2 试验模型各物理量的相似比
Tab.2 Similarity ratio of various physical quantities of the test model

表3 试验模型墙体厚度
Tab.3 Wall thickness of the test model

依据传统砖石古塔砌筑工艺,制作2个一致的中江南塔试验模型分别代表位于山顶和山底的古塔,如图1a所示。为了获得古塔结构在地震作用下的层间变形特征,将加速度计布设在楼板位置处。受限于模型洞口尺寸,无法将加速度传感器置入楼板形心处。考虑到楼板水平向平面内刚度较大,因此将加速度计设置于楼板侧面。为了确定试验模型的加载方向,建立了中江南塔数值结构模型,通过模态分析方法获得了模型的自振频率,得出的EW方向前3阶自振频率分别为1.52、5.98、12.39 Hz,NS方向前3阶自振频率分别为1.52、5.93、12.25 Hz。结果表明,模型结构2个水平方向的自振特征极为接近,因此选择在结构EW方向进行加载,如图1a所示。由于原型结构的八、九层无楼板,所以将七、八、九层视为同一层,共布设7个加速度计于结构上,另外1个加速度计布置在振动台面上,如图1b所示。[KH*1D][XC姜治军2A.TIF; %100%108] [XC姜治军2B.TIF; %100%108]

图1 中江南塔试验模型(a)及加速度传感器布设方式(b)
Fig.1 Test model of the Zhongjiang South Pogado(a)and its acceleration sensor deployment(b)

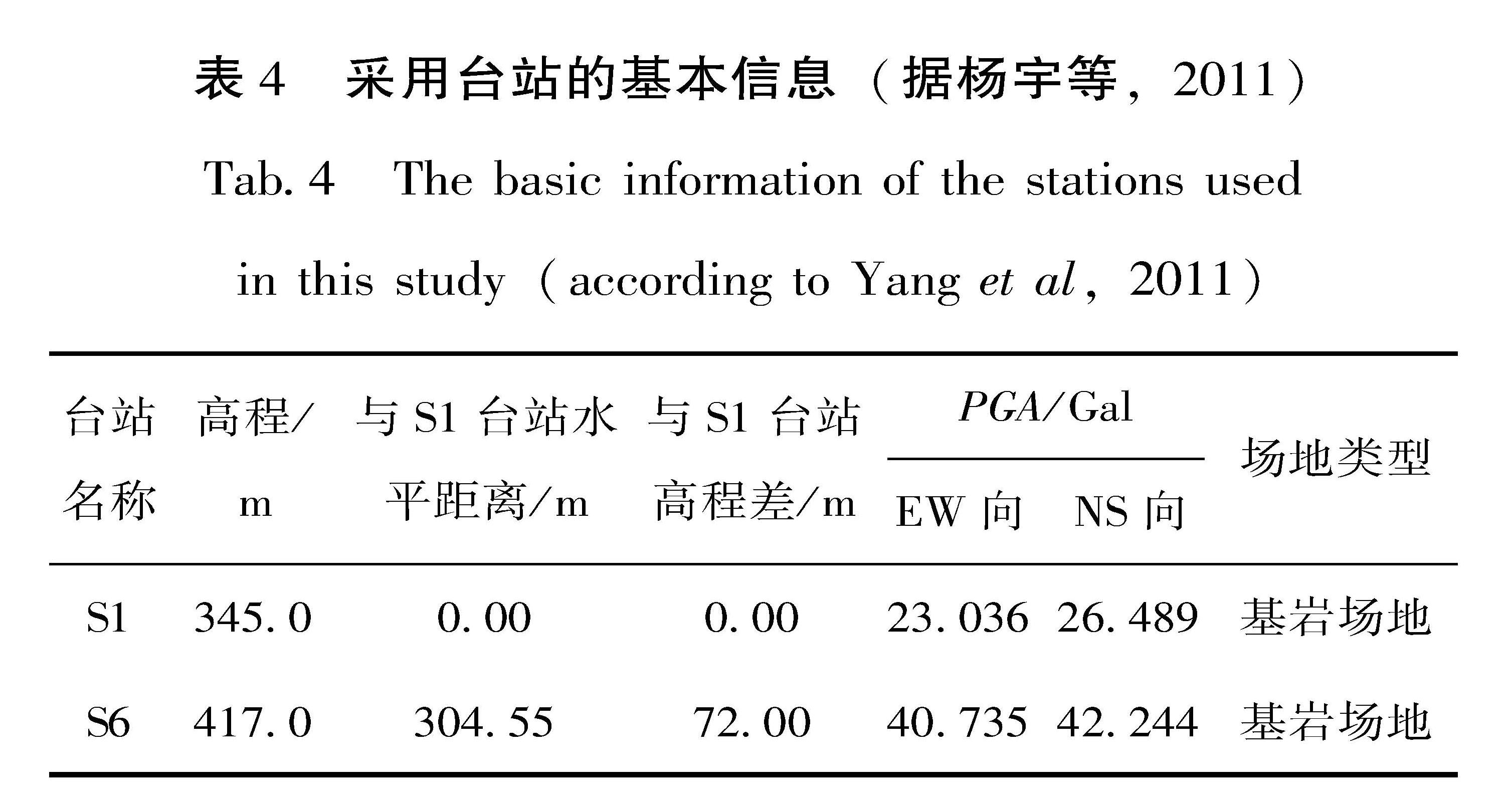
本文旨在研究山体地形对砖石古塔地震反应的影响规律,因此输入地震动应来自山地场地强震动台站。为了能与自由地表结构地震反应进行比较,还需要临近山体的自然地表台站记录。通过筛选,选取了汶川M_S8.0地震发生时位于四川省自贡市西山公园内的地形台阵加速度记录作为地震动输入。该地形台阵包含8个位于不同位置的台站,其位置基本沿山脊分布(图2),其中S1和S6分别为山底和山顶的基岩台站。选取同一次地震发生时S1和S6两个台站的记录作为试验研究的基底输入,可以排除由输入地震动场地条件差异引起的结构反应差别,便于通过比较获得地形效应对古塔地震反应的影响规律。S1和S6台站基本信息见表4。

表4 采用台站的基本信息(据杨宇等,2011)
Tab.4 The basic information of the stations used in this study(according to Yang et al,2011)

图2 自贡地形台阵地形剖面示意(据杨宇等,2011)
Fig.2 Schematic profile of station arrangement (according to Yang et al,2011)

由于本文研究的振动台为水平向单向输入,选用了2个台站EW向分量为输入地震动,其加速度时程及其反应谱如图3所示。由图3及表4可知,2条地震动的卓越周期介于0.2～0.7 s,S6与S1两台站EW向分量的PGA比值为1.768。

为研究地震作用下古塔的损伤演化过程,需开展不同强度的基底输入下的振动台试验。

图3 输入地震动加速度时程(a)及其反应谱(b)
Fig.3 The time history of acceleration(a) and the response spectrum(b)

本次试验采用的基底输入为一组汶川地震的真实记录,需要通过调幅得到不同强度的输入地震动。张江伟等(2017)通过有限元法建立边坡数值模型,定义了山顶与山底地震动的峰值加速度的比值为放大系数,研究输入地震动峰值对放大系数的影响。结果表明输入地震动峰值为100和200 Gal时的放大系数仅相差约9%,因此本文试验暂不考虑输入地震动幅值对地震动放大系数的影响。保持S6、S1台站记录之间的幅值比不变,对其进行调幅,以获得11个幅值的水平向输入地震动。具体为使S1台站记录的峰值加速度分别为20、30、40、50、100、200、300、350、400和450 Gal,分别将S1和S6台站的调幅地震动输入山底古塔和山顶古塔作为地震激励,形成了本试验的11个工况,具体加载制度见表5。

表5 加载制度
Tab.5 The test program

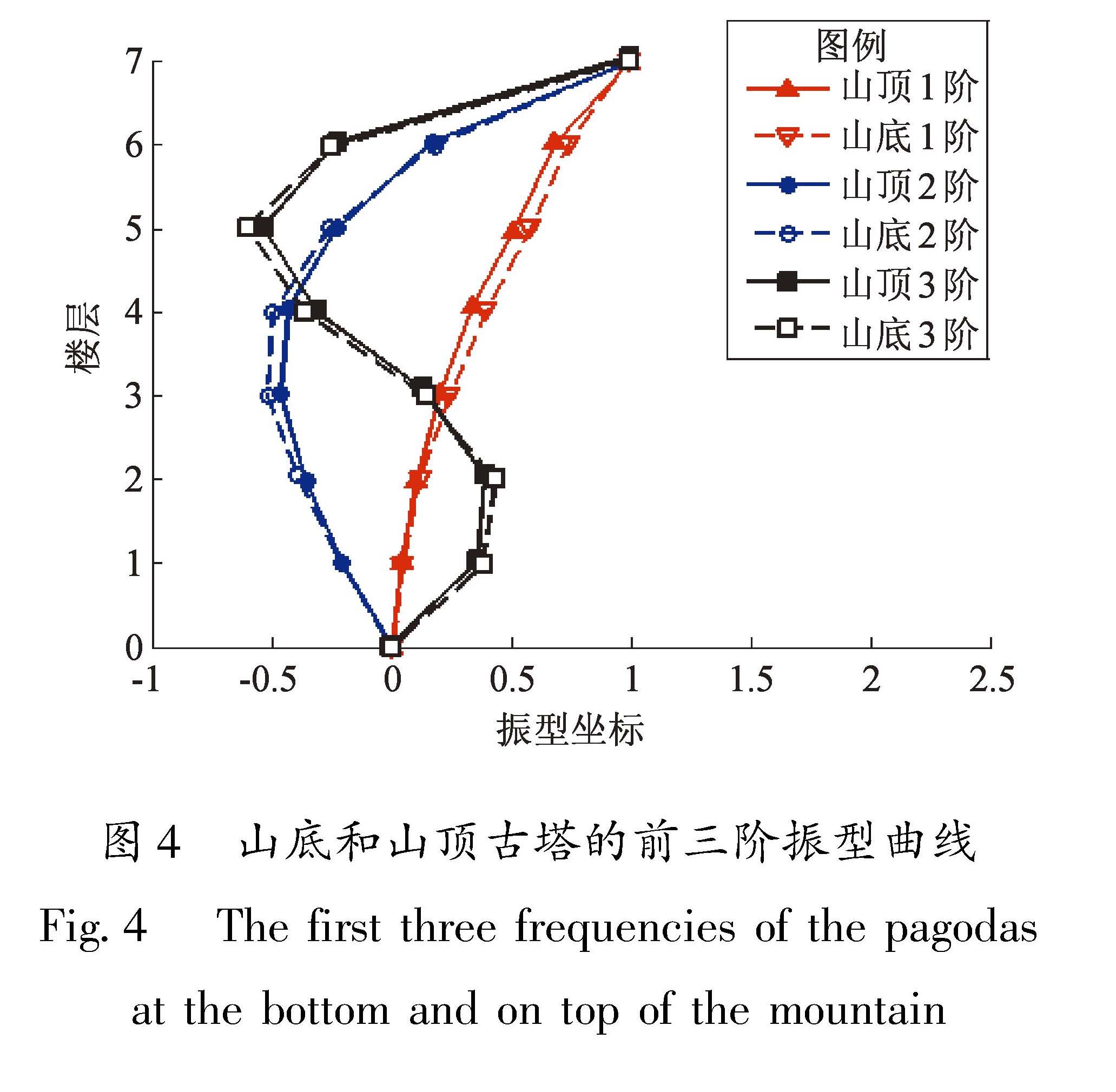
模型动力特性是分析结构地震反应特征的基础。为了获得试验模型动力特性,在各工况之间利用振动台为结构输入白噪声,对结构进行模态分析获得结构的自振频率及模态振型(表6、图4)。同时给出了对中江南塔现场动测得出的自振频率(胡跃祥,2012)。

由图4和表6可知,山底与山顶古塔的前三阶自振频率接近,前三阶振型曲线几乎重合,即两塔的动力特性极为一致,因此结构地震反应的差别可归因于输入地震动的差别。考虑到山顶与山底记录来自同一地震的基岩场地,因此地震动的差别主要源于地形效应。值得注意的是,2座试验模型的自振频率经相似比转化后与原型结构的自振频率十分接近,尤其是基本频率与原结构相差仅为3.88%。

表6 山底和山顶古塔的自振频率
Tab.6 The natural frequencies of the pagodas at the bottom and on top of the mountain

图4 山底和山顶古塔的前三阶振型曲线
Fig.4 The first three frequencies of the pagodas at the bottom and on top of the mountain

结构自振频率可表征结构的整体损伤。图6给出了古塔结构在各工况下的前三阶自振频率变化趋势。由图6可知,当从工况1加载到工况4时,2座古塔的自振频率均未发生明显变化,表明2古塔未发生明显破坏。当加载至工况5、山底地震动幅值为100 Gal时,山底古塔自振频率仅表现出微小变化,但是山顶古塔的自振频率明显减小,其前三阶频率分别减小10%、9%和8%,表明此时山顶古塔结构发生了整体破坏。当加载至工况6、山底地震动幅值为150 Gal时,山底古塔前三阶自振频率均减小6%,山顶古塔的前三阶频率减小幅度约为20%,表明此时2座古塔均发生了明显破坏,尤其山顶古塔的破坏更为严重。当加载至工况7、山底地震动幅值为200 Gal时,山底古塔前三阶自振频率减小约10%,山顶古塔的前三阶频率分别减小33%、29%和28%,此时山顶古塔底部出现贯通裂缝,结构接近倒塌。

图5 各工况下山底及山顶古塔试验现象
Fig.5 Damage to the ancient pagodas at the bottom and on top of the mountain on various working conditions

图6 各工况下山底和山顶古塔结构的前三阶自振频率变化趋势
Fig.6 The variation trend of natural frequencies of the ancient pagodas at the botrom and on top of the mountain on various conditions

为了研究山体地形对砖石古塔地震加速度响应的影响规律,比较了2座古塔各层峰值加速度随楼层的变化趋势,计算了同一测点山顶与山底古塔峰值加速度的比值,如图7所示。结果表明,在各工况下随着结构层数的增加,各层加速度峰值均呈现增加的趋势,且山顶古塔的加速度峰值明显大于山底古塔。峰值加速度的比值表明,山顶古塔峰值加速度为山底古塔的2～3倍,反映了地形效应对结构地震加速度响应的影响,尤其对于砖石古塔结构上部而言,地形效应对结构动力响应的放大影响更加明显。需注意的是,虽然地震动的幅值发生了变化,但是楼层峰值加速度放大倍数几乎不变。

相对位移是指古塔各层与底座的绝对位移之差。为了研究山体地形对砖石古塔的相对位移反应的影响规律,图8给出了山底与山顶古塔最大相对位移随加载工况的变化趋势。由图可知,随着输入地震动峰值加速度的增加,最大相对位移也增加。2座古塔各层最大相对位移随着楼层的增加均呈现增加趋势,其原因为输入地震动卓越频率与结构基本频率比较接近,致使结构发生了以基本振型为主的振动时,模型各层间的最大剪力随高度的减小而增加,使得底层层间剪力最大。

图7 各工况下山底和山顶古塔峰值加速度分布特征
Fig.7 Distribution characteristics of the peak acceleration of the pagodas at the bottom and on top of the mountain on various conditions

图8 各工况下山底和山顶古塔最大相对位移的变化趋势
Fig.8 Trend of the maximum relative displacement of the pagodas at the bottom and on top of the mountain on various conditions

由于模型底层门、窗洞口面积较大,对抗剪能力削弱显著,最终导致其底层发生明显破坏,与试验现象一致。也就是说,试验模型的破坏形式由其自振特性、地震动输入的频谱特征以及结构构造特点共同决定。

为了进一步对比同一工况下2座古塔的最大相对位移关系,本文计算了山顶古塔与山底古塔在同一位置处的最大相对位移比值,如图8所示。从图中可以看出,相同工况下,山顶古塔的最大相对位移明显大于山底古塔,其相差倍数为1.4～4.5。值得注意的是,当山脚地震动幅值为150 Gal时,相对位移的放大倍数显著增加,即此时2座古塔相对位移的差别尤为显著,其原因为此时山顶古塔底部产生水平向贯通裂缝,引起上部结构各层均发生较大的相对位移。

为了分析山体地形对砖石古塔的层间位移角的影响规律,图9给出了2座古塔最大层间位移角随楼层的变化趋势。由图可知,随着古塔高度的增加,最大层间位移角也逐渐增加。为了更加直观地分析地形效应对结构层间位移角的影响,本文计算了同一工况下山顶古塔与山底古塔的各层最大层间位移角的比值,结果显示当山底地震动幅值小于150 Gal时,该比值基本小于2,且数值相近,但是当山底地震动幅值为150 Gal时,该比值接近于4。这表明当结构发生明显的破坏时,层间位移角将显著增加。

图 10给出了山顶与山底古塔地震响应比值随加载工况(自由地表地震动幅值)的变化趋势。由图可进一步看出,对于楼层加速度而言,山顶与山底古塔的加速度峰值比值与自由地表地震动幅值相关性较弱。但是对于楼层最大相对位移和最大层间位移角而言,该比值与自由地表地震动幅值具有显著相关性,即古塔结构楼层相对位移和层间位移角的地形放大效应与地震动强度具有一定相关性。

图9 各工况下山底与山顶古塔最大层间位移角的变化趋势
Fig.9 Trend of maximum story drift of the pagodas on top and at the bottom of the mountain on various conditions

图 10 山顶与山底古塔地震响应比值随工况的变化趋势
Fig.10 The variation trend of the ratio of seismic response along with the variation of the input amplitude