(1.中国地震台网中心,北京 100045; 2.应急管理部 国家自然灾害防治研究院,北京 100085)
(1.China Earthquake Networks Center,Beijing 100045,China)(2.National Institute of Natural Hazards,Ministry of Emergency Management of the People's Republic of China,Beijing 100085,China)
seismicity rate index; seismic activation; seismic quiescence; earthquake prediction; prediction performance; Sichuan-Yunnan region
DOI: 10.20015/j.cnki.ISSN1000-0666.2025.0027
地震预测是世界性科学难题,其研究具有很大的挑战性。虽然地震能否被预测曾经出现过较大争议,但关于地震预测的研究和地震前兆的寻找却从未停止(Gulia et al,2020; Katsumata,Zhuang,2020; Savran et al,2020; Zhang et al,2021; Yu et al,2022a)。其中的典型代表是“地震可预测性合作研究”(Collaboratory for the Study of Earthquake Predictability,CSEP)计划,鼓励全球研究人员定义和发展多种地震预测模型,采用向前地震预测试验、可对比的数据、统一规范的计算标准和严格科学的统计检验方法评估等方式开展国际合作研究,通过对模型的严格统计检验与评估,提高对地震可预测性的认识(Schorlemmer et al,2018)。中国于2009年加入了CSEP计划,2018年成立的中国地震科学实验场成为CSEP 2.0阶段在中国的新测试区(张盛峰,张永仙,2021)。
在各种地震前兆中,地震活动性变化一直扮演着重要角色。其中,地震活动平静和增强作为典型的地震活动性异常受到广泛关注。长期以来,我国主要是基于地震活动图像进行经验预报(呼楠等,2024; Yu et al,2022b)。国外研究者更偏重于使用一些参数来定量分析地震活动性的变化,先后提出了3种比较有代表性的方法分别是ZMAP(Wiemer,Malone,2001)、RTL(Sobolev,Tyupkin,1999)和PI(Rundle et al,2002)。基于这些方法,不少强震前的中小地震平静或增强现象得以被识别和研究(Zhang et al,2017),如2008年汶川MS8.0地震(Huang,2008)、2004年苏门答腊MW9.1地震(Katsumata,2015)和2011年日本东北M9.0地震(Katsumata,2017)前出现的中小地震显著平静。由于地震前兆活动图像往往难以在不同地震前重现,我国的经验预报在半个多世纪的实践中并没有取得显著性突破(石耀霖等,2018),严格定量化的统计预报将是一个发展方向。
为了定量分析小震活动的增强和平静,姜祥华于2019年提出地震发生率指数方法(姜祥华,2020),并将该方法应用到中国地震台网中心日常的震情跟踪工作当中,在不少中强地震前识别到了地震活动显著增强异常,如2020年1月19日新疆伽师MS6.4地震(孟令媛等,2020)、2020年7月23日西藏尼玛MS6.6地震(姜祥华等,2021)和2021年3月19日西藏比如MS6.1地震(田雷等,2021)。本文将详细介绍地震发生率指数方法的原理和算法,然后使用该方法对2014年1月1日—2023年12月31日川滇地区的11次强震开展震例回溯研究,分析总结前兆异常的主要特征,最后对不同时空预测参数下的预报效能进行定量评价,进而认识地震发生率指数异常对强震时间和地点的指示能力。
川滇地区位于青藏高原东南隅,受高原物质侧向挤出的影响,区内构造变形强烈、强震频发。中国地震科学实验场就位于上述区域内部。本文计算所用的ML≥3.0小震目录来自中国地震台网中心国家地震科学数据中心,起始时间选为2009年1月1日。中国地震局于2007年底建成了新一代中国数字地震观测系统,并于2008年10月1日正式提供地震观测报告等数据产品,台网检测能力大幅提升。因此选取2009年1月1日以来的地震目录可确保在数据质量上的统一。2014年1月1日—2023年12月31日,川滇地区先后发生了11次MS≥6.0地震,将这些地震作为预测研究的目标地震。目标地震的起始时间选择为2014年1月1日是因为计算需要选取5年时长作为背景,预报只能从该时间开始。小震和目标地震的震中分布如图1所示。
一次较大地震的发生,通常在短时间内会触发大量余震。为了消除强烈余震活动造成地震活动增强的假象,在数据预处理阶段运用陈凌等(1998)提出的G—C法对地震目录进行余震删除。目录的完备性对计算结果的准确性也有重要影响。本文采用最大曲率法(MAXC)(Wiemer,Wyss, 2000)来估计研究区域内的最小完备震级MC分布。将区域剖分为0.25°×0.25°的网格。对每个网格,挑选距离网格中心50 km内的地震事件用于计算MC。上述网格间距和空间窗口半径与下文计算所用参数一致。圆形窗口内的最小样本数规定为200,小于200则不进行计算。每个样本进行Bootstrap重采样1 000次,从而获得关于MC的误差估计。2009年1月1日—2023年12月31日,川滇地区的最小完备震级和误差如图2所示。MC的最大值为ML2.5,标准差大都小于0.4。本文选择ML3.0作为计算的震级下限,以确保地震的完备性。
图1 2009年1月1日—2023年12月31日川滇地区M≥3.0地震分布
Fig.1 Distribution of M≥3.0 earthquakes that occurred in Sichuan-Yunnan region from Jan.1,2009 to Dec.31,2023
将计算区域按一定间距划分为网格。以每个网格中心为圆心,取半径为r的圆作为采样窗口。对于t时刻,往回取长度为Tb的时间窗t0～t作为背景时段,其中t0=t-Tb,取长度为Tw的时间窗t1～t作为异常探测时段,其中t1=t-Tw。为了定量分析每个网格的地震活动性变化,选取泊松分布作为参考模型。假设在背景时段内发生的地震个数为N,如果地震在时间上均匀发生,则Tw时间内的平均地震发生率λ为:
图2 川滇地区的最小完备震级分布(a)和误差估计(b)
Fig.2 Spatial distribution of MC(a)and error estimation(b)in Sichuan-Yunnan region
根据泊松分布,Tw时间内发生k次地震的概率p(k)为:
记异常探测时段t1～t内实际发生的地震次数为n,定义地震发生率指数SRI(seismicity rate index)为:
式(3)将t1～t内实际发生的地震数映射为0～1的累积概率值,从而实现对地震活动水平的度量。将t在时间上按照一定步长进行滑动就可算出每个网格在不同时刻的SRI值。n越大,SRI值将越大; n越小,SRI值将越小; SRI值接近0或1的程度表征了t1～t时间内地震活动偏离泊松分布预期的程度,刻画了异常探测时段地震发生率与背景地震发生率的差异程度; SRI值越接近1代表地震活动增强越显著,越接近0代表地震活动平静越显著。从假设检验的角度理解,零假设为H0:地震活动在时间上是均匀泊松过程; 备择假设为H1:地震活动在时间上不是均匀泊松过程。SRI值接近0或1的程度表征了对零假设的拒绝程度,揭示了地震活动在时间上非均匀的程度。
本文的计算中,将空间采样窗口半径r设置为50 km,将背景时长Tb设置为1 825 d(5年),将异常探测时长Tw设置为90 d。上述参数设置基于震例回溯经过多次试算后确立,带有一定经验性。计算区域采用0.25°×0.25°的网格进行划分,时间步长设置为5 d,这两个参数主要决定空间上和时间上的分辨率。计算的震级下限为ML3.0。在异常的识别上,分别取0.975和0.025作为地震活动显著增强和显著平静的阈值,即SRI≥0.975的网格为显著增强,SRI≤0.025的网格为显著平静。将由4个以上连续异常网格形成的区域识别为异常区域。
对11次强震开展震例回溯分析,包括2次示例强震的异常演化回溯和11次强震前的异常概况。[HJ2.3mm]对于地震前兆出现的时间和空间范围,学术界没有统一的认识,时间上从地震前几小时到几年不等,异常震中距从几千米到几百千米甚至上千千米不等(Cicerone et al,2009)。在地震前兆异常的认定上,本文约定如下准则:①异常区域需含有4个以上连续异常网格。②异常区域到震中的距离需在200 km以内,如果存在多个异常区域满足条件,将距震中最近者作为前兆异常。③异常与地震的间隔时间需在180 d以内,如果满足条件的异常区域不止一个,则将间隔时间最小者作为前兆异常。
以上3条准则按次序执行,将用于震例的前兆异常分析。准则①要求异常在空间上有一定的聚集规模,这可在一定程度上避免异常的偶然性,排除一些虚假异常。按照0.25°×0.25°的网格大小,即要求异常面积需达到0.25平方度以上。在前兆的物理机制尚不十分明确的情况下,一种常见的做法是根据异常与地震的时空距离来判断其是否为前兆,准则②和③分别限定了前兆异常与地震的最大震中距和最大间隔时间。震例研究显示震中距200 km内和震前180 d内足以搜寻到地震的前兆异常,也足以覆盖各个震例前兆异常时空分布的特征范围。本文中,异常震中距为地震与异常区域内网格的最小欧氏距离。在异常和地震的关联性上,一种合理的倾向是认为时空距离越小者与地震的关联越紧密。因此,准则②和③在前兆异常的认定上附加了就近原则,当有多个符合时空范围要求的异常区域时,优先选取空间距离和时间距离最近者作为前兆异常。就近原则使得每个震例最多只有一个异常能被视为前兆,这样可极大简化对前兆异常的统计分析,突显出最紧密异常的时空分布特征。就近原则还能在很大程度上消除准则②和③中参数设置改变给震例前兆异常分析带来的不确定性,确保前兆异常认定结果的稳定性。
图3显示了2022年6月10日马尔康MS6.0地震前的地震发生率指数分布演化。图中共出现过5个异常满足准则①,即空间上含有4个以上连续异常网格,分别标记为A(图3b～e)、B(图3a、b)、C(图3a、b)、D(图3d～f)和E(图3d～f),这5个异常的震中距分别为23、176、210、218 和258 km。其中异常C、D、E不满足准则②中震中距在200 km以内的要求,不作为马尔康MS6.0地震的前兆异常。异常A和B满足震中距要求,其中异常A离震中更近且出现在震前180 d内,根据准则②附加的就近原则,把异常A视为马尔康MS6.0地震的前兆异常。
前兆异常A始于震前155 d,此时11个增强网格出现于紧邻震中的西南侧。在震前120 d,异常网格数增加到13个,异常强度升高,这种异常特征延续至震前55 d; 在震前50 d,异常强度降低,异常网格数减少至12个; 在震前45 d,异常消失。综上可知,前兆异常A出现于震前155～50 d,异常网格数达11个以上,异常类型为显著增强,震中距为23 km。
除了前兆异常A外,异常B和E也具有较大的面积和较高的强度。异常B出现于震前200～115 d,位于青海省甘德、久治一带,紧邻东昆仑断裂带的玛沁—玛曲段。笔者查看了该区域的小震活动,发现在2021年5月22日玛多MS7.4地震后,该地区的小震活动开始明显增加。岳冲等(2021)计算了玛多MS7.4地震引起的周边断层库仑应力变化,结果显示东昆仑断裂带的玛沁—玛曲段库仑应力变化较大。笔者据此推测该区域的小震增强活动可能为玛多MS7.4地震引起的应力触发所致,异常D的出现应该也是此原因。异常E出现于震前85 d至发震,位于四川省理塘地区,其由2022年3月15—16日理塘地区的小震群活动引起。该小震群共出现了4次ML≥3.0地震,时间上集中在2 d内,空间上集中在半径不超过3 km的圆内。根据笔者的分析经验,这种在时间和空间上高度集中的小震群活动,通常并不会在其附近对应强震。
图4显示了2019年6月17日长宁MS6.0地震前的地震发生率指数分布演化。[JP3]图中显示,包含4个以上连续网格的异常共出现过3个,分别标记为大写字母A(图4a～d)、B(图4b)和C(图4d～f),这3个异常的震中距分别为87、0 和103 km。
图3 2022年6月10日马尔康MS6.0地震前的地震发生率指数异常分布
Fig.3 SRI anomalies before the Maerkang MS6.0 earthquake on June 10,2022
图4 2019年6月17日长宁MS6.0地震前的地震发生率指数异常分布
Fig.4 SRI anomalies before the Changning MS6.0 earthquake on June 17,2019
异常A、B、C均满足震中距在200 km内的要求,其中异常B距离震中最近,根据就近原则把B视为长宁MS6.0地震前兆异常,其出现于震前80 d,异常网格数为8个,异常类型为显著平静。
异常A位于四川省荣县、威远一带,该地区的小震活动从2017年下半年开始急剧增加,主要表现为荣县和威远两处震群活动,异常A正是由这两处震群的增强活动引起。该地区为页岩气开采区,上述两处震群活动可能和页岩气平台的水压致裂作业存在关联(Lei et al,2020)。此外,前兆异常B所在区域也存在着页岩气开采和长期注水采盐活动,Lei等(2020)认为长宁MS6.0地震可能和附近深盐井的长期注水采盐有关,因此,前兆异常B的形成可能还包含了非构造因素。异常C位于四川省雷波县和云南省永善县一带,由永善地区2019年3—5月的多次小震活动引起,这些小震在空间上集中在半径不超过3 km的圆内,为单点地震活动,与强震发生的关联可能并不紧密。
表1为11次强震前的地震发生率指数异常的基本信息。除了2014年10月7日景谷MS6.6地震外,其余10次强震前均出现了地震发生率指数异常。10次强震的异常震中距均小于90 km,计算方法为取异常区域内各网格中心点到震中距离的最小值。异常开始时间为震前155 d至震前5 d,异常结束时间最早是震前80 d,部分震例的异常一直持续至发震时刻。总结上述统计信息可知,10次强震在震中90 km内和震前80 d内均有异常。
表1 川滇地震11次强震前地震发生率指数异常概况
Tab.1 SRI anomalies before 11 strong earthquakes in Sichuan-Yunnan region
表1的统计结果是基于前兆认定准则得到的。准则②中的最大震中距和准则③中的最大间隔时间这两个参数限定了认定前兆异常的空间和时间范围。需要说明的是,只要这两个参数取值不是太小,它们的改变对认定结果影响并不大,这是由于准则②和③都附加了就近原则。由表1可见,历次震例的前兆异常最大震中距为86 km,只要最大震中距大于86 km,不论其取值是否发生变化,由于只挑选距离震中最近的异常,前兆异常的认定结果将保持不变。但当最大震中距小于86 km时,前兆异常的认定结果将依赖于最大震中距,其取值越小,就有越多震例搜寻不到前兆异常。各震例的前兆异常最早开始于震前155 d,最早结束于震前80 d。只要最大间隔时间大于155 d,就能确保完整地统计到前兆异常的展布时间,但当最大间隔时间小于155 d时,一些震例的前兆异常的开始时间将无法被准确统计。当最大间隔时间小于80 d时,前兆异常的认定结果将依赖于最大间隔时间,其取值越小,就有越多震例搜寻不到前兆异常。综上所述,只要最大震中距大于86 km,最大间隔时间大于155 d,这两个参数取值的改变将不影响表1的统计结果。
在异常类型上,只有2019年6月17日长宁MS6.0地震前为地震活动显著平静,其余9次强震前均为地震活动显著增强。侯金欣等(2020)在岩石断层黏滑失稳实验中的声发射观测结果显示,临近失稳,声发射率呈现出增加的特征。本文在绝大多数强震前观察到震中附近短期内地震活动增强,与上述实验室结果较为相似。
图3中除了在震中附近出现异常,在距离震中较远的位置也出现异常。按照前文约定的前兆认定准则,这些异常并非某个强震的前兆。也就是说并不是每个异常区域出现后都会对应发生地震,即存在异常虚报地震的现象,这与地震预报的现状相符(Yu et al,2022b)。在这种情况下,进行预报效能评价就显得尤为重要。
采用R值评分进行预报效能评估(许绍燮,1989),与时空预报相应的计算公式如下:
式中:H为击中率; τ为预报的时空占有率; n为目标地震数; k为击中地震数; T为预报研究总时长; S为预报研究总面积; Ti为第i次预报的时间长度; Si为第i次预报的面积; m为预报的总次数; 符号∪表示将各次预报时空体积取并集。R值评分与国际上常用的Molchan图表法(Molchan,1991)类似,后者更习惯使用漏报率ν和时空占有率τ的曲线来反映预报效能,击中率H=1-ν。R值的含义为真实击中率与随机预报击中概率的差值,取值范围为-1～1,R越大表示预报效能越高,R>0意指优于随机预报。优于随机预报的程度可通过显著性水平来反映,n次地震有k次以上击中的显著性水平α为:
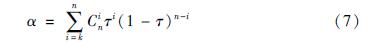
式中:α越小意味着预报效能越高。
基于公式(4)和(7)对不同预测参数下的预报效能进行评估。预测参数有预测半径和预测时长。首先计算时空占有率τ,为此需要先确定预测区域边界。本文先通过简单的聚类识别出异常网格簇,再根据预测半径自动求取预测区域边界,算法细节这里不做展开。作为示例,图5展示了预测半径为90 km时2014年5月16日和2014年9月28日的预测区域边界。在预测时长为80 d时,2014年5月30日盈江MS6.1地震、2014年8月3日鲁甸MS6.5地震和2014年11月22日康定MS6.3地震均为命中地震,2014年10月7日景谷MS6.6地震为漏报地震。
预测半径以10 km为间隔,在70～100 km取值,有4个不同取值; 预测时长以10 d为间隔,在40～110 d取值,有8个不同取值,组合起来共计32对取值。分别计算不同参数组合预测下的R值评分和显著性水平α,结果见表2、图3,其中显著性水平结果以常用对数显示。当预测半径为90 km,预测时长为80 d时,预报效能最佳,R值评分取得最大值0.602 1,同时lg α取得最小值-4.229 3,对应显著性水平α为0.000 059。上述结果表明地震发生率指数异常对川滇地区强震具有较好的短期预报效能。
表2 不同预测参数下地震发生率指数的R值评分
Tab.2 The R scores of SRI according to different prediction parameters
图5 预测半径为90 km时的两个时间的预测区域示例
Fig.5 Two examples of prediction areas when prediction radius is 90 km
表3 不同预测参数下地震发生率指数的显著性水平
Tab.3 Logarithms of significant levels of SRI according to different prediction parameters
如果将α为0.025作为在统计学上具有预报意义的阈值,则lg α低于-1.6的预报参数组合具有预测效力。表3中低于-1.6的参数组合和高于-1.6的参数组合存在明显分界,高于-1.6的参数组合大致形成了一个顶点在左下角的倒三角形,这表明预报时空范围过小时预报效能将变差。当预测时长小于60 d时,地震发生率指数的预报效能将变差,将不再具有统计学意义上的显著性。以上分析表明,地震发生率指数在时间和空间上的预测精度存在着一定的极限。
地震发生率指数的计算涉及3个重要参数,分别是空间采样窗口半径r,背景时长Tb和异常探测时长Tw。通过震例回溯进行多次试算后得出这3个参数的取值分别为50 km、5 a和90 d。采用控制变量法,分别讨论这3个参数对预报效能的影响,每次只考察1个参数的改变对预报效能的影响,其余2个参数在计算中保持不变。计算效能时,预测参数统一采用3.2节中获得的最优解,即预测半径为90 km,预测时长为80 d。
(1)考察r的影响,r依次取值为40、45、50、55 和60 km,Tb=5 a和Tw=90 d保持不变,预报效能如图6a所示。r=50 km时,R值最大,同时α最小,预报效能为最佳。相对于最佳效能,当r<50 km时,预报效能大幅降低,当r>50 km时,预报效能有小幅降低。r越小,采样窗口就越小,就越能反映地震活动的局部信息,但是小的r也会导致采样到的地震数量少,这将不利于探测地震发生率的变化。较大的r有利于保证计算的样本量,但对局部信息的反映较差,在一定程度上也不利于探测异常。从预报效能看,r=50 km是一个较好的折中值。而r<50 km时预报效能较低,原因可能是因为计算样本少导致能被探测到的异常减少,在一些震例前无法探测到异常,这也表明r的取值不能太小。
(2)考察Tb的影响,Tb依次取值为3、4、5、6和7 a,r=50 km和Tw=90 d保持不变,预报效能如图6b所示。在Tb=5 a时,R值最大,α最小,预报效能最佳。相对于最佳效能,当Tb<5 a时,预报效能有所降低,而当Tb>5 a时,预报效能降低较多。这表明作为背景时长,Tb的取值并非越大越好,而5 a是一个较为理想的取值。
(3)考察Tw的影响,Tw依次取值为70、80、90、100和110 d,r=50 km和Tb=5 a保持不变,预报效能如图6c所示。在Tw=90 d时,R值最大,α最小,预报效能最佳。相对于最佳效能,当Tw<90 d时,预报效能大幅降低,当Tw>90 d时,预报效能也有一定幅度的降低。这表明作为异常探测时间窗口长度,Tw的取值既不能太小也不能太大,90 d是一个较为合适的取值。
图6 计算参数r(a)、Tb(b)和Tw(c)对预报效能的影响
Fig.6 Influence of parameter r(a),Tb(b)and Tw(c)on the prediction performance
以上分析表明,计算参数r、Tb和Tw较为优良的一组取值分别为50 km、5 a和90 d。
本文基于地震发生率指数方法开展了对川滇地区强震预测的研究和预报效能评价,主要结论如下:
(1)川滇地区11次震例的研究结果显示,在强震前不到半年内,在震中附近可观察到小震活动的显著变化,主要表现为小震活动显著增强。
(2)预报效能评价结果显示,当预测半径为90 km、预测时长为80 d时,地震发生率指数方法的预报效能最佳,R值评分约为0.60,显著性水平α约为0.000 06,表明地震发生率指数异常应该包含了一定的短期地震前兆信息。
(3)分别考察了3个计算参数对预报效能的影响,结果表明,计算参数r、Tb和Tw较为优良的一组取值分别为50 km、5 a和90 d。
