基金项目:云南省地震局青年地震科学基金(2023K04); 云南省地震工程勘察院有限公司“地震观测网建设”项目(k24-34); 云南省地震局“压缩感知与稀疏反演理论研究”创新团队项目(CXTD202407).
第一作者简介:赵玲云(1995-),工程师,主要从事地震背景噪声和噪声源研究.E-mail:18487202725@163.com.
通信作者简介:庞卫东(1983-),高级工程师,主要从事震害防御研究.E-mail:wdpang1983@qq.com.
(1.云南省地震局,云南 昆明 650224; 2.中国地震局地球物理研究所,北京 100081)
(1.Yunnan Earthquake Agency,Kunming 650224,Yunnan,China)(2.Institute of Geophysics,China Earthquake Administration,Beijing 100081,China)
DOI: 10.20015/j.cnki.ISSN1000-0666.2025.0043
通过地震台站的连续记录计算台站间的噪声互相关函数(Noise Cross-correlation Function,NCF),并提取频散曲线进行速度结构成像是开展地壳速度结构研究的重要方法(Shapiro,2005; Nishida et al,2009)。背景噪声成像无需依赖地震事件,任意台站均可视为一个震源,因而可以提供更为密集的路径覆盖(Weaver,2005)。在噪声相关的研究中,噪声互相关函数近似于格林函数的理论假设能量是均分,即背景噪声能量在三维空间中均匀分布(Snieder,2004; Roux et al,2005)。然而,地球真实背景噪声的噪声源成分复杂,与海洋活动具有明显相关性,在时间和空间上均存在不均匀性,与最初的理论假设不符(Stehly et al,2006; 王伟涛等,2011b),并且这些不均匀性还会体现在NCF上,进而影响到基于噪声的相关研究结果(Tsai,2009; Zeng,Ni,2010)。因而,开展噪声源研究,深入了解噪声信号的构成及其演化特征,可加深对NCF波形中信号的认识,并在基于NCF的地学研究中提供数据质量控制。
NCF技术出现后,基于NCF信号的研究也渐渐开始发展,如Stehly等(2006)提出背景噪声能量流的方法,通过NCF正负半轴信号强度差,对美国加利福尼亚州的台阵进行了噪声源空间分布和季节变化的研究; Yang和Ritzwoller(2008)通过NCF垂直分量中面波信号的信噪比,对全球多个台阵做了不同周期噪声优势分布和季节变化的分析; Tian和Ritzwoller(2015)利用噪声信噪比对Juan de Fuca板块和美国西海岸台站记录到的噪声做了研究。上述噪声分析方法均不能得到噪声信号传播的慢度信息,而慢度信息是确定信号类型和来源的重要因素。
聚束分析方法的出现实现了对噪声信号的慢度分析。时间域下的聚束分析可通过动校正-叠加方法提高噪声信号的信噪比(Rost,Thomas,2002); 而频率域下的聚束分析(f-k分析)则可通过慢度观测有效分离出不同慢度和频率的波场成分,进而了解噪声信号构成和分析噪声信号源方位分布等特征(鲁来玉等,2009; Rost,Thomas,2009)。聚束分析由使用数据的不同分为基于连续数据的聚束分析(Gal et al,2015; Xiao et al,2018)和基于NCF的聚束分析(Harmon et al,2010; Wang et al,2018)。其中,基于NCF的聚束分析方法是研究NCF中信号及来源的一种有效手段。
本文选用位于中国地震科学台阵(ChinArray)二期南部的方形分布台阵,计算该台阵322个台站所有台站对的NCF,并利用基于NCF的台阵聚束方法,对4~30 s的背景噪声做慢度观测,分析了不同频段背景噪声信号的成分组成、方位分布及季节变化等特征。
Wang等(2018)对基于NCF的聚束分析方法做了详细介绍,原理如下:频率域的聚束分析是基于台站间的互谱密度矩阵(Cross-Spectral Density Matrix,CSDM)进行的。CSDM是与频率相关的函数,与时间无关,可由台站的连续数据获得,也可通过NCF获得。在使用连续数据计算CSDM时,要对连续数据进行类似于NCF数据预处理的时间域归一化,选择一定时间窗口,将数据转换为频谱,进而保留频谱的相位信息,并将任意2个台站的相位相乘,得到最终的CSDM。假设CSDM为C(ω,τ),其中τ为时间单元窗,ω为频率。互谱密度矩阵的第i行、第j列即为台站i和台站j在频率ω时的相位延迟,即:
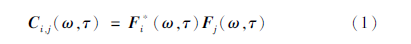
式中:F为傅立叶变换; F为其复共轭; 等式右侧为台站i和j在时间窗τ内在频率域的互相关。
选定台阵中心为参考点,任一台站相对此参考点的位置矢量为r。对于慢度矢量为s的平面波在该台站的响应可以表示为:

忽略研究区域的高程差,假设台阵水平分布,设Δt为r的平面波在频率ω时的时间延迟,则在时间窗为τ时,台阵的聚束输出为:
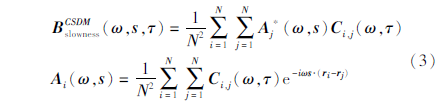
由于CSDM具备共轭转置对称性质,由此:
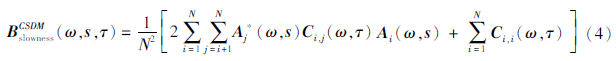
其中矩阵对角线对应于自相关,与源位置无关。本文主要关注噪声源的信息,故仅保留CSDM的非对角线,可得:
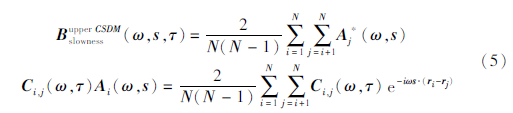
通过式(5)对频率和时间窗做进一步平均便可得对应时段内的聚束输出。
利用叠加后的NCF也可进行聚束分析,其中时间窗τ由获取NCF所用的叠加时段来确定,而CSDM中的矩阵元素可通过对NCF进行傅立叶变换得到。将式(1)中的各元素替换成对应台站对NCF的傅立叶变换,将台站i和j所构成的第k条路径表示为:
rk=rj-ri (6)
慢度矢量为s的平面波在台站间的时间延迟为:
Δti,j=s·rk=s(rj-ri) (7)
已知台阵的台站对数为M=N×(N-1)/2,将式(6)和(7)代入式(5),可得:
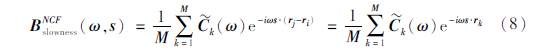
其中NCF是以天为单位进行互相关并叠加得到,我们对所有时间单元进行了时间平均,可略去式(8)中的τ, 1用C~k(ω)来表征时间的平均,并通过台站对构成的路径进行求和,最终的聚束输出结果综合所有路径通过式(8)计算得出。
中国地震科学台阵(ChinArray)探测“喜马拉雅”二期项目在南北地震带北段共布设了678个宽频带台站,该台阵台站均匀分布于1 000 km×1 000 km的观测区域内,平均台间距约为50 km,这一大孔径密集台阵为获取高信噪比的NCF波形提供了保障。考虑到聚束分析会受台阵布局的影响,规则布局且均匀分布的台阵可一定程度避免引入偏差(鲁来玉等,2009; Liu et al,2010)。参考前人经验,本文选用了ChinArray二期南部方形分布的较为规则的台阵(图1),收集了2013年9月—2016年6月该台阵322个地震台站记录到的连续波形数据开展研究。
本文基于Bensen等(2007)的处理流程进行NCF计算,对原始数据进行去均值、趋势和去除仪器响应,抽样至1 Hz后,使用滑动绝对平均方法进行时域归一化,在0.008~0.45 Hz频段进行谱白化,计算单天的NCF。因该台阵都分布在1 000 km以内,主要信号都在±500 s的时间窗内(图2),故对51 681条路径的单天NCF进行了±500 s的截取,共计1 001个点,补零至1 024个点,再进行傅立叶变换,构建出各台站对间的互谱密度矩阵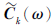 ,分辨率约为0.001 Hz。本文由式(8)利用所有台站对构建的
,分辨率约为0.001 Hz。本文由式(8)利用所有台站对构建的 ,计算得到各频率ω和慢度s对应的聚束输出。在进行聚束输出计算时,慢度区间取为Sx=(-50,+50),Sy=(-50,+50),分别为东西和南北向上的慢度分量,步长为0.2,单位为s/deg。
,计算得到各频率ω和慢度s对应的聚束输出。在进行聚束输出计算时,慢度区间取为Sx=(-50,+50),Sy=(-50,+50),分别为东西和南北向上的慢度分量,步长为0.2,单位为s/deg。
聚束输出结果是慢度矢量和频率的函数,因此可在单频率得到噪声信号在慢度域内的能量分布,实现对单频率噪声信号特征的分析。对单频率聚束输出结果叠加可得到频率范围内噪声信号的综合特征。利用不同时段叠加的NCF进行聚束分析,可进一步分析噪声信号在时间尺度上的演化规律。本文通过2种不同的叠加方式开展了基于NCF的聚束分析,首先以台阵2013—2016年所有时间叠加得的NCF为基础进行聚束计算,得到了研究区内噪声信号的平均特征。其次,对多年不同月份的NCF进行叠加,将每年1月的单天NCF进行叠加来表征1月的NCF,以此类推得到12个月的NCF用于聚束分析,以分析噪声信号随季节的变化。
频率域的聚束分析可以针对不同的频率研究台阵记录信号的慢度特征,并依据慢度及视速度对信号类型进行区分。利用频率域聚束分析方法频率分辨率高的特点,本文对研究区域内不同典型频率的背景噪声信号能量进行分析。
参考赵玲云等(2021)的研究,研究区域台阵NCF的优势能量主要分布在4~8,8~12及12~20 s。因此,本文选择了频带内的0.200 2、0.100 6和0.050 8 Hz 3个典型频率的聚束图像进行分析,对2013—2016年所有时间数据叠加的NCF进行聚束输出,结果如图3所示。图 中 2个白色圆圈由内到外分别对应慢度为25 s/deg(4.5 km/s)和45.5 s/deg(2.5 km/s)[JP3]的面波,而最内侧的黑色圆圈对应慢度为9 s/deg(13 km/s)的体波。从图3可看出,在高频率(0.200 2 Hz)时,噪声能量主要集中在慢度9 s/deg以内,其能量主要由视速度较高的体波信号产生,其对应源区相对于面波信号呈现出更为分散的特征。而在0.100 6 Hz左右,噪声能量主要分布在慢度35 s/deg附近,对应的视速度约为3.3 km/s的面波能量,体波成分的能量相对较弱。在0.050 8 Hz左右,噪声能量主要为近似环状、分布更为均匀的面波能量,且在西南和西北方向上有明显优势分布。观察所有单频率的聚束输出发现,随着周期增大面波能量环有向内迁移的趋势,表明随着周期增大视速度也逐渐增加。面波沿地表传播,其在聚束图像中的视速度可以表征面波的传播速度,这与较长周期面波的传播速度较快的频散特征相符。由上述分析可得,利用聚束分析方法可对噪声信号中的信号类型、优势方向和相对强弱进行有效的分析,相比基于NCF信号对称性的归一化能量流方法(王伟涛等,2011a; 荆涛等,2023; 赵玲云等,2021; 邓明文等,2023)可以提供更多的有效信息。
对不同频率的聚束结果进行叠加和平均,可以得到特定频率内噪声能量的平均分布。相比单频率,平均后的结果更为稳定。
依据全球背景噪声参考模型,4~20 s是噪声能量最强的频段,被定义为地脉动(Peterson,1993)。地脉动是开展地球内部结构成像研究中最常用的噪声信号,将其位于约14 s和5~7 s处的峰值分为第一类地脉动和第二类地脉动,不同频段噪声信号对应着不同的形成机制,因而其相应特征也各不相同(Longuet-Higgins,1950; Hasselmann,1963)。考虑到噪声特征分析的合理性与准确性,本文参考赵玲云等(2021)的研究,将噪声能量划分为4~8、8~12、12~20、20~30 s 4个不同的频段,分别对2013—2016年所有天数叠加所得的NCF计算了4个不同频段的慢度谱,展示了不同频段噪声能量成分和来源方向的分布,如图4所示。图4a、b中5个虚线圆圈由内到外对应的慢度分别为24.7、27.8、31.8、37.1和44.5 s/deg。图4a给出了噪声信号整体的慢度聚束输出结果。在不同频率,体波和面波的噪声能量相对强度具有较大变化,进行全局的能量归一化时会受其影响,本文将慢度输出结果中9 s/deg范围内的体波能量剔除,依据剩余的能量最大值进行归一化,用来反映面波信号的能量分布,如图4b所示。将慢度9 s/deg范围内的体波信号依据其能量最大值进行单独归一化,如图4c所示。
图4 NCF在4个频段的噪声信号整体慢度聚束输出结果(a),及面波(b)和体波(c)信号的能量分布
Fig.4 Slowness beamforming images from NCF in four frequency bands(a),and energy distributions of surface wave(b)and body wave(c)singnals
不同频段的聚束输出结果均表现出很强的方向性,如图4所示。在4~8 s,体波能量强于面波,在90°~150°方向有一较强的面波能量,其慢度约为35 s/deg,对应的视速度约为3 km/s,为瑞利面波。在慢度5 s/deg附近有一个能量较强的优势能量点。基于Kennett和Engdahl(1991)使用ASPEI模型计算得出的体波震相的距离-慢度曲线(Wang et al,2018),笔者判断图4中4~8 s和8~12 s的体波能量的慢度峰值可能对应于远震P波震相,对应视速度约为13 km/s。在8~12 s,存在能量相对4~8 s较强的、来源方向为80°~150°的瑞利面波; 在慢度5 s/deg附近有多个优势能量点,且这些能量点的强度相对面波较弱。在12~20 s,体波成分的能量渐无,面波能量却有多个优势来源方向,主要集中在180°~210°和315°~340°。在20~30 s看不到体波信号,但面波能量却相对加强,优势来源方向也更为突出,分别为100°~135°、170°~210°和315°~360°。
综合分析得出,噪声信号成分具有频率依赖性,在较长周期的频段,面波信号为噪声能量的主要成分,不同频段面波能量的优势来源方向及强弱又有不同。在12~30 s,体波信号很弱,无法观测到; 在较高频率时,体波信号的能量相对增强,面波信号相对减弱。与面波信号相比,体波信号对应的源区较为分散,方位分布上更不均匀。
背景噪声主要是由海洋和固体地球之间的耦合作用产生,其能量变化同海洋活动相关,呈季节变化,且海浪波高的变化同地脉动信号的特征具有较高相关性(Koper,de Foy,2008; Euler et al,2014)。因此,本文以多年单月叠加得到的NCF为输入数据,利用基于NCF的聚束方法构建CSDM,对上述4个频段的季节性变化进行分析。由于王芳等(2020)已对体波信号的季节变化进行了详细讨论,本文着重分析面波信号的季节变化,进而分析面波能量与海洋活动的相关性。通过WAVEWATCH Ⅲ数据库[ZW(DYB,7][KG*3]Tolman H L.2002.Manual and wave user system documentation of WAVEWATCH-III version 2.22.取得2013—2016年全球海浪的高度分布,通过叠加数据获得了12个月的平均海浪波高。聚束结果中,仅显示慢度在28.37~40.5 s/deg的面波部分,根据最大值进行归一化,将能量转化为dB形式; 在中间区域展示了全球海浪平均波高的图像,并将投影中心设为本文选用台阵的台阵中心(34.45°N,104.95°E),以展示全球海洋海浪波高相对于ChinArray二期南部台阵的方位,从而更好地与背景噪声噪声源的变化特征进行对照分析。本文给出了4~8、8~12、12~20、20~30 s 4个不同频段按月进行叠加的聚束结果(图5),以了解噪声能量的季节性变化及其与海洋相对位置的关系。
在4~8 s,全年噪声能量的主要优势来源方向为90°~230°,对应于太平洋海域,并在夏季(4月、7—10月)能量尤其强(图5a)。
在8~12 s,全年噪声能量在东南向(90°~150°)、西南向(180°~245°)和西北向(310°~350°)都较强(图5b)。来源方向对应于太平洋海域的东南向噪声能量最强,且在夏季(5月、7—8月)能量最强; 来源方向对应于印度洋的西南向噪声能量,也在夏季(5—9月)能量相对较强; 而来源方向对应于大西洋北部的西北向噪声能量,则是在冬季(1月和12月)能量较强。
在12~20 s,噪声能量的极大值主要分布于西南向(180°~250°)和西北向(310°~360°),分别对应于印度洋和大西洋北部。其中来源方向对应于印度洋的西南向噪声能量,在夏季(4—9月)能量最强; 来源方向对应于大西洋北部的西北向噪声能量,在1—4月和10—12月能量较强,夏季能量较弱(图5c)。
在20~30 s,部分月份可以观察到一个较为明显的能量环,但也存在能量极大值,分别是东南向(90°~150°)、西南向(170°~250°)和西北向(310°~360°),这些优势来源方向分别对应于太平洋、印度洋和大西洋北部海域(图5d)。其中对应于太平洋的东南向噪声能量在夏季(4月、5月和7月)及秋季(10月和11月)能量较强; 来源方向对应于印度洋的西南向噪声能量,在夏季(4—10月)能量较强; 而来源方向对应于大西洋北部的西北向噪声能量,则是在冬季(1—3月和10—12月)能量较强,夏季能量较弱。
综合观察不同频段的聚束输出结果,发现不同频段噪声能量的优势来源方向不尽相同,随时间呈季节变化,且其随时间的变化规律也各不相同。其中来源方向对应于北半球海域的噪声能量整体呈现出冬季较强、夏季较弱的变化规律,而优势来源方向对应于南半球海域的噪声能量则呈现出夏季较强、冬季较弱的规律,噪声能量随时间的演化规律与全球海洋活动相符。另外,在频率较高的频段,噪声能量在方位上的分布不均匀性更高; 在频率较低的频段上,噪声能量在方位上的分布相对均匀。
聚束分析方法可对噪声源中的体波和面波信号进行完整刻画,具有较高的频率分辨率。本文通过ChinArray二期南部子台阵计算所得的NCF,进行了不同时间尺度的叠加,并利用基于NCF的台阵聚束分析方法对噪声源的特征进行了分析,得到如下结论:
(1)背景噪声中主要为面波信号,同时也有体波信号。在不同频段,二者的相对占比不同。在高频段,体波信号较强,而随着周期变长,面波信号占比逐渐增加,体波信号则减弱。
(2)面波信号的能量方位分布具有不均匀性,且不同周期优势来源方向各不相同。长周期的面波信号相比短周期能量分布更为均匀。
(3)噪声源中的面波信号具有明显的季节性变化:来源方向对应于北半球海域的噪声能量冬季较强、夏季较弱; 来源方向对应于南半球海域的噪声能量夏季较强、冬季较弱。噪声能量随时间的变化规律与全球海洋活动相一致。
背景噪声中蕴含了丰富的地下介质信息,随着噪声互相关技术的成熟,加深对背景噪声噪声源的认识,可进一步促进NCF中的各类信号的精细化分析,推动噪声相关研究的发展。
[HTK]感谢中国地震局地球物理研究所“中国地震科学探测台阵数据中心”提供的数据。