基金项目:国家自然科学基金面上项目(12372143); 广元城投集团科技基金(GYCT-KY-202101).
第一作者简介:邓夕胜(1977-),副教授,主要从事工程结构抗震与防灾的研究.E-mail:dxish@swpu.edu.cn.
通信作者简介:周紫娟(2000-),硕士研究生在读,主要从事工程结构抗震与防灾的研究.E-mail:2413090422@qq.com.
(1.西南石油大学 土木工程与测绘学院,四川 成都 610500; 2.西南交通大学 土木工程学院,四川 成都 610031; 3.福建一建集团有限公司,福建 三明 365001)
(1.School of Civil Engineering and Geomatics,Southwest Petroleum University,Chengdu 610500,Sichuan,China)(2.School of Civil Engineering,Southwest Jiaotong University,Chengdu 610031,Sichuan,China)(3.Fujian No.1 Construction Group Co.,Ltd.,Sanming 365001,Fujian,China)
mainshock-aftershocks; duration; BP neural networks; RC frame structure; fragility surface
DOI: 10.20015/j.cnki.ISSN1000-0666.2025.0052
一次强烈地震后,往往伴随一系列余震(Ruiz-Garcia,2012; Yin,Li,2011)。范宣梅等(2022)对多次主余型地震研究表明,76.2%的地震序列的强余震产生的有效峰值加速度超过主震。工程结构在强余震作用下容易导致二次损伤,为了更加准确评估结构在强余震地震动作用下的抗震性能,有必要对其在主余震序列地震动作用下的易损性开展研究。
国内外学者对主余震序列地震动作用下结构的损伤进行了大量研究,如Wen等(2022)研究了近断层区域主余震序列对结构的累积损伤,发现余震对接近主震卓越周期的结构损伤影响最大; Qiao等(2022)进行了主余震序列作用下的RC框架结构振动台试验,发现多次余震作用下,第二次余震作用对结构有最大的余震影响率; Zhang等(2023)和王新悦(2018)的研究表明,余震会加重结构的损坏,且楼层损伤发展沿结构高度分布不同。以往研究表明结构在主余震序列地震动作用下的损伤更为显著。传统易损性分析要求大样本数据具有较好的稳定性,而由于该方法对输入输出映射关系的描述具有局限性,无法建立可靠概率模型,故无法全面考虑主余震序列地震动作用下结构的易损性分析。
以BP(Back Propagation)神经网络为代表的人工神经网络可以进行大数据样本的分析,并且具有高度准确性。近年来,BP神经网络在多个领域得到广泛应用,如周敉等(2004)、徐峥匀和钱松荣(2022)将BP神经网络应用于桥梁的数据提取以及性能评估; 刘全明(2022)在研究隔振结构优化时采用神经网络的方法建立机器学习模型,最终准确预测了隔振结构的动力响应; 蔡斌等(2019)通过BP神经网络方式对钢筋的温度进行了预测。人工神经网络可以进行大数据样本的分析,并且具有高度准确性。将BP神经网络应用于结构主余震易损性分析,建立易损性模型能避免传统易损性分析对输入输出映射关系描述的局限性。
本文以某多层RC框架结构模型为研究对象,对不同余震持时的主余震序列进行挑选和合成后,选用余震持时和主震强度作为地震动强度参数,结构最大层间位移角作为强度指标,将主震-长持时余震、主震-短持时余震序列地震动组输入到结构中进行增量动力(Incremental Dynamic Analysis,IDA)分析。以IDA分析结果为数据库,借助BP神经网络建立易损性函数,利用该神经网络模型来预测不同极限状态下结构易损性曲面并进行主震-长持时余震和主震-短持时余震作用下结构的损伤分析,绘制基于BP神经网络的易损性曲面,讨论RC框架结构的损伤反应。
人工神经网络是对动物的神经网络开展数学模型模拟,是一种高度非线性的自适应模型(何正风,2016),也可简称为神经网络。神经网络模型由大量神经元的节点搭建而成,神经元对应的数学模型形式为多输入单输出,其内部组成为权值、阈值和激活函数3部分,其中神经网络最常用的3种激活函数为:logsig函数、tansig函数和purelin函数(Hammer,2001)。最常见的神经网络结构为3层,如图1所示。
神经网络性能绝大部分由隐含层数量、隐含层中神经元数量决定。隐含层层数需适量,层数过多会由于算法限制导致训练速度缓慢,一般问题1~2个隐含层就能满足需求,另外需确定合适的神经元数目,神经元数目的确定使用较多的是经验公式法,其具体形式为(Simon,2008):
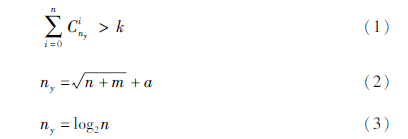
式中:k为数据集的样本数量; ny为隐含层的神经元数目; n为输入参数的个数; m为输出参数的个数; i为区间[0,n]内的常数; a为区间[1,10]内的常数。
在神经网络模型建立过程中,通过经验公式能大致确定隐含层神经元数目,而最终确定仍需在这个范围里进行逐个搜索。
作为一种人工神经网络,BP神经网络是一种按误差逆传播算法进行训练的多层前馈网络。每层神经元与下一层神经元互连,神经元之间不允许同层连接和跨层连接,包括输入层、隐含层和输出层。输入层作用是信息的传递,输出层使用激活函数实现数据的处理,隐含层在一个神经元中可以不只一个,隐含层兼具分析数据和传输作用。神经网络模型的优点在于不需要输入描述映射关系的数学方程式,可以直接学习储存大量输入/输出模式映射关系(程诗焱,2020)。
基于BP神经网络的地震易损性函数(程诗焱等,2021)为:
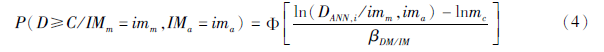
式中:DANN,i/imm,ima为在IMm=imm,IMa=ima条件下BP神经网络模型的输出; P(D≥C/IMm=imm,IMa=ima)为损伤水平C的条件超越概率。
参考一办公楼实例,利用建筑结构设计软件PKPM设计1个6层RC框架结构,抗震设防烈度为Ⅶ度,设计基本地震动加速度为0.10 g,设计地震分组为第二组,特征周期为0.40 s。多遇地震时水平地震影响系数最大值为0.08,结构阻尼比为0.05,结构安全等级为二级,场地类别为Ⅱ类。地面粗糙度为B类,基本风压0.30 kN/m2。楼面荷载:恒荷载为4.8 kN/m2,活荷载2 kN/m2; 屋面荷载:恒荷载为5.6 kN/m2,活荷载为2 kN/m2; 梁上荷载:内墙为7.09 kN/m,外墙为7.9 kN/m; 女儿墙荷载:3.02 kN/m。楼板厚度均为120 mm,混凝土等级为C30,结构一层平面布置及结构剖面如图2所示。
用PKPM中有限元分析板块SATWE计算得到的配筋信息(表1)进行配筋。采用PKPM的配筋信息在结构分析软件SAP2000中建立有限元模型(图3)。定义质量源来表征结构构件的质量,质量源指定为恒载×1+活载×0.5(建筑抗震设计规范(2016年版),GB 50011—2010); 设置塑性铰模拟框架结构屈服和屈服后的性能,塑性铰采用默认铰属性,梁端采用弯矩M铰,柱端采用P-M-M铰,进行静力弹塑性(Pushover)分析。
图2 结构一层平面图(a)及结构剖面图(b)
Fig.2 The plane graph of the building's 1st floor(a)and the building's profile(b)
对建立的有限元模型进行Pushover分析,控制结构的最大推覆位移为高度的1/50,以FEMA356(FEMA 356,2000)为基础,SAP2000能够自动将Pushover分析得到的曲线转换成能力谱,并由此对标准需求谱进行等效从而自动求解性能点。其中结构性能点的基底剪力为4 654.084 kN,顶点位移为72 mm。性能点需求曲线和能力曲线的交点能够满足“大震不倒”设防原则,可见结构具有较大的承载力和变形能力储备。
SAP2000建立的有限元模型第一自振周期T1=1.128 1 s,PKPM建立的模型T1=1.043 5 s,2种模型结构前三阶周期对比见表2,周期误差在10%以内,可见2种软件建立的模型拟合度较高,具有良好的相似性。
由于主余震序列地震动数量较少,为满足研究的需要,本文采用合成的主余震序列地震动进行研究(韩建平,李军,2020; 于晓辉等,2020; 李喜梅等,2021)。不同的主余震序列地震动人工合成方法的区别主要在于余震的调整和选取,其原理为:选取一个主震作为前震,中间插入一段零幅值的加速度时程,之后添加选取的余震,得到一个由主震、零幅值加速度时程、余震构成的主余震序列地震动(张挺,2018)。
考虑余震持时对RC框架结构的影响,在人工合成主余震序列地震动时,将余震持时指标作为余震的选取因素,从PEER地震动数据库中选取不同持时的余震,根据反应谱挑选符合反应谱谱型的主震,据此得到人工主余震序列地震动。参考温卫平等(2021)的方法,在主震地震动和余震地震动之间插入30 s零幅值的时间间隔,以确保主震后的结构有足够的自由振动时间恢复到稳定状态。合成的主余震序列地震动示例如图4所示。
不同持时的余震地震动记录挑选,本质上是以地震动的持时指标作为主要选取因素,在地震动数据库中对余震地震动进行选取。关于持时指标的定义,[HJ]目前国内外学者主要将其分为括号持时、一致持时、重要持时、有效持时4种(孙小云等,2018)。
根据孔令峰(2019)的研究结果,选取重要持时DS5-75作为地震动持时指标。从PEER地震动数据库中挑选20条普通地震动作为主震地震动序列,再根据选取的地震动持时指标挑选20条长持时地震动,对选取的长持时地震动进行谱匹配(孔令峰,2019; Chandramohan et al,2016),消除频谱和幅值的影响,得到与长持时地震动对应的短持时地震动,谱匹配的结果如图5所示。将谱匹配挑选出的不同持时主余震序列地震动进行组合,得到表3所示主震-长持时余震、主震-短持时余震、主震3组地震动各20条。
图5 长(a)、短(b)持时地震动谱匹配结果
Fig.5 The matching of the long-duration(a)and the short-duration(b)ground motion spectra
使用BP神经网络建立综合考虑余震持时和主震强度的向量型IM(Intensity Measure)与结构最大层间位移角之间的关系。选用地震动指标强度IM=[Sa(T1,0.05),CAV]作为预测变量,其中CAV指累积绝对速度(Cumulative Absolute Velocity)。将主震-长持时余震、主震-短持时余震序列地震动组输入到结构中进行IDA分析,将IDA分析结果作为神经网络数据库,利用MATLAB神经网络工具箱构建BP神经网络。
选用只含有单个隐含层的BP神经网络对数据进行处理,输出层输入IDA分析计算的原始数据,隐含层的性能由连接权值确定。输出层的性能由其与隐含层的连接权值及激活函数决定。通过提取训练误差、测试误差、训练时间和相关系数R评估网络性能,经多次训练得到最佳的模型效果,最佳模型的BP神经网络的基本参数设置如下:①迭代次数为3 000次; ②隐含层节点数为5; ③训练算法为Levenberg-Marquardt算法; ④随机选取数据库中70%数据作为网络的训练集,15%数据作为验证集,15%数据作为测试集; ⑤学习速率设置为0.000 5; ⑥误差允许值为0.000 1。确定的BP网络模型示意如图6所示。
根据以上设置构建BP神经网络,并对其进行训练,最佳训练结果示例如图7所示。图中灰色虚线为y=x函数,每个散点代表一个样本数据,其x、y坐标分别代表地震动损伤指标的目标值和输出值,散点越靠近红色直线表示预测结果的误差越小。对比图7a、b可知,主震-长持时及主震-短持时余震地震动作用下的R值分别为0.680 14~0.828 37、0.862 32~0.942 55,主震-短持时余震地震动的拟合效果更好,2种地震动的误差都在可接受范围内。
图7 主震-长持时(a)和主震-短持时(b)余震序列地震动作用下结构的BP神经网络模型训练结果
Fig.7 Results from the training of the BP neural network model for the structures subjected to the ground motion of the mainshocks and their long-duration aftershocks(a)and short-duration(b)aftershocks
根据式(4)使用MATLAB绘制基于BP神经网络的易损性曲面如图8所示。由图8a可见,主震-长持时余震地震动作用下,在结构的轻微破坏到中等破坏阶段,曲面两端变化弧度差异较小,表明在该破坏状态下Sa(T1,0.05)和CAV对结构失效的影响程度相当; 在结构严重破坏阶段,主震Sa(T1,0.05)下的曲面略陡于余震CAV下的曲面; 在结构完全破坏阶段,主震Sa(T1,0.05)下的曲面变化弧度明显大于余震CAV下的曲面,表明主震-长持时余震地震动作用下导致结构最终破坏的因素中主震Sa(T1,0.05)的强度影响占比较大。由图8b可知,主震-短持时余震地震动作用下,在结构的轻微破坏到中等破坏阶段,左右曲面弧度变化基本类似,表明在该破坏状态下,Sa(T1,0.05)和CAV对结构失效的影响程度相当; 在结构严重破坏阶段,主震Sa(T1,0.05)下的曲面与余震CAV下的曲面出现细微差异; 在结构完全破坏阶段,主震Sa(T1,0.05)下的曲面弧度开始明显大于余震CAV下的曲面弧度,同样表明主震-短持时余震地震动作用下主震Sa(T1,0.05)的强度影响是导致结构破坏的主要因素。对比图8a、b可知,2种地震动作用下的曲面差异主要体现在完全破坏阶段,主震-长持时余震中余震CAV的曲面陡于主震-短持时余震中CAV的曲面,表明长持时余震对结构的影响要大于短持时余震对结构的影响。在主余震地震动作用下,造成结构倒塌的主要影响是主震强度。
图8 4种破坏状态时主震-长持时(a)及主震-短持时(b)余震序列地震动作用下结构的易损性曲面
Fig.8 Susceptibility surfaces of structure subjected to the mainshocks and their long-duration(a)and short-duration(b)aftershocks under four damage conditions
将结构的震害等级用相应的结构破环指标量化,由韩建平(2020)的研究和《建筑抗震设计规范(2016年版)》(GB 50011—2010)[KG0.15mm。]可知,结构的破坏状态划分为轻微破坏、中等破坏、严重破坏和完全破坏,性态点对应的性能变量值见表4。
基于BP神经网络模型,罕遇地震作用下Sa=0.218 7 g,取Sa(T1,0.05)=0.218 7 g,CAV=0.2、0.4、0.6、0.8、1.0 g,主震-长持时余震地震动作用下训练出的θmax预测值为0.025 6、0.034 4、0.035 2、0.054 7、0.058 4 g,根据式 (4)计算在4种破坏状态下结构的超越概率; 主震-短持时余震地震动作用下训练出的θmax预测值为0.017 3、0.021 2、0.052 9、0.0570、0.057 3 g,根据式(4)计算出在4种破坏状态下结构的超越概率。2种地震动作用下结构超越概率对比如图9所示。图中BP代表基于BP神经网络,DA代表基于主震Sa(T1,0.05)和余震CAV为地震动强度指标的双变量易损性函数。
由图9得出,罕遇地震作用下,结构一定会达到轻微破坏。在主震-长持时余震地震动作用下,结构的失效概率大于主震-短持时余震地震动作用下的结构失效概率,在结构严重破坏到完全破坏阶段,这种增大更明显。以Sa(T1,0.05)=0.218 7 g,CAV=0.2 g为例,主震-长持时余震地震动作用下,4种破坏状态结构下的失效概率分别为100%、93.11%、65.16%、24.06%; 主震-短持时余震地震动作用下,4种破坏状态下结构的[JP3]失效概率分别为100%、79.28%、65.16%、10.60%,可见主震-长持时余震地震动造成结构更大的失效概率。在该地震动强度下,主震-长持时余震地震动造成结构倒塌的概率比主震-短持时余震地震动增大了1.27倍。基于BP神经网络生成的易损性曲线斜率变化十分明显,2种地震动作用下的结构严重破坏和完全破坏状态斜率都存在“先增大再减小再增大”的趋势,在曲线的平台期,结构的失效概率没有发生较大变化,可能是因为结构在此次持时的余震作用下的损伤没有超过上一个持时的余震作用下的损伤。
图9 4种破坏状态时S/sub>a(T1,0.05)罕遇下主震-长持时(a)和主震-短持时(b)余震序列地震动作用下结构超越概率
Fig.9 The exceeding probability of the structure when the structure is subjected to the rare mainshocks and their long-duration(a)and short-duration(b)aftershocks under four damage conditions
本文建立地震动强度与结构损伤之间的BP神经网络模型,得到地震动强度与结构损伤之间的非线性关系。利用MATLAB建立BP神经网络模型,将IDA分析的数据划分为70%训练集、15%验证集和15%测试集,训练得到效果最佳的神经网络模型。利用该神经网络模型来预测不同主震强度和余震持时地震动下结构的损伤,绘制出基于BP神经网络的结构易损性曲面。考虑罕遇地震下的结构损伤,对Sa(T1,0.05)罕遇下的结构失效概率进行对比,得到以下结论:
(1)BP神经网络最佳训练结果中主震-长持时和主震-短持时余震地震动作用下的R值分别为0.680 14~0.828 37、0.862 32~0.942 55。训练出的最佳BP神经网络模型具有较高可靠性。
(2)在主震-长持时余震和主震-短持时余震这两种地震动作用下结构的易损性曲面差异主要体现在完全破坏阶段,主震-长持时余震地震动中余震CAV的曲面陡于主震-短持时余震地震动中CAV的曲面,可见长持时余震地震动对结构的影响要大于短持时余震地震动。
(3)罕遇地震作用下,主震-长持时余震地震动相较于主震-短持时余震地震动会造成结构更大的失效概率。以Sa(T1,0.05)=0.218 7 g,CAV=0.2 g为例,在该地震动强度下,主震-长持时余震地震动造成结构倒塌的概率比主震-短持时余震地震动增大了1.27倍。采用BP神经网络生成的易损性曲线斜率变化十分明显,能够有效地反映输入输出映射关系。