基金项目:国家自然科学基金项目(42274118,42274080); 云南省地震局地震科技专项(2024ZX03).
第一作者简介:谭 智(1999-),助理工程师,主要从事重力与天然地震联合反演研究.E-mail:2893540431@qq.com.
通信作者简介:石 磊(1984-),研究员,博士,主要从事重力与天然地震联合反演研究.E-mail:shilei@cea-igp.ac.cn.
(1.云南省地震局,云南 昆明 650224; 2.中国地震局昆明地震预报研究所,云南 昆明 650224; 3.中国地震局地球物理研究所,北京 100081; 4.中国地震局震源物理重点实验室,北京 100081; 5.云南省地震局 下关地震监测中心站,云南 大理 671000)
(1.Yunnan Earthquake Agency,Kunming 650224,Yunnan,China)(2.Kunming Institute of Prediction,China Earthquake Administration,Kunming 650224,Yunnan,China)(3.Institute of Geophysics,China Earthquake Administration,Beijing 100081,China)(4.Key Laboratory of Earthquake Source Physics,China Earthquake Administration,Beijing 100081,China)(5.Xiaguan Earthquake Monitoring Center Station,Yunnan Earthquake Agency,Dali 671000,Yunnan,China)
joint inversion of gravity and seismic data; structural coupling; cross-gradient; sequential strategy
DOI: 10.20015/j.cnki.ISSN1000-0666.2025.0056
不同地球物理数据对地下结构的物性参数、空间尺度和深度的敏感性各异,因此,利用多种资料开展联合反演可相互补充和约束,能有效降低单一反演结果的多解性(甘露等,2022),构建更为可靠的模型。相关学者开展了大量研究工作(夏思茹等,2021),为深入了解壳幔结构的组成,理解动力学演化过程和评估潜在地震危险性等提供了重要依据。
目前联合反演方法主要有基于岩石物理关系耦合和结构耦合2类(张佩等,2019; Tu,Zhdanov,2021)。基于岩石物理关系的联合反演利用不同物性参数之间的经验关系来连接多种地球物理模型(Astic et al,2020),所以选取合适的经验关系至关重要。Haber和Oldenburg(1997)最早提出利用模型间的曲率相似性进行联合反演。此后,不同的结构耦合方法被相继提出,如交叉梯度约束(Gallardo,Meju,2003,2004)、梯度点积约束(Molodtsov et al,2011)和联合全变分约束(Li et al,2019)法等。交叉梯度法由于原理简单,易于实现,得到了广泛的发展和应用(Wu et al,2020; Huang et al,2023; 李静等,2023)。
交叉梯度联合反演常采用同步和顺序2种策略。同步策略将单一数据拟合项、交叉梯度项、正则化参数项整合到一个方程系统进行同步反演,需要确定的参数较多,且数据拟合项和交叉梯度项之间交互关系复杂,权重难以确定(Fang et al,2022)。因此Um等(2014)提出将同步反演目标函数解耦,采用顺序反演策略分别进行反演,以降低交叉梯度联合反演的复杂程度和实现难度,[HJ]但该策略中不同地球物理数据的反演和交叉梯度约束完全独立,数据拟合和结构相似性难以同时满足; Gao和Zhang(2018)对其顺序策略的交叉梯度联合反演进行了优化,将不同地球物理资料单独反演的模型更新量引入交叉梯度最小化项,实现了数据拟合与结构相似性之间的平衡; 基于该优化顺序策略,张济东等(2022)进一步提出正反演网格分离法,既保证了反演精度,又提高了计算效率。
地震体波对传播路径中的介质波速敏感,在射线路径交叉密集区具有较高的垂向分辨能力(Aki,Lee,1976)。重力数据对密度变化敏感(Li,Oldenburg,1998),反演结果水平分辨率高。本文利用体波走时和重力资料的不同分辨率特征,基于交叉梯度约束的联合反演方法,将频率域重力反演(Cui,Guo,2019)和近震体波走时反演(Zhang,Thurber,2003)相结合,采用优化的顺序策略,实现了速度模型与密度模型的相似性耦合,并通过理论模型和青藏高原东北缘地区地震观测P波数据对本文方法进行了验证。
频率域反演具有计算速度快、内存需求低等特点,可有效提高重力反演的计算效率(Cui,Guo,2019; Wang et al,2021)。在平面观测面和深度向下为正的假设下,任意深度层的二维密度分布ρ(x',y',z'j)表示为(Cui,Guo,2019):

式中:F2D[·]和F-12D[·]分别表示二维傅立叶正变换和反变换; zj表示反演的深度层; G表示万有引力常数; imgmod(kx,ky,zj)表示深度反褶积滤波因子,其中kx和ky分别为x和y方向的频率; Δg(x,y,0)表示观测面高度为0的重力异常。
依据式(1)逐层计算深度反褶积滤波因子与重力异常频谱的乘积,通过二维傅立叶反变换将其转换至空间域,可获得每层密度分布情况。自上而下逐层组合,即可构建出研究区三维密度分布模型。
本文近震体波走时反演采用双差层析成像方法(tomoDD),该方法由Zhang和Thurber(2003)在双差定位方法基础上,融合绝对走时层析成像方法发展而来。由于地震波到时与震源位置为非线性关系,采用泰勒级数展开进行线性化近似,则地震事件i到台站k的绝对走时残差rik可表示为:

式中:xil(l=1,2,3)表示震源位置; τi是地震事件i的发震时刻; Tik表示地震波到时; wmn表示射线的第m段的第n个网格点(长度为ΔSm)的插值权重系数。同理,地震事件j到台站k的走时残差方程也表示为式(2)的形式。假设邻近地震事件到同一台站的路径相似,事件对走时残差之差rik-rjk(即双差)可以表示为:
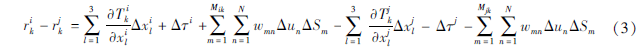
综合利用绝对走时(式2)和相对走时数据(式3),可联合反演地壳三维速度结构及震源参数。
Gallardo和Meju(2003)定义交叉梯度为任意2类地球物理模型梯度场的叉乘,定量衡量模型间的结构相似性。对于速度模型mVp(x,y,z)和密度模型mρ(x,y,z),交叉梯度向量t(mVp,mρ)具体形式为:

当交叉梯度向量值较小时,2类模型结构相似。基于交叉梯度约束的联合反演目标为拟合2类观测数据的同时,实现结构相似性。由于交叉梯度向量与2类模型参数间的非线性关系,本文利用泰勒级数展开并保留一阶项,实现线性化近似:
t(mVp,mρ)=t(m0)+B(m-m0) (5)
式中:m0是2类模型组合的初始模型向量; B是交叉梯度向量t(m0)对模型m0的雅可比矩阵。针对交叉梯度向量t(mVp,mρ)和雅可比矩阵B计算复杂且耗时的问题,则采用Vatankhah等(2022)提出的基于傅立叶变换的快速算法降低计算成本和存储需求。以优化的顺序策略(Gao,Zhang,2018)为基础,开展交叉梯度约束的联合反演。每次迭代,分别执行体波走时反演和频率域重力反演,将各自求解的模型扰动Δm0Vp和Δm0ρ引入到联合反演方程中,实现交叉梯度最小化,得到模型更新量ΔmVp和Δmρ(图1)。联合反演方程表示为:

式中:αVp和αρ分别是调节速度模型扰动量Δm0Vp和密度模型扰动量Δm0ρ之间数量级差异的权重系数,由各自模型扰动量最大绝对值的倒数确定; βt是平衡数据拟合项和交叉梯度项贡献的权重系数,根据L-curve分析(Hansen,O'Leary,1993)确定。基于交叉梯度约束近震体波走时数据与重力异常数据的联合反演流程如图1所示。
为验证本文方法的有效性和反演结果的准确性,建立了一个三维理论速度模型(图2a、表1)。该模型背景速度为6.0 km/s,内嵌3个大小各异但埋深相同的异常体,每个异常体的速度扰动均为+0.3 km/s。网格模型剖分水平方向间距为0.5°,深度间距为5 km。利用速度-密度混合关系(Maceira,Ammon,2009)将理论速度模型转换为密度模型(密度扰动为+0.06 g/cm3)。利用青藏高原东北缘地区的地震事件和台站分布对速度模型进行正演,如图3a所示,图中包含了2008年1月—2019年12月固定台站和2013年9月—2016年3月流动台站记录的MS≥1.5地震震源位置。从台站记录得到理论绝对到时数据和事件对到时差数据,再加入标准差为0.2 s的高斯噪声作为实际走时数据,同时对密度模型正演理论重力异常,加入1%的高斯噪声作为实际重力观测数据(图2b)。不同反演结果与真实模型的相对误差计算公式为:

式中:Vtruepi和ρtruei分别为真实P波速度和密度; Vinvpi和ρinvi分别为反演得到的P波速度和密度; i表示遍历网格节点。相对误差越小,说明反演结果越接近真实模型。
采用体波成像、重力成像和交叉梯度约束的联合成像这3种方法对合成数据进行反演。联合反演过程中(图4),交叉梯度项权重选为9×106(Hansen,O'Leary,1993)。图5为3种方法的反演结果对比,其中图5a分别为5 km深度的真实P波速度模型、体波成像和联合成像的P波速度结果。在此深度处,3个异常体A、B和C的联合反演P波速度(图5a-3)与单独体波反演结果(图5a-2)类似,横向分辨率有所改善,且重力数据的加入明显消除了研究区边缘的射线分布稀疏地区的虚假低速异常。图5b分别为15 km深度处真实密度模型、重力成像和联合反演的密度结果。在此深度处,相较于单独重力反演结果(图5b-2),联合反演密度结果(图5b-1)3个异常体的形态都更接近于真实密度模型(图5b-3),异常体B和C的密度值都得到较好恢复,异常体A由于尺度较小(50 km),与剖分网格水平间距相当,难以准确约束,反演结果与真实值相差0.04 g/cm3。
图2 合成理论速度模型(a)与实际加噪重力异常(b)
Fig.2 The synthetic theoretical velocity model(a)and gravity anomalies with Gaussian noise(b)
图3 青藏高原东北缘地震台阵和MS≥1.5地震事件分布(a)与剩余重力异常(b)
Fig.3 Distribution of seismic stations and MS≥1.5 earthquake events(a),and residual gravity anomalies(b)in the northeastern margin of the Qinghai-Xizang Plateau
图4 交叉梯度与走时数据拟合误差(a)和重力数据拟合误差(b)L-curve
Fig.4 Cross-gradient and traveltime data fitting error L-curve(a),cross-gradientand gravity data fitting error L-curve(b)
图5 真实、单独反演和联合反演构建的P波速度模型(a)和密度模型(b)
Fig.5 P-wave velocity models(a)and density models(b)obtainedfrom true data,solo inversion,and joint inversion
为进一步对比单独反演结果与联合反演结果的差异,分别提取3种方法反演得到穿过异常体中心(37°N)的P波速度结果和密度结果的垂直剖面,如图6所示。单独体波反演速度结果(图6a-2)显示A、B和C共3个异常体的大致形态得到部分恢复,但由于研究区地震震源深度主要集中在5~20 km(夏思茹等,2021),5 km以内体波射线分布稀疏,缺少浅层约束,速度异常向上延伸至地表,且10~15 km深度异常连接在一起,3个异常体边界模糊。联合反演时由于重力数据的引入,更好地约束了浅层速度结构,异常体位置(图6a-3)与真实模型(图6a-1)更为接近。联合反演结果清楚地显示,异常体B与C单独存在,但尺度最小的异常体A仍然难以与中间异常体B完全分开。联合反演与体波单独反演的走时残差均方根接近,但联合反演得到的P波速度模型相对偏差比单独反演小0.05(表2),更接近真实模型。
由于重力的距离平方衰减性质,其对深部结构变化不敏感,且在反演过程中,随着网格单元所在深度的增加,核矩阵中对应元素会急速衰减,导致反演结果趋于地表,无法反映地下结构实际密度分布。深度加权约束能够解决密度反演结果中异常趋于地表的问题(Li,Oldenburg,1998),但其密度结果在深度上的分辨率仍然较低,存在明显的异常底部拖尾现象(图6b-2)。联合反演得到的密度结果(图6b-3)显著改善了这一状况,3个异常体的异常分布明显聚焦,密度结果也更接近真实模型(图6b-1),重力残差均方根为0.92 mGal,明显优于单独反演结果(1.83 mGal)(表2)。
图6 真实、单独反演和联合反演构建的P波速度(a)和密度(b)结果垂直剖面
Fig.6 Vertical profiles of P-wave velocity models(a)and density models(b)obtainedfrom true data,solo inversion,and joint inversion
将单独体波走时反演得到的速度结果与单独重力反演得到的密度结果进行关联,发现并无明显相关性(图7a)。联合反演以结构相似性进行耦合,显著增强了速度与密度结果的相关性,可进一步得出物性参数之间的关系,为基于岩石物理关系耦合开展的联合反演提供更为准确的经验关系,也为地壳物质组成和状态研究提供可靠依据(Moorkamp,2022)。联合反演得到的速度-密度交会点拟合曲线(图7b灰色虚线)与理论模型转换所用的混合关系(图7b黑色实线)(Maceira,Ammon,2009)在6.0~6.1 km/s范围内基本重合,在6.1~6.3 km/s范围内实际密度结果比理论值小0.006 g/cm3。
本文P波走时数据来自夏思茹等(2021)收集的2008年1月—2019年12月青藏高原东北缘地区固定台站记录的MS≥1.5地震震相观测报告和人工挑选的2013年9月—2016年3月流动台站记录的P波到时(图3a)。为确保反演结果的可靠性,反演前对走时数据进行了质量控制和可靠性分析,保证每个地震至少同时被5个台站接收,然后利用和达法(Wadati,1928)拟合P波走时时距曲线,剔除明显偏离曲线的震相数据。经过一系列筛选,最终保留了44个固定台站和232个流动台站记录到的10 569个地震事件中92 910个P波
绝对走时数据及相应的315 821个P波走时差数据。
图7 单独反演结果(a)和联合反演结果(b)的速度-密度交会拟合曲线
Fig.7 The intersection points of velocity and density for the results obtainedfrom solo inversion(a)and joint inversion(b)
布格重力异常数据收集自中国地质调查局,平均测点间距为2~5 km(区域重力调查规范, DZ/T0082—1993)。对数据进行频谱分析,采用大于 0.018 km-1的波数(Shin et al,2007)开展高通滤波去除深层场源(>60 km)引起的区域异常, 获得主要由地壳和上地幔顶部结构引起的剩余异常(图3b)。
图8 单独反演和联合反演后的P波走时残差(a)和重力残差分布(b)
Fig.8 P-wave traveltime residual distribution histogram(a)and gravity residualdistribution maps(b)after solo inversion and joint inversion
初始模型采用夏思茹等(2021)拼合的由背景噪声和面波成像反演得到的S波速度模型,再利用Vp-VS经验关系(Brocher,2005)构建初始P波速度模型。根据研究区的地震事件和台站分布情况进行棋盘测试,结果显示反演网格横向间距为0.5°×0.5°时整体恢复较好。同样利用速度-密度混合关系(Maceira,Ammon,2009)将初始P波速度模型转换为初始密度模型。
基于本文构建的初始模型正演计算得到理论走时与实际走时的残差主要分布在±2 s范围内(图8a中灰色直方图),残差均方根为0.788 s。单独体波反演结果与联合反演结果的走时残差相当(均方根相差0.003 s),集中分布在±1 s范围内(图8a中橙色直方图),反演过程中走时数据的拟合度得到有效提高。
反演前初始密度模型正演的理论重力异常与实际重力异常的残差范围为-60~90 mGal(残差均方根56.21 mGal),单独重力反演(图8b-1)和联合反演(图8b-2)后的重力异常残差主要分布在±20 mGal。单独重力反演后的残差呈现西南高、东北低的特征(图8b-1),与实际剩余异常空间分布特征(图3b)相反,说明反演得到研究区西南部的青藏高原密度值较实际偏低,而东北角的阿拉善地块密度值较实际偏高。联合反演得到的密度结果有效去除了趋势异常(图8b-2),残差主要分布在±5 mGal范围,只在部分构造复杂区存在超过10 mGal的异常残差。
本文对青藏高原东北缘地区实际数据分别进行了单独体波走时成像、单独重力成像和交叉梯度约束的重震联合成像,并对不同方法反演得到的P波速度结果和密度结果进行了对比分析,如图9所示。在5 km深度相比于单独体波成像结果(图9a-1)的联合反演P波速度结果中(图9a-2),共和盆地表现为更显著的低速异常,与浅部沉积层分布相对应。在射线分布稀疏的阿拉善地块,巴彦乌拉山断裂(F1)西北侧为古近-新近系沉积地层,东南侧覆盖第四系松散堆积物(任纪舜等,2013)所导致,联合反演结果(图9a-2)显示:在巴彦乌拉山断裂两侧呈现明显的速度异常差异,与Deng等(2003)对于地表断裂构造的认识和Wang等(2018)得出的深地震测深剖面探测的P波速度结果相同。
图9 青藏高原东北缘地区单独反演和联合反演构建的P波速度(a)和密度(b)结果水平切片
Fig.9 P-wave velocity(a)and density(b)variations from solo and joint inversionin the northeastern margin of the Qinghai-Xizang Plateau
单独体波走时反演结果(图9a-1)显示,在托莱山断裂(F4)附近山脉地区表现为2个独立的高速异常带。而联合反演结果(图9a-2)则显示该区域为一个整体的高速异常带,与杨利荣等(2016)对于地表地质构造走向的认识一致,也与Sun等(2021)使用地震初至震相和PmP震相联合反演的P速度结果相吻合。联合成像结果显示,托莱山—冷龙岭断裂(F4、F5)位于高、低速异常过渡带内。2016年在该断裂带附近发生MS6.4地震,2022年又发生MS6.9地震。这种地震发生在高、低速过渡带的现象在其他地区也出现过(王长在等,2011),推测与壳内低速异常的状态和构造应力的积累有关。
单独重力反演对深部结构的约束较弱,在20 km深度处显示龙首山南缘断裂(F2)与祁连山北缘断裂(F3)之间存在明显低密度异常。而联合反演结果(图9b-2)并无此特征,与董治平和张元生(2007)地震层析成像的结果相吻合。海原断裂带(F7)附近单独重力成像结果(图9b-1)显示为连续展布的高密度异常,走时数据的引入显著提高深部分辨能力。联合反演得到该区域的密度呈间断分布(图9b-2),与大地电磁测深探测得到的电性结构(Xiao et al,2012)、天然地震与人工地震联合反演的速度结果(Sun et al,2019)和重震联合反演得到的密度分布特征(王新胜等,2013)一致。
本文针对实际地下介质复杂、部分地区岩石物理经验关系难以准确确定的问题,提出了一种交叉梯度约束的地震走时与重力联合反演方法。该方法基于优化的顺序策略,利用交叉梯度项将密度模型扰动量与速度模型扰动量相结合。频率域重力反演方法和交叉梯度向量、雅可比矩阵快速计算方法的引入,都有效提高了联合反演方法的计算效率。
理论模型测试显示,联合反演结果有效提高了密度结构的垂向分辨率,明显改善了密度异常底部拖尾现象。重力数据的引入,更好地约束了地壳浅层(地下5 km以内)P波速度结构,提高了横向分辨率。青藏高原东北缘地区实际数据试验表明,联合反演得到的P波速度结果与前人关于地表断裂、沉积层分布的结果对应更好。深部密度结构分布特征与前人关于大地电磁测深探测得到的电性结构、天然地震与人工地震联合反演得到的速度结构认识更为一致,验证了本文方法的可行性和有效性。
中国地震局地球物理研究所地震科学数据中心和中国地震台网中心提供了地震资料,中国地质调查局提供了重力资料,中国科学技术大学张海江教授提供双差层析成像程序,在此一并表示感谢。