虽然三轴不等长椭球体(以下简称“椭球体”)在几何形态上被视为一种更为普遍而又相对简单的形体,但在计算其引力位时却与旋转椭球体、球体、圆柱体以及矩形棱柱体等传统的规则形体有着显著的差异。为此,采用的计算策略是:首先,借助直接积分法求解椭球体内部任意点处的引力位; 然后依据椭球体引力场的特征和麦克劳林定理,将这一内部引力位问题转化为外部引力位问题(刘繁明等,2016); 最后通过对引力位在x、y、z 3个方向上求一、二、三阶偏导数。鉴于椭球体的重力与重力梯度异常表达式比旋转椭球体、球体的推导更加复杂与困难,本文充分发挥编程优势,仅利用椭球体在外部空间任意点P(x,y,z)所引发的重力异常(Δg即Vz)、重力梯度异常(Vxz、Vyz、Vzz)以及重力垂向三阶导数(Vzzz)二重积分计算式就可计算出各阶异常值,不仅降低了数学推导的复杂度,也使结果应用更具普遍性。值得注意的是,与多边形棱柱体在棱边延伸区域易产生场值奇异性不同,椭球体因其光滑闭合的几何特性,在计算引力位时无需考虑畸点所带来的复杂影响。
根据上述计算策略建立椭球体模型,如图1所示。设xoy平面为观测平面,z轴正方向朝下,椭球体位于x、y、z方向的半轴长分别为a、b、c,密度均匀分布的椭球体中心位于坐标原点O(0,0,0)。椭球体模型为:

图1 中心位于原点的椭球体模型
Fig.1 Ellipsoid model with the center at the origin
若椭球体剩余密度为ρ,(ξ,η,ζ)为椭球体内任意一点,该点处体积元为dv=dξdηdζ。根据万有引力公式,在椭球体外部空间任意点P(x,y,z)处的重力异常表达式为:
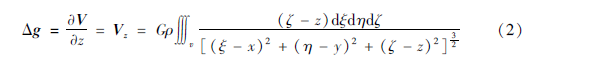
式中:G为万有引力常量6.67×10-11 m3/ (kg?s2)。
由式(2)分别对x、y求一阶偏导数,对z求一阶偏导数和二阶偏导数,得到:
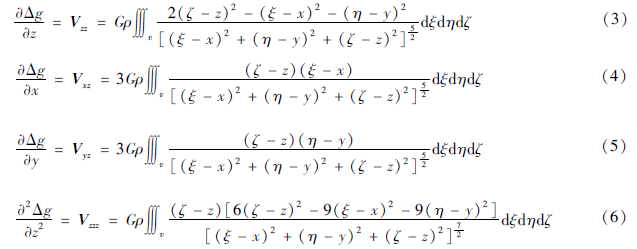
考虑到用式(2)~(6)求积分的解析解比较困难,本文采用数值积分方法求其数值解。
由式(1)可得:
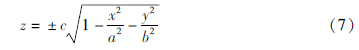
由于(ξ,η,ζ)为椭球体内任意一点,故|ζ|≤|z|,从而可得:
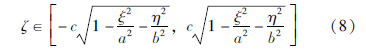
为了减少计算量,提高运行效率,将三重积分转化为二重积分,即对ζ积分,得到关于ξ、η的表达式。考虑ξ、η在xoy平面的取值范围,此时z=0,可得: 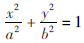 。
。
进一步得到: 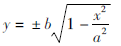
又因点(ξ,η)在椭圆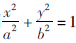 内,则
内,则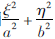 ≤1,故|η|≤|y|,|ξ|≤|x|,从而可得:ξ∈[-a,a],
≤1,故|η|≤|y|,|ξ|≤|x|,从而可得:ξ∈[-a,a], 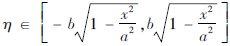 。
。
有关于ξ、η的二重积分表达式如下:
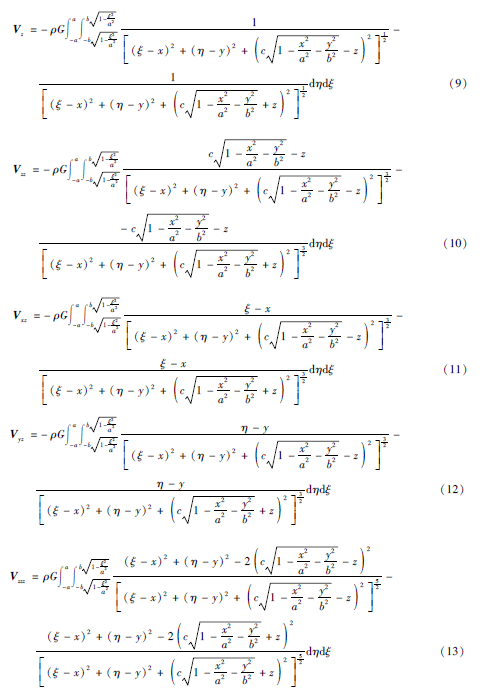
为了进行数值积分,需要把上下限转化为定值,做圆上的极坐标变换,可得:

这个变换的Jacobi行列式为:
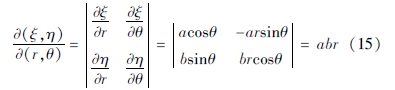
从而得到:
dηdξ=abrdrdθ (16)
由于 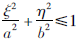 ,则r2≤1,即r∈[0,1], θ是点(ξ,η)与坐标原点的连线与x轴正向的夹角,可取[0,2π]。
,则r2≤1,即r∈[0,1], θ是点(ξ,η)与坐标原点的连线与x轴正向的夹角,可取[0,2π]。
对式(9)~(13)二重积分式中的ξ、η进行替换,则公式可分别变为:

当椭球体中心位于(x0,y0,h),且半轴a、b、c分别平行于x、y、z轴时,只需进行坐标平移,即用(x-x0,y-y0,z-h)代入式(17)~(21)进行计算。
当椭球体中心位于(x0,y0,h),但半轴a、b、c不平行于x、y、z轴时,除需进行坐标平移外,还需进行坐标旋转变换。假定a半轴与xoz平面夹角为α,与xoy平面夹角为β,且0<α,β<π/2时,则可推导出变换前后的坐标关系为:
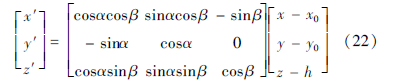
进而可用式(22)中的x'、y'、z'代入式(17)~(21)进行计算。