小波分析方法是一种窗口面积固定但其形状可以改变,即时间窗和频率窗都可以改变的时频局域化分析方法(飞思科技产品研发中心,2005)。换句话说,小波变换具有弹性的时频窗,即在低频时小波变换的时间分辨率较低,而频率分辨率较高; 在高频时小波变换的时间分辨率较高,而频率分辨率较低,因而小波变换可以保证时域分辨率和频域分辨率在各自需要的范围都达到很高的精度。另外,由于小波变换可以采用频域紧支的小波基,因此很大程度上可以避免出现频率之间交叉泄漏的现象(曹晖等,2004)。

小波分析中所用的小波函数具有多样性,可以选择非正交小波、正交小波、双正交小波,甚至线性相关的小波(崔岩飞,李晋平,2003),且应用不同的小波基函数解决同一个问题会得到不同的结果,所以在小波分析方法处理信号的实际应用中(刘希强等,1998,2000; 林大超等,2002; 裴韬等,2004; 陈顺云等,2006; 曾宪伟等,2008),小波基函数选取是否合适,将对信号处理结果的分析和理解产生直接影响,所以对小波基函数的选取是处理和分析信号前必须要做的一项工作。

在不同的应用领域,小波基的选取标准不同,即使在同一应用领域,小波基的选取也没有统一的标准。本文通过比较几种常见小波基函数的幅频特性,并利用不同的小波基函数对模拟地震记录进行时频分析,以期给出可以准确地描述地震信号时频特性的小波基函数。

定义W_n(x)如下(李弼程,罗建书,2003):

W_2n(x)=2^1/2∑_kh_kW_2n(2x-k),

W_2n+1(x)=2^1/2∑_kg_kW_2n(2x-k).(1)

其中,W₀(x)=φ(x),表示尺度函数; W₁(x)=ψ(x),表示小波函数; n=0,1,…。{W_n(x)}^∞_n=0称为由W₀=φ确定的小波包,即正交小波包。此外,在正交小波中,低通滤波器系数{h_n}_n∈Z和高通滤波器系数{g_n}_n∈Z满足

∑_n∈Zh_n-2kh^-_n-2l=δ_k,l, ∑_n∈Zh_n=2^1/2,

g_k=(-1)^kh^-_1-k.(2)

小波包{W_n(x),n∈Z₊}的伸缩平移系{2^j/2W_n(2^jx-k),n∈Z₊,j,k∈Z}称为正交尺度函数φ(x)导出的小波库。其中,Z和Z₊分别表示所有的整数和非负整数。

以Ω ^j_n表示能量有限函数空间L²(R)={f(x)〖JB<1|〗〈f,f〉=∫_R|f(x)|²dz<+∞}(R表示实数集)的闭子空间,若n为任意非负整数,则有

Ω ^j_2n⊥Ω ^j_2n+1,Ω ^j+1_n=Ω ^j_2nΩ ^j_2n+1.(3)

其中,⊥表示正交运算,表示正交和运算。小波包分解能够将变宽的频谱窗进一步分割变细,这一性质用公式表示为

Ω ^j₁=Ω ^j-1₂Ω ^j-1₃

=Ω ^j-2₄Ω ^j-2₅Ω ^j-2₆Ω ^j-2₇

=Λ

=Ω ^j-k_2^kΩ ^j-k_2^k+1ΛΩ ^j-k_2^k+1-1(4)

=Λ

=Ω⁰_2^jΩ⁰_2^j+1ΛΩ⁰_2^j+1-1.

且对于给定的m=0,1,…,2^k-1; k=1,2,…,j; j=0,1,…,有函数系

{2^(j-k)/2W_2^k+m(2 ^j-kx-1)}_l∈Z.(5)

(5)式是空间Ω ^j-k_2^k+m的规范正交基。

设f(x)在子空间Ω ^j_n中的系数为{C^n,j_k,k∈Z},其中

C^n,j_k=∫_Rf(x)2 ^j/2W_n(2 ^jx-k)^-dt.(6)

则在子空间Ω ^j-1_2n和Ω ^j-1_2n+1中的系数{C^2n,j-1_k, C^2n+1,j-1_k, k∈Z}为

{C^2n,j-1_k=∑_l∈Zh^-_1-2kC^n,j_l,

C^2n+1,j-1_k=∑_l∈Zg^-_1-2kC^n,j_l.(7)

若j固定,由(6)式得到小波包基{2 ^j/2W_n(2 ^jx-k),n∈Z₊,k∈Z}下的小波包变换系数。

若f(x)在子空间Ω ^j-1_2n和Ω ^j-1_2n+1中的系数为{C^2n,j-1_k, C^2n+1,j-1_k, k∈Z},则在子空间中Ω ^j_n的系数{C^n,j_k, k∈Z}为

C^n,j_k=∑_l∈Z(h_k-2lC^2n,j-1_k+g_k-2lC^2n+1,j-1_k).(8)

(8)式即小波包重构公式。

对于像地震信号这样的非稳态信号,我们可以通过小波变换或小波包变换等方法进行时频分析,得到信号的局部谱密度信息。

小波基的选取应从一般原则和具体分析对象两个方面考虑。对地震信号进行小波分析时,选择小波基函数的一般原则是:选取的小波基函数具有紧支撑性、对称性和正则性(光滑性)。选择与地震子波形状相近的小波基函数,或以模拟地震子波作为小波基函数(崔岩飞,李晋平,2003)。

小波变换主要有三种算法:连续小波变换、二进小波变换和离散小波变换(李弼程,罗建书,2003)。连续小波变换是一种冗余变换,其逆变换公式不具有唯一性,且信号分解子波在空间两点之间的关联增加了分析解释的困难,而离散的二进正交小波变换则不会出现这种缺陷。选择和构造一个小波基函数要求具有一定的紧支撑性、对称性和正则性。紧支撑性可以保证小波基函数具有优良的时域局部性或频域局部性; 对称性关系到小波的滤波特性是否具有线性相位,可以有效地避免信号处理过程中产生相位畸变,从而不会因相位畸变影响信号重构而造成信号的失真; 正则性主要影响小波系数重构的稳定性。通常对小波要求一定的正则性是为了易于获得光滑的重构曲线,从而减小误差。

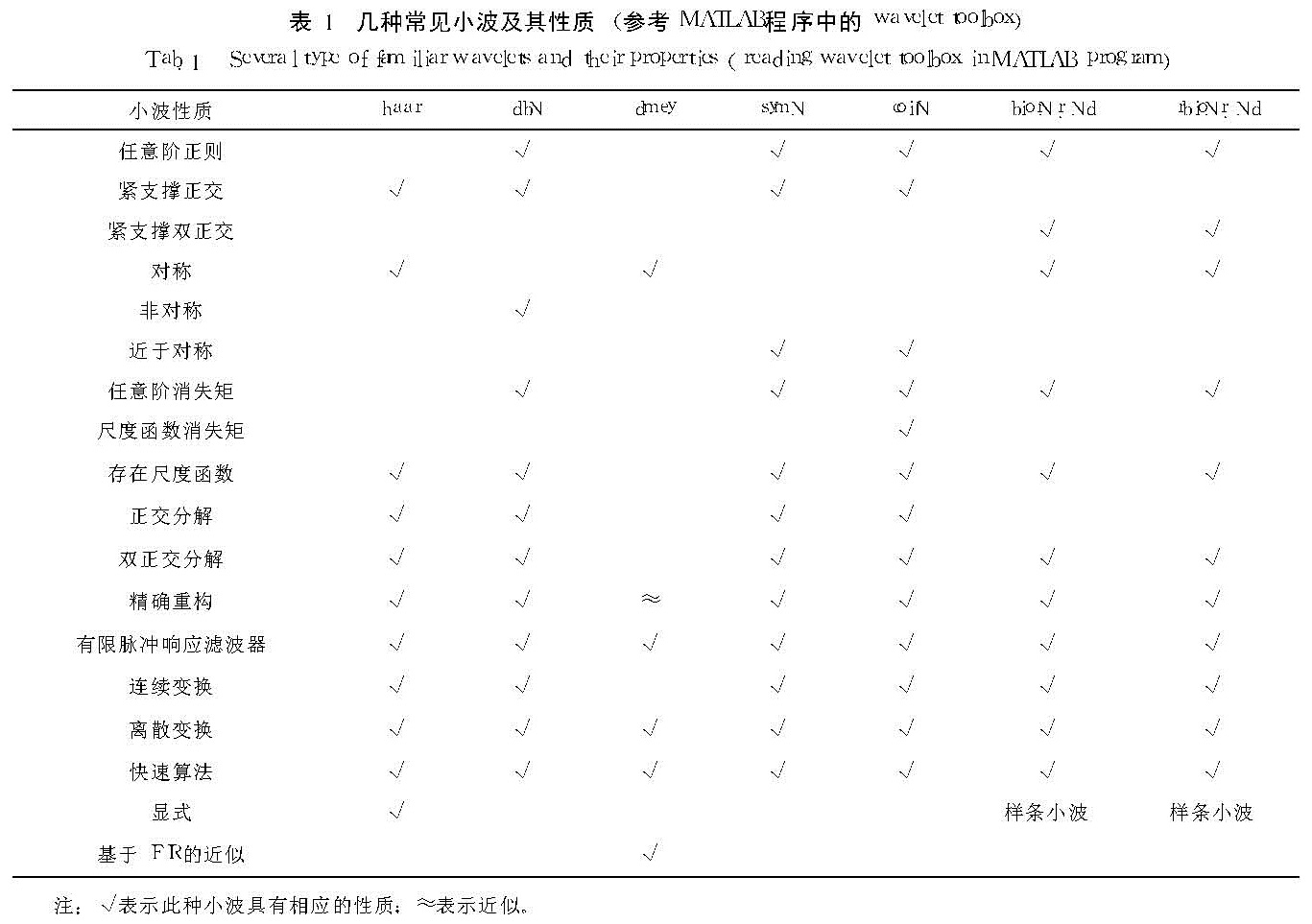
在实际的信号分析处理过程中,小波基函数的紧支撑性、对称性和正则性不可能同时满足(表1)。一般情况下,紧支撑正交小波基缺乏对称性,除haar小波基外所有具有紧支集的实的标准正交小波基都是非对称的。然而,具有对称性的尺度函数和小波函数,可以构造紧支的正则小波基,而且具有线性相位(haar小波除外,主要原

表1 几种常见小波及其性质(参考MATLAB程序中的wavelet toolbox)
Tab.1 Several type of familiar wavelets and their properties(reading wavelet toolbox in MATLAB program)

注:√表示此种小波具有相应的性质; ≈表示近似。

因在于H^haar_n关于1/2Z对称且haar小波基非连续),如dmey小波。另外,如果增加尺度函数φ的光滑度,必然要增加支撑的长度,则空间局部性变差,而光滑度越大,尺度函数的傅立叶变换Φ(ω)趋近于零的速度越快,将Φ(ω)看成带通滤波时,其分辨能力就越高(李弼程,罗建书,2003),因而光滑性和紧支撑性不能兼备。

可用于小波包分解的小波基函数种类很多,这里仅以haar(Haar wavelet)、db8(Daubechies wavelet)、dmey(Discrete Meyer wavelet)、sym11(Symlets wavelet)、coif5(Coiflet wavelet)、bior3.9(Biorthogonal wavelet)、rbio3.9(Reverse Biorthogonal wavelet)为例,对这7种小波基函数的尺度函数和小波函数作频谱分析,两者分别对应于滤波器的低通和高通部分。图1所示左侧一列为小波基函数的尺度函数和小波函数曲线,右侧一列为相应的尺度函数和小波函数的归一化幅频曲线,其中,实线为滤波器低通,虚线为滤波器高通。对比图1中不同小波基函数的幅频曲线,可发现基于db8、dmey、sym11和coif5小波的尺度函数与小波函数的频带中间较为平坦,其中dmey小波的尺度函数与小波函数的频带边缘最为陡直,使得各频带内的分解信号失真较小,在频带边缘的能量泄漏较少,与理想的高通和低通滤波器最为接近。

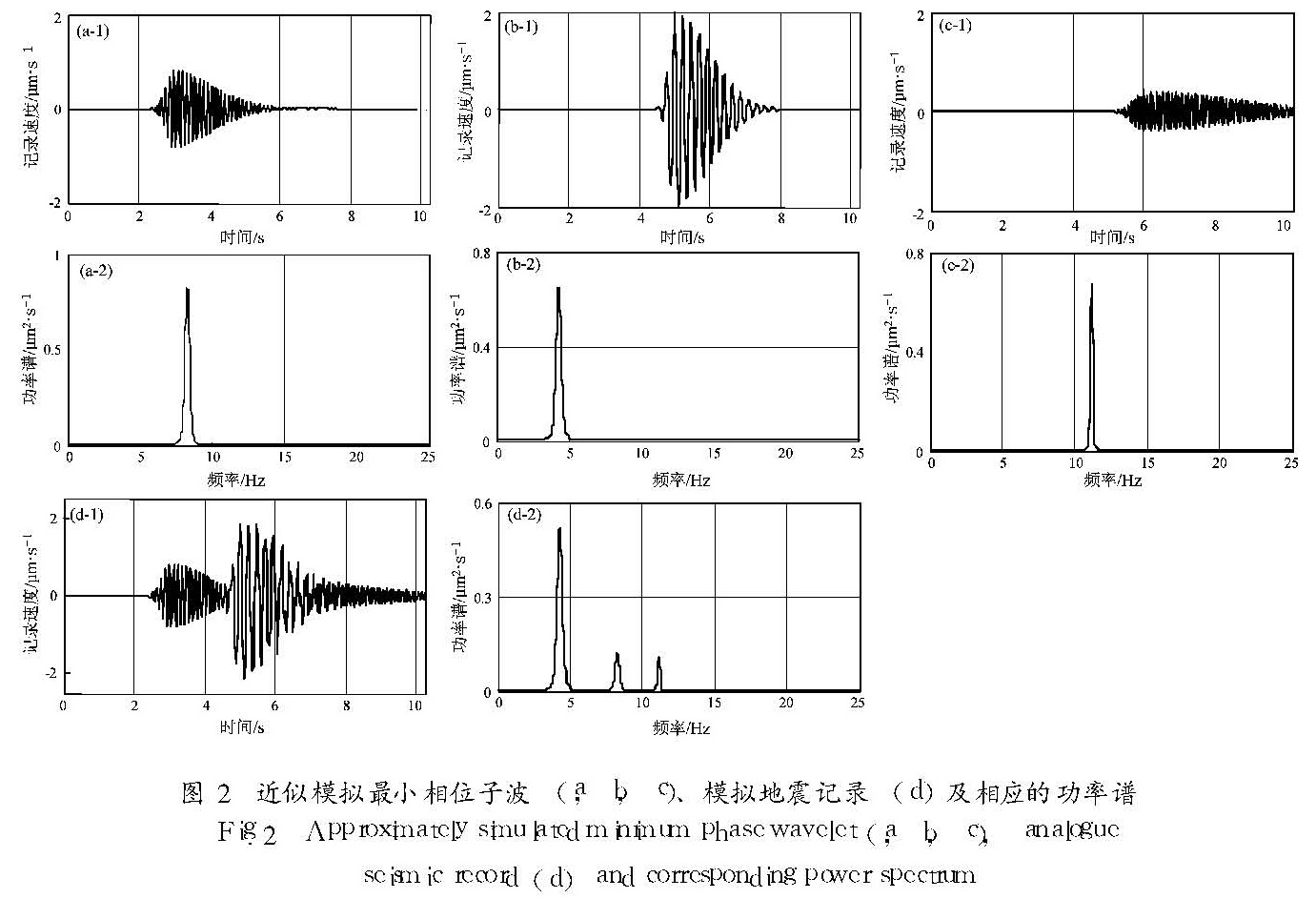
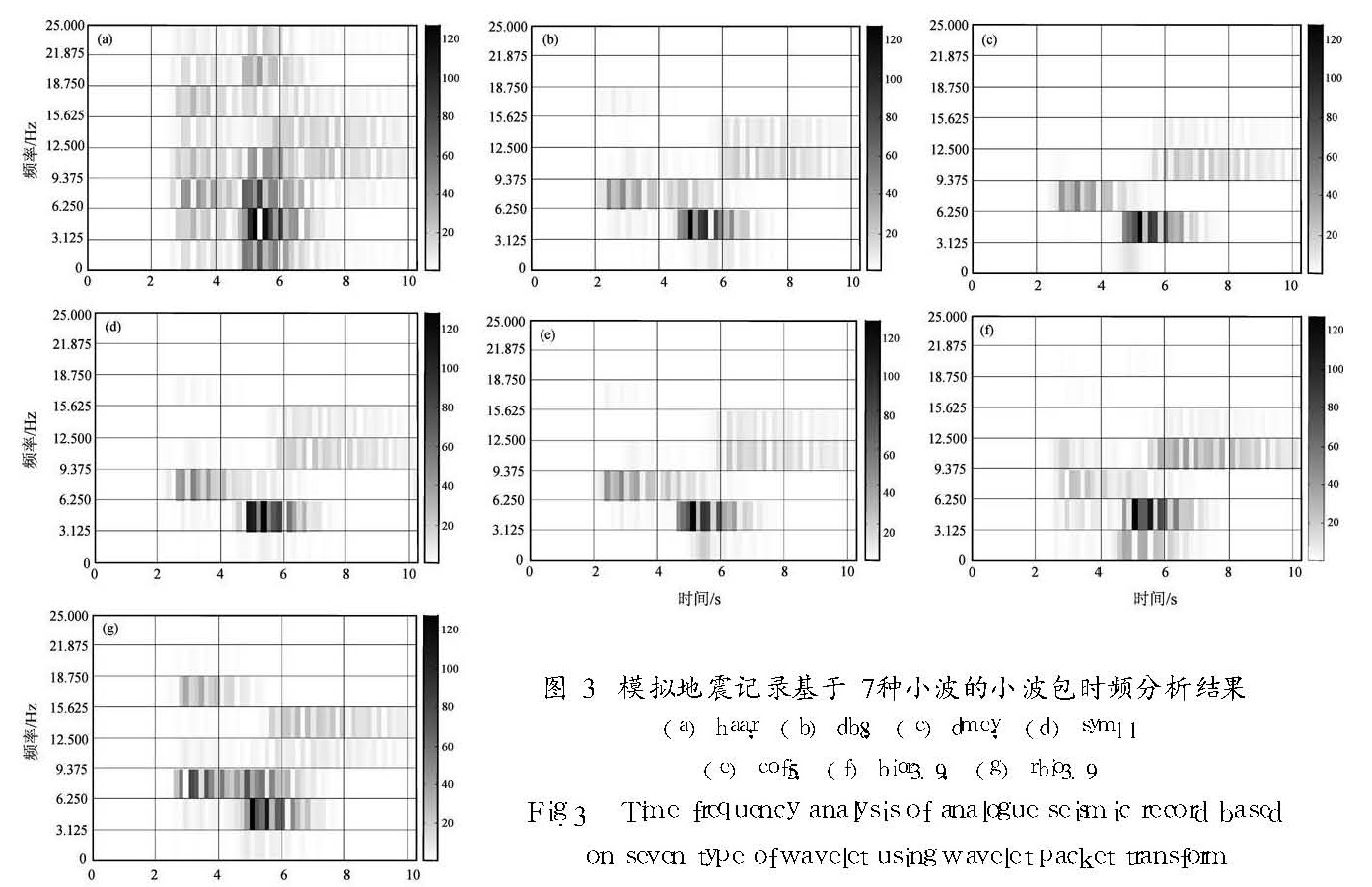
地震记录是震源激发的地震子波与地层反射率函数的褶积,本文利用近似模拟最小相位子波合成模拟地震记录(高静怀等,1996),并采用以上7种小波作为基函数分别对模拟地震记录作时频分析(图2),结果见图3。比较发现,haar小波的时频分析效果比较差,在时间分布和频率分布上均出现了明显的混叠现象。小波db8、sym11、coif5、bior3.9和rbio3.9的时频分析在频率分布上的反映或多或少都存在失真现象,尤其是对高频成分的反映不可靠。与其他六种小波时频分析结果相比,dmey小波可较为准确地描述模拟地震记录信号的时频变化特征。

图1 7种小波的尺度函数与小波函数以及相应的幅频曲线
(a)尺度函数(实线)与小波函数(虚线);(b)尺度函数(实线)与小波函数(虚线)幅频曲线
Fig.1 Scale function and wavelet function of seven type of wavelet and corresponding amplitude-frequency curve

图2 近似模拟最小相位子波(a,b,c)、模拟地震记录(d)及相应的功率谱
Fig.2 Approximately simulated minimum phase wavelet(a,b,c),analogue seismic record(d)and corresponding power spectrum

图3 模拟地震记录基于7种小波的小波包时频分析结果

(e)cofi5;(f)bior3.9;(g)rbio3.9

Fig.3 Time-frequency analysis of analogue seismic record based on seven type of wavelet using wavelet packet transform

本文在分析小波基函数选取原则和比较几种常见的小波基函数幅频特性的基础上,通过对模拟地震记录进行不同小波基函数的小波包时频分析,认为利用dmey小波基函数可以更为准确地描述模拟地震信号的时频变化特征,因此,对地震信号进行小波包时频分析时选取dmey小波基函数较为合适。基于dmey小波基的小波包时频分布可以较好地反映出信号在时间分布和频率分布上的非稳态变化过程。