选取的资料应满足下述两个条件:(1)地震目录要完整,即区域内起算震级及其以上的地震要全部被记录到;(2)为了保证所选取的地震事件的独立性和随机性,要删除大震的前震和余震。

空间平滑地震活动性模型的具体建立步骤如下:

(1)震级分布。在m₀～m_U震级范围内,震级—频度关系(Cornell,1968)表示如下

n(m)=n(m₀)(10^-b(m-m₀)-10^-b(m_U-m₀))/(1-10^-b(m_U-m₀)).(1)

式中,震级下限m₀使用完整地震目录中的起算震级,震级上限m_U在历史最大震级的基础上增加0.5度的震级档。相应的概率密度分布函数为

p(m)=(bln10·10^-b(m_U-m₀))/(1-10^-b(m_U-m₀)).(2)

(2)区域网格化。将研究区域划分为一系列的矩形网格,网格是计算的基本单元,所有的输入输出数据均赋值于单元格的中心,单元格内的地震的震中也都归于单元格的中心。网格的尺寸影响计算结果的分辨率。

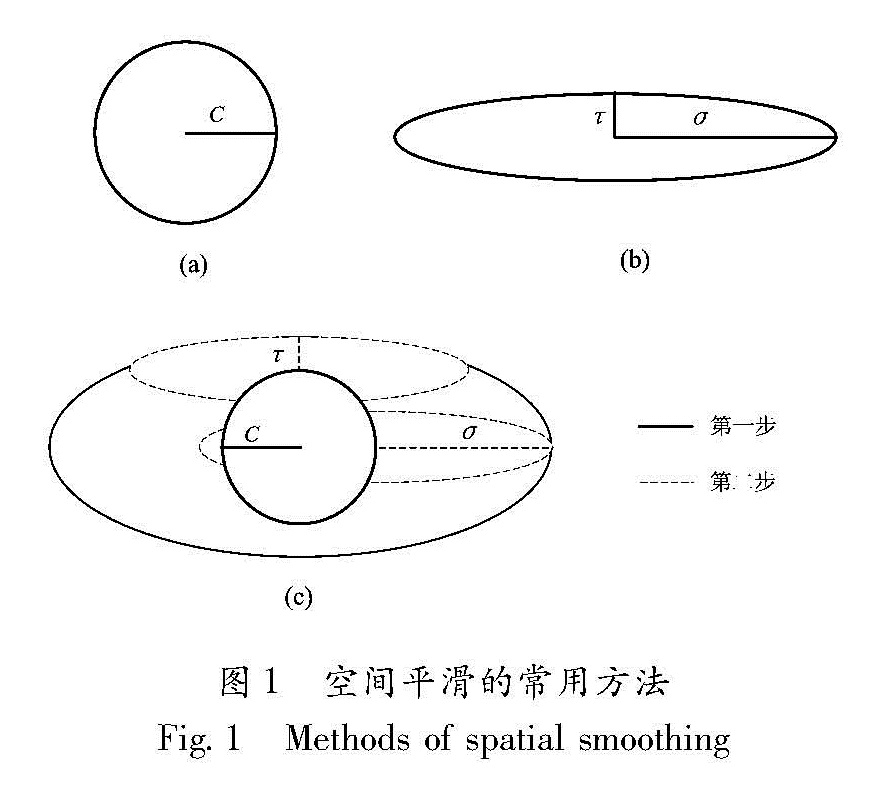
(3)空间平滑地震活动率。常用的平滑过程有一步平滑法(图1a显示圆形高斯平滑,图1b显示椭圆形平滑)和两步平滑法(图1c),椭圆形平滑和两步平滑中的长短轴可以反映地震动沿断裂构造的分布形态。但是,由于缺乏研究区域的定量地震构造模型,本文仅采用一步圆形高斯平滑法,对其它方法不再做进一步的阐述。一步圆形高斯平滑的理论计算公式为

n^-_i(m₀)=(∑_jn_j(m₀)e^{-(Δ_ij /c)2})/(∑_je^{-(Δ_ij /c)2}).(3)

式中,n_i(m₀)为第i网格M≥m₀地震的年发生率; Δ_ij为i,j两个单元格中心的距离; c为相关距离,此参数与地震定位误差有关(Lapajne et al,2003)。

图1 空间平滑的常用方法
Fig.1 Methods of spatial smoothing

将所有地震的震源都看作一个点,震源坐标归到地震所在单元格的中心。单元格的地震危险性可以通过下式计算得到

λ(u>u₀)=∑_in_i(m₀)∫^{m U}_m0P[u>u₀|m,r_i]p_i(m)dm.

(4)

式中,λ为地震动参数u>u₀的年超越概率; n_i(m₀)表示单元格i中大于起算震级m₀的地震年发生率; p_i(m)表示单元格中震源发生m级地震的概率,可由公式(2)计算得到; r_i表示单元格i的中心到目标单元格中心的距离; P[u>u₀|m,r_i]表示距离为r震级为m的地震产生地震动水平u>u₀的条件概率,计算公式为

P[u>u₀|m,r]=1/2Φ^*((lnu₀-lnu(m,r))/(2^1/2σ)).(5)

式中,Φ^*表示补充误差函数; lnu表示衰减关系。

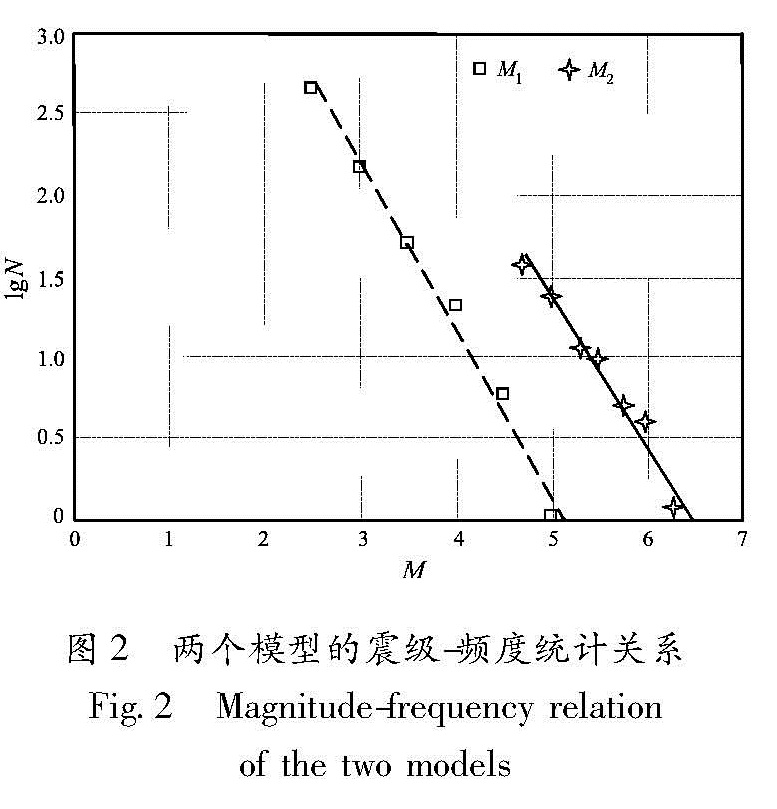
利用最小线性二乘法拟合两个模型的震级—频度关系图(图2)。计算结果表明,M1的b值为0.91,M2的b值为0.96。时间段和震级段不同的两个地震目录,统计的b值基本一致,M2模型的仪器记录可保证是完整的,由此可证明M1地震目录的完整性。M1模型使用的数据时间跨度足够长,起始震级以上的记录完整,最大震级也与地震构造研究的结果一致(刘锁旺,丁忠孝,1990)。M1的震级—频度关系可靠地反映了研究区域的地震活动水平。而M2模型统计时段有限,无法覆盖完整的地震活动周期,b值结果虽然可靠,但是a值(表示地震累积年发生率)偏低,无法反映区域真实的地震活动性水平。

图2 两个模型的震级-频度统计关系
Fig.2 Magnitude-frequency relation of the two models

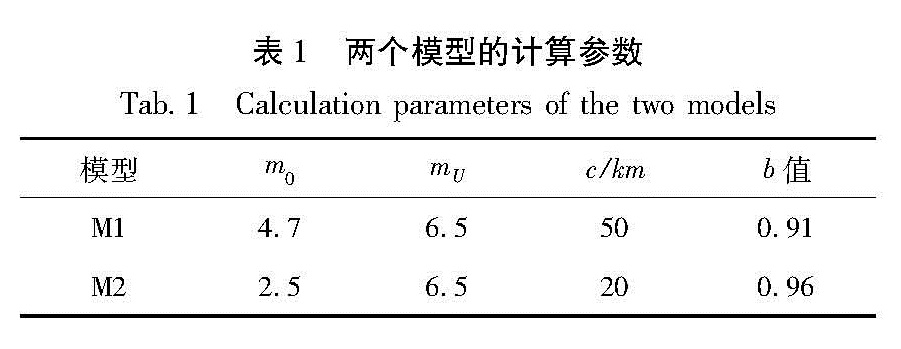
将研究区域划分为5 km×5 km的网格,用经纬度表示约为0.052°×0.045°,两个模型的计算都基于此网格; 震级下限m₀使用地震目录中的起算震级,震级上限m_U在历史最大震级的基础上增加0.5°的震级档; 相关距离c的取值与地震定位误差相关,M1模型中设为50 km,M2模型中设为20 km; 地震动计算的最大影响范围的半径为100 km。两个模型的参数设置如表1所示。

表1 两个模型的计算参数
Tab.1 Calculation parameters of the two models

按照前述的理论方法,计算每个单元格的地震年发生率的值,利用震级—频率关系将其归一化为v_4.0值(M_S≥4地震年发生率)。

图3给出了每个单元格的等值线分布。M1计算的高值的中心位于黄冈、黄石和鄂州交界地区,黄冈东北部、天门北部、咸宁南部和黄石东部受其邻区的辐射影响,v_4.0值也较高。M2计算的结果明显比M1的要低,其结果无法反映区域真实的地震活动水平,这与前面震级—频度关系的分析结果一致。1970年以来,区域的小震活动集中在黄冈东北部、天门北、咸宁西北部和黄石东南地区。

M1和M2的结果对比表明,使用不同的地震目录计算得到的地震活动性分布差异很大,M1(历史地震目录)的计算结果与已有认识较一致(刘锁旺,丁忠孝,1990),而M2(现代仪器记录)虽然有数量很多的小震,但是时间跨度有限,中强震记录不足,计算地震活动性时结果会失真。因此,建立合理的地震活动性分布模型,要求所使用地震目录在时间域中要包含一个完整的地震活动周期,在震级域中要包含一定数量的中强震事件。

由于M2的地震活动性模型无法全面反映区域地震活动性的基本特征,本文仅使用M1的模型计算地震危险性。选用湖北省地震局武汉地震工程研究院给出的湖北及邻区地震动衰减关系,最大影响半径取100 km,计算每个单元格50年超越概率10%的PGA值。

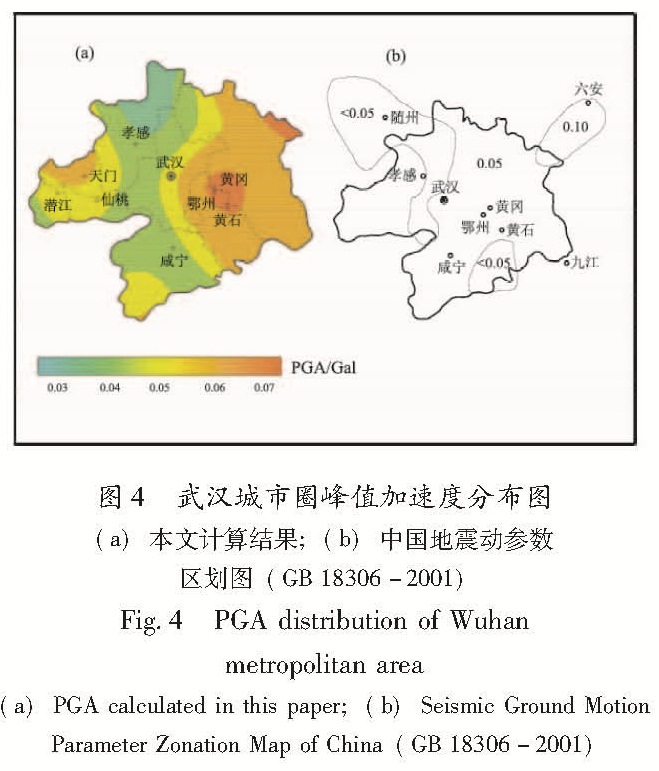
图4a给出了计算区域50年超越概率10%的基岩加速度峰值等值线分布。从图中可知,黄冈、黄石和鄂州交界地区PGA值最高,达0.07 g以上,

图3 两个模型的MS≥4.0地震年发生率分布图
Fig.3 Annual occruuence rate distribution of MS4.0 earthquakes of two models

此区域为襄樊—广济和麻城—团风断裂的交汇处,历史地震活动频繁,曾多次发生5级左右地震; 黄冈东北部PGA值也在0.07 g以上,主要受安徽霍山震源区的控制; 另外,天门北部受钟祥地震活动区的影响,PGA值达0.06 g。孝感大部、武汉西部和咸宁西北部的PGA值都在0.05 g以下,是地震危险性较低的区域。

图4 武汉城市圈峰值加速度分布图(a)本文计算结果;(b)中国地震动参数区划图(GB 18306-2001)
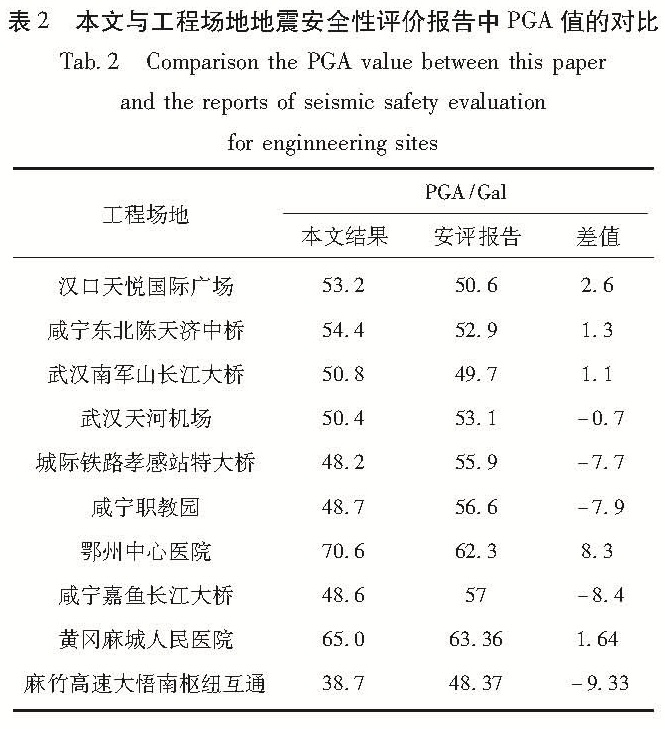
Fig.4 PGA distribution of Wuhan metropolitan area (a)PGA calculated in this paper;(b)Seismic Ground Motion Parameter Zonation Map of China(GB 18306-2001)

为进一步说明本文方法的有效性,表2摘录了研究区域内10个场地地震安全性评价报告 资料来源:武汉地震工程研究院和湖北省地震局地震文献信息中心.给出的50年10%超越概率下的基岩PGA值,10个场地在区域内均匀散布。对比表明,有50%的差值在0.005 g以内,另50%的差值在0.005～0.01 g,最大差值未超过0.01 g。

表2 本文与工程场地地震安全性评价报告中PGA值的对比
Tab.2 Comparison the PGA value between this paper and the reports of seismic safety evaluation for enginneering sites