基金项目:国家科技支撑计划课题(2007BAS18B01).
(1.北京科技大学 土木与环境工程学院,北京 100083; 2.华北科技学院 土木工程系,北京 101601)
(1.Civil and Environmental Engineering School, University of Science and Technology Beijing, Beijing 100083, China)(2. Department of Civil Engineering, North China Institute of Science and Technology, Beijing 101601, China)
seismic signal; WPT; best basis; denoising; dependent threshold
备注
基金项目:国家科技支撑计划课题(2007BAS18B01).
应用最优小波包变换,采用取决于节点噪声时频特征的相关阈值,对模拟地震波到达的加噪合成信号、SDAES 数字声发射仪采集的微震实验信号、NIED观测台站记录的日本2007年能登半岛地震信号进行去噪,并和基于小波变换的其他方法进行了去噪效果比较。结果 表明,该方法获得的信号信噪比(SNR)高、失真低,体现出了总体优越性。
We apply the node-dependent threshold relative to the characteristics of the time-frequency of the noise to the optimum Wavelet Packet Transform(WPT)method to denoise a synthetic noisy signal of the arrival of the simulative seismic wave,an experimental micro-seismic signal collected by a digital acoustic emission instrument, SDAES, and a seismic signal of 2007 Noto Hanto Earthquake in Japan recorded at NIED observatory. We find that the signal denoised by the optimum WPT method has a higher signal-to-noise ratio(SNR)and a lower distortion than those by other methods based on wavelet transform(WT)methods, and the WPT method shows the overall superiority.
引言
地震记录信号信噪比往往比较低,使得地震波到时读取、极性分析、振幅判定较为困难。为了获得有用信息,就必须对记录信号进行消噪。地震信号是非平稳信号,使用时不变滤波方法(如传统傅立叶变换),在信号和噪声频带重叠时滤波效果不够理想(Scherbaum,1996; Douglas,1997)。
小波变换克服了窗口傅立叶变换(Allen,Rabiner,1977)在信号分析上不能同时兼顾时间分辨率和频率分辨率的缺点,通过母小波函数的展缩和平移,时间窗和频域窗都能改变,可以进行多分辨率分析,因而国内外许多研究者将小波分析用于信号的提取及消噪处理。
基于小波变换信号去噪的方法源于小波阈值去噪理论(Donoho,Johnstone,1994)。根据噪声通常表现为高频信号的特性,对小波分解的高频系数进行门限阈值处理,然后对处理后的系数进行小波重构获得恢复信号,该方法受到广泛重视和研究(雷栋等,2006; 张平等,2007)。
假设小波分析信号频谱处于低频带,只对信号的低频分量按小波分解树结构进行时频再分解,所以信号在高频段分辨率较差。小波包变换是小波变换的推广,对低频部分和高频部分都进行二次分解,采用最优基能够根据被分析信号的特征自适应地选择与信号频谱相匹配的频带。因此小波包分解可以将高频噪声和高频信号区分开来,从而获得更理想的去噪效果(Galiana-Merino et al,2003,2007)。
笔者应用最优小波包变换,采用节点噪声时频特征相关阈值,通过Matlab仿真实现了人工合成信号、实验信号和实际地震信号的去噪,并和基于小波变换的其它方法进行去噪效果对比。
1 理论背景
1.1 小波包小波包变换(彭玉华,1999; 刘明才,2005)推广了小波分析,通过一组低、高通正交滤波器H和G,对给定信号进行高频和低频分量多层次分解,使信号的时频特征分解的更加精细,适合于描述和刻画非平稳信号。
令正交小波基的滤波器系数分别为{hk}k∈Z和{gk}k∈Z,并将尺度函数φ(t)改记为u0(t), 小波函数φ(t)改记为u1(t), 由关于φ(t)和φ(t)的两尺度方程(1)式,引进小波包的概念(2)式
{u0(t)=21/2∑k∈Zhku0(2t-k)
u1(t)=21/2∑k∈Zgku1(2t-k).(1)
{u2n(t)=21/2∑k∈Zhkun(2t-k)
u2n+1(t)=21/2∑k∈Zgkun(2t-k).(2)
式(2)所定义的函数集合{un(t); n∈Z+}为由u0=φ 所确定的小波包(正交小波包)。
定义闭包空间Unj=span{2j/2un(2jt-k)}k∈Z^-, n∈Z+, j∈Z。 设gnj(t)∈Unj, gnj(t)可表示为
gnj(t)=2j/2∑k∈Zdnjkun(2jt-k).(3)
则小波包分解的分解算法为
{d2njl=∑k∈Zh^-k-2ldnj+1,k
d2n+1jl=∑k∈Zg^-k-2ldnj+1,k.(4)
重构算法为
dnj+1,l=∑k∈Z(hl-2kd2njk+gl-2kd2n+1jk).(5)
1.2 小波包基的确定对应L2(R)空间的子空间的每一种划分形式就能得到一种小波包基,在众多的小波包基中,笔者采用最优基,可在所需研究的尺度上提供较好的时频分辨率。
给定一个序列的代价函数,在小波库{2j/2un(2jt-k); n∈Z+, k, j∈Z}的所有小波包基中寻找代价函数最小的基即为最优基。
代价函数可定义为任何关于序列的实函数M,而实函数M的选取,最好是那些能够测得系数集中度的可加性代价函数。当序列中的系数大致在相同尺度时,M会大,反之,M会小。对实数序列附加信息成本函数M采用香农熵,则有
M[djl(i)]=-∑idjl(i)2log[djl(i)2],
且0lg0=0.(6)
对小波包分解的每个节点计算成本函数,通过比较某一节点与其子节点的值,获取熵值最低的基。由最小熵确定的最优基,对给定母小波和成本函数提供了最佳选择。
1.3 小波包去噪基于小波的降噪算法大多遵循以下步骤:对信号变换,修改小波系数以减少或消除难以确定的系数,重构系数序列获得所需信号。假设含噪有限长信号可表示为
x(i)=s(i)+z(i)i=0,1,…,N.(7)
其中,x(i)是记录信号; s(i)是感兴趣的信号; z(i)是噪声。 去噪的最终目标是从x(i)中找到s(i)的一个估计信号s^(i),并尽可能与之类似。具体计算方法如下:
(1)小波包变换:计算小波包变换X=Wx,得到与基函数相关的小波包系数序列djl,该系数序列也被噪声污染,可表示为
djl|x=djl|s+djl|z.(8)
式中,djl|x表示记录信号的系数集合; djl|s表示感兴趣信号的系数集合; djl|z表示噪声相关的系数集合。
(2)小波包系数阈值处理:感兴趣信号的能量集中在小波域的少量系数上,其取值必然大于能量分散的噪声的小波包系数值。假设每个小波包系数都受到污染,对它们进行阈值处理,处理的主要方法有硬阈值和软阈值(Donoho,1995):
硬阈值:S^=Th(X,t)={X |X|>=t
0 |X|<t.(9)
软阈值: S^=Th(X,t)
={sgn(X)(|X|-t)|X|>=t
0 |X|<t. (10)
阈值处理以最小化估计系数与期望系数之间的均方差最小化为目的。从L2范数误差最小的观点出发,硬阈值处理方法的估算系数djl|s优于软阈值方法,但其重构信号的光滑性不如软阈值方法。
(3)小波包逆变换:计算小波包逆变换s^=W-1S^得到恢复信号s^。
2 最优基节点阈值去噪
Donoho(1995)去噪的目标是最小化估算信号s^(i)和关注信号s(i)之间的均方差。 由于实际信号s(i)未知, 噪声z(i)也不一定是通常假设的白噪声。因此,如何确定阈值及其量化,直接关系到信号消噪的质量。本文采用最优基节点噪声频谱相关阈值去噪。步骤如下:
(1)在信号x(i)的前几秒内提取噪声样本z'(i);
(2)输入母小波及最高分解层数,对x(i)和z'(i)进行小波包分解,获得小波包树结构;
(3)应用信息成本函数,获得x(i)的最优基, 对噪声z'(i)选择相同的节点集合。小波包分解输出两套系数:djl|x系数和噪声系数djl|z';
(4)相关阈值的确定:
最优基节点噪声方差相关阈值采用通用的阈值公式(10),如下
Th|jl=σjl(2logNjl)1/2. (11)
这里,σjl是噪声的标准方差,N jl是序列djl|(i)|z'的长。对小波包变换系数djl|x阈值处理,得到关注信号s(i)的系数djl|s=djl|x-djl|z',该系数中去除了低幅度的噪声等不期望的信号,保持或缩小关注信号大幅值系数。
最后,对阈值处理后的最优基系数进行重构获得去噪信号。
3 Matlab仿真结果
笔者采用三种方法分别对合成信号、实验信号和实际地震信号进行去噪:(1)采用多尺度小波变换默认阈值去噪(胡昌华等,1999);(2)采用小波变换层相关阈值去噪;(3)采用本文方法,即基于最优小波包基变换节点相关阈值去噪。后两种方法的阈值取决于相应层(或相应节点)的噪声方差和噪声序列长度,可由式(11)确定。
分解应用多种母小波,多个分解层和多种阈值方法实现。为便于比较,以下小波变换均采用小波函数Daubechies 8,最大分解层数为3,软阈值处理。
3.1 合成信号用合成信号模拟震源P波和S波的相继到达情况,假设独立点震源的地震波强度随时间满足指数衰减规律(Aki,Richards,1980; Slawmomir,et al,1994)
m(t,ω,Q,t0)=A0exp[-πω(t-t0)/Q].(12)
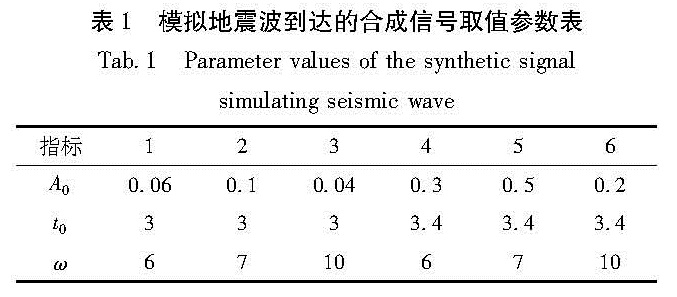
这里,Q为常数,取30; ω为频率; t0为波的初始到达时间。依据这个关系,可以构造一个包含多个频率的合成信号
f(t)={0(0≤t<t01)
∑31misinωi(t-t0i)(t01≤t<t02)
∑61misinωi(t-t0i)(t02≤t<10).(13)
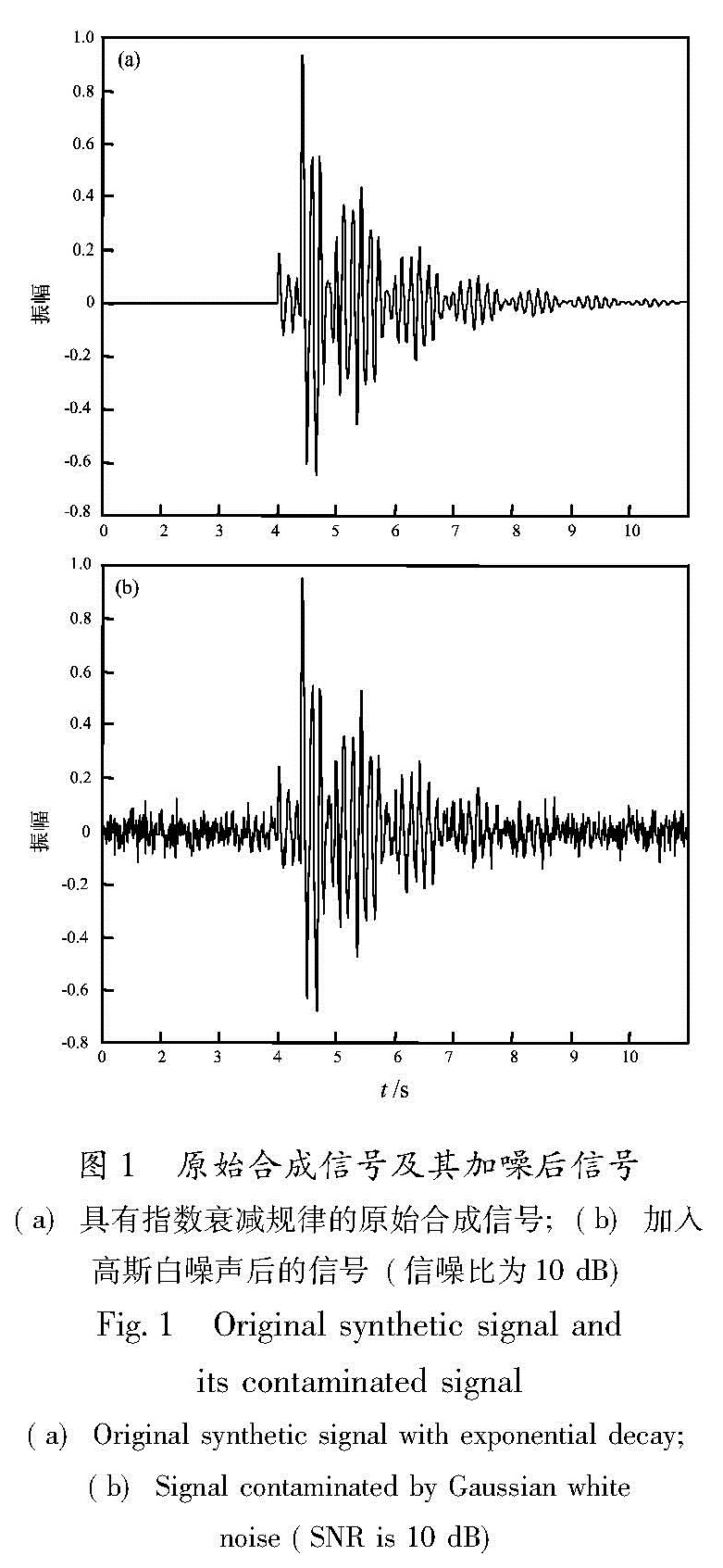
其中,mi=m(t,A0i,ωi,t0i),信号中的基本参数按表(1)给出,采样频率100 Hz,信号终止时刻为10 s。合成的原始信号及其被信噪比为10 dB的高斯白噪声污染后的信号如图1所示。
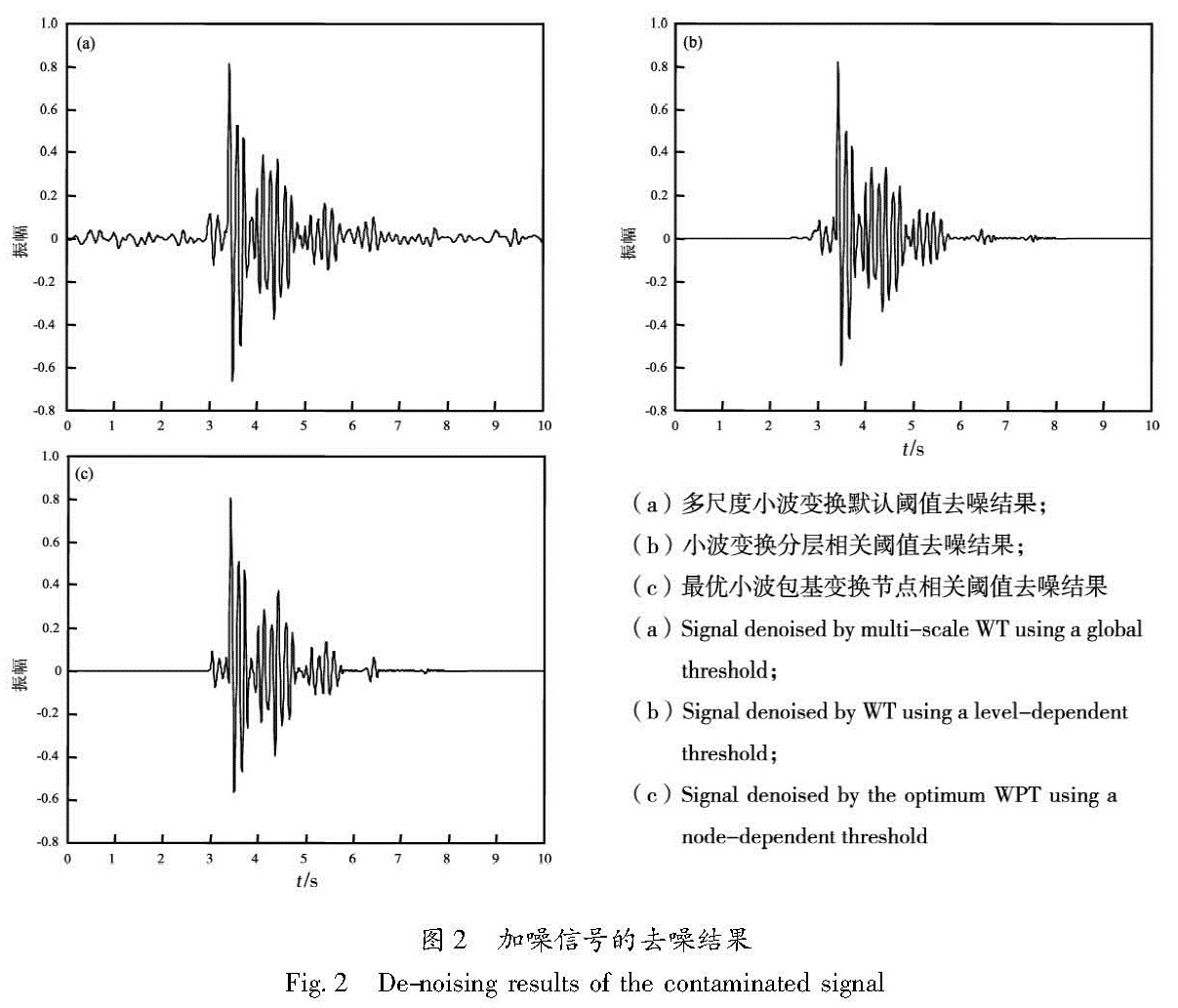
利用信号前2 s(200个样本)的数据来描述噪声。Matlab仿真消噪结果显示:采用小波变换默认阈值去噪,去噪后信号信噪比有所改善,信号前有人为引入的波动信号,第一到达脉冲失真较小(图2a); 利用小波变换分层计算的阈值去噪,信号信噪比很高,第一脉冲到达前产生的人为信号不明显,第一脉冲的最大峰值时间没有延迟或提前,但第一脉冲的到时有明显失真(小波包变换采用默认阈值及节点相关阈值,消噪结果也不理想)(图2b)。图1 原始合成信号及其加噪后信号(a)具有指数衰减规律的原始合成信号;(b)加入高斯白噪声后的信号(信噪比为10 dB)
Fig.1 Original synthetic signal and its contaminated signal(a)Original synthetic signal with exponential decay; (b)Signal contaminated by Gaussian white noise(SNR is 10 dB)笔者利用最优小波包基变换,采用节点相关阈值去噪,去噪信号与加噪前的原始信号非常相似,不但信噪比非常高,第一脉冲到达前也没有产生人为引入的信号,而且第一对脉的到时几乎没有失真,去噪效果最好(图2c)。
3.2 实验信号图3a为SDAES 数字声发射仪采集的近距离微震实验信号,提取信号前2 s(1 250个样本)的数据作为噪声。
去噪结果表明:3种方法对第一脉冲峰值没有产生时间延迟或提前; 采用小波变换默认阈值去噪,信噪比改善不明显,频谱分析表明噪声信号频带与微震信号频带相近,该方法去噪原理类似低通滤波器,因此去噪效果不好(图3b); 采用小波变换分层阈值去噪,信噪比有所提高,但结果仍不够理想(图3c); 最优小波包基变换采用节点阈值去噪,信噪比有很大的提高,虽然结果的幅值较其他方法要低,但不影响到时的取值(图3d),即该方法对低频噪声的去噪效果明显优于以小波变换为基础的其他去噪方法。
图3 实验信号及去噪结果(a)声发射仪采集的微震实验信号;(b)多尺度小波变换默认阈值去噪结果;(c)小波变换分层相关阈值去噪结果;(d)最优小波包基变换节点相关阈值去噪结果
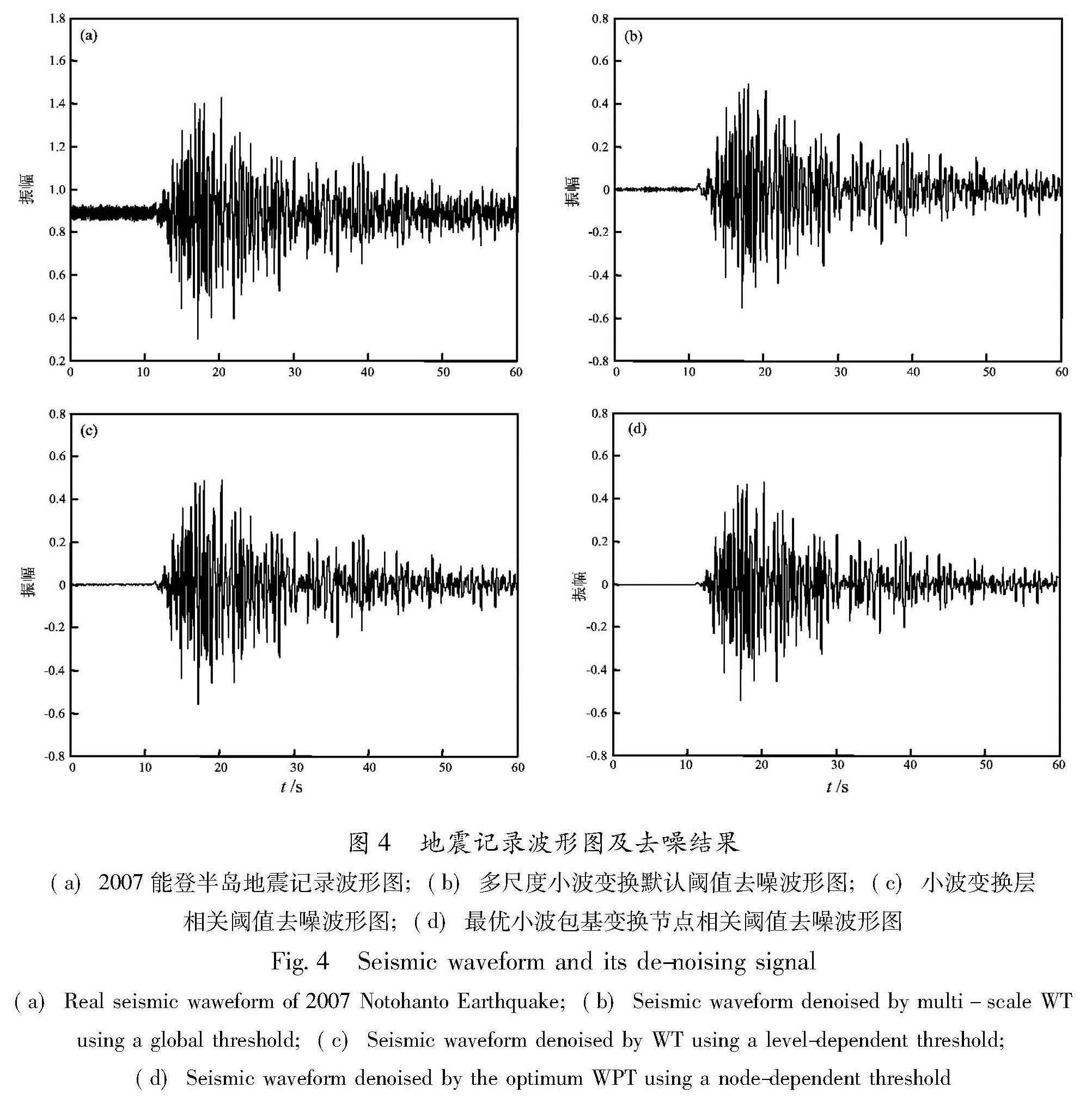
Fig.3 Experimemtal signal and its de-noising signal(a)Experimental micro-seismic signal collected by SDAES digital acoustic emission instrument; (b)Signal denoised by multi-scale WT using a global threshold;(c)Signal denoised by WT using a level-dependent threshold;(d)Signal denoised by the optimum WPT using a node-dependent threshold3.3 地震信号图4a为2007年3月25发生在日本能登半岛地震的记录波形图,数据源于NIED(K-NET)强震观测台站。地震图信噪比不足以精确确定到达时间,应用上述3种方法消噪,采用震前10 s(1000个样本)记录的环境噪声数据来描述。
类似前面的结果,最优小波包基变换采用节点相关阈值去噪在信噪比上优于小波变换为基础的去噪结果(图4b~d)。
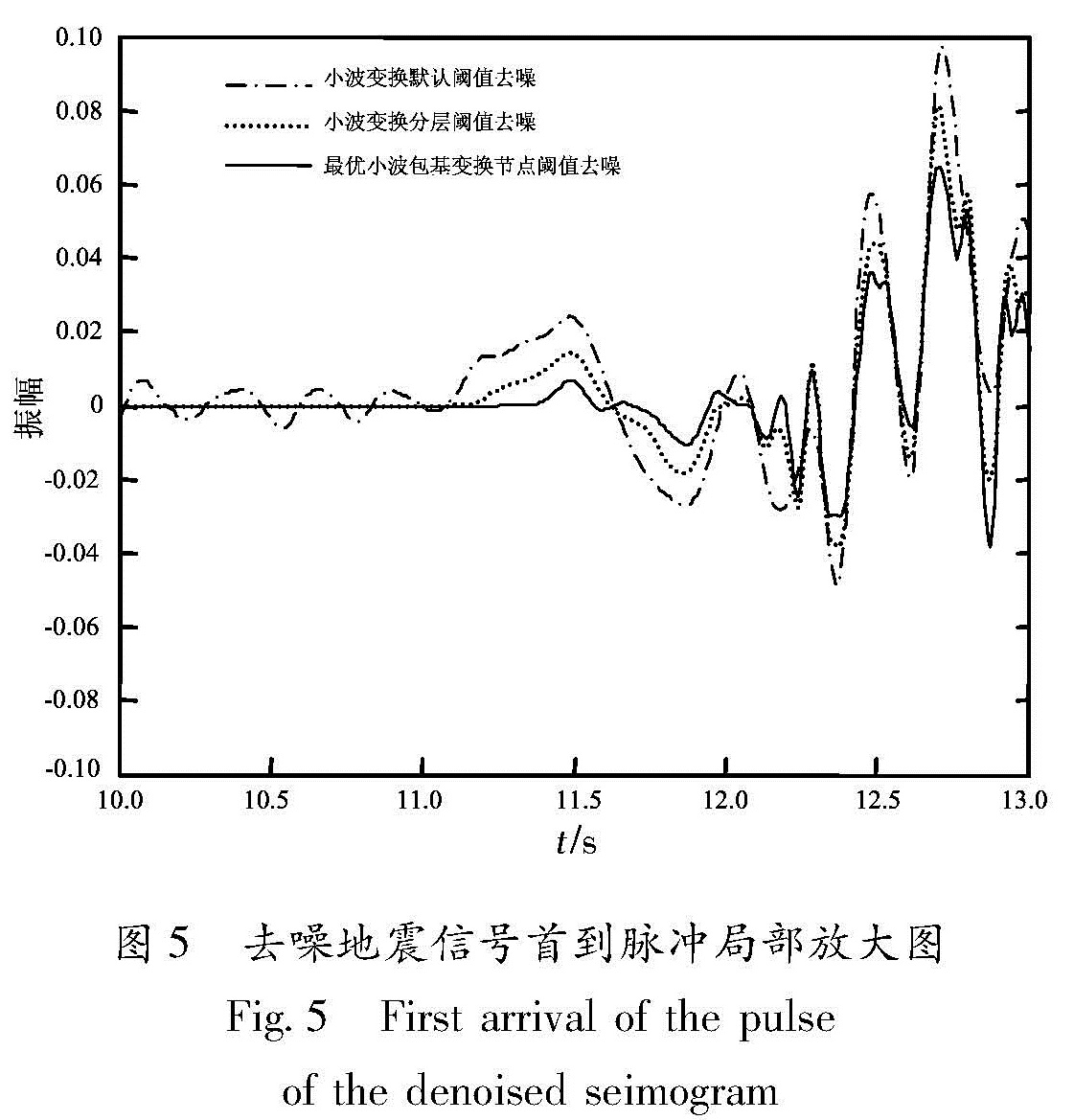
图5是图4去噪结果的第一到达脉冲的局部放大图。由图5可见:尽管3种方法得到的第一脉冲的峰值幅值不同,但位置一致,而第一脉冲的到达时间存在明显差异。根据上述合成信号和实验信号的分析结果以及地震波形图的频谱分析推断:应用小波变换方法去噪,信号的到时有可能存在人为引入的信号波动误差; 采用最优小波包基变换节点阈值,去噪后信号第一脉冲的到时位置更准确。
分析:小波包变换将信号在低频部分和高频部分都进行了精细分解; 采用最优基能够根据该信号的特征自适应地选择相应的频带,使之与信号频谱相匹配; 采用节点相关阈值消噪使信号的去噪效果最佳。这表明本文采用的去噪方法为后续分析提供的信号更可靠。
4 结论
笔者采用基于小波(包)变换的几种方法对合成信号、实验信号和实际地震信号进行了阈值去噪。结果表明:三种方法去噪信号初到峰值位
图4 地震记录波形图及去噪结果(a)2007能登半岛地震记录波形图;(b)多尺度小波变换默认阈值去噪波形图;(c)小波变换层相关阈值去噪波形图;(d)最优小波包基变换节点相关阈值去噪波形图
Fig.4 Seismic waveform and its de-noising signal(a)Real seismic waweform of 2007 Notohanto Earthquake;(b)Seismic waveform denoised by multi-scale WT using a global threshold;(c)Seismic waveform denoised by WT using a level-dependent threshold; (d)Seismic waveform denoised by the optimum WPT using a node-dependent threshold
置一致; 采用多尺度小波变换默认阈值去噪,去噪信号信噪比不高,第一脉冲前会产生一些人为引入的振荡信号; 采用小波变换分层阈值去噪,能给出比默认阈值要好的信噪比,但第一脉冲的到时有明显失真; 由于小波包变换对信号分解精细,采用最优基能使时频分解动态适应信号特征,节点相关阈值消噪使信号的去噪效果最佳,最终能获得高信噪比,低失真的去噪信号,第一脉冲的到时也更准确,总体上表现出优越性。
- 胡昌华,张军波,夏伟,等.1999.基于Matlab的系统分析与设计——小波分析[M].西安:西安电子科技大学出版社,217-232.
- 雷栋,胡祥云,张素芳.2006.小波理论及其在地震监测中的应用[J].地震研究,29(1):103-106.
- 刘明才.2005.小波分析及其应用[M].北京:清华大学出版社,88-97.
- 彭玉华.1999.小波变换与工程应用[M].北京:科学出版社.
- 张平,山秀明,毛玉平.2007.基于小波多分辨率分析的地磁脉动信号提取[J].地震研究,30(2):179-181.
- Aki K,Richards P G.1980.Quantitative seismology:theory and methods,Vol I [M].San Francisco:W H Freeman and Company.
- Allen J,Rabiner L.1977.A unified approach to short-time Fourier analysis and synthesis[J].Proc IEEE,65(11):1558-1564.
- Donoho D,Johnstone I M.1994.Ideal spatial adaptation by wavelet shrinkage[J].Biometrika,81(3):425-455.
- Donoho D.1995.De-noising by soft-thresholding[J].IEEE Trans Inform Theory,41(3):613-627.
- Douglas A.1997.Bandpass filtering to reduce noise on seismograms:is there a better way? [J].BSSA,87(3):770-777.
- Galiana-Merino J J,Rosa-Herranz J,Giner J,et al.2003.De-noising of short-period seismograms by wavelet packet transform[J].BSSA,93(6):2334-2562.
- Galiana-Merino J J,Rosa-Herranz J,Jáuregui P,et al.2007.Wavelet transform methods for azimuth estimation in local three-component seismograms[J].BSSA,97(3):793-803.
- Scherbaum P.1996.Of poles and zeros:Fundamentals of digital seismology[M].Hinham:Kluwer press.
- Slawmomir J,Gibowicz,Andrzej K.1994.An Introduction to Mining Seismology[M].New York:Academic Press.