(1.北京大学 地球与空间科学学院,北京100871; 2.黑龙江省地震局,黑龙江 哈尔滨 150090)
(1.School of Earth and Space Sciences,Peking University,Beijing 100871,China)(2.Earthquake Administration of Heilongjiang Province,Harbin 150090,Heilongjiang,China)
displacement field; stress field; seismic landslide; finite element method; dynamic
备注
利用基于FEPG的有限元新模型,从动力学的角度对地震中断层的破裂过程进行了研究,探讨其对边坡的位移场、应力场的动态影响,从而用数值模拟的方法印证了现有的地震滑坡动力学模型理论。
Using a new finite element model based on the Finite Element Program Generator,we research the fault rupture process in the earthquake from the viewpoint of dynamics, and discuss the dynamic effect on displacement field and stress field of slope from the new model.Therefore we use the method of numerical simulation to prove the existing earthquake-inducing landslide dynamics model theories.
引言
2008年汶川8.0级地震诱发了惨重的破坏性地震地质灾害,触发了约5万处滑坡,滑坡灾害造成的人员死亡约占地震总死亡人数的1/3。地震滑坡因其巨大的致灾力引起了人们广泛的关注(李为乐等,2011)。目前对滑坡现象发育分布规律的统计的研究已较为成熟,而对其动力学机理的研究尚处于初步阶段。汶川地震所造成的许多巨型、高速、远程滑坡已超过了现有的认知水平。从动力学的角度,采用数值模拟方法来验证相关滑坡概念模型及推断的研究还比较少。
滑坡是指斜坡的局部稳定性受破坏,在重力作用下岩体或其他碎屑沿一个或多个破裂滑动面向下做整体滑动的过程与现象。地震是触发滑坡灾害的主要因素之一,地震震级ML>4.0时便会触发滑坡灾害。一次大型地震可以诱发数万处滑坡,分布范围可达 1×105 km2,地震滑坡造成的生命财产损失可以占到整个地震造成损失的 50%,甚至更多。
由于对滑坡产生的机理及其动力学过程并不清晰,学者们提出了许多不同的观点。Celebi(1987)研究了1985年Central Chile地震时的地形放大及场地放大,认为在主震及余震中,地面运动在不同地质条件的场地及山脊处确实得到放大; Geli等(1988)指出,地形放大效应随坡度的增大而增大; 毛彦龙等(1998)认为坡体波动震荡在斜坡岩土体变形破坏过程中产生三种效应:累进破坏效应、启动效应和启程加速效应。本文利用基于FEPG(Finite Element Program Generator)的有限元新模型,从动力学的角度研究断层破裂引发地震,及其之后一段时间内的位移场和应力场的连续变化过程,进而研究其对边坡广义荷载场的动态影响,从而验证上述理论观点。
1 基于FEPG的有限元新模型方法
由于均匀各向同性弹性半空间的地震位错理论不能给出考虑非均匀介质和非均匀应力场的理论解,特别是一个有复杂边界条件和多条独立断层的理论解。为了克服地震位错理论的这些局限性,本文使用了一种有限元新模型来研究地震断层的发震加强,及其周围介质的位移场和应力场的连续变化的现象。该模型可以考虑介质和构造应力场的不均匀性,以及介质内部位移场、应力场的演化(胡才博,2009a)。
在本文使用的新模型中,将发震断层看作是有一定厚度的断层带,这是新模型与地震位错理论、利用分裂节点技术(Melosh,Aaefsky,1980)的有限元法的一个不同之处,后面两种方法都将断层视为没有厚度的几何面。岩石力学实验、野外地质考察和地震波记录都表明伴随着地震的发生,发震断层的力学性质发生了改变(Jaeger,Cook,1979)。因此新模型可以将地震看作是在应力场作用下由于断层带介质的突然破坏或损伤而产生的失稳事件。
在新模型中,将断层带介质视为横观各向同性弹性材料,通过降低断层带的剪切模量来模拟地震或断层错动。本文所采用的新方法是动力学方法,而所有基于地震位错理论的方法都是运动学方法。
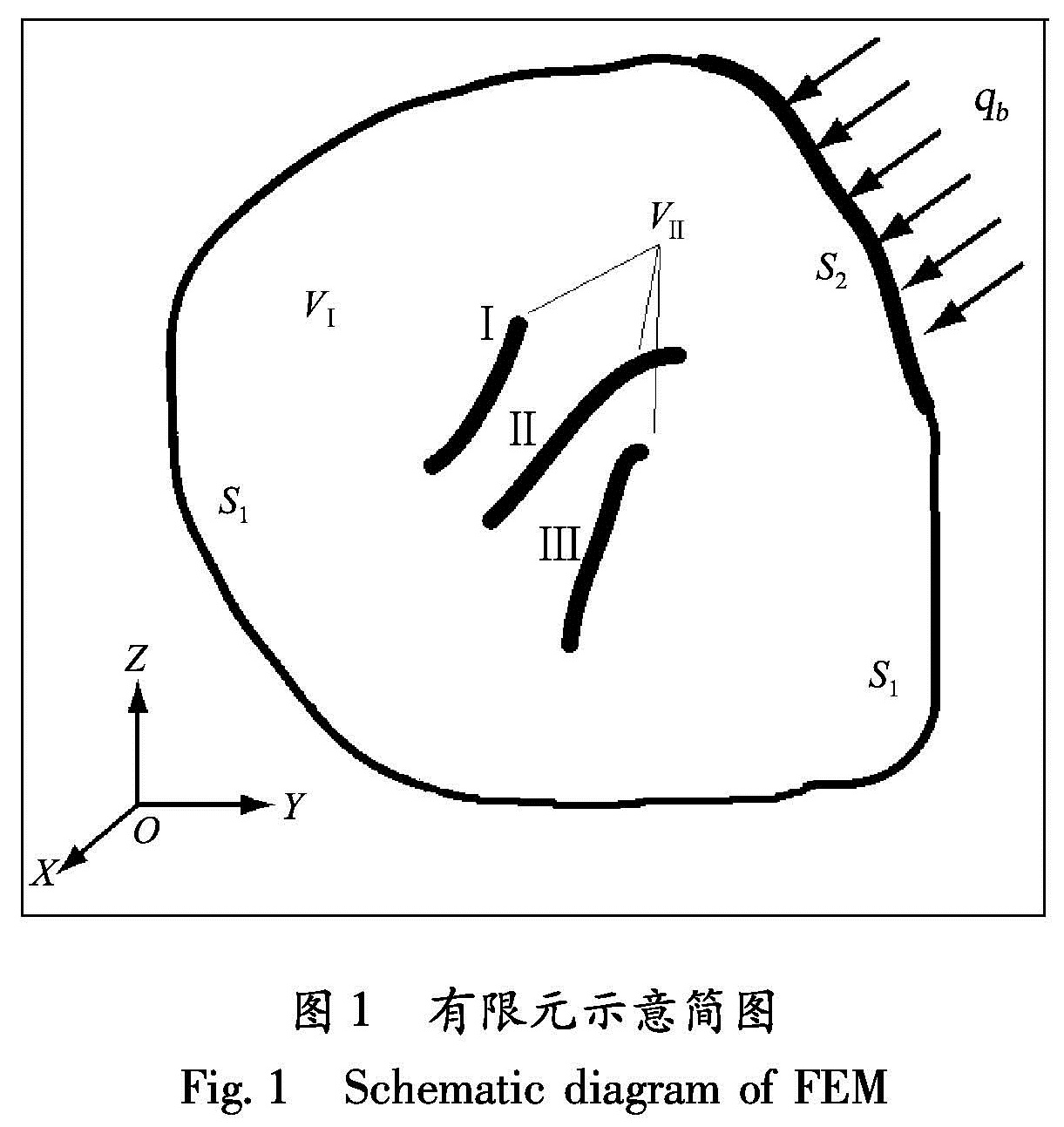
设研究区域V分为两个部分(图1):VⅠ和VⅡ,其中下标Ⅰ和Ⅱ分别表示断层外部和内部区域,也就是说在区域VⅠ内没有断层,而VⅡ由断层带(图1中的黑粗线)构成。区域的边界分为S1和S2两个部分。在S1上指定位移u, 在S2上指定分布面力qb(可由最大和最小主压应力σ1和σ3表示)(胡才博等,2009a,2009b)。
地震之前弹性材料矩阵、应变、应力可表示为DⅠ0,εⅠ0和σⅠ0=DⅠ0εⅠ0(区域VⅠ内),DⅡ0,εⅡ0和σⅡ0(区域VⅡ内)。地震之后,区域VⅠ的DⅠ0不发生变化,应变为εⅠ=εⅠ0+ΔεⅠ,应力为σⅠ=DⅠ0εⅠ,其中ΔεⅠ为地震引起的应变增量。地震之后,区域VⅡ的DⅡ=DⅡ0-ΔDⅡ,应变为εⅡ=εⅡ0+ΔεⅡ,应力为σⅡ=DⅡεⅡ,其中ΔDⅡ0为用来模拟地震发生的断层带内的弹性材料参数的减少量。由弹性力学平衡方程,根据迦辽金有限元法(Jaeger,Cook,1979),可以推得
∫VⅠε~TσⅠdV+∫VⅡε~TσⅡdV
=∫VⅠu~TγⅠdV+∫VⅡu~TγⅡdV+∫S2u~Tqbds.(1)
将上面提及的关系式代入(1)式,并根据虚功原理——内力(应力)的虚功等于外力的虚功,有限元新模型的公式可以表示为(蔡永恩,殷有泉,1997)
∫Vε~TD0ε0dV=∫Vu~TγdV+∫S2u~Tqbds,(2)
∫Vε~TD0ΔεdV=∫VⅡεu~TΔDⅡεⅡ0dV.(3)
其中,u~和ε~分别表示虚位移和虚应变向量,两者皆满足弹性力学几何方程。u、ε和σ分别表示需要求解的位移、应变和应力。体力γ可由重力得到。上面提及的所有变量都采用向量形式。
有限元新方法求解震前节点位移U0和同震位移ΔU的方程由式(2)、(3)得到:
K0(DⅠ0,DⅡ0)U0=F0,(4)
D(DⅠ0,DⅡ0,ΔDⅡ)ΔU=ΔF(U0).(5)
其中,K0和F0分别为震前刚度矩阵和节点载荷,K为震后刚度矩阵(断层带内部的材料参数有所减小),ΔF是由震前位移U0或者震前应力场计算得到的节点载荷增量。可以看出,同震位移ΔU不仅与断层带内部材料参数变化有关,而且与震前位移U0有关。式(4)仅仅计算震前位移场U0,它由边界S1上的位移和边界上的构造应力决定。式(5)可用来计算由第(i-1)次地震的位移场U0引起的第i次地震的同震位移场ΔU。第i次地震的震后位移场为(U0+ΔU),作为第(i+1)次地震的震前位移场,并用来计算第(i+1)次地震的同震位移场。可以看出利用式(4)和式(5)能得到地震序列的位移场和应力场的连续演化。这是有限元新模型与王仁等(1980)提出有限元方法、Gomberg和Ellis(1993)提出的边界元方法最主要的不同之处。
2 有限元方法的应用
设计该有限元计算模型如图2所示,其相关参数如下:
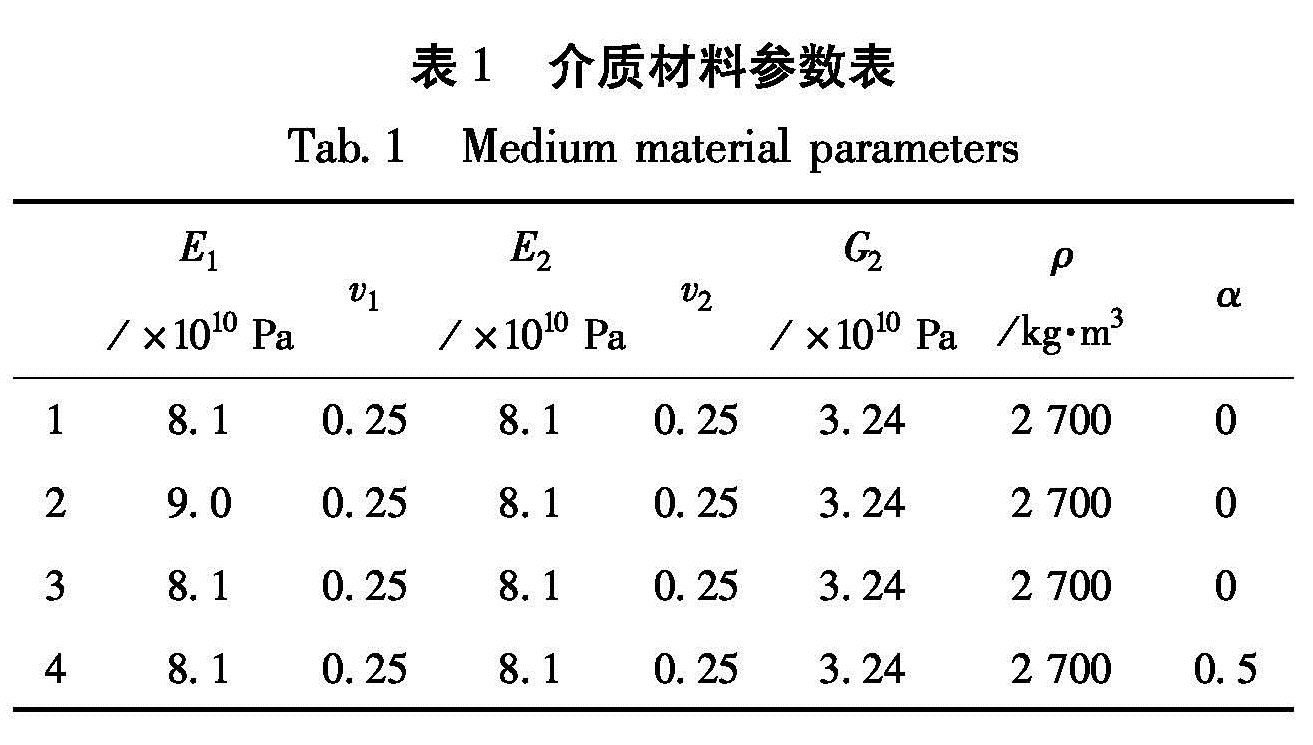
模型尺寸设为1 000,模型右侧深度为500,左侧深度为540,断层宽度为4,莫霍面在模型右侧深度为300,断裂倾角60°贯穿地壳,莫霍面以下计算深度取为200,模型左右与底面的浅灰色吸收边界宽度为8(图2),重力加速度g取为9.8 m/s,通过将断层带内部剪切模量G2从32.4 GPa降低到3.24 GPa来模拟地震。地震发生起始破裂点位于断裂中上部,对应于图2中A点,纵向距地表深度为100。模型边界条件为左右边界法向约束,下边界完全约束,上边界自由。模型材料分为4类,其材料参数见表1,其中,E为杨氏模量,v为泊松比,G为剪切模量,ρ为密度,α为阻尼系数。
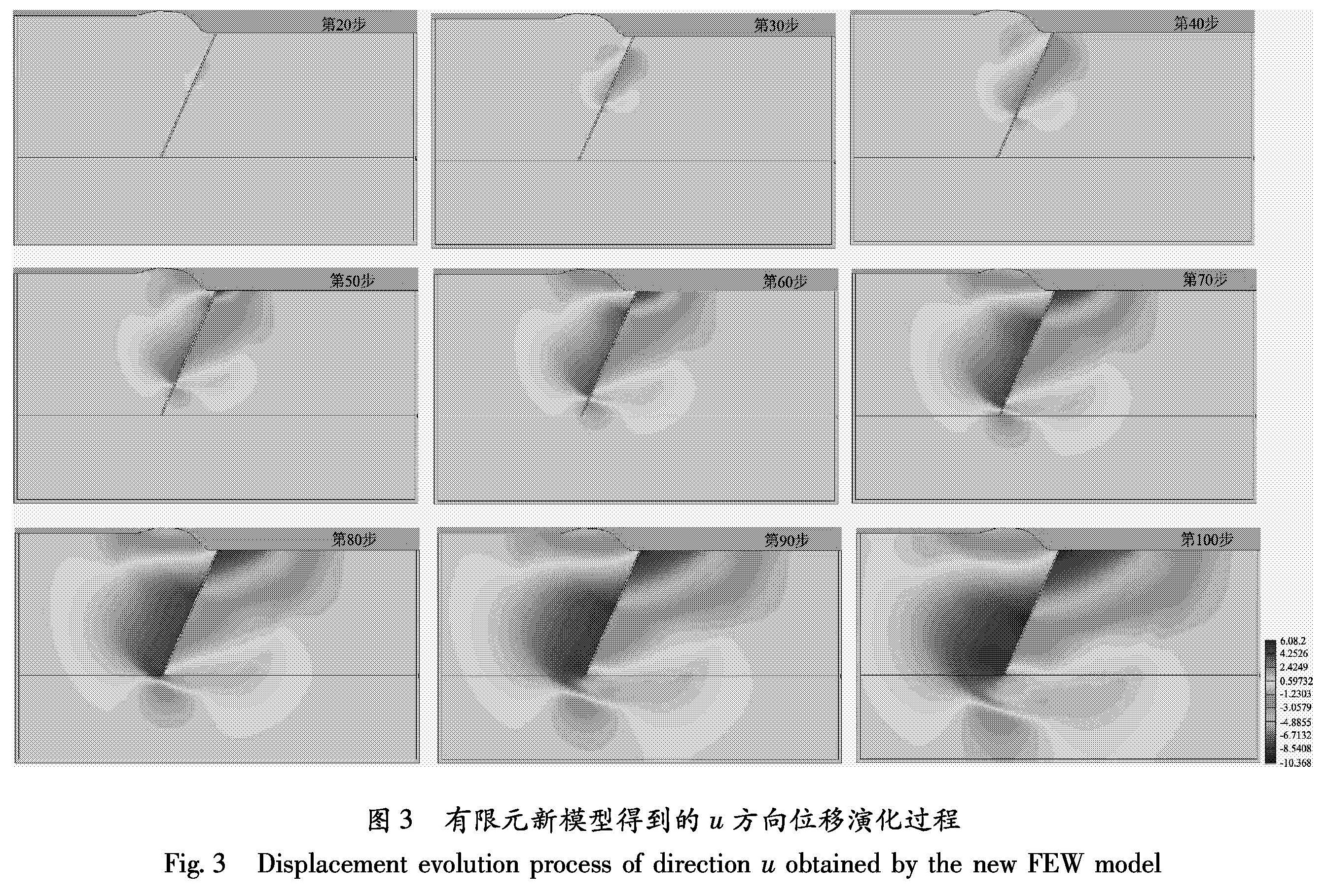
该有限元模型共划分67 855个单元,68 392个节点,共计算了100步,模拟了从地震产生至其波场在介质中传播5 s的全过程。图3、4列出了利用有限元新方法模拟得到的地震发生后5 s,内介质内位移场和应力场在u方向(即x方向)变化的过程,从第20步开始,间隔10步直到100步。由图3可以发现,在山坡部u方向位移的极大值自第70步起出现在山坡顶部,即淡蓝色的区域。图4中u方向正应力自第50步左右,在山坡顶部
图2 有限元模型
(1,2,3,4为介质材料标号,A点为初始破裂点)
Fig.2 FEM model(1、2、3、4 represent medium material number,A represents initial rupture point)图3 有限元新模型得到的u方向位移演化过程
Fig.3 Displacement evolution process of direction u obtained by the new FEW model出现远高于相邻区域的绿色负值; 并沿地表向模型左侧传播,经过调查后发现该绿色高负值产生于山坡与水平地表交汇处。
下面以靠近断层面近表面坡部的4个点为例分析地震对其作用(图5)。这4个点的位移、应力演化如图6、图7所示,横坐标是时间步数。
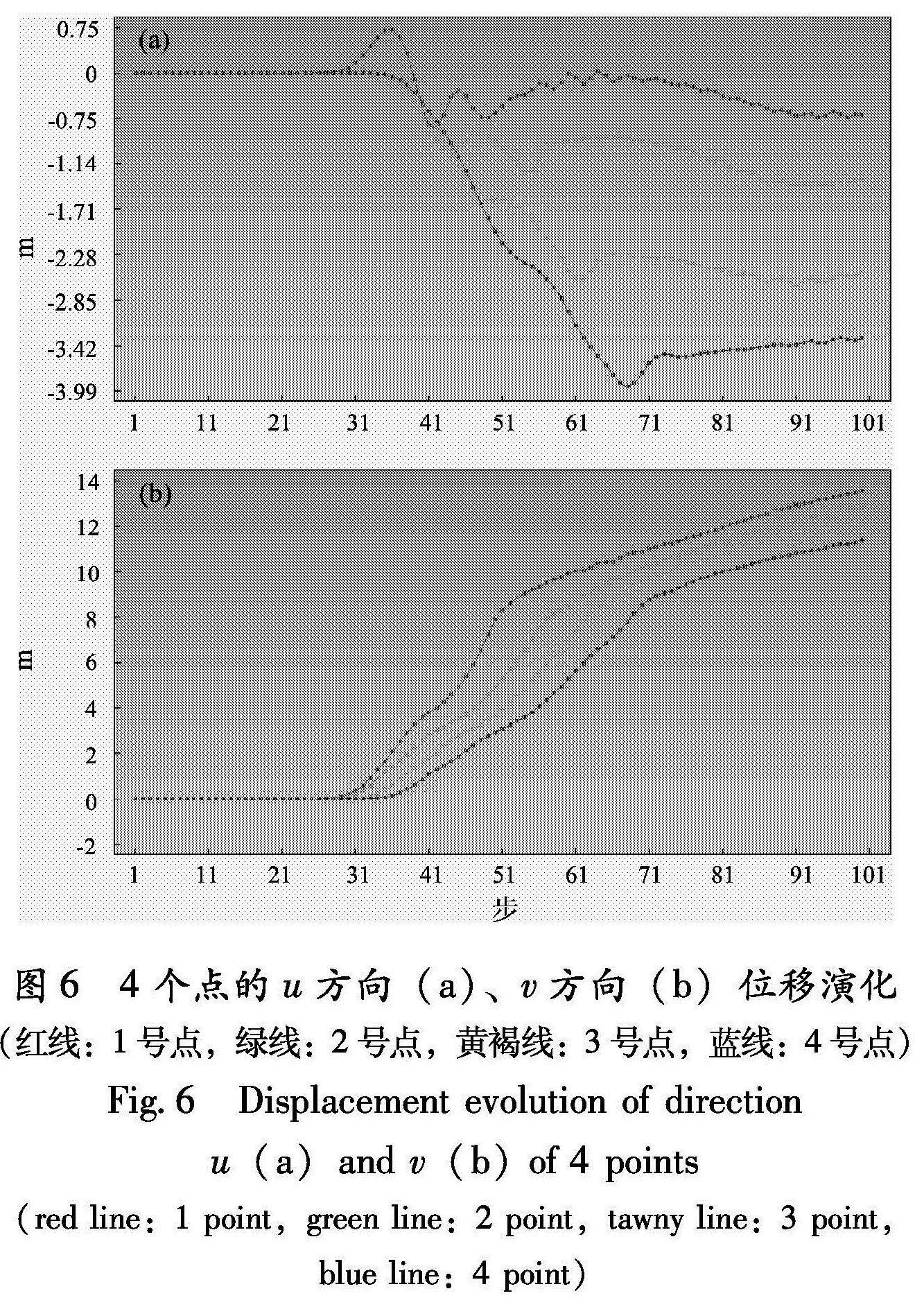
由图6a可以看出,点1由于接近地表水平面,故先有u的正方向的运动,然后恢复并向u的反方向运动,然后逐渐震荡,最后值趋于u的反方向,点2,3,4的运动趋势比较一致,点4靠近坡顶,其
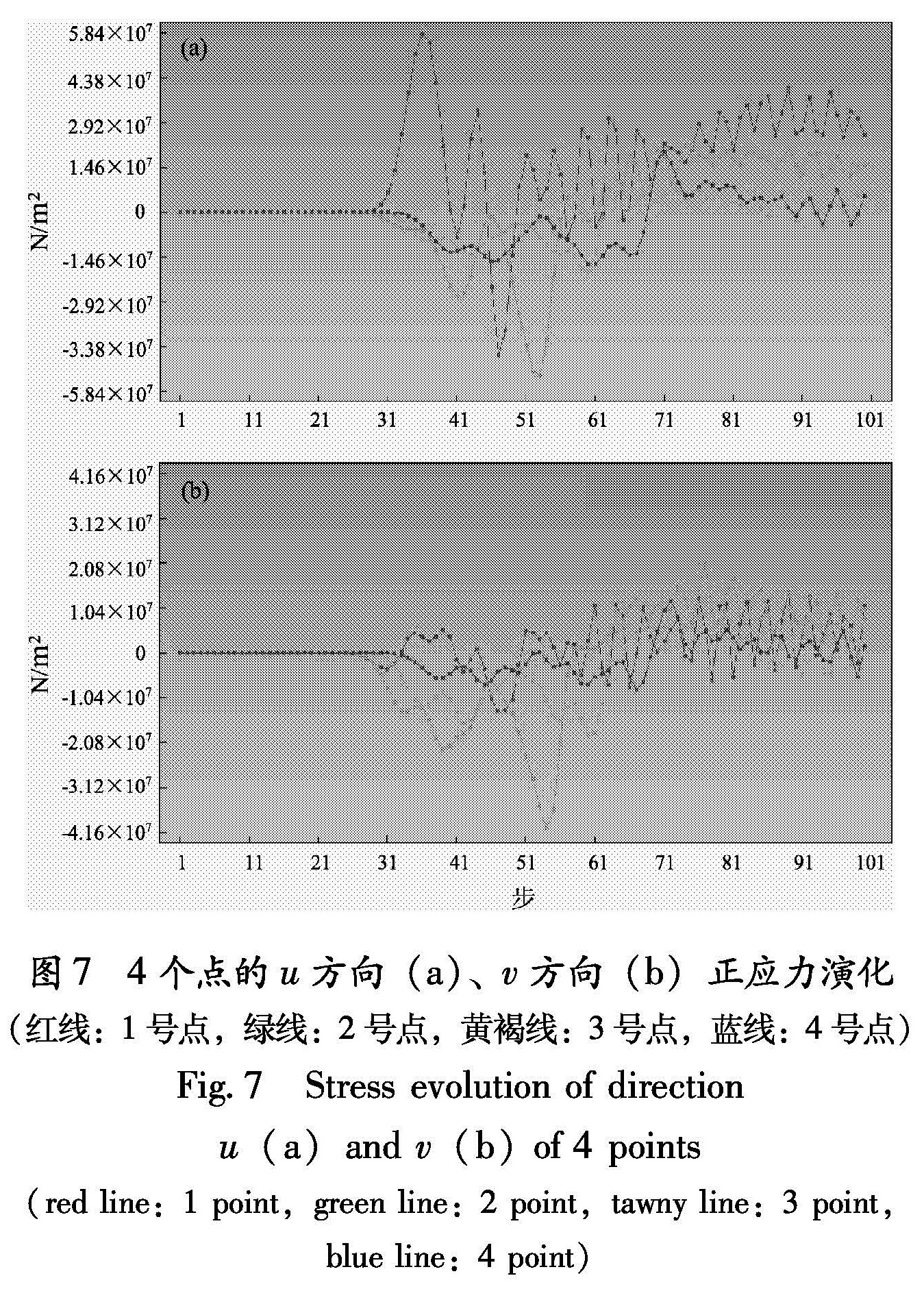
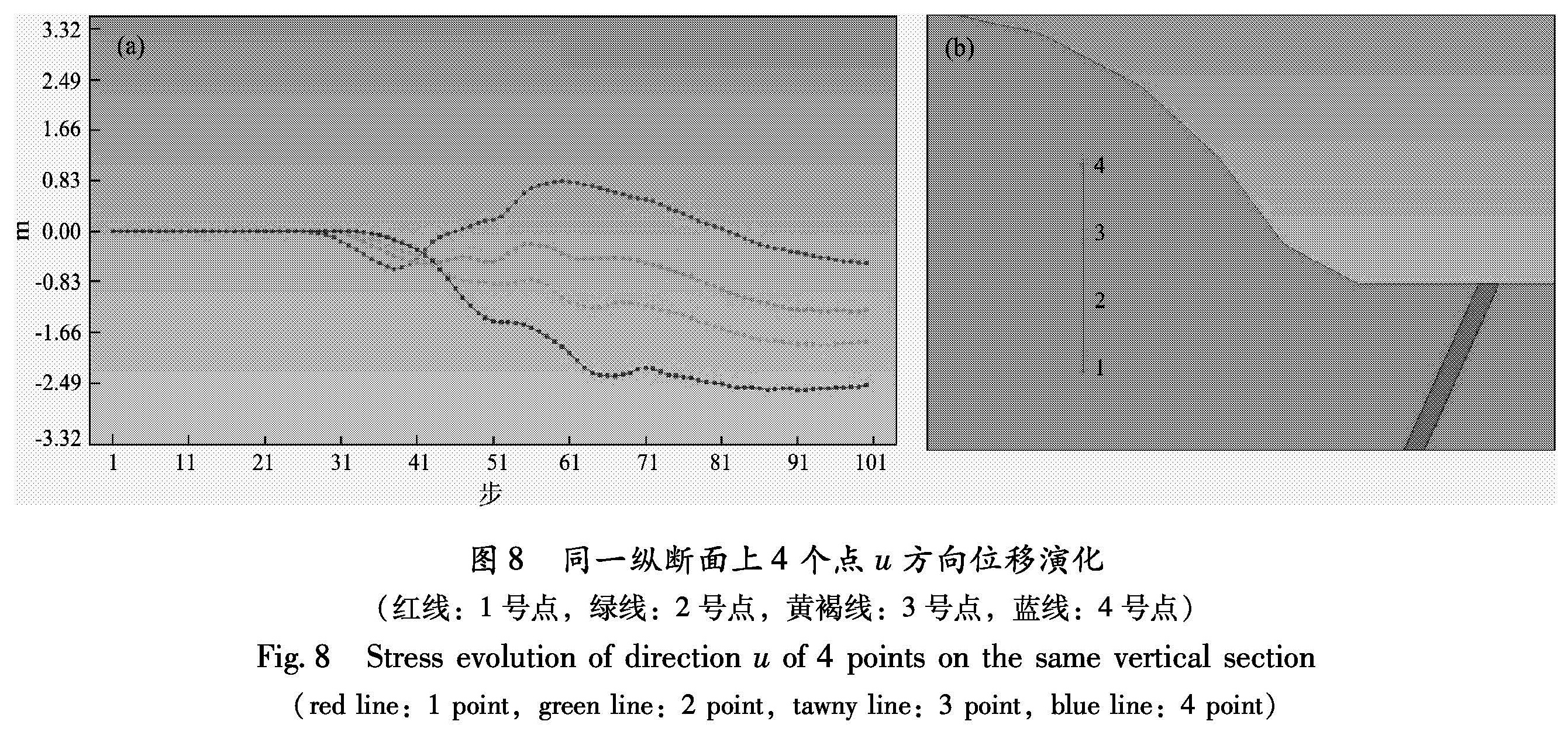
位移变化最大。图6b中,4个点的运动比较一致,都是向v的正方向即向上运动。图7a中,由于点1靠近地表水平面,而该断裂带在地表有出露,故在地震作用下地表有破裂,所以点1受其影响而应力变化较大; 从点2、3、4的位移变化可以看出地震对山体的影响,这3个点的应力值皆是距离越近波动越大,距离越远波动越小,考虑到地震传播的速度与到达各点的先后,可以看出其波动频率比较接近。图7b中,v方向的正应力变化从数值上看较u方向小,但其波动频率接近,值得注意的是点2的u、v方向正应力波动极值最大,这与其所处地形与坡度有关。笔者还对山体内部不同点的位移与应力场进行了比对。综合来看,无论同一水平面还是同一纵断面上,所取的4个观察点的v方向位移的变化非常接近,且类似于图6b。所取同一水平面上4个观察点u方向位移的变化趋势接近于图6a中蓝色曲线,相对变化范围不大,同一纵断面上4个点的u方向位移如图8所示,可见水平面以下以u正方向运动为主,水平面以上以其反方向运动为主。
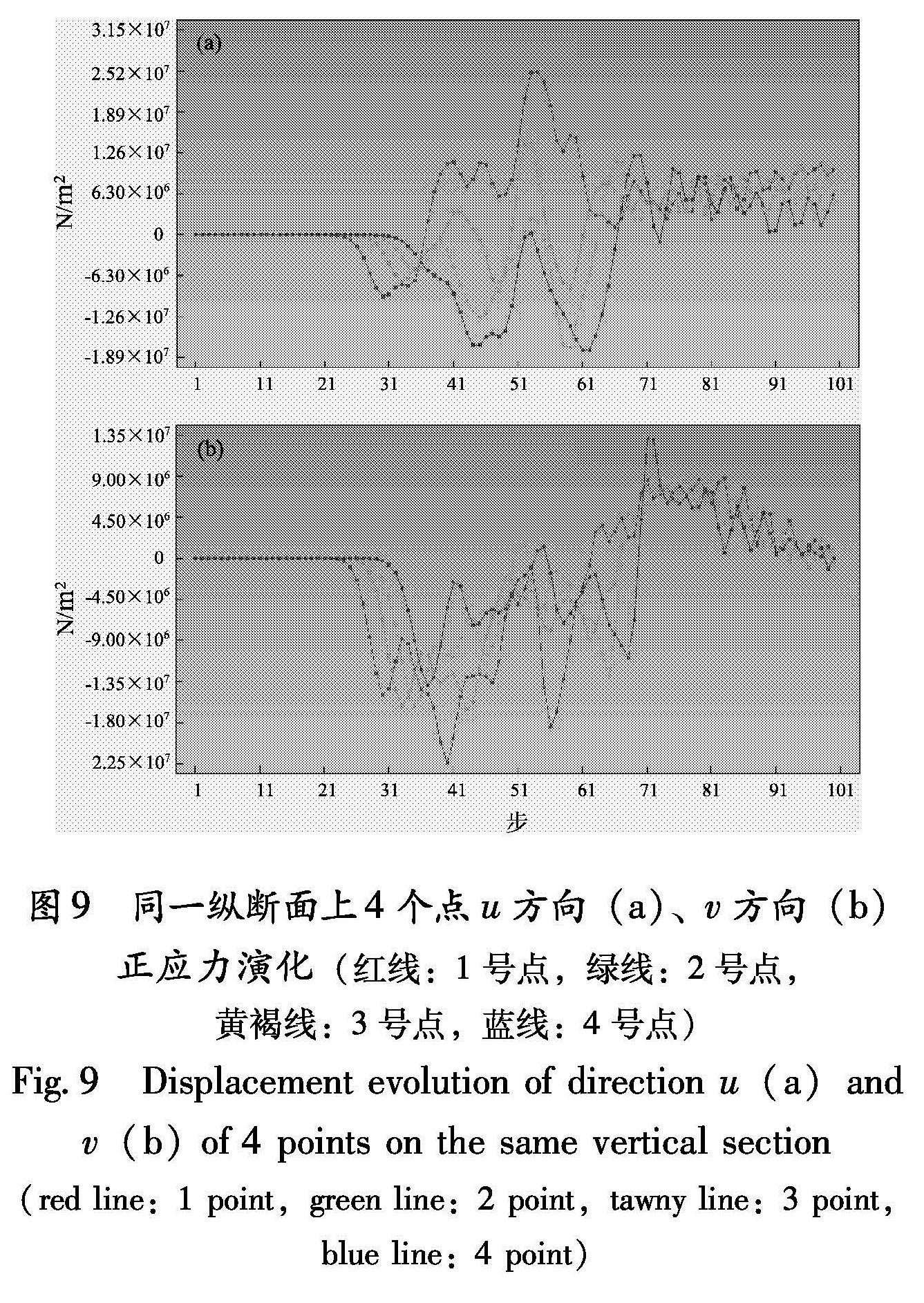
图8中的4个点在u、v方向正应力变化频率较一致,振幅逐渐衰减,如图9所示。
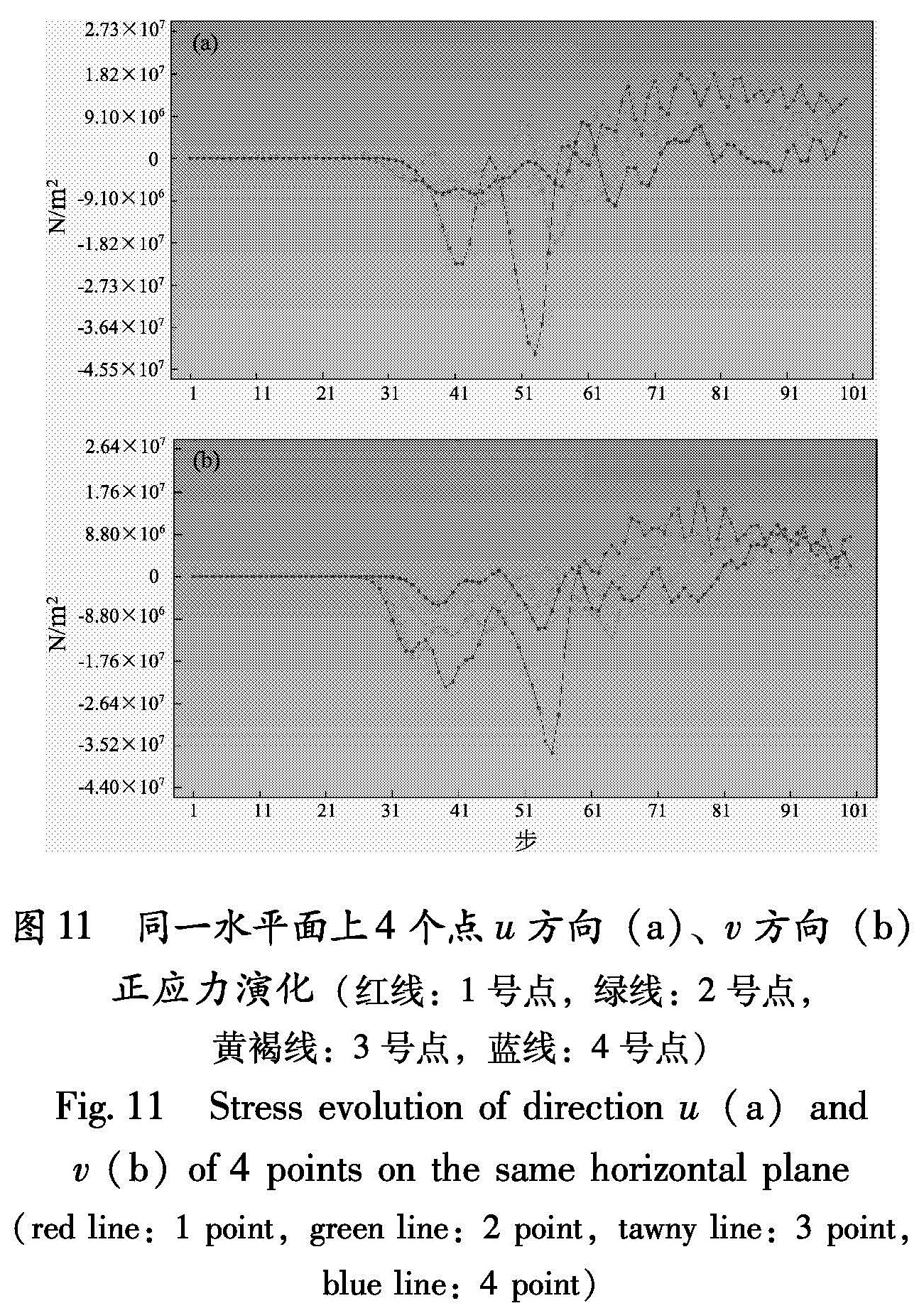
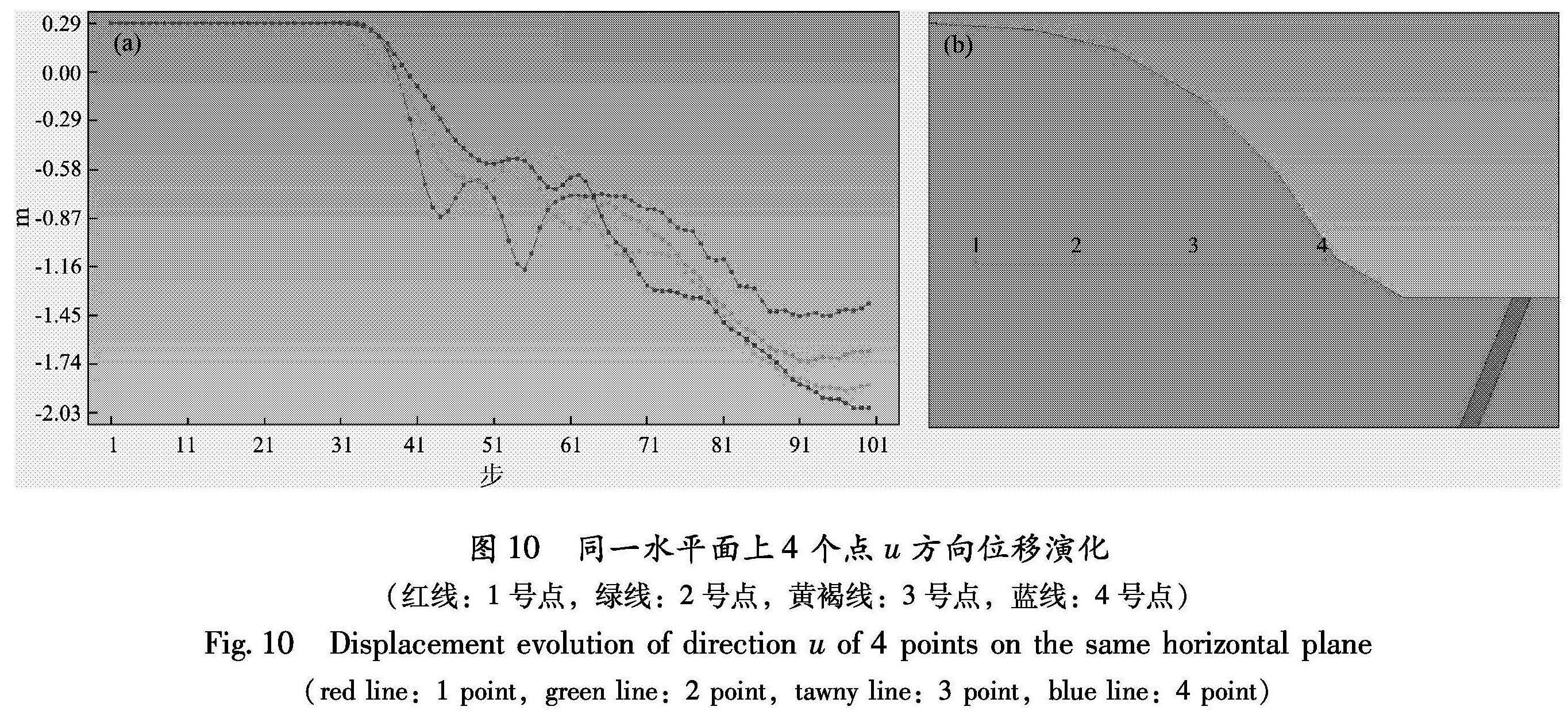
同一水平面上4个点的u方向位移变化趋势如图 10所示,其u、v方向正应力的变化频率接近,振幅逐渐减小,如图 11所示。
综上所述,可见在地震作用下,整体而言,山体表面与内部的变化规律接近,但山体接近地表处的位移、应力比山体内部大。在山体接近表面的部位,以坡度较陡、地形变化最大的2号点的应力变化最为突出,位移则是接近山坡顶部的4号点变化最大,可见边坡破坏容易在2号点与山坡顶部发生。由此可以佐证Celebi和Jullien(1988)的地形放大效应理论与Geli(1987)的观点,即地形放大效应随坡度的增大而增大。各个观察点u、v方向正应力的频繁变化也表明了地震时对坡体的波动震荡,由此可能会在岩土内部产生附加应力,进而造成应力集中,产生累进破坏效应。
图6 4个点的u方向(a)、v方向(b)位移演化(红线:1号点,绿线:2号点,黄褐线:3号点,蓝线:4号点)
Fig.6 Displacement evolution of direction u(a)and v(b)of 4 points(red line:1 point,green line:2 point,tawny line:3 point,blue line:4 point)图7 4个点的u方向(a)、v方向(b)正应力演化(红线:1号点,绿线:2号点,黄褐线:3号点,蓝线:4号点)
Fig.7 Stress evolution of direction u(a)and v(b)of 4 points(red line:1 point,green line:2 point,tawny line:3 point,blue line:4 point)图8 同一纵断面上4个点u方向位移演化(红线:1号点,绿线:2号点,黄褐线:3号点,蓝线:4号点)
Fig.8 Stress evolution of direction u of 4 points on the same vertical section(red line:1 point,green line:2 point,tawny line:3 point,blue line:4 point)图9 同一纵断面上4个点u方向(a)、v方向(b)正应力演化(红线:1号点,绿线:2号点,黄褐线:3号点,蓝线:4号点)
Fig.9 Displacement evolution of direction u(a)and v(b)of 4 points on the same vertical section(red line:1 point,green line:2 point,tawny line:3 point,blue line:4 point)图 11 同一水平面上4个点u方向(a)、v方向(b)正应力演化(红线:1号点,绿线:2号点,黄褐线:3号点,蓝线:4号点)
Fig.11 Stress evolution of direction u(a)and v(b)of 4 points on the same horizontal plane(red line:1 point,green line:2 point,tawny line:3 point,blue line:4 point)3 结论与讨论
本文使用了基于FEPG的有限元新模型,从动力学的角度来模拟断层破裂发生地震后的位移场和应力场的连续变化,通过该方法可以直观地观察到地震对边坡的广义荷载场的动态影响,并对数值模拟结果进行了分析和讨论,验证了部分学者对滑坡的动力学机理的观点,即地震的地形放大效应与地形放大效应随坡度增大而增大。
值得注意的是,由于本次模型设计为整个山体被看作是均匀的物质,无法体现滑坡体部分与山体的差异影响,从而对滑坡体的累进破坏效应、启动效应、启程加速效应等理论讨论不充分,这会在以后的工作中用人为设定滑坡体等方法来进行进一步探讨。
- 蔡永恩,殷有泉.1997.热弹性问题的有限元方法及程序设计[M].北京:北京大学出版社.
- 胡才博,周一杰,蔡永恩.2009a.如何用有限元新模型研究地震触发和应力场连续演化[J].中国科学D辑:地球科学,39(5):546-555.
- 胡才博.2009b.研究地震触发和应力场连续演化的新方法[D].北京:北京大学.
- 李为乐,伍霁,吕宝雄.2011.地震滑坡研究回顾与展望[J].灾害学,26(3):103-108.
- 毛彦龙,胡广韬,赵法锁,等.1998.地震东出发滑坡提滑动的机理[J].西安工程学院学报,20(4):45-48.
- 王仁,何国琦,殷有泉,等.1980.华北地区地震前已规律的数学模拟[J].地震学报,2(1):32-42.
- Celebi M.1987.Topographic and geological amplification determined from strong motion an after shock records of 3 March,1985 Chile earthquake[J].BSSA,77(4):1141-1147.
- Geli L,Bard P Y,Jullien B.1988.The effects of topography on earthquake ground motion:a review and new result[J].BSSA,78(1):42-63.
- Gomberg J,Ellis M.1993.3D-Def:A User's Manual[R].USGS Openfile Report:93-547.
- Jaeger J C,Cook N G W.1979.Fundamentals of Rock Mechanics[M].London:3rd ed,Chapman and Hall.
- Melosh H J,Aaefsky A D.1980.The dynamic origin of subduction zone topography[J].Geophys J R Astro Soc,60(3):333-354.