基金项目:云南省人民政府十项措施监测预报项目(JYB-20080601-5)资助.
(1.云南师范大学 旅游与地理科学学院,云南 昆明 650000; 2.云南省地震局,云南 昆明 650224)
(1.School of Tourism and Geographical Sciences,Yunnan Normal University,Kunming 650000,Yunnan,China)(2.Earthquake Administration of Yunnan Province,Kunming 650224,Yunnan,China)
Yunnan region; earthquake sequence; maximum strong aftershock; main shock magnitude; b-value intercept
备注
基金项目:云南省人民政府十项措施监测预报项目(JYB-20080601-5)资助.
利用1965~2012年云南地区的181次地震序列资料,分别用4种不同的方法得到主震和最大余震的震级关系式分别为:b值截距法Mmax=-0.44+1.03Mb±0.4; 最大后续余震法Mmax=-0.23+1.00Mm±0.4; 主震震级估算最大余震法Mmax=-0.71+0.89M±0.4; 主震与最大余震震级差法:主震震级在5.0~5.9级之间,Mmax=M-1.2,在6.0~7.9级之间,Mmax=M-1.0。用这4种方法对2009年7月9日姚安6.0级地震和2012年9月7日彝良5.6、5.7级地震序列中的最大强余震进行估算,结果符合较好。统计结果显示最大强余震发生在主震后前3天的比例高达60%,这一结果可为最大强余震的时间判定提供依据。
Basing on the 181 earthquake sequences in Yunnan region from 1965 to 2012,we respectively obtained four relation formulas between the main shock and the largest aftershock by four methods:Mmax=-0.44+1.03Mb ± 0.4 in the b-value intercept method,Mmax=-0.23+1.00Mm ± 0.4 in the maximum subsequent aftershocks method,Mmax=-0.71+0.89M±0.4 in the maximum aftershock estimated by main shock magnitude method,and Mmax=M-1.2 for M5.0~5.9 main shock,Mmax=M-1.0 for M6.0~7.9 main shock in the magnitude difference of main shock and aftershock method. We estimated the maximum magnitude of aftershock sequences of Yaoan M6.0 earthquake on Jul.9,2009 and Yiliang M5.6,5.7 earthquakes on Sep.7,2012 by four methods and obtained that the theory and actual maximum magnitudes of aftershock sequences agreed well. The statistic results showed that the proportion of maximum aftershocks occurred in the first three days after the main shock up to 60%,which may provide the basis for the time judgment of the maximum aftershock.
引言
最大余震震级判断是破坏性地震震后趋势分析的重要内容,对震后灾区救灾和恢复重建工作部署意义重大。钱晓东和秦嘉政(2008),吕晓健等(2007)研究表明,一次强震或者大震之后,短时间内会相继发生一系列高强度、高密度的余震,如果强余震震级大且发生时间距离主震时间比较长时,可能对震中附近地区造成比主震更严重的破坏。因此,地震趋势判定中最大强余震估算尤为重要。例如,1970年1月5日通海7.8级地震,2月5日发生5.7级最大余震,而在主震后第3个月的3月13日还发生了5.5级强余震。
从20世纪60年代起,全球地震研究国家有计划地开展了一系列科学研究,取得了丰硕的成果,对地震趋势判定、类型判定方法,尤其是最大余震估算方法,发表了诸多研究成果。刘正荣(2004)提出了b值判定方法,利用频度衰减判定地震类型; 蒋海昆等(2006)认为主震断层性质与其前兆表现及余震性质关系密切,主震断层特性是影响余震序列性质的重要因素; 皇甫岗等(2010)对云南地震类型进行研究,结合活动构造和震源机制,分区讨论了云南地震类型; 钱晓东等(2011)利用云南地震序列频度衰减,对最大后续强余震进行研究; 王碧泉等(1979)、谷继成等(1979)、任雪梅等(2009)采用了统计特征推断法研究余震序列的特征并推算出最大余震; 姚殿义等(1994)将韦布尔分布应用到地震序列中,通过经验数据画成韦布尔—时间曲线,考察曲线随着时间变化时反映出的强余震关系,进而实现对强余震的预测; Madahizadeh1和Allamehzad(2009)利用人工神经网络法对汶川地震后的余震序列进行研究和预测; 张智等(1989)利用b值的G-R曲线在横轴上的截距预报最大余震。早在1990年,中国地震局地震学分析预报方法程式指南(国家地震局科技监测司,1990)就将最大余震计算作为重要震后趋势判定参数,20多年来,这些参数整体预测效果如何?尤其是针对云南这样一个破坏性地震多发地区,应该怎样应用这些参数?这方面的成果还不多见。
本文系统研究了云南近200次地震序列资料,对常用的估算最大余震方法进行了总结,提出了新的计算云南地震序列最大余震经验公式,并进行了检验。
1 资料
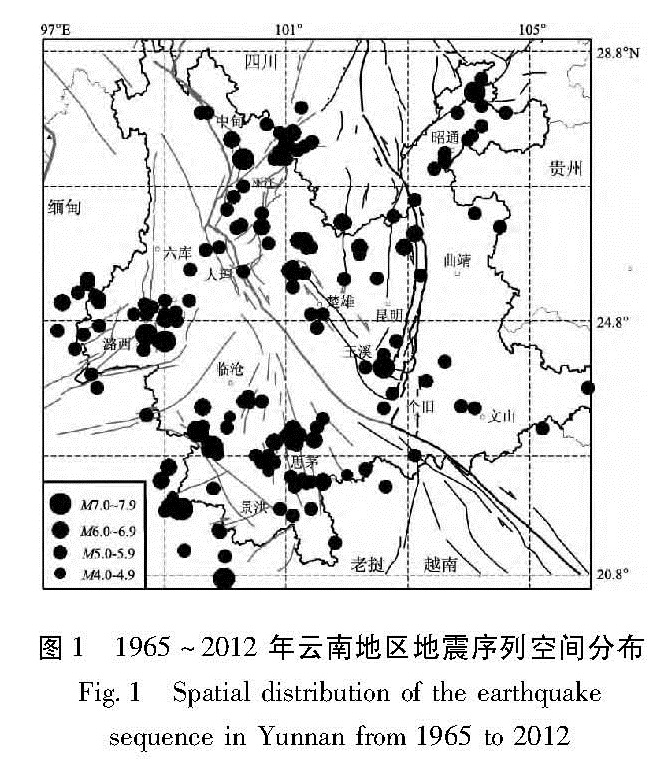
云南地区是我国地震活动最频繁的地区之一,主要分布3条中强地震活动带:鲜水河—安宁河—小江地震带、金沙江—红河地震带和腾冲—澜沧江地震带等(苏有锦,秦嘉政,2001)。本文选取1965~2012年云南地区181次地震序列,5级地震截止时间为震后3个月,6级地震截止时间为震后0.5年,7级地震截止时间为震后1年作为研究样本。地震类型分为5类:孤立型、主震余震型(主余型)、双震型、前震型和震群型。在所研究181次地震序列中,主余型地震为92次,占51%; 双震型地震为54次,占30%; 孤立型地震为11次,占6%; 震群型地震为13次,占7%; 其中有直接前震地震为11次,占7%。从序列主震震级来看,5.0~5.9级132次,占72%; 6.0~6.9级30次,占17%; 7.0~7.9级9次,占5%。云南地区6级以上地震共计39次,主余型为24次,占62%; 双震型为14次,占36%; 前震型1次,占2%。可见,云南地区地震类型以主余型地震为主,双震次之。
2 云南最大余震的估算
3 实例检验〖*4〗3.1 2009年7月9日姚安6.0级地震序列
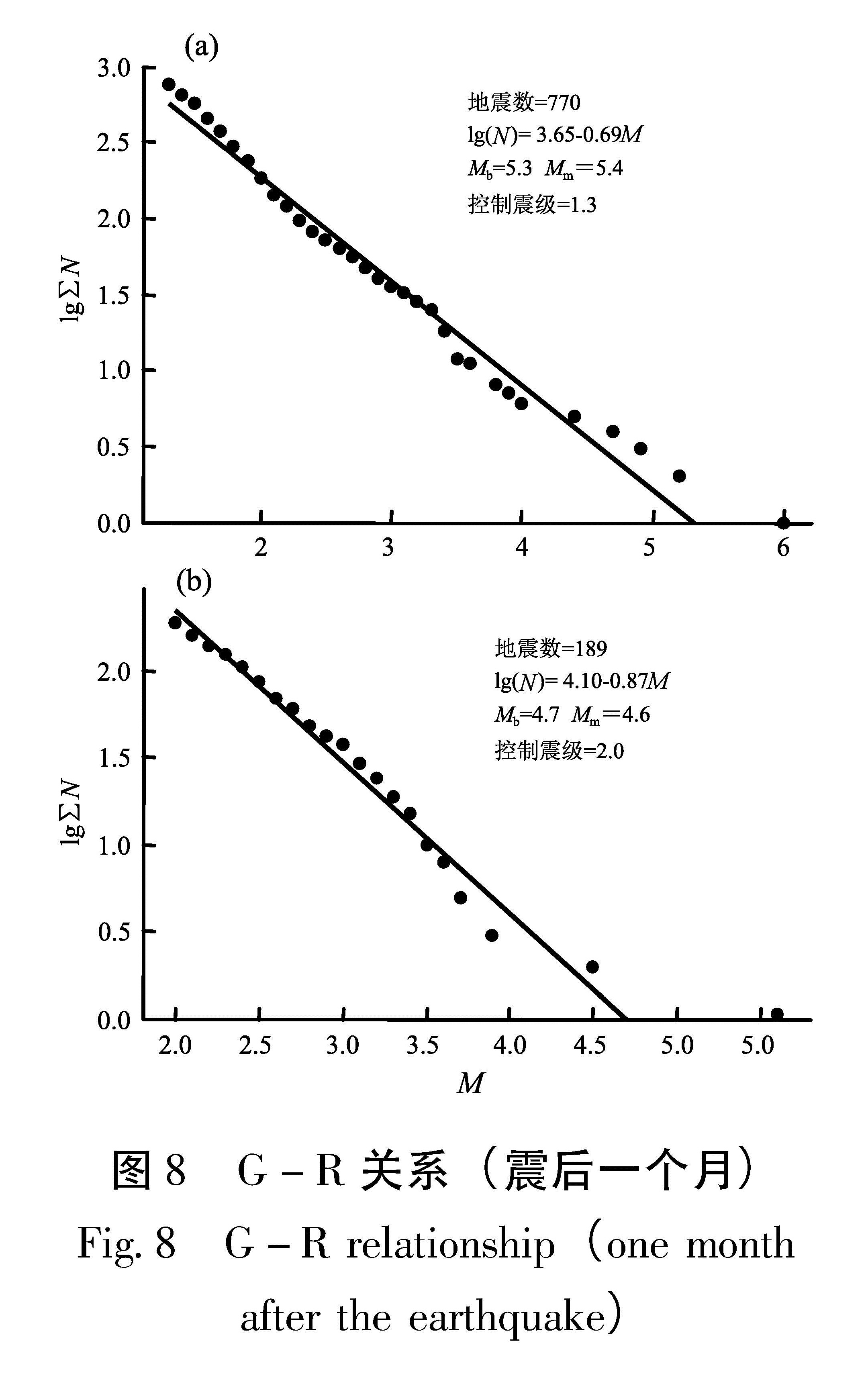
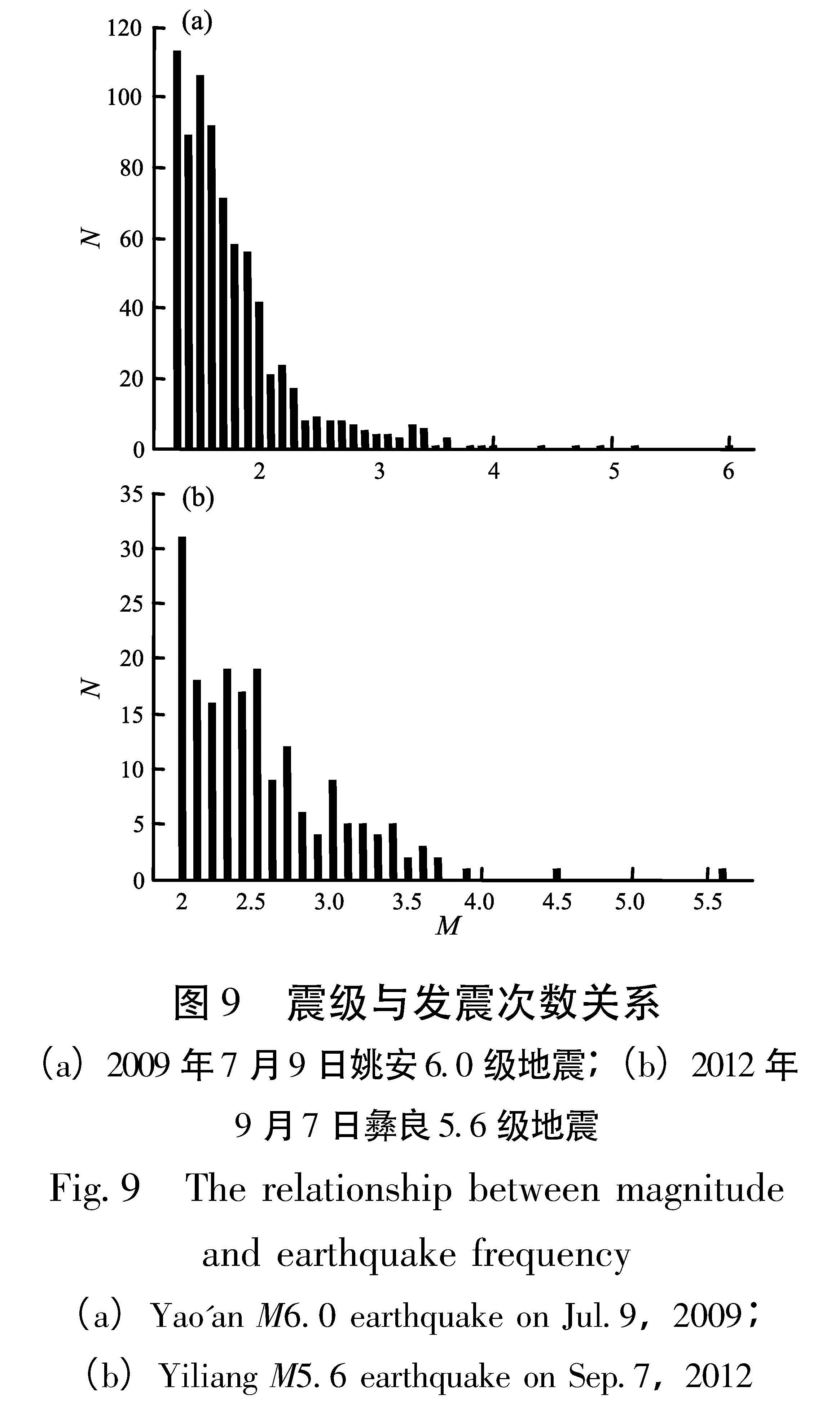
2009年7月9日姚安发生6.0级地震,截至2009年8月9日,云南地震台网共记录到余震770次,其中3.0~3.9级地震25次、4.0~4.9级地震4次、5.0~5.9级地震1次,最大余震为7月10日5.2级。为了检验该序列的最大余震是否已经发生,首先,用主要震级粗略估算,利用(12)式得Mmax=4.8,利用(10)式得到Mmax=4.6。其次,再作相对精确估算,通过震级—频度分布可知控制震级为1.3级,图8a给出地震序列的G-R关系拟合直线,得到a=3.65,b=0.69,由b值截距法求得Mmax=5.0,由最大后续余震法求得Mmax=5.2。最后,进行统计分析,4种不同方法求得的最大余震都在5.2级以下,意味着未来该序列最大余震不会超过5.2级。由于在震后一天的7月10日发生了一次5.2级余震,可以判定该序列最大余震已经发生,实际情况,该序列其后未发生大于5.2级的余震。
3.2 2012年9月7日彝良5.7,5.6级地震序列2012年9月7日彝良5.6、5.7级地震,截至2012年10月7日,云南地震台网共记录到余震188次,其中3.0~3.9级地震36次、4.0~4.9级地震1次,最大余震为9月7日4.5级地震。为了检验该序列最大余震是否已经发生,首先,用主要震级作粗略估算,利用(11)式得Mmax=4.4,利用(10)式得Mmax=4.2。其次,再作相对精确估算,通过震级—频度分布可知控制震级为2.0级,
图8b给出地震序列的G-R关系拟合直线,得到a=4.10,b=0.87,由b值截距法求得Mmax=4.4,由最大后续余震法求得Mmax=4.3。最后,进行统计分析,四种不同方法求得的最大余震都在4.5级之下,也就是说未来该序列最大余震不会超过4.5级。由于震后一个小时发生过一次4.5级余震,因此可以判定该序列最大余震已经发生,实际情况是其后该序列未发生过大于4.5级余震。图9 震级与发震次数关系
(a)2009年7月9日姚安6.0级地震;(b)2012年9月7日彝良5.6级地震
Fig.9 The relationship between magnitude and earthquake frequency(a)Yao'an M6.0 earthquake on Jul.9,2009;(b)Yiliang M5.6 earthquake on Sep.7,20124 结论与讨论
(1)通过对云南地区181次地震序列资料,统计分析,得到云南地区地震序列最大余震的4种求解公式,分别为:b值截距法Mmax=-0.44+1.03Mb±0.4; 最大后续余震法Mmax=-0.23+1.00Mm±0.4; 主要震级法Mmax=-0.71+0.89M±0.4; 震级差法:主震震级在5.0~6.9级之间Mmax=M-1.2,在7.0~7.9级,Mmax=M-0.8。
(2)用4种求解公式对2009年7月9日姚安6.0级和2012年9月7日彝良5.7,5.6级地震序列最大余震震级进行计算检验,结果显示4种方法符合均较好。
(3)对最大强余震发生时间进行统计的结果表明,60%的最大强余震发生在主震后的前3天,这个结果可以在实际应用中对快速判定地震趋势提供有益的参考。
(4)在此之前,很多学者利用b值截距法求过最大余震,但与实际最大余震存在误差,导致G-R关系式出现误差的主要原因可能是地震序列统计时间不够长造成大震缺失; 小震没有记录不全。
(5)对最大余震震级影响最大的参数是b值,如果b值偏大,求得最大余震也偏大; 反之亦然。b值不仅影响Mb,且Mm也由b值决定,因此b值的误差、样本的完整性和震级下限的选取都直接影响Mb和Mm的取值,同时影响最大余震的估算结果。因此,对b值的把握就成了整个式子准确度的关键。应用G-R关系式对a、b值估算时,所用地震序列需满足以下条件(韩渭宾,2003):(1)确定余震的起始时间;(2)余震数目必须大于50次;(3)确定起始震级;(4)对(1)式应用最小二乘法拟合的地震数目要大于5个;(5)最大震级和最小震级之差必须大于1.5级;(6)震级使用统一标准MS,以此确保b值的准确性,减小最大余震估算产生的误差。
2.1 b值截距法Mb古登堡和里希特在研究世界地震活动时,根据全球各大地震区6级以上地震数目的统计发现,地震的震级与频度有以下关系(Gutenberg,Richter,1942):
lgN=a-bM.(1)
式(1)反映了地震序列中大小地震的比例关系及其变化,亦称G-R关系式,式中a和b两个参数可根据一定地区、一定时间的地震目录统计估算得到。N为震级大于等于M的地震次数,近年来,很多学者采用累积频度代替N,因此,求b值截距时采用累积频度作图法,根据地震序列的累积地震频度—震级的lgN-M图作线性延长与M轴交点的横截距就是震级Mb。地震序列的b值曲线是用来估算最大余震的可靠方法(吴开统等,1984,1986)。张智等(1989)研究b值截距法,表明它可以被用来预报序列的最大余震。
2.2 最大后续余震法Mm若(1)式中N采用非累积频度Nm,则可表示为
Nm=10a-bm.(2)
式中,Nm为一定震级区间(M±0.5)内的地震数(频度)。假定(2)式是连续的,根据刘正荣(1979)对(2)式积分结果,在震级范围[Mmin,Mmax]内的地震总数N为
N=∫ MmaxMmin10a-bMdM=(10a)/(bln10)(10-bMmin-10-bMmax).(3)
假定最大地震有n次,其震级为Mmax,Mmax>Mmin按照(2)式有10a=n10bMmax,代入(3)式有
Mmax=1/(b)lg(1+(bNln10)/n)+Mmin,(4)
若最大地震只有1次,即n=1,则
Mmax=1/(b)lg(1+bNln10)+Mmin.(5)
当(3)式积分结果只有1次地震时(N=1),积分上、下限都不能用恰当的震级表示出来,取N=1时上、下限之间的重心表示地震震级,这与N=1/2时积分下限相当,令(5)式中N=1/2,积分下限Mmin写为最大震级Mm,有
Mm=Mmax-1/blg(1+0.5bln10),(6)
将(6)式代入(5)式有
Mm=1/blg(1+bNln10)-1/blg(1+0.5bln10)+Mmin.(7)
(7)式为由地震总数N、b值和控制震级Mmin求序列最大后续地震震级Mm公式。
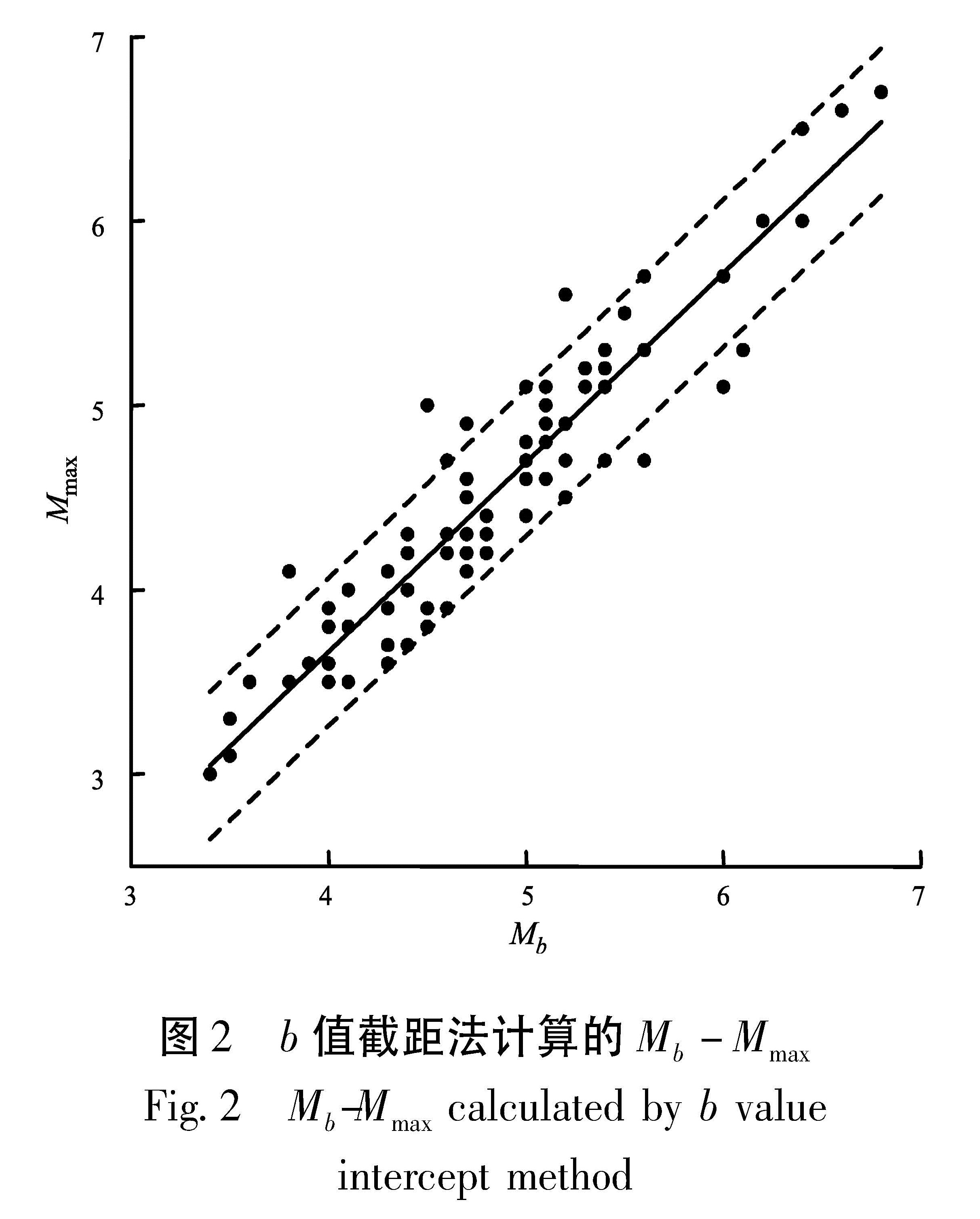
2.3 b值截距法和最大后续余震法结果利用上述二种方法计算了云南地区地震序列的最大余震震级。从b值截距Mb方法(图2)可知,误差为0.4,两条误差线之内的数据点占总数据点的比例为92%,直线方程为
Mmax=-0.44+1.03Mb±0.4.(8)
根据(8)式,已知Mb可以估算出最大余震震级。
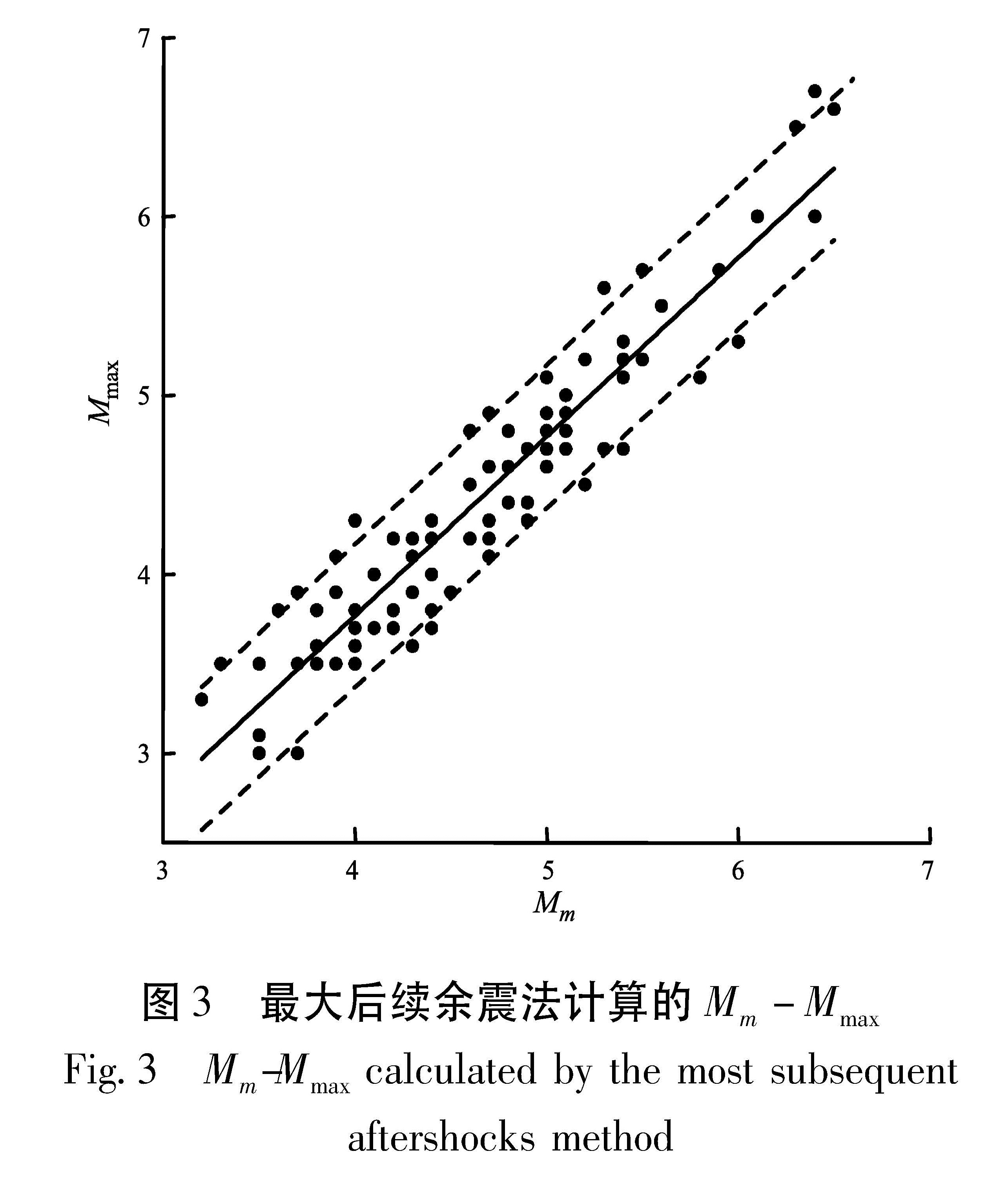
从最大后续余震方法(图3)可知,误差=0.4,二条误差线内的数据点占总数据点的比例为89%,直线方程为
Mmax=-0.23+1.00Mm±0.4.(9)
根据(9)式,已知Mm可以估算出最大余震震级。
图2 b值截距法计算的Mb-Mmax
Fig.2 Mb-Mmax calculated by b value intercept method图3 最大后续余震法计算的Mm-Mmax
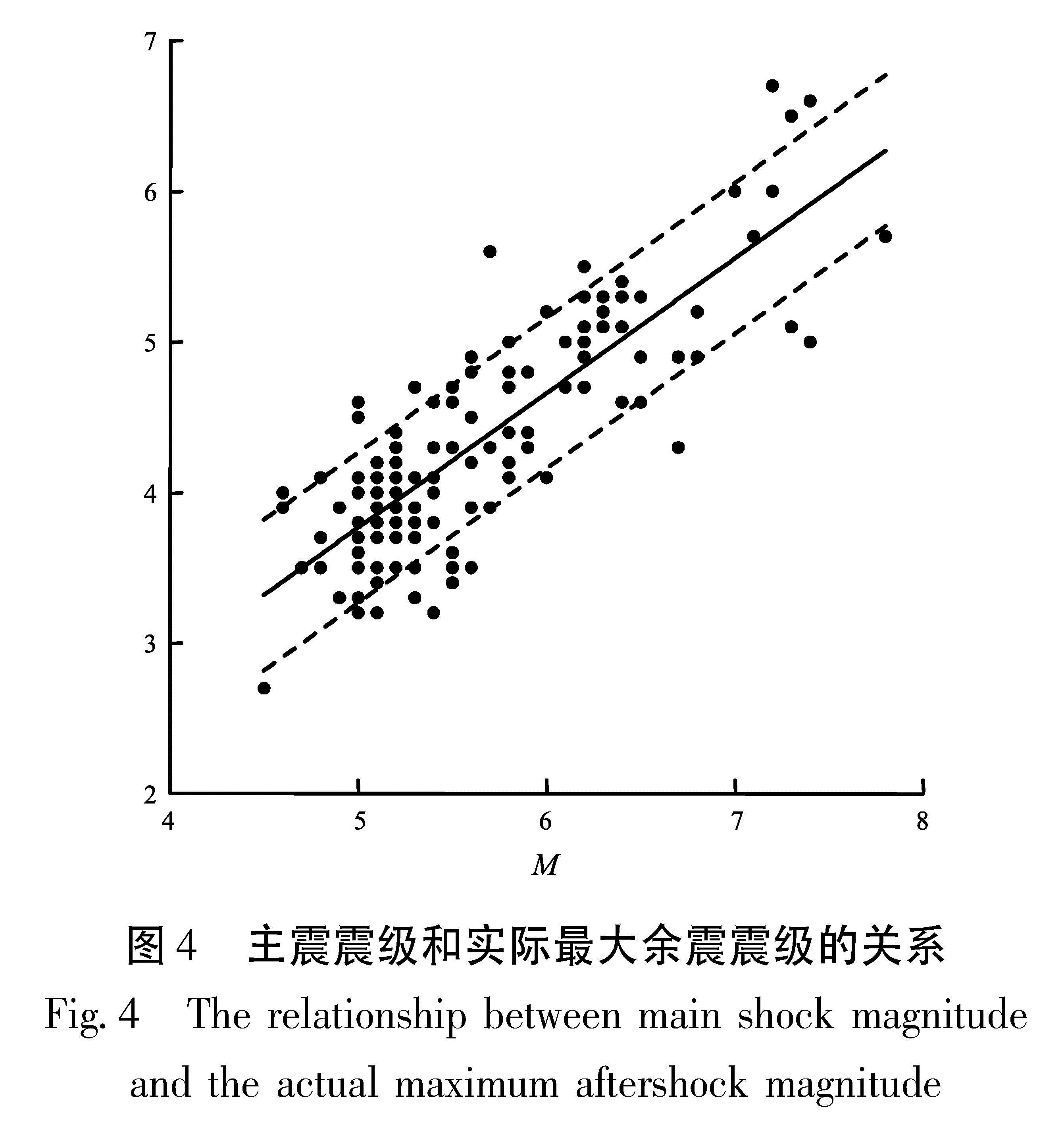
Fig.3 Mm-Mmax calculated by the most subsequent aftershocks method2.4 由主震震级估算最大余震2.4.1 主震震级和实际最大余震震级的关系从181次地震序列中选取主震M和实际最大余震Mmax,根据二元分析方法得到主震M和实际最大余震Mmax的线性关系式为
Mmax=-0.71+0.89M±0.4.(10)
根据(10)式,已知主震震级M就可以估算出实际最大余震震级。此公式与蒋海昆等(2006)得出的中国大陆地区地震最大余震和主震震级关系是一致的。从图4可以看出,主震震级M和最大余震震级成正相关,同时结果也符合吴开统等(1984)得出的最大余震震级一般比主震小1.2级的巴特定律。
2.4.2 主震与最大余震的震级差如果知道主震震级和最大余震的震级差之间存在的关系,根据经验,当主震发生后可以迅速地估算出最大余震震级。这点在实际地震预测中有很重要的意义,主震发生时,地震序列资料还不完整,此时,可以只通过主震震级就得出最大余震震级的范围,给救援财产和抢救生命提供参考。
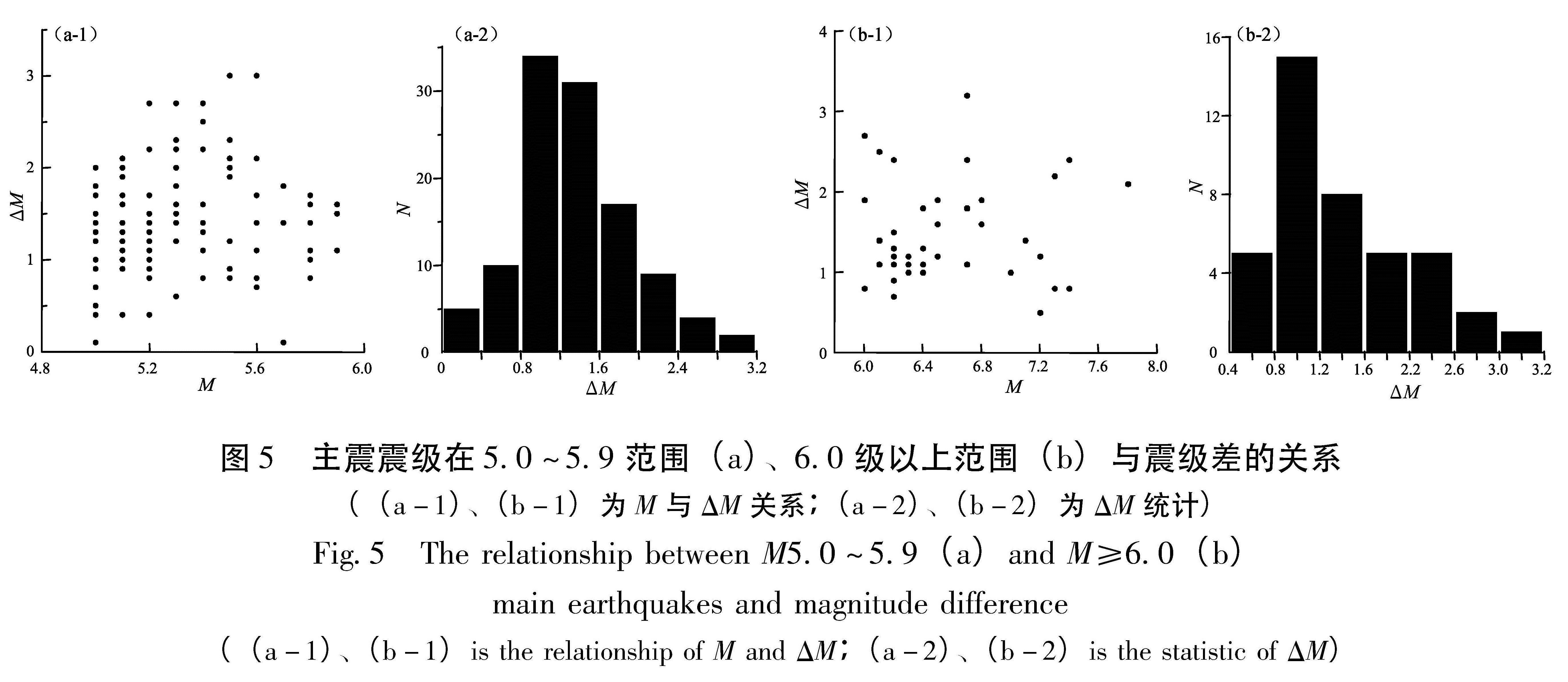
图5 主震震级在5.0~5.9范围(a)、6.0级以上范围(b)与震级差的关系
((a-1)、(b-1)为M与ΔM关系;(a-2)、(b-2)为ΔM统计)
Fig.5 The relationship between M5.0~5.9(a)and M≥6.0(b)main earthquakes and magnitude difference((a-1)、(b-1)is the relationship of M and ΔM;(a-2)、(b-2)is the statistic of ΔM)图5(a-1)为主震范围在5.0~5.9级地震震级与震级差的关系,图5(a-2)为震级差的统计图,以0.4级统计一次。震级差在0.8~1.6之间的地震数量为60多个,占75%。0.8~1.6的中值为1.2,作为粗略估算,取ΔM=1.2,就可以估算出主震范围在5.0~5.9级地震的实际最大余震震级:
Mmax=M-1.2.(11)
图5(b-1)为主震范围在6.0级以上地震震级与震级差的关系,图5(b-2)为震级差的统计图。以0.4级统计一次。震级差在0.8~1.2之间的地震数量为15个。0.8~1.2的中值为1.0,作为粗略估算,取ΔM=1.0。由此我们可以算出主震范围在6.0级以上地震的实际最大余震震级:
Mmax=M-1.0.(12)
所得地震余震范围结论在近似条件下与bath定律一致。
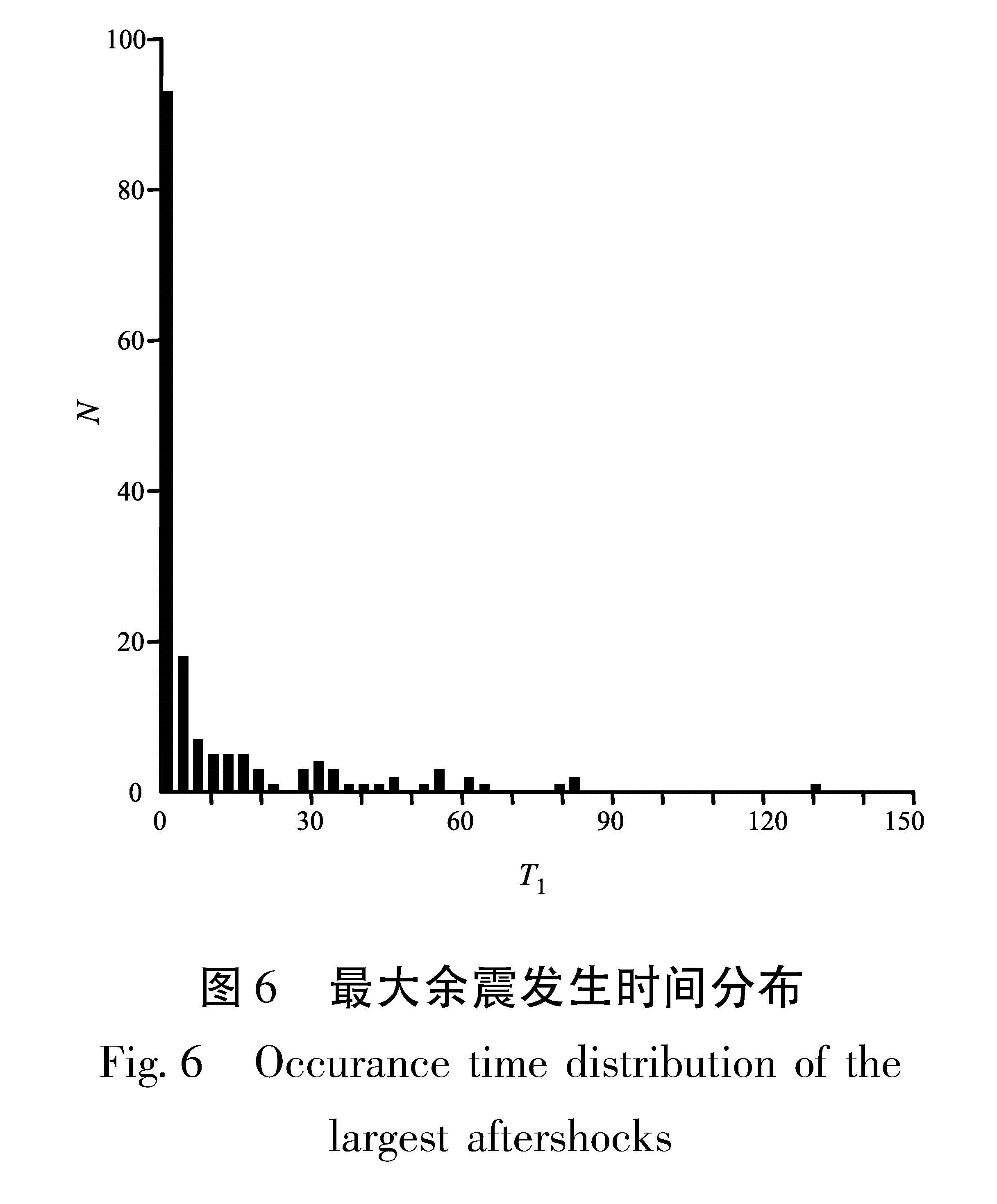
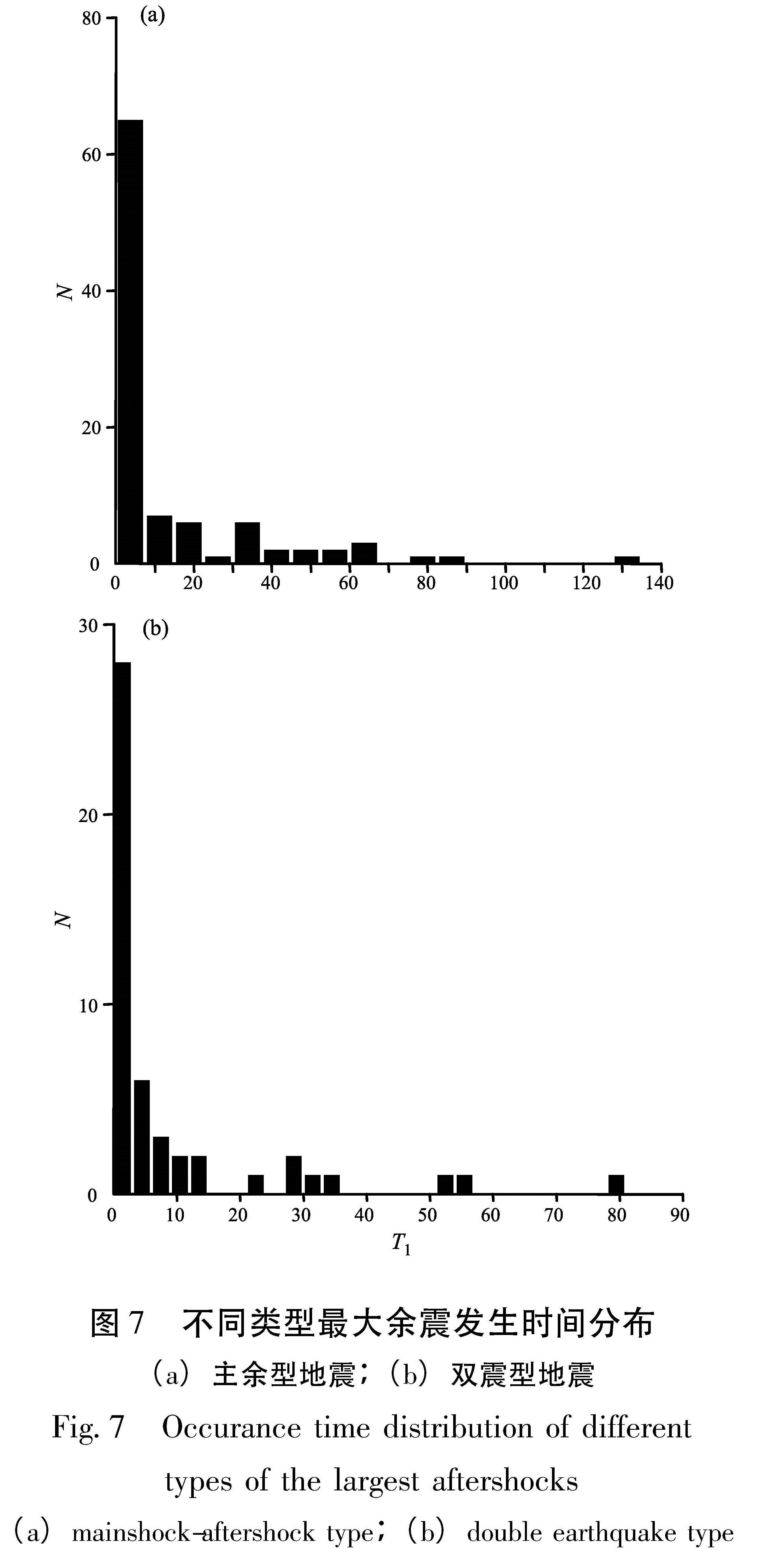
2.5 最大余震发生时间图6显示了最大余震的发生时间分布,根据余震种类不同,最大余震发生时间分布也不同。由图7a可以看出,主余型地震总数为92次,3 d内发生的地震个数有63个,占68%。3~6 d内的地震个数下降到6个。在主震后的一个月和60 d左右,出现最大余震发生的优势时间段; 由图7 b可以看出,双震型地震总数为49个,3 d内发生的个数有28个,占57%。3~6 d内的地震数有6个,比例下降到了12%。在主震地震后1个月前后,出现最大余震发生的优势时间段,其次为50 d附近容易发生强余震。统计结果表明有60%的最大强余震发生在主震后的前3 d,这个结果可以在实际应用中对快速判定地震趋势提供有益的参考。
云南的7级地震最大余震在地震后3天之内发生得很少,1970年以来的地震除1996年丽江7.0级地震外,其余的都是在20天后发生的。我们选取的181次地震中有9次7.0级以上地震,最大余震发生的优势时间段为20天后。- 谷继成,谢小碧,赵丽.1979.强余震的时间分布特征及其理论解释[J].地球物理学报,22(1):33-45.
- 国家地震局科技监测司.1990.地震学分析预报方法程式指南[M].北京:地震出版社,20-28.
- 韩渭宾.2003.b值在地震预测中的三类应用及其物理基础与须注意的问题[J].四川地震,(1):1-5.
- 皇甫岗,陈颙,秦嘉政,等.2010.云南地震活动性[M].昆明:云南科技出版社,94-108.
- 蒋海昆,曲延军,李永莉,等.2006.中国大陆中强地震余震序列的部分统计特征[J].地球物理学报,49(4):1110-1117.
- 刘正荣.2004.b值特征研究[M]//刘正荣地震预报方法.北京:地震出版社,33-37.
- 吕晓健,高孟潭,高战武,等.2007.强余震与主震地面运动分布比较研究[J].地震学报,29(3):295-301.
- 钱晓东,秦嘉政,刘丽芳.2011.云南地区现代构造应力场研究[J].地震地质,33(1):91-106.
- 钱晓东,秦嘉政.2008.用b值截距估算汶川8.0级地震序列最大余震[J].地震研究,31(增刊):436-441.
- 任雪梅,高孟潭,刘爱文,等.2009.1900年以来我国西南地区强余震统计特征[J].震灾防御技术,4(2):200-208.
- 苏有锦,秦嘉政.2001.川滇地区强地震活动与区域新构造运动的关系[J].中国地震,17(1):24-34.
- 王碧泉,杨锦英,王春珍.1979.强余震的准周期性[J].地震学报,1(2):154-165.
- 吴开统,焦远碧,吕培苓.1986.b值研究进展综述[J].地震,(5):50-53.
- 吴开统,焦远碧,王志东.1984.华北地区的晚期强余震特征[J].西北地震学报,6(2):35-43.
- 姚殿义,刘家琦,李幼铭.1994.逐步波形反演方法及应用[J].中国地震,10(3):230-237.
- 张智,吴开统,焦远碧.1989.b值横截距预报强余震震级的方法探讨[J].中国地震,5(4):59-69.
- Gutenberg B.,Richter C.F..1942.Earthquake Magnitude,Intersity,Energy,and Accerleration[J].Bull.Seism.Sor.Amer,32:163-191.
- Madahizadeh R.,Allamehzadeh M..2009.Prediction of Aftershocks Distribution Using,Artificial Neural Networks and its Application on the May 12,2008 Sichuan Earthquake[J].Archive of SID,JSEE,11(3):111-120.