橡胶隔震支座是由一层钢板一层橡胶经高温硫化而成的(日本建筑学会,2006),其外表面通常设置一定厚度的橡胶保护层来保护内部结构。影响橡胶隔震支座耐久性的因素非常多,主要包括:橡胶材料的老化、橡胶隔震支座的徐变、疲劳(GB/T 20688.1-2007; 全国橡胶与橡胶制品标准化技术委员会橡胶杂品分技术委员会,广州大学工程抗震研究中心,2009)。支座性能的改变是由长期恒定作用、地震荷载作用、行车荷载作用及使用环境中的各种光、热、氧、化学介质等因素引起的(周福霖,1997; 苏经宇等,2012)。橡胶隔震支座的力学性能直接关系到隔震结构在遭遇地震时的响应及抗震性能,因此对橡胶隔震支座性能随时间老化变化规律开展研究是非常必要的。

目前,对于橡胶隔震支座老化性能的研究主要是依靠热老化试验(裴若娟,唐家祥,1993; 许斌,唐家祥,1995)和试样实测(李杨海,2009)两种方法。但对橡胶隔震支座性能随时间老化的实测,非常耗时耗力,试验成本非常昂贵,获得的数据却很有限。另外,对于橡胶隔震支座的老化性能开展的试验研究,通常只是采集初始状态(老化前)和终止状态(老化后)时的力学性能指标且均采用人工加速老化的试验方法。对试验数据的处理,通常是采用回归分析的方法,在得到回归公式后进行预测,但是对于隔震支座老化性能这种“贫数据”的情况,回归分析的方法在老化性能预测方面具有明显的局限性。

邓聚龙(1993)于20世纪80年代提出了灰色理论,该理论已经广泛应用于农业、经济、医疗、工业、管理、气象、教育、历史等几十个领域,取得较好的经济效益,并取得了许多重大成果(刘思峰,党耀国,2010)。灰色理论以“部分信息已知、部分信息未知”的“小样本”、“贫信息”不确定性系统为研究对象,主要通过对“部分”已知信息的生成、开发,提取有价值的信息,实现对系统运行行为、演化规律的正确描述和有效监控(党耀国,刘思峰,2009)。橡胶隔震支座老化性能试验数据符合这种“小样本”、“贫信息”的特点,预测其老化性能可以采用此方法。

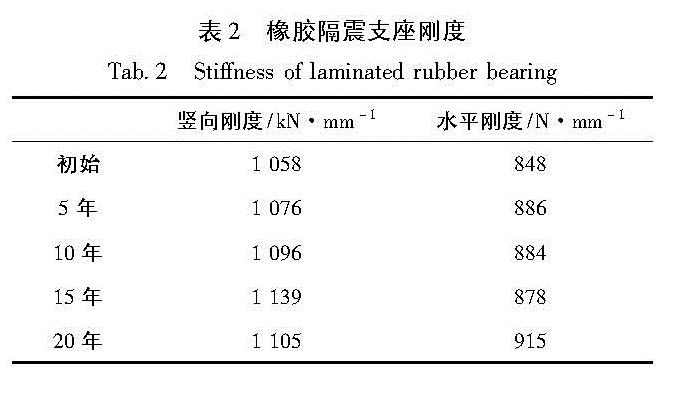
本文采用的研究数据来源于Morita等(2009)对直径500 mm的橡胶隔震支座(表1)跟踪20年研究所得到的性能指标(表2)。

表1 橡胶隔震支座参数
Tab.1 Parameters of laminated rubber bearing

表2 橡胶隔震支座刚度
Tab.2 Stiffness of laminated rubber bearing

初始值:

X⁽⁰⁾={x⁽⁰⁾(1), x⁽⁰⁾(2), x⁽⁰⁾(3), x⁽⁰⁾(4)}.

(1)对X⁽⁰⁾作一次累加生成(1-AGO),得到:

X⁽¹⁾={x⁽¹⁾(1), x⁽¹⁾(2), x⁽¹⁾(3), x⁽¹⁾(4)}.

(2)对X⁽¹⁾作紧邻值生成。令

z⁽¹⁾(k)={0.5x⁽¹⁾(k)+0.5x⁽¹⁾(k-1)},

得到: Z⁽¹⁾={z⁽¹⁾(2),z⁽¹⁾(3),z⁽¹⁾(4)}.

于是, B=[-z⁽¹⁾(2),1

-z⁽¹⁾(3),1

-z⁽¹⁾(4),1

], Y=[-x⁽⁰⁾(2),1

-x⁽⁰⁾(3),1

-x⁽⁰⁾(4),1

].

(3)对参数a^{^}=(a,b)^T进行最小二乘估计: 得到:

a^{^}=(B^TB)^-1B^TY.

(4)确定模型:(dx⁽¹⁾)/(dt)+ax⁽¹⁾=b,及时间响应式: x^{^}(k+1)=(x⁽⁰⁾(1)-b/a)e^-ak+b/a。

(5)还原数列序列x^{^}(k+1)=x^{^(1)}(k)-x^{^(0)}(k-1),依次得到: x^{^(0)}(1), x^{^(0)}(2), x^{^(0)}(3), x^{^(0)}(4)。

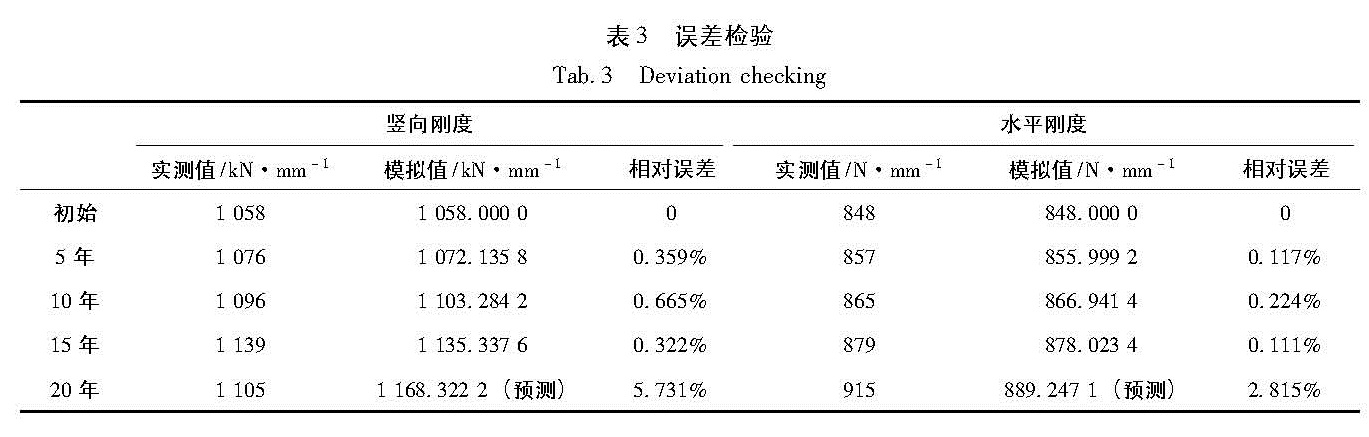
(6)对结果进行误差检验:用灰色预测方法得到的老化性能(水平与竖向刚度)预测值与实测值的对比见表3。

表3 误差检验
Tab.3 Deviation checking

以上采用前15年的数据建立GM(1,1)模型,以建立的GM(1,1)模型对隔震支座使用了20年后的竖向刚度及水平刚度进行预测,并将实测结果与预测结果作了比较。由表3可知:对于隔震支座在使用了20年后的竖向刚度预测存在5.731%的误差,而对于水平刚度的预测则相对误差较小,仅相差2.815%。从比较结果来看,采用灰色系统理论对隔震支座的力学性能预测具有较高的精度。

在作灰色系统预测时,建立合理的GM(1,1)灰色模型,确保GM(1,1)在原点的精度非常重要。为了提高GM(1,1)在原点的精度通常可以采用全数据GM(1,1)模型、新息GM(1,1)模型及新陈代谢GM(1,1)模型。

新息GM(1,1)模型可将不断进入系统的扰动因素考虑进去,GM(1,1)模型要将每一个新得到的数据送入X⁽⁰⁾中,重新建立GM(1,1)模型,即原始数列为X⁽⁰⁾={x⁽⁰⁾(1),x⁽⁰⁾(2),…,x⁽⁰⁾(n)},当获得第n+1个数据后,重新构造数列:

X⁽⁰⁾={x⁽⁰⁾(1), x⁽⁰⁾(2),…, x⁽⁰⁾(n), x⁽⁰⁾(n+1)}.

随时间的推移,老的信息将越来越不适应新情况,新陈代谢GM(1,1)模型将最新获得的信息

考虑进来,同时舍弃最老的信息,即原始数列为X⁽⁰⁾={x⁽⁰⁾(1),x⁽⁰⁾(2),…,x⁽⁰⁾(n)},当获得第n+1个数据后,舍弃最老信息,加入新获得的信息,重新构造数列:

X⁽⁰⁾={x⁽⁰⁾(2),…,x⁽⁰⁾(n),x⁽⁰⁾(n+1)}.

就本文算例来说,以使用了20年的隔震支座力学性能参数作为新获得的信息,分别建立新息GM(1,1)模型和新陈代谢GM(1,1)模型。

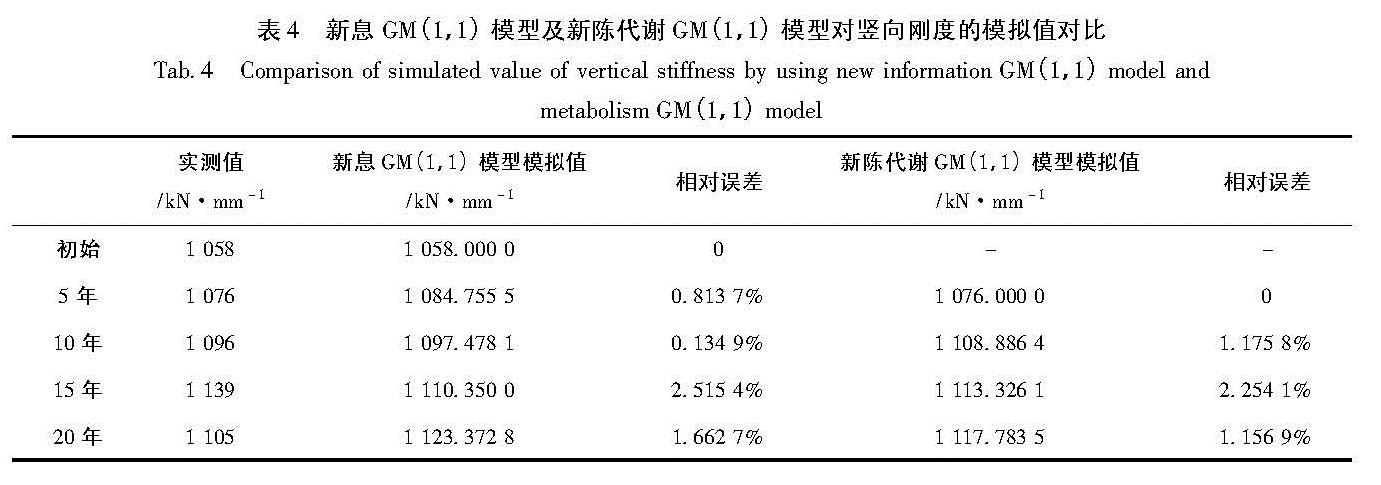
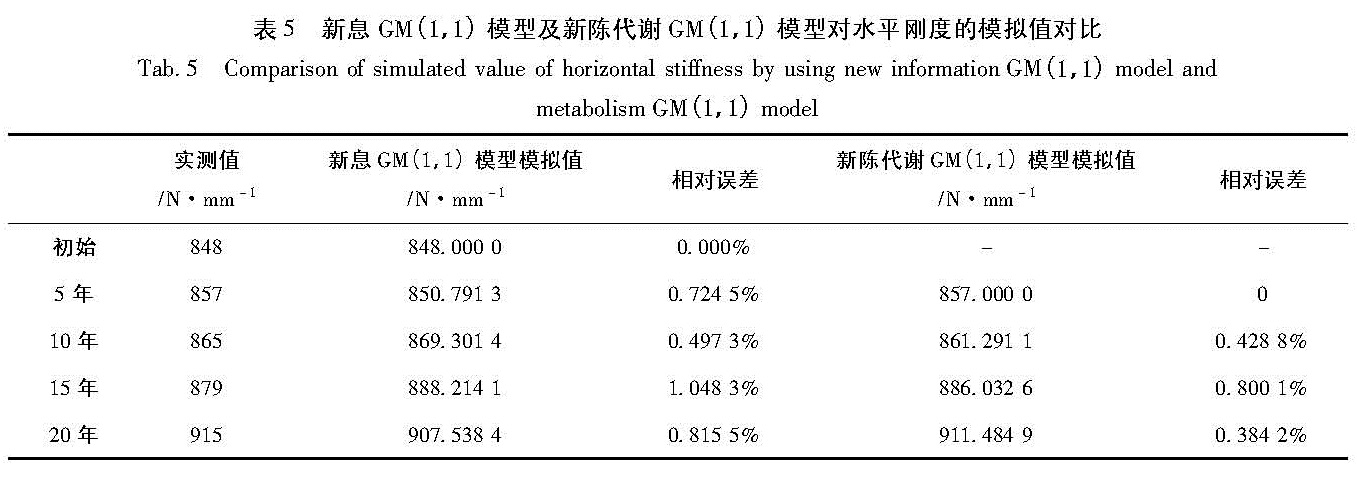
为了对使用了30年后的隔震支座力学性能情况作预测,分别采用新息GM(1,1)模型(即在上述GM(1,1)模型中加入使用了20年的隔震支座力学性能参数)和新陈代谢模型(即初始数据舍去,并新加使用了20年的隔震支座力学性能参数),并将得到的结果作相应的对比,结果见表4,表5。可见,相对来说由新陈代谢模型求得的模拟值误差小于新息模型。

为预测橡胶隔震支座使用25年、30年、35年、40年的力学性能,作发展带预测。将上述建立的3种GM(1,1)模型所对应的估计参数序列

表4 新息GM(1,1)模型及新陈代谢GM(1,1)模型对竖向刚度的模拟值对比
Tab.4 Comparison of simulated value of vertical stiffness by using new information GM(1,1)model and metabolism GM(1,1)model

表5 新息GM(1,1)模型及新陈代谢GM(1,1)模型对水平刚度的模拟值对比
Tab.5 Comparison of simulated value of horizontal stiffness by using new information GM(1,1)model and metabolism GM(1,1)model

a^{^}₍₁₎=[a_i,b_i]^T(1,2,3),列出如下:

a^{^}₍₁₎=[a₁,b₁]^T=[-0.028 638 666

1 026.557 005 955],

a^{^}₍₂₎=[a₂,b₂]^T=[-0.011 660 325 27

1 066.106 857 96],

a^{^}₍₃₎=[a₃,b₃]^T=[-0.000 399 571 96

1 102.373 074 59].

因为

-a_min=min_1≤i≤3{-a_i}=0.000 399 571 96=-a₃,

-a_max=max_1≤i≤3{-a_i}0.028 638 666=-a₁.

所以发展带上界序列响应式为

{x^{^(0)}_s(k+1)=x⁽⁰⁾(1)-(b₁)/(a₁))e^-a₁k+(b₁)/(a₁)

=36 903.142 33e^{0.028 638 666k}-35 845.142 33,

x^{^(0)}_s(k+1)=x^{^(1)}_s(k+1)-x^{^(1)}_s(k).

即: x^{^(0)}_s(k+1)=1 041.866 723e^{0.286 386 66k}.

由此得最高预测值:x^{^(0)}_s(6), x^{^(0)}_s(7), x^{^(0)}_s(8), x^{^(0)}_s(9),分别与第25年、30年、35年、40年对应,以下类似。

x^{^(0)}_s(6)=1 202.265 097,

x^{^(0)}_s(7)=1 237.194 138,

x^{^(0)}_s(8)=1 273.137 962,

x^{^(0)}_s(9)=1 310.126 051.

因X⁽⁰⁾₃的起点为x⁽⁰⁾(2),故发展带下界序列时间响应式为

{x^{^(1)}_s(k+1)=(x⁽⁰⁾(2)-(b₃)/(a₃))e^-a₃k+(b₃)/(a₃)

=276 964.499 9e^{0.003 995 719 6k}-275 888.499 9,

x^{^(0)}_s(k+2)=x^{^(1)}_s(k+2)-x^{^(1)}_s(k+1)

=1 104.464 446e^{0.003 995 719 6k}.

{x^{^(1)}_u(k+2)=(x⁽⁰⁾(2)-(b₃)/(a₃))e^-a₃k+(b₃)/(a₃)

=276 964.499 9e^{0.003 995 719 6k}-275 888.499 9,

x^{^(0)}_u(k+2)=x^{^(1)}_u(k+2)-x^{^(1)}_u(k+1)

=1 104.464 446e^{0.003 995 719 6k}.

由此可得竖向刚度最低预测值为

x^{^(0)}_u(6)=1 122.258 778,

x^{^(0)}_u(7)=1 126.751 981,

x^{^(0)}_u(8)=1 131.263 172,

x^{^(0)}_u(9)=1 135.792 425.

由竖向刚度最高值和竖向刚度最低值得到基本预测值:

x^{^(0)}(6)=1/2[x^{^(0)}_s(6)+x^{^(0)}_u(6)]=1 162.261 938,

x^{^(0)}(7)=1/2[x^{^(0)}_s(7)+x^{^(0)}_u(7)]=1 181.973 06,

x^{^(0)}(8)=1/2[x^{^(0)}_s(8)+x^{^(0)}_u(8)]=1 202.200 567,

x^{^(0)}(9)=1/2[x^{^(0)}_s(9)+x^{^(0)}_u(9)]=1 222.959 238,

对于水平刚度数据,按照相同的方法,得到水平刚度最高预测值为

x^{^(0)}_s(6)=937.668 343 4,

x^{^(0)}_s(7)=964.603 912 5,

x^{^(0)}_s(8)=992.313 235 9,

x^{^(0)}_s(9)=1 020.818 541.

水平刚度最低预测值为

x^{^(0)}_u(6)=900.614 297 1,

x^{^(0)}_u(7)=912.126 773 6,

x^{^(0)}_u(8)=923.786 413 1,

x^{^(0)}_u(9)=935.595 096 7.

由水平刚度最高值和水平刚度最低值得到基本预测值:

x^{^(0)}(6)=1/2[x^{^(0)}_s(6)+x^{^(0)}_u(6)]=919.141 320 3,

x^{^(0)}(7)=1/2[x^{^(0)}_s(7)+x^{^(0)}_u(7)]=938.365 343 1,

x^{^(0)}(8)=1/2[x^{^(0)}_s(8)+x^{^(0)}_u(8)]=958.049 824 5,

x^{^(0)}(9)=1/2[x^{^(0)}_s(9)+x^{^(0)}_u(9)]=978.206 818 6.

为了直观清晰表示,将3种模型的模拟、预测结果绘图如图1、2所示。

图1 竖向刚度模拟及预测值对比
Fig.1 Comparison of simulated and predicted value of vertical stiffness

图2 水平刚度模拟及预测值对比
Fig.2 Comparison of simulated and predicted value of horizontal stiffness

与此同时,本文还结合上述几种灰色预测模型,对隔震支座的竖向刚度及水平刚度进行了使用40年后的发展带预测,得出的竖向刚度基本预测值为1 222.96 kN/mm,比初始值增大了15.592%,水平刚度基本预测值为978.21 N/mm,比初始值增大了15.355%。这个预测结果与日本试验得到的结论经过30～60年老化后,水平剪切刚度提高约20%(周福霖,1997)相一致。

本文采用3种橡胶隔震支座的性能随时间的老化作了相应的模拟、预测,由结果可知:灰色系统预测理论用于隔震支座老化性能的模拟预测具有较高的精度。对于一些重要的隔震建筑、隔震桥梁的监测,可以抽样检测隔震支座的力学性能,并在这基础上采用灰色系统预测理论对隔震支座力学性能随时间的老化进行预测,从而为预测隔震结构的抗震性能提供必要的依据。