基金项目:国家自然科学基金(51278027)、国家自然科学基金重点(51038006)和城市地下空间开发利用中的基础理论和关键技术研究创新团队(PMX2013_014210_00016)联合资助.
(1.北京建筑大学 工程结构与新材料北京高等学校工程研究中心,北京 100044; 2.北京工业大学 建筑工程学院,北京 100124)
(1. Beijing Higher Institution Engineering Research Centre of Structural Engineering and New Materials,University of Civil Engineering and Architecture,Beijing 100044,China)( 2. College of Architecture and Civil Engineering,Beijing University of Technolog
Self-centering Moment-resisting Frame(SC-MRFs); steel structure; plane frame; static elastic-plastic; high-strength steel
备注
基金项目:国家自然科学基金(51278027)、国家自然科学基金重点(51038006)和城市地下空间开发利用中的基础理论和关键技术研究创新团队(PMX2013_014210_00016)联合资助.
运用ABAQUS有限元软件对一榀四层两跨平面钢框架进行静力弹塑性分析,分别计算钢材强度为Q345、Q420和Q460三榀自复位钢框架,探讨自复位平面钢框架的抗震性能,并着重讨论钢材强度对自复位性能的影响。结果 表明,钢材强度的提高对减小结构塑性、残余侧移有较明显的作用,但未彻底避免柱底塑性的产生。对相对内转角和摩擦耗能也有一定影响,但是对钢绞线预应力影响不大。
The static elastic-plastic analysis of a four-story two-bay Self-centering Steel Moment-resisting Plane Frame(SC-MRFs)are conducted by FEA software ABAQUS,and three SC-MRFs with different steel strength of Q345,Q420 and Q460 are calculated. The seismic performance of SC-MRFs and the effect of steel strength on self-centering capability are discussed. The results indicate that the increment of steel strength has an obvious effect on decrement of structural plasticity and residual drift,but it can't completely avoid the plasticity of column bottom. Besides,it also affects connection relative rotation to some degree and friction energy dissipation,but has little influence on the loss of prestressing steel strand.
引言
与传统钢框架不同,自复位钢框架梁与柱通过槽钢和预应力钢绞线连接,在地震作用下,梁柱截面张开,通过梁腹板与槽钢之间的摩擦耗散能量。开口之后预应力钢绞线伸长,钢绞线的拉力提供框架自复位的恢复力。传统钢框架节点一般采用刚接节点,在地震作用下,梁端承担弯矩,通过梁端塑性变形耗散地震能量。但是在1994年美国北岭地震和1995年日本阪神地震中大量钢框架发生脆性破坏,主要集中在梁柱翼缘焊接部位。震后残余变形大,修复难度大、成本高(Miller,1998)。为了避免此类问题,1997年Garlock提出了自复位钢框架结构,力求实现结构在震后无需修复或稍加修复即可恢复其使用功能(Garlock et al.,2007)。本文运用ABAQUS有限元软件对一榀四层两跨腹板摩擦耗能的自复位平面钢框架进行静力弹塑性分析(石亦平,周玉蓉,2006; 马晓峰,2013),分别选取钢材强度为Q345、Q420和Q460三榀自复位钢框架,探讨自复位平面钢框架的抗震性能和自复位性能,并着重讨论钢材强度对平面钢框架受力性能的影响,为进一步试验研究做准备。
1 模型构造及尺寸
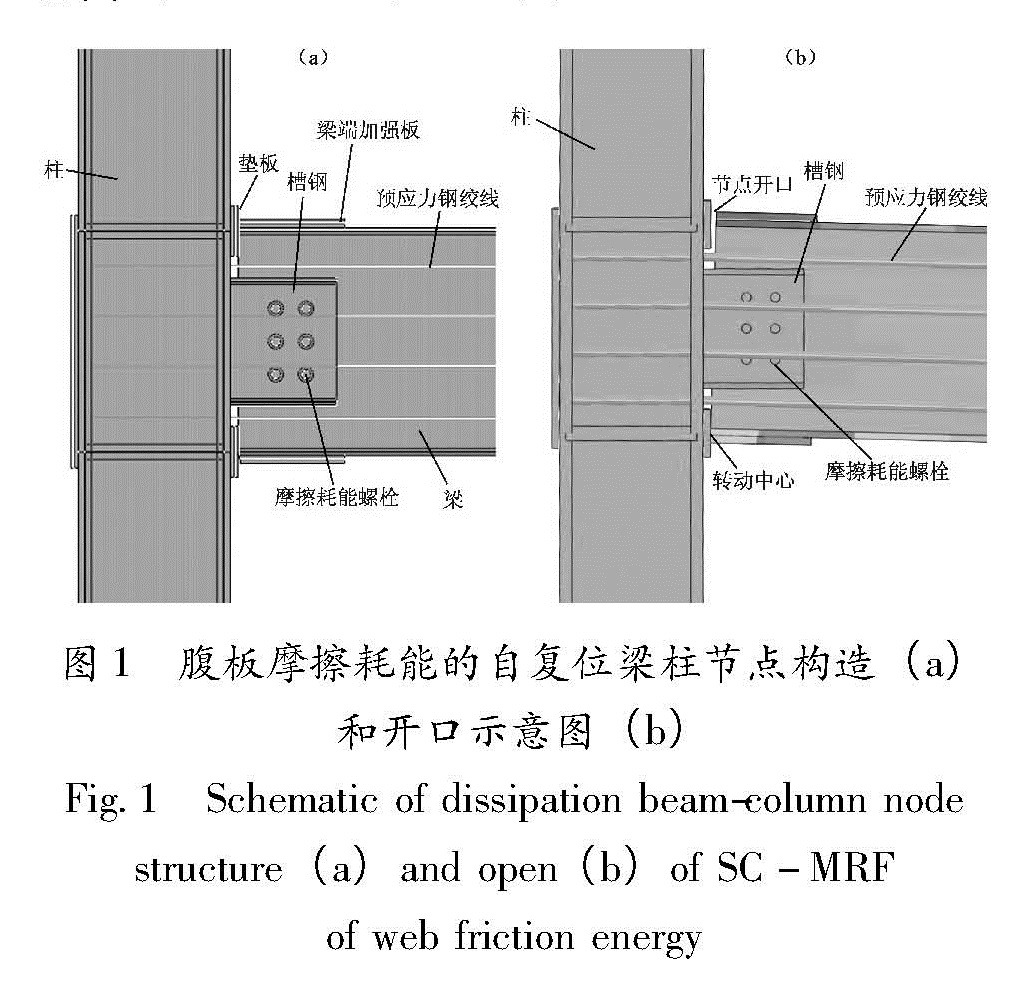
腹板摩擦耗能的自复位梁柱节点构造如图1a所示,槽钢与柱翼缘焊接,与梁腹板通过高强螺栓连接。通过槽钢与梁腹板之间的摩擦耗散地震能量,与梁平行的预应力索将梁柱压紧,并提供恢复力,使结构在地震作用后能恢复到原来位置。图1b为腹板摩擦耗能的自复位梁柱节点的开口示意图(Ricles et al.,2010)。
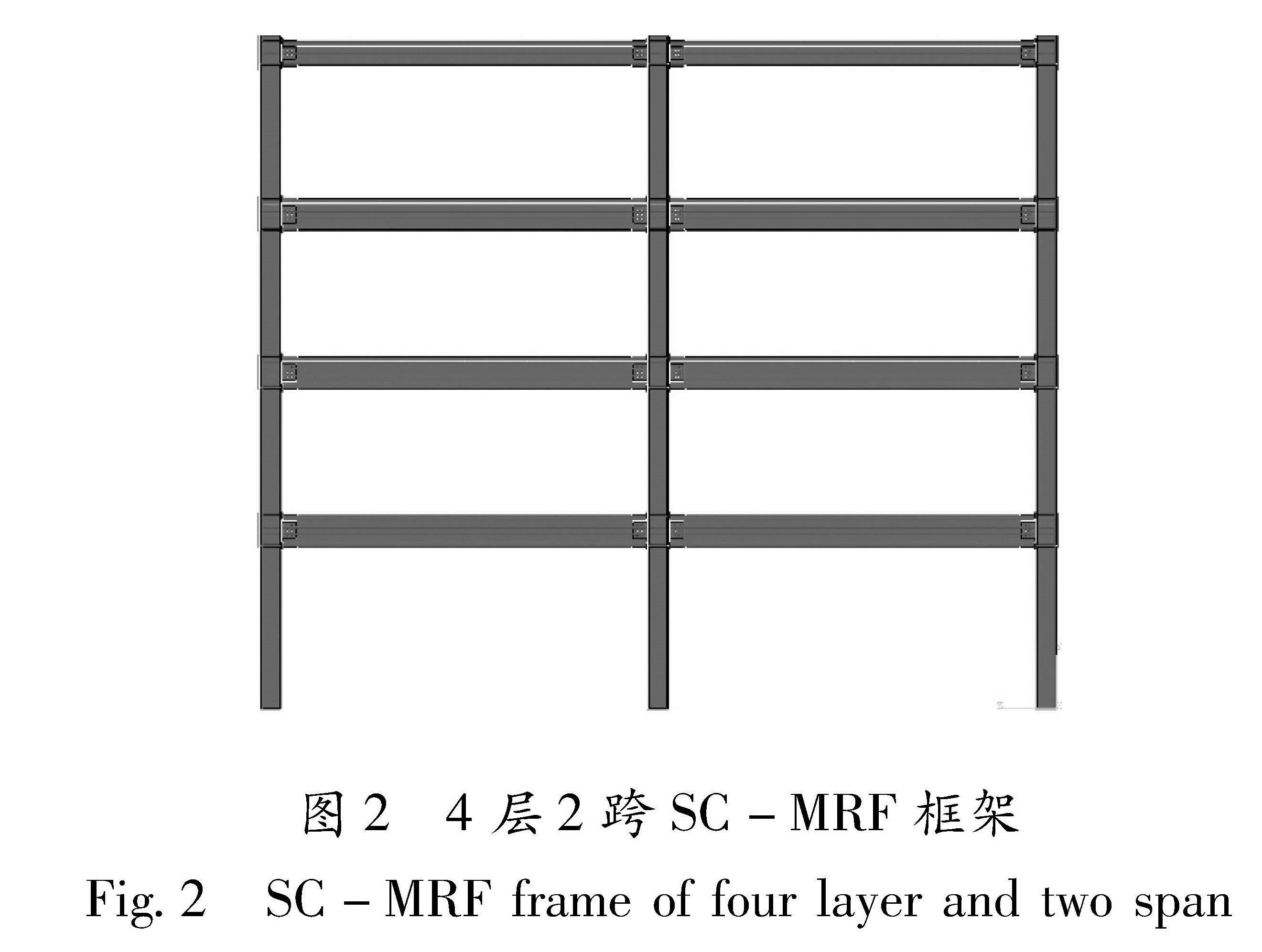
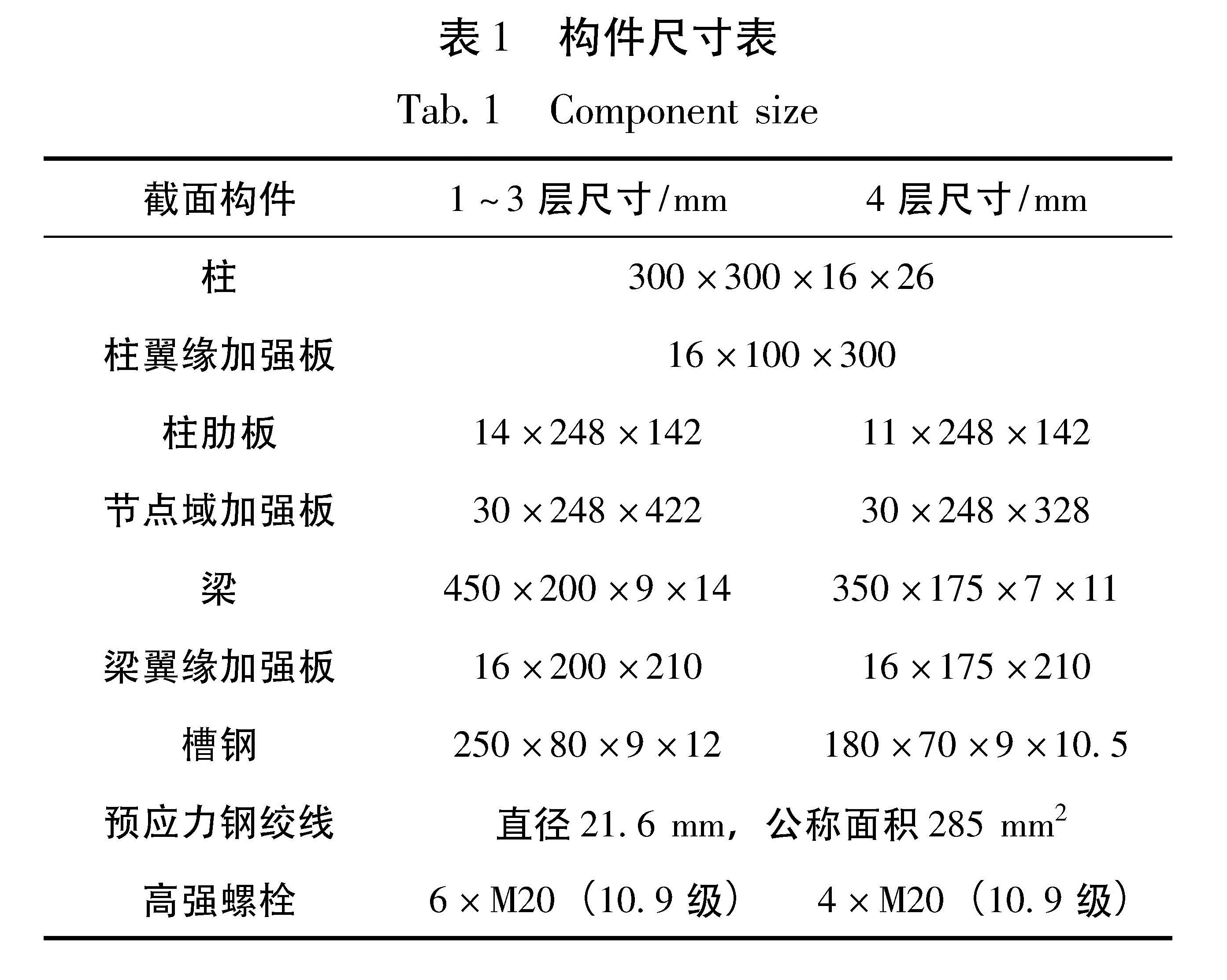
本文四层两跨自复位平面钢框架模型参考Garlock等(2005)的试验框架,底层层高2.75 m,二至四层层高均为2.25 m(图2),构件尺寸详见表1。梁腹板两侧均与槽钢之间设置黄铜板摩擦耗能件,摩擦系数为0.35(Tsai et al.,2008)。预应力钢绞线公称直径21.6 mm,公称截面积为285 mm2,钢绞线分布在梁腹板两侧,沿梁高均匀布置,一至三层每层8根,四层6根。为考察不同预应力值对框架中节点自复位性能的影响,对各层预应力钢绞线施加不同的初始预应力值。单根钢绞线的初始预拉力一至四层分别为114 kN、108 kN、72 kN和40 kN。槽钢与梁腹板采用10.9级M20高强螺栓连接,每个螺栓预紧力为155 kN。顶层每个槽钢布置4个高强螺栓,其它层布置6个构件尺寸详见表1。本文主要分析三榀平面框架模型,其截面尺寸和构选等条件均相同,仅钢材强度不同。钢材强度分别为Q345、Q420和Q460级,分别称作框架S-1、框架S-2和框架S-3。图1 腹板摩擦耗能的自复位梁柱节点构造(a)
和开口示意图(b)
Fig.1 Schematic of dissipation beam-column node structure(a)and open(b)of SC-MRF of web friction energy2 构件材料性能
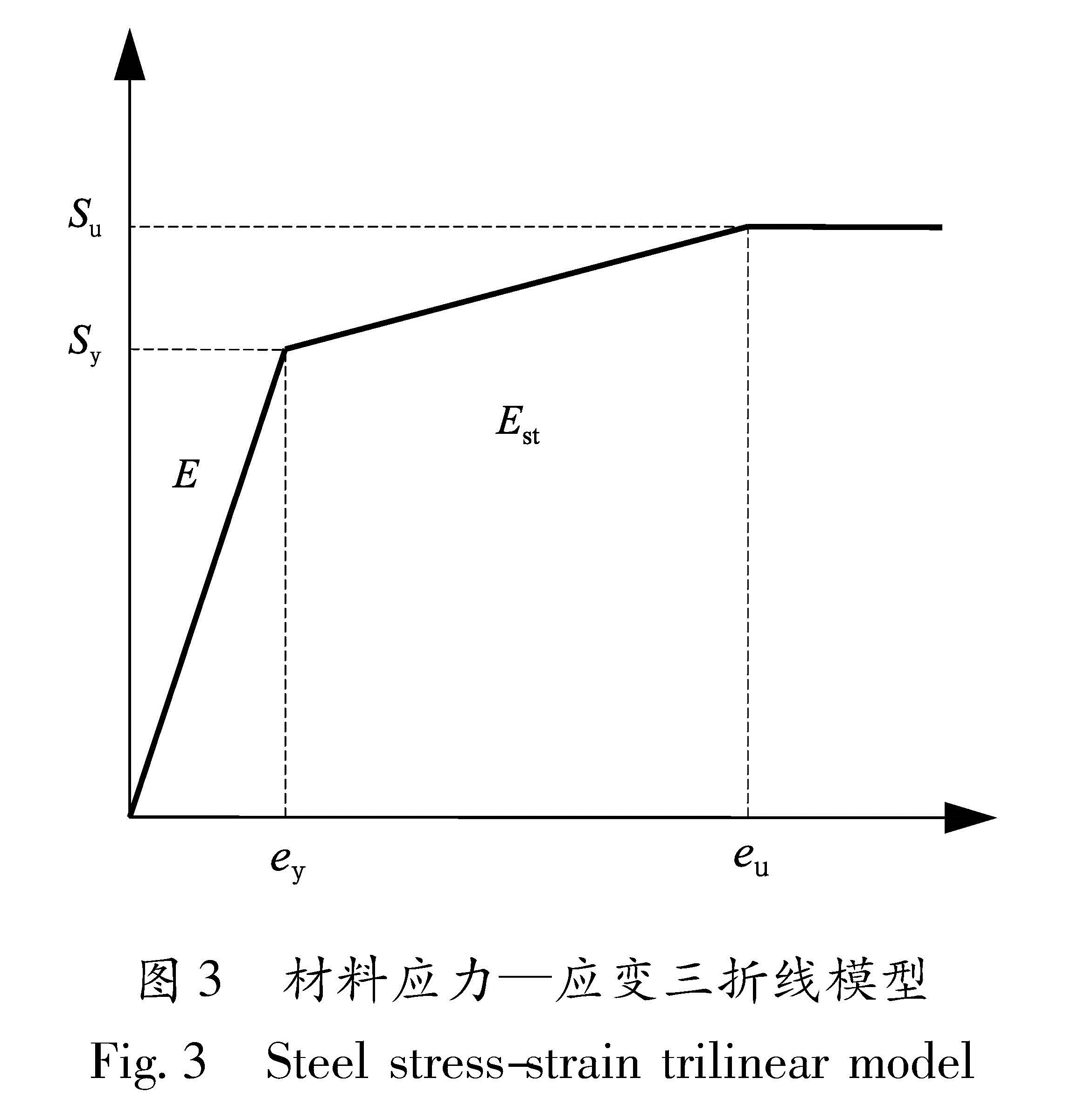
钢材Q345、Q420、Q460的应力—应变关系曲线均采用只考虑强化阶段三折线模型(戴国欣等,2012)(图3)。Q345取σy=345 MPa,εy=0.17%,E=2.06×105 MPa,σu=480 MPa,εu=2.1%,泊松比v=0.3; Q420取σy=420 MPa,εy=0.2%,E=2.06×105 MPa,σu=520 MPa,εu=2.6%,泊松比v=0.3。Q460取σy=460 MPa(陆新征等,2009),εy=0.22%,E=2.06×105 MPa,σu=550 MPa,εu=2.4%,泊松比v=0.3。预应力钢绞线只定义其弹性,E=2.06×105 MPa,热膨胀系数αs=0.14×10-6·c-1,泊松比v=0.3(预应力钢结构技术规程,2006; 低合金高强度结构钢,2008)。
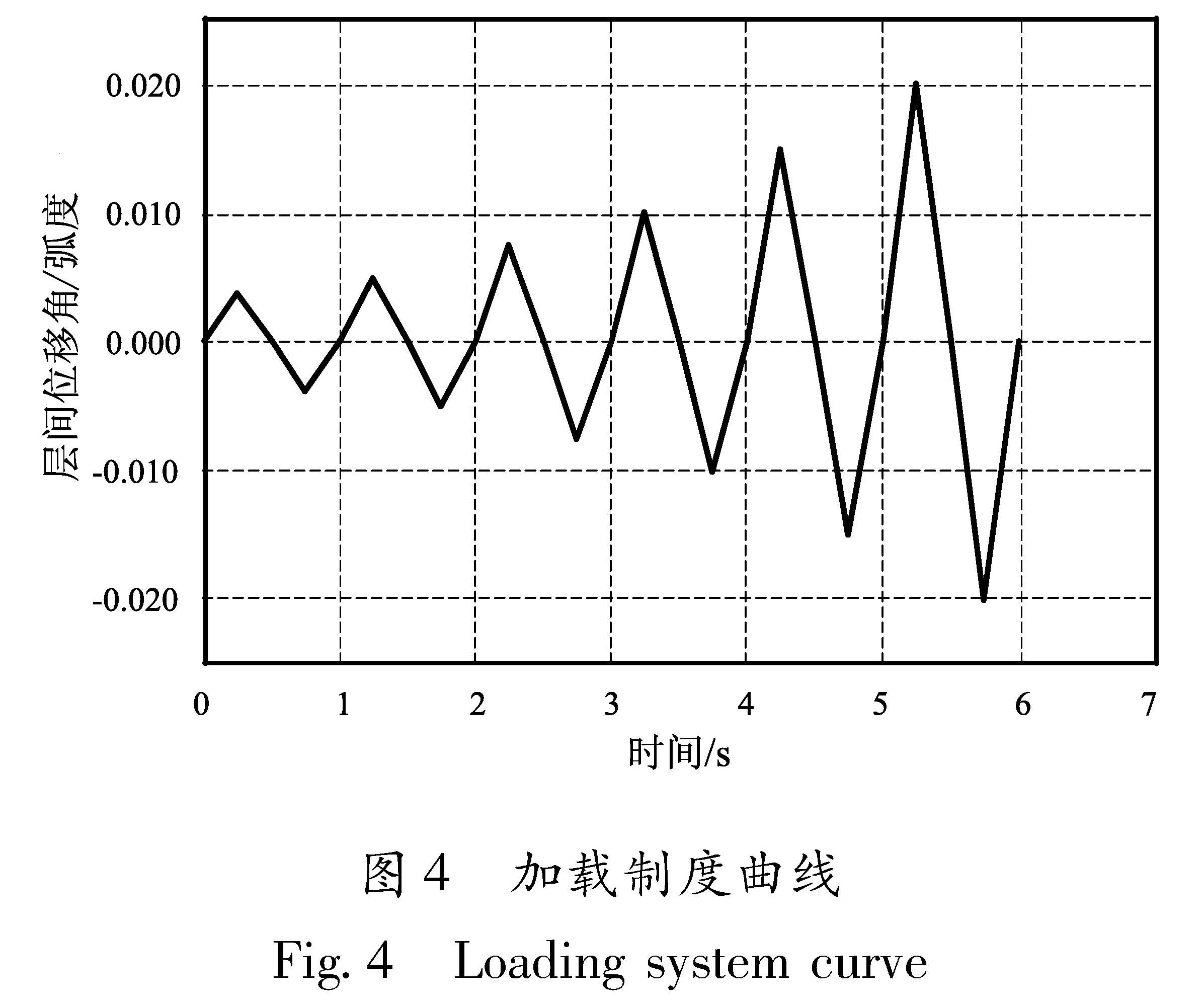
3 加载制度
分析过程中采用倒三角位移循环加载模式加载至层间位移角2%时,停止加载,放开位移约束(陆新征等,2009)(图4)。各级层间位移角分别为0.375%、0.5%、0.75%、1%、1.5%和2%(FEMA-350,2000)。
4 结果分析对比
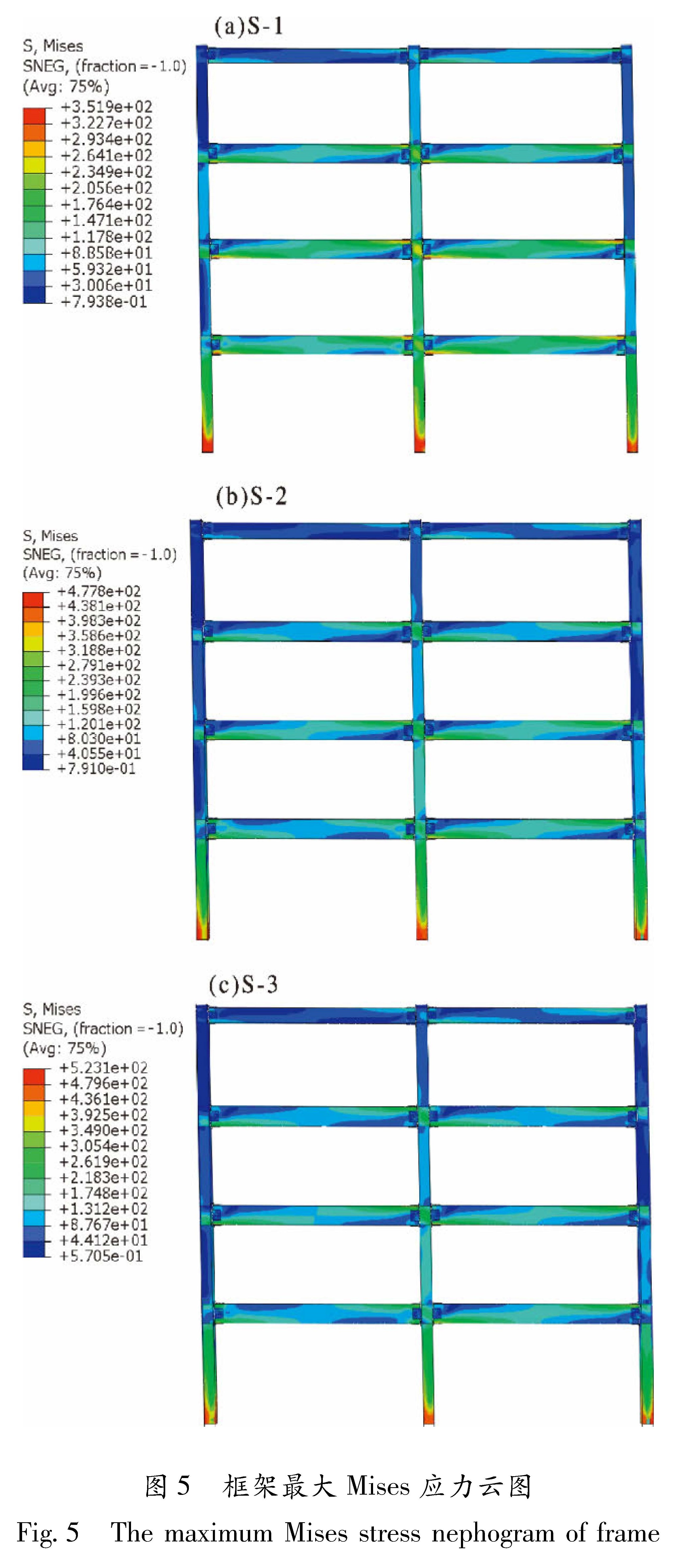
4.1 Mises应力由于预应力钢绞线有初始预拉力,梁在加载
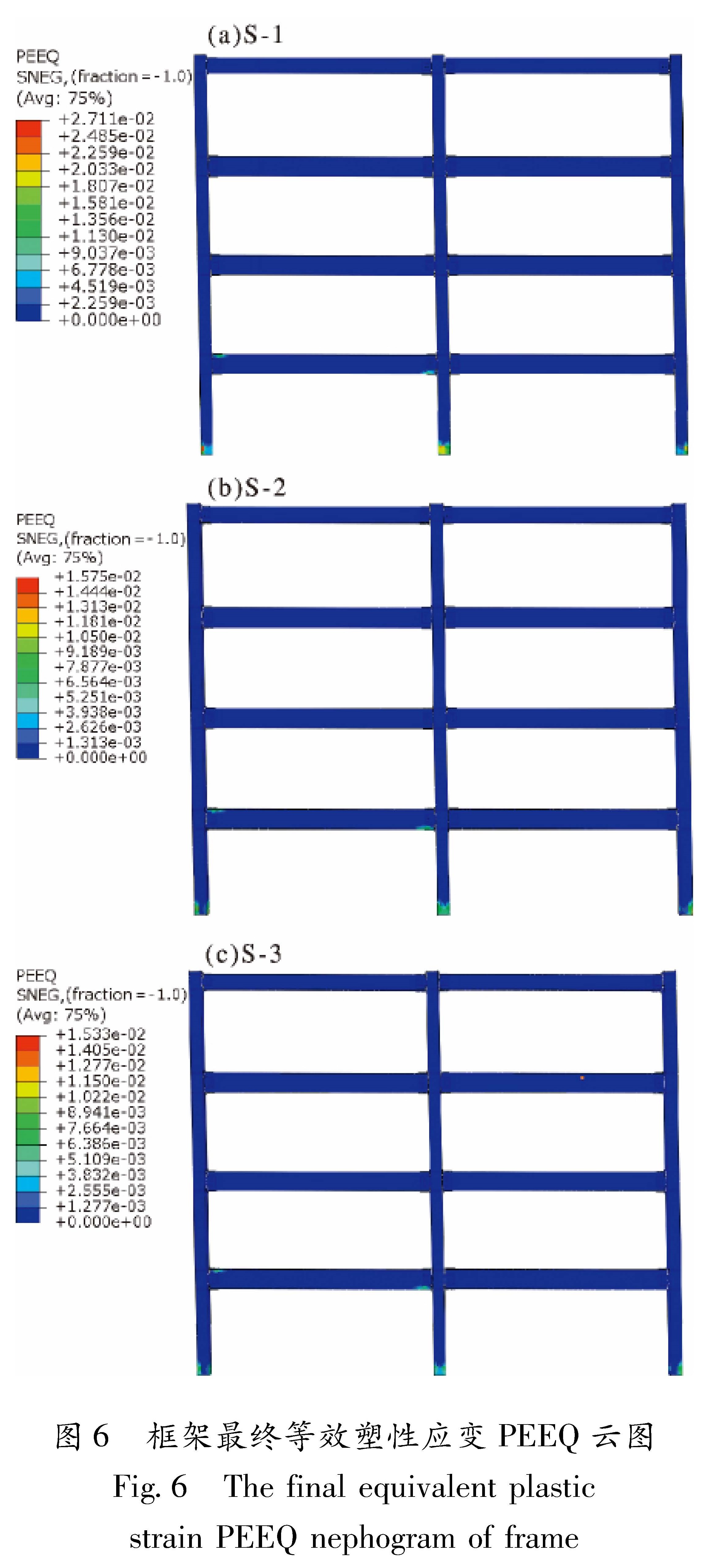
前就处于受压状态,最大应力位于一层梁上层翼缘。随着加载过程的进行,最大应力位置逐渐转移到柱底翼缘处。层间位移角为2%时,框架S-1最大应力位于左柱柱底翼缘,数值达351.9 MPa。框架S-2最大应力位于右柱柱底翼缘,数值达477.8 MPa。框架S-3最大应力位于中柱柱底翼缘,数值达523.1 MPa(图5)。4.2 塑性应变自复位框架塑性只在柱底与一层梁出现,自复位梁出现塑性主要是由加载部位处局部受力过大导致,柱子塑性主要是加载后期层间位移角过大导致。塑性应变的发展过程与Mises应力发展过程基本一致,S-1、S-2塑性最早出现于层间位移角1%的加载循环,层间位移角为1%时,等效塑性应变分别1.794E-3和2.077E-4。加载至层间位移角2%时,最大等效塑性应变PEEQ分别增至2.71E-2和1.575E-2。塑性S-3最早出现于层间位移角为1.5%的加载循环,层间位移角为1.5%时,等效塑性应变为3.173E-3。加载至层间位移角为2%时,最大等效塑性应变PEEQ为1.533E-2,如图6所示。由此可见,随着钢材强度等级的提高,自复位钢框架柱底等效塑性应变减小的趋势明显。提高钢材强度虽不能完全消除塑性,但延缓了塑性最早出现的时间,使自复位钢框架具备更大的弹性侧移能力。
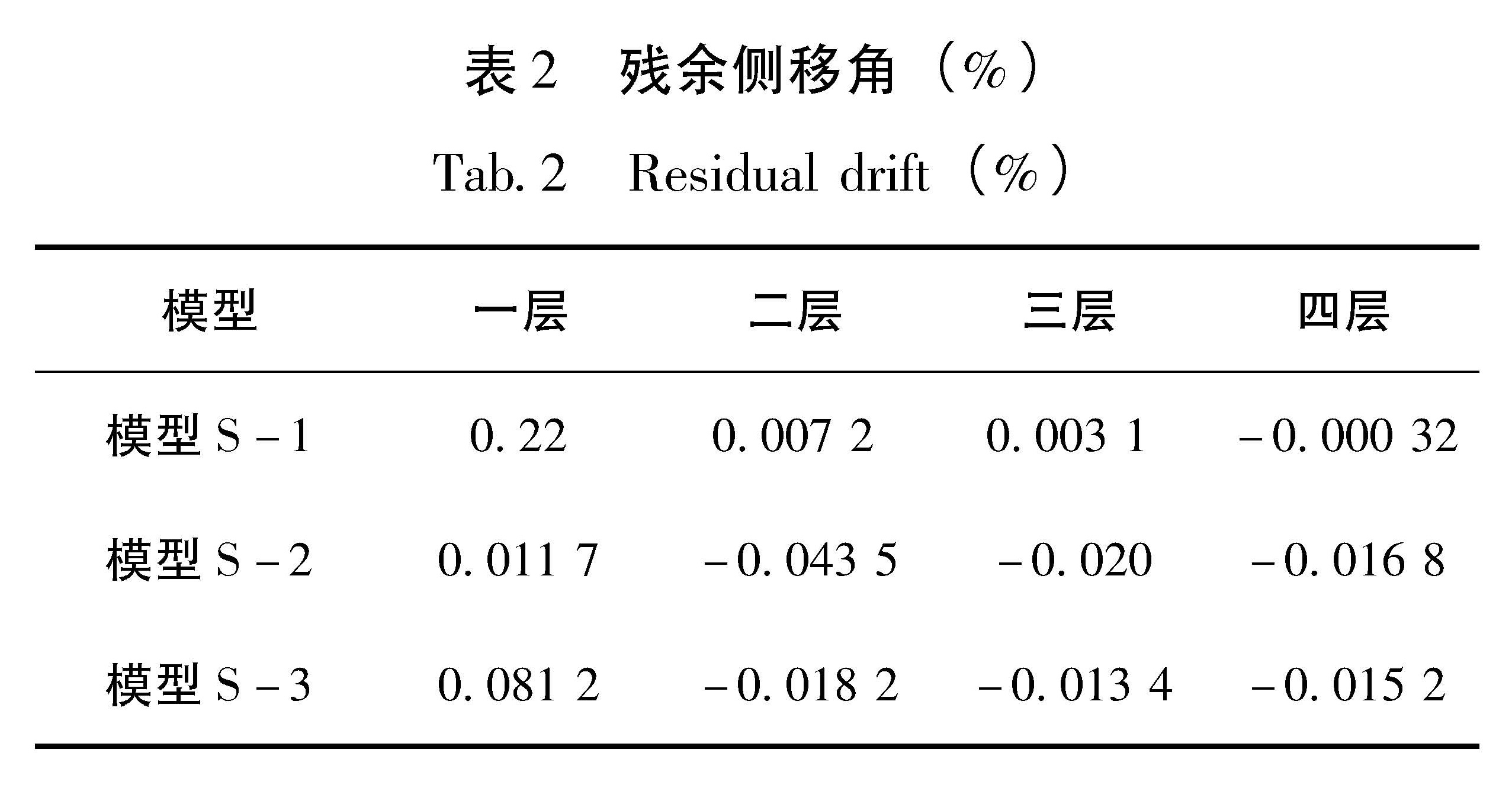
4.3 残余变形表2为三榀框架的残余侧移角,表中层间侧移角为正号表示框架往左侧偏移,负号表示框架往右侧偏移。从表中可以看出,三榀框架的残余侧移角均很小,最大残余侧移角仅为框架S-1底
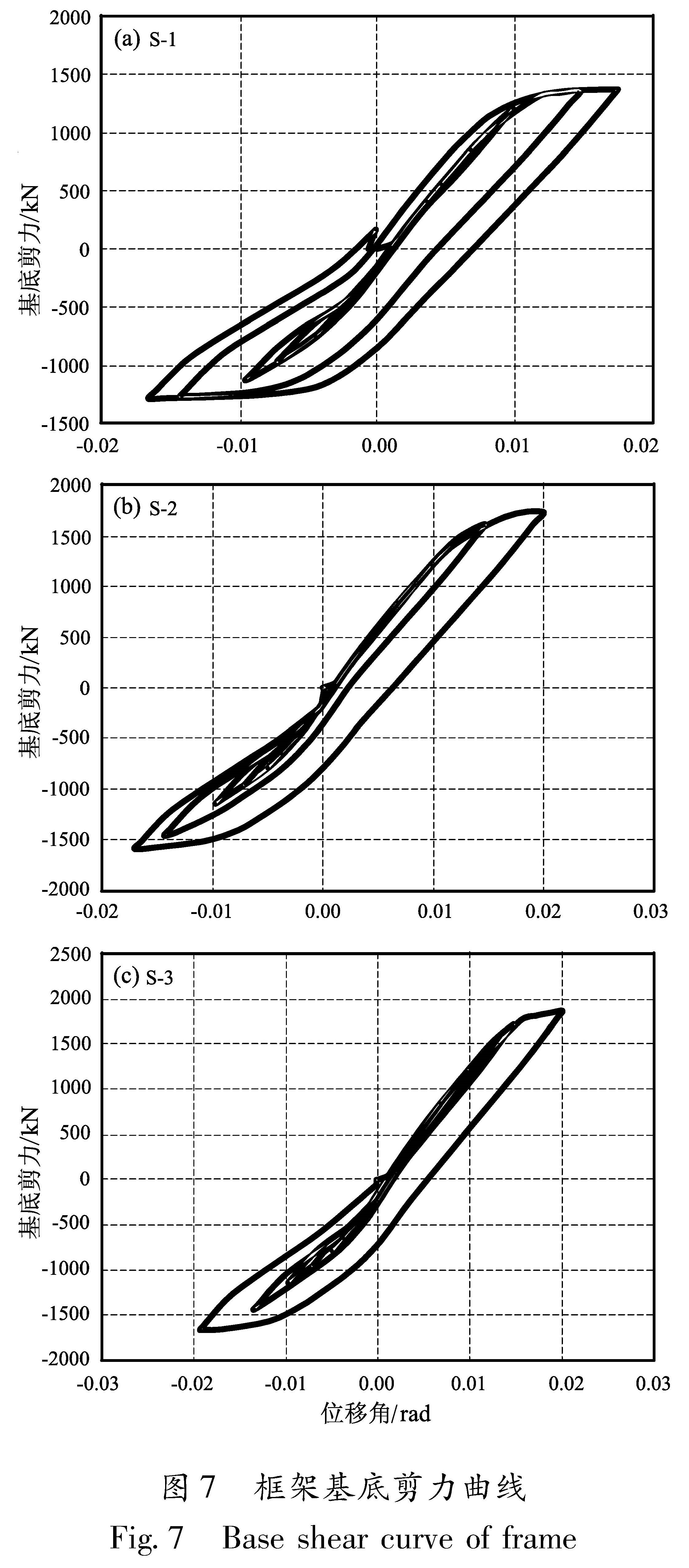
层的0.22%,表示自复位钢框架有很好的自复位性能,残余侧移角小。其中S-1残余侧移角主要集中在底层,二至四层残余侧移角甚至小于其他两榀更高强度钢框架相应层数的残余侧移角,其主要原因为S-1钢材强度低,底层塑性发展严重,变形主要集中在底层。同时,钢材强度等级提高至S-2,最大残余侧移角明显减小,但S-3与S-2相比并无明显变化,这说明钢材强度提高到一定程度能提升自复位钢框架的自复位能力,再继续提高效果不明显。4.4 基底剪力与层间侧移角的关系曲线三榀框架基底剪力与层间侧移角的关系曲线
如图6所示。S-1最大基底剪力为1 367.1 kN,S-2 和S-3分别增至1 732.6 kN、1 862.27 kN。由图7a可以看出S-1的基底剪力与层间侧移明显比S-2和S-3饱满,这由于S-1柱底塑性发展较S-2和S-3严重。S-1与S-2塑性发展主要出现在层间侧移角为1.5%和2%时的加载循环,S-3则主要出现在层间侧移角为2%时的加载循环,这同样说明钢材强度提高延缓了柱底塑性的发展。
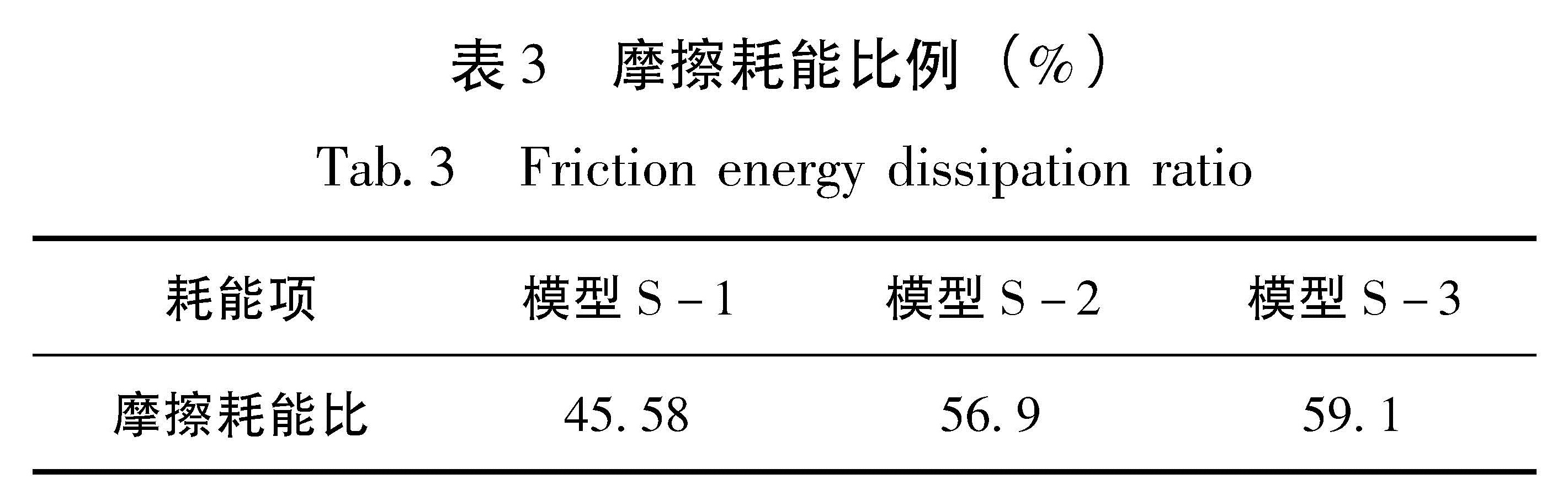
4.5 摩擦耗能框架梁柱节点通过槽钢处摩擦来消耗能量。整个加载中,三榀框架S-1,S-2和S-3总的输入能量分别为1.73×105 J,1.46×105 J和1.45×
105 J。摩擦消耗的能量分别为7.9×104 J,8.3×104 J和8.57×104 J。整个加载过程累积的耗能比例详见表3。 随着钢材强度等级的提高,整个加载过程三榀框架消耗的总能量降低,摩擦耗能增大,累积摩擦耗能比例增大趋势明显。图8为框架每个加载循环摩擦耗能占该圈总能量的比例曲线。由图可知,三榀框架单循环最大摩擦耗能比均位于位移角为1%加载循环。位移角
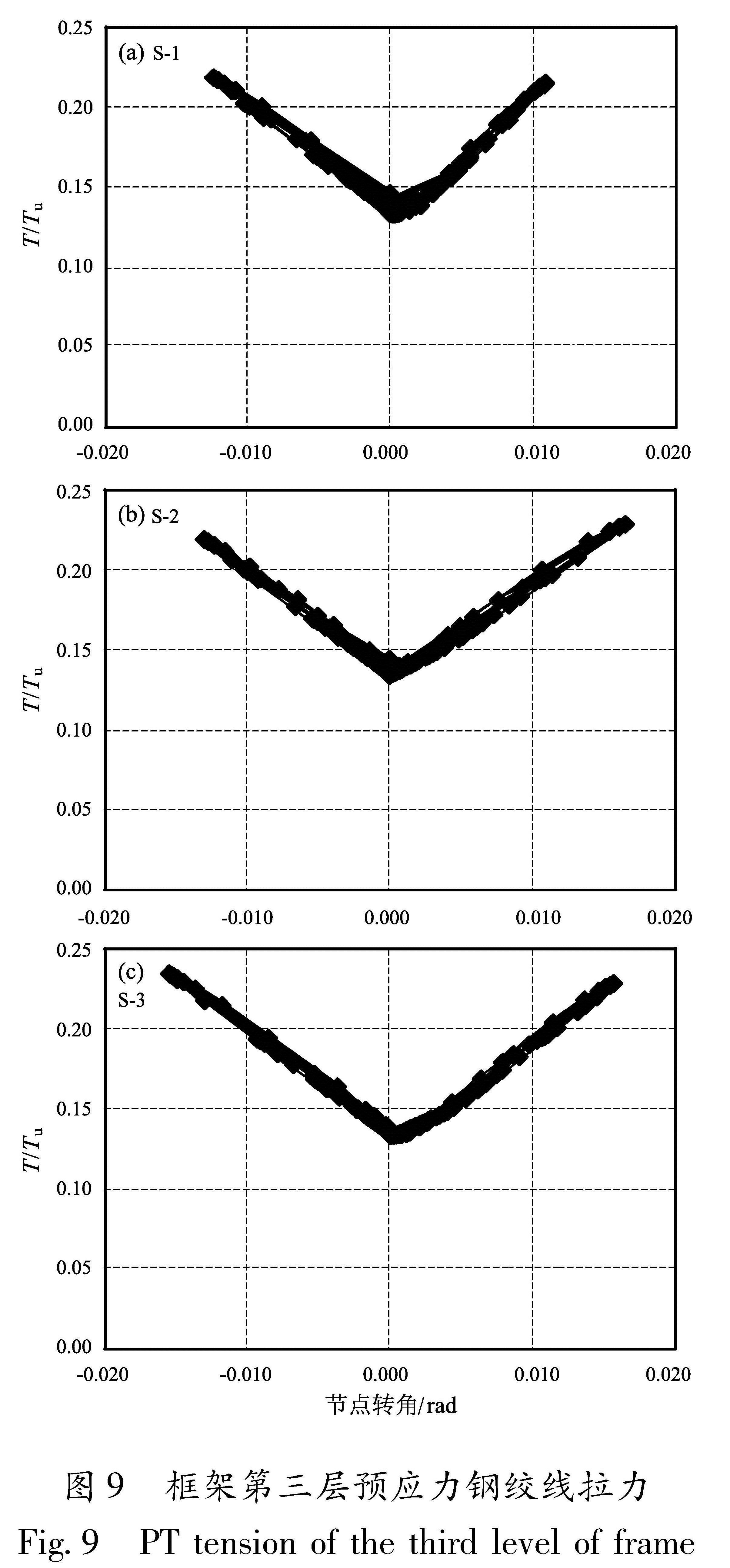
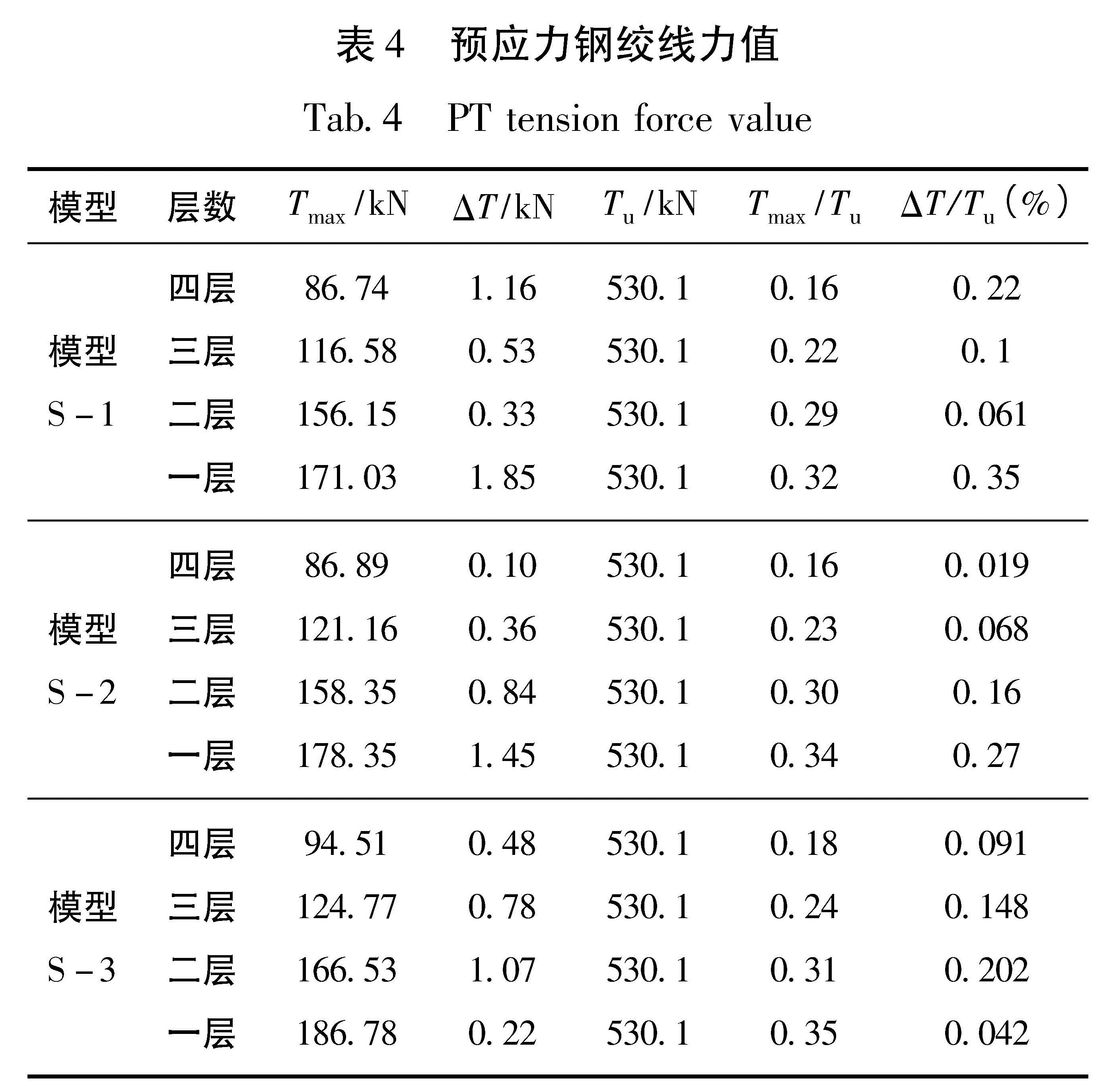
1%时,S-1、S-2和S-3框架摩擦耗能比分别高达92.84%、94.68%和94.75%。S-1和S-2在位移角1.5%加载循环下降明显,S-3则在位移角为2%加载循环下降明显,这与塑性发展趋势相符。4.6 钢绞线预应力梁柱截面张开时,预应力钢绞线伸长,索力值增大,梁柱截面闭合后,预应力索基本恢复到原来的长度和索力值(潘振华等,2011; Garlock et al.,2005)。由于篇幅有限,笔者仅列出三榀框架第三层预应力钢绞线拉力与层间位移的关系,如图9所示,详细数据列于表4中,表中Tmax为最大预应力钢绞线拉力,ΔT为预应力损失,Tu为钢绞线极限抗拉强度(Ricles et al.,2010)。钢绞线在S-3一层最大索力为0.35 Tu,远远小于钢绞线的极限索力,同时可以看出,钢材强度对预应
力钢绞线的受力影响不大。从表4可知,钢绞线最大预应力值为186.78 kN,远小于钢绞线的屈服荷载530.1 kN,同时预应力钢绞线的力值损失较小,随着强度提高,损失值略有下降。最大损失为S-1的一层钢绞线,数值为1.85 kN。
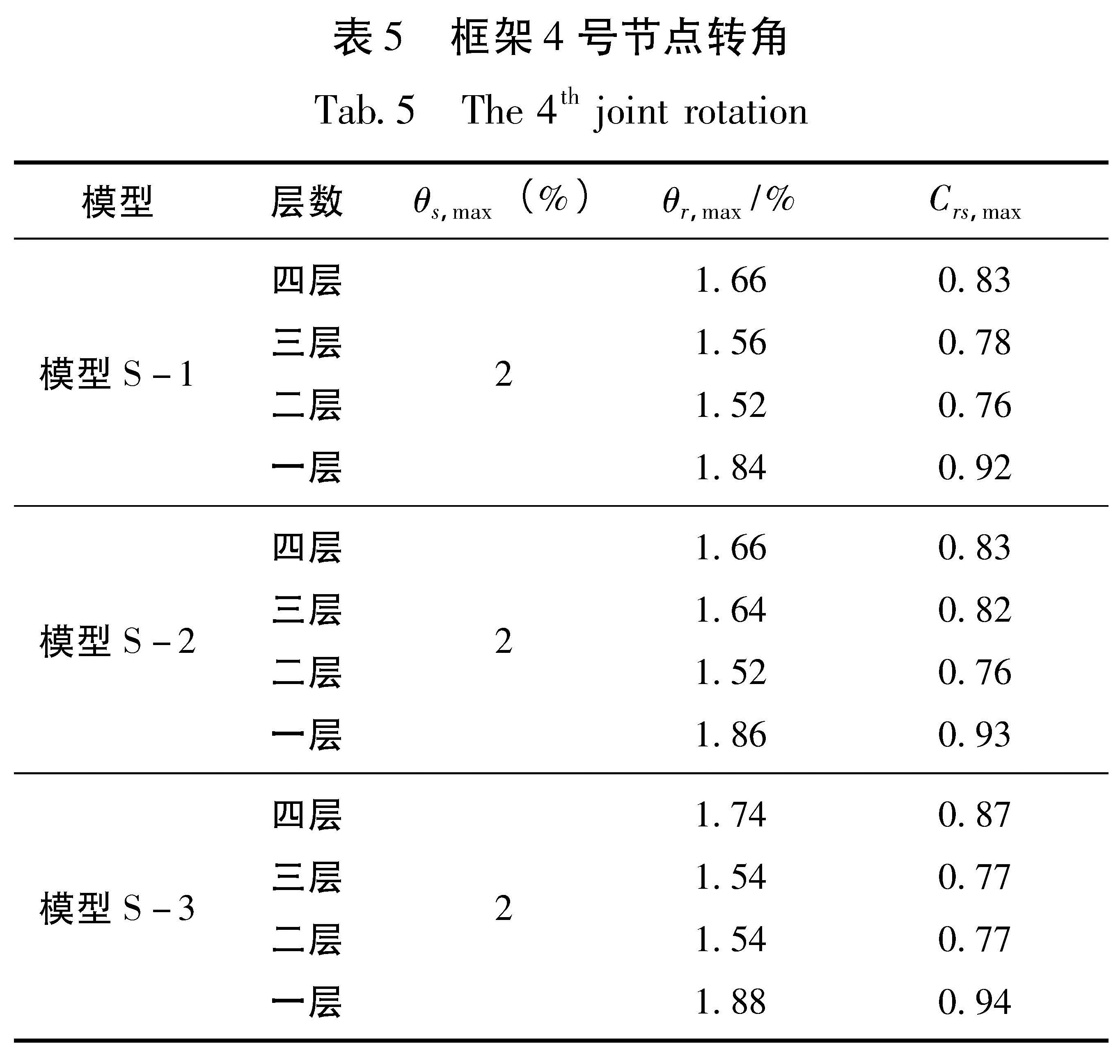
4.7 框架节点性能当三榀框架层间侧移角达到一定数值、节点弯矩达到临界开口弯矩时,梁柱截面脱开,开始出现内转角,框架恢复到初始位置后,内转角也随之减小为零,梁柱截面重新闭合(Lin et al.,2013)。由于篇幅有限,笔者仅讨论框架4号节点的转动能力,其它节点的规律类似。4号节点详细数据详见表5,Qs,max为最大层间侧移角,Qr,max为最大相对转角,Crs,max由Qr,max/Qs,max计算得出(Ricles,2010; Lin et al.,2013)。由表中数据可知,四层框架内转角均小于层间位移角,底层和四层略大于二三层,数据均大于0.7,表明自复位钢框架节点有较好的转动能力。横向比较三榀框架同层节点的内转角数值,发现提高钢材强度等级,主体构件塑性变形减小,导致框架内转角略有增大。
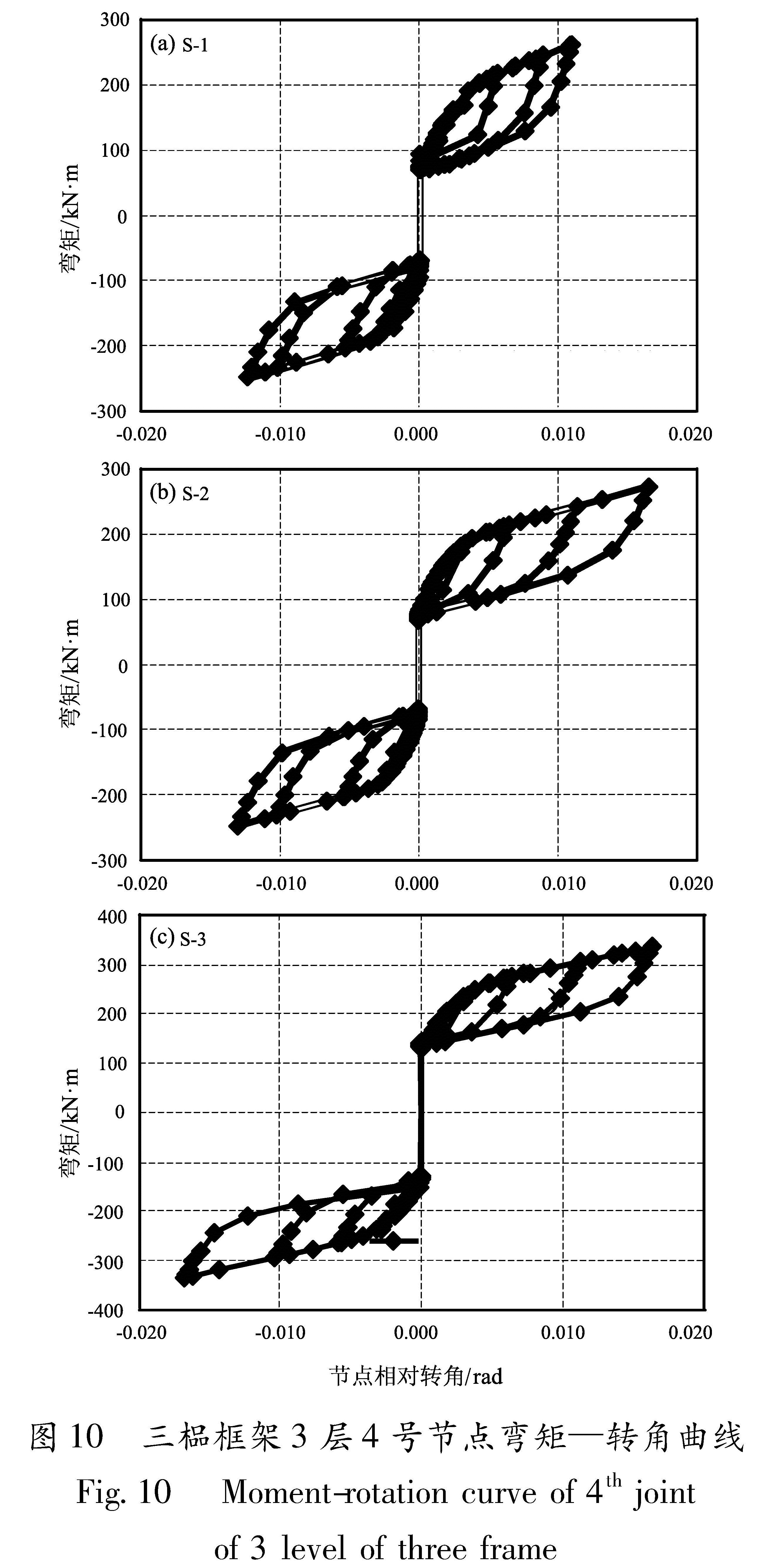
图 10中三榀框架的三层4号节点的弯矩—转角曲线除转角大小稍有差异外,其它基本一致,这表明钢材强度对节点的弯矩—转角曲线影响不明显。
表5 框架4号节点转角
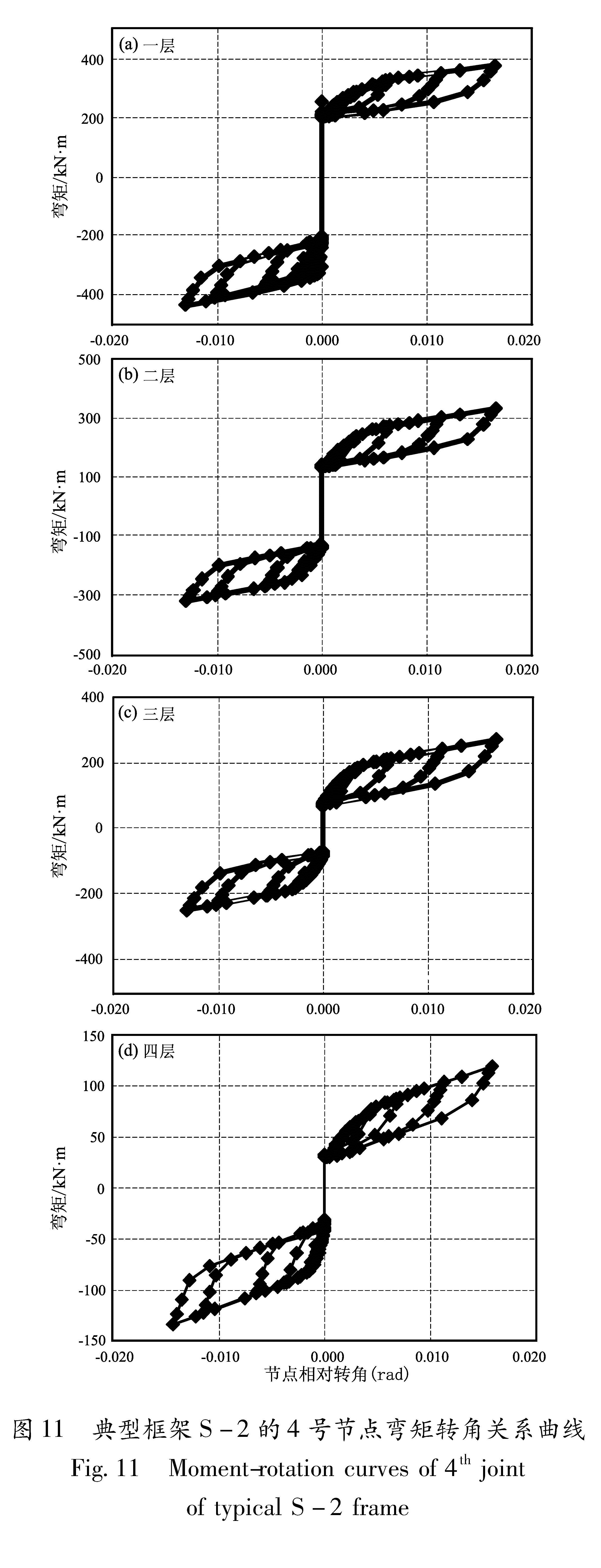
Tab.5 The 4th joint rotation对典型框架S-2的4号节点弯矩转角关系进行分析(图 11),发现节点临界开口弯矩沿层数逐层减小。摩擦耗能面积由于螺栓数不同和节点相对转角大小差异而略有不同。图 10 三榀框架3层4号节点弯矩—转角曲线
Fig.10 Moment-rotation curve of 4th joint of 3 level of three frame图 11 典型框架S-2的4号节点弯矩转角关系曲线
Fig.11 Moment-rotation curves of 4th joint of typical S-2 frame5 结论
通过对钢材强度分别为Q345、Q420和Q460等级的三榀四层两跨平面自复位钢框架进行静力弹塑性分析,得出以下结论:
(1)不同钢材等级的三榀自复位平面钢框架均能实现自复位机制,有较好的自复位性能,钢框架残余变形较小。这对减小震后修复成本和修复难度均有重要意义。
(2)随着框架钢材强度等级的提高,自复位钢框架的Mises应力增大,塑性明显减小。自复位柱底虽不能完全避免进入塑性,但是提高钢材强度等级大大延缓了框架塑性的发展。
(3)提高自复位钢框架钢材强度等级,框架摩擦耗能的比例明显增大,最大耗能的合理层间侧移角在1%至1.5%之间。
(4)随着钢材强度等级的提高,自复位钢框架梁柱节点的内转角亦略有增大。
(5)提高钢材强度对钢绞线索力的大小和预应力损失影响较小,对各层节点的弯矩—转角关系影响也不大。
(6)钢材强度从Q345提高至Q420,残余侧移角减小幅度大,自复位钢框架的自复位能力提升明显,性价比较高。继续提高至Q460,框架的自复位能力继续提高,但幅度相对低,性价比不高。
- 戴国欣,王飞,施刚,等.2012.Q345与Q460结构钢材单调和循环加载性能比较[J].工业建筑,42(1):13-17.
- 陆新征,叶列平,缪志伟.2009.建筑抗震弹塑性分析——原理、模型与ABAQUS,MSC.MARC和SAP 2000上的实践[M].北京:中国建筑工业出版社.
- 马晓峰.2013.ABAQUS 6.11 有限元分析从入门到精通[M].北京:清华大学出版社.
- 潘振华,潘鹏,叶列平,等.2011.自复位钢框架节点有限元模拟及参数分析[J].建筑结构学报,32(3):35-42.
- 石亦平,周玉蓉.2006.ABAQUS有限元分析实例详解[M].北京:机械工业出版社.
- FEMA-350.2000.Recommended Seismic Design Criteria For New Steel Moment-Frame Buildings[R].Federal Emergency Management Agency.
- Garlock M.,Ricles J.M.,Sause R..2005.Experimental Studies on Full-scale Posttensioned Steel Connections[J].J.Struct.Eng.,131(3):438-448.
- Garlock M.,Sause R.,Rides J..2007.Behavior and design of post-tensioned sted frame system[J].J.Struct.Eng.,133(3):389-399.
- Lin Y. C.,Sauser P.E.,ASCEM.,et al.2013.Seismic Performance of a Large-scale Steel Self-centering Moment Resisting Frame:MCE Hybrid Simulations and Quasi-static Pushover Tests[J].J.Struct.Eng.,139:1227-1236.
- Miller D.K.,1998.Lessons Learned from the Northridge Earthquake[J].Engineering Structure,20:249-260.
- Ricles J.M.,Sause R.R.,Lin Y.C.,et al.2010.Self-centering Moment Connections for Damage-free Seismic Response of Steel MRFs[C]//Structures Congress 2010.Reston Virginia:American Society of Civil Engineers,955-966.
- Tsai K.C.,Chou C.C.,Lin C.L.,et al.2008.Seismic Self-centering Steel Beam-to-column Moment Connections Using Bolted Friction Devices[J].Earthquake Engng.Struct.Dyn.,37:627-645.
- CECS 212—2006,预应力钢结构技术规程[S].
- GB/T 1591-2008,低合金高强度结构钢[S].