基金项目:中国地震局星火科技项目(xh12074)资助.
(1.陕西工业职业技术学院 土木工程学院,陕西 咸阳 712000; 2.中国地震局第二监测中心,陕西 西安 710054; 3.西安科技大学 测绘科学与技术学院,陕西 西安 710054)
(1.School of Civil Engineering,Shaanxi Polytechnic Institute,Xianyang 712000, Shaanxi, China)(2. The Second Crust Monitoring and Application Center, CEA, Xi'an 710054, Shaanxi, China)(3. College of Science and Technology of Surveying and Mapping, Xi'an University ofScience and Technology,Xi'an 710054, Shaanxi, China)
grey relational analysis; interfere factor evaluation; correlation degree evaluation model; Wozitan site; cross-fault deformation
备注
基金项目:中国地震局星火科技项目(xh12074)资助.
采用跨断层场地垂直形变观测数据和气象站气象数据等资料,利用灰色关联分析法构建了适于本类数据的灰色关联模型,对影响因素与形变值之间的关联度进行了研究,同时提出了一个关联度评价模型用于计算关联度阈值,将计算所得的关联度与阈值进行比较来筛选干扰因素。通过对窝子滩场地和大泉口场地计算的结果进行分析,结果表明该模型能在一定程度上定量确定干扰因素对形变的影响程度,可应用于跨断层监测场地的形变分析。
Using the vertical deformation observation data of cross-fault site and meteorological data of meteorological station, we build a grey relational model for this kind of data by the grey relational analysis method, and study the associated degrees between effect factors and deformation value. At the same time, we also present an associated degree evaluation model for calculating the threshold value of associated degree, and compare the calculation proceeds of associated degrees with threshold value to filter the interference factors. Through analyzing the calculating results of Wozitan and Daquakou observation sites, the result indicates that the obtained model can quantifiably determined the effect of interference factor on the deformation to a certain degree, which can be applied to the deformation analysis of other cross-fault monitoring sites.
引言
地震监测场地中监测点的形变异常通常是地震前兆信息的一个非常重要的指标,也是短临地震预报的重要基础。因此对影响其变化的因素的研究也具有重要意义。目前所观测到的形变异常是多源的,并非全是地壳应力活动的地表反应,导致形变资料异常变化有多种干扰因素。这些干扰因素既有外界因素如自然现象(干旱、冰冻、降水、蒸发以及气温变化等),也有观测场地自身因素如测点稳定性、测线长短、走向、是否跨断层、断层活动性以及场地周围植被情况等。降水量的变化可引起标石点位的上升或下沉,导致观测曲线出现明显的变化,水准与温度、气压、蒸发量有的呈正相关关系,有的呈负相关关系(楼关寿等,2010)。为了研究气温、气压、降雨量等因素对形变异常的影响程度,本文以窝子滩场地和大泉口场地为例搜集了2002~2011年的水准、气温、气压及降雨量的数据,用灰色关联分析法分析其影响程度。
灰色关联分析法是用关联度来确定比较因子对参考因子的影响程度的。所谓的关联度表征的是序列的变化态势,各个序列的变化态势总是按一定的量级和趋势变化的,因此比较序列与参考序列的关联度表现为二者间量级大小变化的相近性与发展趋势的相似性(肖新平等,2005)。邓聚龙(2002)提出经典的基于点灰色关联分析模型以距离来表示关联度; 梅振国(1992)提出的绝对关联度模型以斜率差来表示关联度,它克服了灰色关联分析模型关联系数会受两级最大、最小绝对差和样本量影响以及关联系数、关联度受分辨率系数影响等缺陷; 唐五湘(1995)提出的T型关联度模型克服了绝对关联度模型不具一致性、不具有序数效应和不满足负相关等缺陷(唐五湘,1994); 孙玉刚和党耀国(2008)提出的改进的T型关联度模型又进一步克服了一些模型缺陷; 刘勇等(2012)提出的灰色绝对关联度模型解决了序列曲线间负相关性问题,并且满足一定模型性质,也是一种以斜率来表示关联度的模型; 余步雷等(2013)提出的新灰色综合关联度模型综合考虑了序列曲线的相似性和相近性,是一种考虑比较全面的模型但是并不能从模型计算结果上反映出两序列间的负相关性。目前所提出的模型并不具有普遍适用性,每种模型的提出都有其适用范围,而监测点的水准高差数据与在气象站收集的气温、气压、降水量数据均为时间序列数据,所以为了适应数据的特点克服关联模型的不足,本文构建了以时间序列曲线相似性为基础的灰色关联分析模型,并以此模型进行灰色关联分析。
1 模型的建立
为了保证建模的质量和系统分析结果的正确性,必须对原始数据进行变换和处理,使其消除量纲并具有可比性。其中数据变换包括初值化变换、均值化变换、归一化变换、区间值化变换等(邓聚龙,2002)。由于高差数据与气温、气压、降雨量等数据的变化量不在同一个量级上,这里通过区间值化变换的方法消除量纲、归一化后进行灰色关联分析。
1.1 消除数据量纲设X0=(x0(1),x0(2),…,x0(n))为系统参考序列,系统相关因素系列为
Xi=(xi(1),xi(2),…,xi(n)),(i=1,2,…,m).(1)
设yi(k)表示序列经区间值变化后某一时刻对应的无量纲值。
令ximin=MIN(Xi),ximax=MAX(Xi), 有
zi(k)=(xi(k)-ximin)/(ximax-ximin).(2)
1.2 计算关联度形变数据和气温气压降雨量等观测数据均为时间序列,令Δxi(k)=zi(k)-zi(k-1), Δxi(k)表示相邻两时刻数值之差,由于序列为等时间间隔序列,在此将时间间隔视为1,Δxi(k)可表示为斜率。关联度计算公式为
S0 i(k)={sgn(Δx0(k)·Δxi(k))1/(1+〖JB<2|〗〖JB<1*|〗Δx0(k)〖JB>1*|〗-〖JB<1*|〗Δxi(k)〖JB>1*|〗〖JB>2|〗+(〖JB<1*|〗Δx0(k)2-Δxi(k)2〖JB>1*|〗)/(〖JB<1*|〗Δx0(k)Δxi(k)〖JB>1*|〗)) Δx0(k)·Δxi(k)≠0,
0 Δx0(k)·Δxi(k)=0.(3)
ε0i=1/(n-1)∑nk=2ε0i(k).(4)
其中,(k=2,3,…,n),(i=1,2,…,m)。sgn(Δx0(k)·Δxi(k))为符号函数, 当Δx0(k)·Δxi(k)>0时取“+”,当Δx0(k)·Δxi(k)<0时取“-”。
2 模型的基本性质
2.1 规范性由(3)、(4)式可得,〖JB<1*|〗ε0i〖JB>1*|〗≤1。
2.2 相似性Δxi(k)表示变化率,〖JB<1*|〗Δx0(k)〖JB>1*|〗-〖JB<1*|〗Δxi(k)〖JB>1*|〗是斜率差,〖JB<2|〗〖JB<1*|〗Δx0(k)〖JB>1*|〗-〖JB<1*|〗Δxi(k)〖JB>1*|〗〖JB>2|〗越小,(〖JB<1*|〗Δx0(k)2-Δxi(k)2〖JB>1*|〗)/(〖JB<1*|〗Δx0(k)Δxi(k)〖JB>1*|〗)也越小,ε0i(k)越大,曲线在k点的相似度越高; 反之,ε0i(k)越小,曲线在k点的相似度越低。
2.3 正负相关性由sgn(Δx0(k)·Δxi(k))={1 Δx0(k)·Δxi(k)>0,
-1 Δx0(k)·Δxi(k)<0.可知, sgn(Δx0(k)·Δxi(k))为1时为正相关, 相反
为负相关。
2.4 平行性若序列X0=(x0(1),x0(2),…,x0(n))与Xi=(xi(1),xi(2),…,Xi(n))满足x0(k)=xi(k)+c; c为常数,(i=1,2,…,m),(k=1,2,…,n), 则序列X0与Xi平行。由式(2)、(3)可得〖JB<1*|〗ε0i〖JB>1*|〗=1,即该模型满足平行性。
2.5 一致性若序列与X0=(x0(1),x0(2),…,x0(n))与Xi=(xi(1),xi(2),…,Xi(n))满足x0(k)=axi(k); a为常数,(i=1,2,…,m),(k=1,2,…,n)。由式(2)、(3)可得〖JB<1*|〗ε0i〖JB>1*|〗=1,即该模型满足一致性。
3 关联度评价模型
对灰色关联分析得出的关联度进行排序,只能得到各种比较因子对参考因子的不同影响程度,并不能确定在关联度值为多大时比较因子会对参考因子产生显著影响。如果能给定一个确定的阈值,当关联度大于该阈值时我们就认为比较因子对参考因子有显著影响,当小于该阈值认为比较因子对参考因子的影响较小。这样就可以通过灰色关联分析法筛选我们认为可能会对参考因子产生影响的影响因子,有利于对参考因子进行分析和研究。
现讨论灰色关联曲线曲率最大点处的关联度值作为关联度阈值。曲率计算公式为
K=(〖JB<1*|〗y″〖JB>1*|〗)/((1+y'2)3/2).(5)
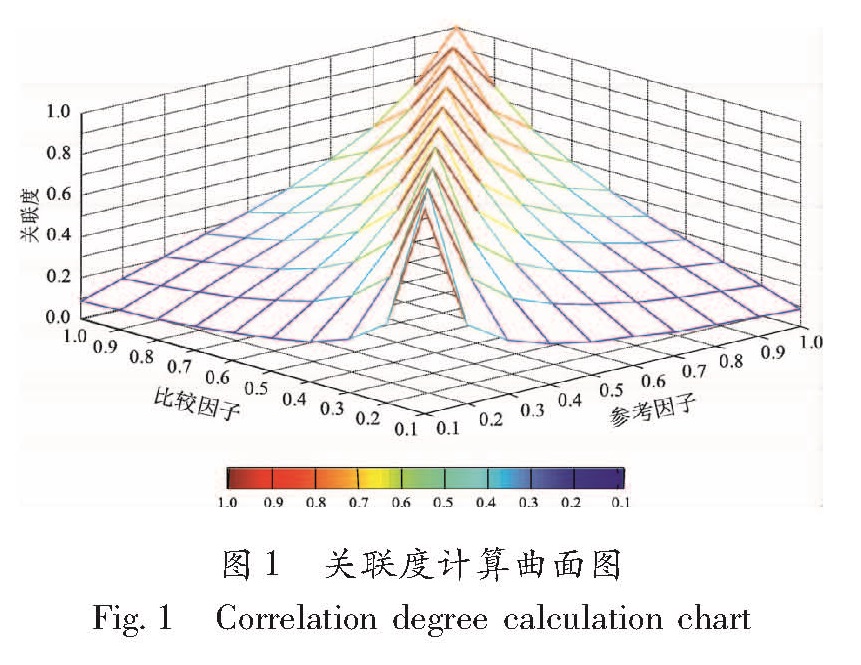
由式(3)可知,当取Δx0∈[0,1], Δxi∈[0,1]时, 且ε0i(Δx0,Δxi)为偶函数, ε0i∈[0,1]。 以Δx0为x轴, Δxi为y轴, ε0i为z轴建立空间直角坐标系如图1。
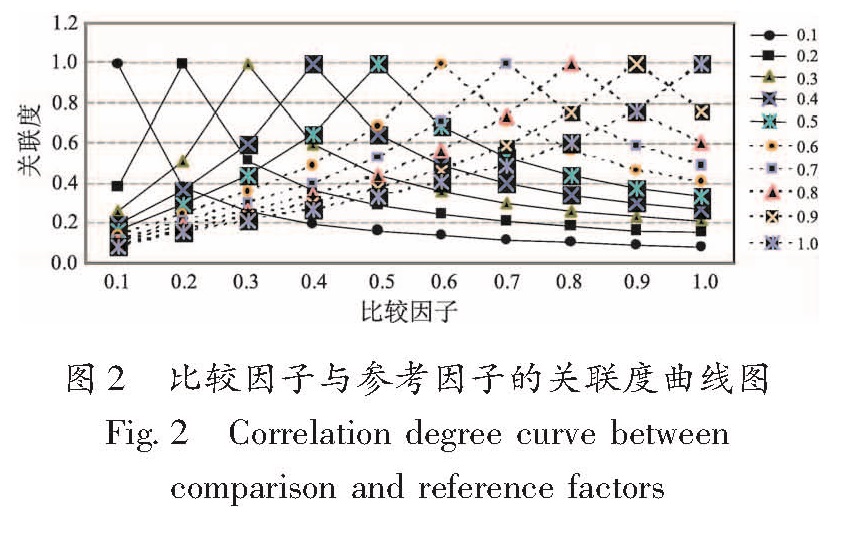
由图1可知,当给定参考因子一个固定值时,令Δx0=0.1,0.2,…,1,得到比较因子与参考因子的关联度曲线图(图2)。以比较因子与参考因子的关联度曲线最大曲率处的关联度值作为关联度阈值,但Δx0取不同值时的关联度曲线也不相同,最终导致得到的关联度阈值不唯一。由图2可知,关联度阈值随着Δx0取值的增大而不断增大,在一系列的关联度阈值中,取最大值作为最终的关联度阈值以涵盖所有取值。即令Δx0=1,Δx0∈[0,1],用最小二乘拟合多项式拟合y=ε0i(x)。 设g(x)=a1xn+a2xn-1+…+an-1x+an,利用最小二乘法计算多项式系数,满足一定拟合精度后,以g(x)计算关联度阈值。
现以g(x)=a1x6+a2x5+…+a5x+a6为例计算得到的关联度值。
最终解得g(x)=2.811 14x6-6.564 47x5+6.047 022x4-1.888 8x3-0.201 18x2+0.786 807x+0.009 944 5,将g(x)代入式(5)得到函数K(x)。令K'(x)=0计算曲率最大的点,解得x=0.792; 将其代入g(x)得g(0.792)=0.595 504。最终得到该模型关联度阈值约为0.6。根据经验,两因素的关联度大于0.6便认为其关联性显著(邓聚龙,2002; 刘思峰等,2004; 傅立,1992; 徐国祥,2005),计算结果与经验值相符。
4 模型在地震形变分析中的应用
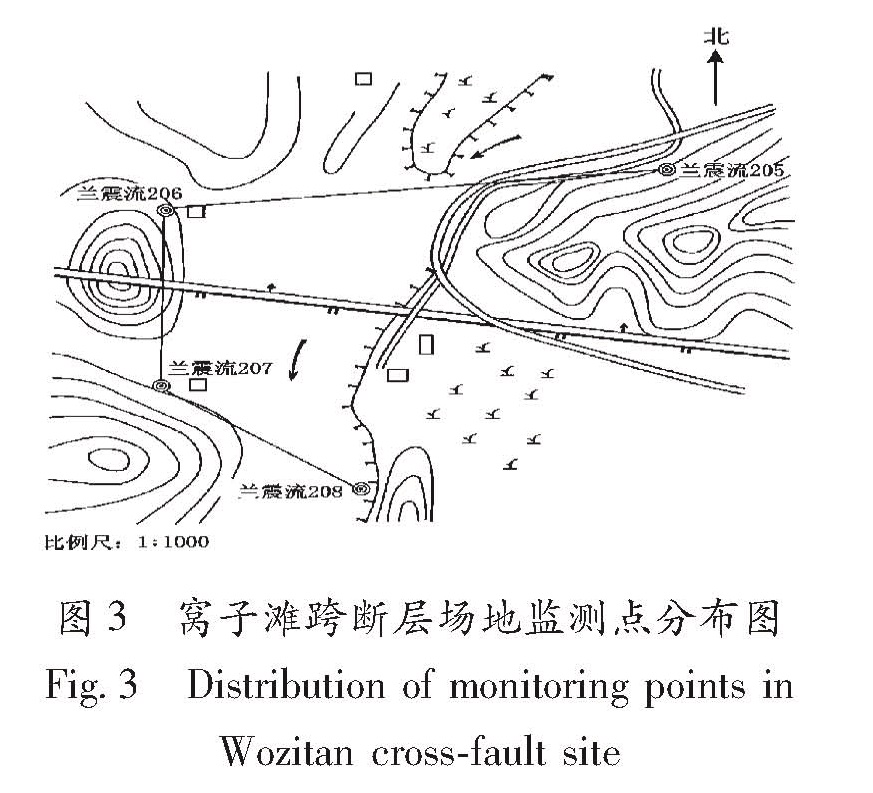
4.1 窝子滩场地窝子滩场地位于甘肃省靖远县水泉乡窝子滩(104.57°E,36.89°N),由兰州地震研究所于1981年7月选点建立,场地类型为水准观测场地。该场地为跨断层场地,断层产状为走向:N280°,倾向:N,倾角:62°。窝子滩场地中监测点的形变可能受到周围环境(气温、气压、降雨量)的影响,现利用上述模型计算2002~2011年窝子滩场地高差变化与气温、气压、降雨量等因素间的关联度。图3为窝子滩场地监测点分布图,图中东西走向的双线为该场地断层的概略位置。
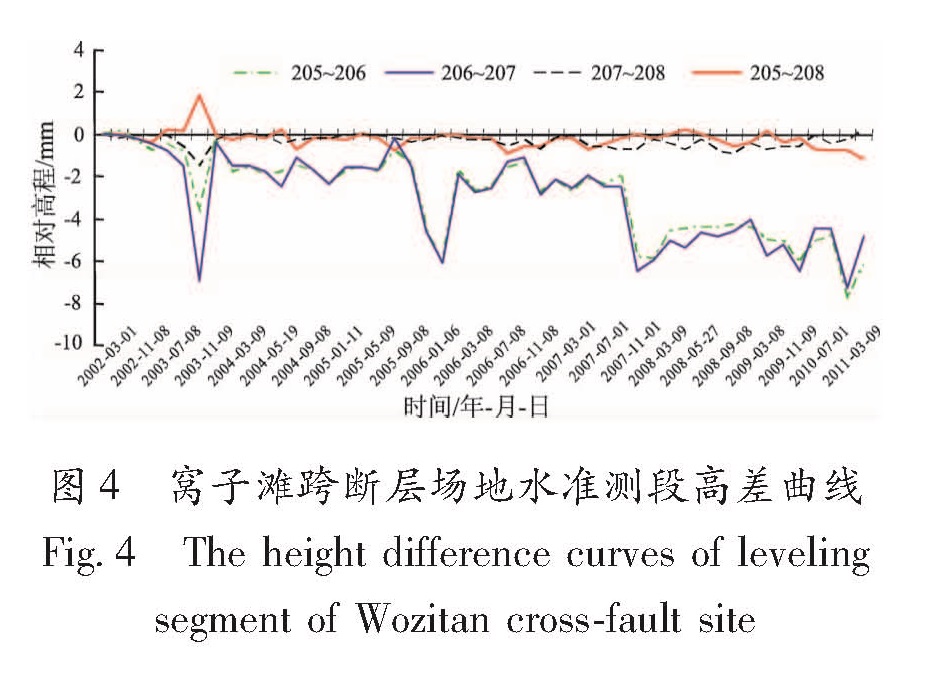
由图4 可看出206-207测段与207-208测段高差波动正常,而205-206、208-205测段高差波动出现异常,据此可推断出205号监测点出现异常。4个监测点构成一个闭合水准路线,将闭合差作为零,为得到205号点的相对高程值,这里将205-206测段和208-205测段的高差值的平均值作为205号点的相对高程值(图5a)。
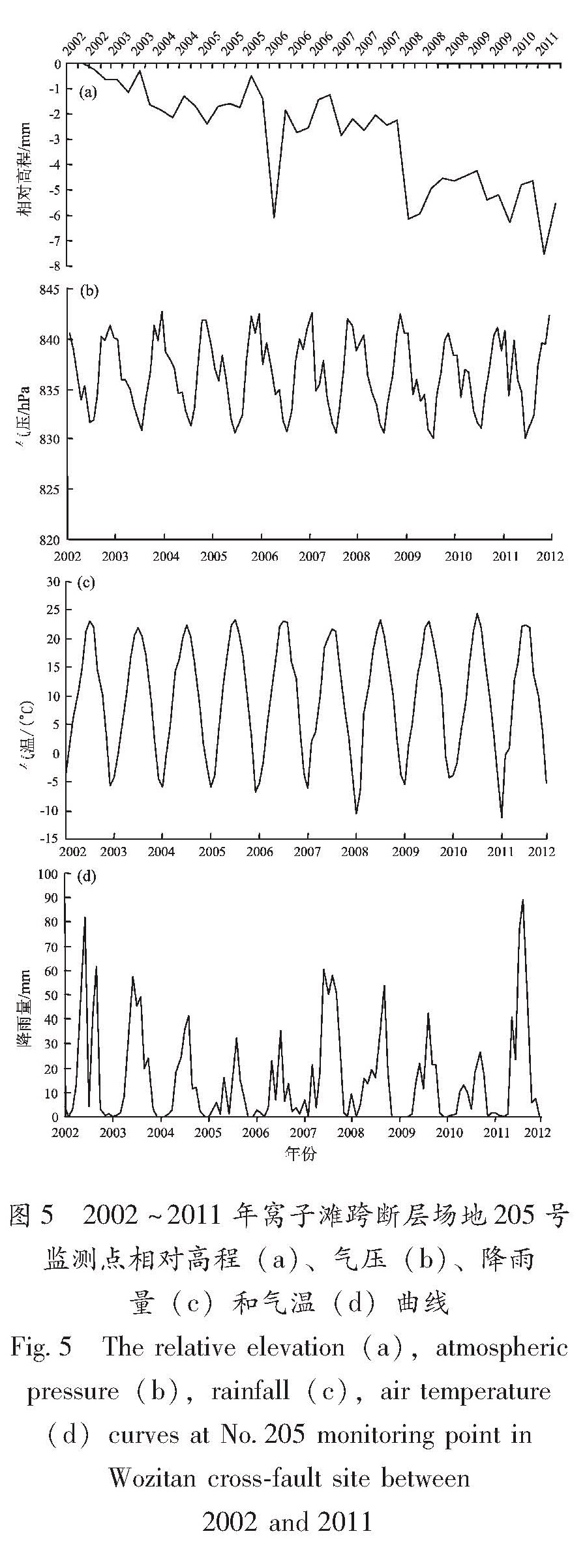
从图5可以看出,2002~2011年205号监测点的高程整体呈直线下降,局部存在波动,在2006年1月和2009年1月有明显的异常变化。2002~2011年205号监测点气温、气压、降雨量都具有明显的季节性,气压变化总体在835 hPa上下波动具规律性,局部存在随机性的扰动; 气温的变化更具规律性,并且变化稳定; 每年降雨量总体趋势随季节变化明显,但降水量的变化随机性比较强。
2002~2011年205号监测点气温、气压的总体趋势稳定,而高程总体呈直线下降趋势,表明气温、气压对监测点形变没有影响; 205号监测点在2006年1月和2009年1月出现明显的异常变化,但同期的气温、气压也没有出现较为明显的异常变化,表明气温、气压对窝子滩场地监测点的形变异常也没有明显的影响。
考虑到降水量对地形变的影响比较显著(胡惠民,1984),雨季的总降雨量和连续干旱天数对对地形变有着显著的影响,并且其对地形变的干
扰具有滞后效应。对比图5a和5d,205号监测点的高程变化并没有出现与雨季—旱季相同的交替变化规律,并且其两个异常的变化均发生在1月份,不符合降雨对地形变的影响规律,因此在窝子滩场地降雨量对其形变的影响可以忽略。图4 窝子滩跨断层场地水准测段高差曲线
Fig.4 The height difference curves of leveling segment of Wozitan cross-fault site下面通过灰色关联分析模型计算气温、气压、降水量与高程变化的关联度来确定这些形变异常的干扰因素对地形变的影响程度。
图5 2002~2011年窝子滩跨断层场地205号
监测点相对高程(a)、气压(b)、降雨量(c)和气温(d)曲线
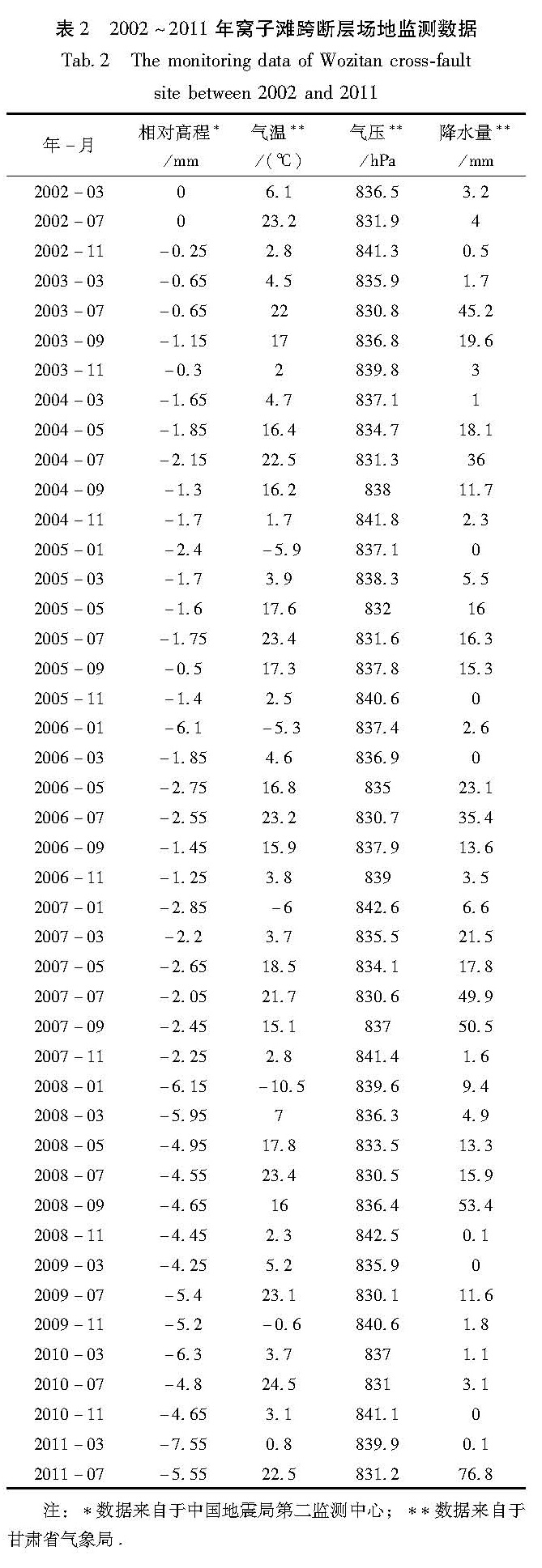
Fig.5 The relative elevation(a),atmospheric pressure(b),rainfall(c),air temperature(d)curves at No.205 monitoring point in Wozitan cross-fault site between 2002 and 2011表2 2002~2011年窝子滩跨断层场地监测数据
Tab.2 The monitoring data of Wozitan cross-fault site between 2002 and 2011注:*数据来自于中国地震局第二监测中心; **数据来自于甘肃省气象局.
由表3得出,窝子滩场地气温、气压、降水量与205号监测点的高程变化的关联度非常小,远远小于关联度阈值,另外观察表3,发现在相同的数据列中既存在正值又存在负值,这说明在同一数据列中,数据之间既存在正相关又存在负相关,这种矛盾恰恰说明了其关联度很低。综上可认为在窝子滩场地气温、气压、降水量对形变异常的影响并不大。205号点的形变异常可能是受地壳应力活动或其他干扰因素的影响而导致的。另外关联度计算结果与图5所反映的信息一致说明该模型可应用于跨断层场地形变异常干扰因素的评价分析中。
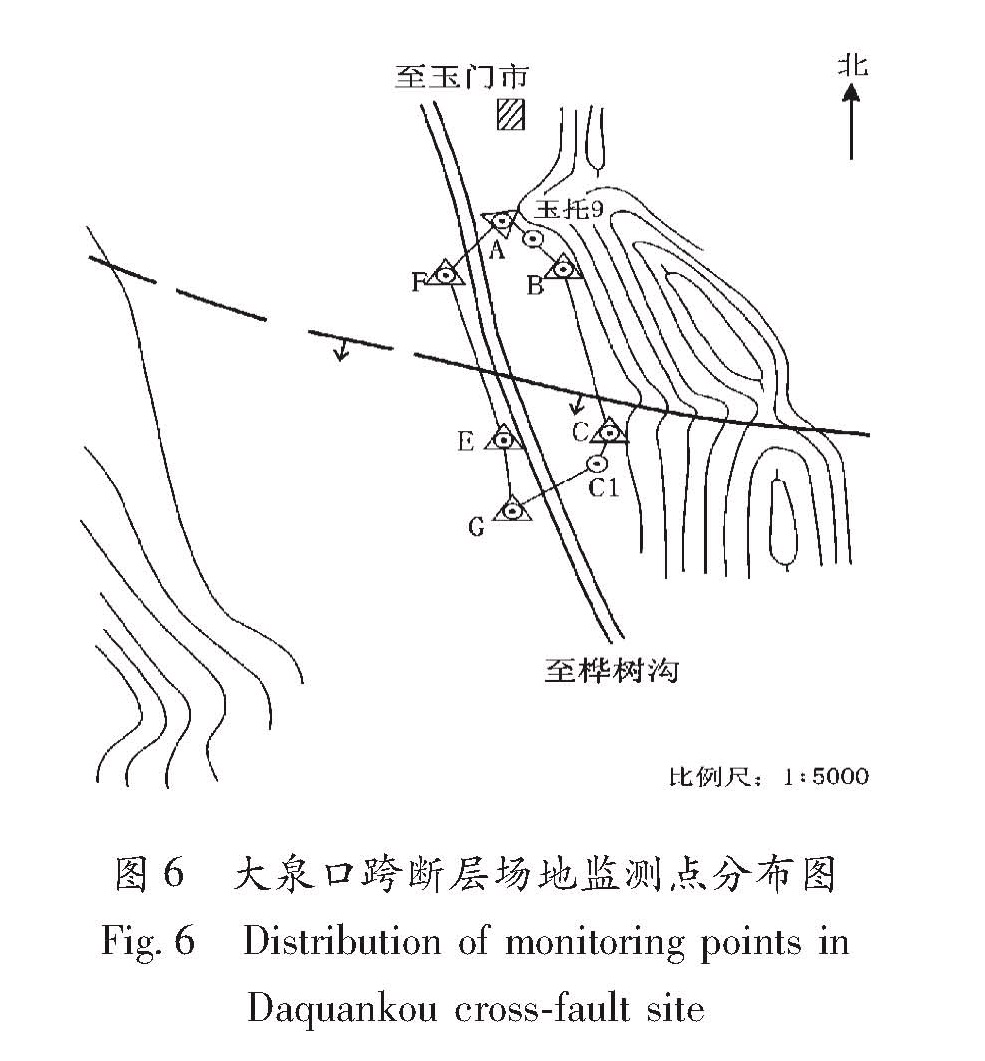
4.2 大泉口场地大泉口场地位于甘肃省肃南县大泉口(97.70°E,39.51°N)。该场地由中国地震局第二监测中心于1988年6月埋设。场地位于昌马—古浪断裂西段,该断层在场地附近走向近东西,总体走向N70°W,倾向SW,倾角70°~80°。图6中东西走向虚线为断层的概略位置。
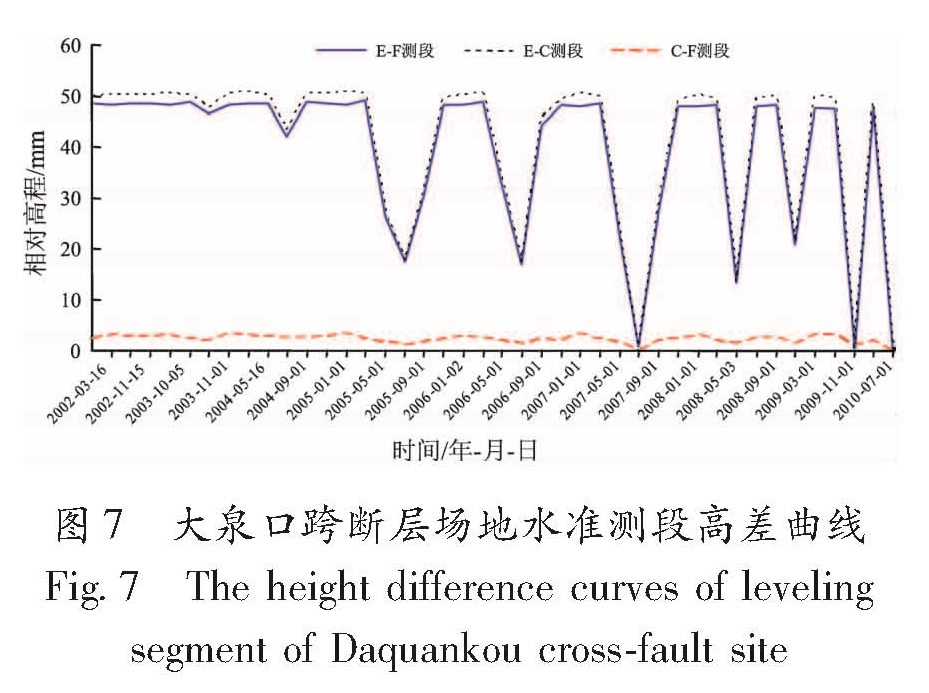
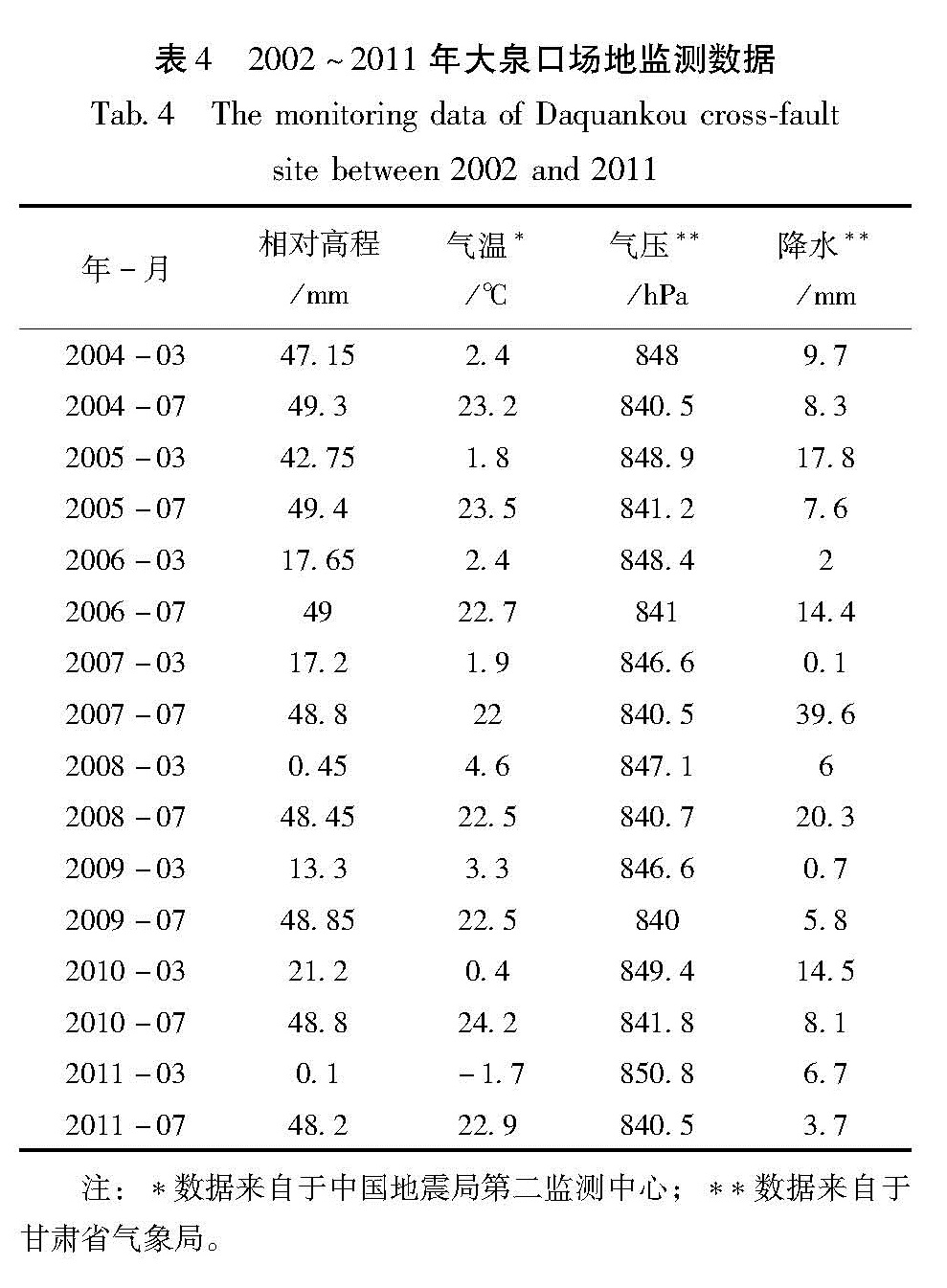
以大泉口场地中的一个闭合环线为例进行分析(图7)。E-C测段与E-F测段、C-F测段构成闭合环线,C-F测段高差波动无异常,E-C测段与E-F测段出现巨幅变化,据此可推断出监测点E出现异常。观察时间轴可知此变化具有明显的季节性。为得到E号点的相对高程值,这里将E-C测段与E-F测段的高差值的平均值作为E号点的相对高程值(图8a)。图7 大泉口跨断层场地水准测段高差曲线
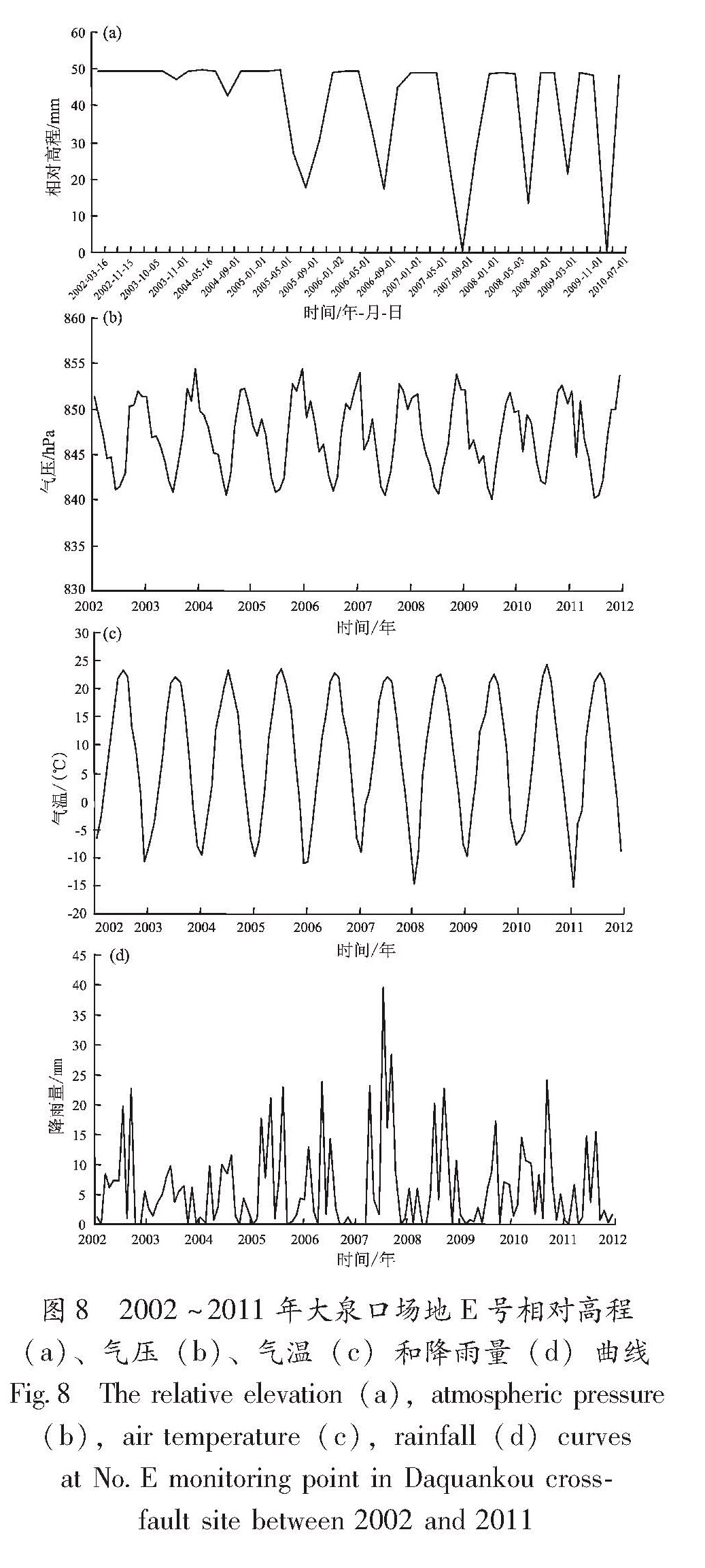
Fig.7 The height difference curves of leveling segment of Daquankou cross-fault site由图8可知,大泉口场地E号监测点具有显著的周期性特征,同时气温、气压、降雨量等均具有季节性特征。从数据曲线上,气温、气压图像整体规律为围绕某一值上下波动,呈周期性变化,而监测点的波动图像与降雨量图像则呈出以某一值为最大值或最小值,周期性出现峰值的规律。图8 2002~2011年大泉口场地E号相对高程(a)、气压(b)、气温(c)和降雨量(d)曲线
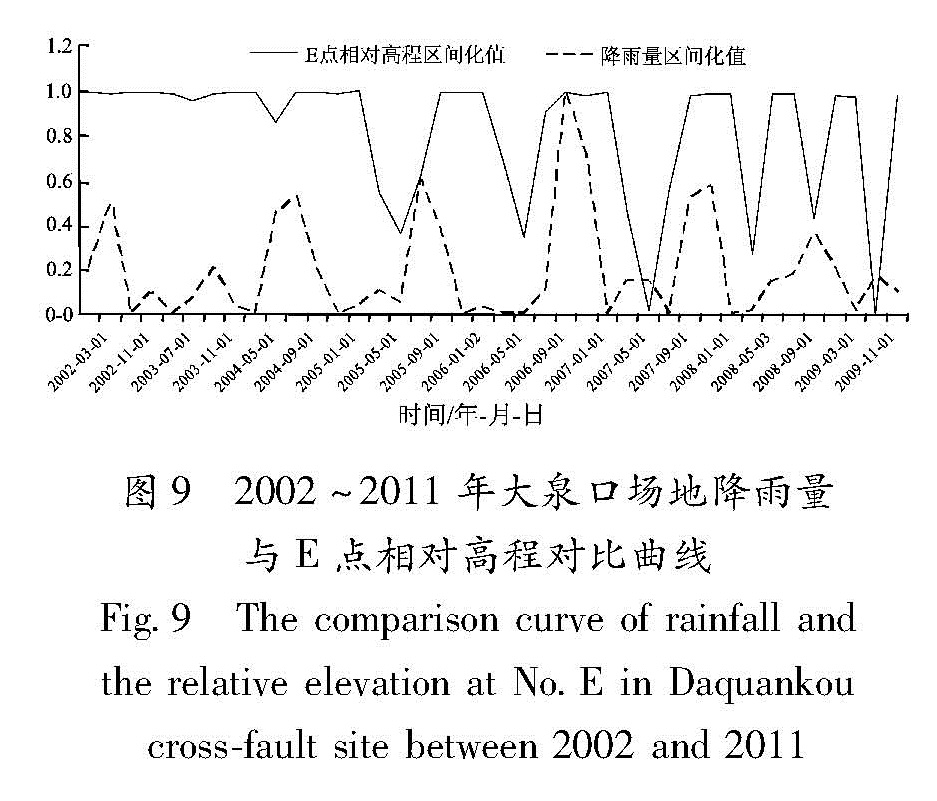
Fig.8 The relative elevation(a),atmospheric pressure (b),air temperature(c),rainfall(d)curves at No.E monitoring point in Daquankou cross-fault site between 2002 and 2011由图9可得降雨量对E点的高程有一定的影响,且影响是滞后的、负相关的。其大致规律为:大泉口场地每年的7月至第二年的1月降雨量较小,E点的高程也随之逐渐降低,到1月份降至最低,每年的1~7月降雨较丰富,E点高程也随之 升高,至5月升至最高点,并以此进行周期性变化。图9 2002~2011年大泉口场地降雨量与E点相对高程对比曲线
Fig.9 The comparison curve of rainfall and the relative elevation at No.E in Daquankou cross-fault site between 2002 and 2011下面通过上述模型计算关联度验证上述结论:
注:*数据来自于中国地震局第二监测中心; **数据来自于甘肃省气象局。
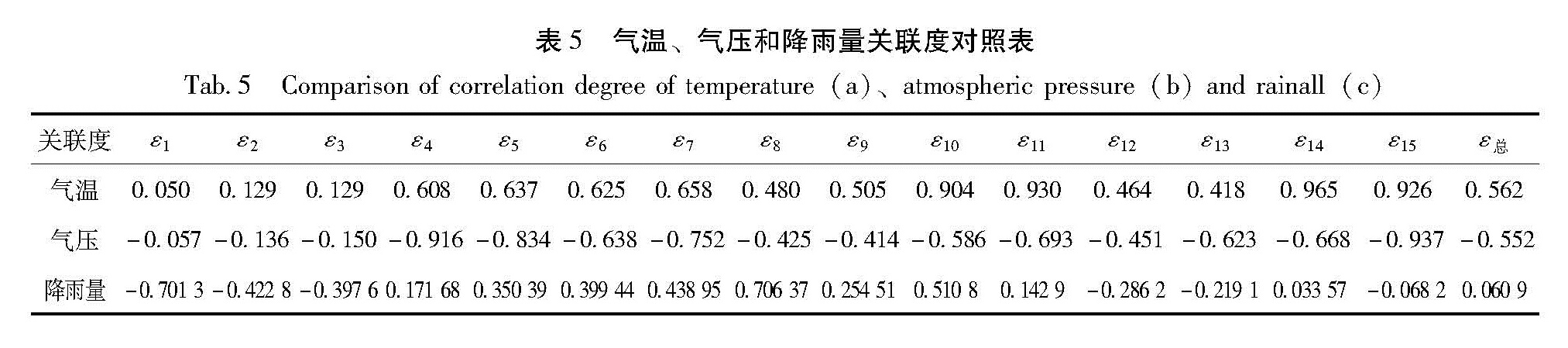
表5 气温、气压和降雨量关联度对照表
Tab.5 Comparison of correlation degree of temperature(a)、atmospheric pressure(b)and rainall(c)由表5可以看出,E点的高程与温度表现出很大的关联度,并且与温度呈正相关的关系; E点的高程与气压关联度也比较显著,并且与气压呈负相关的关系。对于具有滞后影响的降雨量来看,该模型并没有很好地表现出来,由于降雨量对高程影响的滞后时间也不固定,所以通过模型计算出的结果与实际不相符。由此可得在大泉口场地监测点E点高程受到了气温、气压、降雨量等环境因素的影响较明显,但由于模型对滞后影响上的计算存在缺陷,在计算降雨量的关联度时结果出现了失真。
影响因子对参考因子的影响滞后是一个复杂的过程。目前还没有一个有效的模型进行识别,必须进行人工干预识别。对于具有滞后效应的干扰因素的有效识别,也是今后需要深入研究和探讨的问题。
5 结语
通过以上分析,本文提出的灰色关联计算模型能较真实反映干扰因素对形变的影响程度,具有很好的模型性质,比如满足平行性、一致性,并且能反映正负相关性。该模型反映的是曲线相似程度,并不能反映曲线的相近程度,单从数学模型角度来看,该模型还有待进一步的改进。窝子滩场地气温、气压、降雨量对高差的关联度与关联度阈值比较结果得到气温、气压、降水量等因素对高差的影响程度很小,其形变异常可能是由地壳应力活动或其他干扰因素引起的。大泉口场地受到环境因素的影响较大,在分析其异常值时需要考虑到环境因素所造成的影响。本文对于关联度评价模型只是做了初步探讨,该模型对数据的要求比较严格,必须要等间隔时间序列才能得到良好的计算结果,而且对于有滞后效应的影响因素其评价效果并不理想,在对此类影响因子的分析上该模型还有待进一步研究。
本文在撰写过程中得到杨永崇教授的帮助,在此向他表示衷心感谢。
- 邓聚龙.2002.灰理论基础[M].武汉:华中科技大学出版社.
- 傅立.1992.灰色系统理论及其应用[M].科学出版社.
- 胡惠民,顾国华,胡思勇.1984.人工降雨地形变实验[J].地壳形变与地震,4(3):257-260.
- 刘思峰,党耀国,方志耕.2004.灰色系统理论及其应用[M].北京:科学出版社.
- 刘勇,刘思峰,Jeffrey Forrest.2012.一种新的灰色绝对关联度模型及其应用[J].中国管理科学,20(5):173-174.
- 楼关寿,周伟,金鹏,等.2010.跨断层形变干扰因素的调查[J].大地测量与地球动力学,30(增刊):68-74.
- 梅振国.1992.灰色绝对关联度及其计算方法[J].系统工程,10(5):43-45.
- 孙玉刚,党耀国.2008.灰色T型关联度的改进[J].系统工程理论与实践,4(1):135-139.
- 唐五湘.1994.灰色绝对关联度的缺陷[J].系统工程,12(5):59-62.
- 唐五湘.1995.T型关联度及其计算方法[J].数理统计与管理,14(1):34-37.
- 肖新平,宋中民,李峰.2005.灰技术基础及其应用[M].北京:科学出版社,50-53.
- 徐国祥.2005.统计预测和决策[M].上海财经大学出版社.
- 余步雷,周宗放,谢茂森.2013.新灰色综合关联度模型及其应用[J].技术经济,30(1):85-89.